Energy Scheduling of PV–ES Inverters Based on Particle Swarm Optimization Using a Non-Linear Penalty Function
Abstract
1. Introduction
- (1)
- With the non-linear penalty function method, the penalty factor in the iterative process is continuously updated to make the search result closer to the optimal value.
- (2)
- The particle swarm optimization algorithm serves as the search engine, combining the non-linear penalty function method to optimize the charge/discharge scheduling of energy storage batteries and the power transactions between users and the grid, thereby achieving enhanced user economic benefits.
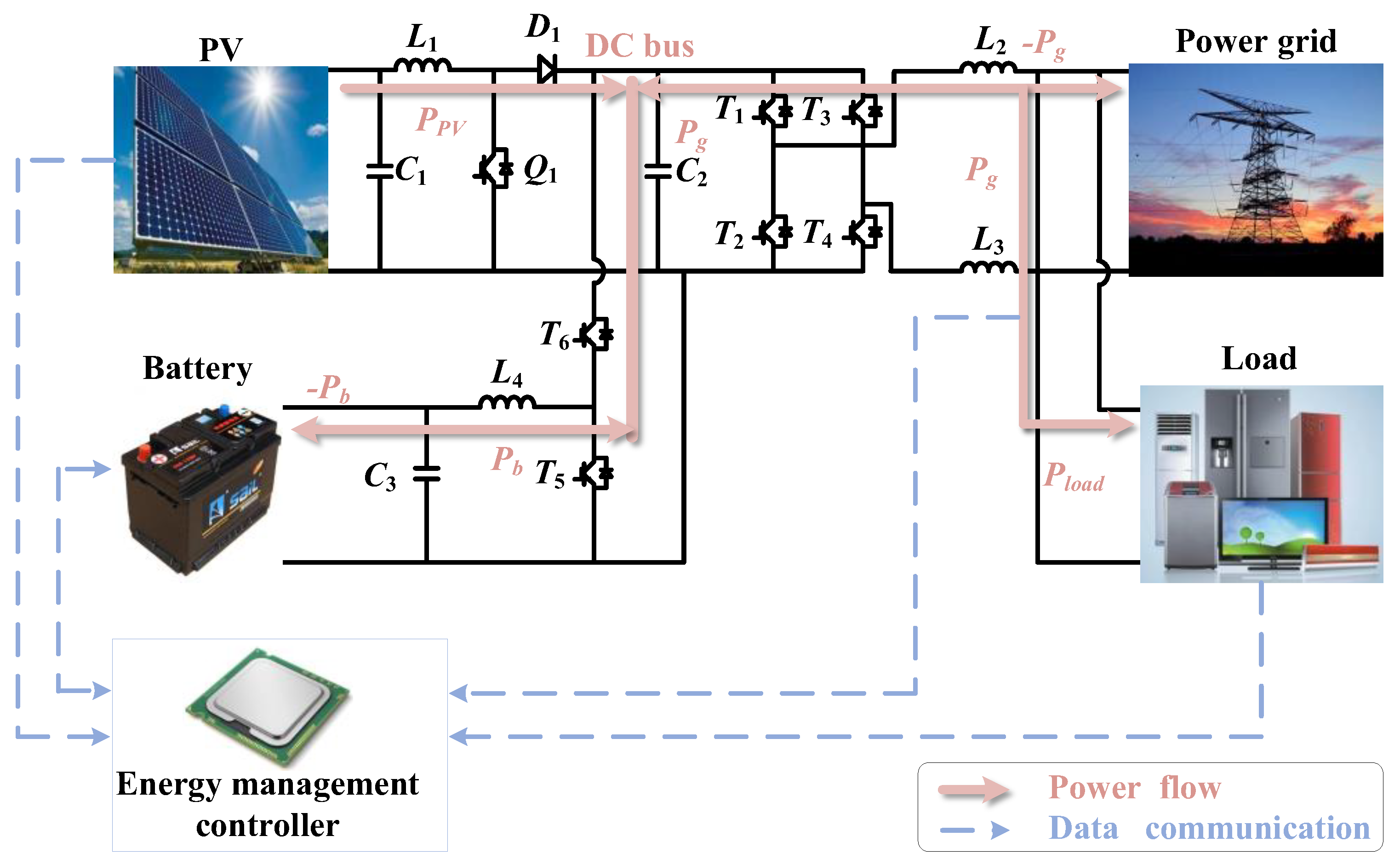
2. System Model
2.1. System Structure
2.2. Mathematical Model
2.2.1. Objective Function
2.2.2. Constraint Condition
3. Penalty Function
3.1. Traditional Penalty Function
3.2. Non-Linear Penalty Function
4. Particle Swarm Optimization Based on Non-Linear Penalty Function
4.1. Algorithm Steps
- Initialize the particle swarm, including the velocity and position of each particle.
- Calculate the fitness (objective function value) of each particle.
- For each particle, compare its fitness with its historical pbest. If superior, update pbest.
- For each particle, compare its fitness with the historical gbest. If superior, update gbest.
- Adjust particle velocity and position according to the following equations:
- f.
- Terminate the process if the iteration counts or precision condition is met; otherwise, return to step b.
4.2. Comparison with Other Advanced Algorithms
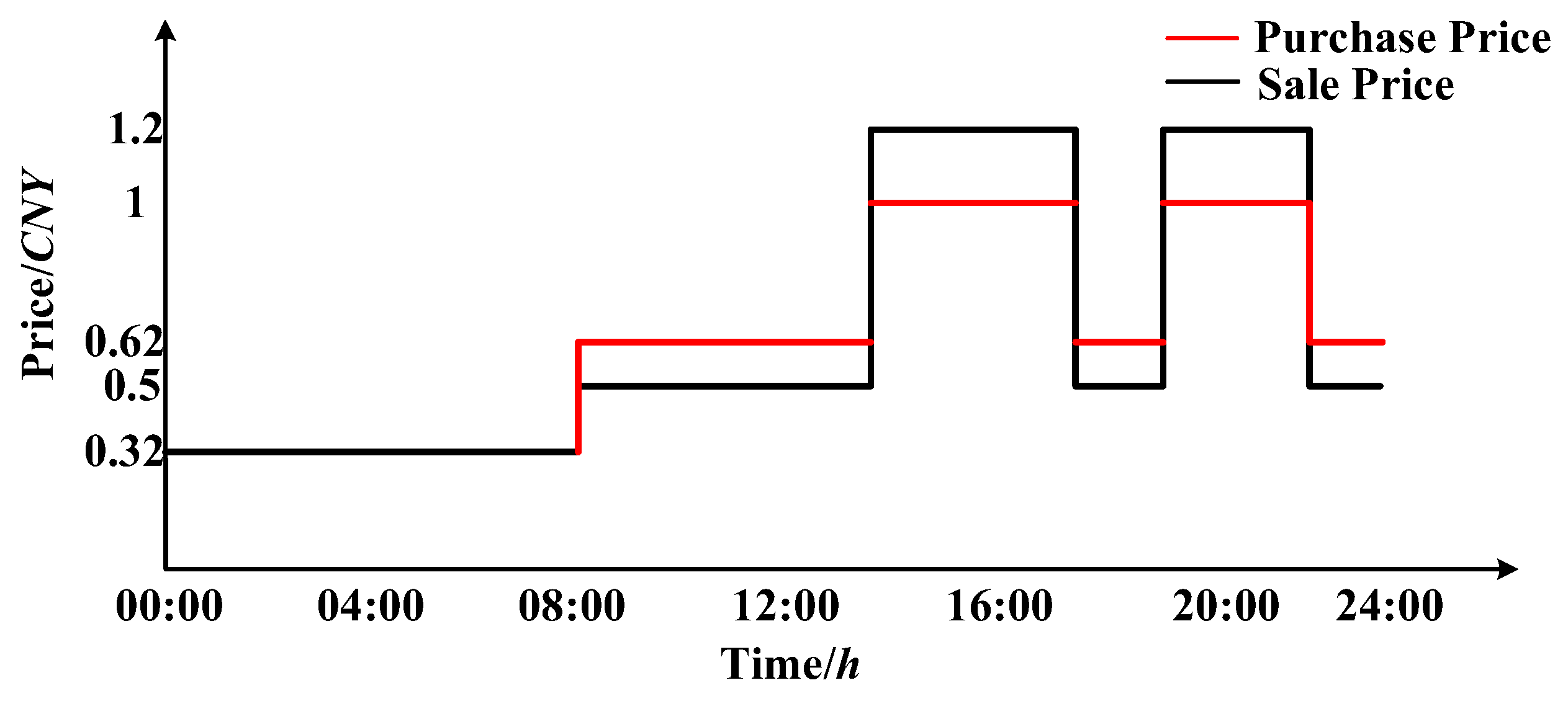
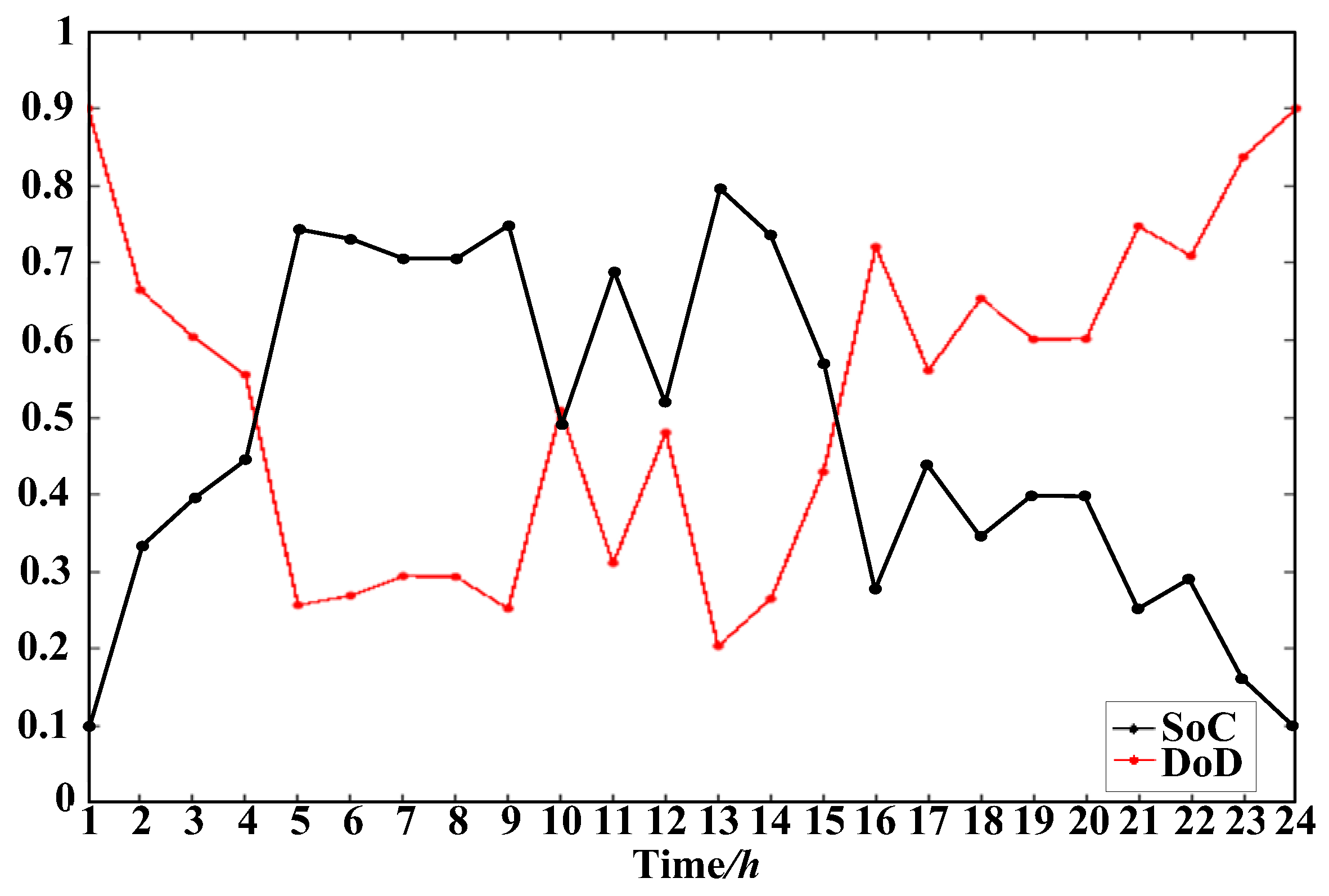
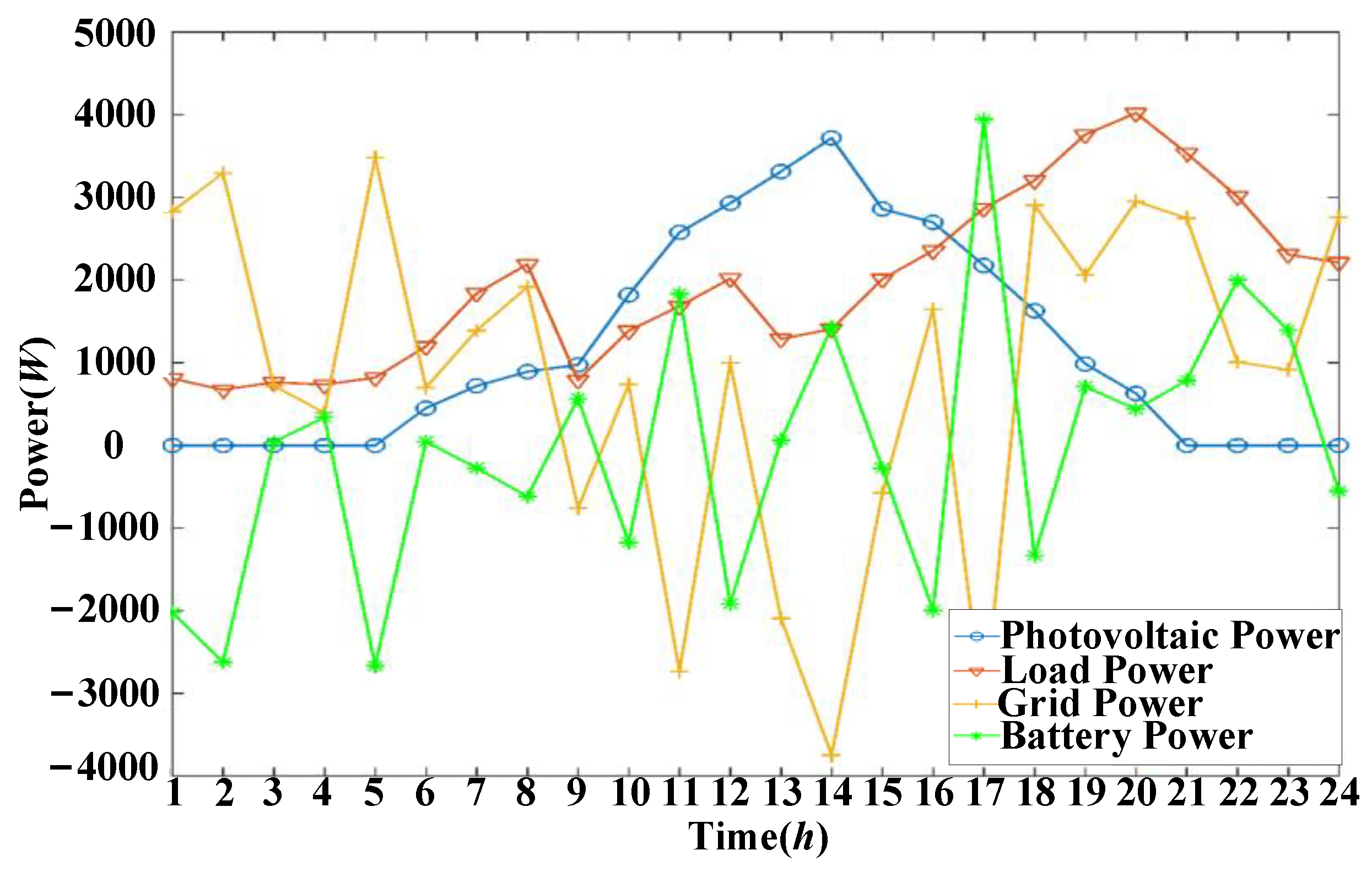
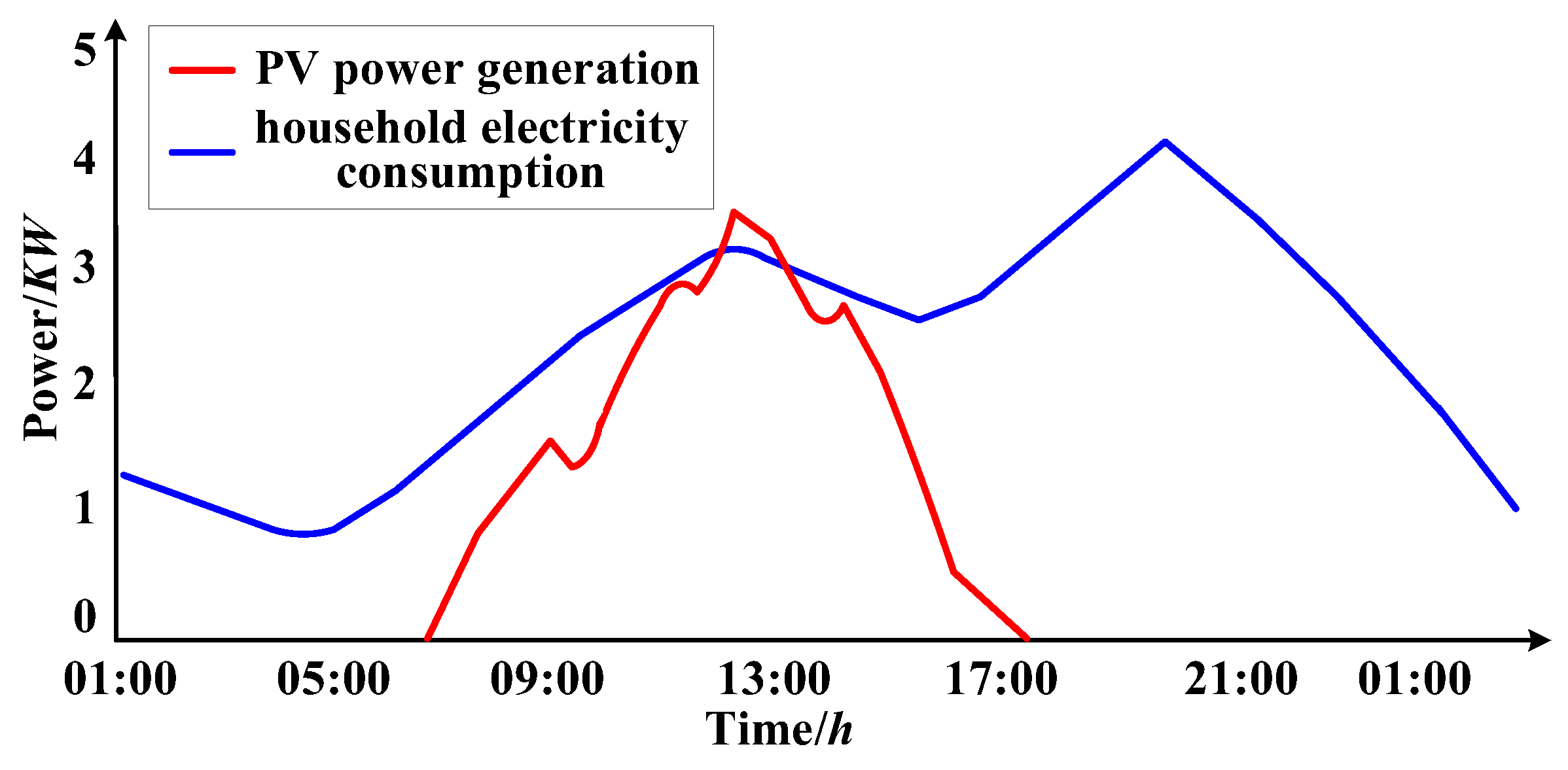
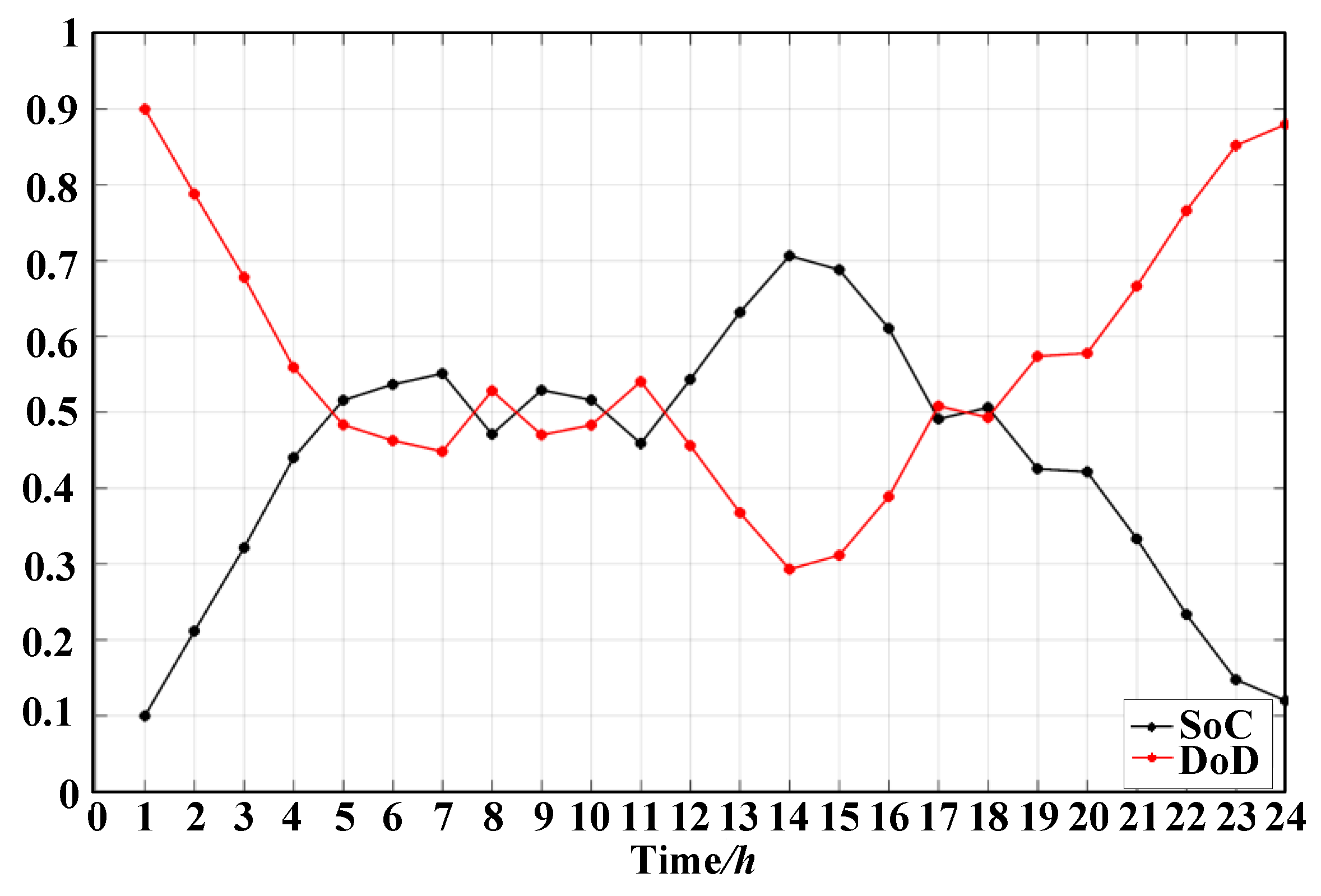
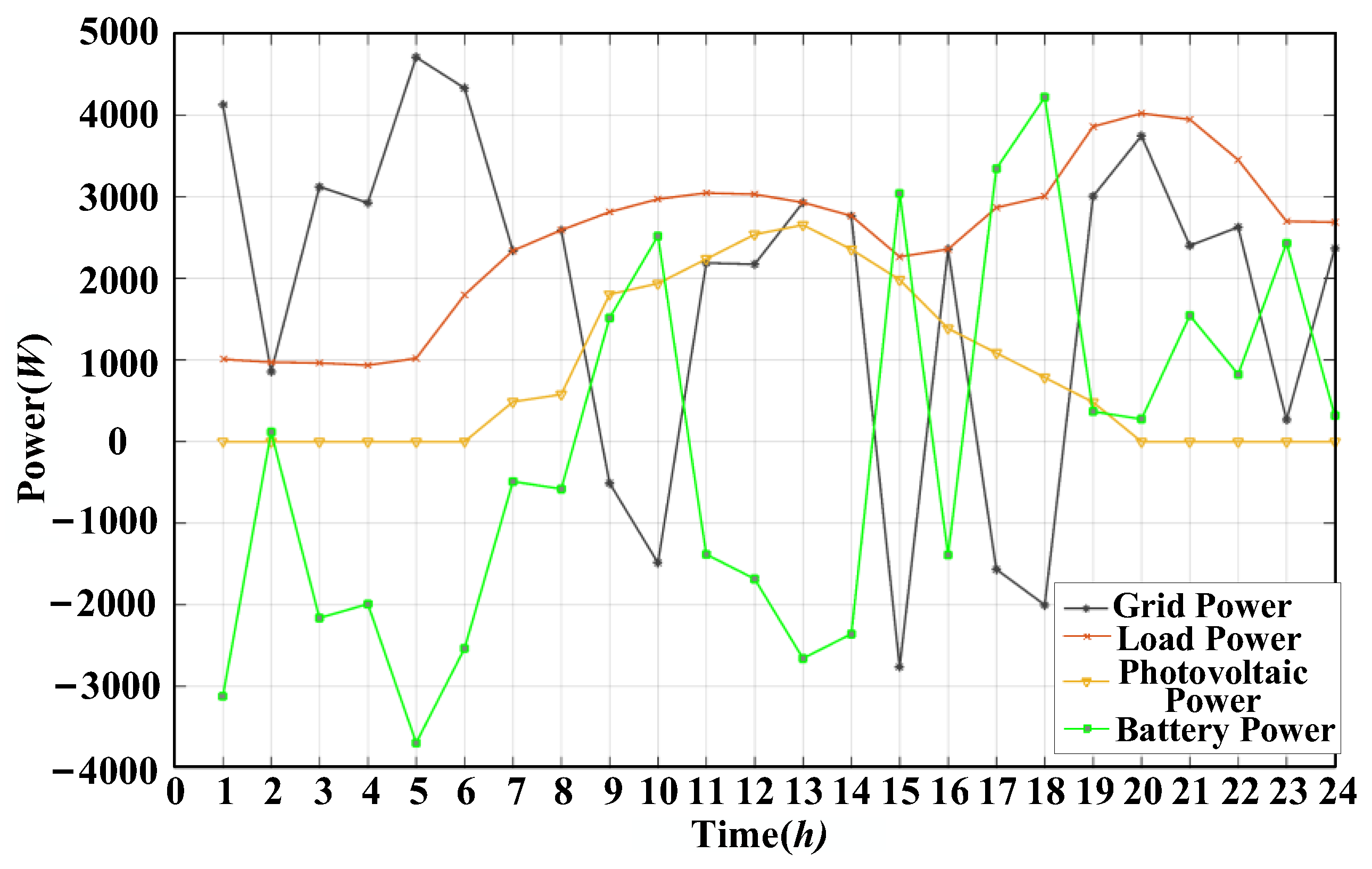
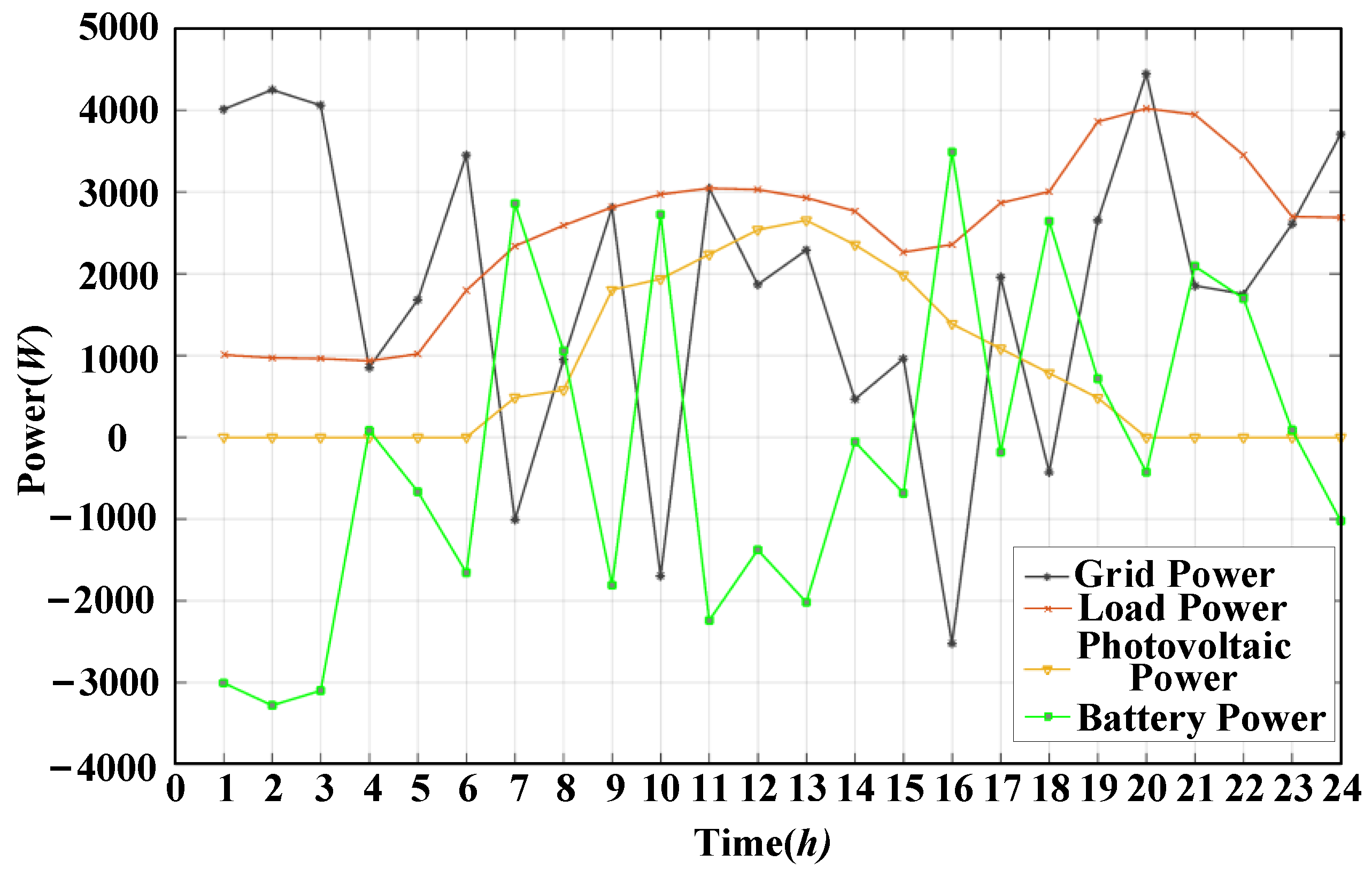
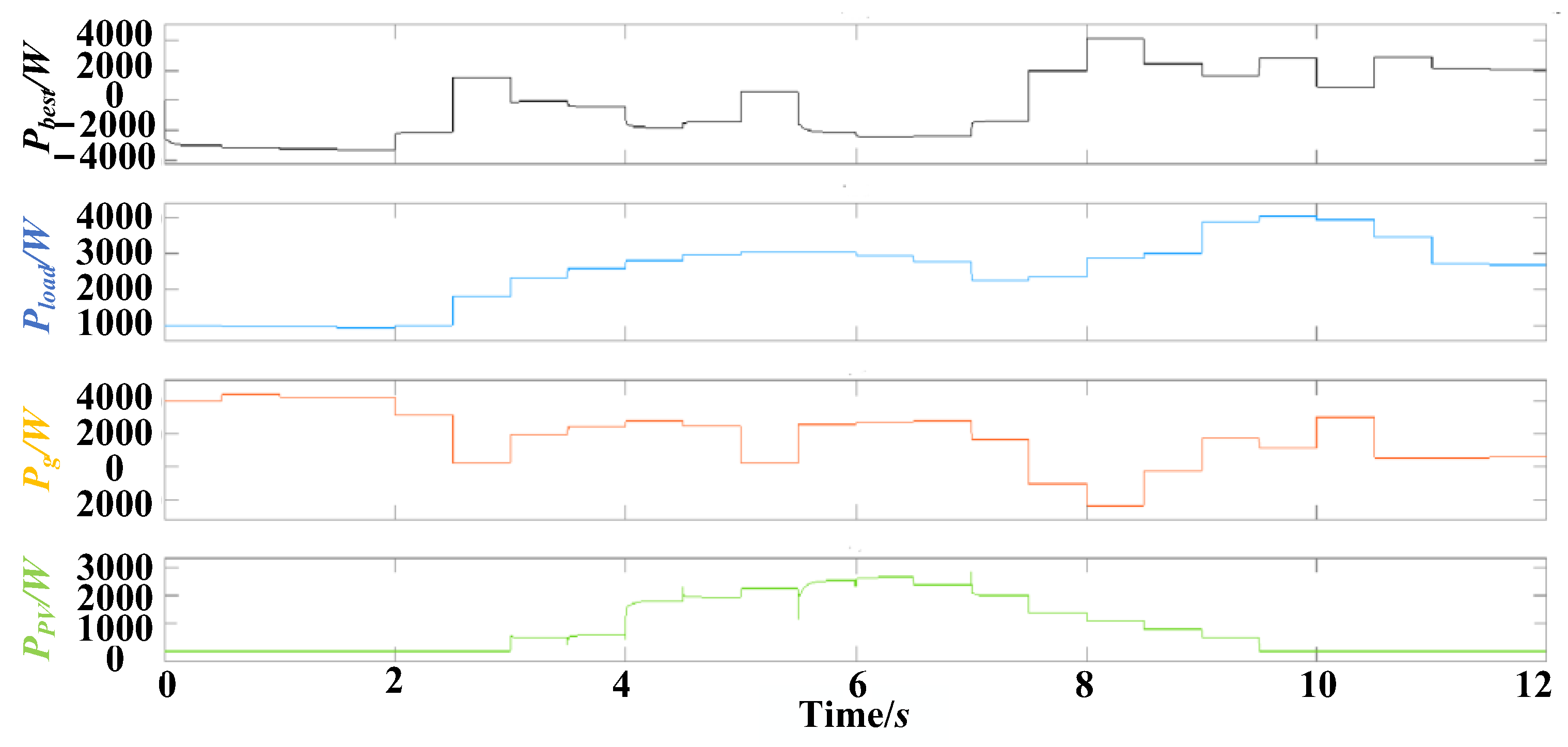
5. Simulation Results
5.1. Example I
5.2. Example II
6. Results Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Chiang, H.D. Online and Look-Ahead Determination of the Renewable Admissible Region for Managing the Uncertainty of Renewables: Theory and Some Applications. IEEE Trans. Power System. 2024, 39, 5609–5619. [Google Scholar]
- Yu, Z.; Chi, Y.; Lin, J.; Liu, F.; Li, J.; Song, Y.; Ren, Z.; Lu, C.; Ji, M. Joint Multi-stage Planning of Renewable Generation, HESS, and AESS for Deeply Decarbonizing Power Systems with High-penetration Renewables. IEEE Trans. Sustain. Energy 2024, 1–16. [Google Scholar] [CrossRef]
- Michal, J.; Homaee, O.; Opalkowski, D.; Najafi, A.; Leonowicz, Z. On the Forecastability of Solar Energy Generation by Rooftop Panels Pointed in Different Directions. IEEE Trans. Sustain. Energy 2024, 15, 699–702. [Google Scholar]
- Kharazi, S.; Amjady, N.; Nejati, M.; Zareipour, H. A New Closed-Loop Solar Power Forecasting Method with Sample Selection. IEEE Trans. Sustain. Energy 2024, 15, 687–698. [Google Scholar] [CrossRef]
- Pranith, S.; Kumar, S.; Singh, B.; Bhatti, T.S. Robust Control System Tuner and Cascaded Adaptive Vectorial Filter-Based PV-Battery System with a Dual-Loop ANF-PLL. IEEE Trans. Ind. Electron. 2024, 71, 16419–16429. [Google Scholar] [CrossRef]
- Xu, J.; Zhong, J.; Kang, J.; Dong, W.; Xie, S. Stability Analysis and Robust Parameter Design of DC-Voltage Loop for Three-Phase Grid-Connected PV Inverter Under Weak Grid Condition. IEEE Trans. Ind. Electron. 2024, 71, 3776–3787. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, X.; Tu, C.; Che, L.; Xiao, F.; Hou, Y. A Multi-timescale Energy Management Strategy for Advanced Cophase Traction Power Supply System with PV and ES. IEEE Trans. Transp. Electrif. 2025, 11, 859–869. [Google Scholar] [CrossRef]
- Ramos, E.R.; Leyva, R.; Liu, Q.; Vazquez, S.; Farivar, G.G.; Townsend, C.D.; Tafti, H.D.; Pou, J. Discontinuous PWM Operation of a Single-Phase PV Generator with Low-Voltage Energy Storage. IEEE Trans. Ind. Electron. 2025, 72, 2997–3007. [Google Scholar] [CrossRef]
- Zafar, R.; Pota, H.R. Multi-Timescale Coordinated Control with Optimal Network Reconfiguration Using Battery Storage System in Smart Distribution Grids. IEEE Trans. Sustain. Energy 2023, 14, 2338–2350. [Google Scholar] [CrossRef]
- Hafiz, F.; Awal, M.A.; de Queiroz, A.R.; Husain, I. Real-time stochastic optimization of energy storage management using deep learning-based forecasts for residential PV applications. IEEE Trans. Ind. Appl. 2020, 56, 2216–2226. [Google Scholar] [CrossRef]
- Shirsat, A.; Tang, W. Data-Driven Stochastic Model Predictive Control for DC-Coupled Residential PV-Storage Systems. IEEE Trans. Energy Convers. 2021, 36, 1435–1448. [Google Scholar] [CrossRef]
- Ye, Y.; Qiu, D.; Wu, X.; Strbac, G.; Ward, J. Model-free real time autonomous control for a residential multi-energy system using deep reinforcement learning. IEEE Trans. Smart Grid 2020, 11, 3068–3082. [Google Scholar] [CrossRef]
- Lin, Y.; McPhee, J.; Azad, N.L. Comparison of deep reinforcement learning and model predictive control for adaptive cruise control. IEEE Trans. Intell. Veh. 2021, 6, 221–231. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, Z.; Yan, Z. Energy storage optimization technology for source-grid-load-storage microgrid based on particle swarm optimization algorithm. Electrotech. Technol. 2020, 14, 13–15. [Google Scholar]
- Jia, Y.; Li, W.; Zhao, M. Optimal configuration of wind-PV-storage system using penalty function improved particle swarm optimization algorithm. Acta Energ. Sol. Sin. 2019, 7, 2071–2077. [Google Scholar]
- Hoffmeister, F.; Sakai, S. Problem-Independent Handling of Constraints by Use of Metric Penalty Functions. Evol. Program. 1996, 870, 289–294. [Google Scholar]
- Homaifar, A.; Qi, X.C.; Lai, H.S. Constrained Optimization via Genetic Algorithms. Simulation 1994, 62, 242–253. [Google Scholar] [CrossRef]
- Kazarlis, S.; Petridis, V. Varying Fitness Functions in Genetic Algorithms: Studying the Rate of Increase of the Dynamic Penalty Terms. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Tessema, B.; Yen, G.G. An Adaptive Penalty Formulation for Constrained Evolutionary Optimization. IEEE Trans. Syst. Man Cybern. Part-A Syst. Humans 2009, 39, 565–578. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Zaman, F.; Guerrero, J.M. Energy scheduling of community microgrid with battery cost using particle swarm optimization. Appl. Energy 2019, 254, 113723. [Google Scholar] [CrossRef]
- Lu, Z.D. Improvement and Application Research of Hybrid Particle Swarm Optimization Algorithm. Ph.D. Thesis, Yanshan University, Qinhuangdao, China, 2020. [Google Scholar]
- Hu, T.Q.; Zhang, X.X.; Cao, X.Y. A hybrid particle swarm optimization algorithm with dynamically adjusted inertia weight. Electron. Opt. Control 2020, 27, 16–21. [Google Scholar]
- Hao, H.; Zhang, T.Y. Research on optimal load distribution of generating units based on improved particle swarm optimization algorithm. Sci. Technol. Innov. Her. 2019, 16, 106–108. [Google Scholar]







| Item | This Work | Reference [10] | Reference [11] | Reference [12] | Reference [13] |
|---|---|---|---|---|---|
| Approaches | PSO based on non-linear penalty function | DP | SMPC | DRL | DRL |
| Advantages and disadvantages | Continuously update the penalty factor in the iterative process to make the search result closer to the optimal value | The course of dimensionality in dynamic programming plays a prime role in limiting its applications | Low computation complexity and can easily incorporate the updated values of the uncertainty forecasts | The necessity of a complex computational framework | Similar performances as SMPC when the modeling errors are small |
| Item | Value |
|---|---|
| Rated voltage of battery (V) | 120 |
| Power of battery (Ah) | 40 |
| Power of charging and discharging for battery (kW) | 5 kW |
| Rated voltage of grid (V) | 220 |
| Frequency of grid (Hz) | 50 |
| Switching frequency (kHz) | 20 |
| Inductor of inverter (mH) | 1.3 |
| Inductor of boost converter (mH) | 0.65 |
| Inductor of battery (mH) | 0.65 |
| Capacitor of DC bus (uF) | 2820 |
| Controller | Intel Core i5-4600U |
| Operation Parameters | Pg_max (kW) | Pbc_max (kW) | Pbd_max (kW) | SoCmin (%) | SoCmax (%) | σ (%) |
|---|---|---|---|---|---|---|
| Value | 5 | 4.5 | 5 | 10 | 90 | 7 |
| Operation Parameters | Iterations | Population Size | wmax | wmin | D | c1s | c2s | c1l | c2l |
|---|---|---|---|---|---|---|---|---|---|
| Value | 600 | 8000 | 0.9 | 0.4 | 24 | 0.5 | 2.5 | 2.5 | 0.5 |
| Types of Penalty Functions | Daily Electricity Cost (CNY) | ||
|---|---|---|---|
| Average | Maximum | Minimum | |
| Non-linear penalty function method | 9.64 | 10.38 | 8.95 |
| Penalty factor: 50 | 10.56 | 11.98 | 10.42 |
| Penalty factor: 500 | 11.82 | 12.84 | 10.61 |
| Penalty factor: 5000 | 12.14 | 13.72 | 11.29 |
| Types of Penalty Functions | Daily Electricity Cost (CNY) | ||
|---|---|---|---|
| Average | Maximum | Minimum | |
| Non-linear penalty function method | 17.92 | 18.87 | 16.37 |
| Penalty factor: 50 | 23.35 | 24.20 | 21.01 |
| Penalty factor: 500 | 24.21 | 25.42 | 22.59 |
| Penalty factor: 5000 | 22.47 | 22.94 | 20.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Song, W.; Sun, K. Energy Scheduling of PV–ES Inverters Based on Particle Swarm Optimization Using a Non-Linear Penalty Function. Electronics 2025, 14, 2272. https://doi.org/10.3390/electronics14112272
Wang L, Song W, Sun K. Energy Scheduling of PV–ES Inverters Based on Particle Swarm Optimization Using a Non-Linear Penalty Function. Electronics. 2025; 14(11):2272. https://doi.org/10.3390/electronics14112272
Chicago/Turabian StyleWang, Lei, Wenle Song, and Kai Sun. 2025. "Energy Scheduling of PV–ES Inverters Based on Particle Swarm Optimization Using a Non-Linear Penalty Function" Electronics 14, no. 11: 2272. https://doi.org/10.3390/electronics14112272
APA StyleWang, L., Song, W., & Sun, K. (2025). Energy Scheduling of PV–ES Inverters Based on Particle Swarm Optimization Using a Non-Linear Penalty Function. Electronics, 14(11), 2272. https://doi.org/10.3390/electronics14112272






