Self-Supervised Interpolation Method for Missing Shallow Subsurface Wavefield Data Based on SC-Net
Abstract
1. Introduction
- (1)
- We developed a deep interpolation network model named SC-Net, which incorporates our specifically designed spatial-channel feature fusion module to effectively integrate global and local features while capturing long-range dependencies. This approach proves particularly suitable for seismic data interpolation applications, as it reduces interpolation errors and generates reconstructed waveforms that more closely approximate the actual seismic waveforms. We conducted experimental tests under high missing-data conditions and achieved promising results.
- (2)
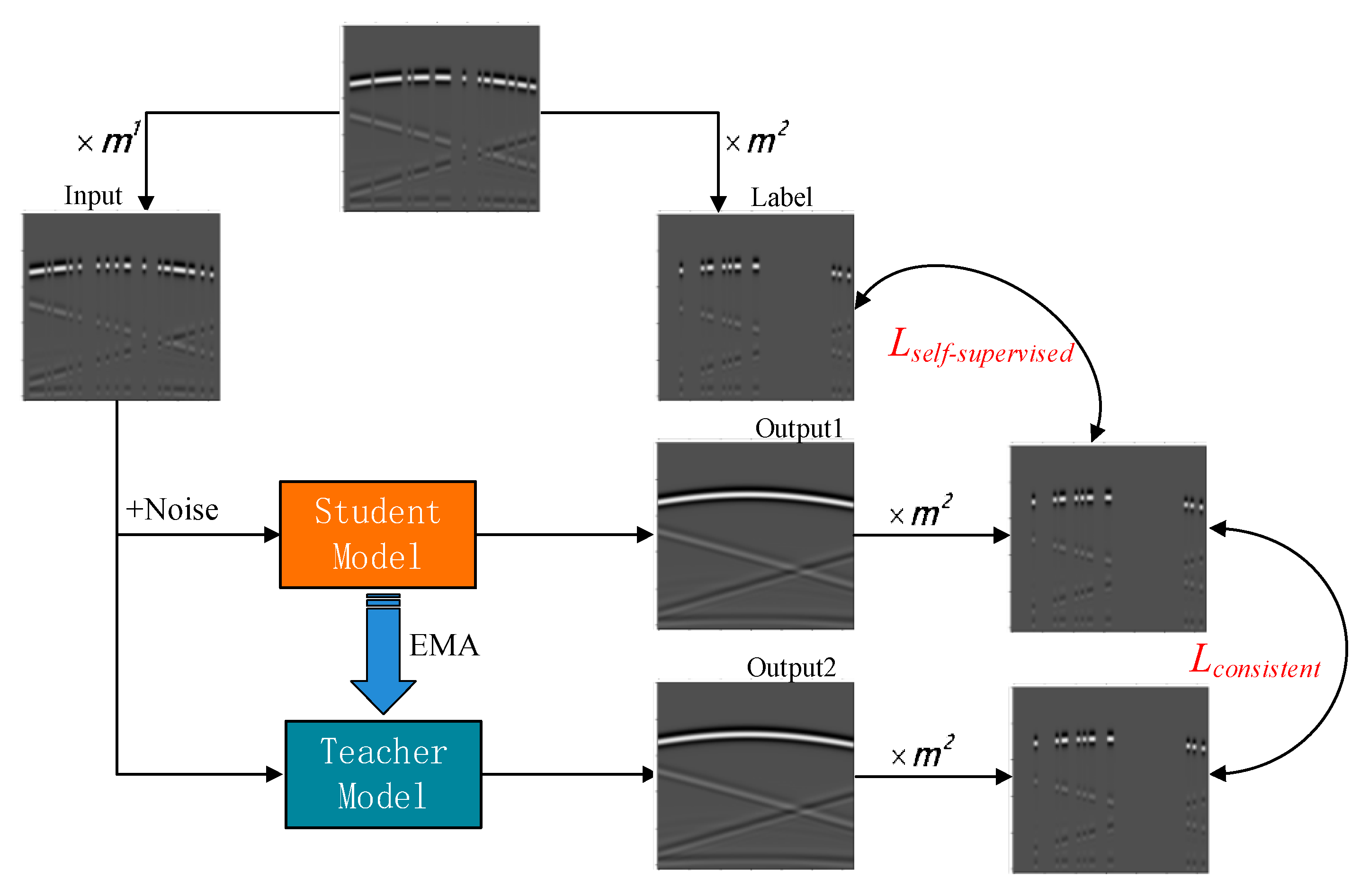
- Building upon the Mean Teacher model, we propose a plug-and-play training method for missing data. This approach enables training using only incomplete seismic data while enhancing network stability, making it adaptable to various complex real-world conditions.
- (3)
- To mitigate the challenge of insufficient real data for effective network training, we utilize a hybrid training approach combining simulated and real data. By jointly training the model with a large number of numerically simulated samples and a small set of real data samples, we enhance the model’s adaptability to shallow geological conditions, improve the generalization capability of the network model, and increase the accuracy of real seismic data interpolation. During our simulation experiments, we introduced Gaussian noise with varying amplitude percentages to the test data. The resulting outputs under different ablation scenarios demonstrate that our training framework can effectively enhance the network’s robustness to a certain extent.
2. Methods
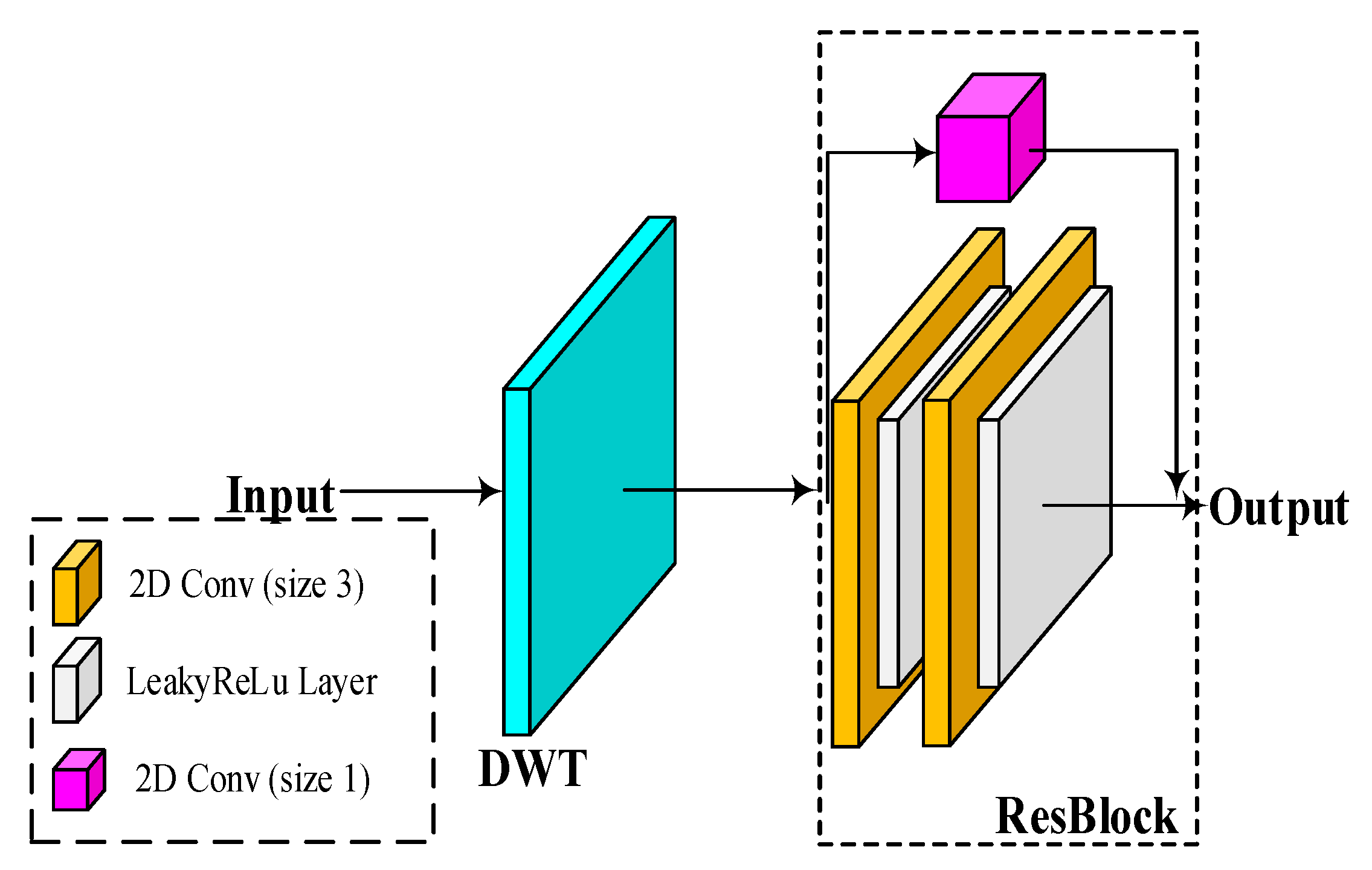
2.1. Spatial and Channel Feature Fusion Network (SC-Net)
2.1.1. Sampling Layer
- Wavelet down-sampling layer
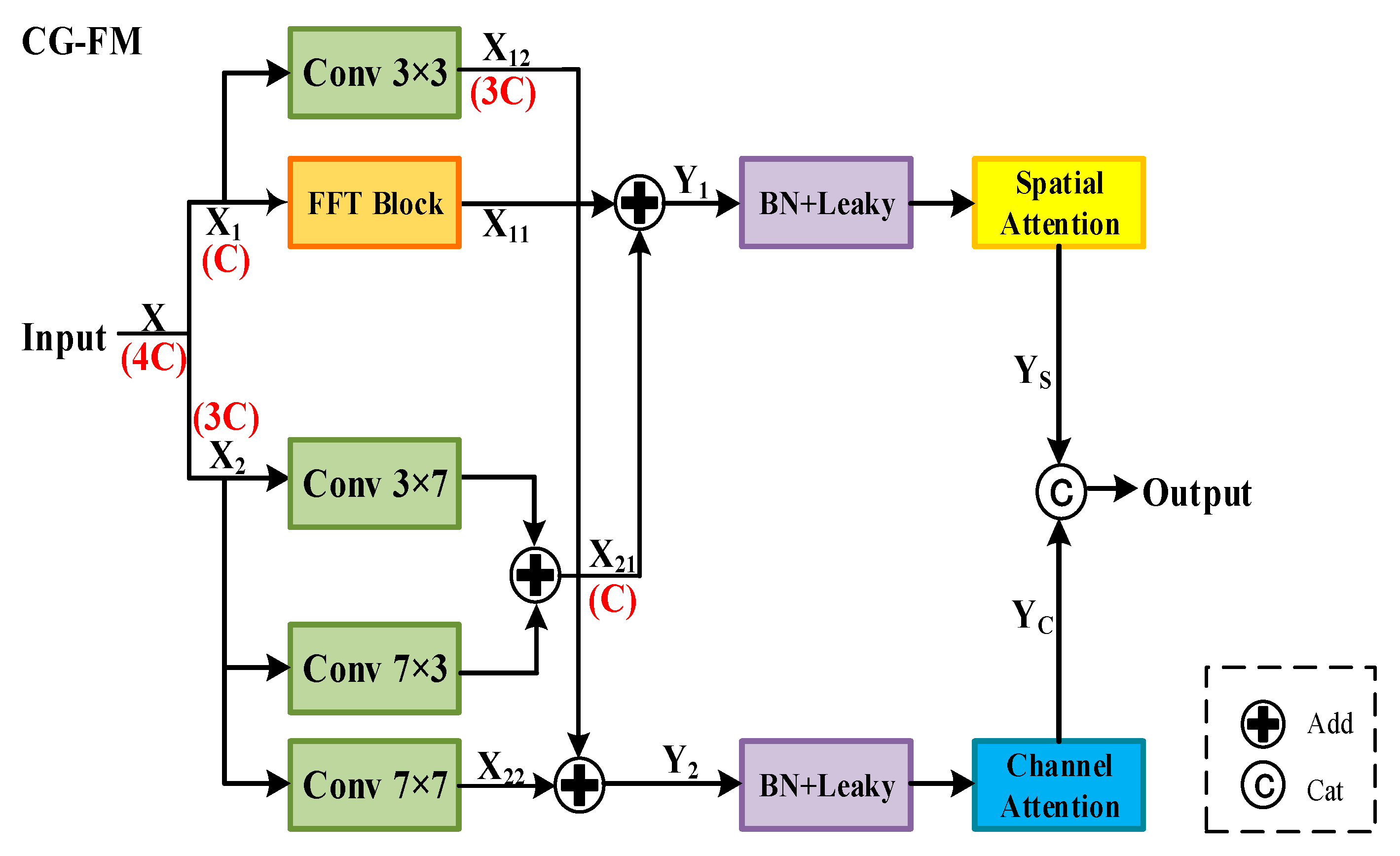
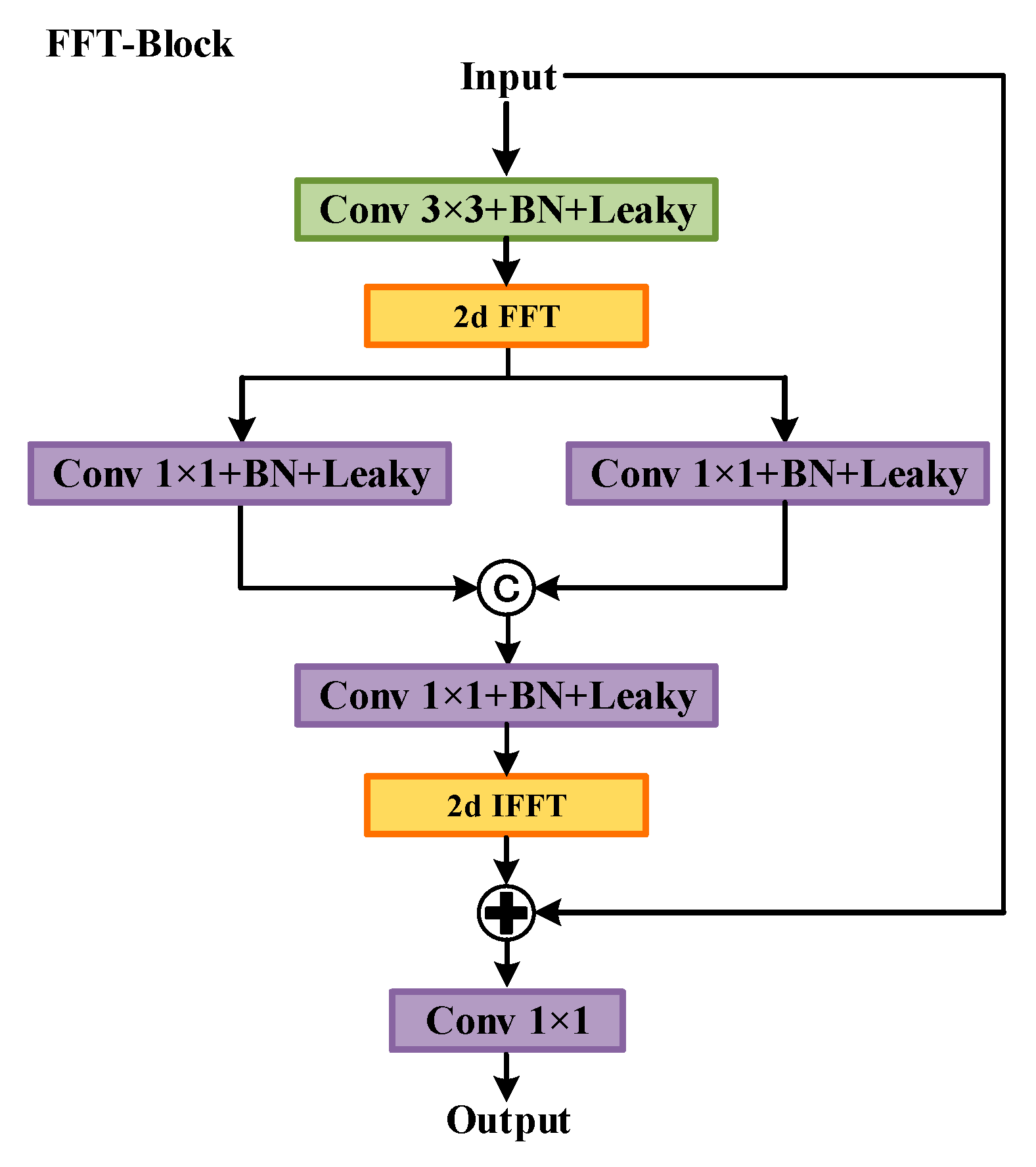
2.1.2. Spatial-Channel Feature Fusion Module (SC-FM)
- 2.
- Spatial attention block
- 3.
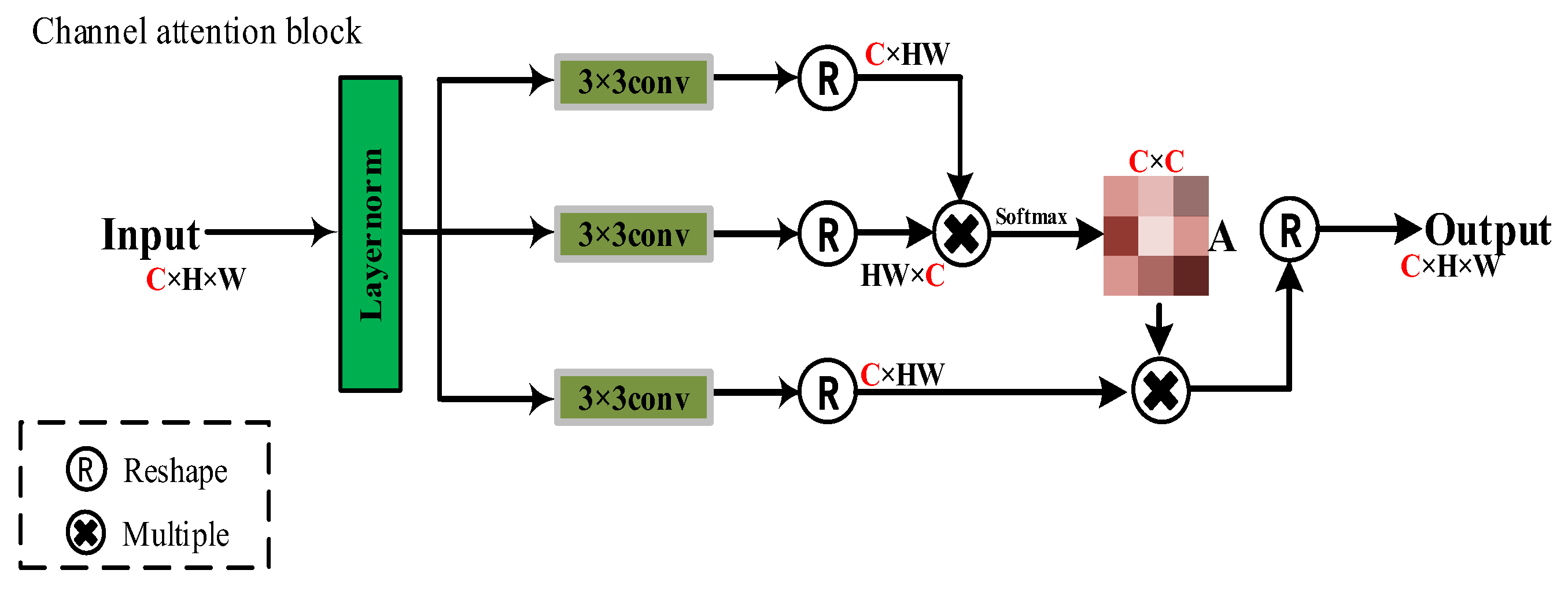
- Channel attention block
- 4.
- FFT block
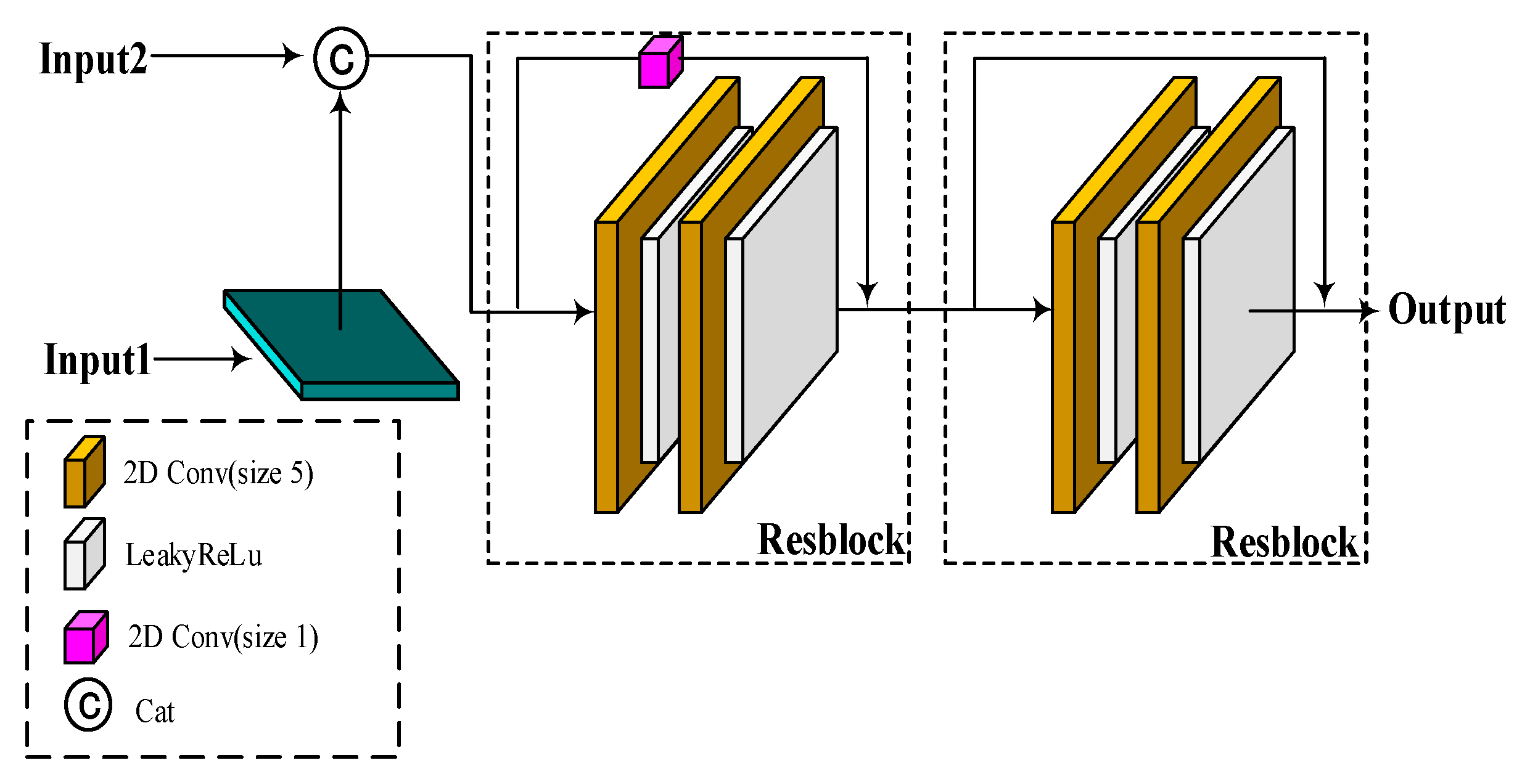
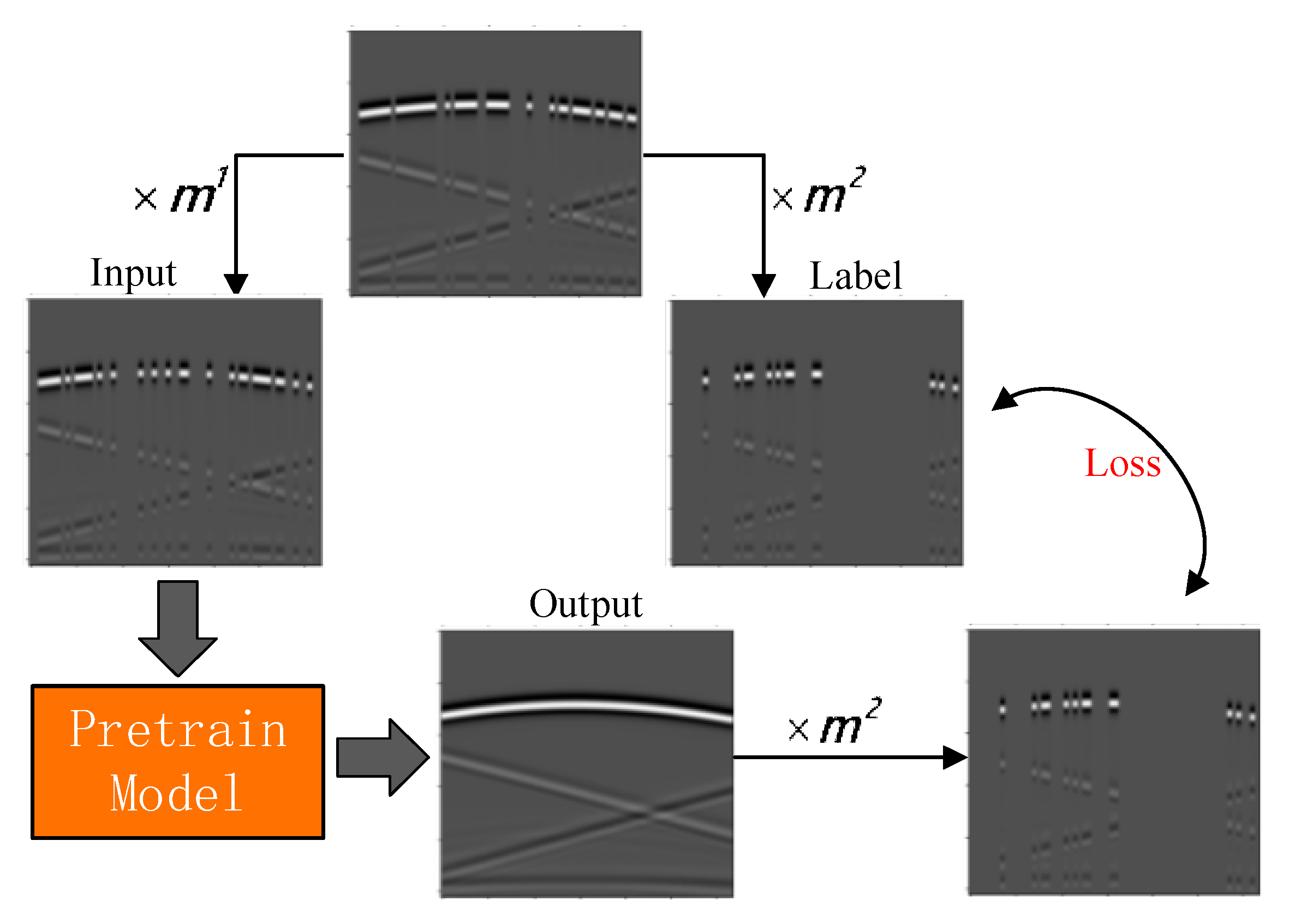
2.2. Self-Supervised Training Method for Missing Data
3. Results
3.1. Construction of Simulated Training Dataset
3.2. Construction of Actual Training Dataset
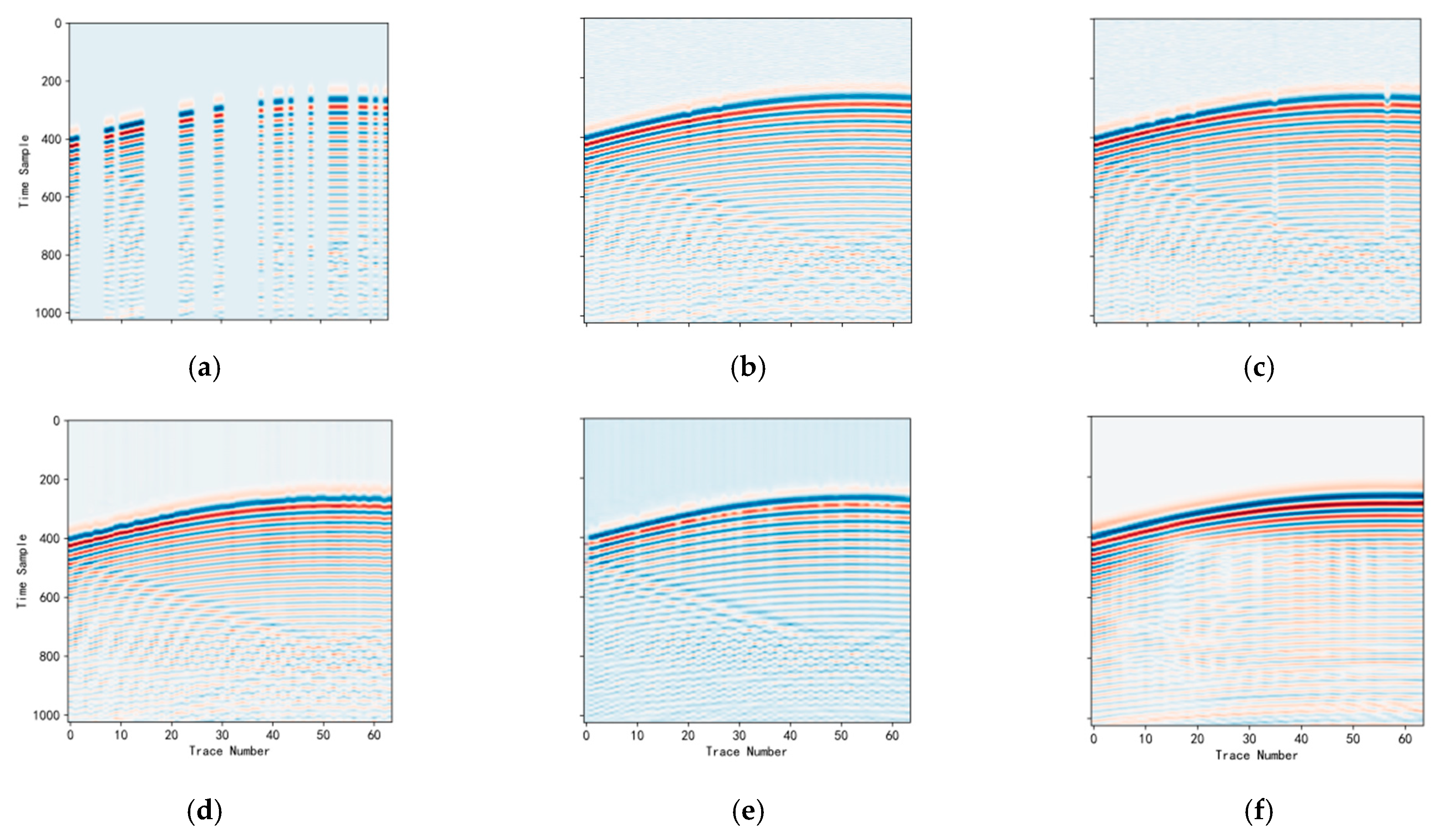
3.3. Training and Results
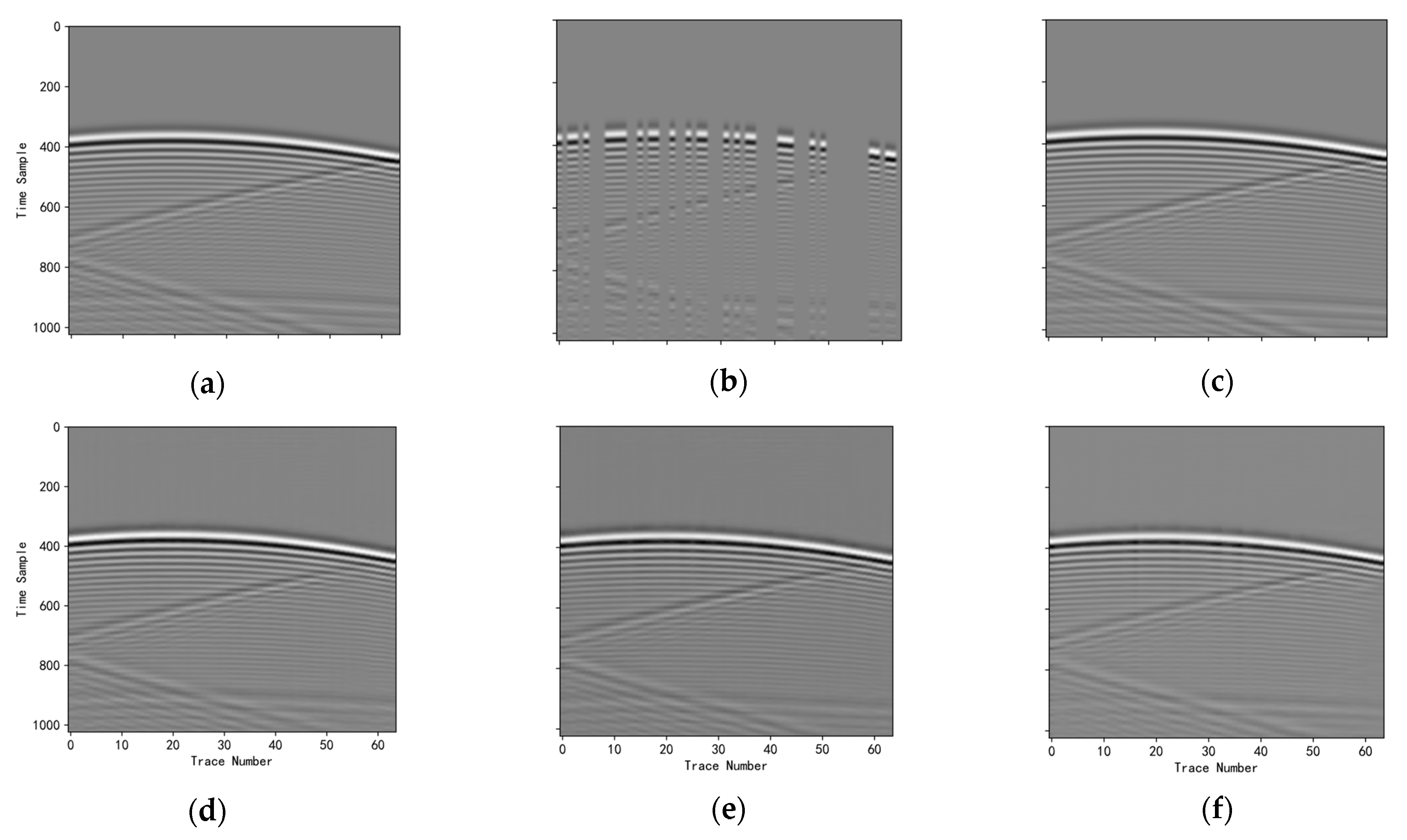
3.3.1. Ablation Studies
3.3.2. Network Effectiveness Comparison Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stolt, R.H. Seismic Data Mapping and Reconstruction. Geophysics 2002, 67, 890–908. [Google Scholar] [CrossRef]
- Fomel, S. Seismic Reflection Data Interpolation with Differential Offset and Shot Continuation. Geophysics 2003, 68, 733–744. [Google Scholar] [CrossRef]
- Oropeza, V.; Sacchi, M. Simultaneous Seismic Data Denoising and Reconstruction via Multichannel Singular Spectrum Analysis. Geophysics 2011, 76, V25–V32. [Google Scholar] [CrossRef]
- Ma, J.W. Three-Dimensional Irregular Seismic Data Reconstruction via Low-Rank Matrix Completion. Geophysics 2013, 78, V181–V192. [Google Scholar] [CrossRef]
- Chen, Y.K.; Zhang, D.; Huang, W.L.; Zu, S.; Jin, Z.; Chen, W. Damped Rank-Reduction Method for Simultaneous Denoising and Reconstruction of 5D Seismic Data. In Proceedings of the SEG Technical Program Expanded Abstracts, Dallas, TX, USA, 16–21 October 2016; Society of Exploration Geophysicists: Dallas, TX, USA, 2016; pp. 4075–4080. [Google Scholar]
- Porsani, M. Seismic Trace Interpolation Using Half-Step Prediction Filters. Geophysics 1999, 64, 1461–1467. [Google Scholar] [CrossRef]
- Naghizadeh, M.; Sacchi, M.D. Multistep Autoregressive Reconstruction of Seismic Records. Geophysics 2007, 72, V111–V118. [Google Scholar] [CrossRef]
- Wu, G.; Liu, C.; Liu, D.; Liu, Y.; Zheng, Z. Seismic Data Interpolation Beyond Continuous Missing Data Using High-Order Streaming Prediction Filter. Chin. J. Geophys. 2023, 66, 1220–1231. [Google Scholar]
- Pathirage, C.S.N.; Li, J.; Li, L.; Hao, H.; Liu, W.; Ni, P. Structural damage identification based on autoencoder neural networks and deep learning. Eng. Struct. 2018, 172, 13–28. [Google Scholar] [CrossRef]
- Wang, Z.X.; Wang, S.D.; Zhou, C.; Cheng, W. Dual Wasserstein Generative Adversarial Network Condition: A Generative Adversarial Network-Based Acoustic Impedance Inversion Method. Geophysics 2022, 87, R401–R411. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, S.D.; Wang, Z.X.; Cheng, W. Absorption Attenuation Compensation Using an End-To-End Deep Neural Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Liu, G.C.; Du, J.; Li, C.; Qi, J. Low-Frequency Extrapolation of Prestack Viscoacoustic Seismic Data Based on Dense Convolutional Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Li, F.; Liu, H.; Yang, X.; Zhao, M.; Yang, C.; Zhang, L. Reconstruction of Acoustic Curve Based on U-Net Neural Network. Period. Ocean. Univ. China 2023, 53, 86–92. [Google Scholar]
- Liu, X.; Sun, Y. Seismic Signal Denoising Based on Convolutional Neural Network with Residual and Attention Mechanism. J. Jilin Univ. (Earth Sci. Ed.) 2023, 53, 609–621. [Google Scholar]
- Wan, X.; Gong, X.; Cheng, Q.; Yu, M. Eliminating Low-Frequency Noise in Reverse-Time Migration Based on DeCNN. J. Jilin Univ. (Earth Sci. Ed.) 2023, 53, 1593–1601. [Google Scholar]
- Jia, Y.N.; Ma, J.W. What Can Machine Learning Do for Seismic Data Processing? An Interpolation Application. Geophysics 2017, 82, V163–V177. [Google Scholar] [CrossRef]
- Siahkoohi, A.; Kumar, R.; Herrmann, F. Seismic Data Reconstruction with Generative Adversarial Networks. In Proceedings of the 80th EAGE Conference and Exhibition, Copenhagen, Denmark, 11–14 June 2018; European Association of Geoscientists and Engineers: Copenhagen, Denmark, 2018; pp. 1–5. [Google Scholar]
- Wang, B.F.; Zhang, N.; Lu, W.K.; Wang, J. Deep-Learning-Based Seismic Data Interpolation: A Preliminary Result. Geophysics 2019, 84, V11–V20. [Google Scholar] [CrossRef]
- Kaur, H.; Pham, N.; Fomel, S. Seismic Data Interpolation using CycleGAN. In Proceedings of the SEG Technical Program Expanded Abstracts, San Antonio, TX, USA, 19–20 September 2019; Society of Exploration Geophysicists: San Antonio, TX, USA, 2019; pp. 2202–2206. [Google Scholar]
- Xiong, Y.; Cheng, J. Efficient Seismic Data Interpolation using Deep Convolutional Networks and Transfer Learning. In Proceedings of the 81st EAGE Conference and Exhibition, London, UK, 3–6 June 2019; European Association of Geoscientists and Engineers: London, UK, 2019; pp. 1–5. [Google Scholar]
- Zheng, H.; Zhang, B. Intelligent Seismic Data Interpolation via Convolutional Neural Network. Prog. Geophys. 2020, 35, 721–727. [Google Scholar]
- Wang, Y.Y.; Wang, B.F.; Tu, N.; Geng, J. Seismic Trace Interpolation for Irregularly Spatial Sampled Data Using Convolutional Auto-Encoder. Geophysics 2020, 85, V119–V130. [Google Scholar] [CrossRef]
- Xu, G.; Liao, W.; Zhang, X.; Li, C.; He, X.; Wu, X. Haar wavelet downsampling: A simple but effective downsampling module for semantic segmentation. Pattern Recognit. 2023, 143, 109819. [Google Scholar] [CrossRef]
- Cui, Y.; Alois, K. Dual-domain strip attention for image restoration. Neural Netw. 2024, 171, 429–439. [Google Scholar] [CrossRef] [PubMed]
- Fang, W.; Fu, L.; Wu, M.; Yue, J.; Li, H. Irregularly sampled seismic data interpolation with self-supervised learning. Geophysics 2023, 88, V175–V185. [Google Scholar] [CrossRef]
- Tarvainen, A.; Harri, V. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; Available online: https://dl.acm.org/doi/10.5555/3294771.3294885 (accessed on 1 October 2025).
- Hwang, S.; Jeon, S.; Ma, Y.S. Byun, H. WeatherGAN: Unsupervised multi-weather image-to-image translation via single content-preserving UResNet generator. Multimedia Tools Appl. 2022, 81, 40269–40288. [Google Scholar] [CrossRef]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Proceedings of the International Workshop on Deep Learning in Medical Image Analysis, Granada, Spain, 20 September 2018; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Liu, P.; Zhang, H.; Zhang, K.; Lin, L.; Zuo, W. Multi-level wavelet-CNN for image restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–23 June 2018; pp. 773–782. [Google Scholar]



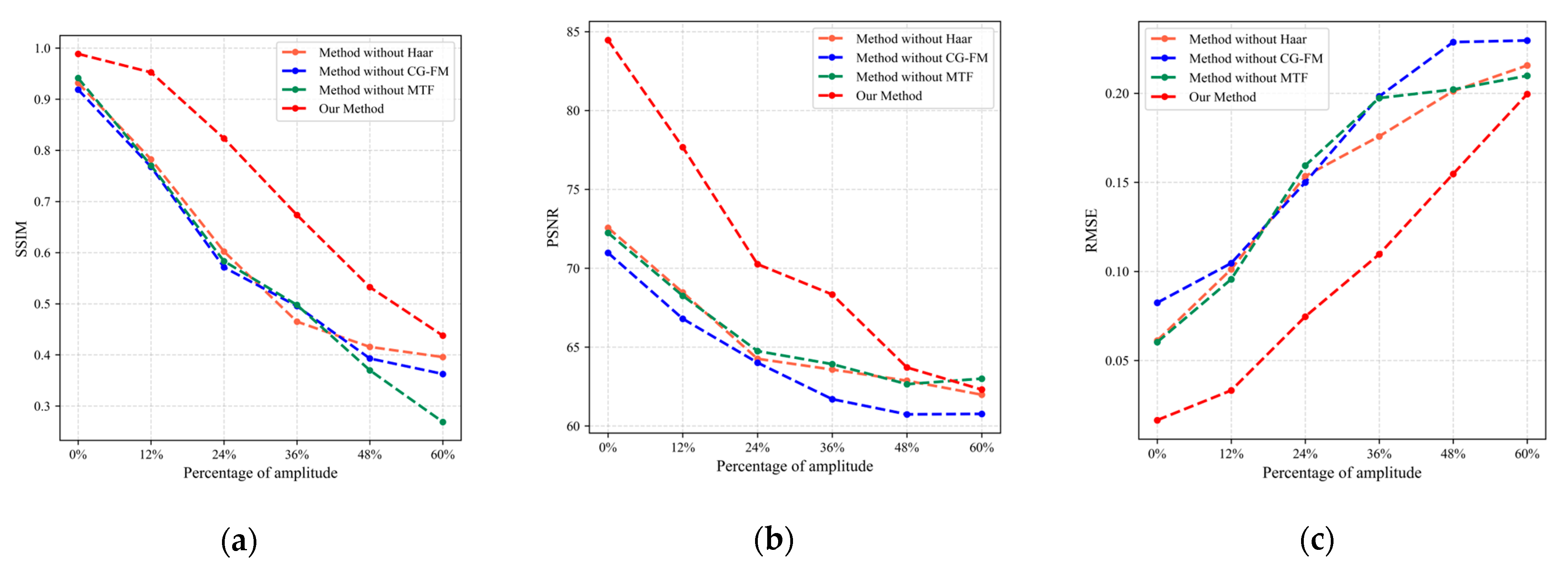

| Method | Metrics | 0% | 12% | 24% | 36% | 48% | 60% |
|---|---|---|---|---|---|---|---|
| Our Method | SSIM | 0.9886 | 0.9524 | 0.8232 | 0.6736 | 0.5324 | 0.4376 |
| PSNR | 84.4673 | 77.6743 | 70.2573 | 68.3341 | 63.7064 | 62.3021 | |
| RMSE | 0.0165 | 0.0332 | 0.0746 | 0.1096 | 0.1547 | 0.1995 | |
| Method-without Haar | SSIM | 0.9316 | 0.7824 | 0.6021 | 0.4650 | 0.4156 | 0.3957 |
| PSNR | 72.5634 | 68.4632 | 64.2573 | 63.5732 | 62.8673 | 61.9774 | |
| RMSE | 0.0612 | 0.1012 | 0.1534 | 0.1758 | 0.2012 | 0.2156 | |
| Method- without CG-FM | SSIM | 0.9188 | 0.7676 | 0.5712 | 0.4954 | 0.3929 | 0.3627 |
| PSNR | 70.9758 | 66.7961 | 64.0112 | 61.6954 | 60.7342 | 60.7594 | |
| RMSE | 0.0824 | 0.1046 | 0.1499 | 0.1982 | 0.2287 | 0.2296 | |
| Method-without MTF | SSIM | 0.9412 | 0.7702 | 0.5832 | 0.4976 | 0.3698 | 0.2689 |
| PSNR | 72.2414 | 68.2536 | 64.7463 | 63.9175 | 62.6476 | 62.9965 | |
| RMSE | 0.0603 | 0.0956 | 0.1594 | 0.1973 | 0.2021 | 0.2098 |
| Method | SSIM | PSNR | RMSE |
|---|---|---|---|
| SC-Net | 0.9212 | 76.5483 | 0.0332 |
| MWCNN | 0.8951 | 73.5850 | 0.0533 |
| U-Net++ | 0.8679 | 71.3622 | 0.0588 |
| U-Resnet | 0.8566 | 71.1639 | 0.0642 |
| CAE | 0.6953 | 69.0816 | 0.0796 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Yuan, Z.; Xu, L.; Liu, R.; Li, J. Self-Supervised Interpolation Method for Missing Shallow Subsurface Wavefield Data Based on SC-Net. Electronics 2025, 14, 4185. https://doi.org/10.3390/electronics14214185
Wang L, Yuan Z, Xu L, Liu R, Li J. Self-Supervised Interpolation Method for Missing Shallow Subsurface Wavefield Data Based on SC-Net. Electronics. 2025; 14(21):4185. https://doi.org/10.3390/electronics14214185
Chicago/Turabian StyleWang, Limin, Zhilei Yuan, Lina Xu, Rui Liu, and Jian Li. 2025. "Self-Supervised Interpolation Method for Missing Shallow Subsurface Wavefield Data Based on SC-Net" Electronics 14, no. 21: 4185. https://doi.org/10.3390/electronics14214185
APA StyleWang, L., Yuan, Z., Xu, L., Liu, R., & Li, J. (2025). Self-Supervised Interpolation Method for Missing Shallow Subsurface Wavefield Data Based on SC-Net. Electronics, 14(21), 4185. https://doi.org/10.3390/electronics14214185






