Abstract
Intrusion detection is essential to cybersecurity. However, the curse of dimensionality and class imbalance limit detection accuracy and impede the identification of rare attacks. To address these challenges, this paper proposes the high-dimensional feature sequence temporal convolutional network (HiSeq-TCN) for intrusion detection. The proposed HiSeq-TCN transforms high-dimensional feature vectors into pseudo-temporal sequences, enabling the network to capture contextual dependencies across feature dimensions. This enhances feature representation and detection robustness. In addition, a few-shot reinforcement strategy adaptively assigns larger loss weights to minority classes, mitigating class imbalance and improving the recognition of rare attacks. Experiments on the NSL-KDD dataset show that HiSeq-TCN achieves an overall accuracy of 99.44%, outperforming support vector machines, deep neural networks, and long short-term memory models. More importantly, it significantly improves the detection of rare attack types such as remote-to-local and user-to-root attacks. These results highlight the potential of HiSeq-TCN for robust and reliable intrusion detection in practical cybersecurity environments.
1. Introduction
As Internet technologies become deeply embedded in daily life, network systems now serve as indispensable platforms for communication and information sharing across diverse domains, from individuals to national defense. However, the inherent openness of network infrastructure, combined with the exponential growth of data, has significantly increased their vulnerability to cyber threats [1,2,3]. Recent reports from Kaspersky Lab indicate that over one billion distinct types of malware were detected globally in the past year, with more than 2.7 million new variants identified each day on average [4]. These threats include various forms of malicious software, including viruses, trojans, worms, and ransomware, that leverage phishing schemes, malicious links, and software vulnerabilities to penetrate systems and exfiltrate or compromise sensitive data. With cyber threats continuing to grow in both scale and sophistication, safeguarding the security and resilience of network systems poses a critical challenge. Consequently, advancing research in cyber security and developing robust, effective defense technologies have become pressing global priorities.
Intrusion detection technology is designed to monitor and identify potential security threats or malicious activities within computer systems and network environments. It serves as a fundamental component in safeguarding network security and ensuring the stable operation of information systems [5]. Intrusion detection technologies are typically deployed in a distributed architecture, with detectors strategically positioned at critical nodes throughout the target network. These detectors continuously collect data such as network traffic, system logs, and user activity patterns. The collected data are analyzed using predefined rule sets, statistical models, or machine learning frameworks. When suspicious behaviors are detected, especially those matching known malicious activity signatures, the intrusion detection generates an alert to enable a timely response [6].
Intrusion detection technologies are classified into signature-based and anomaly-based approaches. Signature-based methods detect intrusions by matching network traffic against known attack signatures. While efficient and low in false positives, they are ineffective against novel or evolving threats [7,8]. In contrast, anomaly-based detection identifies deviations from normal network behavior, enabling the discovery of unknown or zero-day attacks [9,10]. This approach offers greater adaptability and is well-suited for complex, dynamic environments. Among various anomaly detection techniques, machine learning has become a mainstream solution due to its superior capabilities in data processing and pattern recognition. By modeling large-scale network traffic, machine learning enables automated feature extraction and accurate, real-time intrusion detection, supporting the development of intelligent and adaptive cybersecurity systems [11,12,13].
Traditional machine learning techniques have been extensively utilized in network anomaly detection. Representative frameworks include K-nearest neighbors (KNNs), Bayesian networks, support vector machines (SVMs), random forests, and decision trees, which have demonstrated favorable performance in a range of detection tasks [14,15,16]. However, as network attacks become increasingly frequent and sophisticated, these conventional shallow learning models exhibit limited capacity to cope with the complexity and diversity of modern attack patterns, thereby restricting their effectiveness in dynamic and large-scale network environments.
In recent years, deep learning has gained significant attention in the field of intrusion detection. Compared to traditional shallow machine learning methods, deep learning models offer enhanced feature extraction capabilities and superior nonlinear representation power, enabling the automatic discovery of latent patterns from large-scale, high-dimensional network traffic data [17,18]. These advantages contribute to notable improvements in the accuracy and robustness of anomaly detection. Deep learning models widely used in intrusion detection include convolutional neural networks (CNNs) for spatial feature extraction, as well as deep neural networks (DNNs), long short-term memory (LSTM) networks, transformer models, and temporal convolutional networks (TCNs) for learning features across multiple dimensions [19,20,21].
Intrusion detection systems operating in complex network environments typically encounter several challenges:
- (1)
- Information extraction bottleneck under the curse of dimensionality: High-dimensional features exhibit complex inter-correlations, and treating them as independent inputs hampers effective pattern extraction and reduces detection performance.
- (2)
- Difficulty in capturing long-range feature dependencies: Correlations often exist across distant feature dimensions, while traditional methods struggle to reliably capture these contextual dependencies, limiting the quality of feature representation.
- (3)
- Severe class imbalance: Intrusion datasets are usually dominated by normal traffic, while samples of certain attack categories are scarce. This imbalance causes models to be biased toward majority classes, resulting in degraded detection performance for minority attack types.
To address these challenges, this study proposes an intrusion detection framework based on TCN. The key contributions are as follows:
- (1)
- Novel high-dimensional feature sequence modeling: The static high-dimensional feature vectors are innovatively reinterpreted as pseudo time-series inputs. TCN is employed to model contextual dependencies among feature dimensions, enabling more effective extraction of complex feature patterns and improving information utilization compared to traditional static feature extraction methods.
- (2)
- Integration of TCN for intrusion detection: A TCN-based detection framework is developed to leverage its strengths in capturing long-range dependencies and sequential features within network traffic. This framework enhances the accuracy and robustness of anomaly detection by comprehensively modeling temporal characteristics.
- (3)
- Small-sample enhancement mechanism: A few-shot reinforcement strategy is applied by assigning fixed, predefined weights to minority attack categories during training. Higher weights are allocated to rare classes to amplify their contribution to the overall loss. This approach strengthens the learning of minority classes, improves detection accuracy for rare attacks, and ensures robust performance across all classes.
2. Related Works
2.1. Traditional Machine Learning
Traditional machine learning methods typically employ supervised learning to build classification models capable of distinguishing between normal and anomalous behaviors. Representative frameworks include KNNs, Bayesian networks, SVMs, random forests, and decision trees.
KNNs are distance-based classification methods that remain attractive for small-scale datasets due to its simplicity and interpretability. The earliest application of KNN to intrusion detection was presented [22], where program behavior was modeled as documents using system call frequency features for classification. Building on this idea, Li et al. employed KNNs to design an intrusion detection system for wireless sensor networks in the Internet of things [23]. Their approach detected behavioral anomalies and reliably distinguished abnormal nodes from normal ones. Enhancements to the ad hoc on-demand distance vector routing protocol further improved detection efficiency.
Bayesian networks model conditional dependencies among features through probabilistic inference, enabling the handling of uncertainty to a certain extent. A wrapper-based intrusion detection framework was proposed [24], which integrates feature selection to remove irrelevant attributes and reduce computational complexity, and employs a Bayesian network as the base classifier for attack type prediction.
SVMs construct decision boundaries based on the maximum margin criterion, demonstrating strong generalization performance, particularly in high-dimensional feature spaces. Mukkamala et al. investigated intrusion detection using neural networks and support vector machines [25]. Their study focused on extracting behavioral features and constructing classifiers to detect anomalies and known intrusions in real time. An analysis of SVM-based intrusion detection techniques was presented [26]. It covered data collection, preprocessing, training, testing, and decision-making.
Random forests and decision trees, as ensemble learning methods, improve model stability and robustness. They also provide advantages in evaluating feature importance and capturing nonlinear relationships. An intrusion detection system was developed using a random forest classifier to address the complexity of network traffic data [27]. The model achieved efficiency with a low false alarm rate and a high detection rate. Rai et al. proposed a decision tree-based intrusion detection framework [28]. Their method enhanced feature selection and split value determination. Information gain was used to identify relevant features, and the split strategy reduced bias toward frequent values.
2.2. Deep Learning
Representative deep learning models include CNNs, DNNs, and sequence-oriented architectures such as LSTM, Transformer, and TCN models.
CNNs extract local spatial features using convolutional operations. They are effective for images and spatial data, benefiting from parameter sharing and sparse connectivity, which reduce computation and improve generalization. Chen et al. introduced a novel convolutional neural network for intrusion detection in dynamic IoT environments [29]. By integrating the synaptic intelligence framework, their model mitigates catastrophic forgetting during continuous learning and reduces training complexity. Furthermore, they proposed a custom loss function to address class imbalance and gradient vanishing, and applied quantization-aware training to enhance model deployment on resource-constrained IoT devices.
DNNs consist of multiple fully connected layers. They capture complex high-dimensional features through nonlinear transformations and apply to various tasks. However, they are less sensitive to spatial structures. The study [30] designed a DNN for network intrusion detection, employing SMOTE and random sampling to mitigate class imbalance in the CICIDS 2017 dataset. Their model achieved a high accuracy of 99.68% with a minimal loss of 0.0102, demonstrating strong predictive performance.
LSTM networks are a type of recurrent neural network. They use gating mechanisms to solve the vanishing gradient problem. LSTM networks excel at modeling long-term dependencies in sequences. They are widely used in time series and natural language processing. Adetunji et al. [31] proposed a parameter-tuned LSTM network for intrusion detection, employing sequential learning to classify attacks such as denial of service (DoS), probe scan (Probe), remote-to-local (R2L), and user-to-root (U2R) attacks. Their model achieved 99.65% validation accuracy and 99.9% recall on the CICIDS dataset, while keeping false positive and false negative rates low. An LSTM-based intrusion detection model was developed to improve IoT security by identifying both known and emerging attack patterns [32]. Evaluation on the CIC-IoT2023 dataset showed 98.75% accuracy and an F1 score of 98.59%, highlighting its strong performance across diverse IoT traffic scenarios.
Transformer models use self-attention to capture global dependencies in sequences. They enable parallel computation and improve training efficiency. Transformers handle long sequences and multimodal data and are now a leading sequence modeling architecture. A transformer-based framework for network intrusion detection was proposed [33] to capture long-term network behaviors often overlooked by traditional intrusion detection methods. The framework allows for modular replacement of transformer components and was evaluated using architectures such as generative pre-trained transformer 2 and bidirectional encoder representations from transformers across multiple benchmark datasets.
TCNs use causal and dilated convolutions to capture dependencies over multiple temporal scales. They ensure stable training and effectively model long-range temporal patterns. The study [34] developed an intrusion detection framework for Intelligent Connected Vehicles. By treating message sequences as natural language, the model employs bidirectional sliding windows and stacked TCN residual blocks for feature extraction, while additive feature fusion enhances anomaly detection. A focal causal TCN was proposed [35] to detect rare cyber attacks in industrial IoT environments. The approach treats intrusion detection as a binary task and gives priority to minority attacks using a tree-structured descending scheme. This design mitigates data imbalance and lowers computational overhead while maintaining high detection accuracy.
Traditional machine learning methods have demonstrated reasonable performance across various intrusion detection scenarios. However, these shallow models generally depend on handcrafted features and often struggle to capture complex patterns in high-dimensional and dynamic network traffic. In contrast, deep learning models provide significant advantages by automatically extracting sophisticated features and modeling nonlinear relationships within large-scale, high-dimensional network data. Despite these benefits, several challenges remain due to the intrinsic characteristics of network traffic data. Specifically, the combination of high dimensionality and weak correlations among features limits effective information propagation. Moreover, many approaches rely on static feature representations, which reduce the ability to capture complex dependencies. In addition, class imbalance is severe in intrusion datasets because normal traffic far exceeds attack samples. This imbalance causes models to be biased toward majority classes and leads to poor detection performance on minority attack types. Addressing these challenges is essential to improve the effectiveness of deep learning-based intrusion detection systems.
3. Proposed HiSeq-TCN
The basic structure of HiSeq-TCN is illustrated in Figure 1. HiSeq-TCN transforms input vectors into sequences, extracts context-aware features using TCN, and applies class-weighted loss to address class imbalance. The model consists of three tightly integrated modules: sequential modeling of high-dimensional features, which transforms feature vectors into ordered sequences suitable for convolutional processing; multi-scale feature extraction via residual TCN, which captures both local and long-range dependencies across feature dimensions; and classification with manually assigned class weights guided by a few-shot reinforcement strategy to improve sensitivity to minority classes. Each component is described in detail below with corresponding formulations.
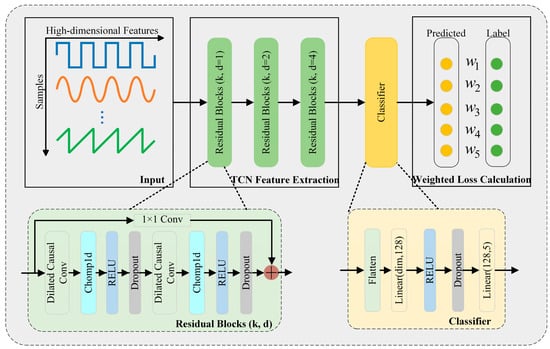
Figure 1.
The basic structure of the HiSeq-TCN model.
In this study, we did not manually select or define specific communication features to detect particular types of attacks. Instead, our model utilizes all available high-dimensional feature sequences and learns the intrinsic differences among them through the similarity measurement and graph-based representation. This approach enables the model to identify various attacks, such as DoS, by capturing global feature correlations rather than relying on a limited set of predefined attributes.
3.1. Sequential Modeling of High-Dimensional Features
In network intrusion detection, the input data are typically represented as high-dimensional feature vectors. However, traditional models that treat these features as unordered often fail to capture the latent dependencies among them. To address this, HiSeq-TCN reformulates each feature vector as a pseudo-temporal sequence, enabling the use of temporal convolution to extract contextual correlations across feature dimensions.
Let denote the feature vector of the -th sample. This vector is viewed as a one-dimensional sequence , where denotes the number of feature dimensions. For a batch of samples, the input tensor is represented as .
To ensure consistent feature scale and avoid dominance by large-valued features during convolution operations, all feature dimensions are normalized using the min–max scaling method. The normalization parameters (minimum and maximum values) were computed only from the training set and then applied to the test sets to prevent data leakage. The normalized feature is given by Equation (1).
where and denote the minimum and maximum feature values within the training data, respectively.
To maintain input-output dimensional alignment for residual connections, HiSeq-TCN applies causal convolution with appropriate zero-padding. The padding introduces extra elements at the sequence boundary, which are subsequently removed using a Chomp1d operation to preserve the original sequence length. The output of the convolutional operation is described in Equation (2).
where denotes convolution and represents the kernel weights.
3.2. Multi-Scale Feature Extraction with Residual TCN Blocks
To effectively model both local and long-range dependencies among feature dimensions, HiSeq-TCN employs a stack of residual temporal convolutional network (TCN) blocks. Each block consists of two dilated causal convolution layers, which expand the receptive field without increasing the number of parameters. The use of residual connections further ensures stable training and facilitates deep network construction.
Figure 2 depicts the structure of dilated causal convolutions. At any given time step, the causality of these convolutions is determined solely by data from previous time steps, and information from future time steps is inaccessible. The dilatation behavior of the output is as follows: as the number of convolutional layers increases, the dilation factors grow, indicating an expanding gap between sampling points. Consequently, can capture more historical information from the input sequence through skip connections.
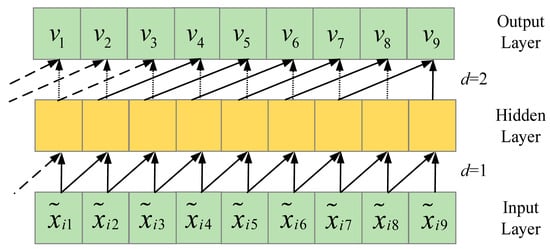
Figure 2.
The structure of dilated causal convolutions.
These dilation factors provide with a larger receptive field, allowing it to extract more input data while minimizing computational cost. In this context, the receptive field defines the range of historical input that can be effectively captured. A larger receptive field enhances the extraction of historical information, thereby improving prediction performance.
Let the input to the first residual block be . In each residual block, a dilated convolution with dilation rate and kernel size is applied. The dilation rate increases exponentially with depth, given by , where and denotes the total number of residual blocks. The dilated convolution at position computes the output as shown in Equation (3).
Within each residual block, the output is computed as Equations (4)–(6).
where is a projection of to match the dimensions of , implemented via a convolution when necessary. This is given by Equation (7).
The receptive field of the final output feature serves as a key measure of the capability of the model to capture feature interactions over distance. After layers of exponentially increasing dilation, the receptive field is as shown in Equation (8).
This ensures that each output element integrates information from a wide range of input features, thus enabling the model to learn both fine-grained and global patterns indicative of intrusion behavior.
3.3. Classification with Weighted Loss Optimization
After multi-scale feature extraction, the final output is flattened into a vector and passed through a fully connected network for classification. Let denotes the trainable parameters. The classification process is defined as shown in Equations (9) and (10).
where denotes the number of traffic classes, including normal and various attack types.
To mitigate the problem of class imbalance, a few-shot reinforcement strategy is integrated into the training process. In this strategy, class weights are introduced to increase the relative contribution of minority classes in the overall loss function, which allows the model to learn more discriminative representations for these classes. Let denote the complete set of classes, and represent the subset of minority classes. The class weights for each class c are formally defined as shown in Equation (11).
For samples, let be the logits and be the ground-truth label. The weighted cross-entropy loss is shown in Equation (12).
This corresponds to the standard log-softmax form. Using the softmax probabilities provides an interpretable probability representation, and the loss can equivalently be written as shown in Equation (13).
3.4. Implementation Workflow and Complexity Analysis
HiSeq-TCN is an efficient and scalable intrusion detection framework that integrates sequential modeling, multi-scale temporal convolution, and class imbalance–aware optimization. Given a batch of high-dimensional feature vectors, each instance is first standardized to ensure numerical stability and consistent gradient propagation. For each of the feature dimensions, the mean and standard deviation are computed across the batch, and each feature value is normalized accordingly. The normalized feature vector is then reshaped into a pseudo-temporal sequence, enabling temporal convolution to model dependencies across feature dimensions.
The core of HiSeq-TCN consists of stacked residual blocks. Each block contains two dilated causal convolutional layers with filters of kernel size , where the dilation rate increases exponentially with depth. This design allows the receptive field to grow rapidly while maintaining computational efficiency. Each convolution is followed by ReLU activation, dropout, and a Chomp operation to preserve sequence length. When the input and output dimensions differ, a convolution is used for dimension alignment before residual addition.
The final feature representation is flattened and passed through a two-layer fully connected classifier. The first layer maps a vector of length to 128 hidden units, followed by ReLU and dropout. The second layer maps the hidden units to output classes, producing class probabilities via the softmax function.
To address class imbalance, class weights are manually set using a few-shot reinforcement strategy. The normal class is assigned a weight of 1, while minority classes are given higher weights according to the experimental setup defined in Section 4.4. These weights remain fixed during training, proportionally modulating the contribution of each sample to the loss. The processing of HiSeq-TCN is illustrated in the following pseudocode in Algorithm 1.
| Algorithm 1 HiSeq-TCN Processing Procedure |
| Input: Feature matrix , labels vector of length Output: Predicted probability matrix 1: for each feature dimension to : 2: for each sample to : 3: Normalize 4: Reshape to sequence format with shape 5: Set 6: for each residual block to : 7: Set dilation 8: Apply 9: Apply 10: If input and output dimensions differ: 11: Apply Conv1D for alignment 12: Add residual connection to 13: Flatten into 14: 15: 16: Assign fixed class weights as specified in Section 4.4. 17: Compute weighted cross-entropy loss 18: |
The total number of parameters in HiSeq-TCN can be grouped into three components:
Convolutional layers: Each residual block contains two dilated Conv1D layers, each with filters of kernel size . Across , this contributes approximately parameters.
Residual projections: When dimension alignment is required, a convolution is used. Assuming it occurs in every block, this adds approximately parameters.
Fully connected layers: The first layer has parameters, and the second has parameters.
Thus, the total parameter count is given by Equation (14).
In terms of computation per forward pass:
Convolutional layers: Each Conv1D processes sequences of length , costing about operations per layer. Across all blocks, this totals approximately operations.
Fully connected layers: The first layer costs operations, and the second costs operations.
The overall forward-pass complexity per batch is shown in Equation (15).
Linear scaling with and ensures that HiSeq-TCN remains computationally efficient and suitable for real-time intrusion detection, even in high-dimensional and large-scale network environments.
4. Experiments and Results
The experiments employ the NSL-KDD dataset, an enhanced version of the KDD Cup 1999 dataset with redundant records removed. It preserves the original attack patterns while reducing duplication, resulting in a more balanced and challenging benchmark. The dataset comprises five categories: normal traffic (Normal) and four attack types—Probe, DoS, R2L, and U2R. Probe refers to reconnaissance and scanning attacks, such as port scanning. DoS represents denial-of-service attacks, for example, SYN flood. R2L corresponds to remote-to-local attacks, such as password guessing. U2R denotes user-to-root attacks, such as buffer overflow.
To further illustrate the detection capabilities of our system, Table 1 summarizes the key indicators and patterns captured for each attack type.

Table 1.
Key indicators and patterns for different attack types.
The original training and test sets were merged. The data were then split into new training and test sets using 80%:20% stratified sampling, ensuring consistent class proportions in both. Table 2 shows the sample distribution.

Table 2.
Class distribution of NSL-KDD dataset.
According to Table 2, Normal, Probe, and DoS traffic constitute the majority of the dataset, with 61,643, 42,708, and 11,261 samples in the training set, respectively, and 15,411, 10,677, and 2816 samples in the testing set. In contrast, R2L and U2R are severely underrepresented, with only 2999 and 202 samples in the training set and 750 and 50 samples in the testing set, collectively accounting for less than 2% of the total data. Such a pronounced class imbalance often results in reduced detection accuracy for the minority classes.
To comprehensively evaluate the performance of the proposed model in multi-class classification tasks, both class-wise and weighted average metrics are adopted in this study. The notations and corresponding formulas are defined as follows.
Let denote the total number of classes, and represent the class index (). The evaluation is based on the following definitions: denotes the true positives for class , denotes the false positives for class , denotes the false negatives for class , denotes the number of actual samples in class , defined as , and is the total number of samples, given by .
For each class , the basic performance metrics are defined as follows.
Precision:
Recall:
F1-Score:
To obtain the overall performance across all classes, weighted average metrics are computed, where the weight of each class corresponds to its support (i.e., the number of actual samples in that class).
Weighted Precision:
Weighted Recall:
Substituting gives the following:
This value is equivalent to the overall Accuracy.
Weighted F1-Score:
These weighted metrics provide a balanced evaluation in the presence of class imbalance, ensuring that each class contributes proportionally to the overall performance assessment.
4.1. Model and Experimental Setup
Each high-dimensional feature vector was treated as a pseudo-temporal sequence in a fixed order. This sequence was fed into the HiSeq-TCN model for feature extraction. The extraction stage uses stacked TCN residual blocks. Each block includes the following: two dilated causal convolution layers with dilation factors 1, 2, and 4; a Chomp1d operation to keep the output length consistent; ReLU activation and dropout for nonlinearity and regularization; 1 × 1 convolution and residual connection for feature fusion. The extracted features were flattened and passed through two fully connected layers to produce five class probabilities. Weighted cross-entropy loss was used. Class weights were based on sample counts and later tuned for R2L and U2R.
The HiSeq-TCN model was trained in a supervised learning manner using labeled datasets. Specifically, the NSL-KDD benchmark dataset was employed, which contains predefined labels indicating both normal and attack types of network traffic. This labeling enables the model to learn discriminative patterns between licit and illicit communications during training.
All experiments were carried out using the PyTorch framework (version 2.5.1, CUDA 11.8) on a workstation equipped with an AMD Ryzen 9 5900X 12-Core Processor CPU, 32 GB RAM, and an NVIDIA RTX 1660 GPU (6 GB VRAM). The model was trained for 70 epochs using the Adam optimizer with an initial learning rate of 0.001, which was decayed by a factor of 0.5 after 50 epochs. The batch size was set to 64, and no early-stopping strategy was applied. To ensure the reproducibility of results, a fixed random seed of 43 was used throughout all experiments, except for cases where multiple random seeds (41–45) were employed to compute the averaged results.
4.2. Performance Comparison
HiSeq-TCN was compared with SVM, DNN, and LSTM. Table 3 shows the overall accuracy and per-class accuracy on the test set. Each experiment was independently conducted five times under different random seeds (41, 42, 43, 44, and 45), while keeping all other settings identical. The average performance results across the five runs are reported in Table 3. Using results averaged over multiple random seeds helps reduce randomness and provides a more reliable evaluation of model performance.

Table 3.
Comparison of intrusion detection classification accuracy of different models.
It can be seen from Table 3 that the HiSeq-TCN model achieved an overall accuracy of 99.43% ± 0.0002, outperforming SVM, DNN, and LSTM by 1.67%, 1.03%, and 0.23%, respectively. Specifically, for the Normal class, it reached 99.55% ± 0.0009, surpassing SVM and DNN by 1.28% and 0.99%, and slightly exceeding LSTM by 0.31%. For the Probe class, the accuracy was 99.92% ± 0.0004, exceeding SVM, DNN, and LSTM by 1.74%, 0.21%, and 0.05%, respectively. In the DoS class, HiSeq-TCN achieved 99.40% ± 0.007, outperforming SVM and DNN by 1.21% and 2.06%, and slightly surpassing LSTM by 0.07%. For the R2L class, the model obtained 91.31% ± 1.36, exceeding SVM and DNN by 7.65% and 5.98%, and slightly higher than LSTM by 2.42%. In the U2R class, its accuracy reached 80.40% ± 0.64, slightly surpassing LSTM by 1.20% and significantly exceeding SVM and DNN by 10.40% and 10.80%, respectively. These results indicate that HiSeq-TCN consistently delivers strong performance across both majority and minority classes. The inclusion of standard deviations demonstrates that the model performance is stable across five independent experimental runs under different random seeds (41–45), providing a more reliable and robust evaluation.
To ensure fair comparison with prior studies, additional experiments were conducted using the official NSL-KDD dataset splits. The results of multiple intrusion detection models under this setting are provided in Appendix A.
To ensure a more comprehensive evaluation of model performance, additional indicators including Precision, Recall, and F1-Score were introduced beyond the overall accuracy, as shown in Table 4. It can be observed that the proposed HiSeq-TCN achieves superior results across all metrics, demonstrating its effectiveness and robustness in intrusion detection tasks. These complementary metrics provide a more balanced and objective view of model performance under multiple evaluation dimensions. The Precision, Recall, and F1-Score reported in this study are calculated under the weighted average scheme.

Table 4.
Comparison of multi-metric intrusion detection performance of different models.
To further evaluate the generalization ability of the proposed model on modern network intrusion scenarios, additional experiments were conducted on the Edge-IIoT dataset (2022) [36]. The comparative results are provided in Appendix B.
As illustrated in Figure 3, the radar plot confirms that HiSeq-TCN achieved consistently high and balanced performance across all classes. It demonstrated high accuracy for majority classes, including Normal, Probe, and DoS, while substantially improving detection of minority classes, such as R2L and U2R. By effectively narrowing the performance gap between common and rare attacks, HiSeq-TCN exhibits robustness in identifying both frequent and infrequent attack types. This balanced performance is consistent with its overall accuracy of 99.44%, indicating reliable detection across all categories without compromising recognition of rare attacks.
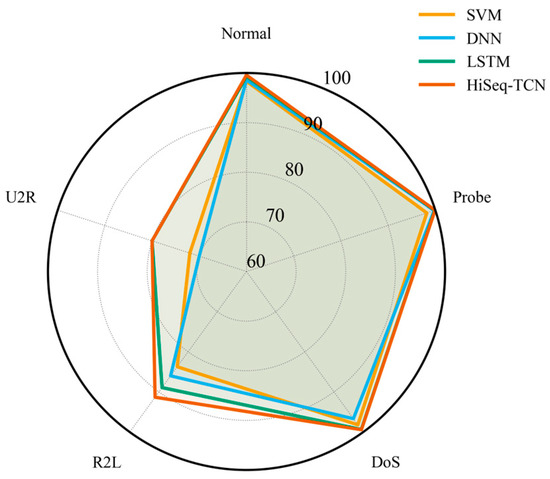
Figure 3.
Radar plot comparing multiple models.
To provide a clear comparison between the predicted and actual classes in the test set, confusion matrices for the four classification models are presented in Figure 4. Subfigures (a) through (d) correspond to the SVM, DNN, LSTM, and HiSeq-TCN models, respectively. As shown in Figure 4, HiSeq-TCN achieves the highest concentration of samples along the diagonal, reflecting more accurate predictions across all classes. In particular, the misclassification of minority classes such as R2L and U2R is markedly reduced compared with SVM and DNN, and is comparable to or better than LSTM. For majority classes including Normal, Probe, and DoS, HiSeq-TCN also maintains high precision with fewer off-diagonal errors. These results confirm that HiSeq-TCN achieves reliable detection of both frequent and infrequent attack categories while maintaining consistently high overall accuracy.
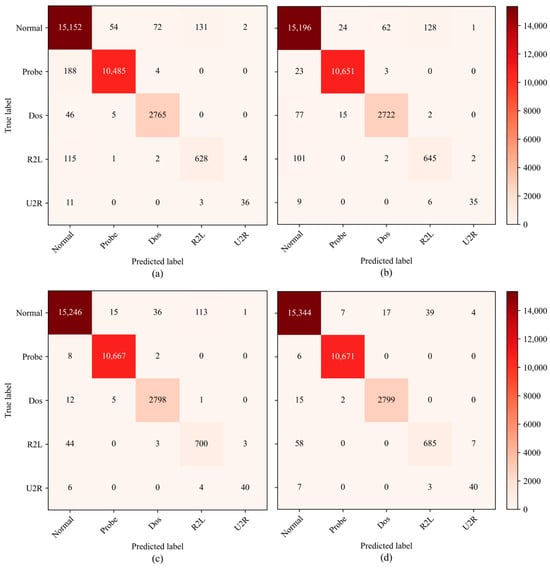
Figure 4.
Confusion matrix comparing multiple models. (a) SVM; (b) DNN; (c) LSTM; (d) HiSeq-TCN.
4.3. Structural Parameter Optimization
Different channel sizes and residual block depths were evaluated, and the results are summarized in Table 5.

Table 5.
Comparison of classification accuracy under different model parameter settings.
It can be seen from Table 5 that the three-layer network with channel dimensions of 16-32-16 achieved the highest classification accuracy of 99.44% while maintaining relatively low model complexity. In contrast, increasing the channel width to 32-32-64 or 16-32-64 slightly reduced the accuracy to 99.40% and 99.39%, respectively. Similarly, extending the architecture to four layers with a 16-32-48-64 configuration and dilation factors of 1, 2, 4, and 8 did not yield any improvement, as the accuracy remained at 99.40%. These observations indicate that the three-layer 16-32-16 configuration is sufficient to capture temporal dependencies in the data. Further increasing the network depth or channel width only adds parameters. This raises computational overhead and increases the risk of overfitting, without improving classification performance.
To ensure a fair and comprehensive evaluation, we conducted additional parameter tuning for the LSTM model. The results are shown in Appendix C. Different network configurations were tested to examine the effects of layer depth and hidden dimensions on classification accuracy. These supplementary experiments further confirm that, even after hyperparameter tuning, the performance difference between HiSeq-TCN and LSTM remains consistent, indicating the robustness and stability of the proposed HiSeq-TCN model.
4.4. Optimizing Weights for Minority Classes
Due to the limited number of samples for R2L and U2R classes, different weighting schemes were evaluated in the loss function. The weights for Normal, Probe, and DoS classes were fixed at 1, while those for R2L and U2R were gradually increased. The results are presented in Table 6.

Table 6.
Performance comparison under different weighting schemes for R2L and U2R classes.
As illustrated in Table 6, increasing the class weights from 1:1 to 1.2:2 produced moderate improvements, with R2L accuracy rising from 91.33% to 93.20% and U2R accuracy from 80.00% to 84.00%. Further adjustment to 1.5:3 yielded additional gains, as R2L increased to 94.53% and U2R improved to 86.00%. The best performance was observed at a ratio of 2:4, where R2L reached 94.93% and U2R remained at 86.00%, representing overall improvements of 3.6% and 6.0% compared with the baseline. When the weights were further increased to 2.2:4, performance declined, with R2L slightly dropping to 94.67% and U2R decreasing to 84.00%, indicating that excessive weighting may amplify noise in minority class samples. These results demonstrate that a ratio of 2:4 provides the most effective balance, significantly enhancing rare class detection without reducing the accuracy of majority classes.
To systematically assess the impact of different class-weighting schemes on the detection performance of minority attack classes, a 3D bar chart was generated, as shown in Figure 5, illustrating the classification accuracy for R2L and U2R attacks under various weight ratios. In Figure 5, the x-axis represents the R2L weight, the y-axis represents the U2R weight, and the z-axis indicates the corresponding classification accuracy (%). As shown in Figure 5, increasing the weights from 1:1 to 1.2:2 and 1.5:3 consistently improves accuracy for both attack types. The highest performance occurs at a weight ratio of 2:4, with R2L achieving 94.93% and U2R reaching 86.00%, indicating this ratio as the optimal trade-off. Further increasing the weight to 2.2:4 slightly reduces accuracy for both classes, suggesting that excessive weighting may introduce noise from minority class samples. Overall, the results demonstrate that the 2:4 weighting scheme effectively enhances detection of rare attacks without compromising the performance of majority classes.
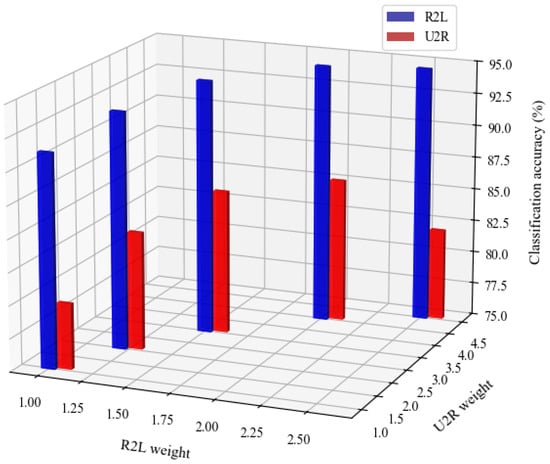
Figure 5.
Bar charts illustrating the classification accuracies of R2L and U2R under various R2L-to-U2R weight ratios.
5. Conclusions
This paper introduces HiSeq-TCN, a high-dimensional feature sequence modeling approach based on temporal convolutional networks for intrusion detection. The proposed method tackles challenges arising from the curse of dimensionality and severe class imbalance in complex network environments. By treating feature vectors as pseudo-temporal sequences and applying a class-weighted loss function, HiSeq-TCN effectively captures contextual dependencies. This approach improves detection rates for rare attack types. Experiments on the NSL-KDD dataset show that HiSeq-TCN outperforms traditional models like SVM, DNN, and LSTM. It achieves an overall accuracy of 99.44%. The model demonstrates significantly improved accuracy on the minority classes R2L and U2R, surpassing other methods by a clear margin. Structural optimization confirms that a three-layer residual block balances accuracy and complexity well. These results demonstrate that a ratio of 2:4 provides the most effective balance, significantly enhancing rare class detection without reducing the accuracy of majority classes. Hence, this configuration was regarded as the optimal setting in our study. This setting boosts minority class detection without harming performance on majority classes. Although the results are promising, this study only evaluates one dataset. The NSL-KDD dataset is comprehensive, but further tests on other datasets and real-world scenarios are needed. Future work will extend the evaluation of HiSeq-TCN to additional datasets and real network environments to validate its practical effectiveness. Efforts will also focus on real-time deployment and reducing false alarm rates to enhance the model’s robustness and reliability in real-world intrusion detection.
Author Contributions
Conceptualization, Y.P. and M.W.; methodology, Y.P. and Y.T.; software, W.G.; validation, Y.P., Y.T. and W.G.; formal analysis, Y.P.; investigation, F.L.; resources, M.W.; data curation, Y.T.; writing—original draft preparation, Y.P.; writing—review and editing, M.W. and Y.T.; visualization, W.G.; supervision, M.W.; project administration, M.W.; funding acquisition, M.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Chongqing Municipal Education Commission Scientific and Technological Research Projects including the key project KJZD-K202302401 and the youth projects KJQN202302402 and KJQN202202401.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
This work was supported by the Chongqing Key Laboratory of Public Big Data Security Technology.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A

Table A1.
Comparison of intrusion detection classification accuracy of different models on the official NSL-KDD dataset split.
Table A1.
Comparison of intrusion detection classification accuracy of different models on the official NSL-KDD dataset split.
| Models | Total Accuracy | Normal | Probe | Dos | R2L | U2R |
|---|---|---|---|---|---|---|
| SVM | 72.35 ± 1.68 | 92.75 ± 3.12 | 61.75 ± 6.36 | 63.68 ± 6.71 | 5.34 ± 6.43 | 2.20 ± 7.26 |
| DNN | 75.86 ± 1.34 | 93.56 ± 2.88 | 71.34 ± 5.78 | 64.58 ± 5.14 | 7.43 ± 3.68 | 3.50 ± 6.35 |
| LSTM | 77.02 ± 1.19 | 94.36 ± 2.23 | 81.87 ± 4.09 | 66.23 ± 4.58 | 15.31 ± 1.89 | 6.5 ± 4.35 |
| HiSeq-TCN | 79.03 ± 0.31 | 94.74 ± 1.92 | 84.51 ± 3.38 | 66.52 ± 3.47 | 18.41 ± 0.19 | 7.7 ± 2.56 |
Appendix B

Table A2.
Comparison of intrusion detection classification accuracy of different models on the Edge-IIoT dataset (2022).
Table A2.
Comparison of intrusion detection classification accuracy of different models on the Edge-IIoT dataset (2022).
| Models | Total Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| SVM | 92.56 ± 0.46 | 92.24 ± 1.02 | 92.56 ± 0.46 | 91.91 ± 0.85 |
| DNN | 92.89 ± 0.25 | 92.33 ± 0.96 | 92.89 ± 0.25 | 91.93 ± 0.54 |
| LSTM | 93.64 ± 0.03 | 93.46 ± 0.18 | 93.64 ± 0.03 | 92.74 ± 0.14 |
| HiSeq-TCN | 94.94 ± 5 × 10−4 | 95.78 ± 0.19 | 94.94 ± 5 × 10−4 | 94.60 ± 0.02 |
Appendix C

Table A3.
Classification accuracy of the LSTM model under different parameter settings.
Table A3.
Classification accuracy of the LSTM model under different parameter settings.
| Network Architecture | Number of Layers | Classification Accuracy |
|---|---|---|
| 32-32-64 | 3 | 99.11 |
| 16-32-64 | 3 | 99.15 |
| 16-32-16 | 3 | 99.21 |
| 16-32-48-64 | 4 | 99.12 |
References
- Liao, H.J.; Lin, C.H.R.; Lin, Y.C.; Tung, K.Y. Intrusion detection system: A comprehensive review. J. Netw. Comput. Appl. 2013, 36, 16–24. [Google Scholar] [CrossRef]
- Humayed, A.; Lin, J.; Li, F.; Luo, B. Cyber-physical systems security—A survey. IEEE Internet Things J. 2017, 4, 1802–1831. [Google Scholar] [CrossRef]
- Redino, C.; Nandakumar, D.; Schiller, R.; Choi, K.; Rahman, A.; Bowen, A.; Weeks, M.; Shaha, A.; Nehila, J. Zero day threat detection using graph and flow based security telemetry. In Proceedings of the 2022 International Conference on Computing, Communication, and Intelligent Systems (ICCCIS), Greater Noida, India, 4–5 November 2022; pp. 655–662. [Google Scholar]
- A Distribution of Exploits Used in Attacks by Type of Application Attacked, May 2020. 2024. Available online: https://securelist.com/kaspersky-security-bulletin-2020-2021-eu-statistics/102335/#vulnerable-applications-used-by-cybercriminals (accessed on 19 October 2025).
- Diana, L.; Dini, P.; Paolini, D. Overview on intrusion detection systems for computers networking security. Computers 2025, 14, 87. [Google Scholar] [CrossRef]
- Vasilomanolakis, E.; Karuppayah, S.; Mühlhäuser, M.; Fischer, M. Taxonomy and survey of collaborative intrusion detection. ACM Comput. Surv. 2015, 47, 1–33. [Google Scholar] [CrossRef]
- Maseer, Z.K.; Kadhim, Q.K.; Al-Bander, B.; Yusof, R.; Saif, A. Meta-analysis and systematic review for anomaly network intrusion detection systems: Detection methods, dataset, validation methodology, and challenges. IET Netw. 2024, 13, 339–376. [Google Scholar] [CrossRef]
- Ravindran, V.K.; Ojha, S.S.; Kamboj, A. A comparative analysis of signature-based and anomaly-based intrusion detection systems. Int. J. Latest Technol. Eng. Manag. Appl. Sci. 2025, 14, 209–214. [Google Scholar] [CrossRef]
- Park, H.; Shin, D.; Park, C.; Jang, J.; Shin, D. Unsupervised machine learning methods for anomaly detection in network packets. Electronics 2025, 14, 2779. [Google Scholar] [CrossRef]
- Almseidin, M.; Al-Sawwa, J.; Alkasassbeh, M. Anomaly-based intrusion detection system using fuzzy logic. In Proceedings of the 2021 International Conference on Information Technology (ICIT), Amman, Jordan, 14–15 July 2021; pp. 290–295. [Google Scholar]
- Dardouri, S.; Almuhanna, R. A deep learning/machine learning approach for anomaly based network intrusion detection. Front. Artif. Intell. 2025, 8, 1625891. [Google Scholar] [CrossRef]
- Schummer, P.; Del Rio, A.; Serrano, J.; Jimenez, D.; Sánchez, G.; Sánchez, Á. Machine learning-based network anomaly detection: Design, implementation, and evaluation. AI 2024, 5, 2967–2983. [Google Scholar] [CrossRef]
- Atassi, R. Anomaly detection in IoT networks: Machine learning approaches for intrusion detection. Fusion Pract. Appl. 2023, 13, 126–134. [Google Scholar] [CrossRef]
- Belavagi, M.C.; Muniyal, B. Performance evaluation of supervised machine learning algorithms for intrusion detection. Procedia Comput. Sci. 2016, 89, 117–123. [Google Scholar] [CrossRef]
- Abuali, K.M.; Nissirat, L.; Al-Samawi, A. Advancing network security with AI: SVM-based deep learning for intrusion detection. Sensors 2023, 23, 8959. [Google Scholar] [CrossRef]
- Moharam, M.H.; Hany, O.; Hany, A.; Mahmoud, A.; Mohamed, M.; Saeed, S. Anomaly detection using machine learning and adopted digital twin concepts in radio environments. Sci. Rep. 2025, 15, 18352. [Google Scholar] [CrossRef]
- Al-Ajlan, M.; Ykhlef, M. GAN-AHR: A GAN-based adaptive hybrid resampling algorithm for imbalanced intrusion detection. Electronics 2025, 14, 3476. [Google Scholar] [CrossRef]
- Wu, Y.; Zou, B.; Cao, Y. Current status and challenges and future trends of deep learning-based intrusion detection models. J. Imaging 2024, 10, 254. [Google Scholar] [CrossRef]
- Ye, X.; Cui, H.; Luo, F.; Wang, J.; Xiong, X.; Zhang, W.; Yu, J.; Zhao, W. Daily insider threat detection with hybrid TCN transformer architecture. Sci. Rep. 2025, 15, 28590. [Google Scholar] [CrossRef]
- Tseng, S.M.; Wang, Y.Q.; Wang, Y.C. Multi-class intrusion detection based on transformer for IoT networks using CIC-IoT-2023 dataset. Future Internet 2024, 16, 284. [Google Scholar] [CrossRef]
- He, Z.; Wang, X.; Li, C. A Time series intrusion detection method based on SSAE, TCN and Bi-LSTM. Comput. Mater. Contin. 2024, 78, 845–871. [Google Scholar] [CrossRef]
- Liao, Y.; Vemuri, V.R. Use of k-nearest neighbor classifier for intrusion detection. Comput. Secur. 2002, 21, 439–448. [Google Scholar] [CrossRef]
- Li, W.; Yi, P.; Wu, Y.; Pan, L.; Li, J. A new intrusion detection system based on KNN classification algorithm in wireless sensor network. J. Electr. Comput. Eng. 2014, 2014, 240217. [Google Scholar] [CrossRef]
- Kabir, M.R.; Onik, A.R.; Samad, T. A network intrusion detection framework based on Bayesian network using wrapper approach. Int. J. Comput. Appl. 2017, 166, 13–17. [Google Scholar] [CrossRef]
- Mukkamala, S.; Janoski, G.; Sung, A. Intrusion detection using neural networks and support vector machines. In Proceedings of the 2002 International Joint Conference on Neural Networks, Honolulu, HI, USA, 12–17 May 2002; pp. 1702–1707. [Google Scholar]
- Bhati, B.S.; Rai, C.S. Analysis of support vector machine-based intrusion detection techniques. Arab. J. Sci. Eng. 2020, 45, 2371–2383. [Google Scholar] [CrossRef]
- Farnaaz, N.; Jabbar, M.A. Random forest modeling for network intrusion detection system. Procedia Comput. Sci. 2016, 89, 213–217. [Google Scholar] [CrossRef]
- Rai, K.; Devi, M.S.; Guleria, A. Decision tree based algorithm for intrusion detection. Int. J. Adv. Netw. Appl. 2016, 7, 2828. [Google Scholar]
- Chen, H.; Wang, Z.; Yang, S.; Luo, X.; He, D.; Chan, S. Intrusion detection using synaptic intelligent convolutional neural networks for dynamic internet of things environments. Alex. Eng. J. 2025, 111, 78–91. [Google Scholar] [CrossRef]
- Osa, E.; Orukpe, P.E.; Iruansi, U. Design and implementation of a deep neural network approach for intrusion detection systems. Adv. Electr. Eng. Electron. Energy 2024, 7, 100434. [Google Scholar] [CrossRef]
- Adetunji, O.J.; Ibitoye, O.T. Development of an intrusion detection model using long short term memory algorithm. In Proceedings of the IEEE 5th International Conference on Electro-Computing Technologies for Humanity (NIGERCON), Ado Ekiti, Nigeria, 26–28 November 2024; pp. 1–5. [Google Scholar]
- Jony, A.I.; Arnob, A.K.B. A long short-term memory based approach for detecting cyber attacks in IoT using CIC-IoT2023 dataset. J. Edge Comput. 2024, 3, 28–42. [Google Scholar] [CrossRef]
- Manocchio, L.D.; Layeghy, S.; Lo, W.W.; Kulatilleke, G.K.; Sarhan, M.; Portmann, M. Flowtransformer: A transformer framework for flow-based network intrusion detection systems. Expert Syst. Appl. 2024, 241, 122564. [Google Scholar] [CrossRef]
- Mei, Y.; Han, W.; Lin, K. Intrusion detection for intelligent connected vehicles based on bidirectional temporal convolutional network. IEEE Netw. 2024, 38, 113–119. [Google Scholar] [CrossRef]
- Miryahyaei, M.; Fartash, M.; Akbari Torkestani, J. Focal causal temporal convolutional neural networks: Advancing IIoT security with efficient detection of rare cyber-attacks. Sensors 2024, 24, 6335. [Google Scholar] [CrossRef]
- Ferrag, M.A.; Friha, O.; Hamouda, D.; Maglaras, L.; Janicke, H. Edge-IIoTset: A new comprehensive realistic cyber security dataset of IoT and IIoT applications for centralized and federated learning. IEEE Access 2022, 10, 40281–40306. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).