Acoustic Emission from GaN-on-Sapphire Structures
Abstract
1. Introduction
2. Materials and Methods
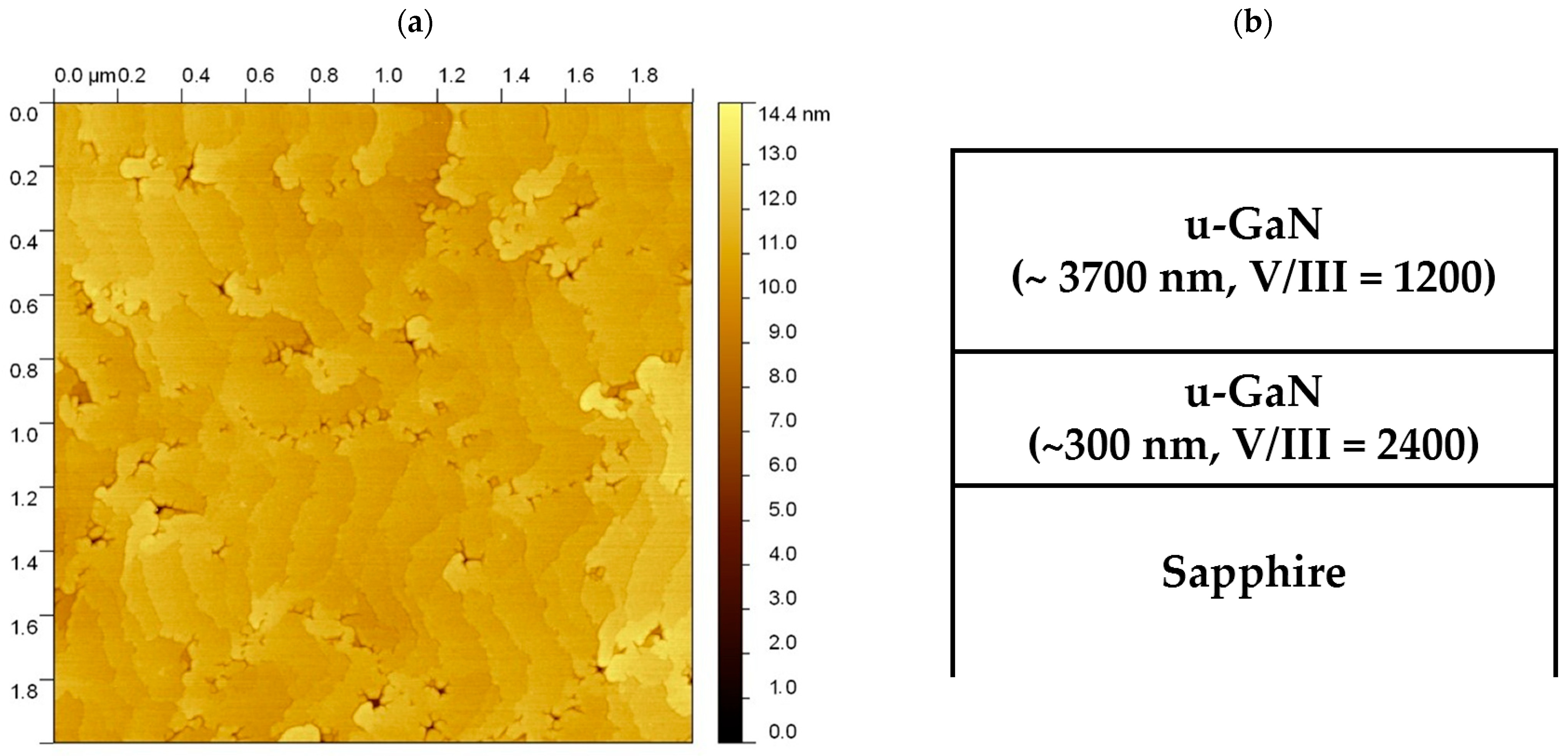
2.1. Test Structures
2.2. Measurements
3. Results
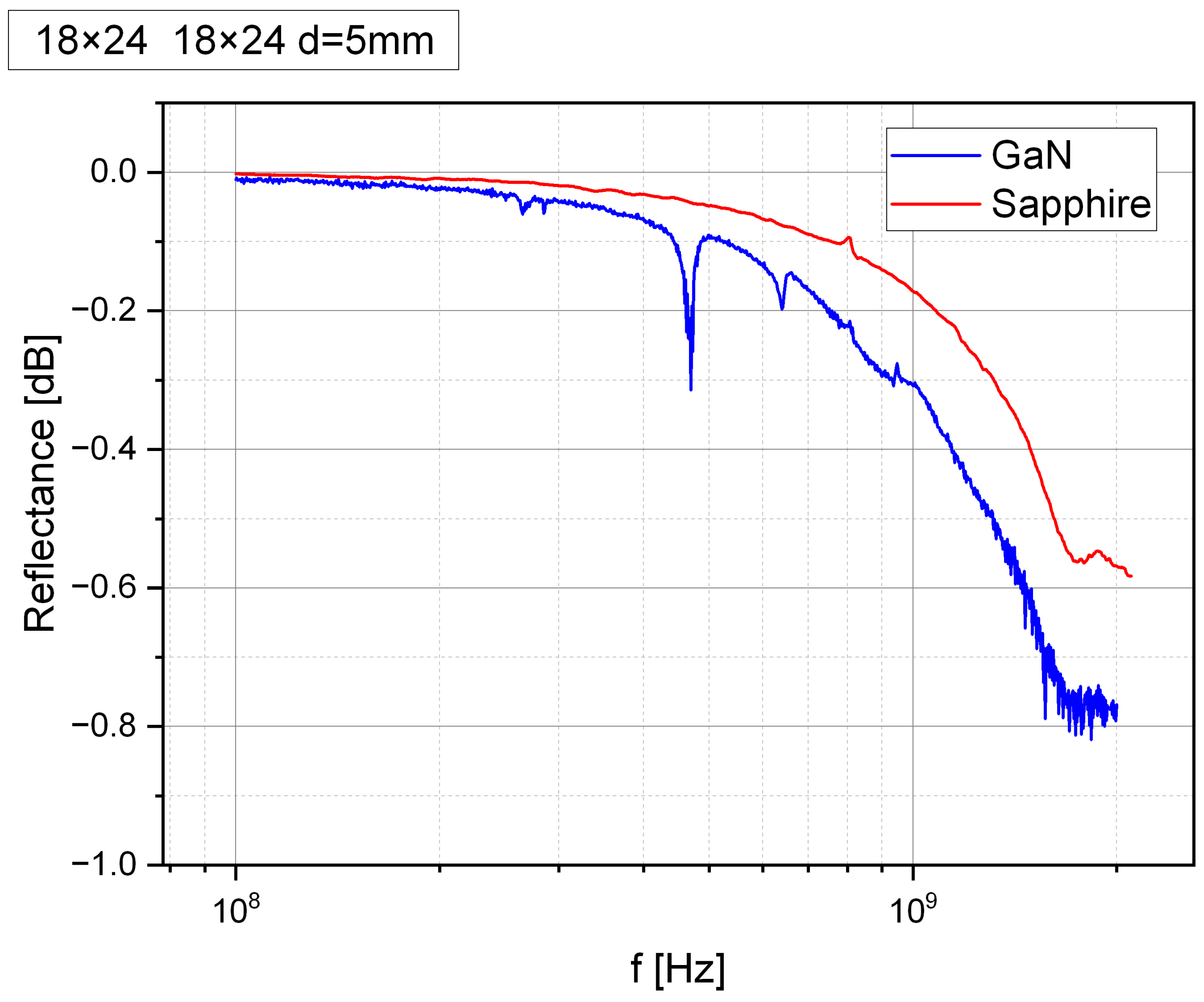
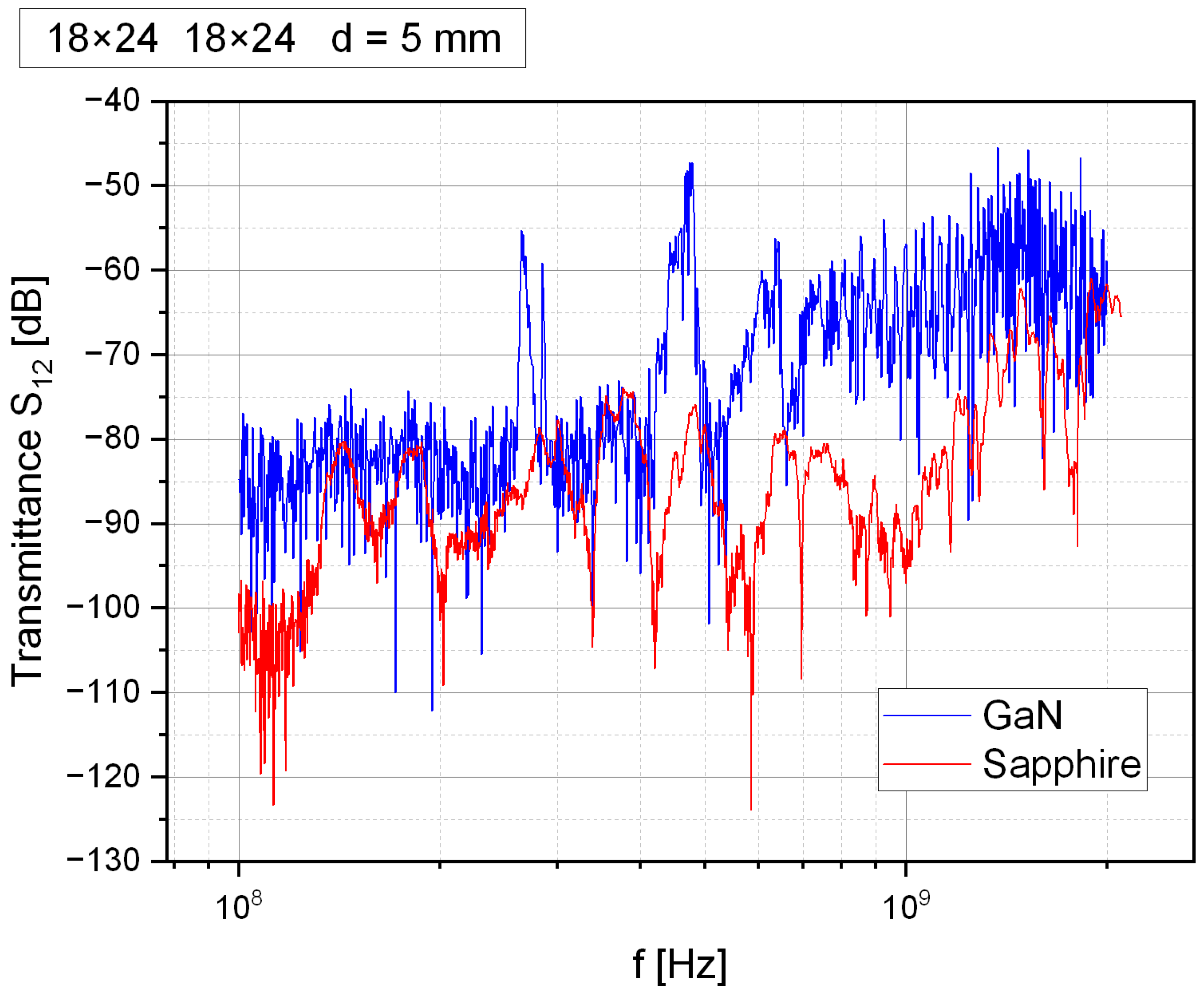
3.1. Identification of Acoustic Modes
3.2. Analysis of Resonance, Antiresonance, and Electromechanical Coupling
3.3. Electrode Loading Analysis
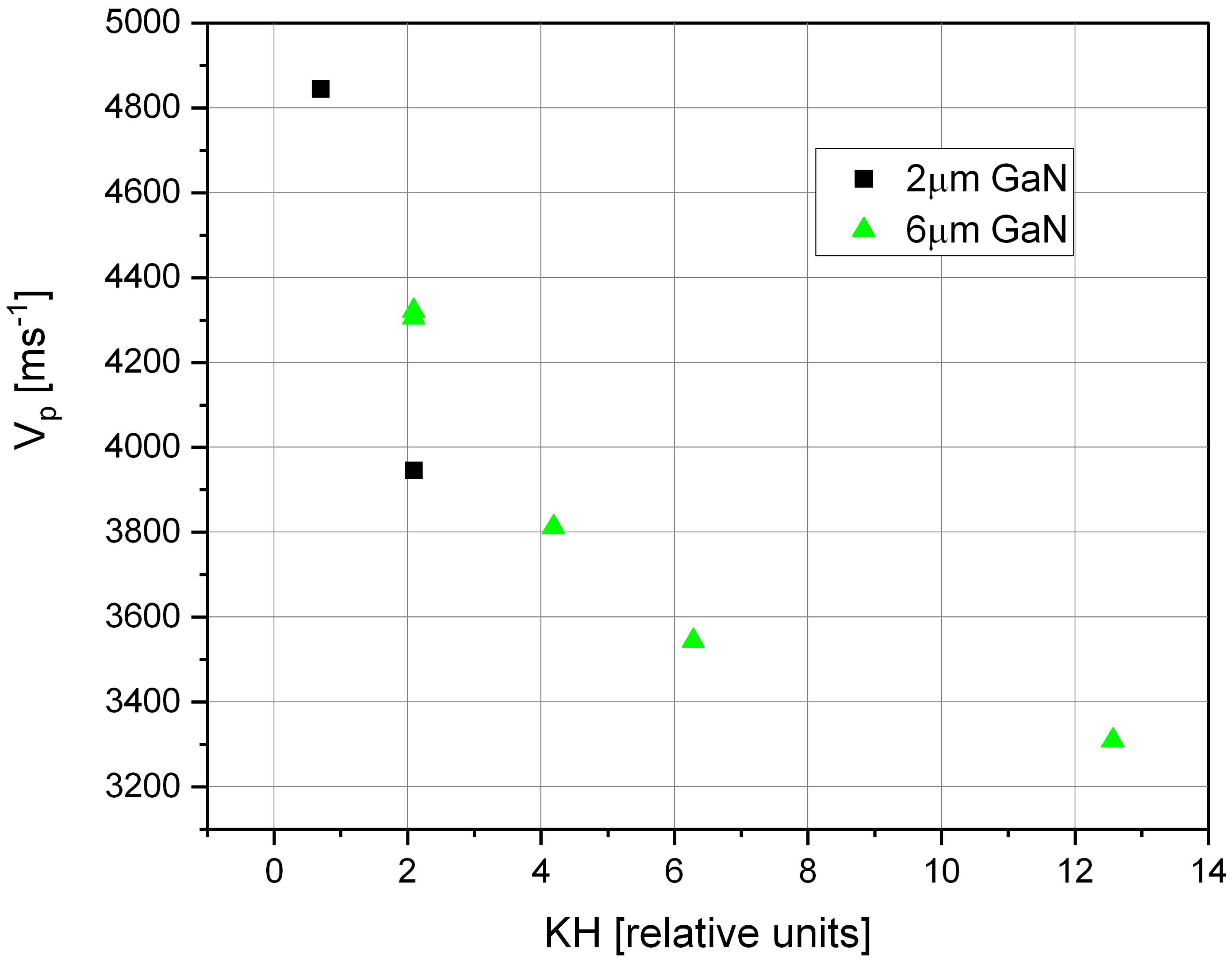
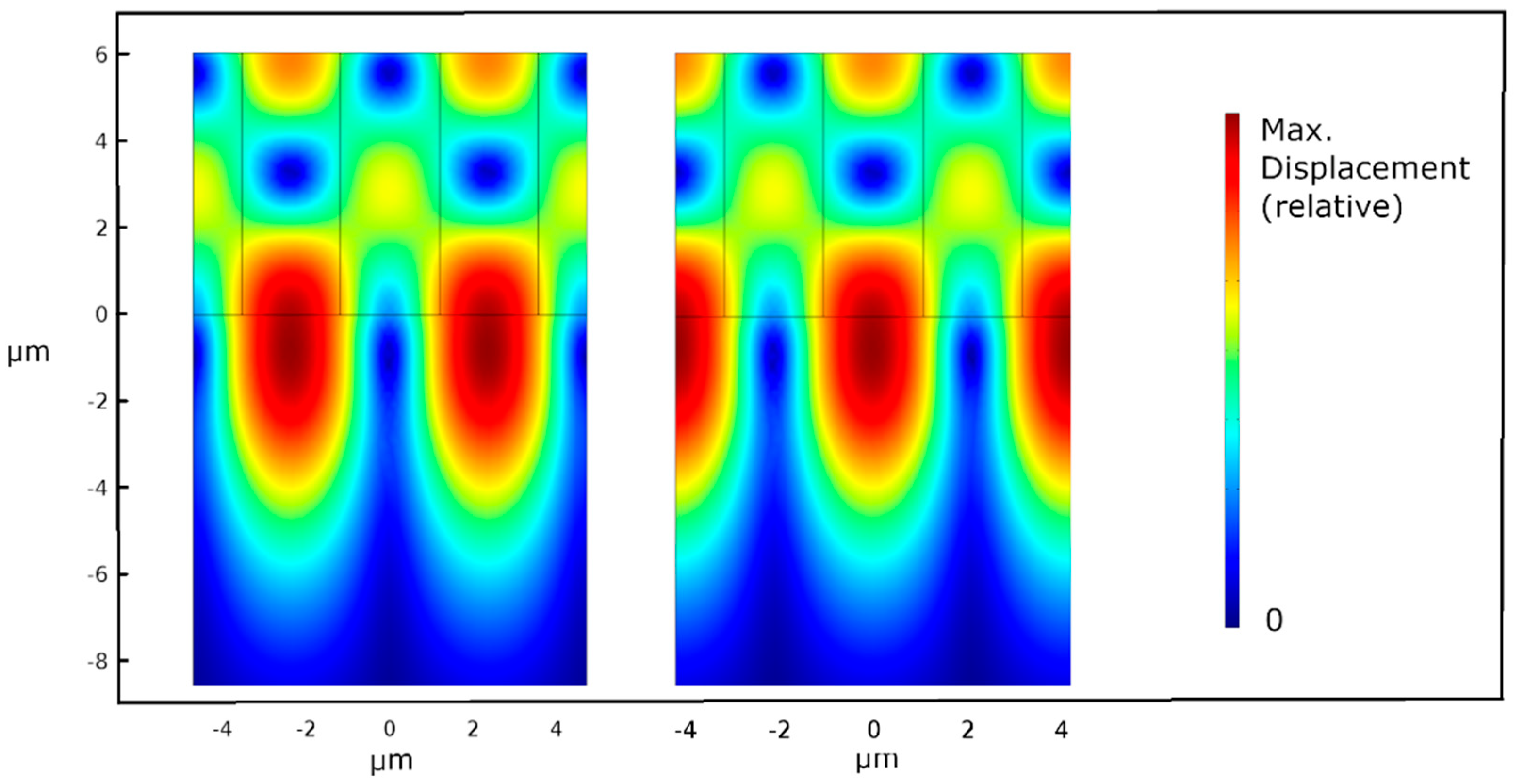
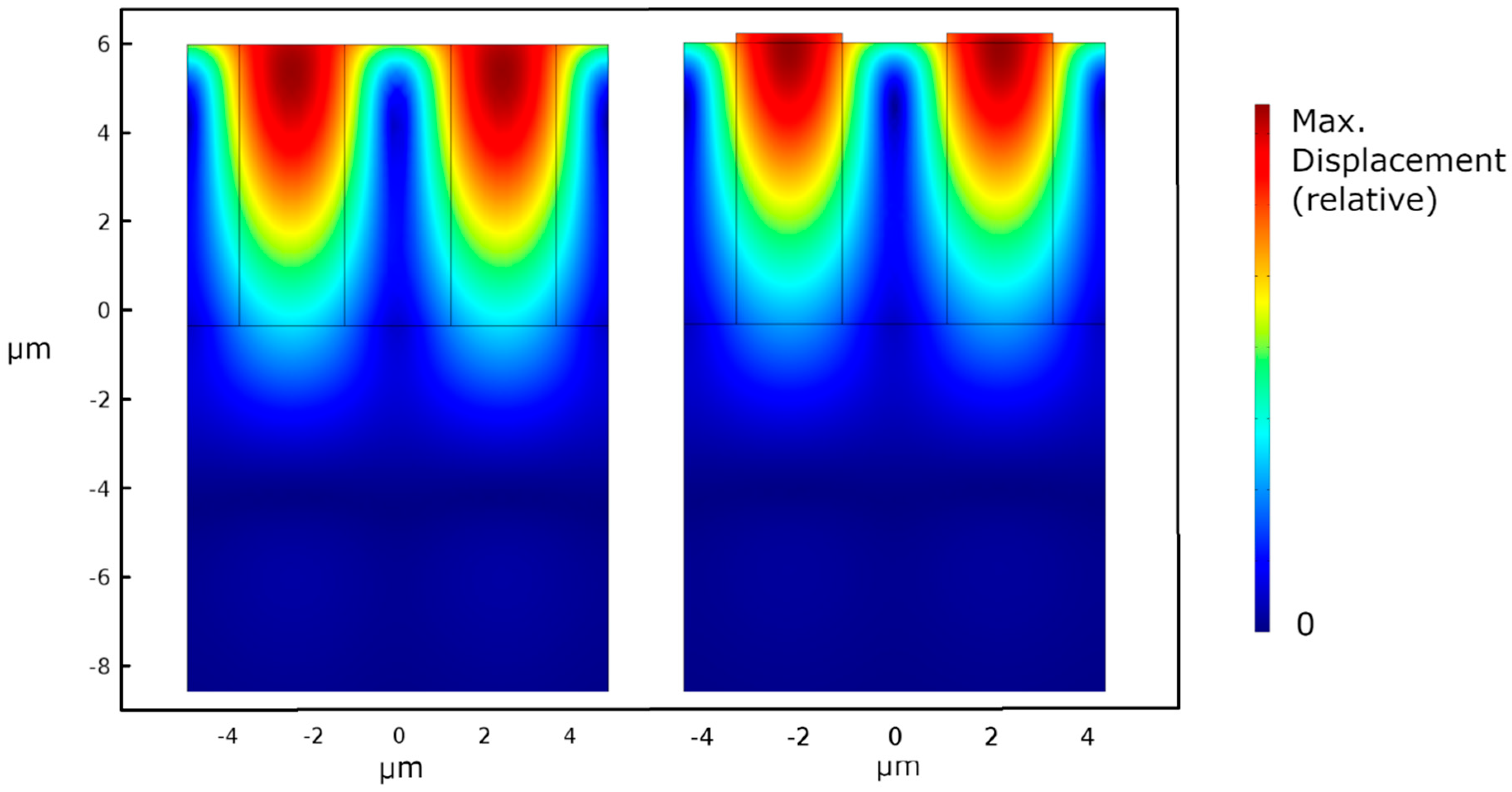
3.4. Energy Confinement Analysis
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wośko, M. Optimisation of LT-GaN nucleation layer growth conditions for the improvement of electrical and optical parameters of GaN layers. Opt. Appl. 2019, 49, 167–176. [Google Scholar] [CrossRef]
- Macherzynski, W.; Gryglewicz, J.; Stafiniak, A.; Prazmowska, J.; Paszkiewicz, R. Formation process and properties of ohmic contacts containing molybdenum to AlGaN/GaN heterostructures. Adv. Electr. Electron. Eng. 2016, 14, 83–88. [Google Scholar] [CrossRef]
- Macherzyński, W.; Stafiniak, A.; Paszkiewicz, B.; Gryglewicz, J.; Paszkiewicz, R. Microanalysis of the Ti/Al and Ti/Al/Mo/Au ohmic contacts metallization to AlGaN/GaN heterostructures. Phys. Status Solidi (A) Appl. Mater. Sci. 2016, 213, 1145–1149. [Google Scholar] [CrossRef]
- COMSOL AB. COMSOL Multiphysics®, Version 4.3; COMSOL AB: Stockholm, Sweden, 2025.
- Rais-Zadeh, M.; Gokhale, V.J.; Ansari, A.; Faucher, M.; Theron, D.; Cordier, Y.; Buchaillot, L. Gallium nitride as an electromechanical material. J. Microelectromechan. Syst. 2014, 23, 1252–1271. [Google Scholar] [CrossRef]
- Bernstein, B.T. Elastic constants of synthetic sapphire at 27 °C. J. Appl. Phys. 1963, 34, 169–172. [Google Scholar] [CrossRef]
- Bernardini, F.; Fiorentini, V. First-principles calculation of the piezoelectric tensor d of III–V nitrides. Appl. Phys. Lett. 2002, 80, 4145–4147. [Google Scholar] [CrossRef]
- Almirall, A.; Oliveri, S.; Daniau, W.; Margueron, S.; Baron, T.; Boulet, P.; Ballandras, S.; Chamaly, S.; Bartasyte, A. High-frequency surface acoustic wave devices based on epitaxial Z-LiNbO3 layers on sapphire. Appl. Phys. Lett. 2019, 114, 162905. [Google Scholar] [CrossRef]
- Pedrós, J.; Calle, F.; Grajal, J.; Riobóo, R.J.J.; Takagaki, Y.; Ploog, K.H.; Bougrioua, Z. Anisotropy-induced polarization mixture of surface acoustic waves in GaN/c-sapphire heterostructures. Phys. Rev. B 2005, 72, 75306. [Google Scholar] [CrossRef]
- Mueller, A.; Giangu, I.; Stavrinidis, A.; Stefanescu, A.; Stavrinidis, G.; Dinescu, A.; Konstantinidis, G. Sezawa propagation mode in GaN on Si surface acoustic wave type temperature sensor structures operating at GHz frequencies. IEEE Electron. Device Lett. 2015, 36, 1299–1302. [Google Scholar] [CrossRef]
- Fu, Y.Q.; Luo, J.; Nguyen, N.; Walton, A.; Flewitt, A.; Zu, X.; Li, Y.; McHale, G.; Matthews, A.; Iborra, E.; et al. Advances in piezoelectric thin films for acoustic biosensors, acoustofluidics and lab-on-chip applications. Prog. Mater. Sci. 2017, 89, 31–91. [Google Scholar] [CrossRef]
- Farnell, G.W.; Adler, E.L. Elastic wave propagation in thin layers. Phys. Acoust. 2012, 9, 35–127. [Google Scholar] [CrossRef]
- Jaafar, M.M.; Wee, M.F.M.R.; Nguyen, H.-T.; Hieu, L.T.; Rai, R.; Sahoo, A.K.; Dee, C.F.; Chang, E.Y.; Majlis, B.Y.; Tee, C.A.T. Surface Acoustic Wave Propagation of GaN/Sapphire Integrated with a Gold Guiding Layer. Sensors 2023, 23, 2464. [Google Scholar] [CrossRef] [PubMed]
- Jaafar, M.M.; Mohd Razip Wee, M.F.; Dee, C.F.; Chang, E.Y.; Majlis, B.Y. Sezawa Guided Mode on Periodic Grooves of GaN/Sapphire Substrate. Electron. Mater. Lett. 2022, 18, 415–421. [Google Scholar] [CrossRef]
- Caliendo, C.; Benetti, M.; Cannatà, D.; Laidoudi, F.; Petrone, G. Experimental and Theoretical Analysis of Rayleigh and Leaky-Sezawa Waves Propagating in ZnO/Fused Silica Substrates. Micromachines 2024, 15, 974. [Google Scholar] [CrossRef] [PubMed]
- Gaso Rocha, M.I.; Jimenez, Y.; Laurent, F.A.; Arnau, A. Love Wave Biosensors: A Review. In State of the Art in Biosensors—General Aspects; IntechOpen: London, UK, 2013. [Google Scholar] [CrossRef]
- Caliendo, C.; Sait, S.; Boubenider, F. Love-mode MEMS devices for sensing applications in liquids. Micromachines 2016, 7, 15. [Google Scholar] [CrossRef]
- Liu, B.; Chen, X.; Cai, H.; Ali, M.M.; Tian, X.; Tao, L.; Yang, Y.; Ren, T. Surface acoustic wave devices for sensor applications. J. Semicond. 2016, 37, 021001. [Google Scholar] [CrossRef]
- Auld, B.A.; Green, R.E. Acoustic Fields and Waves in Solids: Two Volumes. Phys. Today 1974, 27, 63–64. [Google Scholar] [CrossRef]
- Paszkiewicz, B.K.; Gierz, L. Pseudo-bulk SAW transducers fabricated in GaN epitaxial layers grown on sapphire substrate. In Journal of Physics: Conference Series; IOP Publishing: Bristol, England, 2021. [Google Scholar] [CrossRef]
- Bu, G.; Ciplys, D.; Shur, M.; Schowalter, L.J.; Schujman, S.; Gaska, R. Electromechanical coupling coefficient for surface acoustic waves in single-crystal bulk aluminum nitride. Appl. Phys. Lett. 2004, 84, 4611–4613. [Google Scholar] [CrossRef]
- Woods, R.C.; Boroumand, F.A. Comments on ‘Epitaxially grown GaN thin-film SAW filter with high velocity and low insertion loss’. IEEE Trans. Electron. Devices 2006, 53, 173–176. [Google Scholar] [CrossRef]
- Neighbours, J.R.; Alers, G.A. “Elastic constants of silver and gold. Phys. Rev. 1958, 111, 707–712. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Yang, Z.; Xia, H.; Zhang, C.; Wei, X. Surface acoustic wave based microfluidic devices for biological applications. Sensors Diagn. 2023, 2, 507–528. [Google Scholar] [CrossRef]

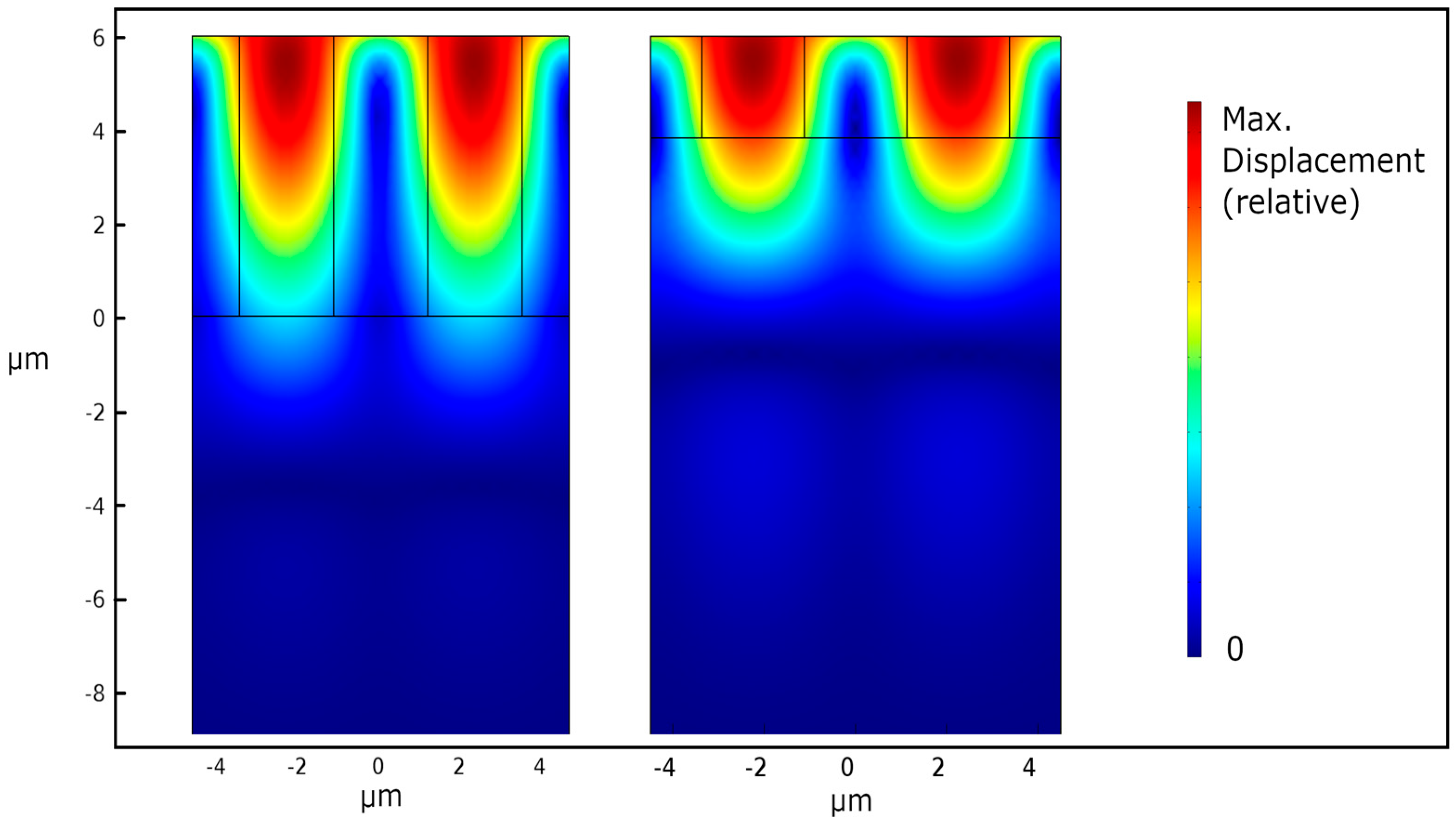
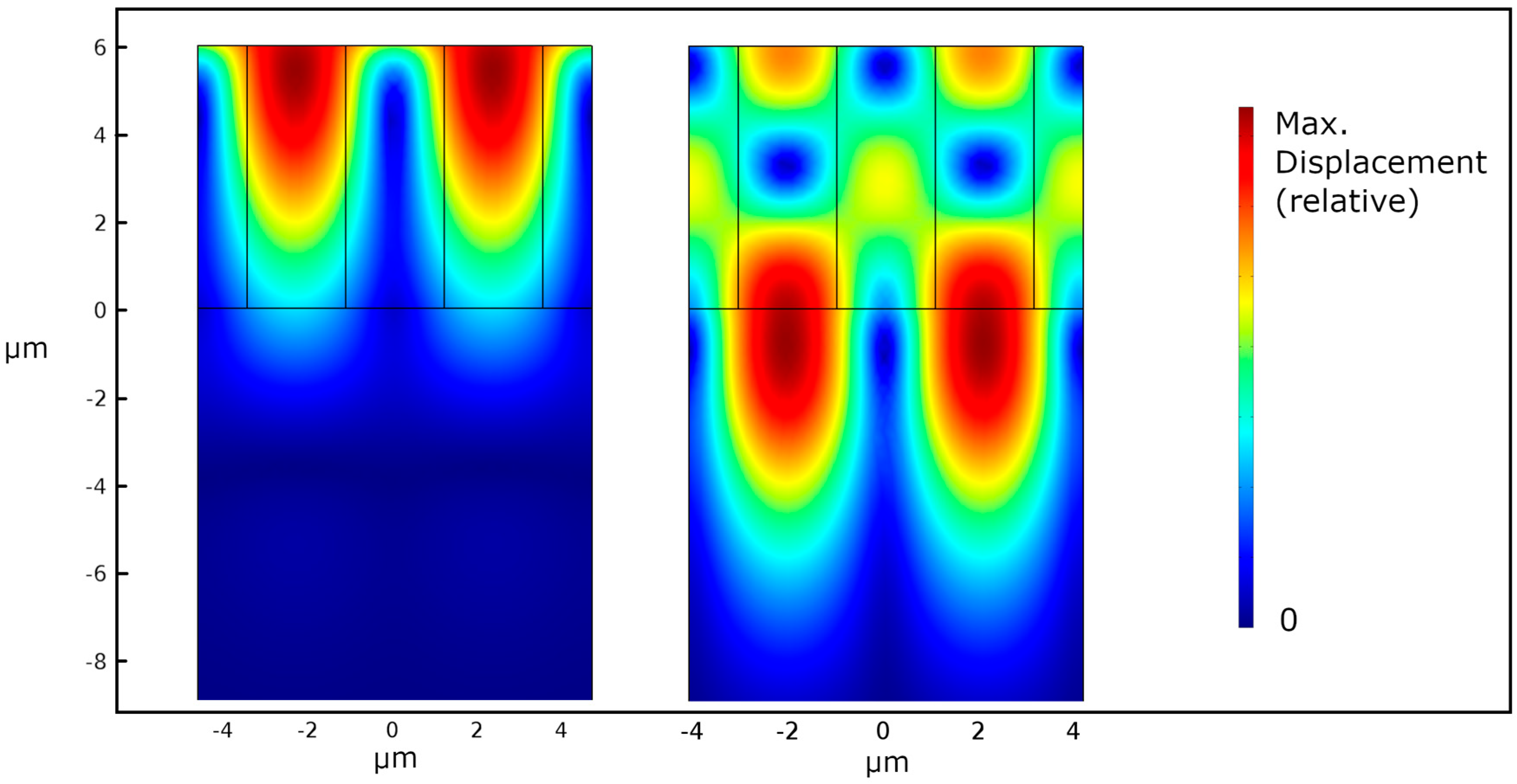
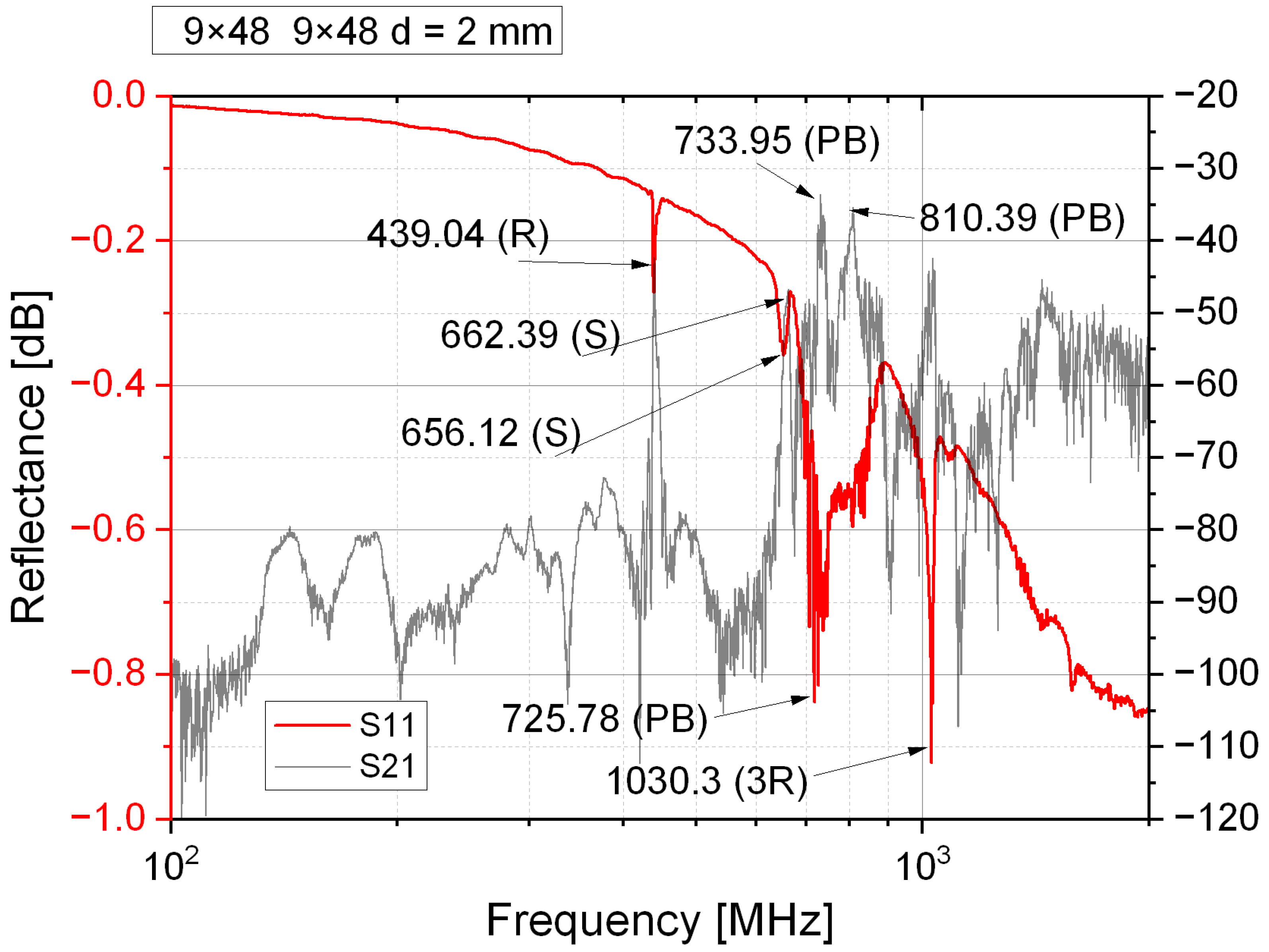
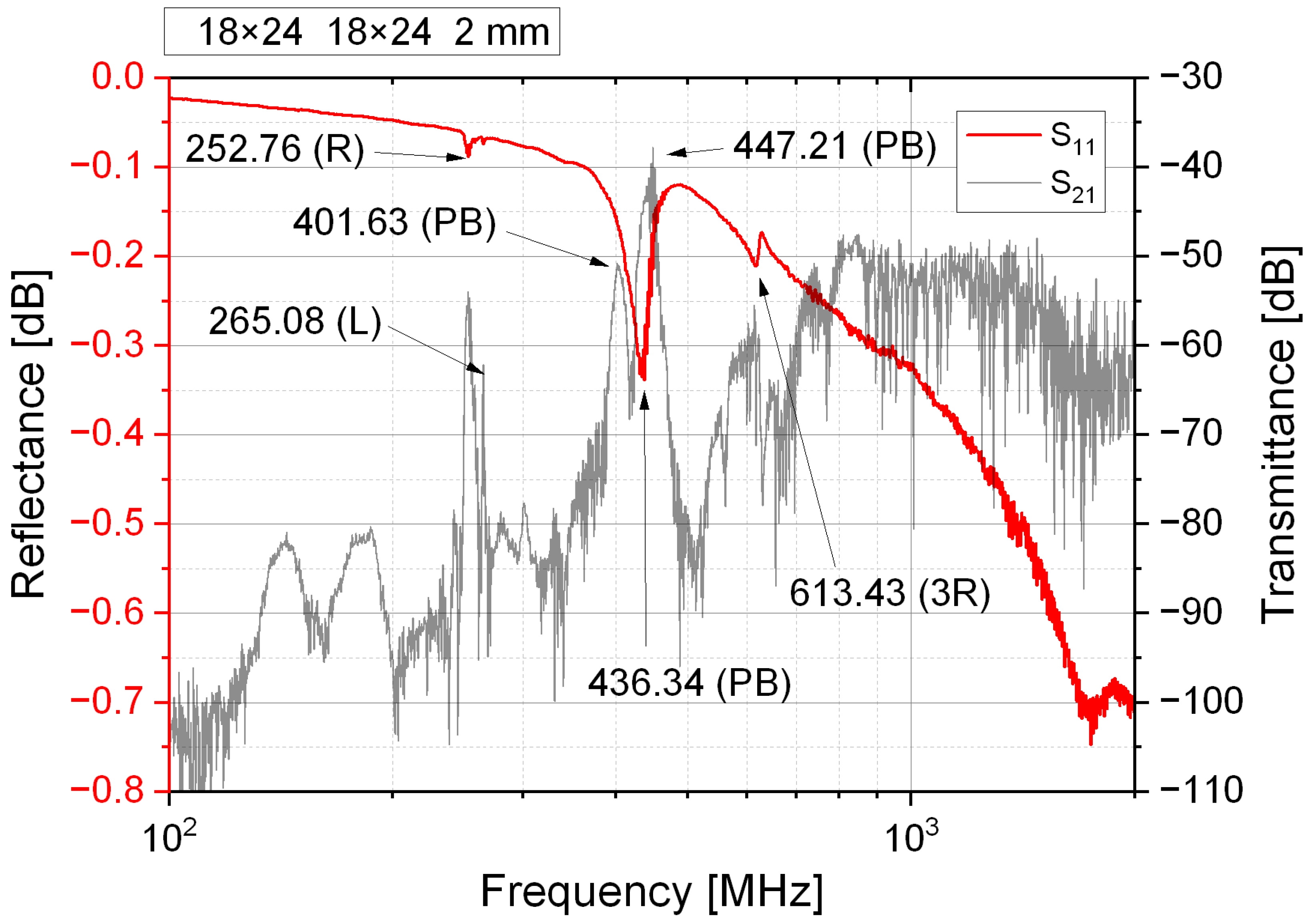


| Configuration | λ [μm] | Repetition Number |
|---|---|---|
| 01 | 18 | 24 |
| 01 | 18 | 12 |
| 01 | 9 | 48 |
| 0011 | 18 | 24 |
| Parameter | Tensor Element | Value |
|---|---|---|
| Stiffness, cij, [GPa] | c11 | 390 |
| c33 | 398 | |
| c44 | 105 | |
| c12 | 145 | |
| c13 | 106 | |
| Piezoelectric coefficient, eij, [Cm−2] | e16 | −0.3 |
| e31 | −0.289 | |
| e33 | 0.464 | |
| Relative permittivity | ϵr | 8.9 |
| Parameter | Tensor Element | Value |
|---|---|---|
| Stiffness, cij, [GPa] | c11 | 490 |
| c33 | 492 | |
| c44 | 146 | |
| c13 | 114 | |
| c14 | −23 | |
| Relative permittivity | ϵr | 9.4 |
| Mode | KH | k2 |
|---|---|---|
| Rayliegh | 1.4 | 0.096% |
| Rayliegh | 4.2 | 0.098% |
| Sezawa | 4.2 | 0.048% |
| Mode | KH | Max. Displacement [nm] | n [%] |
|---|---|---|---|
| Rayliegh | 1.4 | 7.6 | 60.2 |
| Rayliegh | 4.2 | 2.1 | 96.6 |
| Sezawa | 4.2 | 3.2 | 38.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paszkiewicz, B.K.; Paszkiewicz, B.; Dziedzic, A. Acoustic Emission from GaN-on-Sapphire Structures. Electronics 2025, 14, 4146. https://doi.org/10.3390/electronics14214146
Paszkiewicz BK, Paszkiewicz B, Dziedzic A. Acoustic Emission from GaN-on-Sapphire Structures. Electronics. 2025; 14(21):4146. https://doi.org/10.3390/electronics14214146
Chicago/Turabian StylePaszkiewicz, Bartlomiej K., Bogdan Paszkiewicz, and Andrzej Dziedzic. 2025. "Acoustic Emission from GaN-on-Sapphire Structures" Electronics 14, no. 21: 4146. https://doi.org/10.3390/electronics14214146
APA StylePaszkiewicz, B. K., Paszkiewicz, B., & Dziedzic, A. (2025). Acoustic Emission from GaN-on-Sapphire Structures. Electronics, 14(21), 4146. https://doi.org/10.3390/electronics14214146







