A Hybrid Frequency Decomposition–CNN–Transformer Model for Predicting Dynamic Cryptocurrency Correlations
Abstract
1. Introduction
2. Literature Review
2.1. Multivariate Time Series Forecasting
2.2. Transformer Models
2.3. Hybrid Models
3. Data Description
4. Methods
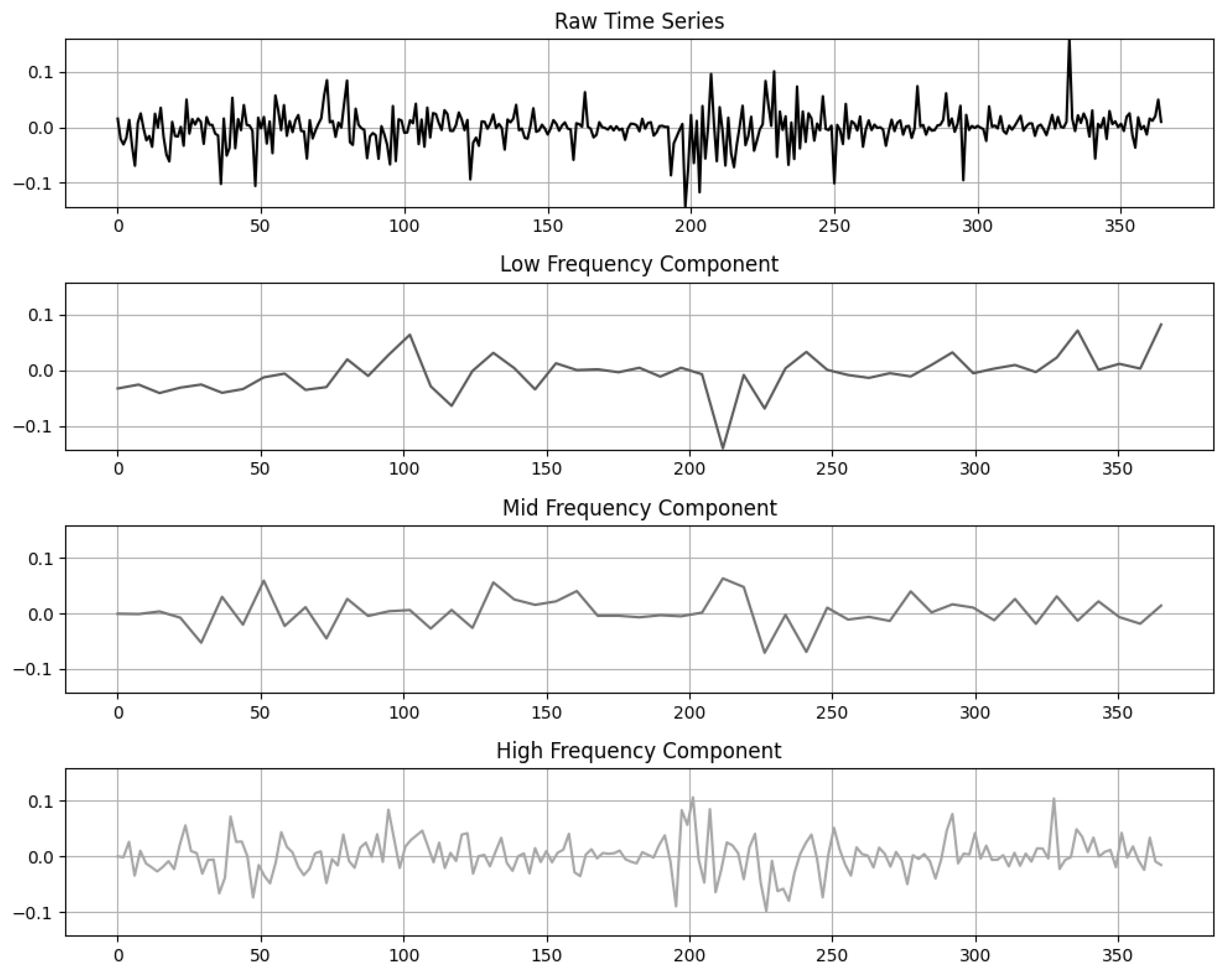
4.1. Frequency Decomposition
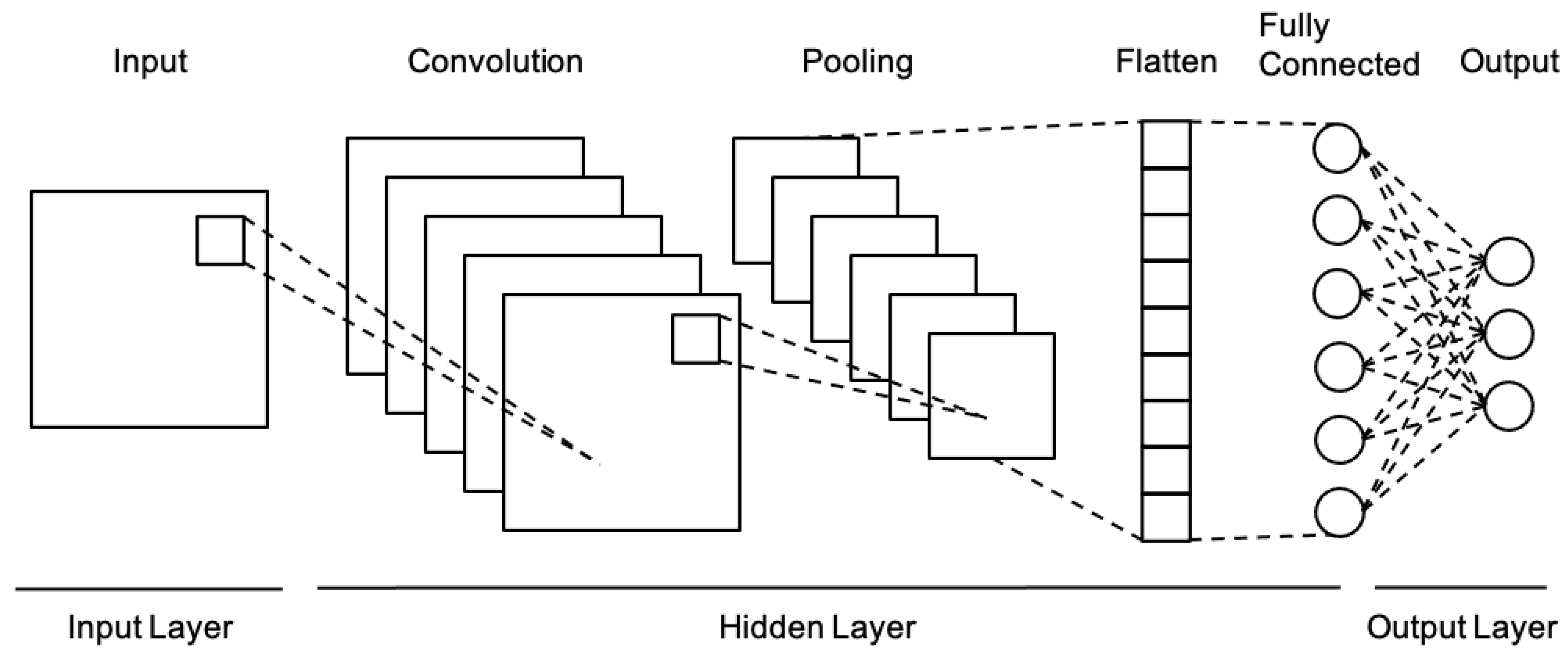
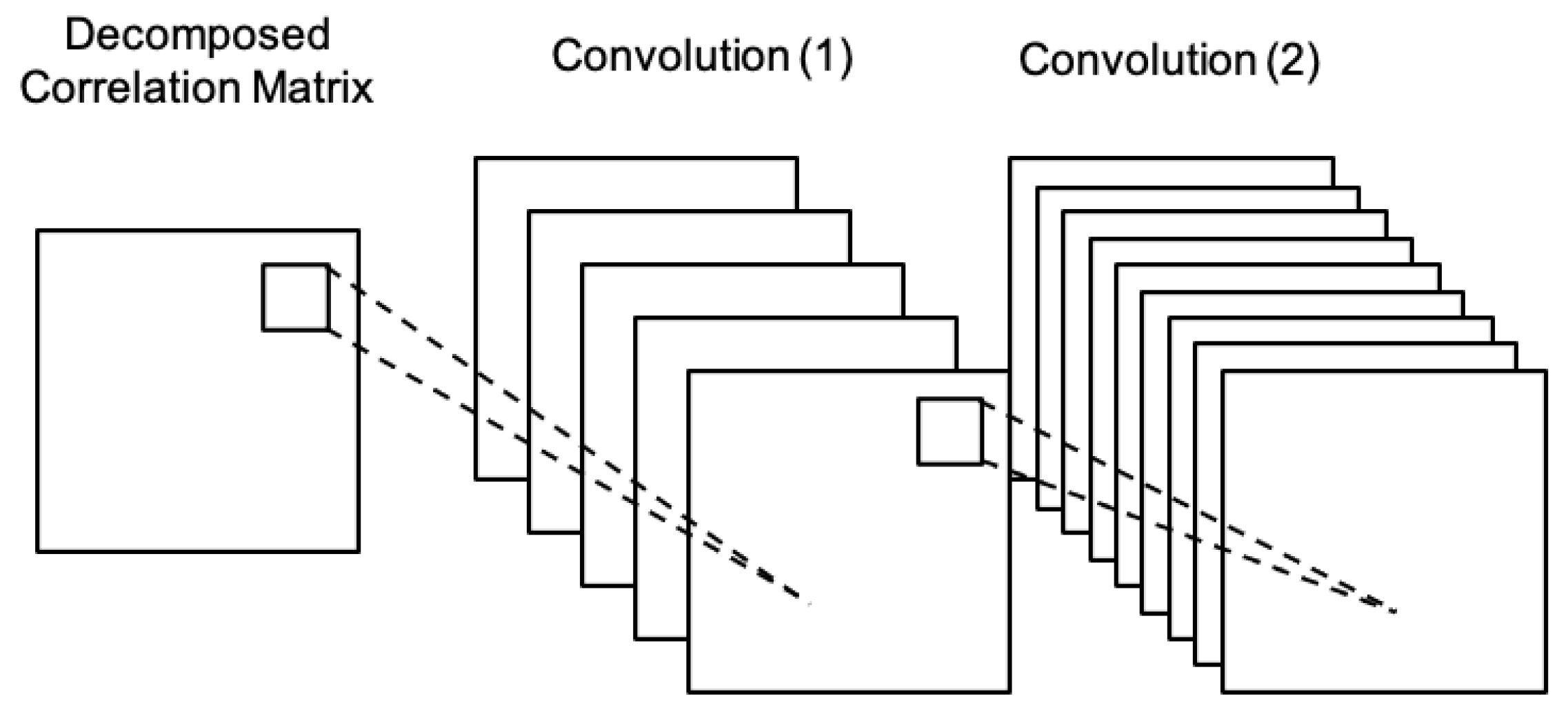
4.2. Convolutional Neural Networks
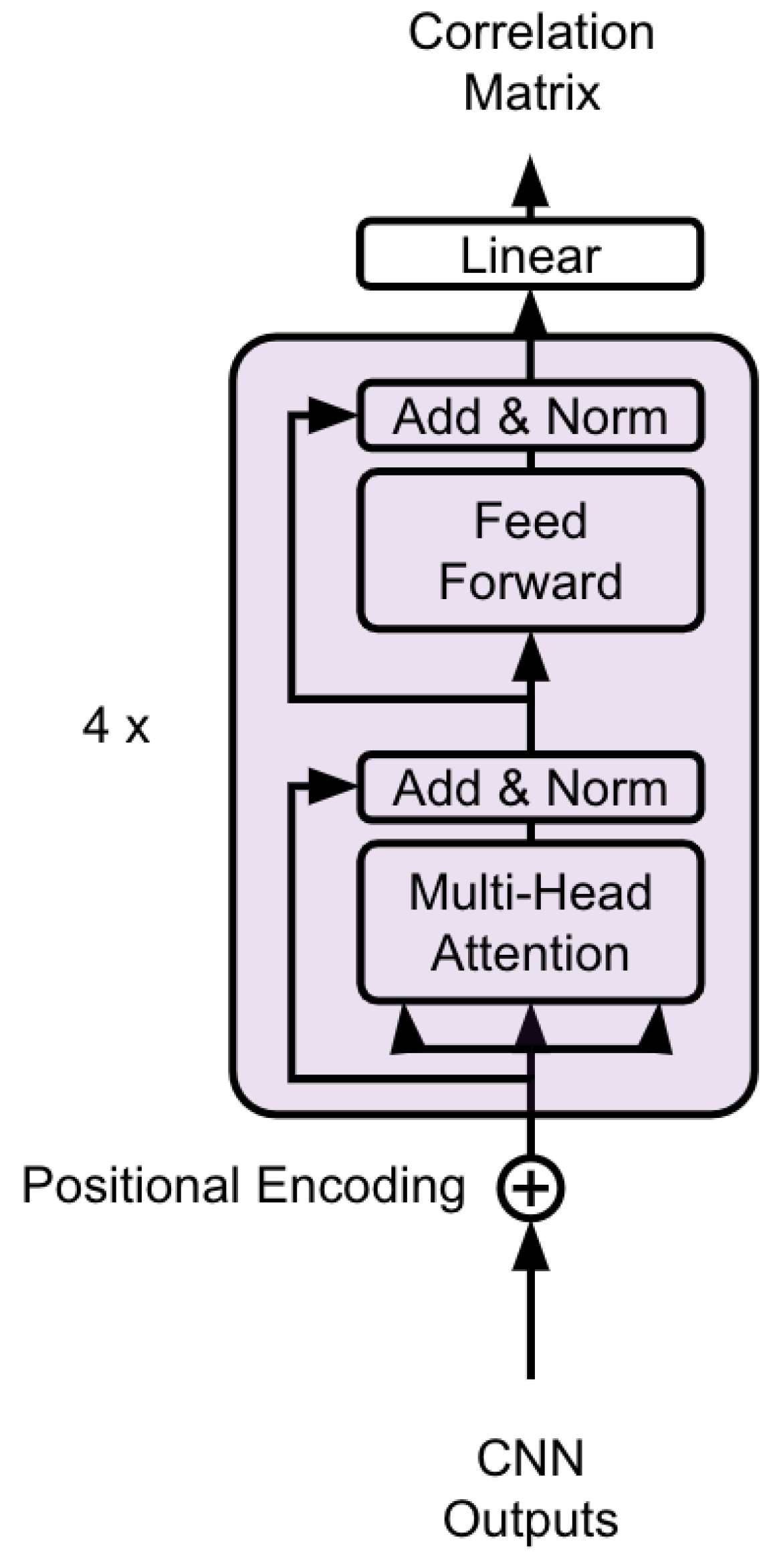
4.3. Transformer
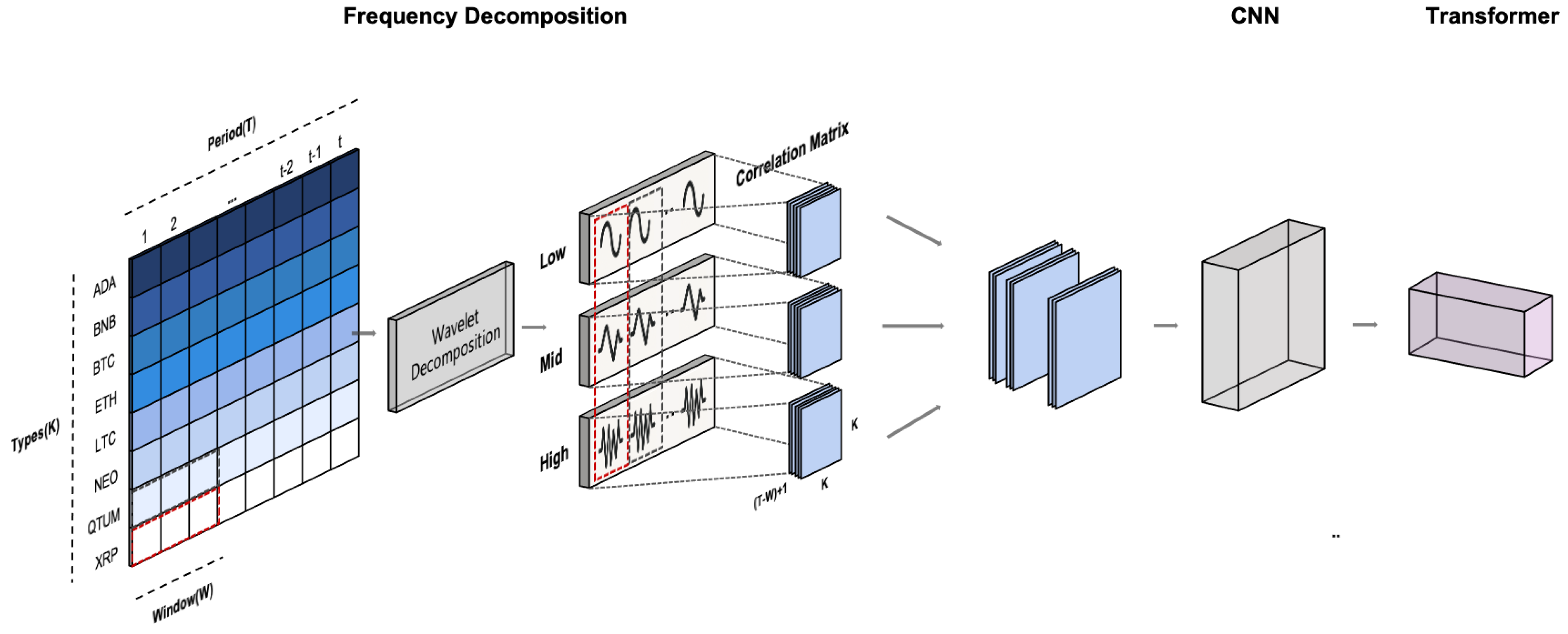
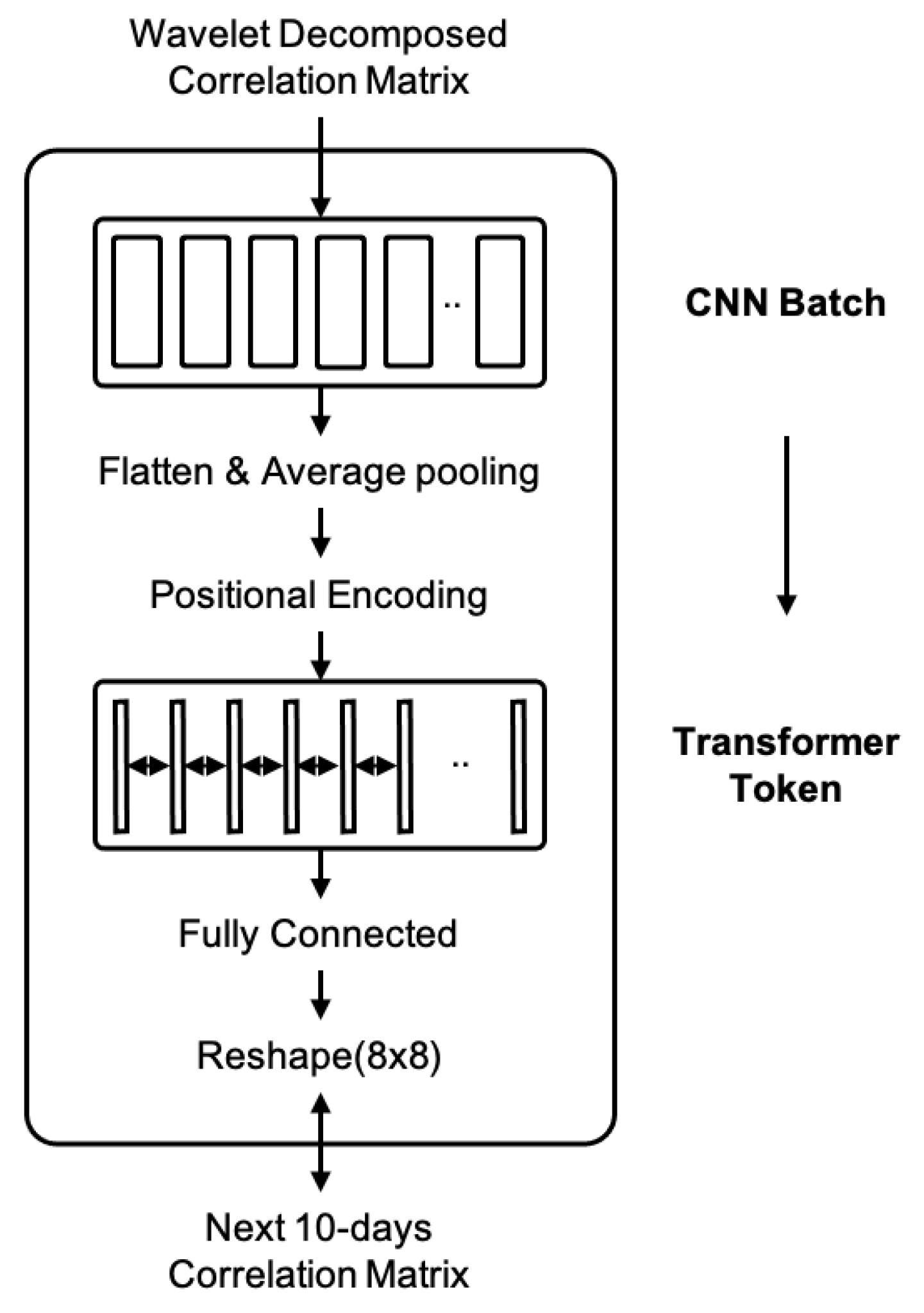
4.4. The Proposed Model
4.5. Model Training
- CNN parameters: The kernel size (kernel_size) was set to [3, 5], and the embedding dimension (d_model)—which determines the output dimension of the second convolutional layer—was selected from [32, 64, 128]. Additionally, the batch size for the CNN output, which is subsequently used as the input embedding sequence size for the Transformer, was chosen from [64, 128, 256, 512].
- Transformer parameters: The number of heads in multi-head attention (nhead) was selected from [2, 4], and the number of Transformer layers (num_layers) from [2, 4]. The dimension of the feed-forward network (dim_feedforward) was set to [256, 512], and the activation function (activation) was selected between ReLU and GELU.
- Optimization parameters: The optimizer was chosen between Adam, AdamW, and RMSprop, and the learning rate (lr) was set to [0.001, 0.0005]. To prevent overfitting and promote stable training, a learning rate scheduler was employed, which automatically reduced the learning rate when the validation loss plateaued.
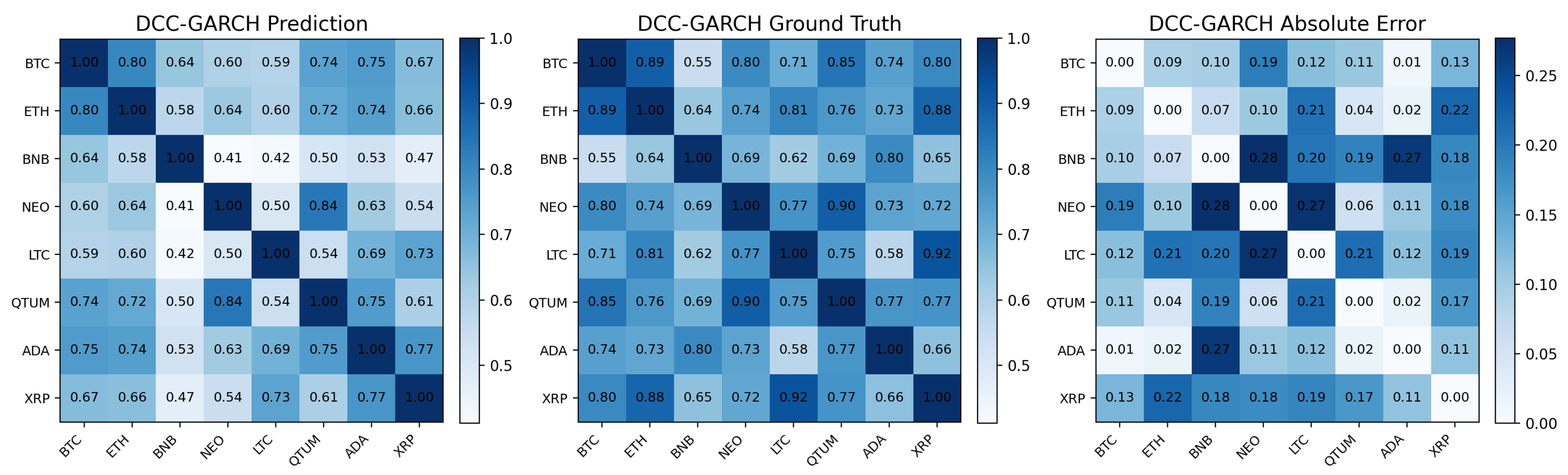
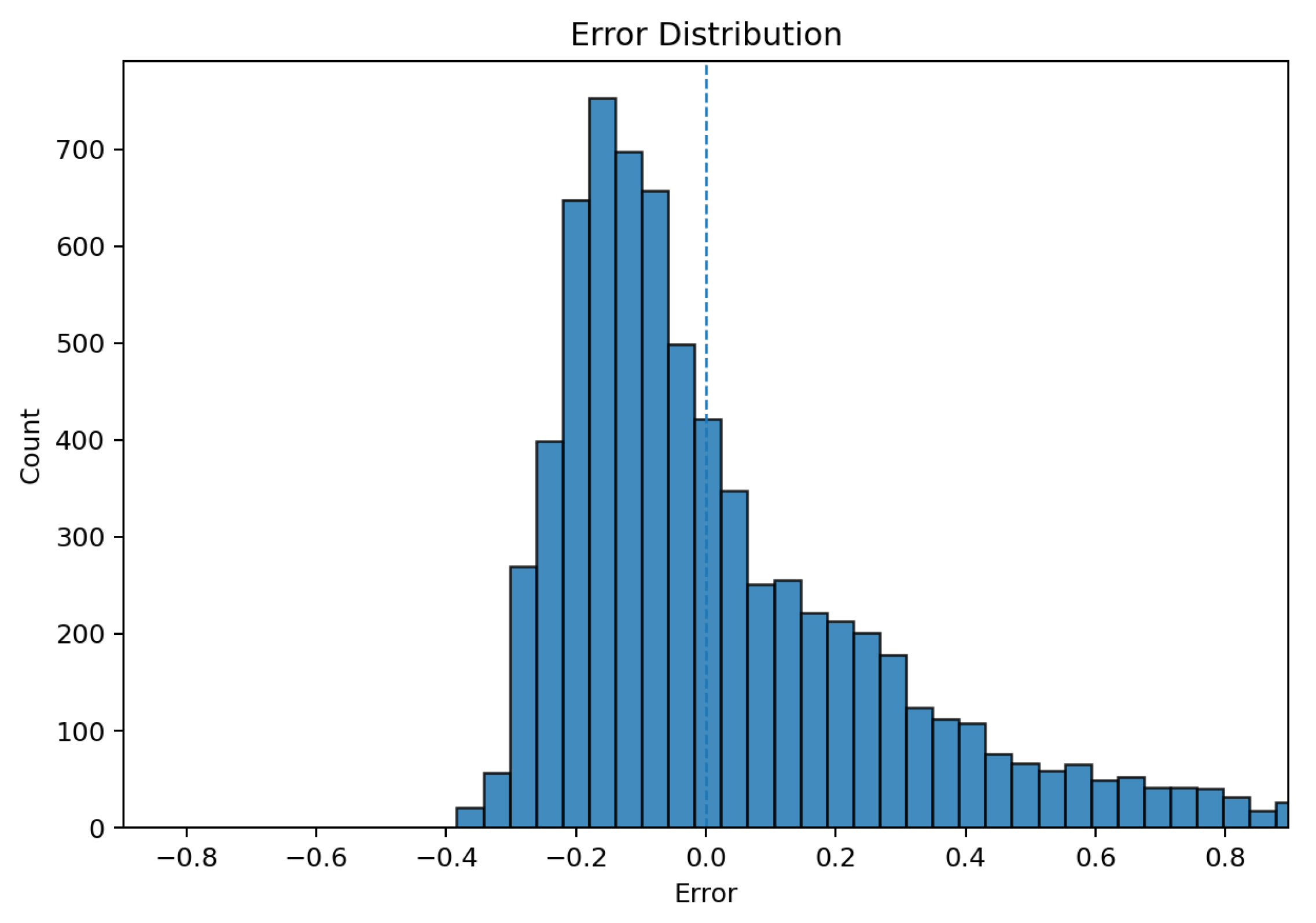
5. Results
The Proposed Model
6. Discussion and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Order Granting Approval of Proposed Rule Changes to List and Trade Shares of Spot Bitcoin Exchange-Traded Products; Securities Exchange Act Release 34-99306; U.S. Securities and Exchange Commission: Washington, DC, USA, 2024.
- Liu, Y.; Tsyvinski, A. Risks and Returns of Cryptocurrency. Rev. Financ. Stud. 2021, 34, 2689–2727. [Google Scholar] [CrossRef]
- Borri, N. Conditional tail-risk in cryptocurrency markets. J. Empir. Financ. 2019, 50, 1–19. [Google Scholar] [CrossRef]
- Bouri, E.; Kamal, E.; Kinateder, H. FTX Collapse and systemic risk spillovers from FTX Token to major cryptocurrencies. Financ. Res. Lett. 2023, 56, 104099. [Google Scholar] [CrossRef]
- Sims, C.A. Macroeconomics and Reality. Econometrica 1980, 48, 1–48. [Google Scholar] [CrossRef]
- De Livera, A.M.; Hyndman, R.J.; Snyder, R.D. Forecasting time series with complex seasonal patterns using exponential smoothing. J. Am. Stat. Assoc. 2011, 106, 1513–1527. [Google Scholar] [CrossRef]
- Jung, G.; Choi, S.Y. Forecasting foreign exchange volatility using deep learning autoencoder-LSTM techniques. Complexity 2021, 2021, 6647534. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.S.; Choi, S.Y. Forecasting the S&P 500 index using mathematical-based sentiment analysis and deep learning models: A FinBERT transformer model and LSTM. Axioms 2023, 12, 835. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting. Adv. Neural Inf. Process. Syst. 2019, 32, 5243–5253. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–14 December 2021; Curran Associates, Inc.: Red Hook, NY, USA, 2021; Volume 34, pp. 22419–22430. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; Volume 162, pp. 27268–27286. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are Transformers Effective for Time Series Forecasting? Proc. AAAI Conf. Artif. Intell. 2023, 37, 10913–10921. [Google Scholar] [CrossRef]
- Xu, J.; Cao, L. Copula variational LSTM for high-dimensional cross-market multivariate dependence modeling. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 16233–16247. [Google Scholar] [CrossRef]
- Widiputra, H.; Mailangkay, A.; Gautama, E. Multivariate CNN-LSTM model for multiple parallel financial time-series prediction. Complexity 2021, 2021, 9903518. [Google Scholar] [CrossRef]
- Lu, W.; Li, J.; Li, Y.; Sun, A.; Wang, J. A CNN-LSTM-based model to forecast stock prices. Complexity 2020, 2020, 6622927. [Google Scholar] [CrossRef]
- Zha, W.; Liu, Y.; Wan, Y.; Luo, R.; Li, D.; Yang, S.; Xu, Y. Forecasting monthly gas field production based on the CNN-LSTM model. Energy 2022, 260, 124889. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of Conditional Value-at-Risk. J. Risk 2000, 2, 21–41. [Google Scholar] [CrossRef]
- Bollerslev, T. A conditionally heteroskedastic time series model for speculative prices and rates of return. Rev. Econ. Stat. 1987, 69, 542–547. [Google Scholar] [CrossRef]
- Barbierato, E.; Gatti, A.; Incremona, A.; Pozzi, A.; Toti, D. Breaking Away From AI: The Ontological and Ethical Evolution of Machine Learning. IEEE Access 2025, 13, 55627–55647. [Google Scholar] [CrossRef]
- Reinsel, G.C. Elements of Multivariate Time Series Analysis; Springer: New York, NY, USA, 1993. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, revised ed.; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Chen, W.; Wang, W.; Peng, B.; Wen, Q.; Zhou, T.; Sun, L. Learning to Rotate: Quaternion Transformer for Complicated Periodical Time Series Forecasting. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), Washington, DC, USA, 14–18 August 2022; pp. 146–156. [Google Scholar] [CrossRef]
- Liu, S.; Yu, H.; Liao, C.; Li, J.; Lin, W.; Liu, A.X.; Dustdar, S. Pyraformer: Low-Complexity Pyramidal Attention for Long-Range Time Series Modeling and Forecasting. In Proceedings of the International Conference on Learning Representations (ICLR 2022), Virtual Event, 25–29 April 2022. [Google Scholar]
- Zhang, Y.; Yan, J. Crossformer: Transformer Utilizing Cross-Dimension Dependency for Multivariate Time Series Forecasting. In Proceedings of the ICLR, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Kim, J.; Park, S. A Convolutional Transformer Model for Multivariate Time Series Prediction. IEEE Access 2022, 10, 101319–101329. [Google Scholar] [CrossRef]
- Allen, J. Short term spectral analysis, synthesis, and modification by discrete Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 2003, 25, 235–238. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 11, 674–693. [Google Scholar] [CrossRef]
- Bhowmick, A.; Chandra, M. Speech enhancement using voiced speech probability based wavelet decomposition. Comput. Electr. Eng. 2017, 62, 706–718. [Google Scholar] [CrossRef]
- Lu, W.; Ghorbani, A.A. Network anomaly detection based on wavelet analysis. EURASIP J. Adv. Signal Process. 2008, 2009, 837601. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Li, J.; Wu, J. Multilevel wavelet decomposition network for interpretable time series analysis. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2437–2446. [Google Scholar]
- Berger, T. Forecasting based on decomposed financial return series: A wavelet analysis. J. Forecast. 2016, 35, 419–433. [Google Scholar] [CrossRef]
- Tang, Q.; Shi, R.; Fan, T.; Ma, Y.; Huang, J. Prediction of financial time series based on LSTM using wavelet transform and singular spectrum analysis. Math. Probl. Eng. 2021, 2021, 9942410. [Google Scholar] [CrossRef]
- Fernández-Macho, J. Wavelet multiple correlation and cross-correlation: A multiscale analysis of Eurozone stock markets. Phys. A Stat. Mech. Its Appl. 2012, 391, 1097–1104. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef] [PubMed]
- Alshingiti, Z.; Alaqel, R.; Al-Muhtadi, J.; Haq, Q.E.U.; Saleem, K.; Faheem, M.H. A deep learning-based phishing detection system using CNN, LSTM, and LSTM-CNN. Electronics 2023, 12, 232. [Google Scholar] [CrossRef]
- Luo, A.; Zhong, L.; Wang, J.; Wang, Y.; Li, S.; Tai, W. Short-term stock correlation forecasting based on CNN-BiLSTM enhanced by attention mechanism. IEEE Access 2024, 12, 29617–29632. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A survey on vision transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 87–110. [Google Scholar] [CrossRef]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in time series: A survey. arXiv 2022, arXiv:2202.07125. [Google Scholar]
- Lin, T.; Wang, Y.; Liu, X.; Qiu, X. A survey of transformers. AI Open 2022, 3, 111–132. [Google Scholar] [CrossRef]
- Ahmed, S.; Nielsen, I.E.; Tripathi, A.; Siddiqui, S.; Ramachandran, R.P.; Rasool, G. Transformers in time-series analysis: A tutorial. Circuits Syst. Signal Process. 2023, 42, 7433–7466. [Google Scholar] [CrossRef]
- Ghosh, S.; Manimaran, P.; Panigrahi, P.K. Characterizing multi-scale self-similar behavior and non-statistical properties of fluctuations in financial time series. Phys. A Stat. Mech. Its Appl. 2011, 390, 4304–4316. [Google Scholar] [CrossRef]
- Gudelek, M.U.; Boluk, S.A.; Ozbayoglu, A.M. A deep learning based stock trading model with 2-D CNN trend detection. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–8. [Google Scholar]
- Livieris, I.E.; Pintelas, E.; Pintelas, P. A CNN–LSTM model for gold price time-series forecasting. Neural Comput. Appl. 2020, 32, 17351–17360. [Google Scholar] [CrossRef]
- Chen, J.F.; Chen, W.L.; Huang, C.P.; Huang, S.H.; Chen, A.P. Financial time-series data analysis using deep convolutional neural networks. In Proceedings of the 2016 7th International Conference on Cloud Computing and Big Data (CCBD), Macau, China, 16–18 November 2016; pp. 87–92. [Google Scholar]
- Zeng, Z.; Kaur, R.; Siddagangappa, S.; Rahimi, S.; Balch, T.; Veloso, M. Financial time series forecasting using CNN and transformer. arXiv 2023, arXiv:2304.04912. [Google Scholar] [CrossRef]
- Bui, N.K.H.; Chien, N.D.; Kovács, P.; Bognár, G. Transformer Encoder and Multi-features Time2Vec for Financial Prediction. arXiv 2025, arXiv:2504.13801. [Google Scholar]
- Izadi, M.A.; Hajizadeh, E. Time Series Prediction for Cryptocurrency Markets with Transformer and Parallel Convolutional Neural Networks. Appl. Soft Comput. 2025, 177, 113229. [Google Scholar] [CrossRef]
- Higham, N.J. Computing the nearest correlation matrix—A problem from finance. IMA J. Numer. Anal. 2002, 22, 329–343. [Google Scholar] [CrossRef]
- Celık, S. The more contagion effect on emerging markets: The evidence of DCC-GARCH model. Econ. Model. 2012, 29, 1946–1959. [Google Scholar] [CrossRef]
- Shiferaw, Y.A. Time-varying correlation between agricultural commodity and energy price dynamics with Bayesian multivariate DCC-GARCH models. Phys. A Stat. Mech. Its Appl. 2019, 526, 120807. [Google Scholar] [CrossRef]
- Ringim, S.H.; Alhassan, A.; Güngör, H.; Bekun, F.V. Economic policy uncertainty and energy prices: Empirical evidence from multivariate DCC-GARCH models. Energies 2022, 15, 3712. [Google Scholar] [CrossRef]



| Asset | Mean | Std.Dev. | Min | Max | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| BTC | 0.0009 | 0.0348 | −0.5026 | 0.1784 | −1.2519 | 20.4016 |
| ETH | 0.0006 | 0.0455 | −0.5905 | 0.2338 | −1.1268 | 15.1670 |
| BNB | 0.0016 | 0.0474 | −0.5823 | 0.5324 | −0.3706 | 21.6922 |
| NEO | −0.0007 | 0.0562 | −0.5024 | 0.3690 | −0.3738 | 8.4099 |
| LTC | −0.0002 | 0.0487 | −0.4867 | 0.2635 | −0.7146 | 9.9519 |
| QTUM | −0.0008 | 0.0591 | −0.6260 | 0.4043 | −0.4986 | 11.5918 |
| ADA | 0.0004 | 0.0524 | −0.5331 | 0.2864 | −0.2299 | 7.0560 |
| XRP | 0.0004 | 0.0538 | −0.5387 | 0.5487 | 0.5689 | 18.4507 |
| Hyperparameters | Setting |
|---|---|
| Kernel Size | 3 |
| 128 | |
| Batch Size | 256 |
| Number of Heads () | 4 |
| Number of Transformer Layers | 4 |
| Feedforward Dimension | 256 |
| Activation Function | GELU |
| Learning Rate | 0.001 |
| Optimizer | AdamW |
| Model | MSE | MAE | RMSE | Cosine Sim. | Frobenius Norm |
|---|---|---|---|---|---|
| WCT (Proposed) | 0.06176 | 0.17248 | 0.24852 | 0.94646 | 1.78960 |
| Wavelet-Decomposed CNN | 0.06634 | 0.17909 | 0.25757 | 0.94252 | 1.87537 |
| Wavelet-Decomposed Transformer | 0.06500 | 0.17345 | 0.25494 | 0.94532 | 1.84685 |
| CNN Transformer | 0.06132 | 0.17983 | 0.24763 | 0.94624 | 1.83247 |
| DCC-GARCH | 0.06635 | 0.18725 | 0.25759 | 0.94332 | 1.92294 |
| Currency | MSE | MAE | RMSE | Cosine Similarity |
|---|---|---|---|---|
| BTC | 0.05405 | 0.16291 | 0.23248 | 0.95725 |
| ETH | 0.05848 | 0.15899 | 0.24184 | 0.95268 |
| BNB | 0.06208 | 0.17898 | 0.24916 | 0.94430 |
| NEO | 0.04627 | 0.15144 | 0.21510 | 0.96522 |
| LTC | 0.07766 | 0.18676 | 0.27868 | 0.92751 |
| QTUM | 0.05871 | 0.17529 | 0.24231 | 0.95275 |
| ADA | 0.05586 | 0.16339 | 0.23634 | 0.95576 |
| XRP | 0.08098 | 0.20206 | 0.28457 | 0.92533 |
| Baseline | DM (MSE) | p-Value (MSE) | DM (MAE) | p-Value (MAE) |
|---|---|---|---|---|
| WC | −2.221 | 0.027 | −2.445 | 0.015 |
| WT | −2.114 | 0.036 | −0.405 | 0.686 |
| CT | 0.605 | 0.546 | −6.973 | 0.000 |
| DCC-GARCH | −3.279 | 0.001 | −6.979 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.-W.; Kwon, D.; Choi, S.-Y. A Hybrid Frequency Decomposition–CNN–Transformer Model for Predicting Dynamic Cryptocurrency Correlations. Electronics 2025, 14, 4136. https://doi.org/10.3390/electronics14214136
Kang J-W, Kwon D, Choi S-Y. A Hybrid Frequency Decomposition–CNN–Transformer Model for Predicting Dynamic Cryptocurrency Correlations. Electronics. 2025; 14(21):4136. https://doi.org/10.3390/electronics14214136
Chicago/Turabian StyleKang, Ji-Won, Daihyun Kwon, and Sun-Yong Choi. 2025. "A Hybrid Frequency Decomposition–CNN–Transformer Model for Predicting Dynamic Cryptocurrency Correlations" Electronics 14, no. 21: 4136. https://doi.org/10.3390/electronics14214136
APA StyleKang, J.-W., Kwon, D., & Choi, S.-Y. (2025). A Hybrid Frequency Decomposition–CNN–Transformer Model for Predicting Dynamic Cryptocurrency Correlations. Electronics, 14(21), 4136. https://doi.org/10.3390/electronics14214136







