Exploring Uncertainty in Medical Federated Learning: A Survey

Abstract

The adoption of artificial intelligence (AI) in healthcare requires not only accurate predictions but also a clear understanding of its reliability. In safety-critical domains such as medical imaging and diagnosis, clinicians must assess the confidence in model outputs to ensure safe decision making. Uncertainty quantification (UQ) addresses this need by providing confidence estimates and identifying situations in which models may fail. Such uncertainty estimates enable risk-aware deployment, improve model robustness, and ultimately strengthen clinical trust. Although prior studies have surveyed UQ in centralized learning, a systematic review in the federated learning (FL) context is still lacking. As a privacy-preserving collaborative paradigm, FL enables institutions to jointly train models without sharing raw patient data. However, compared with centralized learning, FL introduces more complex sources of uncertainty. In addition to data uncertainty caused by noisy inputs and model uncertainty from distributed optimization, there also exists distributional uncertainty arising from client heterogeneity and personalized uncertainty associated with site-specific biases. These intertwined uncertainties complicate model reliability and highlight the urgent need for UQ strategies tailored to federated settings. This survey reviews UQ in medical FL. We categorize uncertainties unique to FL and compare them with those in centralized learning. We examine the sources of uncertainty, existing FL architectures, UQ methods, and their integration with privacy-preserving techniques, and we analyze their advantages, limitations, and trade-offs. Finally, we highlight key challenges—scalable UQ under non-IID conditions, federated OOD detection, and clinical validation—and outline future opportunities such as hybrid UQ strategies and personalization. By combining methodological advances in UQ with application perspectives, this survey provides a structured overview to inform the development of more reliable and privacy-preserving FL systems in healthcare.

1. Introduction

The current situation in healthcare is characterized by escalating expenses, aging populations, precision medicine, universal health coverage, and a surge in non-communicable diseases, coupled with the global impact of the COVID-19 pandemic [1]. Meanwhile, the digital transformation of healthcare information through big data and medical imaging has led to the emergence of FL as a promising approach. However, data privacy and security concerns remain significant barriers to widespread adoption. Privacy breaches, exemplified by major incidents such as the 2015 Anthem breach (78.8 million health records) and the 2019 American Medical Collection Agency (AMCA) breach, affecting over 25 million patients, have highlighted the urgent need for robust measures to protect sensitive information. International information protection laws, as shown in Table 1, such as HIPAA, GDPR, APPI, and the Personal Information Protection Law, have been enacted to address these concerns. These laws aim to safeguard user privacy and regulate data usage [2].

To ensure privacy-preserving and collaborative learning, FL [3,4] has emerged as a promising paradigm for the training of models across decentralized institutions without sharing raw data. However, in medical imaging, FL faces several challenges: limited and noisy annotations due to privacy regulations and labeling costs, non-IID client distributions caused by demographic and device heterogeneity, and reduced transparency that undermines clinical trust [5,6,7]. These issues highlight the need for UQ, which can identify unreliable clients or noisy data, provide calibrated confidence under heterogeneity, and improve interpretability in safety-critical applications [8]. In this context, three major forms of uncertainty become particularly important: data uncertainty, arising from measurement errors, sampling variability, or inconsistent labels [9]; model uncertainty, introduced by local optimization and aggregation variability in decentralized training [10]; and distributional uncertainty, driven by inter-site heterogeneity or personalization biases across clients [11,12]. Addressing and quantifying these uncertainties is essential in building reliable, robust, and trustworthy federated medical AI systems.

Various approaches have been proposed to manage uncertainty in FL. Bayesian methods provide a principled framework for incorporating prior knowledge, estimating posterior distributions, and quantifying parameter uncertainty [13]; conformal prediction constructs prediction regions with guaranteed error rates [14]; deterministic evidential methods offer alternative mathematical formulations to capture ambiguity in predictions [15]; and ensemble techniques enhance reliability by combining multiple models or predictions [16]. Leveraging these methods, researchers have begun to adapt UQ to federated healthcare settings, recognizing its critical role in building safe, reliable, and privacy-preserving medical AI systems [17]. In safety-critical domains, UQ highlights potential failure cases, thereby improving transparency and clinical trust. Recent studies have explored diverse strategies, including Bayesian neural networks (BNNs) and conformal prediction adapted to decentralized training, ensemble learning and distillation for robustness under heterogeneous data, and meta-learning for rapid adaptation in data-scarce domains. Privacy-preserving techniques such as differential privacy (DP), secure aggregation, and homomorphic encryption (HE) have also been combined with UQ [17], although they may introduce additional uncertainty or degrade utility due to noise injection, overhead, or approximation errors. Overall, existing efforts can be broadly grouped into two main directions, Bayesian federated learning (BFL) and federated conformal prediction (FCP), with other approaches—such as evidential models, fuzzy theory, and verification-based techniques—remaining less common. These developments illustrate the growing importance of FL-UQ as a pathway toward reliable, trustworthy, and privacy-conscious medical AI, although current work remains fragmented and lacks systematic synthesis, as summarized in Figure 1.

Table 1. International organizations’ laws for data privacy protection.

Ref.	Law	Country/Region	Focus
[18]	Health Insurance Portability and Accountability Act (HIPAA)	United States of America	Bill regarding health insurance and liability
[19]	Personal Information Protection and Electronic Documents Act (PIPEDA)	Canada	The provisions and directives govern personal information utilization by private individuals or companies in their business operations
[20]	Act on the Protection of Personal Information (APPI)	Japan	An improved process for regulating the use of data to prevent leakage, loss, and damage
[21]	General Data Protection Regulation (GDPR)	European Union	Comprehensive legislation that has broad scope and is systematically designed to cover a wide range of applications
[22]	California Consumer Privacy Act (CCPA)	California (United States)	A detailed law for safeguarding consumer privacy rights and regulating the acquisition, use, and disclosure of personal information by business operations
[23]	Personal Information Protection Law (PIPL)	China	A systematic and comprehensive law specifically designed to safeguard personal data, having broad scope and applicable to various sectors

Table 1. International organizations’ laws for data privacy protection.

Ref.	Law	Country/Region	Focus
[18]	Health Insurance Portability and Accountability Act (HIPAA)	United States of America	Bill regarding health insurance and liability
[19]	Personal Information Protection and Electronic Documents Act (PIPEDA)	Canada	The provisions and directives govern personal information utilization by private individuals or companies in their business operations
[20]	Act on the Protection of Personal Information (APPI)	Japan	An improved process for regulating the use of data to prevent leakage, loss, and damage
[21]	General Data Protection Regulation (GDPR)	European Union	Comprehensive legislation that has broad scope and is systematically designed to cover a wide range of applications
[22]	California Consumer Privacy Act (CCPA)	California (United States)	A detailed law for safeguarding consumer privacy rights and regulating the acquisition, use, and disclosure of personal information by business operations
[23]	Personal Information Protection Law (PIPL)	China	A systematic and comprehensive law specifically designed to safeguard personal data, having broad scope and applicable to various sectors

This research aims to provide a comprehensive analysis of the integration of FL and UQ in healthcare. We investigate the coexistence and interaction of uncertainties unique to federated learning—distinguishing them from those in centralized deep learning—and develop strategies to mitigate their impacts on model reliability and robustness. Our survey covers variants of FL, UQ methods, and medical applications, including distributed machine learning, with attention to security considerations such as secure multi-party computation, differential privacy, and homomorphic encryption [24]. To achieve this, we conducted a systematic literature review of publications emerging between 2020 and 2024 from IEEE, Google Scholar, ScienceDirect, ACM, and Nature. Using Boolean search strings such as “Federated Learning”, “Uncertainty Quantification”, “Healthcare”, “Distributed Machine Learning”, and “Medical”, we retrieved 2216 articles, from which 147, were selected after rigorous filtering for relevance and quality. These works were analyzed to synthesize key themes, challenges, and methods, enabling us to provide a holistic understanding of FL-UQ for medical imaging and to highlight distinctions from existing surveys, as summarized in

Table 2. Comparison with related surveys. Our work is distinct in providing a dedicated review of UQ in FL for medical imaging.

Survey	Focus	Domain (General FL vs. Medical FL)	Difference from This Work
[25]	Sources, taxonomy, quantification, calibration, and applications of uncertainty in centralized learning.	General (Centralized ML)	Does not consider FL scenarios.
[26]	Trustworthy clinical AI with UQ; introduces structural uncertainty, methods to align segmentation uncertainty with clinical needs, and evaluation protocols.	Medical FL (Clinical AI)	Focuses on medical image analysis, but does not focus on FL.
[6]	Review of FL in heterogeneous scenarios (device, data, model heterogeneity) and corresponding solutions.	General FL	Heterogeneity is analyzed, but uncertainty is not explicitly considered as a solution framework.
[27]	Comprehensive review of trustworthy FL; taxonomy covers interpretability, transparency, privacy, robustness, fairness, accountability.	General FL	Mentions uncertainty within trustworthiness, but does not focus on UQ as a central theme.
[28]	Systematic review of robust FL; classifies 244 studies into eight themes (regularization, optimizers, DP, aggregation, etc.).	General FL	While robustness is discussed, uncertainty is not systematically reviewed as a core dimension.
This work (2025)	UQ in FL for medical application; taxonomy of uncertainty sources, Bayesian and conformal methods, privacy–uncertainty trade-offs, and clinical applications.	Medical FL	A comprehensive review analyzing uncertainty in FL, with an emphasis on medical scenarios.

.

This survey provides a comprehensive overview of UQ in explainable medical FL, emphasizing its role in building trustworthy and privacy-preserving AI systems. The key contributions of this work are as follows.

1.

Analysis of sources of uncertainty and comprehensive categorization of uncertainty in FL: We analyze how uncertainty arises in FL and interacts in medical settings, and we distinguish between data, model, and distributional uncertainties.

2.

Review of state-of-the-art UQ methods integrated with FL: We summarize and compare various approaches—including Bayesian methods, conformal prediction, ensemble-based techniques, evidential models, and meta-learning—highlighting their strengths and limitations in addressing privacy, data and model heterogeneity, and annotation scarcity.

3.

In-depth analysis of BFL and FCP: We provide an in-depth discussion of both server- and client-side BFL approaches, along with recent advances in applying conformal prediction to heterogeneous and non-exchangeable FL data.

4.

Mapping to real-world medical applications: We highlight five representative use cases: COVID-19 prognosis, tumor segmentation, breast cancer detection, large-scale radiological networks, and breast density classification. These examples illustrate how UQ enhances clinical reliability and interpretability in medical imaging.

5.

Identification of open challenges and future opportunities: We summarize unresolved issues such as robust UQ under non-IID data, computational efficiency, out-of-distribution (OOD) detection, and clinical explainability, outlining promising directions for future research.

The remainder of the study is structured as follows. Section 2 discusses a preliminary study focusing on the FL background and its types. Moving forward, Section 3 presents an overview of UQ techniques in FL. In Section 4, we discuss federated Bayesian learning methods. In Section 5, federated conformal prediction is discussed, followed by Section 6, which presents other FL-UQ methods. Section 7 highlights federated medical applications. Then, in Section 8, uncertainty-related challenges are presented, and, lastly, Section 9 concludes the current survey.

2. Federated Learning Background

FL, first introduced by Google in 2016, was designed to overcome the limitations of data silos while emphasizing the protection of data privacy [29]. An example of its application involved implementing joint learning for Google Keyboard’s next-word prediction on mobile devices [30]. The advancement of FL has expanded its reach across various fields [31], with the medical domain being a notable beneficiary. Applying FL to train models on real-world health data collected from different hospitals and institutions has been shown to enhance the quality of medical diagnosis. As a specialized form of distributed machine learning, FL enables the development of joint models while preserving privacy. This design directly addresses many of the privacy issues inherent in conventional distributed learning. In this setting, multiple parties collaboratively update a shared model using only their local datasets, without exposing raw patient information [32].

FL is a decentralized approach that preserves data privacy by aggregating locally computed updates on local devices to create a shared model, enhancing the user experience with learning models [29]. FL emerges as an extension of the fundamental principles of distributed machine learning. Distributed machine learning, in turn, represents the amalgamation of machine learning techniques with distributed architectures. The concept of machine learning has gained significant prominence since the 1980s, demonstrating remarkable success in tasks such as classification and prediction. It has even achieved or exceeded human-level performance in speech, image, and text prediction and classification [33].

As is evident from the above, FL offers the advantage of training models without uploading private data. Furthermore, since FL primarily focuses on model training rather than individual data samples, it mitigates the risk of data leakage. This characteristic makes FL an ideal framework for developing machine learning applications that involve privacy-sensitive electronic medical records [34]. Ref. [35] proposed “SVeriFL”, a privacy-preserving successive verifiable FL approach. They introduced a well-designed protocol based on BLS signatures and multi-party security, enabling the verification of parameter integrity when uploaded by participants and the correctness of results provided by the server, while also allowing participants to validate the consistency of the aggregation results.

Beyond privacy-preserving protocols, recent research has also explored the combination of FL with modern model architectures such as Transformers. For example, the Federated Transformer (FeT) framework [36] introduces a multi-party vertical FL scheme designed to address the practical challenges of loosely linked data across institutions. By leveraging Transformer encoders within a vertical FL pipeline, FeT improves representation learning under limited feature overlap while ensuring privacy-preserving aggregation. Although such Transformer-based FL approaches are still in their early stages compared to convolutional or ensemble methods, they highlight the growing interest in adapting advanced neural architectures to the federated setting, particularly in medical domains, where data are heterogeneous and distributed across institutions. In parallel, multimodal FL has gained increased attention, with paradigms such as FedMBridge [37] enabling bridgeable learning across diverse modalities and FedMFS [38] proposing selective modality communication to improve efficiency in multimodal fusion. These studies demonstrate the potential of extending FL to more complex and clinically relevant multimodal data scenarios.

Currently, two prominent frameworks dominate the field of FL: the TensorFlow framework and the WeBank Fate framework [39]. Alongside these, other derivative frameworks exist, including Flower [40], which introduces unique features to facilitate large-scale FL experiments. FL has thus emerged as the most extensively adopted privacy-preserving technology for industrial and medical AI applications in next-generation advancements [41].

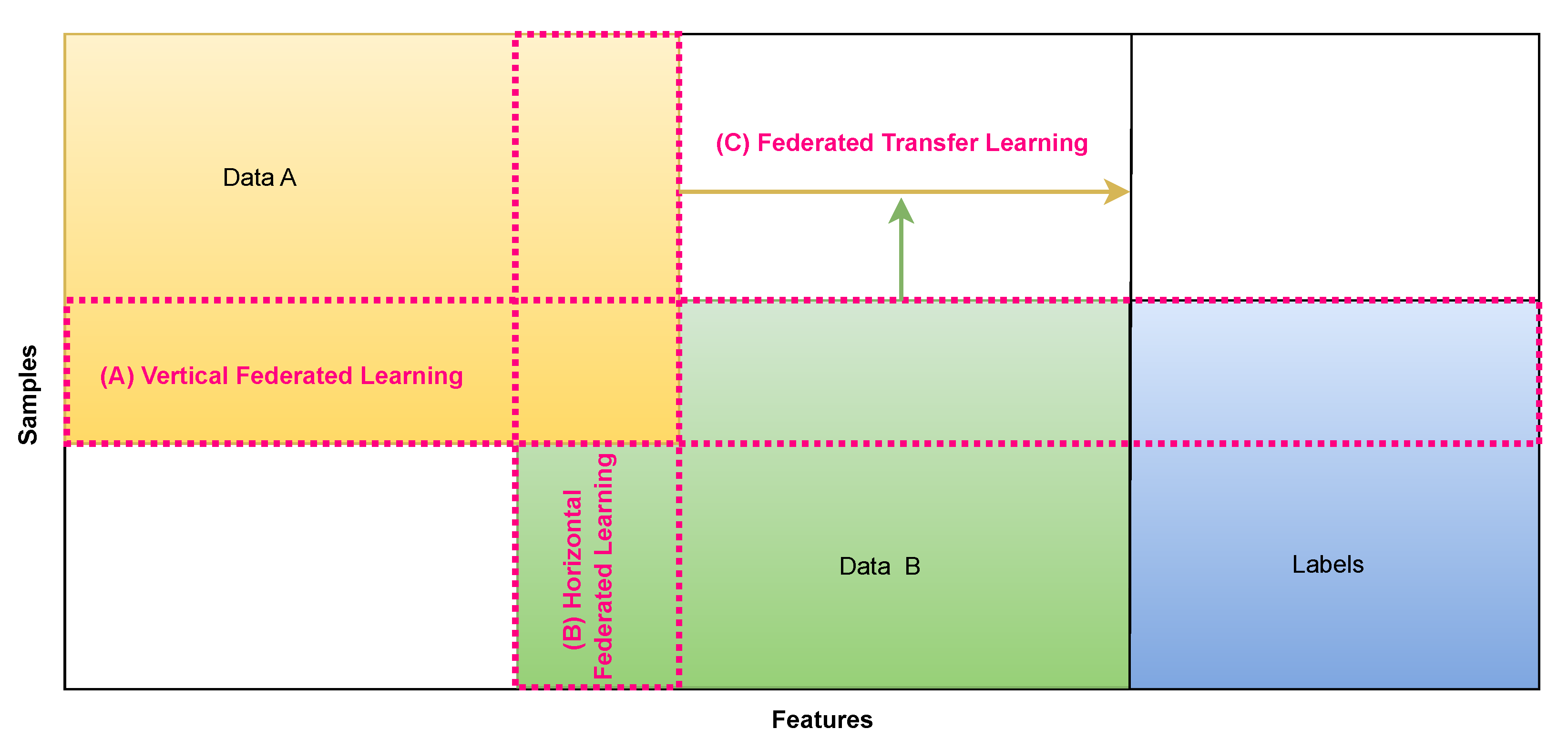
2.1. Federated Learning Categories

FL can be categorized into three types based on the data sample space and data feature space distribution among participants. These categories include vertical federated learning, horizontal federated learning, and federated transfer learning. Ref. [42] has served as the foundation for subsequent enhancements and refinements in federated learning algorithms.

2.1.1. Horizontal Federated Learning

Horizontal federated learning is distinguished by substantial overlap in data feature spaces distributed among various data sources, while significant differences are observed in the data sample space. A notable intersection exists in data attributes like gender and age, with minimal overlap in intermediate samples [43]. This concept is depicted in Figure 2. For instance, certain user characteristics, such as gender, blood type, pulse, and blood pressure, may be shared between hospitals, but the specific user groups may vary.

2.1.2. Vertical Federated Learning

Vertical federated learning exhibits substantial overlap in data samples within the data sample space but relatively little overlap in the data features among the data sources. In other words, there is minimal similarity in data attributes like gender and age between the two sides of the data. At the same time, there is a significant intersection in the middle portion of the data samples [44]. This concept is illustrated in Figure 2. For instance, most individuals in these groups may be the same when considering hospitals and pharmacies within the same city. However, there is limited similarity in terms of patient-specific data characteristics.

2.1.3. Federated Transfer Learning

Federated transfer learning stands apart from vertical and horizontal FL. It typically involves minimal overlap in data characteristics across different data sources and limited overlap in the data sample space [45]. Essentially, this approach entails a lack of similarity in characteristics such as gender and age between the two sides of the data, along with minimal overlap in the data samples. This concept is illustrated in Figure 2. For instance, when considering hospitals and pharmacies in different cities, not only are these groups composed of distinct individuals, but the characteristics of the patients also do not exhibit significant overlap.

2.2. Federated Learning Steps

Figure 3 illustrates the federated learning model training process. In general, FL can be divided into four steps.

• Local Optimization: In the context of FL, local optimization refers to the initial step where each participating client trains its local model using its own local data. This localized training allows the model to adapt to the unique characteristics of each client’s data. Local optimization is a crucial phase in FL as it ensures that local models are fine-tuned based on local data while preserving data privacy.
• Global Aggregation: Global aggregation is the subsequent step in federated learning. In this phase, participating clients send their local model updates (not the raw data) to a central server. The central server aggregates these updates to update the global model. The global model is the result of collaboration among all clients, merging their localized knowledge to create a comprehensive model. Global aggregation represents the collaborative aspect of federated learning.
• Personalization: Due to the heterogeneity of client data and models, personalization is a common step in federated learning. Personalization involves integrating information from different participants and introducing personalized elements into the global model. Personalization can enhance the model’s performance on heterogeneous data and cater to the unique demands of different clients.
• Test: The final phase of federated learning is the test step. The testing phase evaluates the model’s performance and ensures its effectiveness and robustness across various client scenarios. Personalization and testing help to validate the effectiveness of federated learning and ensure that the global model caters to diverse use cases.

3. Uncertainty in Federated Learning

3.1. Uncertainties in Federated Learning Process

Federated learning is a decentralized machine learning paradigm that enables multiple clients to collaboratively train a shared model without exchanging raw data. Formally, let $D=\{D_1,\dots ,D_M\}$ denote the collection of datasets distributed across M clients, where each client m holds local data $D_m={\left\{(x_i,y_i)\right\}}_{i=1}^{N_m}$ with $N_m$ samples. The objective of FL is to optimize a global model $f_w$ parameterized by weights w over the union of all client datasets:

$$f_w:\to ,\underset{w}{\min }\sum _{m=1}^M{\displaystyle \frac{|D_m|}{\left|D\right|}}l(w;D_m),$$

(1)

where $l(w;D_m)$ denotes the empirical risk on client m and $\left|D\right|={\sum }_m\left|D_m\right|$ is the total data size.

In practice, training a federated model consists of multiple steps that correspond to different sources of uncertainty.

1.

The data acquisition step:

The collection and annotation of local datasets at each client institution, often subject to noise, incompleteness, or privacy-driven perturbations.

2.

The local optimization step:

Each client optimizes its model locally using stochastic procedures such as gradient descent on private data.

3.

The global aggregation step:

The central server aggregates model updates from heterogeneous clients, producing a global model.

4.

The personalization step:

The adaptation of the global model to local data distributions to handle heterogeneity across clients.

5.

The testing and deployment step:

The global or personalized models are evaluated and applied in real-world scenarios.

Each of these steps introduces potential sources of uncertainty that propagate through the entire FL process. We identify five main factors that critically affect uncertainty in federated learning:

• The quality and reliability of data acquisition at distributed clients;
• The randomness and instability of local training;
• The variance and communication noise in global aggregation;
• The distributional shifts introduced by personalization across heterogeneous clients;
• The robustness of predictions under out-of-distribution or temporally shifted test data.

In the following, we describe each step of the FL pipeline in more detail, highlight the corresponding sources of uncertainty, and explain how these uncertainties are propagated and compounded. Finally, we introduce a taxonomy of uncertainty types in federated learning and discuss their implications for trustworthy medical AI.

3.1.1. Data Acquisition in Federated Medical Learning

In federated medical learning, the data acquisition step corresponds to the collection and annotation of patient information at distributed healthcare institutions. Each client m holds its own dataset $D_m={\left\{(x_i,y_i)\right\}}_{i=1}^{N_m}$, where $x_i$ may represent a medical image (e.g., MRI, CT scan, histopathology slide) or electronic health record features, and $y_i$ is the corresponding label (e.g., diagnosis, segmentation mask, survival outcome). For a real-world clinical case $\omega$ from space Ω, the observed medical measurement can be expressed as

$$x|\omega \sim p_{x|\omega },$$

(2)

and the associated target annotation is given by

$$y|\omega \sim p_{y|\omega }.$$

(3)

The local dataset $D_m$ thus consists of realizations $\{x_i,y_i\}$ sampled from the distribution of patients admitted to institution m. When aggregated across multiple hospitals, the global dataset $D={\bigcup }_{m=1}^M{D}_m$ represents a highly heterogeneous and potentially noisy collection of medical records.

Two principal sources of uncertainty arise already at this stage. First, the coverage of the patient population space Ω is often incomplete. Individual hospitals may only address specific demographics, disease subtypes, or imaging protocols, leading to non-representative data. This creates distribution shifts across clients and reduces the generalizability of the global model.

Factor I: Variability in Medical Populations and Protocols Each clinical site acquires data from its own patient cohort under specific imaging devices and acquisition protocols. This leads to distribution shifts in terms of demographics, disease prevalence, and scanner characteristics. When the distribution of a new patient sample differs from that of the training data, the global model is exposed to uncertainty, which can cause degraded prediction accuracy.

Second, medical data acquisition and annotation are prone to errors. Images may contain artifacts from patient movement or machine calibration; electronic health records may have missing values; and labels (e.g., tumor boundaries, pathology grading) may vary across annotators due to inter-observer variability. In addition, privacy regulations (e.g., HIPAA, GDPR) may require the removal or obfuscation of sensitive features, effectively introducing artificial noise.

Factor II: Noise, Missing Data, and Labeling Errors Measurement errors, annotation inconsistencies, and privacy-driven data suppression introduce uncertainty in the training data. These imperfections reduce the reliability of local updates and propagate to the global model, increasing the predictive variance.

In summary, already at the data acquisition stage, federated medical learning inherits substantial uncertainty due to heterogeneous populations, diverse acquisition protocols, and noisy or incomplete annotations. These factors lay the foundation for non-IID distributions across clients, which propagate through subsequent steps of local training and global aggregation.

3.1.2. Local Optimization in Federated Medical Learning

In federated medical learning, each client (e.g., a hospital) trains its model locally on its private dataset $D_m$. This process can be formalized as learning local parameters $w_m$ by minimizing the empirical risk:

$$w_m^{*}\sim p(w_m\mid D_m,s),$$

(4)

where s denotes the model configuration (e.g., network architecture, optimizer choice). The training of $w_m$ is stochastic, influenced by random initialization, mini-batch sampling, and optimizer dynamics. Moreover, local datasets in medicine are often small, imbalanced, or noisy, leading to unstable convergence. For instance, a rural hospital may only collect cases of certain demographics, whereas a specialized center may only provide data from severe cases, producing very different local optima $w_m^{*}$. This variability across clients propagates uncertainty into the global model.

Factor III: Randomness and Bias in Local Training Uncertainty arises due to stochastic optimization and the limited, biased, or imbalanced nature of local medical datasets. Even with the same model configuration, two hospitals may produce highly divergent local updates, making the reliability of local models inherently uncertain.

3.1.3. Global Aggregation in Federated Medical Learning

Once local updates ${\left\{w_m^{*}\right\}}_{m=1}^M$ are obtained, the server aggregates them to form the global model $w_g$. The most common approach is weighted averaging:

$$w_g=\sum _{m=1}^M{\displaystyle \frac{|D_m|}{\left|D\right|}}{w}_m^{*},$$

(5)

with $\left|D\right|={\sum }_m\left|D_m\right|$. However, aggregation introduces additional uncertainty. First, heterogeneity among local updates leads to variance in the aggregated parameters. Second, communication channels are imperfect: packet loss, quantization, and compression can distort updates during transmission. Third, proxy datasets sometimes used to stabilize aggregation may not reflect the true distribution, further biasing the global model. Consequently, even if each local model is well trained, the global update may be noisy or unstable.

Factor IV: Variance and Noise in Global Aggregation Uncertainty is introduced when combining heterogeneous and potentially conflicting local updates. This is further amplified by communication noise or the use of proxy datasets, which can distort the aggregation and reduce the reliability of the global model.

3.1.4. Personalization in Federated Medical Learning

In medical FL, the global model $w_g$ obtained after aggregation may not perform optimally on all clients due to data heterogeneity. Personalization aims to adapt $w_g$ to a client’s local distribution, yielding $w_m^{\mathrm{pers}}$. Formally, this can be seen as a fine-tuning process:

$$w_m^{\mathrm{pers}}\sim p(w_m\mid w_g,D_m),$$

(6)

where $D_m$ is the client’s local dataset. However, personalization itself introduces uncertainty. Different hospitals may adapt $w_g$ in inconsistent ways depending on their data biases, leading to integration variance across clients. For example, a model fine-tuned on pediatric data may deviate significantly from one adapted to geriatric populations, and both may diverge from the global model. This tension between global consistency and local specialization represents a unique uncertainty source in FL.

Factor V: Uncertainty from Personalized Adaptation While personalization improves local accuracy, it introduces uncertainty by creating distributional divergence across clients. This may enhance performance in one medical center but undermine generalization across the federation.

3.1.5. Testing and Deployment in Federated Medical Learning

After training and personalization, federated models are evaluated and deployed in clinical practice. At this stage, uncertainty arises from several factors. First, models may encounter out-of-distribution (OOD) inputs, such as new disease variants or imaging protocols not seen during training. Second, temporal shifts occur as patient populations and clinical practices evolve over time. Third, the prediction confidence itself may be miscalibrated, with models appearing overconfident in cases where they are unreliable.

Formally, for a new test input $x^{*}$, the predictive distribution depends on whether the deployed model is the global model or a personalized local model. For the global model, we have

$$p(y^{*}\mid x^{*},w_g),$$

(7)

whereas, for a personalized client m, the inference is based on

$$p(y^{*}\mid x^{*},w_m^{\mathrm{pers}}).$$

(8)

In both cases, the predictive distribution may deviate strongly if $x^{*}$ lies outside the training support or if the model has not been calibrated.

In a medical context, these uncertainties directly affect patient safety: a miscalibrated cancer detection model that confidently misclassifies an OOD sample poses critical risks. Therefore, reliable UQ during deployment is essential for clinical trust.

Factor VI: Prediction and Deployment Uncertainty Uncertainty at deployment arises from out-of-distribution samples, temporal distribution shifts, and miscalibrated confidence estimates. For personalized models, this uncertainty is further affected by the adaptation from $w_g$ to $w_m^{\mathrm{pers}}$. Without principled UQ, clinicians may misinterpret unreliable predictions, reducing trust in federated models.

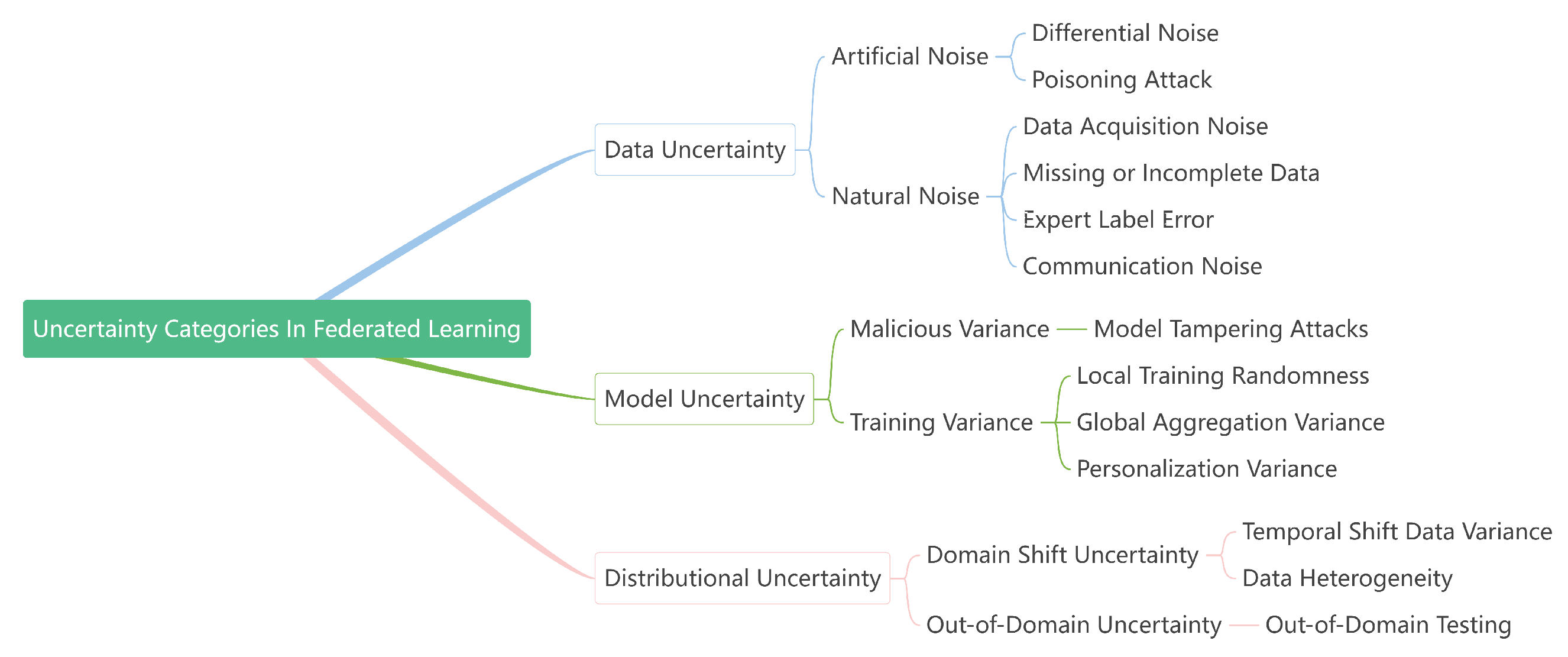
3.2. Uncertainty Categories in Federated Learning

In summary, uncertainty in FL can be categorized into three types: data uncertainty, model uncertainty, and distributional uncertainty, as listed in Figure 4.

Data uncertainty. Data uncertainty in FL refers to instability introduced by noisy, incomplete, or diverse data across distributed clients. In the medical domain, this may result from imaging artifacts, annotation errors, or missing patient records. Moreover, privacy-preserving techniques such as differential privacy deliberately inject random noise into local updates, which further increases the predictive variability. In distributed settings, adversarial or malicious clients can also introduce corrupted updates, amplifying uncertainties. Thus, data uncertainty encompasses noise in data acquisition, the incompleteness of annotations, communication noise, and privacy-induced perturbations.

Model uncertainty. Model uncertainty arises from limitations in the construction and training of federated models. It reflects the instability of model parameters w under heterogeneous and noisy data distributions and is particularly relevant in medical FL, where data are often scarce and imbalanced. In addition, model uncertainty can be used to quantify the effects of model tampering or adversarial manipulations, which are realistic threats in decentralized environments. From a generalization perspective, measuring model uncertainty is crucial to prevent overfitting and to ensure reliable performance across unseen clinical data.

Formally, the Bayesian framework provides a principled way to reason about model and data uncertainty [46]. Model uncertainty is captured as a distribution over parameters w, while data uncertainty is captured as a distribution over predictions $y^{*}$ given parameters w:

$$\begin{array}{cc}\hfill p(y^{*}\mid x^{*},D)& =\int \underset{\mathrm{Data}}{\underbrace{p(y^{*}\mid x^{*},w)}}\underset{\mathrm{Model}}{\underbrace{p(w\mid D)}}dw.\hfill \end{array}$$

(9)

Here, $p(w\mid D)$ is the posterior over the parameters and is generally intractable. Ensemble methods approximate this posterior by averaging over multiple models [47], while Bayesian inference applies Bayes’ theorem [48]:

$$p(w\mid D)={\displaystyle \frac{p(D\mid w)p\left(w\right)}{p\left(D\right)}},$$

(10)

where $p\left(w\right)$ denotes the prior and $p(D\mid w)$ is the likelihood. Loss functions such as cross-entropy or the mean squared error can be derived from log-likelihood maximization [49]. Although exact inference is infeasible, variational and Monte Carlo approximations make Bayesian reasoning practical in FL.

Distributional uncertainty. As discussed in Section 3.1, distributional uncertainty refers to the unpredictability arising from differences in underlying data distributions. It becomes evident when test or deployment distributions shift over time. Formally, distributional uncertainty can be modeled by introducing an intermediate latent variable $\mu$ describing the predictive categorical distribution:

$$p(y^{*}\mid x^{*},D)=\int \int \underset{\mathrm{Data}}{\underbrace{p(y\mid \mu )}}\underset{\mathrm{Distributional}}{\underbrace{p(\mu \mid x^{*},w)}}\underset{\mathrm{Model}}{\underbrace{p(w\mid D)}}d\mu dw.$$

(11)

Here, $p(\mu \mid x^{*},w)$ captures uncertainty over the categorical distribution itself (e.g., modeled via a Dirichlet prior on the softmax output [50]). This formulation highlights the hierarchy: model uncertainty affects distributional uncertainty, which in turn affects data uncertainty.

Although distributional uncertainty is relatively underexplored in centralized learning, it becomes a dominant challenge in FL due to the ubiquity of heterogeneity. Ignoring this uncertainty can significantly degrade the testing performance across clients with diverse and evolving data distributions.

3.3. Comparison with Centralized Learning

While the above analysis highlights the sources of uncertainty within the federated learning pipeline, it is also useful to contrast these with those in conventional centralized training. In centralized learning, all data are pooled into a single repository, which reduces heterogeneity but does not eliminate intrinsic data noise or model limitations. By contrast, federated learning introduces additional sources of uncertainty due to client-specific biases, non-IID distributions, aggregation noise, and personalization divergence.

Table 3. Comparison of uncertainty sources and their impacts on UQ performance in centralized vs. FL.

Uncertainty Category	Centralized Learning	Federated Learning	Performance Impact (Centralized → FL)
Data uncertainty	Large centralized datasets average out label and sensor noise, leading to better-calibrated predictions.	Small, site-specific datasets amplify noise; heterogeneous labeling policies increase variability.	Calibration error increases (worse calibration).
Model uncertainty	Unified optimization and access to full data reduce epistemic uncertainty; confidence better reflects correctness.	Aggregation across clients with limited and diverse data increases epistemic uncertainty; harder to align confidence.	Calibration error increases; reliability of uncertainty decreases.
Distributional uncertainty	Less severe since all data distributions are pooled centrally; OOD samples easier to detect.	Client heterogeneity and non-IID data induce strong distribution shifts; unseen client distributions at server side.	OOD detection performance decreases.

summarizes the main uncertainty types, together with commonly used evaluation metrics and the typical performance shifts observed when moving from centralized to federated settings.

3.4. Privacy-Preserving Mechanisms, Uncertainty, and Security Trade-Offs

Privacy-preserving mechanisms are indispensable in federated medical learning, yet they inevitably affect uncertainty estimation and model reliability. Two commonly used techniques are differential privacy (DP) and homomorphic encryption (HE).

Differential Privacy (DP). DP protects patient-level information by adding random noise to model updates before transmission. This improves confidentiality but directly amplifies data uncertainty. For example, in federated medical imaging tasks, strong privacy budgets (e.g., $ϵ<1$) have been shown to increase calibration errors (higher ECE and NLL) and degrade the out-of-distribution (OOD) detection performance, as the injected noise obscures informative gradients. Thus, while DP ensures rigorous privacy guarantees, it introduces a quantifiable trade-off between confidentiality and reliable UQ.

Homomorphic Encryption (HE). HE enables secure aggregation on encrypted updates, ensuring that the server cannot access raw model parameters. Unlike DP, HE does not inject stochastic noise, but it introduces additional model uncertainty due to the computational overhead, approximation errors in encrypted arithmetic, and increased communication latency. These factors can destabilize global optimization, thereby affecting the consistency of confidence estimates across clients.

Attacks and UQ Mitigation. Despite DP and HE, adversarial threats such as model inversion attacks remain possible, where an attacker reconstructs private patient information from gradients or model outputs. UQ provides a complementary defense: highly uncertain predictions can signal potential leakages or adversarial manipulation, enabling early detection and mitigation. For example, uncertainty-aware anomaly detection can identify abnormal gradient patterns indicative of inversion or reconstruction attempts.

Implications. Overall, DP and HE strengthen security but introduce new challenges for uncertainty-aware federated learning. Balancing these trade-offs requires adaptive privacy budgets, hybrid cryptographic protocols, and the integration of UQ methods not only for reliability but also as an auxiliary defense mechanism against privacy attacks in medical AI.

3.5. Uncertainty Quantification Objective in Federated Learning

3.5.1. Security

In this context, security refers to protecting federated learning systems from adversarial threats and failures, following the well-established CIA triad: confidentiality, integrity, and availability.

Confidentiality: Ensuring that the privacy of each participant’s raw data and model updates is preserved during the federated learning process. This involves techniques such as secure aggregation, homomorphic encryption, and differential privacy to prevent information leakage or unauthorized access during communication.

Integrity: Ensuring the correctness and trustworthiness of model updates in the presence of potentially malicious or faulty clients. This includes defending against poisoning and backdoor attacks, using Byzantine-resilient aggregation, anomaly detection, and update auditing to maintain model reliability.

Availability: Maintaining the ability of the federated system to operate and serve models even under failures or attacks (e.g., denial-of-service, stragglers, or communication faults). This can be achieved with fault-tolerant orchestration, asynchronous protocols, and robust communication mechanisms.

3.5.2. Robustness

Robust Communication: In the distributional setting of federated learning, we typically require numerous rounds of communication, which may result in new noise and errors. It is crucial to develop mechanisms to handle disconnections or failures of participating parties to ensure that the learning process can continue seamlessly without interruptions. These methods typically model the noise and errors in communication.

Non-Typical Data: Ensuring that the federated model remains effective and accurate when dealing with non-typical data, such as noisy and extreme data, thus preventing it from making incorrect predictions.

Missing or Incomplete Data: Due to the privacy demands of federated learning, we usually need to deal with missing or incomplete data.

3.5.3. Generalization

Non-IID Data: The heterogeneity of federated learning environments often breaks the fundamental hypothesis that traditional deep learning relies upon. Effectively coping with this situation usually involves modeling the distributional uncertainties. Avoiding Overfitting: Due to the privacy and distributed requirements of federated learning, data aggregation is frequently performed. Ensuring that the federated model does not overfit the data of a single participant can lead to good performance on new data.

3.5.4. Availability

Efficiency: Ensuring that model updates and the communication overhead in federated learning are controlled and efficient.

Performance: Federated learning implicitly increases the overall complexity of the deep learning model, and effectively tuning the additional global aggregation and personalization weights is crucial for performance.

4. Bayesian Federated Learning (BFL)

This section summarizes relevant studies concerning Bayesian federated learning (BFL), one of the primary categories in uncertainty-related federated learning. We explore different approaches within Bayesian learning (BL) and highlight their respective advantages. BFL effectively incorporates BL principles into FL. This integration utilizes the inherent advantages of BL to address challenges in FL.

4.1. BFL Preliminaries

Bayesian federated learning (BFL) represents a promising solution to overcome the challenges encountered in FL. BFL integrates Bayesian learning (BL) principles into FL frameworks. This integration enhances model robustness and also improves performance, especially when data are limited. BFL effectively addresses uncertainties and process-oriented challenges, offering superior model interpretability. These advances benefit applications such as financial forecasting, disease modeling, and disaster prediction [51].

Although a standardized definition for Bayesian federated learning (BFL) is currently absent, BFL can be viewed as combining the mechanisms of FL and Bayesian learning (BL). Unlike conventional FL, a BFL system seeks to obtain not only point estimates of model parameters but also their full posterior distributions. Specifically, let $D={\left\{D_m\right\}}_{m=1}^M$ denotes all client datasets. BFL aims to learn the global posterior $p(w_g\mid D)$ at the server and the local posteriors $p(w_m\mid D_m)$ on each client m based on its local dataset $D_m={\left\{(x_i^m,y_i^m)\right\}}_{i=1}^{N_m}$. A shared prior distribution $p\left(w\right)$ can be placed on all model parameters to enable Bayesian inference.

The posterior of the global model parameters is

$$p(w_g\mid D)={\displaystyle \frac{p(D\mid w_g)p\left(w_g\right)}{p\left(D\right)}}.$$

(12)

Similarly, the posterior of the local parameters on client m is

$$p(w_m\mid D_m)={\displaystyle \frac{p(D_m\mid w_m)p\left(w_m\right)}{p\left(D_m\right)}}.$$

(13)

In non-personalized BFL, the local parameters $w_m$ are regularized to be close to the global parameters $w_g$. A common federated optimization objective is

$$\underset{w_m,w_g}{\arg \min }\sum _{m=1}^M{\displaystyle \frac{|D_m|}{\left|D\right|}}\ell (w_m;D_m)+\lambda {\parallel w_m-w_g\parallel }^2,$$

(14)

where $\ell (w_m;D_m)$ is the local training loss and $\lambda$ controls the regularization strength.

The true posteriors $p(w_m,w_g\mid D)$ are intractable, so BFL typically employs variational inference (VI) to approximate them with tractable variational distributions $q_{\theta }(w_m,w_g)$. This leads to the following evidence lower bound (ELBO) objective:

$${\mathcal{L}}_{\mathrm{ELBO}}\left(\theta \right)={\mathbb{E}}_{q_{\theta }(w_m,w_g)}\left[\log p(D\mid w_m,w_g)\right]-\mathrm{KL}\left(q_{\theta }(w_m,w_g)\parallel p(w_m,w_g)\right).$$

(15)

Minimizing the Kullback–Leibler (KL) divergence between the variational and true posteriors forms the core objective of BFL. This probabilistic formulation distinguishes BFL from standard FL by enabling uncertainty-aware global aggregation and personalized local adaptation.

BFL tasks and methods can be classified from both Bayesian and federated perspectives. From the Bayesian side, BFL includes client-side methods such as federated Bayesian privacy (FBP), Bayesian neural networks (BNNs) for local models, Bayesian optimization (BO) for local training, and Bayesian non-parametric (BNP) models for dynamic FL. Server-side BFL methods include Bayesian model ensemble (BME), Bayesian posterior decomposition (BPD), and Bayesian continual learning (BCL) for the aggregation of local updates into a global posterior. From the FL perspective, BFL methods can also be categorized as heterogeneous, hierarchical, dynamic, personalized, or hybrid variants.

4.1.1. Approximation Methods for Federated Bayesian Inference

The core of BFL involves computing the global posterior distribution $p\left(\theta \right|D)$, where $D={\cup }_{i=1}^N{D}_i$ is the union of all local datasets. This is computationally intractable for complex models, so two main approximation approaches are commonly used. Each faces distinct challenges in FL.

Variational inference (VI) frames inference as an optimization problem. It approximates the true posterior $p\left(\theta \right|D)$ with a simpler distribution $q(\theta ;\lambda )$ by minimizing the KL divergence:

$${\lambda }^{*}=\arg \underset{\lambda }{\min }\mathrm{KL}(q(\theta ;\lambda )\parallel p\left(\theta \right|D))$$

(16)

In FL, this becomes a distributed optimization problem where clients collaborate to learn global variational parameters.

Markov Chain Monte Carlo (MCMC): This method approximates the posterior by generating samples. These methods are highly accurate. However, they are iterative and require access to the full dataset for each update and pose a significant challenge in FL. For example, a Metropolis–Hastings step requires evaluating the likelihood $p\left(D\right|{\theta }^{\prime })$ for a proposed parameter ${\theta }^{\prime }$, which is distributed across clients.

$$\alpha =\min \left(1,{\displaystyle \frac{p\left({\theta }^{\prime }\right){\prod }_{i=1}^{N}p\left(D_i\right|{\theta }^{\prime })q\left(\theta \right|{\theta }^{\prime })}{p\left(\theta \right){\prod }_{i=1}^{N}p\left(D_i\right|\theta )q\left({\theta }^{\prime }\right|\theta )}}\right)$$

(17)

Federated Variational Inference (FVI)

FVI leverages the additive structure of the ELBO objective. A common strategy is to use a global variational approximation $q(\theta ;\lambda )$ parameterized by $\lambda$. The server maintains $\lambda$ and iteratively refines it by aggregating stochastic gradients from clients:

$$\mathcal{L}\left(\lambda \right)=\sum _{i=1}^N{E}_{q(\theta ;\lambda )}\left[\log p\left(D_i\right|\theta )\right]-\mathrm{KL}(q(\theta ;\lambda )\parallel p\left(\theta \right))$$

(18)

The Algorithm 1 shows the pseudocode of FVI.

Algorithm 1 Federated Variational Inference

1: Server initializes global variational parameters ${\lambda }^{\left(0\right)}$ 2: for round $t=1$ to T do 3:     Server sends ${\lambda }^{(t-1)}$ to participating clients 4:     for each client i in parallel do 5:          Compute local gradient: $g_i^{\left(t\right)}={\nabla }_{\lambda }{\mathcal{L}}_i\left({\lambda }^{(t-1)}\right)$ 6:          Optionally apply differential privacy noise. 7:      end for 8:      Server aggregates: ${\lambda }^{\left(t\right)}={\lambda }^{(t-1)}+\eta {\sum }_i{\displaystyle \frac{|D_i|}{\left|D\right|}}{g}_i^{\left(t\right)}$ 9: end for

Challenges: FVI can suffer from client drift due to non-IID data, and the choice of the variational family $\mathcal{Q}$ imposes a trade-off between flexibility and computational and/or communication costs.

Federated MCMC Methods

This type of method aims to generate samples from the global posterior without centralizing the data. One prominent approach is to run local MCMS chains on each client and periodically synchronize them at the server. Further approaches are as follows.

Likelihood-Weighted MCMC: Clients compute the local likelihood

$$p\left(D_i\right|\theta )=\prod _{x\in D_i}p\left(x\right|\theta )$$

(19)

which is multiplied at the server for the global acceptance decision.

Local–Global MCMC: This alternates between local sampling and global synchronization:

$${\theta }_i^{\left(k\right)}\sim p\left(\theta \right|D_i,{\theta }_{\mathrm{global}}^{(k-1)})$$

(20)

Federated MCMC: These methods are often more communication-intensive than VI. Algorithm 2 shows the pseudocode.

Algorithm 2 Consensus-Based Federated MCMC

Require: Initial global parameters ${\theta }^{\left(0\right)}$, number of rounds T, local steps L 1: for round $t=1$ to T do 2:    Server broadcasts the current global parameter estimate ${\theta }^{(t-1)}$ to all clients. 3:    for each client $i=1$ to N in parallel do 4:       Client i initializes a local MCMC chain (e.g., Langevin dynamics) from ${\theta }^{(t-1)}$: $${\theta }_i^{\left(l\right)}\leftarrow {\theta }_i^{(l-1)}+{\displaystyle \frac{ϵ}{2}}{\nabla }_{\theta }\log p\left({\theta }_i^{(l-1)}\right|D_i)+\sqrt{ϵ}\mathcal{N}(0,I),\mathrm{for}l=1,\dots ,L$$ 5:       Client i sends a summary of its local chain (e.g., the mean ${\mu }_i^{\left(t\right)}$) to the server. 6:    end for 7:    Server aggregates local summaries to form a new global estimate. Under a Gaussian approximation, this can be $${\theta }^{\left(t\right)}={\left(\sum _{i=1}^N{\Sigma }_i^{-1}\right)}^{-1}\left(\sum _{i=1}^N{\Sigma }_i^{-1}{\mu }_i^{\left(t\right)}\right)$$ 8: end for Ensure: Set of global samples $\left\{{\theta }^{\left(t\right)}\right\}$ approximating $p\left(\theta \right|D)$

4.2. Global BFL (Server Side)

The methods of server-side Bayesian federated learning (BFL) encompass the global aggregation or decomposition of updated local models. This research paper provides a comprehensive review and identifies two server-side BFL techniques: (1) Bayesian model ensemble (BME) and (2) Bayesian posterior decomposition (BPD). Furthermore, BFL exhibits applicability in various other settings, such as continual learning, using Bayesian continual learning (BCL) approaches.

4.2.1. Bayesian Model Ensemble (BME) for Federated Learning Aggregation

Bayesian learning (BL) models employ stochastic (e.g., MCMC) or deterministic (e.g., VI) techniques, as introduced by [52,53], to quantify posterior distributions over model parameters. Stochastic methods involve approximating the posterior distribution through random sampling, as outlined by [54]. Consequently, each sample can be considered a Bayesian model ensemble (BME) base learner.

Within the framework of Bayesian model ensemble (BME)-based federated learning, FedBE [55] constructs a global posterior distribution (e.g., Gaussian or Dirichlet) from client parameters during each aggregation round. An ensemble model is then obtained by drawing MCMC samples from this posterior and applied to unlabeled data to produce pseudo-labels. The pseudo-labeled set is subsequently used to refine the global model through stochastic weighted averaging. FedPPD follows a related idea and proposes three aggregation mechanisms, one of which mirrors the ensemble strategy of FedBE. The distinction lies in the local training stage: while FedBE relies on point estimation to derive client parameters, FedPPD instead incorporates a Bayesian neural network (BNN) to model client updates.

Using a Bayesian model ensemble (BME) in server-side FL enables the more effective implementation of Bayesian inference by leveraging information from all clients and mitigating potential model performance degradation, particularly in the case of local models trained on non-IID data. Compared to other approximation methods, the sampling approach used in BME is simpler and offers higher accuracy. However, obtaining an accurate ensemble model requires more samples, increasing the devices’ computational requirements. Additionally, directly obtaining a specific global parameter through BME is not feasible. Therefore, alternative methods for distilling an appropriate global parameter are necessary for client learning in the subsequent communication round.

4.2.2. Bayesian Posterior Decomposition (BPD) for Federated Learning

In many machine learning applications, dividing a complex model into a set of simpler sub-models is both essential and challenging [56]. To address this, model decomposition is often employed. Within Bayesian learning, Bayesian posterior decomposition (BPD) achieves this by partitioning the global model’s posterior into multiple local posteriors.

In Bayesian posterior decomposition (BPD)-based federated learning, FedPA [57] decomposes the global posterior into the product of client-specific posteriors during each communication round by enforcing a uniform prior and assuming independence across local datasets. The parameters of the global posterior are estimated using federated least squares. However, direct computation is expensive in both communication and computation. To address this, the task is reformulated as an optimization problem and solved by sampling. Because independently approximating local posteriors may not yield an accurate global approximation, FedEP [58] improves upon FedPA by applying expectation propagation to obtain a better global model. Similarly, ref. [59] adopts the same decomposition strategy as FedPA but incorporates quantized Langevin stochastic dynamics (QLSD), transmitting compressed gradients to reduce the communication overhead. Unlike these methods, FOLA employs BPD to express the global posterior as a weighted product of local posteriors without imposing restrictive assumptions. VIRTUAL [60] also applies BPD for server-side aggregation, where the global posterior in each round is decomposed into the product of the previous global posterior and the ratios of client posteriors from the current round, helping to mitigate catastrophic forgetting.

Most FL methods commonly employ naive parameter averaging, such as FedAVG, for model aggregation. However, this approach can lead to performance degradation when dealing with local data that exhibit statistical heterogeneity. In contrast, by decomposing the global posterior model, BPD-based FL models demonstrate enhanced stability on heterogeneous data. Moreover, BPD offers the advantage of improved interpretability in FL models. Nevertheless, BPD also presents certain challenges in the FL context. Firstly, it may necessitate additional algorithms to aid in model learning, which can result in substantial computational overhead or intractability. Secondly, certain decomposition methods may impose strong constraints that are often impractical to satisfy when solving real-world problems.

4.2.3. Bayesian Continual Learning for Continual FL

Continual learning addresses the challenge of training models on datasets that arrive sequentially and may evolve over time [61]. In Bayesian learning, this is achieved by reusing the posterior from a previous task as the prior for the next, forming the basis of Bayesian continual learning (BCL).

Within FL, FOLA [62] applies BCL by constructing the global posterior as the product of local posteriors in each round, rather than relying on a simple mixture. This design improves the robustness when handling non-IID client data. Similarly, pFedBayes updates the prior of each local model with the global distribution obtained from the previous round, improving both the performance and interpretability. Although they share the same foundation, the two methods differ in two ways. First, pFedBayes derives the global distribution incrementally through local model averaging, while FOLA aggregates local posteriors directly. Second, pFedBayes uses BNNs for clients, whereas FOLA relies on conventional neural networks.

Applying Bayesian continual learning (BCL) to FL allows us to benefit from the accumulated knowledge gathered from previous communication rounds. This online learning approach often leads to improved learning performance. However, a complex prior distribution can introduce significant computational overhead to the modeling process and may only provide limited performance gains. Finding the right balance between utilizing BCL and selecting an appropriate prior distribution for FL poses a challenging task. It requires careful consideration to achieve a trade-off that maximizes the advantages of BCL while avoiding excessive computational costs and potential limitations in performance improvement.

4.3. Local BFL (Client Side)

Different Bayesian techniques cater to the client’s needs and facilitate the learning of local models. Local methods (client side) encompass (1) Bayesian optimization (BO), (2) Bayesian neural networks (BNNs), (3) federated Bayesian privacy (FBP), and (4) Bayesian non-parametrics (BNP). These methods are selected based on individual clients’ unique objectives and requirements.

4.3.1. BO Bayesian Federated Learning Learning Optimization

Bayesian optimization (BO) is commonly used to optimize the hyperparameters of deep neural networks (DNNs) sequentially. It has also been applied in FL approaches. The study [63] proposed a federated Bayesian optimization (FBO) framework called FTS, which utilizes BO to optimize local models in each communication round. FTS employs a Gaussian process (GP) as a surrogate model for the objective and acquisition functions, using Thompson sampling and random Fourier features to enhance scalability and information exchange. The FTS algorithm guarantees convergence even with non-IID data. In a different study [64], BO is employed for traffic flow prediction (TFP) in FL. Unlike FTS, their FBO approach dynamically adjusts the weights of local models using BO, avoiding performance degradation with heterogeneous data. The acquisition function in FBO for TFP is based on the expected improvement, addressing the scalability challenges associated with GP. The application of Bayesian optimization (BO) in FL demonstrates its effectiveness in achieving robust learning performance, particularly for non-IID local datasets. BO possesses inherent properties that contribute to this robustness. Compared to traditional optimization algorithms, BO offers a simpler and more convenient implementation process. However, when considering the practicality of federated Bayesian optimization (FBO), challenges arise when dealing with models involving substantial data points. Additionally, the convergence rate of FBO is relatively slow, indicating the need for further investigation and improvement to enhance its efficiency.

4.3.2. Bayesian Neural Networks (BNN)

The study [65] introduced Bayesian neural networks (BNNs), combining Bayesian inference with neural networks. In FL, BNNs are integrated in various ways. Ref. [51] proposed pFedBayes, using BNNs to train local models in each communication round. pFedBayes employs variational inference (VI) to approximate posterior distributions at the client level and aggregates models at the server level. Sadilek et al [66] extended pFedBayes by updating local parameters again after BNN updates, addressing non-IID data challenges. FedPPD [67] also uses BNNs for local models but approximates posterior distributions using Markov Chain Monte Carlo (MCMC). FedPPD employs a Bayesian dark knowledge method to distill posterior distributions into a single DNN per client, sent to the server for aggregation.

The integration of Bayesian neural networks (BNNs) in FL offers several advantages, including the ability to quantify local uncertainty and improve robustness by leveraging deep neural networks (DNNs) for task learning. BNNs also enhance learning performance in FL settings with limited data. However, the adoption of BNNs in FL presents its own set of challenges. Firstly, training local models with BNNs incurs significant computational and memory costs, particularly when dealing with large-scale local model parameters. Secondly, selecting appropriate prior distributions for local model parameters becomes challenging, particularly when complex relationships between model outputs and parameters cannot be accurately estimated. These challenges must be addressed to exploit the potential benefits of BNNs in FL.

4.3.3. Federated Bayesian Privacy (FBP)

FL models have primarily focused on preserving privacy in federated learning, communication, and aggregation, often making differential privacy advancements, as [68] demonstrates. Differential privacy methods encompass techniques such as simple statistics, object perturbation, and output perturbation. The study [69] introduced Bayesian differential privacy (BDP), which considers the randomness of local data. BDP ensures client privacy, instance privacy, and joint privacy through a privacy loss accounting method. In another study [70], KL divergence is used to quantify Bayesian privacy loss during data restoration. This approach forms the basis for the federated deep learning for private passport (FDL-PP) method, which is designed to mitigate FL restoration attacks and enhance privacy preservation.

Bayesian differential privacy (BDP) and the federated deep learning for private passport (FDL-PP) method represent advancements in relaxing constraints on existing FL differential privacy approaches by incorporating uncertainty. While BDP and FDL-PP offer improved privacy preservation, it is important to note that they may still face limitations when applied to complex FL and BL settings and more stringent privacy-preserving requirements. Further research and development are necessary to address these challenges and enhance the applicability of privacy-preserving techniques in FL.

4.3.4. Bayesian Non-Parametric Models for Dynamic Federated Learning

Dynamic learning is facilitated by Bayesian non-parametric (BNP) models, as demonstrated by [71]. In Bayesian federated learning (BFL), BNP models utilize Gaussian or Beta-Bernoulli processes (BBP). In GP-based federated learning, pFedGP, proposed by [72], employs a Gaussian process (GP) classifier to train the local model for every client while sharing a common kernel method across all clients. FedLoc, introduced by [73], also utilizes GP to train local models for regression tasks. However, unlike pFedGP, FedLoc does not handle non-IID [31] data in the federated learning setting. In contrast to these approaches, FedCor, developed by [74], employs GP to predict changes in loss and selects clients to be activated in each communication round based on these loss changes. It is important to note that FedCor is specifically designed for the cross-silo federated learning framework, where the learning performance significantly deteriorates when dealing with non-IID data.

Bayesian non-parametric (BNP) models offer the advantage of adaptable model complexity to effectively train local models in FL, surpassing the limitations of parametric methods, as demonstrated by [75]. BNP models can flexibly adjust to the data, enabling more efficient learning. However, it is important to note that the complexity of BNP models increases as the number of data grows, which poses computational challenges for clients dealing with large datasets in the FL setting. This computational requirement for BNP models in FL can potentially limit their scalability and practicality in real-world scenarios. Further research and optimization are needed to address the computational burden associated with BNP models and enhance their applicability in FL systems.

4.4. Other Bayesian Federated Learning Studies

4.4.1. Calibrated Bayesian Federated Learning

The study [76] presents an algorithm called $\beta$-Predictive Bayes for Bayesian federated learning. The algorithm addresses the challenges in terms of communication costs, performance with heterogeneous data, and calibration in FL. It operates in a single round of communication and aims to produce well-calibrated models with accurate uncertainty estimates. The proposed $\beta$-Predictive Bayes algorithm was evaluated on various regression and classification datasets, demonstrating its superiority in calibration compared to other baselines, even with increasing data heterogeneity. The paper provides access to the code for the algorithm, enabling further exploration and replication in experiments.

Additionally, it highlights the limitations of existing Bayesian FL techniques, such as the Bayesian Committee Machine (BCM), which can suffer from calibration issues and produce overconfident predictions. To address these limitations, the authors apply the $\beta$-Predictive Bayes algorithm, which combines the advantages of the BCM and a mixture model over local predictive posteriors. This approach results in an ensemble model that is then distilled into a single model to be sent back to clients. The proposed algorithm offers improved calibration and accurate uncertainty estimates, making it suitable for FL scenarios with limited training data or high variance. While the paper does not provide specific details about the scalability and computational efficiency of the algorithm, it highlights its effectiveness in addressing the challenges of FL. It provides a valuable contribution to the field.

4.4.2. Bayesian FL Using Meta-Variational Dropout

Ref. [77] proposes a Bayesian meta-learning framework, named Meta-Variational Dropout (MetaVD), for personalized federated learning (PFL). The method tackles the issues of overfitting and divergence among client models that often arise from limited and non-IID data in conventional federated learning. MetaVD employs a shared hypernetwork to infer client-specific dropout rates, which supports effective personalization under data heterogeneity. In addition, it integrates a posterior aggregation scheme that leverages dropout uncertainty across clients, thereby improving convergence on non-IID distributions. Experimental results on multiple FL benchmarks confirm the effectiveness of MetaVD, showing strong classification accuracy and reliable uncertainty calibration, particularly for out-of-distribution clients. The approach also provides model compression, alleviating overfitting and lowering the communication overhead. Overall, MetaVD represents a novel solution to key FL challenges, achieving notable gains in personalization, stability, and efficiency.

Despite its contributions, the cited paper has certain limitations. While MetaVD demonstrates notable performance in FL scenarios, the experiments focus mainly on sparse and non-IID datasets, potentially limiting its generalizability to other data distributions. Further investigation of diverse FL settings would enhance our understanding of MetaVD’s robustness and effectiveness. Secondly, although the paper presents the advantages of model compression through MetaVD’s integration of variational dropout (VD), it does not extensively explore the implications of this model compression technique. A more comprehensive analysis of the trade-off between model size reduction and predictive performance would further elucidate the benefits and limitations of this approach. Lastly, while the authors emphasize the posterior adaptation view of meta-learning and the posterior aggregation view of Bayesian FL, they could provide additional insights into the theoretical underpinnings and implications of these perspectives, strengthening the theoretical foundation of MetaVD.

4.4.3. Integrated Multiple Uncertainty Approaches in FL

This research study [78] integrates different approaches for UQ in federated deep learning, focusing on achieving trustworthy machine learning and preserving data privacy. The authors investigate prominent methods such as MC dropout, stochastic weight averaging Gaussian (SWAG), and deep ensembles, demonstrating their effectiveness in the FL framework. The empirical evaluation confirms that these approaches enable reliable UQ on out-of-distribution data without significant additional communication. The paper emphasizes that, while all methods perform well, deep ensembles and MC dropout offer the better identification of out-of-distribution data and misclassified instances based on uncertainty. Overall, this research provides valuable insights into UQ in federated deep learning, serving as a baseline for future developments in the field.

While the cited paper presents valuable insights, there are a few limitations. First, the empirical evaluation is limited to specific datasets and may not fully capture the generalizability of the proposed approaches across different domains. Further experiments on diverse datasets would strengthen the validity and reliability of the findings. Additionally, the paper focuses on integrating existing UQ methods into FL, without introducing novel techniques. Future research could explore the development of new approaches tailored specifically to UQ in federated deep learning, potentially addressing some of the limitations of the current methods.

4.4.4. Minimization of Uncertainty for Personalized FL (Semi-Supervised) Systems

The study [79] proposes a semi-supervised learning paradigm for personalized FL to overcome challenges such as data heterogeneity, a lack of knowledge for personalized global models, and performance fairness. It allows partially labeled or unlabeled clients to seek labeling assistance from data-related clients, leveraging supervised training on pseudo-labels to improve performance. The paper introduces a data relation metric based on uncertainty estimation to select trustworthy helpers and presents a helper selection protocol for efficiency. Experimental results demonstrate the method’s superiority, especially in highly heterogeneous settings with partially labeled data.

However, the method assumes the availability of data-related clients for labeling assistance, which may not always be feasible in practical scenarios. The effectiveness of the method relies on the presence of suitable data-related clients. Additionally, while the paper focuses on performance fairness, it does not explicitly address privacy concerns about exchanging labeled and unlabeled data between clients. Future research should explore privacy-preserving mechanisms to ensure data security in the proposed personalized FL paradigm.

4.4.5. Bayesian Method for Personalized FL

The study [80] introduces a new methodology for personalized FL by introducing a Bayesian approach called FedPop. The paper addresses the limitations of existing FL approaches by incorporating UQ and handling issues related to personalization in cross-silo and cross-device settings. The FedPop framework combines fixed common population parameters and random effects to model client data heterogeneity. It utilizes a new class of federated stochastic optimization algorithms based on Markov chain Monte Carlo (MCMC) methods to ensure convergence and enable UQ. The suggested methodology is robust to client drift and practical for inference on new clients and allows for efficient computation and memory usage. The paper provides non-asymptotic convergence guarantees and demonstrates the performance of FedPop in various personalized FL tasks.

While FedPop offers several advantages, there are some limitations to consider. The paper does not extensively discuss the scalability of the approach, particularly in scenarios with a large number of clients or high-dimensional data. The computational requirements of MCMC-based optimization algorithms may become a limitation when dealing with complex models or resource-constrained devices. Additionally, the paper does not provide an extensive comparison with other state-of-the-art personalized FL methods, which could further highlight the advantages and limitations of the FedPop approach. Future research should explore these aspects to assess the scalability and performance of FedPop in real-world FL scenarios.

Table 4. Representative works on BFL.

Ref.	Focus/Setting	Main Contribution
[55]	Bayesian model ensemble (BME) for FL	Introduces FedBE, which constructs a global posterior from client parameters and samples via MCMC to form an ensemble model; applies pseudo-labeling and knowledge distillation to improve aggregation on non-IID data.
[67]	Posterior aggregation with Bayesian neural networks (BNNs)	Extends FedBE by incorporating BNNs at the client side; uses Bayesian dark knowledge distillation to aggregate local posteriors more effectively.
[57]	Posterior decomposition (FedPA)	Proposes Bayesian posterior decomposition (BPD) by factorizing the global posterior into local posteriors under strong constraints; solves via optimization with sampling.
[58]	Expectation propagation (FedEP)	Extends FedPA with expectation propagation to approximate a global posterior, improving robustness to heterogeneity.
[59]	Quantized Langevin dynamics (QLSD) for BPD	Applies BPD with QLSD-based client updates, compressing gradients to reduce communication costs.
[60]	Variational continual learning (VIRTUAL)	Decomposes the global posterior into the product of previous and current round distributions, mitigating catastrophic forgetting in continual FL.
[62]	Bayesian continual learning	Uses product of local posteriors to form the global posterior, enabling robust continual FL on non-IID data.
[51]	Personalized FL with BNNs	Employs variational inference with BNNs for client models; local priors are updated with global posteriors to improve personalization.
[63]	Federated Bayesian optimization (FBO)	Introduces Gaussian process-based BO to optimize local hyperparameters in each round; ensures convergence under non-IID data.
[64]	FBO for traffic flow prediction	Adapts FBO to dynamically adjust client weights in traffic prediction, addressing heterogeneity with an expected improvement acquisition function.
[69]	Bayesian differential privacy (BDP)	Incorporates randomness of local data to ensure client, instance, and joint privacy in FL.
[70]	Federated deep learning for private passport (FDL-PP)	Uses KL divergence to quantify privacy leakage and design privacy-preserving mechanisms against restoration attacks.
[72]	Bayesian non-parametrics (Gaussian Processes)	Introduces GP-based personalized FL, sharing kernels across clients for classification tasks.
[73]	FedLoc with Gaussian Processes	Uses GP models for regression tasks in FL; lacks handling of non-IID distributions.
[74]	FedCor with GP client selection	Predicts loss changes with GP and activates clients accordingly, designed for cross-silo FL.
[76]	Calibrated BFL	Proposes a single-round ensemble method improving calibration over BCM; distills predictive ensembles into a global model.
[77]	Bayesian meta-variational dropout for PFL	Introduces MetaVD using hypernetworks for client-specific dropout rates, enabling personalization and model compression in non-IID settings.
[78]	UQ approaches in FL	Benchmarks MC dropout, SWAG, and deep ensembles for UQ in FL; shows that deep ensembles and MC dropout perform best for OOD detection.
[79]	Semi-supervised personalized FL	Introduces uncertainty-based helper selection to improve learning with partially labeled clients; leverages pseudo-labeling for fairness and performance.
[80]	Bayesian personalized FL with population priors	Combines population parameters and client-specific random effects; employs MCMC-based optimization with convergence guarantees, robust to client drift.

summarizes the mentioned Bayesian federated learning (BFL) families, their foci, and key ideas. As a predominant uncertainty-aware paradigm in FL, BFL grounds predictions in posterior reasoning and yields calibrated, principled uncertainty estimates. However, practical deployments must balance computational/communication overheads, prior/model misspecification, and brittleness under non-IID data and privacy noise. Emerging directions include scalable posterior representations, communication-efficient VI/MCMC, continual Bayesian updates, and calibrated personalization via hierarchical/empirical priors. These considerations motivate the complementary perspective of federated conformal prediction, which offers distribution-free coverage guarantees and can be combined with BFL to improve the reliability in heterogeneous clinical environments.

5. Federated Conformal Prediction

This section summarizes representative studies on federated conformal prediction (FCP), a principal uncertainty-aware paradigm in FL that provides distribution-free, finite-sample coverage guarantees for prediction sets across clients. Unlike Bayesian approaches that model posteriors over parameters, FCP calibrates a (possibly pre-trained) predictor post hoc and is therefore model- and loss-agnostic, making it attractive for heterogeneous, privacy-sensitive deployments. Recent works extend CP to federated settings by relaxing exchangeability, accounting for client heterogeneity (covariate/label shift), and improving systems’ efficiency and robustness.

5.1. FCP Preliminaries

Let $\mathcal{D}=(z_1,\dots ,z_n)$ represent a dataset of size n, where each element $z_i=(x_i,y_i)$ denotes an input–output pair sampled from a distribution $\mathcal{P}$. The input domain is $\mathcal{X}$, the output domain is $\mathcal{Y}$, and together they define the sample space $\mathcal{Z}=\mathcal{X}\times \mathcal{Y}$. For a target coverage level $1-\alpha \in (0,1)$, the task is to construct a prediction set ${\mathrm{\Gamma }}^{1-\alpha }:\mathcal{X}\to \mathrm{subsets}\mathrm{of}\mathcal{Y}$ such that, for a fresh draw $(X,Y)\sim \mathcal{P}$,

$$\mathbb{P}!\left(Y\in {\mathrm{\Gamma }}^{1-\alpha }\left(X\right)\right)\ge 1-\alpha .$$

(21)

We say that ${\mathrm{\Gamma }}^{1-\alpha }$ covers Y when $Y\in {\mathrm{\Gamma }}^{1-\alpha }\left(X\right)$. A prediction region is regarded as valid if it satisfies condition (21), which is also referred to as the coverage guarantee or validity property.

Assessing the uncertainty associated with model predictions is essential in risk-aware decision making. Prediction sets provide probabilistic bounds for the target variable, indicating regions where future outcomes are expected to lie with a specified confidence level. One can build prediction regions via parametric likelihood/Bayesian modeling or by using distribution-free methods that make no distributional assumptions. Conformal prediction (CP) is a simple, distribution-free framework that wraps around any underlying predictive model to produce valid prediction sets. CP is notable because it achieves finite-sample validity under mild assumptions. Originating from the work of Vovk and Shafer on finite random sequences [81], CP is popular due to its simplicity and low computational cost [82,83], with applications across domains [84,85,86]. Current research roughly comprises three branches: (i) algorithmic variants tailored to specific learners, e.g., quantile regression [87,88], k-NN [89], density estimators [90], survival analysis [91,92], and risk control [93]; (ii) relaxing exchangeability to handle distribution shift [94,95,96,97,98]; and (iii) improving efficiency/sharpness [88,99,100,101,102]. The time-series algorithms that we focus on fall mainly within the latter two branches.

We now formalize CP and introduce the required notation.

Given $(X,Y)\sim \mathcal{P}$ and target coverage $1-\alpha \in (0,1)$, CP seeks a valid predictor ${\mathrm{\Gamma }}^{1-\alpha }$ such that

$$\mathbb{P}\left(Y\in {\mathrm{\Gamma }}^{1-\alpha }\left(X\right)\right)\ge 1-\alpha .$$

(22)

Validity alone is trivial (e.g., take ${\mathrm{\Gamma }}^{1-\alpha }\left(x\right)=\mathcal{Y}$). In practice, we also seek efficiency/sharpness, i.e., regions with small measurements (length/area/volume), while maintaining validity.

Let $\mathcal{D}=(z_1,\dots ,z_n)$. Split (or inductive) CP partitions $\mathcal{D}$ into a proper training set ${\mathcal{D}}_{\mathrm{train}}=(z_1,\dots ,z_m)$ with $m<n$ and a calibration set ${\mathcal{D}}_{\mathrm{cal}}$ of size $n-m$.

A key component is the non-conformity score $\mathcal{S}:{\mathcal{Z}}^m\times \mathcal{Z}\to \mathbb{R}$, which measures how atypical a sample z is relative to ${\mathcal{D}}_{\mathrm{train}}$. A common regression choice is the absolute residual under a model $\widehat{f}$ trained on ${\mathcal{D}}_{\mathrm{train}}$:

$$\mathcal{S}\left((x,y),{\mathcal{D}}_{\mathrm{train}}\right):=|y-\widehat{f}\left(x\right)|.$$

(23)

When unambiguous, we write $\mathcal{S}(z,\widehat{f})$.

Train a predictor $\widehat{f}$ on ${\mathcal{D}}_{\mathrm{train}}$; compute calibration scores $s_i=\mathcal{S}(z_i,\widehat{f})$ for $z_i\in {\mathcal{D}}_{\mathrm{cal}}$. Let

$$q_{1-\alpha }=Q\left({\displaystyle \frac{\lceil (n_{\mathrm{cal}}+1)(1-\alpha )\rceil }{n_{\mathrm{cal}}+1}},{\left\{s_i\right\}}_{i\in \mathrm{cal}}\cup \{\infty \}\right),$$

where $n_{\mathrm{cal}}=\left|{\mathcal{D}}_{\mathrm{cal}}\right|$ and $Q(p,·)$ is the empirical p-quantile. Then, the $(1-\alpha )$ prediction set at a new x is

$${\mathrm{\Gamma }}^{1-\alpha }\left(x\right)=\left\{y\in \mathcal{Y}:\mathcal{S}\left((x,y),\widehat{f}\right)\le q_{1-\alpha }\right\}.$$

Regarding exchangeability, the data points $z_1,\dots ,z_n$ and the test point $z_{n+1}$ are exchangeable:

$$(z_1,\dots ,z_{n+1})\stackrel{d}{=}(z_{\pi \left(1\right)},\dots ,z_{\pi (n+1)}),$$

for any permutation $\pi$ of $\{1,\dots ,n+1\}$. Exchangeability is weaker than IID and often reasonable. Later, we review variants that relax this assumption to handle distribution shift.

For scores $s_{1:n}=\{s_1,\dots ,s_n\}$, define the empirical p-quantile

$$Q(p,s_{1:n}):=\inf \left\{s^{\prime }:{\displaystyle \frac{1}{n}}\sum _{i=1}^n\mathbf{1}\{s_i\le s^{\prime }\}\ge p\right\}.$$

(24)

As shown in Algorithm 3, the above is split CP. Full CP avoids splitting but retrains the model n times (leave one out), which is often impractical for deep models. Although we focus on regression, CP extends to classification, segmentation, and outlier detection; see Vovk et al. [81], Angelopoulos and Bates [83].

Algorithm 3 Split Conformal Prediction (Regression)

Require: Dataset $\mathcal{D}={\left\{(x_i,y_i)\right\}}_{i=1}^n$, learning algorithm $\mathcal{A}$, test input $x_{n+1}$, target confidence $1-\alpha$ Ensure: Prediction region ${\mathrm{\Gamma }}^{1-\alpha }\left(x_{n+1}\right)$   1: Randomly split $\mathcal{D}$ into ${\mathcal{D}}_{\mathrm{train}}$ and ${\mathcal{D}}_{\mathrm{cal}}$ with $|{\mathcal{D}}_{\mathrm{cal}}|=n_{\mathrm{cal}}$   2: Train $\widehat{f}\leftarrow \mathcal{A}\left({\mathcal{D}}_{\mathrm{train}}\right)$   3: Compute calibration scores ${\mathbf{s}}_{\mathrm{cal}}\leftarrow \{\mathcal{S}((x_i,y_i),\widehat{f}):(x_i,y_i)\in {\mathcal{D}}_{\mathrm{cal}}\}$   4: Compute $q_{1-\alpha }\leftarrow Q\left({\displaystyle \frac{\lceil (n_{\mathrm{cal}}+1)(1-\alpha )\rceil }{n_{\mathrm{cal}}+1}},{\mathbf{s}}_{\mathrm{cal}}\cup \{\infty \}\right)$   5: return ${\mathrm{\Gamma }}^{1-\alpha }\left(x_{n+1}\right)\leftarrow \{y:\mathcal{S}((x_{n+1},y),\widehat{f})\le q_{1-\alpha }\}$

5.2. Federated Conformal Prediction (FCP) Methodology

Conformal prediction (CP) is becoming increasingly popular as it provides a reliable framework for accurately measuring uncertainty. The key benefit of this approach is its simplicity when applying it as a post-processing step to pre-trained models, offering assurances independent of the data distribution and with minimal assumptions. Implementing this method is vital in guaranteeing forecasts’ dependability, as it can tackle prevalent obstacles, including inaccurately calibrated probabilities generated by models, which often lead to excessively huge prediction sets. Nevertheless, despite its merits, it encounters notable obstacles, particularly in FL settings. One significant constraint is its strong dependence on the data exchangeability criterion, which often fails to be satisfied in real-world scenarios. Due to computing limitations, the current approaches to addressing non-exchangeability are not practically viable for more complex scenarios. This poses a significant obstacle to the extensive implementation of CP, particularly in crucial fields like healthcare and protecting patient confidentiality. Effective UQ is critical to FL, where several clients cooperatively train models while maintaining decentralized training data. Despite recent progress in FL, the UQ subject is only partially resolved. Incorporating federated models into clinical practice may face inadequate calibration and limited interpretability. These issues might result in the misuse of technologies in critical decision-making processes. Conformal prediction’s capacity to provide prediction sets that include true labels with a specified coverage guarantee is a notable solution to these difficulties.

The study [103] discusses a methodology for improving conformal prediction, a statistical method used to generate prediction sets with a pre-determined degree of confidence. The main objective is to enhance the adaptive prediction sets (APS) method, which primarily relies on softmax probabilities. The distribution of these probabilities frequently exhibits a long-tailed pattern, including several low-probability classes, leading to needlessly huge prediction sets. Furthermore, ref. [104] explores the intricacies of federated inference over wireless channels. The research offers valuable insights into effectively handling uncertainty in dispersed contexts, a crucial factor to consider regarding real-time medical monitoring and treatments.

In 2023, Plassier et al. made notable progress in FCP by presenting two research studies. Each study focused on a key issue in medical federated learning: the diversity of data and the occurrence of label changes. The initial study [105] explores the intricacies of conformal prediction in varied data ecosystems, emphasizing the necessity of resilient predictive models that can uphold accuracy despite the diverse data distributions commonly found in medical contexts. The second research work [106] focuses on efficiency, specifically optimizing conformal prediction to tackle label shifts, which are inconsistencies in label distributions among various data sources. These articles improve the comprehension and demonstrate the practicality of FCP by guaranteeing that predictive models are responsive to the intricacies of medical data, maintain privacy, remain relevant in many situations, and sustain a high level of dependability. Lastly, ref. [107] presents innovative methods for distribution-free federated learning. The paper underscores the importance of enhancing model robustness and reliability through conformal prediction techniques, thereby paving the way for the broader adoption of FCP in medical applications.

Moreover, based on the existing research, we classify federated conformal prediction (FCP) into two broader categories. The subsequent subsections summarize research on these broader perspectives, specifically addressing data heterogeneity and alleviating exchangeability assumptions in federated learning settings. These categories cover a variety of methodologies and technologies that address the specific issues presented by diverse data and the limits of typical conformal prediction methods in unconventional data scenarios.

These collective efforts in exploring and refining the realms of conformal prediction and federated conformal prediction underscore these methodologies’ pivotal role in shaping the future of medical federated learning, particularly in ensuring that predictions are data-driven, context-aware, and clinically reliable.

5.3. FCP Under Data Heterogeneity

Data heterogeneity is a critical challenge in federated learning, particularly in medical settings, where data are sourced from diverse institutions, each with unique patient populations, data collection protocols, and device configurations. This diversity in data can lead to significant inconsistencies and biases in model training and performance.

The study [106] addresses this issue directly. The paper explores how conformal prediction can be tailored to work effectively in environments with non-exchangeable data distributions. By focusing on calibration for data uncertainty, the study offers strategies to improve prediction reliability in federated learning settings characterized by data diversity. Similarly, the study [105] delves into the complexities introduced by statistical heterogeneity, specifically label shifts across different datasets. The research presents methods to maintain prediction accuracy and reliability even when the underlying data distribution varies, ensuring that the predictive models remain robust and clinically relevant.

The study [108] introduces federated conformal prediction (FCP) to tackle the issue of data heterogeneity in federated learning. The authors recognize that the diversity of data among clients contradicts the principles of exchangeability necessary for conformal prediction. To address this problem, the paper presents the notion of partial exchangeability. The FCP framework offers both theoretical assurances and empirical assessments in the presence of diverse data, showcasing its efficacy in enhancing reliability and accuracy in practical situations. The study extends the application of conformal prediction to the federated learning context and presents a realistic method for integrating meaningful uncertainty quantification in dispersed and diverse contexts. The empirical assessments encompass several medical imaging datasets, emphasizing the actual implementation of the FCP framework. In summary, it provides a solution for situations when data privacy and heterogeneity are major considerations.

Recent advances have further pushed the boundaries of FCP. Li et al. [109] proposed FCP-Pro, a prototype similarity-based federated conformal prediction algorithm that addresses data heterogeneity and label distribution shifts. By introducing the Prototype-Based Adaptive Prediction Set (PAPS) score function and integrating label shift and similarity calibration weighting, FCP-Pro achieves significantly smaller prediction sets while preserving theoretical coverage guarantees. Extensive experiments on CIFAR-10, CIFAR-100, and ImageNet demonstrate that FCP-Pro provides tighter and more reliable uncertainty estimates compared to prior FCP approaches, even under non-IID distributions. This work represents a notable step toward making conformal prediction more practical and trustworthy in federated medical learning scenarios. In summary, these studies highlight the importance of addressing data heterogeneity to ensure that the predictive models are accurate, equitable, and generalizable across different medical contexts.

5.4. Alleviating Exchangeable Assumptions in FCP

Conventional conformal prediction methods frequently depend on the concept of exchangeability, which assumes that the data points may be interchanged without altering the result. Nevertheless, this assumption might be too limiting and invalid in practical situations, particularly in federated learning environments.

The paper [108] presents a new method that relaxes the exchangeability assumption. The study introduces federated conformal predictors to improve the reliability in federated learning environments. The research offers a flexible and realistic framework for quantifying uncertainty in distributed learning settings. It achieves this by assuring calibration under partial exchangeability, which is less strict. In addition, the study [107] investigates techniques for federated learning that do not rely on assumptions about the data distribution. The work presents conformal prediction algorithms that do not depend on the conventional assumption of exchangeable data, thereby improving the resilience and dependability of the models. This strategy is especially advantageous for medical federated learning, as the data distribution across multiple nodes may differ.

These contributions are crucial in developing federated learning and conformal prediction approaches, providing more flexible and dependable tools for quantifying uncertainty in complicated, real-world situations.

5.5. Byzantine-Robust Federated Conformal Prediction

Although federated conformal prediction (FCP) provides statistical coverage guarantees for uncertainty quantification, it is highly vulnerable to Byzantine failures, where a fraction of malicious clients may arbitrarily manipulate their contributions. This limitation poses significant risks in sensitive domains such as healthcare, where adversarial behavior can severely undermine the reliability of predictive models.

The work [110] introduces Rob-FCP, the first certifiably Byzantine-robust framework for federated conformal prediction. The method is designed to guarantee reliable coverage even in the presence of malicious clients. Specifically, the authors establish theoretical bounds on the coverage under Byzantine threats and further propose a malicious client number estimator to handle cases when the exact fraction of attackers is unknown. The estimator is accompanied by rigorous theoretical guarantees, ensuring that the calibration process remains valid under adversarial conditions. Extensive experiments on benchmark datasets and real-world medical data demonstrate that Rob-FCP maintains near-ideal coverage and competitive prediction set sizes despite Byzantine manipulations, whereas conventional FCP approaches degrade significantly.

These contributions advance the robustness of conformal prediction in federated learning, providing a critical safeguard for its deployment in high-stakes applications. By integrating conformal prediction with Byzantine resilience, Rob-FCP offers both theoretical assurance and empirical effectiveness, paving the way for reliable uncertainty quantification in adversarial federated environments.

Table 5. Representative works on federated conformal prediction (FCP).

Ref.	Focus/Setting	Main Contribution
[107]	Distribution-free federated learning with conformal predictions	Introduces conformal prediction methods that relax distributional assumptions, ensuring validity without requiring exchangeability; improves resilience in heterogeneous medical federated learning.
[108]	Federated conformal predictors for distributed UQ	Proposes a general framework for federated conformal prediction under partial exchangeability; provides calibration guarantees across distributed clients.
[111]	One-shot federated conformal prediction	Develops a one-shot FCP method that reduces communication costs while maintaining uncertainty calibration; especially useful in bandwidth-constrained federated settings.
[105]	FCP under label shift	Introduces methods to handle federated UQ when data across clients suffer from label shift; adapts conformal prediction to non-identical distributions.
[104]	Reliable UQ over wireless channels	Explores federated inference with conformal prediction in wireless communication systems; addresses challenges of reliability and uncertainty propagation over noisy channels.
[110]	Byzantine-robust FCP	Proposes Rob-FCP, the first certifiably Byzantine-robust FCP framework; provides theoretical coverage guarantees under adversarial clients and validates on benchmark and medical datasets.

summarizes representative federated conformal prediction (FCP) works, their settings, and the main contributions. As a complementary uncertainty-aware paradigm to Bayesian FL, FCP provides distribution-free, finite-sample coverage guarantees across clients but, in practice, must balance larger prediction sets under shift, sensitivity to the calibration set composition, and the overhead of cross-site quantile aggregation under communication constraints. Emerging directions include partial/group-wise exchangeability for heterogeneous cohorts, label shift-aware calibration, one-shot and bandwidth-aware protocols for wireless deployments, and certifiably Byzantine-robust FCP. Together, these advances position FCP as a practical layer atop FL pipelines—and a natural companion to BFL—combining posterior reasoning with coverage guarantees to enhance reliability in real-world, heterogeneous medical environments.

5.6. Conformal Prediction Under Non-IID Challenges

Conformal prediction (CP) provides distribution-free, finite-sample guarantees for prediction sets under the assumption of exchangeability (a stronger condition than IID). The non-IID nature of FL data directly violates this assumption, threatening the validity of the coverage guarantee $\mathbb{P}(Y_{\mathrm{test}}\in C\left(X_{\mathrm{test}}\right))\ge 1-\alpha$.

1.

Localized CP: Each client i calibrates its own prediction sets $C_i\left(x\right)$ using its local calibration set $D_i^{\mathrm{cal}}$. This ensures valid coverage for the client’s local data distribution but sacrifices global consistency.

$$C_i\left(x\right)=\{y:s(x,y)\le Q_{1-\alpha }\left(\{s(x_j,y_j):(x_j,y_j)\in D_i^{\mathrm{cal}}\}\right)\}$$

2.

Weighted/Marginal CP: This method pools conformity scores from all clients but reweights them to account for distribution shifts. Suppose that a test sample comes from a target distribution $P_{\mathrm{test}}$. The quantile $Q_{1-\alpha }$ is calculated from a mixture of the empirical distributions of the scores from each client, weighted by the similarity between $P_{\mathrm{test}}$ and each $P_i$.

$$\widehat{F}\left(s\right)=\sum _{i=1}^N{w}_i{\widehat{F}}_i\left(s\right),\mathrm{where}{w}_i\propto {\displaystyle \frac{d{P}_{\mathrm{test}}}{d{P}_i}}\left(\mathrm{estimated}\right)$$

(25)

The prediction set is then $C\left(x\right)=\{y:s(x,y)\le {\widehat{F}}^{-1}(1-\alpha )\})$. This provides marginal coverage over the minxture distribution.

3.

Cluster-based CP: If clients can be clustered into groups with similar distributions ${\left\{P_C\right\}}_{C=1}^C$, CP can be applied within each cluster, offering a balance between local and global performance.

Challenges: The core challenge is that, without strong assumptions about the relationship between the client distribution $P_i$ and the test distribution $P_{\mathrm{test}}$, it is impossible to guarantee conditional or group-wise coverage. Current FCP research focuses on making the best use of distributed data under practical assumptions to provide approximately valid and efficient prediction sets.

In summary, conformal prediction offers a lightweight and distribution-free framework for uncertainty quantification in federated learning. Its finite-sample coverage guarantees and intuitive prediction sets make it attractive for clinical decision support. However, its performance degrades under non-exchangeable or highly heterogeneous client data, where calibration can become unreliable. Compared to Bayesian methods, conformal prediction is computationally more efficient but less flexible in modeling complex prior structures or learning under continual updates. These trade-offs motivate hybrid strategies, such as applying conformal calibration to Bayesian or ensemble models, which can combine efficiency with principled uncertainty reasoning to improve robustness in real-world federated medical applications.

6. Other Uncertainty-Related Federated Learning

In addition to BFL and FCP, a few other uncertainty-related federated learning works exist. These works are relatively scarce, so we summarize them in this section, as shown in

Table 6. Other representative works on uncertainty quantification in federated learning.

Ref.	Focus/Setting	Main Contribution
[112]	Federated learning for distributed hospital EHR data	Proposes one of the earliest frameworks for uncertainty-aware federated learning on electronic health records, highlighting the importance of robustness in medical applications.
[113]	Fuzzy consensus in federated medical systems	Introduces fuzzy consensus mechanisms integrated with federated learning, enabling reliable decision making under uncertainty in distributed medical environments.
[114]	Federated learning with uncertainty in medical data	Demonstrates application of uncertainty-aware federated learning for medical datasets, showing how uncertainty handling improves reliability across institutions.
[115]	Sugeno integral for federated learning with unbalanced data	Applies Sugeno fuzzy integrals to handle uncertainty and imbalance in federated datasets, improving robustness of decision fusion.
[116]	Federated similarity-based learning with incomplete data	Proposes a similarity-based fuzzy approach for federated learning, explicitly addressing missing or incomplete client data while retaining uncertainty quantification.
[9]	Uncertainty quantification in heterogeneous health data	Explores uncertainty-aware FL methods in healthcare, focusing on heterogeneity across hospitals and proposing techniques to calibrate prediction reliability.
[16]	Fed-ensemble: ensemble models for FL	Develops ensemble-based methods in federated learning that improve generalization and provide uncertainty quantification, showing superior calibration compared to single models.
[9]	Federated fuzzy neural networks	Presents fuzzy neural networks with evolutionary rule learning in FL, combining fuzzy logic and neural networks to model uncertainty in distributed settings.
[15]	Dirichlet-based UQ for personalized FL	Introduces Dirichlet posterior networks for uncertainty quantification in personalized FL, improving calibration and adaptability to client heterogeneity.
[110]	Byzantine-robust FCP	Extends conformal prediction to adversarial federated environments; Rob-FCP certifiably guarantees coverage under Byzantine failures, validated in healthcare settings.

.

6.1. Fuzzy Theory-Based Method

The first category of work combines fuzzy theory with federated learning. Refs. [114,115,116] applied interval-valued fuzzy set theory in the logistic regression model for missing or imprecise data. Furthermore, ref. [117] proposes a federated fuzzy neural network (FedFNN) with evolutionary rule learning (ERL) to cope with non-IID issues as well as data uncertainties. On the other hand, ref. [113] introduced the fuzzy consensus algorithm, employing the fuzzy controller (Takagi–Sugeno system) for federated learning result aggregation to achieve the final decision. To elaborate further, each client classifier’s classification results are regarded as fuzzy variables, where membership is categorized as poor/average/good based on the prediction probability. Ultimately, these results are combined using t-norm operations to obtain the final result.

6.2. Evidential Model-Based Methods

In personalized federated learning (PFL), local models may fail when exposed to out-of-distribution (OOD) data, whereas the global model can often provide more reliable predictions. To address this, ref. [15] proposed a Dirichlet-based uncertainty-guided approach that dynamically balances between local and global knowledge. Specifically, they adopt the frameworks of posterior networks (PostNet) [118] and natural posterior networks (NatPN) [119], where the network outputs are directly interpreted as parameters of a Dirichlet distribution, enabling the explicit modeling of both aleatoric and epistemic uncertainty.

Unlike Bayesian federated learning approaches, the network parameters in this framework remain deterministic during forward passes, and uncertainty is derived from the Dirichlet predictive distribution rather than weight sampling. A key contribution of the work is the correction of a flaw in the NatPN training loss that previously hindered the proper disentanglement of uncertainty types. The resulting method, named FedPN, allows clients to selectively rely on global predictions when local models exhibit high epistemic uncertainty, while preserving personalization when local predictions are confident.

Empirical evaluations demonstrate that FedPN achieves state-of-the-art performance on heterogeneous image datasets and exhibits superior robustness to OOD samples. This shows the promise of Dirichlet-based methods in bridging uncertainty quantification and personalization in federated learning.

6.3. Ensemble-Based Methods

Model ensembling is a widely used approach for UQ, as it reduces the variance in predictions by combining outputs from multiple models. A classical method is deep ensembles, where multiple models are trained with different random initializations on the same dataset, and their predictions are averaged during inference [9]. This technique provides reliable UQ by capturing the variability arising from random initialization and stochastic training.

In the context of FL, ensembling becomes particularly attractive because of the inherently distributed nature of the setting. Multiple clients can be treated as an ensemble of models, naturally enabling variance estimation across their predictions. Three primary ensembling strategies in FL have been discussed in the literature [16]: (i) ensembles of local models, where each client’s model is treated as an independent ensemble member—this preserves privacy and simplicity but diverges from the collaborative nature of FL; (ii) ensembles of global models, which train multiple global models with different random seeds and then average their predictions—while preserving collaboration, this approach significantly increases the computational and communication overhead; (iii) ensembles with multiple coordinators, where clients are divided into subgroups coordinated by separate servers—this improves the scalability but introduces coordination complexity and risks fragmentation in learning.

To address these limitations, Fed-ensemble was recently proposed [16]. Instead of maintaining a single global model, Fed-ensemble simultaneously trains an ensemble of K models, each randomly assigned to clients in every communication round. Predictions are obtained via averaging across these models, while personalization can be achieved by client-dependent weighting. Importantly, Fed-ensemble introduces no additional communication cost compared with single-model FL, yet it improves generalization, naturally supports UQ through prediction variance, and offers a Bayesian interpretation as variational inference over a Gaussian mixture posterior. Empirical studies across multiple benchmark datasets (e.g., MNIST, CIFAR-10/100, FEMNIST, Shakespeare, and OpenImage) and a real-world 3D printing task demonstrate that Fed-ensemble consistently outperforms single-model baselines, especially under non-IID data distributions.

In summary, ensemble-based methods represent a powerful line of work to enable reliable UQ in FL. While classical deep ensembles highlight the value of variance reduction through diversity, FL-specific approaches such as Fed-ensemble illustrate how ensembling can be adapted to distributed, heterogeneous, and privacy-sensitive environments.

6.4. Verification-Based Methods

Boughorbel et al. [112] proposed one of the first uncertainty-aware approaches for federated learning on distributed hospital EHR data, called the Federated Uncertainty-Aware Learning Algorithm (FUALA). The key idea is to integrate verification steps into the training loop so that aggregation weights are adjusted according to the estimated uncertainty of each client. Specifically, in each training round, the central server randomly selects a client model as a proxy and redistributes it to other clients for evaluation. Each client then acts as a cross-validation fold, producing a generalization score that reflects distributional uncertainty. Clients with lower uncertainty (i.e., better cross-validation performance) receive higher aggregation weights, while unreliable updates are down-weighted.

In addition to uncertainty-aware aggregation, FUALA also incorporates an ensemble mechanism at inference time. Instead of relying solely on the aggregated global model, the method retains the final local “heads” from participating clients, and predictions are obtained from this ensemble. The variance among these predictions provides a direct estimate of the predictive uncertainty, which is especially valuable in clinical tasks where confidence calibration is critical.

FUALA was evaluated on a large-scale cohort of 87,000 pregnant women for preterm birth prediction. Compared to standard FedAvg, the method not only achieved higher accuracy but also demonstrated superior robustness under out-of-distribution conditions, underscoring the practical value of incorporating uncertainty into federated training. This work highlights how verification-based strategies can operationalize uncertainty quantification in FL, particularly for heterogeneous medical datasets where cross-site validation is essential.

7. Federated Learning in Medical Applications

The impact of federated learning may be relatively modest in the initial training iterations; however, its effectiveness improves with subsequent rounds of iteration [120]. Notably, all participants benefit from federated learning, particularly those with minimal or negligible data [121].

Table 7. Various medical applications of federated learning concerning FL devices, datasets, and models.

Ref.	Dataset	Application(s) in Healthcare	Variations of Devices	Algorithm/Model
[34]	Distributed electronic medical records	Predicting mortality and hospital stay time	5, 10, 15, 50	Patient clustering, federated machine learning
[122]	Patient data not shared	Facilitating multi-institutional collaborations	10	Federated learning
[123]	Medical imaging	Cross-domain federated learning	2	Cross-domain federated learning
[124]	Electroencephalography	Hierarchical heterogeneous horizontal federated learning	3	Hierarchical heterogeneous horizontal federated learning
[125]	Population-based disease prediction	Disease prediction	10	Federated graph learning with network inpainting
[126]	Simulated cross-institutional psychiatric setting	Violent incident prediction	2	Federated learning
[127]	COVID-19 detection	COVID-19 detection	5	Federated learning with generative adversarial networks
[120]	Clinical benchmark data	Performance assessment	10	Federated learning
[128]	COVID-19 lung abnormalities in CT	COVID-19 lung abnormality detection	3	Federated deep learning
[129]	Chest X-ray images	COVID-19 screening	4	Federated learning
[130]	Brain anomaly detection	Unsupervised brain anomaly detection	5	Federated disentangled representation learning
[131]	EHR	Mortality prediction in hospitalized COVID-19 patients	5	Machine learning approach
[66]	SARS-CoV-2 and MIMIC-III	Privacy-first health research	1000 to 10,000	Federated learning
[132]	Electronic Medical Records	Predicting clinical outcomes in COVID-19 patients	20	Federated machine learning
[133]	T1w MRI	Alzheimer’s disease classification	3	Conditional mutual learning
[134]	Gigapixel whole-slide images	Computational pathology analysis	4	Weakly supervised federated learning
[135]	Dermatology Atlas (DA)	Sustainability of healthcare data analysis IoT systems	200	Federated deep learning
[136]	Dermatology medical images (DMI)	Securing healthcare data using robust zero-watermarking	4	Federated learning with sparse autoencoder
[137]	ISIC 2018	Enhancing data processing capability in Healthcare IoT	5	Many-objective optimization

summarizes representative applications of FL in healthcare, most of which are based on experimental datasets or benchmark studies.

To move beyond controlled settings, it is equally important to examine deployments of FL in real-world clinical environments. In the following, we highlight several landmark studies that demonstrate the clinical feasibility of FL, where heterogeneous patient data, incomplete modalities, and institutional constraints are inherent challenges.

7.1. Federated COVID-19 Prognosis

One landmark application of FL in the medical domain was conducted by Dayan et al. [132], who leveraged FL to train a predictive model for COVID-19 patients across 20 institutions worldwide without sharing raw data. The resulting model, named the Electronic Medical Record CXR AI Model (EXAM), was designed to predict patients’ future oxygen requirements based on chest X-rays and electronic health record data.

The EXAM model reported strong predictive performance, achieving an average area under the ROC curve (AUC) above 0.92. Relative to models trained separately at single institutions, the federated approach improved the AUC by 16% and enhanced the generalizability by 38%, highlighting the benefits of joint training across diverse healthcare environments. The study drew on datasets spanning four continents and further validated the model at three external sites, confirming both its robustness and cross-institutional applicability.

From a methodological standpoint, the EXAM framework employed a centralized FL setup with the FedAvg [138] algorithm for aggregation. Additionally, the study implemented differential privacy to safeguard sensitive patient information, showing that privacy-preserving techniques can be integrated into FL pipelines without significant loss of predictive accuracy.

One limitation highlighted by the authors was that the decentralized nature of FL made further exploratory analyses beyond the aggregated training results challenging. Nevertheless, the study stands out as one of the largest real-world FL deployments in healthcare to date, demonstrating the feasibility and clinical value of FL for large-scale medical AI, especially in urgent global health contexts such as the COVID-19 pandemic.

From a UQ perspective, calibrated uncertainty estimates in this setting could further help clinicians to identify borderline cases of oxygen requirement, prioritize the monitoring of high-uncertainty patients, and reduce the risk of overconfident false predictions in triage decisions.

7.2. Federated Breast Cancer Detection

The Open Consortium for Decentralized Medical Artificial Intelligence (ODELIA), funded by the European Union’s Horizon Europe program, began on 1 January 2023, with the aim of advancing healthcare AI through the use of swarm learning [139]. In contrast to conventional federated learning, swarm learning removes the need for a central coordinating server, enabling fully decentralized training and offering stronger safeguards against privacy and regulatory challenges in medical data sharing.

Over a planned five-year period, ODELIA aims to develop an open-source swarm learning framework and apply it to create AI algorithms for breast cancer detection on MRI scans. This effort leverages a vast distributed database collected across multiple European countries, with the objective of enhancing AI development speeds, model performance, and generalizability for clinical deployment. By directly tackling the challenges of data privacy, ethical constraints, and fragmented datasets, ODELIA highlights the potential of decentralized learning approaches in domains such as cancer screening, where the centralization of data is often impractical.

The consortium consists of 12 academic and industry partners from across Europe, including institutions in Austria, Germany, Spain, Greece, the Netherlands, Belgium, Switzerland, and the United Kingdom (University of Cambridge). By establishing a collaborative infrastructure for decentralized AI training, ODELIA is expected to not only accelerate innovation in breast cancer detection but also provide a scalable blueprint for broader applications of swarm learning in healthcare AI.

Integrating UQ into such swarm learning frameworks could provide radiologists with probabilistic confidence in MRI-based tumor detection, improving trust in automated screening pipelines and helping to stratify cases for secondary expert review.

7.3. Federated Tumor Segmentation

One of the most representative applications of FL in the medical imaging domain is the Federated Tumor Segmentation (FeTS) Challenge. As the first large-scale real-world FL initiative in medical imaging, FeTS v1.0 [140] aimed to identify optimal weight aggregation strategies for the training of consensus models across geographically distributed institutions, while preserving data localization and privacy. The challenge evaluated the generalization capabilities of FL-based brain tumor segmentation models on previously unseen, institution-specific data, highlighting the potential of FL in real-world healthcare scenarios.

Building upon this foundation, FeTS v2.0 [141] focused on the OOD sample generalization performance for glioblastoma detection. It organized the largest real-world medical FL deployment to date, spanning 71 sites across six continents, and led to the creation of the largest glioblastoma dataset to date, comprising 6314 patients. Compared with publicly trained models, the federated model achieved a 33% improvement in surgical target tumor contour accuracy and a 23% improvement in whole-tumor contour accuracy. These results underscore FL’s potential to enhance model performance in clinical practice and pave the way for subsequent research efforts.

A key insight from the FeTS challenges is that data quality issues often become apparent only after model training, typically when comparing FL models against publicly trained baselines. Moreover, the findings showed that simply increasing the amount of data does not necessarily lead to performance gains if the data quality is insufficient. The project employed a centralized FL framework based on the FedAvg [138] algorithm and was built on the OpenFL framework [142], demonstrating both the opportunities and challenges of deploying FL in heterogeneous and privacy-sensitive clinical environments.

Here, UQ methods such as ensembles or conformal prediction could highlight regions with high predictive uncertainty in tumor boundaries, guiding neurosurgeons toward safer resection margins and reducing risks in radiotherapy planning.

7.4. Federated Learning in Large-Scale Radiological Cooperative Network

The German Radiological Cooperative Network (RACOON) [143,144], a nationwide initiative involving 38 hospitals, has pioneered one of the first real-world FL deployments in radiology. Researchers within RACOON conducted a multi-institutional FL experiment and published a comprehensive practical guide for the development and deployment of FL infrastructure in radiological settings [145].

The study described the implementation of a centralized FL approach across six hospitals, where a segmentation model was trained for lung pathology detection. The performance of the federated approach was compared with that of simpler alternatives such as local model training and model ensembling, demonstrating the added benefits of FL despite its increased complexity.

Beyond the technical aspects, the guide also addressed organizational structures, legal requirements, experimental design, and evaluation strategies, offering a holistic framework for institutions aiming to adopt FL in medical imaging. This work not only highlights the feasibility of deploying FL in a real-world clinical network but also provides a blueprint for overcoming hurdles in governance, infrastructure, and workflow integration.

For radiology networks like RACOON, UQ can quantify prediction reliability across hospitals with varying scanner quality and protocols, enabling clinicians to adapt decision thresholds and ensuring safer integration into routine diagnostic workflows.

7.5. Federated Breast Density Classification

Roth et al. [146] provided one of the earliest real-world implementations of FL in breast imaging. The study investigated whether FL could improve performance in breast density classification by leveraging data from seven clinical institutions without centralizing patient data.

The federated model achieved an average improvement of 6.3% compared with locally trained models and demonstrated a 45.8% relative gain in generalizability when evaluated on external test datasets. These findings highlight FL’s ability to address data fragmentation across institutions and to improve model robustness in clinical settings with limited data availability. This work serves as empirical evidence that FL can outperform traditional deep learning pipelines in real-world medical imaging, particularly by enhancing cross-institutional generalization—a critical factor for reliable deployment in heterogeneous healthcare environments.

Incorporating UQ here could allow radiologists to interpret confidence-adjusted breast density scores, minimizing false positives in high-density cases and supporting more personalized risk communication to patients.

8. Uncertainty-Related Challenges and Future Directions in Federated Learning

The integration of UQ is critical in building trustworthy and robust federated models in healthcare. However, the distributed and heterogeneous nature of FL introduces profound and unique challenges for reliable UQ. This section outlines these primary challenges and suggests promising avenues for future research.

8.1. Key Challenges

8.1.1. Scalable UQ Under Extreme Data Heterogeneity

Medical institutions differ in terms of patient populations, imaging devices, and acquisition protocols, which naturally leads to statistical heterogeneity such as covariate shift and label shift. This diversity introduces significant uncertainty into model training and evaluation. Furthermore, clinical data often contain noisy labels, incomplete annotations, and systematic errors, which may amplify predictive uncertainty and degrade model robustness.

Challenges: How can we develop UQ methods that maintain accuracy and proper calibration across highly non-exchangeable data distribution? Additionally, how can we identify and mitigate the impact of low-quality clients without direct access to their raw data, while keeping computational costs manageable?

8.1.2. Federated OOD Detection and Monitoring

Once deployed, FL models inevitably encounter distribution shifts. Detecting these OOD samples is a primary defense against model failure but is exceptionally difficult in a federated setting, where the global data distribution is unseen.

Challenges: How can we develop effective, privacy-preserving mechanisms that utilize uncertainty metrics to reliably identify out-of-distribution (OOD) samples at the client level and initiate robust model retraining or adaptation protocols?

8.1.3. Clinical Validation and Interpretability

For clinical adoption, uncertainty estimates must be more than a technical metric; they must be interpretable and actionable for clinicians. A poorly communicated result can be useless or even dangerous.

Challenges: How can we establish a standardized framework for the clinical validation of UQ methods and design intuitive interfaces that translate uncertainty scores into transparent, actionable decision support?

8.1.4. Personalization vs. Generalization

Personalized FL improves performance on local data but risks overfitting and reduced cross-site generalization.

Challenges: How can uncertainty information guide personalization and aggregation strategies to achieve both local accuracy and global robustness?

8.1.5. Resource-Efficient UQ

Ensemble-based and Bayesian FL approaches are computationally expensive, requiring multiple local training steps or the probabilistic modeling of parameters. This burden is further amplified in multi-center medical settings.

Challenges: How can we design lightweight, scalable UQ methods that provide uncertainty estimates without requiring multiple model evaluations or dramatically increasing the local computational and communication overhead for clients?

8.1.6. Trustworthiness Under Adversarial Conditions

FL is vulnerable to adversarial updates or poisoned data contributions that can deliberately increase and destabilize models.

Challenges: How can we leverage UQ not just for data uncertainty but also as a tool for detecting anomalous client behavior and mitigating malicious attacks to ensure the system’s overall robustness and trustworthiness?

8.1.7. Meaningful Uncertainty Aggregation

Each client may produce different uncertainty estimates due to homogenous data. Aggregating such estimates in a meaningful way is non-trivial.

Challenges: How can we design an aggregation mechanism that preserves both model performance and informative, well-calibrated global uncertainty estimates from divergent local contributions?

8.2. Future Directions

While several avenues exist for advancing UQ in medical FL, not all are equally urgent. Among these, two directions stand out as the most critical: out-of-distribution (OOD) detection, which directly impacts patient safety by reducing the risk of erroneous predictions in clinical workflows, and regulatory compliance, since alignment with frameworks such as those of the FDA or the EU AI Act is a prerequisite for deployment in real-world healthcare systems. These challenges demand immediate attention and should be prioritized in future research.

8.2.1. Robust OOD Detection for Patient Safety

A critical and urgent direction is improving out-of-distribution (OOD) detection under federated constraints. In real-world clinical practice, encountering data that deviate from the training distribution is inevitable, and misclassification in such cases can have severe consequences for patient safety. Future research should focus on designing communication-efficient, federated OOD detection mechanisms that remain reliable under client heterogeneity, thereby ensuring that the clinical deployment of FL systems prioritizes safety and robustness.

8.2.2. Federated Uncertainty for Model Governance

Developing protocols where uncertainty metrics are continuously monitored across the federation can serve as a key tool for model governance. This includes automated retraining triggers and data quality audits at participating sites and overall system health monitoring, creating a more robust and maintainable FL ecosystem for healthcare.

Beyond technical performance, aligning UQ with regulatory frameworks is a prerequisite for real-world deployment. Concretely, UQ can be mapped to the FDA’s Good Machine Learning Practice (GMLP) principles and the SaMD pathway as follows. Data quality and representativeness: report site- and subgroup-stratified performance with uncertainty and quantify coverage/calibration under non-IID clients. Model design and training: pre-specify calibration targets (e.g., ECE thresholds) and risk coverage operating points; document conformal coverage guarantees and update policies. Transparency and human factors: adopt clinician-facing uncertainty displays (e.g., prediction intervals, conformal set size, deferral flags) with clear interpretive guidance. Monitoring and change control: implement uncertainty- and OOD-based drift monitors and define pre-determined change control plan (PCCP) triggers (e.g., coverage shortfall, rising OOD rate) to govern retraining and recalibration. Analytical validation: include calibration/coverage metrics (ECE, Brier, risk–coverage curves, conformal coverage) alongside accuracy/AUC. Clinical validation: demonstrate site-level generalizability with uncertainty-aware endpoints and pre-defined non-inferiority margins; report failure modes identified by OOD detectors. Labeling/IFU: provide instructions for interpreting uncertainty and deferral logic (e.g., thresholds that trigger expert review). Postmarket surveillance: specify an uncertainty/OOD monitoring plan, periodic recalibration, and CAPA hooks. Risk management (ISO 14971): link hazards from miscalibration or OOD usage to mitigations (deferral, secondary imaging, expert escalation). These concrete mappings would transform UQ from a purely technical add-on into a compliance-enabling mechanism that supports safe, auditable, and updatable SaMD.

While this mapping focuses on FDA guidance, similar regulatory trends are emerging globally. The EU Artificial Intelligence Act designates most medical AI systems as high-risk, emphasizing transparency, human oversight, and continuous post-deployment monitoring—principles that naturally align with UQ-driven governance. Likewise, ongoing efforts by the IMDRF SaMD Working Group highlight explainability, lifecycle management, and real-world performance evaluation, all of which can be operationalized through uncertainty monitoring and adaptive recalibration. Incorporating these perspectives further situates UQ as a cornerstone of trustworthy and internationally harmonized medical AI.

8.2.3. Hybrid and Hierarchical UQ Methods

Future work should explore combining the strengths of different UQ paradigms (e.g., model-based [Bayesian] and data-based [ensemble]). A promising direction is developing a hierarchical UQ framework that separates uncertainty into its distinct components (aleatoric, epistemic, and client-specific) at different levels of the federation process, allowing for more nuanced aggregation and interpretation.

8.2.4. UQ-Aware Personalization Algorithms

Aggregation and personalization strategies should explicitly incorporate uncertainty. This could involve uncertainty-weighted aggregation, where client updates are dynamically weighted based on the reliability of their uncertainty estimates, and UQ-guided personalization, allowing clients to adapt models not just for accuracy but for better uncertainty calibration on their local data.

8.2.5. Benchmarks and Standardized Clinical Evaluation

The field urgently requires comprehensive benchmarks featuring real-world non-IID medical data splits and standardized evaluation metrics beyond accuracy (e.g., calibration error, OOD detection AUC).

8.2.6. Lightweight and Approximate UQ Techniques

Research into single-model UQ methods (e.g., spectral-normalized neural Gaussian processes, deterministic uncertainty quantification) is crucial for FL. Techniques that provide a reasonable estimate with a single forward pass would dramatically reduce the computational barrier to widespread UQ adoption in large-scale FL systems.

In summary, future work on UQ in FL must balance breadth with prioritization. While hybrid designs, personalization, benchmarks, lightweight methods, and governance frameworks are all important, the most urgent priorities are (i) advancing OOD detection to safeguard patient safety and (ii) operationalizing regulatory alignment by explicitly mapping UQ practices to GMLP and the SaMD pathway (including PCCP-driven monitoring and recalibration). Addressing these will pave the way for other innovations and accelerate the clinical translation of federated medical AI.

9. Discussion

In clinical practice, uncertainty estimates are vital for safe and reliable decision making. Predictive intervals and calibrated confidence scores help clinicians to judge when AI outputs can be trusted for immediate action and when additional tests or expert review are needed. This not only safeguards patient safety but also clarifies responsibility by framing AI recommendations as probabilistic guidance rather than absolute decisions. By integrating such measures into workflows like diagnosis, treatment planning, and risk assessment, federated learning models become more clinically meaningful and supportive of real-world healthcare needs.

To strengthen the practical relevance of UQ in FL, we include concrete, workflow-level scenarios showing how predictive intervals, calibrated confidence, and OOD detection change decisions. (i) Diagnostic triage—breast cancer screening: A federated classifier provides a calibrated probability and a conformal prediction set for each mammogram. Benign ases with high confidence (e.g., $p<0.05$, set size $=1$ with “benign”) proceed to routine follow-up, whereas “borderline” cases (e.g., $0.45\le p\le 0.55$ or conformal set size $>1$ containing {benign, malignant}) are auto-flagged for second reading and adjunct ultrasound/DBT to reduce false negatives. Site-specific thresholds are tuned to meet a target risk–coverage curve while maintaining per-client conformal coverage. (ii) Surgical/radiotherapy planning—glioma or lung tumor: A federated segmentation model outputs voxel-wise uncertainty and boundary-predictive intervals. Regions where the 95% boundary interval exceeds a safety margin (e.g., >3 mm near eloquent cortex or >5 mm adjacent to major vessels) trigger margin expansion or the acquisition of contrast-enhanced MRI; low-uncertainty contours allow tighter planning of target volumes, balancing local control with toxicity. (iii) Treatment escalation—COVID-19/ICU deterioration: A federated risk model reports a 24 h deterioration risk interval (e.g., 95% PI $[0.18, 0.36]$). If the interval overlaps with an escalation threshold (e.g., 0.30), the nursing frequency and telemetry are increased, labs/imaging are expedited, and an early senior review is triggered; if the interval is confidently below the threshold, routine care continues. In all scenarios, an OOD detector (e.g., scanner protocol shift or rare subtype) routes atypical cases to expert review and suppresses automated recommendations until recalibration. These examples show how UQ signals are translated into concrete triage rules, margin adjustments, and escalation triggers, making FL models actionable at the point of care.

Recent benchmarks such as MedMNIST [147] and FLamby [148] provide standardized datasets that can be leveraged to evaluate UQ methods in federated medical imaging tasks. MedMNIST includes lightweight, preprocessed medical image datasets (e.g., breast ultrasound, retina, chest X-ray) that facilitate reproducibility and rapid prototyping. FLamby, on the other hand, offers a comprehensive federated learning benchmark suite with clinically relevant datasets for tasks such as heart segmentation, prostate MRI analysis, and cancer detection. Integrating UQ methods with these benchmarks allows for fair comparisons across studies and helps to substantiate claims regarding the robustness, generalizability, and clinical applicability of FL models.

While the above discussion emphasizes clinical relevance, a balanced method-level comparison is also necessary under federated constraints. As discussed in Table 3, FL typically worsens calibration and OOD detection relative to centralized training; the choice of UQ method must therefore account for computational and communication limitations, clinician-facing interpretability, and robustness to client heterogeneity. We summarize four representative families—Bayesian, conformal, ensemble, and evidential—along these axes in

Table 8. Balanced comparison of UQ methods for federated medical learning along three key axes.

Method	Comp./Comm. in FL	Calibration and Interpretability	Robustness to Non-IID/OOD
Bayesian (BNNs/VI/MC dropout)	High client compute for VI/sampling; larger payload if transmitting moments; potentially more rounds.	Strong probabilistic calibration; credible intervals are principled but may require tooling for clinician-facing display.	Moderate; sensitive to priors and heterogeneity; improves with hierarchical priors and personalization.
Conformal prediction	Low–moderate compute; minimal comm. (calibration scores/thresholds); easy to plug into FL pipelines.	Finite-sample marginal coverage under exchangeability; intervals/coverage guarantees are clinician-friendly.	Coverage degrades under non-exchangeable client data; per-client or clustered calibration mitigates this.
Ensembles	High compute (K models) and comm. (K updates); distillation reduces cost but may dilute uncertainty fidelity.	Typically strong calibration; (dis)agreement is intuitive to interpret.	Often strong OOD behavior in practice, but overhead is substantial in FL.
Evidential	Single-pass inference; low client compute/comm.; no sampling.	Compact Dirichlet/evidence-based uncertainty; needs post hoc calibration or regularization for reliability.	Moderate; sensitive to misspecification and severe non-IID without targeted regularization.

.

In practice, Bayesian and ensemble approaches tend to yield stronger calibration and OOD behavior but at higher computational and communication costs in FL; conformal prediction is lightweight and interpretable but requires per-client or clustered calibration to maintain coverage under non-IID conditions; evidential methods are efficient and workflow-friendly yet benefit from targeted regularization and post hoc calibration under distribution shift. Hybrid designs are attractive: conformal “wrappers” around evidential or distilled ensembles for low-cost coverage guarantees; communication-aware Bayesian inference (e.g., fewer Monte Carlo passes, server-side posterior approximation) to limit the payload; and client-specific temperature scaling or risk coverage tuning to restore reliability under heterogeneity. No single method is uniformly superior—the choice should be guided by site resources (compute/bandwidth), the required calibration and interpretability, and the expected degree of distribution shift across participating hospitals.

10. Conclusions

This survey highlights the central role of UQ in enabling safe, reliable, and privacy-preserving medical federated learning. We classified uncertainty into data, model, and distributional sources; reviewed key approaches such as Bayesian federated learning (BFL) and federated conformal prediction (FCP); and mapped them to real-world medical applications including tumor segmentation, breast cancer detection, and COVID-19 prognosis. While advances show that UQ can enhance reliability and clinical interpretability, challenges such as handling non-IID data, computational efficiency, and robust out-of-distribution detection still limit large-scale clinical deployment. Looking forward, actionable priorities include developing hybrid and lightweight UQ frameworks that balance rigor with efficiency, designing personalization and aggregation schemes that explicitly account for uncertainty, creating benchmarks with standardized calibration and OOD metrics, and aligning methods with regulatory requirements (e.g., FDA, EU AI Act). By embedding these strategies, UQ can evolve from a technical safeguard into a practical clinical tool—enhancing safety, guiding decision making, and fostering the equitable adoption of federated medical AI worldwide.