Statistical Analysis of the Sum of Double Random Variables for Security Applications in RIS-Assisted NOMA Networks with a Direct Link
Abstract
1. Introduction
1.1. Backgrounds and Concerns
1.2. State of the Art
1.3. Motivations and Contributions
- We provide a comprehensive review of the statistics of a single random variable plus the sum of double RVs, including an analysis of the cumulative distribution function (CDF) and/or the probability density function (PDF) for cascaded channels with an optimal RIS phase shifter. This plays a core approach in guiding how to analyze the performance analysis of RIS-aided networks in general and RIS-secured systems in particular.
- We propose a novel communication strategy that combines the mutual benefits of NOMA encoding and an RIS phase shifter by allocating higher power levels for untrusted nodes while optimally configuring the RIS phase shifter. This helps achieve the following three goals: enhancing legitimate channel quality, serving untrusted nodes, and reducing leaks of eavesdropping activities.
- In addition to that, we provide detailed guidance on how to achieve the CDF and PDF for cascaded channels with random RIS phase shifters, which lays the foundation for measuring the impacts of untrusted parties.
- Capitalizing on the CDF and PDF in modeling channel characteristics, we derive closed-form expressions for the secrecy effective capacity and SOP, considering both exact and asymptotic analysis in high signal-to-noise ratio (SNR) regions. This serves as an effective way for probing key insights into system designs, such as the secrecy ergodic slope or diversity order gain.
- Through simulation results based on the Monte Carlo method, we not only demonstrate the efficacy of our proposed communication method in favor of RIS-secured undertaking but also exhibit several impacts of system parameters, which reflects the importance of choosing a resource power allocation policy and transmission target data rate.
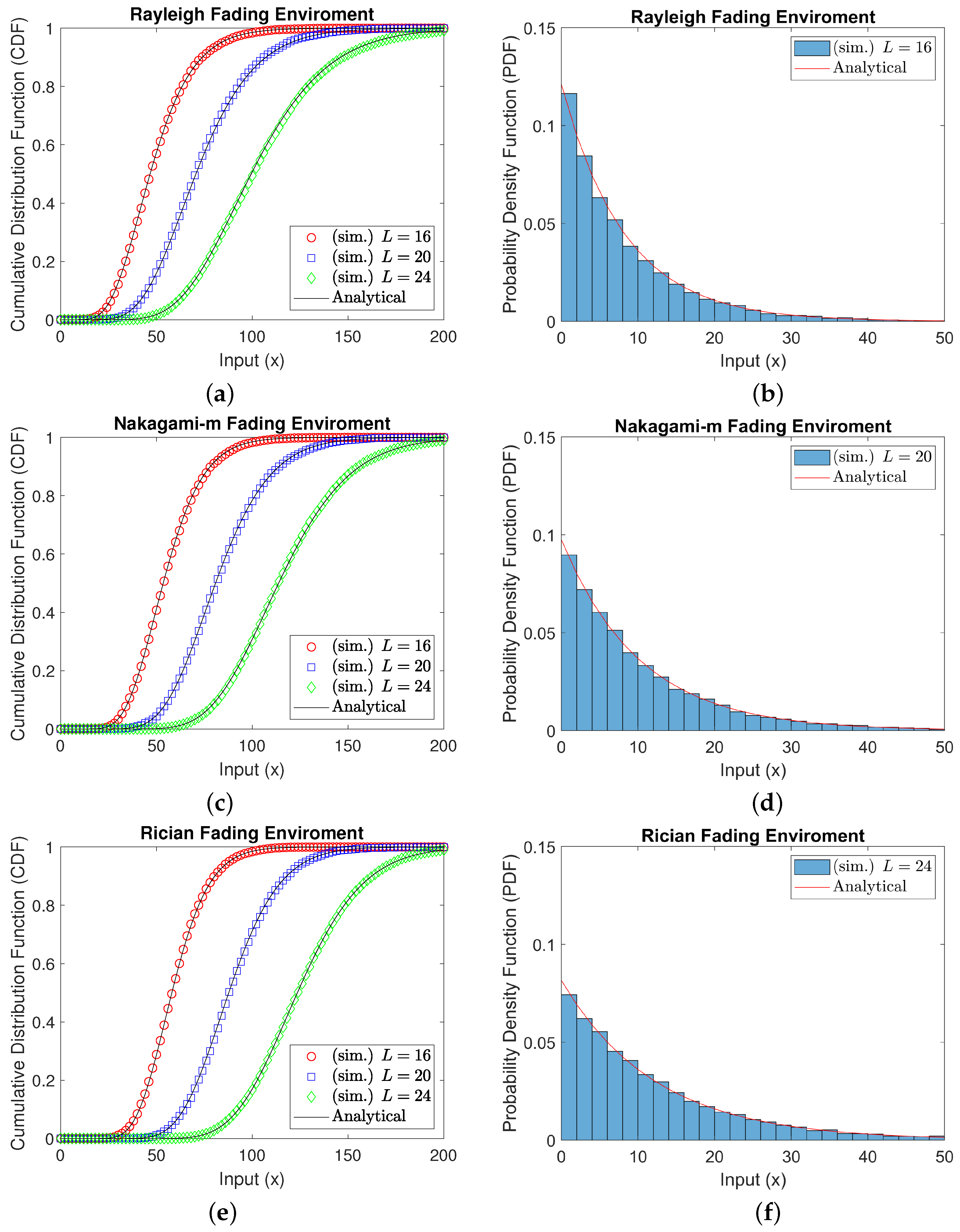
1.4. Review of the Statistics of Single Random Variable Plus the Sum of Double Random Variables
1.4.1. Rayleigh Fading Environment
1.4.2. Nakagami-m Fading Environment
1.4.3. Rician Fading Environment
2. System Model
2.1. Model Description
- Bob has optimal cascaded channel gains to perform SIC in descending power order.
- Bob’s information is protected better from Willie’s eavesdropping since the signal strength of Bob () is much lower than that of Willie (). If Willie wants to optimally wiretap Bob’s information (), he needs to perform SIC to first decode their signal (), then remove their signal from the received signal using SIC to obtain Bob’s signal (), and finally intercept Bob’s information ().
2.2. Legitimate Channels of Link Sources: RIS and Bob
2.3. Eavesdropping Channels of Link Sources: RIS and Willie
- Step 1: Denote by , with . Let us rewrite Q asSince the weighted sum of a uniform RV is a uniform RV, is uniformly distributed within . Accordingly, we can derive the following:
- Step 2: Making use of the relation between circularly symmetric complex Gaussian noise, we can map into the exponential distribution with inverse variance , i.e.,Making use of ([70] Equation (3.351.2)), the CDF of can be derived as
3. Performance Evaluation Framework
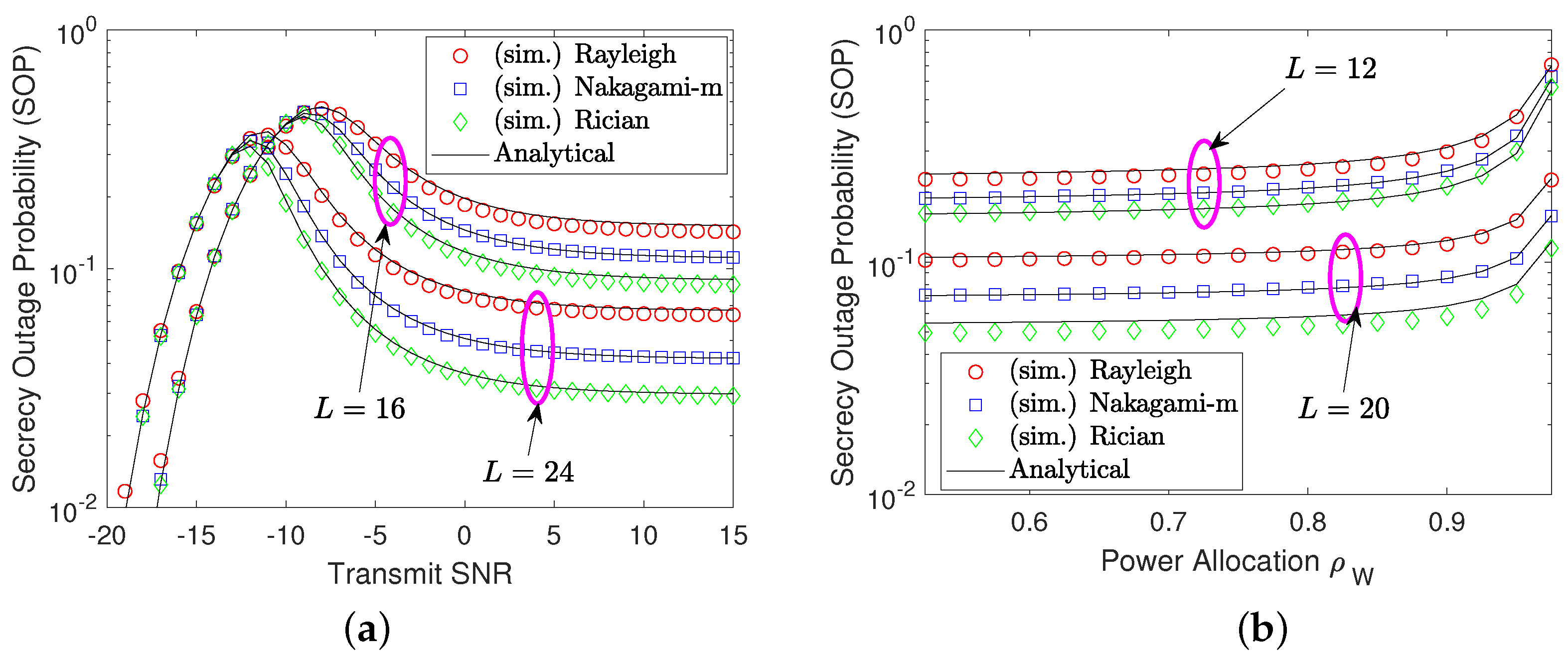
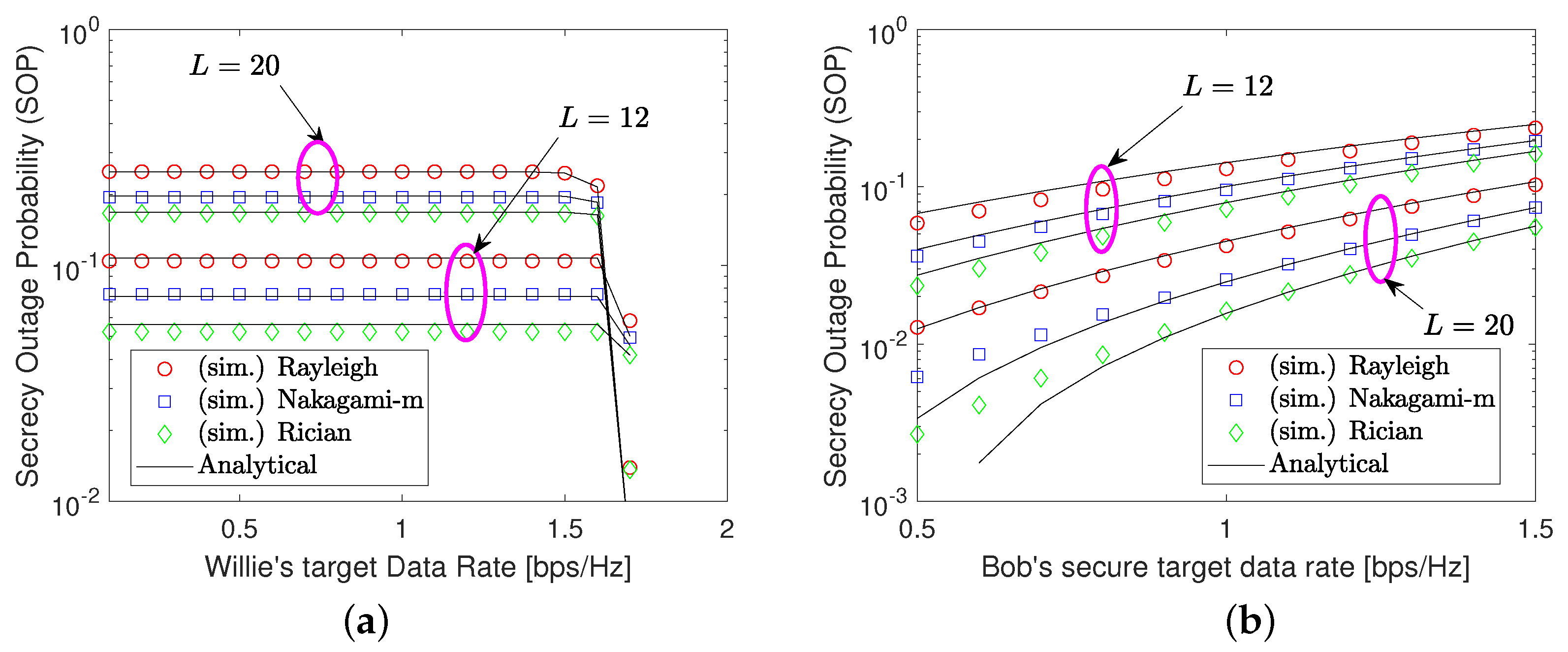
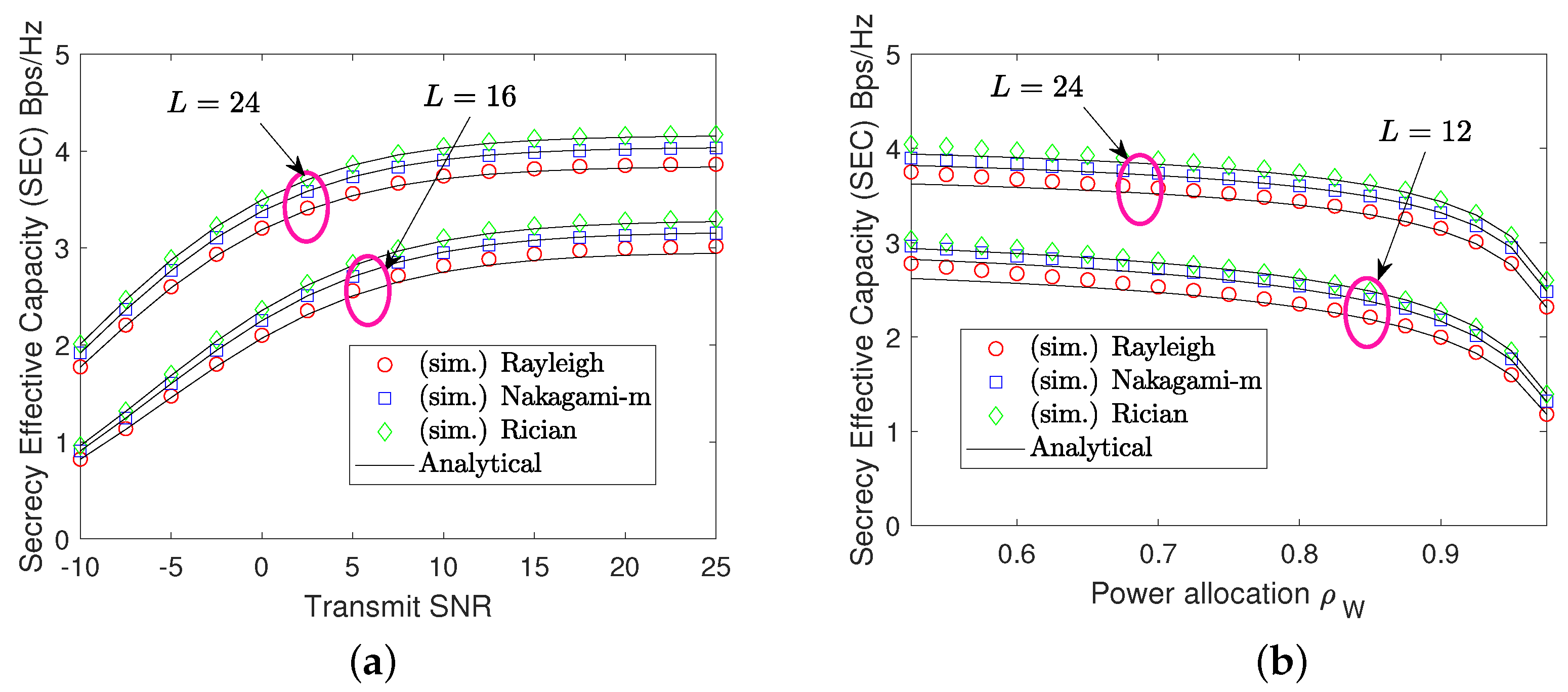
3.1. SEC Analysis
3.2. SOP Analysis
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mahdi, M.N.; Ahmad, A.R.; Qassim, Q.S.; Natiq, H.; Subhi, M.A.; Mahmoud, M. From 5G to 6G Technology: Meets Energy, Internet-of-Things and Machine Learning: A Survey. Appl. Sci. 2021, 11, 8117. [Google Scholar] [CrossRef]
- Sufyan, A.; Khan, K.B.; Khashan, O.A.; Mir, T.; Mir, U. From 5G to beyond 5G: A Comprehensive Survey of Wireless Network Evolution, Challenges, and Promising Technologies. Electronics 2023, 12, 2200. [Google Scholar] [CrossRef]
- Aouedi, O.; Vu, T.H.; Sacco, A.; Nguyen, D.C.; Piamrat, K.; Marchetto, G.; Pham, Q.V. A Survey on Intelligent Internet of Things: Applications, Security, Privacy, and Future Directions. IEEE Commun. Surv. Tutor. 2024. [Google Scholar] [CrossRef]
- Le, M.; Huynh-The, T.; Do-Duy, T.; Vu, T.H.; Hwang, W.J.; Pham, Q.V. Applications of Distributed Machine Learning for the Internet-of-Things: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2024, 1. [Google Scholar] [CrossRef]
- Vu, T.H.; Jagatheesaperumal, S.K.; Nguyen, M.D.; Van Huynh, N.; Kim, S.; Pham, Q.V. Applications of Generative AI (GAI) for Mobile and Wireless Networking: A Survey. IEEE Internet Things J. 2024, 1. [Google Scholar] [CrossRef]
- Le, A.T.; Vu, T.H.; Duy, T.T.; Tu, L.T.; Voznak, M. Analysis of PHY-Layer Security and Covert Communication in Hybrid Power-Frequency Multiple Access Systems. IEEE Wirel. Commun. Lett. 2024, 1. [Google Scholar] [CrossRef]
- Saito, Y.; Benjebbour, A.; Kishiyama, Y.; Nakamura, T. System-level performance evaluation of downlink non-orthogonal multiple access (NOMA). In Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 8–11. [Google Scholar] [CrossRef]
- El-Sayed, M.M.; Ibrahim, A.S.; Khairy, M.M. Power allocation strategies for Non-Orthogonal Multiple Access. In Proceedings of the 2016 International Conference on Selected Topics in Mobile & Wireless Networking (MoWNeT), Cairo, Egypt, 11–13 April 2016; pp. 11–13. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Ding, Z.; Nallanathan, A.; Hanzo, L. Nonorthogonal Multiple Access for 5G and Beyond. Proc. IEEE 2017, 105, 2347–2381. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vu, T.H.; Tu, L.T.; Duy, T.T.; Nguyen, Q.S.; da Costa, D.B. A Low-Complexity Relaying Protocol for Cooperative Short-Packet NOMA-Based Spectrum Sharing Systems. IEEE Trans. Veh. Technol. 2024, 73, 9044–9049. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Ding, Z.; Wang, Z.; Chen, S.; Hanzo, L. A Survey of Non-Orthogonal Multiple Access for 5G. IEEE Commun. Surv. Tutor. 2018, 20, 2294–2323. [Google Scholar] [CrossRef]
- Vaezi, M.; Baduge, G.A.A.; Liu, Y.; Arafa, A.; Fang, F.; Ding, Z. Interplay Between NOMA and Other Emerging Technologies: A Survey. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 900–919. [Google Scholar] [CrossRef]
- Björnson, E.; Wymeersch, H.; Matthiesen, B.; Popovski, P.; Sanguinetti, L.; De Carvalho, E. Reconfigurable Intelligent Surfaces: A signal processing perspective with wireless applications. IEEE Signal Process. Mag. 2022, 39, 135–158. [Google Scholar] [CrossRef]
- Van Chien, T.; Papazafeiropoulos, A.K.; Tu, L.T.; Chopra, R.; Chatzinotas, S.; Ottersten, B. Outage Probability Analysis of IRS-Assisted Systems Under Spatially Correlated Channels. IEEE Wirel. Commun. Lett. 2021, 10, 1815–1819. [Google Scholar] [CrossRef]
- Björnson, E.; Özdogan, Ö.; Larsson, E.G. Intelligent Reflecting Surface Versus Decode-and-Forward: How Large Surfaces are Needed to Beat Relaying? IEEE Wirel. Commun. Lett. 2019, 9, 244–248. [Google Scholar] [CrossRef]
- Björnson, E.; Özdogan, Ö.; Larsson, E.G. Reconfigurable Intelligent Surfaces: Three Myths and Two Critical Questions. IEEE Commun. Mag. 2021, 58, 90–96. [Google Scholar] [CrossRef]
- Özdogan, Ö.; Björnson, E.; Larsson, E.G. Intelligent Reflecting Surfaces: Physics, Propagation, and Pathloss Modeling. IEEE Wirel. Commun. Lett. 2019, 9, 581–585. [Google Scholar] [CrossRef]
- Pei, X.; Yin, H.; Tan, L.; Cao, L.; Li, Z.; Wang, K.; Zhang, K.; Björnson, E. RIS-Aided Wireless Communications: Prototyping, Adaptive Beamforming, and Indoor/Outdoor Field Trials. IEEE Trans. Commun. 2021, 69, 8627–8640. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, S.; Zheng, B.; You, C.; Zhang, R. Intelligent Reflecting Surface-Aided Wireless Communications: A Tutorial. IEEE Trans. Commun. 2021, 69, 3313–3351. [Google Scholar] [CrossRef]
- Mei, W.; Zheng, B.; You, C.; Zhang, R. Intelligent Reflecting Surface-Aided Wireless Networks: From Single-Reflection to Multireflection Design and Optimization. Proc. IEEE 2022, 110, 1380–1400. [Google Scholar] [CrossRef]
- Zheng, B.; You, C.; Mei, W.; Zhang, R. A Survey on Channel Estimation and Practical Passive Beamforming Design for Intelligent Reflecting Surface Aided Wireless Communications. IEEE Commun. Surv. Tutor. 2022, 24, 1035–1071. [Google Scholar] [CrossRef]
- Nguyen, B.C.; Hoang, T.M.; Tran, P.T.; Nguyen, T.N.; Phan, V.D.; Minh, V.; Voznak, M. Cooperative Communications for Improving the Performance of Bidirectional Full-Duplex System With Multiple Reconfigurable Intelligent Surfaces. IEEE Access 2021, 9, 134733–134742. [Google Scholar] [CrossRef]
- Vu, T.H.; Nguyen, T.V.; da Costa, D.B.; Kim, S. Intelligent Reflecting Surface-Aided Short-Packet Non-Orthogonal Multiple Access Systems. IEEE Trans. Veh. Technol. 2022, 71, 4500–4505. [Google Scholar] [CrossRef]
- Vu, T.H.; Nguyen, T.V.; Pham, Q.V.; da Costa, D.B.; Kim, S. STAR-RIS-Enabled Short-Packet NOMA Systems. IEEE Trans. Veh. Technol. 2023, 72, 13764–13769. [Google Scholar] [CrossRef]
- Vo, D.T.; Nguyen, T.N.; Le, A.T.; Phan, V.D.; Voznak, M. Holographic Reconfigurable Intelligent Surface-Aided Downlink NOMA IoT Networks in Short-Packet Communication. IEEE Access 2024, 12, 65266–65277. [Google Scholar] [CrossRef]
- Le, A.T.; Nguyen, T.N.; Tu, L.T.; Tran, T.P.; Duy, T.T.; Voznak, M.; Ding, Z. Performance Analysis of RIS-Assisted Ambient Backscatter Communication Systems. IEEE Wirel. Commun. Lett. 2023, 13, 791–795. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Vinh, N.V.; Nguyen, B.C.; Minh, B.V. On performance of RIS-aided bidirectional full-duplex systems with combining of imperfect conditions. Wirel. Netw. 2024, 30, 649–660. [Google Scholar] [CrossRef]
- Phu, L.S.; Nguyen, T.N.; Voznak, M.; Nguyen, B.C.; Hoang, T.M.; Minh, B.V.; Tran, P.T. Improving the Capacity of NOMA Network Using Multiple Aerial Intelligent Reflecting Surfaces. IEEE Access 2023, 11, 107958–107971. [Google Scholar] [CrossRef]
- Vu, T.H.; Jee, A.; da Costa, D.B.; Kim, S. STAR-RIS Empowered NOMA Systems with Caching and SWIPT. IEEE Open J. Commun. Soc. 2023, 5, 379–396. [Google Scholar] [CrossRef]
- Vu, T.H.; Pham, Q.V.; Nguyen, T.T.; da Costa, D.B.; Kim, S. Enhancing RIS-Aided Two-Way Full-Duplex Communication With Nonorthogonal Multiple Access. IEEE Internet Things J. 2024, 11, 19963–19977. [Google Scholar] [CrossRef]
- Tam, D.T.; Nguyen, B.C.; Lam, S.C.; Van Vinh, N.; Nguyen, T.N. SER performance of millimeter-wave communications with multiple reconfigurable intelligent surfaces and transmit antenna selection. AEU-Int. J. Electron. Commun. 2023, 160, 154517. [Google Scholar] [CrossRef]
- Pham, X.N.; Nguyen, B.C.; Thi, T.D.; Van Vinh, N.; Minh, B.V.; Kim, T.; Nguyen, T.N.; Le, A.V. Enhancing data rate and energy efficiency of NOMA systems using reconfigurable intelligent surfaces for millimeter-wave communications. Digit. Signal Process. 2024, 151, 104553. [Google Scholar] [CrossRef]
- Quang, P.M.; Kien, N.T.; Duy, T.T.; An, N.H.; Tung, N.T.; Le, A.V. Performance Evaluation Of Reconfigurable Intelligent Surface Aided Multi-Hop Relaying Schemes With Short Packet Communication. Adv. Electr. Electron. Eng. 2024, 22, 97–106. [Google Scholar] [CrossRef]
- Vu, T.H.; Kim, S. Performance Analysis of Full-Duplex Two-Way RIS-Based Systems With Imperfect CSI and Discrete Phase-Shift Design. IEEE Commun. Lett. 2022, 27, 512–516. [Google Scholar] [CrossRef]
- Nguyen, S.Q.; Le, A.T.; Thien, H.T.; Kharel, R. Outage Performance Analysis of STAR-RIS-NOMA Networks under Imperfect CSI. Adv. Electr. Electron. Eng. 2024, 22, 260–270. [Google Scholar] [CrossRef]
- Vu, T.H.; Nguyen, T.N.; Nguyen, T.T.; Kim, S. Hybrid Active-Passive STAR-RIS-based NOMA Systems: Energy/Rate-Reliability Trade-offs and Rate Adaptation. IEEE Wirel. Commun. Lett. 2024, 14, 238–242. [Google Scholar] [CrossRef]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Sanenga, A.; Mapunda, G.A.; Jacob, T.M.L.; Marata, L.; Basutli, B.; Chuma, J.M. An Overview of Key Technologies in Physical Layer Security. Entropy 2020, 22, 1261. [Google Scholar] [CrossRef] [PubMed]
- Tran, M.; Tu, L.T.; Minh, B.V.; Nguyen, Q.S.; Rejfek, L.; Lee, B.M. Security and Reliability Analysis of the Power Splitting-Based Relaying in Wireless Sensors Network. Sensors 2024, 24, 1300. [Google Scholar] [CrossRef]
- Ha, D.H.; Nguyen, T.N.; Tran, M.H.; Li, X.; Tran, P.T.; Voznak, M. Security and reliability analysis of a two-way half-duplex wireless relaying network using partial relay selection and hybrid TPSR energy harvesting at relay nodes. IEEE Access 2020, 8, 187165–187181. [Google Scholar] [CrossRef]
- Tran Tin, P.; Nguyen, T.N.; Sang, N.Q.; Trung Duy, T.; Tran, P.T.; Voznak, M. Rateless codes-based secure communication employing transmit antenna selection and harvest-to-jam under joint effect of interference and hardware impairments. Entropy 2019, 21, 700. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Yang, L.; Alouini, M.S. Physical Layer Security for Cooperative NOMA Systems. IEEE Trans. Veh. Technol. 2018, 67, 4645–4649. [Google Scholar] [CrossRef]
- Xiang, Z.; Yang, W.; Pan, G.; Cai, Y.; Song, Y. Physical Layer Security in Cognitive Radio Inspired NOMA Network. IEEE J. Sel. Top. Signal Process. 2019, 13, 700–714. [Google Scholar] [CrossRef]
- Cao, K.; Wang, B.; Ding, H.; Lv, L.; Dong, R.; Cheng, T. Improving Physical Layer Security of Uplink NOMA via Energy Harvesting Jammers. IEEE Trans. Inf. Forensics Secur. 2020, 16, 786–799. [Google Scholar] [CrossRef]
- Gong, C.; Yue, X.; Zhang, Z.; Wang, X.; Dai, X. Enhancing Physical Layer Security With Artificial Noise in Large-Scale NOMA Networks. IEEE Trans. Veh. Technol. 2021, 70, 2349–2361. [Google Scholar] [CrossRef]
- Vu, T.H.; Pham, Q.V.; da Costa, D.B.; Debbah, M.; Kim, S. Physical-Layer Security in Short-Packet NOMA Systems with Untrusted Near Users. In Proceedings of the 2023 IEEE International Conference on Communications Workshops (ICC Workshops), Rome, Italy, 28 May–1 June 2023; p. 2023-01. [Google Scholar] [CrossRef]
- Le, A.T.; Vu, T.H.; Tu, N.H.; Nguyen, T.N.; Tu, L.T.; Voznak, M. Active Reconfigurable Repeater-Assisted NOMA Networks in Internet-of-Things: Reliability, Security, and Covertness. IEEE Internet Things J. 2024, 1. [Google Scholar] [CrossRef]
- Zhang, J.; Du, H.; Sun, Q.; Ai, B.; Ng, D.W.K. Physical Layer Security Enhancement With Reconfigurable Intelligent Surface-Aided Networks. IEEE Trans. Inf. Forensics Secur. 2021, 16, 3480–3495. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, C.; Jiang, C.; Jia, F.; Ge, J.; Gong, F. Improving Physical Layer Security for Reconfigurable Intelligent Surface Aided NOMA 6G Networks. IEEE Trans. Veh. Technol. 2021, 70, 4451–4463. [Google Scholar] [CrossRef]
- Cao, K.; Ding, H.; Lv, L.; Su, Z.; Tao, J.; Gong, F. Physical-Layer Security for Intelligent-Reflecting-Surface-Aided Wireless-Powered Communication Systems. IEEE Internet Things J. 2023, 10, 18097–18110. [Google Scholar] [CrossRef]
- Khoshafa, M.H.; Ngatched, T.M.N.; Ahmed, M.H. RIS-Aided Physical Layer Security Improvement in Underlay Cognitive Radio Networks. IEEE Syst. J. 2023, 17, 6437–6448. [Google Scholar] [CrossRef]
- Yang, L.; Yuan, Y. Secrecy outage probability analysis for RIS-assisted NOMA systems. Electron. Lett. 2020, 56, 1254–1256. [Google Scholar] [CrossRef]
- Chen, Q.; Li, M.; Yang, X.; Alturki, R.; Alshehri, M.D.; Khan, F. Impact of Residual Hardware Impairment on the IoT Secrecy Performance of RIS-Assisted NOMA Networks. IEEE Access 2021, 9, 42583–42592. [Google Scholar] [CrossRef]
- Gong, C.; Yue, X.; Wang, X.; Dai, X.; Zou, R.; Essaaidi, M. Intelligent Reflecting Surface Aided Secure Communications for NOMA Networks. IEEE Trans. Veh. Technol. 2021, 71, 2761–2773. [Google Scholar] [CrossRef]
- Ahmed, T.; Badrudduza, A.S.M.; Islam, S.M.R.; Islam, S.H.; Ibrahim, M.; Abdullah-Al-Wadud, M. Enhancing Physical Layer Secrecy Performance for RIS-Assisted RF-FSO Mixed Wireless System. IEEE Access 2023, 11, 127737–127753. [Google Scholar] [CrossRef]
- Le, S.P.; Nguyen, H.N.; Nguyen, N.T.; Van, C.H.; Le, A.T.; Voznak, M. Physical layer security analysis of IRS-based downlink and uplink NOMA networks. EURASIP J. Wirel. Commun. Netw. 2023, 2023, 1–26. [Google Scholar] [CrossRef]
- Li, X.; Pei, Y.; Yue, X.; Liu, Y.; Ding, Z. Secure Communication of Active RIS Assisted NOMA Networks. IEEE Trans. Wirel. Commun. 2023, 23, 4489–4503. [Google Scholar] [CrossRef]
- Xie, Z.; Liu, Y.; Yi, W.; Wu, X.; Nallanathan, A. Physical Layer Security for STAR-RIS-NOMA: A Stochastic Geometry Approach. IEEE Trans. Wirel. Commun. 2023, 23, 6030–6044. [Google Scholar] [CrossRef]
- Ghadi, F.R.; Kaveh, M.; Wong, K.K.; Martín, D. Physical Layer Security Performance of Cooperative Dual-RIS-Aided V2V NOMA Communications. IEEE Syst. J. 2024, 18, 2074–2084. [Google Scholar] [CrossRef]
- Khoshafa, M.H.; Ahmed, G.; Ngatched, T.M.N.; Di Renzo, M. Aerial Reconfigurable Intelligent Surfaces-Enabled Secured Wireless Communications: Performance Analysis and Optimization. IEEE Trans. Commun. 2024, 1. [Google Scholar] [CrossRef]
- Le, A.T.; Hieu, T.D.; Nguyen, T.N.; Le, T.L.; Nguyen, S.Q.; Partila, P. Physical layer security analysis for RIS-aided NOMA systems with non-colluding eavesdroppers. Comput. Commun. 2024, 219, 194–203. [Google Scholar] [CrossRef]
- Badarneh, O.S. Statistics of the Product of Two α-F Variates with Applications. IEEE Commun. Lett. 2021, 25, 1761–1765. [Google Scholar] [CrossRef]
- Tegos, S.A.; Tyrovolas, D.; Diamantoulakis, P.D.; Liaskos, C.K.; Karagiannidis, G.K. On the Distribution of the Sum of Double-Nakagami-m random vectors and application in randomly reconfigurable surfaces. IEEE Trans. Veh. Technol. 2022, 71, 7297–7307. [Google Scholar] [CrossRef]
- Minh, B.V.; Tran, P.T.; Pham, T.-H.T.; Le, A.T.; Le, S.-P.; Partila, P. Statistics of the Sum of Double Random Variables and Their Applications in Performance Analysis and Optimization of Simultaneously Transmitting and Reflecting Reconfigurable Intelligent Surface-Assisted Non-Orthogonal Multi-Access Systems. Sensors 2024, 24, 6148. [Google Scholar] [CrossRef] [PubMed]
- Silva, H.S.; Lourenço, G.B.L.C.; Queiroz, W.J.L.; Oliveira, A.S.R.; Madeiro, F.; Badarneh, O.S. On the Sum of α-F and Double α-F VariatesWith Application to MRC and RIS. IEEE Commun. Lett. 2022, 26, 2894–2898. [Google Scholar] [CrossRef]
- Van Chien, T.; Tu, L.T.; Khalid, W.; Yu, H.; Chatzinotas, S.; Di Renzo, M. RIS-Assisted Wireless Communications: Long-Term Versus Short-Term Phase Shift Designs. IEEE Trans. Commun. 2024, 72, 1175–1190. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, P.T.; Vozňák, M. Power splitting–based energy-harvesting protocol for wireless-powered communication networks with a bidirectional relay. Int. J. Commun. Syst. 2018, 31, e3721. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Minh, T.H.Q.; Tran, P.T.; Voznak, M.; Duy, T.T.; Nguyen, T.L.; Tin, P.T. Performance enhancement for energy harvesting based two-way relay protocols in wireless ad-hoc networks with partial and full relay selection methods. Ad Hoc Netw. 2019, 84, 178–187. [Google Scholar] [CrossRef]
- Hoang, T.M.; Nguyen, B.C.; Thang, N.N.; Tran, M.; Tran, P.T. Performance and optimal analysis of time-switching energy harvesting protocol for MIMO full-duplex decode-and-forward wireless relay networks with various transmitter and receiver diversity techniques. J. Frankl. Inst. 2020, 357, 13205–13230. [Google Scholar] [CrossRef]
- Jeffrey, A.; Zwillinger, D. Table of Integrals, Series, and Products; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Nguyen, T.N.; Tran Tin, P.; Ha, D.H.; Voznak, M.; Tran, P.T.; Tran, M.; Nguyen, T.L. Hybrid TSR–PSR alternate energy harvesting relay network over Rician fading channels: Outage probability and SER analysis. Sensors 2018, 18, 3839. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.N.; Quang Minh, T.H.; Tran, P.T.; Vozňák, M. Energy harvesting over Rician fading channel: A performance analysis for half-duplex bidirectional sensor networks under hardware impairments. Sensors 2018, 18, 1781. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, P.T.; Minh, T.H.Q.; Voznak, M.; Sevcik, L. Two-way half duplex decode and forward relaying network with hardware impairment over Rician fading channel: System performance analysis. Elektron. Elektrotechnika 2018, 24, 74–78. [Google Scholar] [CrossRef]
- Meijer G-Function: Integration. Wolfram Research. Available online: http://functions.wolfram.com/07.34.21.0013.01 (accessed on 30 December 2024).
| Context | Our Work | [52,53,54,55,56,57,58,59,60,61] | [49] | [46] |
|---|---|---|---|---|
| Generalized Fading Channels | Yes | No | No | No |
| PLS with RIS systems | Yes | Yes | Yes | No |
| Joint beamforming and power allocation | No | No | Yes | Yes |
| Modified NOMA combining RIS design | Yes | No | No | No |
| SOP | Yes | Yes | Yes | No |
| SEC | Yes | Yes/No | No | Yes |
| Free untrusted user | Yes | No | No | No |
| Parameter | Notation | Values |
| Number of RIS elements | L | {16,24} |
| Number of RIS elements | L | {16,24} |
| Power allocation coefficient for Willie’s signal | ||
| Power allocation coefficient for Bob’s signal | ||
| Target data rate for Willie’s signal | bps/Hz | |
| Secured target data rate for Bob’s signal | bps/Hz | |
| Rayleigh parameters | Notation | Values |
| Inverse scale parameter of link to | ||
| Inverse scale parameter of link to | ||
| Inverse scale parameter of link to | ||
| Inverse scale parameter of link to | 1 | |
| Inverse scale parameter of link to | ||
| Nakagami-m | Notation | Values |
| Shape parameter of link to | ||
| Shape parameter of link to | 2 | |
| Shape parameter of link to | ||
| Shape parameter of link to | ||
| Shape parameter of link to | 1 | |
| Rician parameters | Notation | Values |
| Rician factor of link to | 2 | |
| Rician factor of link to | 2 | |
| Rician factor of link to | 3 | |
| Rician factor of link to | 3 | |
| Rician factor of link to | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, S.-Q.; Tran, P.T.; Minh, B.V.; Duy, T.T.; Le, A.-T.; Rejfek, L.; Tu, L.-T. Statistical Analysis of the Sum of Double Random Variables for Security Applications in RIS-Assisted NOMA Networks with a Direct Link. Electronics 2025, 14, 392. https://doi.org/10.3390/electronics14020392
Nguyen S-Q, Tran PT, Minh BV, Duy TT, Le A-T, Rejfek L, Tu L-T. Statistical Analysis of the Sum of Double Random Variables for Security Applications in RIS-Assisted NOMA Networks with a Direct Link. Electronics. 2025; 14(2):392. https://doi.org/10.3390/electronics14020392
Chicago/Turabian StyleNguyen, Sang-Quang, Phuong T. Tran, Bui Vu Minh, Tran Trung Duy, Anh-Tu Le, Lubos Rejfek, and Lam-Thanh Tu. 2025. "Statistical Analysis of the Sum of Double Random Variables for Security Applications in RIS-Assisted NOMA Networks with a Direct Link" Electronics 14, no. 2: 392. https://doi.org/10.3390/electronics14020392
APA StyleNguyen, S.-Q., Tran, P. T., Minh, B. V., Duy, T. T., Le, A.-T., Rejfek, L., & Tu, L.-T. (2025). Statistical Analysis of the Sum of Double Random Variables for Security Applications in RIS-Assisted NOMA Networks with a Direct Link. Electronics, 14(2), 392. https://doi.org/10.3390/electronics14020392







