Multiscale Convolution-Based Efficient Channel Estimation Techniques for OFDM Systems

Abstract

With the advancement of wireless communication technology, the significance of efficient and accurate channel estimation methods has grown substantially. Recently, deep learning-based methods are being adopted to estimate channels with higher precision than traditional methods, even in the absence of prior channel statistics. In this paper, we propose two deep learning-based channel estimation models, CAMPNet and MSResNet, which are designed to consider channel characteristics from a multiscale perspective. The convolutional attention and multiscale parallel network (CAMPNet) accentuates critical channel characteristics by utilizing parallel multiscale features and convolutional attention, while the multiscale residual network (MSResNet) integrates information across various scales through cross-connected multiscale convolutional structures. Both models are designed to perform robustly in environments with complex frequency domain information and various Doppler shifts. Experimental results demonstrate that CAMPNet and MSResNet achieve superior performance compared to existing channel estimation methods within various channel models. Notably, the proposed models show exceptional performance in high signal-to-noise ratio (SNR) environments, achieving up to a 48.98% reduction in mean squared error(MSE) compared to existing methods at an SNR of $25\mathrm{dB}$. In experiments evaluating the generalization capabilities of the proposed models, they show greater stability and robustness compared to existing methods. These results suggest that deep learning-based channel estimation models have the potential to overcome the limitations of existing methods, offering high performance and efficiency in real-world communication environments.

1. Introduction

In the fifth-generation (5G) wireless communication system, orthogonal frequency division multiplexing (OFDM) has been widely adopted due to its high bandwidth efficiency and robustness against multipath fading and delay [1]. OFDM offers resistance to frequency-selective fading by dividing data across multiple subcarriers and efficiently utilizes spectral resources without interference by leveraging the orthogonality between subcarriers. However, signals passing through a communication channel are subject to distortion caused by the channel characteristics, necessitating a channel estimation process to mitigate these distortions [2]. Channel estimation serves to identify the characteristics of the channel and recover distorted signals, thereby maintaining signal quality. This process is a essential step in OFDM systems, as it determines the impact of channel characteristics on the quality of received signals [3]. As a result, precise channel estimation is regarded as a fundamental technology in OFDM systems [4]. In general, the channel is measured using pilot signals at predefined time–frequency positions that are known to both the transmitter and the receiver. Pilot-based signals transmitted from the transmitter traverse the channel and reach the receiver, where the receiver extracts the pilot signals to estimate the channel characteristics. The estimated channel response is then utilized to compensate for signal distortion, restoring the transmitted signal. In OFDM systems, coherent modulation and detection methods are employed, among which accurate channel information is necessary for the coherent detection of received signals [1]. 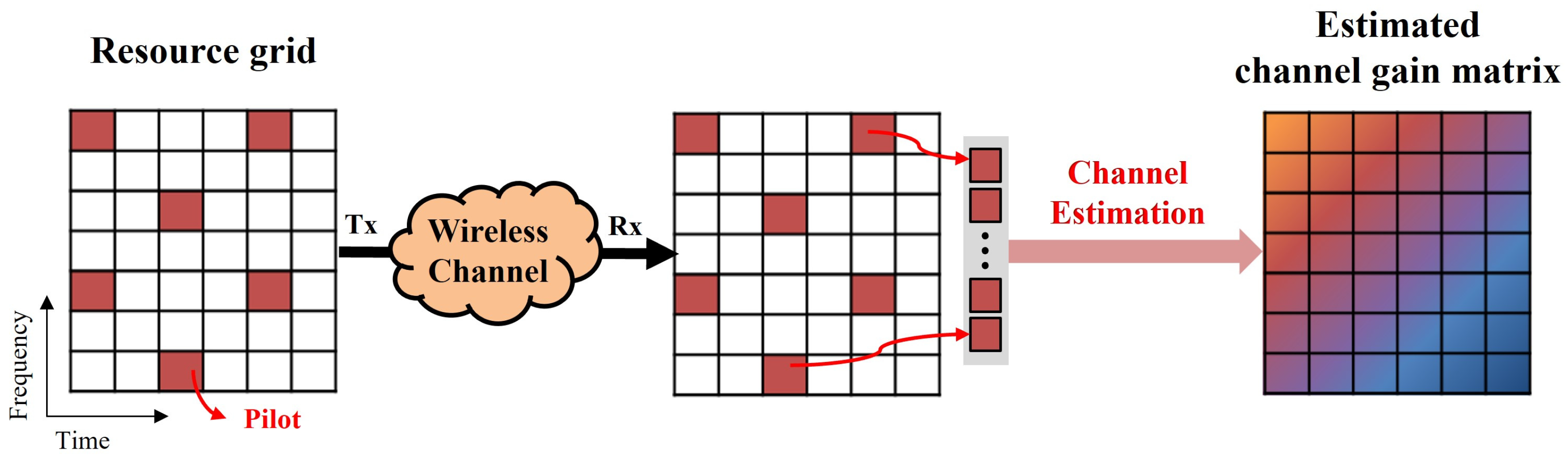Figure 1 illustrates the overall process of channel estimation in a single-input single-output (SISO) OFDM system.

Traditional channel estimation methods include the least square (LS) and minimum mean square error (MMSE) method [5]. The LS method is practical due to its simplicity but lacks estimation accuracy. In contrast, the MMSE provides highly accurate estimates but relies on prior channel statistics and has a high computational cost, making it challenging to apply in practical channel environments. Moreover, these conventional methods are not suitable for high-speed mobility scenarios [6]. To address these limitations, deep learning-based methods have recently been proposed, offering improved accuracy in channel estimation without additional prior channel information. For example, studies in [7,8,9,10] introduced deep learning models based on neural networks with fully connected layers. These models demonstrated superior performance across various channel conditions, highlighting the potential of deep learning for channel estimation. Additionally, It has been demonstrated that deep learning is more effective than traditional methods in realistic communication environments in [11,12] Other approaches, including those by [13,14,15,16], treated the channel as a two-dimensional (2D) image. These methods utilized convolutional operations to extract channel characteristics, enabling more accurate channel estimation. Specifically, ReEsNet [17] extracts only the pilot signals from the received signal to use as input data, significantly reducing the computational load of the model. It also demonstrated the ability to perform effective channel estimation by employing residual connections. Interpolation-ResNet [18] significantly reduced model complexity and achieved superior performance by utilizing bilinear interpolation instead of deconvolution to restore the extracted pilot signals to the original signal size, as is done in the ReEsNet structure. Recurrent neural networks (RNNs) and long short-term memory (LSTM) models were applied in [19,20,21,22] to capture the temporal dynamics of channel characteristics. Furthermore, generative models like GANs and diffusion models have been employed in channel estimation. The models proposed in [23,24,25,26] reproduced channel responses using their generative frameworks. Through the numerous studies mentioned above, it has been demonstrated that various deep learning methods can achieve superior performance compared to MMSE, even without prior information about the channel. However, channel estimation methods based on time series models and generative models generally require high computational complexity, which may render them unsuitable for real-time applications. Therefore, to design a practical and accurate channel estimation model, we aim to develop a model based on convolutional operations that require relatively low computational complexity while effectively capturing channel characteristics.

In this paper, we propose CAMPNet and MSResNet, which are advancements of the ReEsNet [17] and Interpolation-ResNet [18] models, respectively. Both models incorporate multiscale convolutional layers with different filter sizes, aiming to incorporate information from diverse perspectives based on filter size through their multiscale structures. By employing structures with varying filter sizes, the input pilot signals can be processed to integrate information across multiple resolutions. This approach enables more comprehensive feature representations compared to single-scale information, allowing for a more precise reflection of the channel’s spatial–frequency characteristics.

Convolutional attention and multiscale parallel network (CAMPNet) is a model based on ReEsNet, retaining the residual connection structure and transposed convolutional layers used in ReEsNet to restore the original signal size from the pilot signals. The model introduces convolutional attention and multiscale parallel residual block (CAMPResBlock), which integrates parallel operations and convolution-based attention mechanisms to enhance feature extraction. The use of a dilated convolutional layer in the parallel block of the CAMPResBlock allows the model to consider a broader receptive field without increasing parameters. Additionally, the convolutional attention mechanism in the convolution attention block of the CAMPResBlock focuses on important regions within the received pilot signals, facilitating more precise channel estimation.

The multiscale residual network (MSResNet) is an advanced model based on Interpolation-ResNet, utilizing an interpolation layer instead of transposed convolutional operations to restore the pilot signals to their original size with reduced computational complexity. The core of MSResNet lies in the multiscale residual block (MSResBlock), which performs convolution operations with filters of varying sizes, enabling the extraction of channel characteristics across multiple scales. Moving beyond the approach of simply utilizing filters of the same size for learning, MSResBlock considers a broader range of pilot signals and effectively integrates information at various scales by cross-connecting the features extracted from different filters.

Both CAMPNet and MSResNet demonstrate superior performance compared to traditional channel estimation methods and existing deep learning-based methods. The key contributions of this paper are as follows:

• We propose the CAMPNet, which incorporates parallel operations and convolutional attention mechanisms. The parallel operations utilize both standard and dilated convolutions, allowing the model to extract features over a wider receptive field without increasing the number of parameters. Additionally, the convolutional attention mechanism is designed to prioritize and emphasize the critical parts of the received pilot signal. These approaches enable CAMPNet to effectively capture channel characteristics in multiscale perspectives, resulting in more precise channel estimation compared to existing methods.
• We propose the MSResNet, which is a model that employs a multiscale convolutional structure. MSResNet leverages MSResBlock to extract features at multiple scales using filters of varying sizes. The features obtained from different scales are fused through cross-connections, enabling the integration of rich, multilayered information that is unattainable with single-scale approaches.
• The proposed models outperform existing deep learning-based methods and traditional channel estimation methods in the Extended Pedestrian A (EPA) and Extended Typical Urban (ETU) channel models under varying mobility conditions. Furthermore, the proposed models demonstrated strong generalization performance even in testing environments that were different from the trained channel models and exhibited stable and adaptive performance in experiments with various Doppler shifts. These results confirm that the proposed models are well suited for practical deployment in real-world communication environments.

2. Related Works

2.1. Channel Estimation

Traditional channel estimation methods include least square (LS) and minimum mean square error (MMSE). The LS estimates the channel by minimizing the discrepancy between the transmitted and received signals, offering practicality and low computational complexity. However, it suffers from low accuracy in channel estimation. In contrast, the MMSE improves estimation accuracy by calculating the covariance between the channel and received signal alongside the autocorrelation of the received signal based on LS-derived channel information. This method effectively handles noise and interference but relies on prior channel information. If the prior information does not align with the actual channel conditions, MMSE performance can degrade significantly.

To address the limitations of traditional methods, deep learning-based channel estimation models have been developed. ChannelNet [2] is one such model designed for pilot-based channel estimation. It treats the received pilot signal as a low-resolution image, enhances its resolution using SRCNN [27], and then applies DnCNN [28] to restore the high-resolution channel estimation. ReEsNet [17] focuses only on extracted pilot signals to identify channel characteristics and reconstructs the full channel size using a transposed convolutional layer. This model achieves superior performance compared to traditional methods, even with a reduced number of learnable parameters. Interpolation-ResNet [18], similar to ReEsNet, uses only pilot signals for channel estimation but replaces the transposed convolution operation with bilinear interpolation. This approach maintains high estimation accuracy while significantly reducing the computational complexity and the number of learnable parameters. Deep learning-based channel estimation models effectively address the shortcomings of traditional methods, offering more robust and reliable performance across diverse channel environments.

2.2. Vision Attention Mechanism

The attention mechanism was originally designed for natural language processing and has proven highly effective in enabling deep learning models to focus on significant features while minimizing irrelevant information. By utilizing queries, keys, and values derived from the input data, this mechanism enhances the model’s capability to more effectively capture the underlying characteristics of the data. Its usefulness has led to widespread adoption across various fields, including computer vision, where it has been adapted to suit diverse data types and tasks. In particular, in the field of computer vision, attention mechanisms are employed to emphasize critical regions within 2D images.

For instance, SE-Net [29] applies attention along the channel dimension to assess inter-channel importance. It consists of two stages: the squeeze stage, which summarizes global channel characteristics via global average pooling; and the excitation stage, which calculates channel importance using a fully connected layer. This approach enhances model performance by prioritizing significant channels. CBAM [30] is a model that combines channel attention and spatial attention. Channel attention computes the importance of channels using average pooling and max pooling, while spatial attention identifies spatial relevance through the same operations applied to spatial dimensions. By integrating both channel and spatial information, CBAM significantly improves model effectiveness. ECA [31] simplifies the SE-Net structure by replacing the fully connected layer with convolution operations in the channel attention mechanism. This simplication reduces computational complexity, making the structure more efficient and suitable for integration into various networks.

Attention methods have also been introduced in deep learning-based channel estimation models. HA02 [32] incorporates the transformer encoder structure into channel estimation, leveraging the multihead attention mechanism to extract input data characteristics and thereby improving channel estimation accuracy. Similarly, AttenReEsNet [33] integrates attention at the channel level within the structure of ReEsNet. By utilizing a fully connected layer in attention module, it achieves more precise channel estimation by effectively emphasizing significant features. These advancements illustrate the adaptability and utility of attention mechanisms across various domains, including deep learning-based channel estimation methods.

3. Preliminaries

3.1. OFDM

Assuming a single-input single-output (SISO) downlink scenario in an OFDM system, the relationship between the transmitted signal $x(t)$ and the received signal $y(t)$ at time t can be expressed as follows:

$$y(t)=g(t)\otimes x(t)+z(t),$$

(1)

where $z(t)$ denotes the additive white Gaussian noise (AWGN), while $g(t)$ represents the pulse response of the Rayleigh fading channel. The OFDM system operates in frames comprising $N_s$ OFDM symbols, with the channel impulse response assumed to vary slowly within a single frame. If the maximum path delay is shorter than the cyclic prefix, the OFDM symbol in the frequency domain can be expressed as follows:

$$\mathbf{Y}=\mathbf{H}\circ \mathbf{X}+\mathbf{Z},$$

(2)

where $\mathbf{H},\mathbf{X},\mathbf{Y},\mathbf{Z}\in {\mathbb{C}}^{{\mathit{N}}_{\mathit{f}}\times {\mathit{N}}_{\mathit{s}}}$ represent the channel gain matrix, the symbol matrix to be transmitted in the current frequency domain, the received symbol matrix, and the discrete Fourier transform of the AWGN noise matrix, respectively. $N_f$ denotes the length of the fast Fourier transform (FFT) used in the OFDM receiver, and ∘ represents the element-wise multiplication operation. The transmitted OFDM symbol comprises both data and pilot symbols. In the data symbol, all subcarriers carry modulated signals, whereas in the pilot symbol, specific subcarriers are reserved as pilots, following a method akin to the 5G demodulation reference signal approach [34], with the remaining subcarriers set to zero. These pilot signals facilitate channel estimation, allowing the receiver to extract pilot subcarriers, perform frequency domain channel estimation, and predict the channel gain for the entire frame. In this paper, only the pilot symbols were extracted and utilized as input data, which can be represented as follows:

$${\mathit{Y}}_{\mathrm{p}}={\mathit{H}}_{\mathrm{p}}\circ {\mathit{X}}_{\mathrm{p}}+{\mathit{Z}}_{\mathrm{p}}.$$

(3)

where ${\mathit{Y}}_{\mathrm{p}},{\mathit{H}}_{\mathrm{p}},{\mathit{X}}_{\mathrm{p}},{\mathit{Z}}_{\mathrm{p}}\in {\mathbb{C}}^{N_{{\mathrm{p}}_f}\times N_{{\mathrm{p}}_s}}$ represent the received signal, channel gain matrix, transmitted signal, and noise matrix of extracted pilot symbols, respectively. $N_{{\mathrm{p}}_f}$ and $N_{{\mathrm{p}}_s}$ denote the number of subcarriers and OFDM symbols of the pilot signal, respectively.

3.2. LS

The LS method performs channel estimation by minimizing the Euclidean distance between $\mathbf{Y}$ and $\mathbf{H}\circ \mathbf{X}$. The channel gain estimated using LS can be expressed as follows:

$${\widehat{\mathbf{H}}}_{\mathrm{p}}^{\mathrm{LS}}=\frac{{\mathbf{Y}}_{\mathrm{p}}}{{\mathbf{X}}_{\mathrm{p}}},$$

(4)

where ${\mathbf{X}}_{\mathrm{p}}$ and ${\mathbf{Y}}_{\mathrm{p}}$ denote the transmitted and received pilot signal matrix, respectively, while ${\widehat{\mathbf{H}}}_{\mathrm{p}}\in {\mathbb{C}}^{N_{{\mathrm{p}}_f}\times N_{{\mathrm{p}}_s}}$ represents the channel gain matrix estimated by the LS method. As is evident from the above equation, deriving the LS is computationally simple, leading to low complexity and high practicality. However, it has the limitation of low channel estimation accuracy, and its performance degrades significantly in environments with low signal-to-noise ratios (SNRs).

3.3. MMSE

The MMSE method performs channel estimation by minimizing the Euclidean distance between $\mathbf{H}$ and ${\widehat{\mathbf{H}}}_{\mathrm{LS}}$. The linear MMSE estimation for the pilot ODFM symbols [35] is expressed as follows:

$${\widehat{\mathbf{H}}}_{\mathrm{p}}^{\mathrm{MMSE}}={\mathit{R}}_{{\mathbf{HH}}_{\mathrm{p}}}{({\mathit{R}}_{{\mathbf{H}}_{\mathrm{p}}{\mathbf{H}}_{\mathrm{p}}}+\mathbf{I}\frac{{\mathsf{\sigma }}_N^2}{{\mathsf{\sigma }}_X^2})}^{-1}{\widehat{\mathbf{H}}}_{\mathrm{p}}^{\mathrm{LS}},$$

(5)

where $\mathbf{H}$ represents the channel gain matrix, while ${\mathbf{H}}_{\mathrm{p}}$ denotes the estimated channel gain matrix using pilot symbols. The term ${\mathsf{\sigma }}_N^2/{\mathsf{\sigma }}_X^2$ corresponds to the inverse of the SNR, where the scalar values ${\mathsf{\sigma }}_N^2$ and ${\mathsf{\sigma }}_X^2$ represent the average power of the additive white Gaussian noise (AWGN) and the transmitted signal, respectively. The matrix ${\mathit{R}}_{{\mathit{HH}}_{\mathrm{p}}}$ is the cross-correlation that numerically measures the similarity between the channel gain matrix ${\mathit{H}}_{\mathrm{p}}$—obtained through pilot signals—and the actual channel gain matrix $\mathbf{H}$. Meanwhile, the matrix ${\mathit{R}}_{{\mathit{H}}_{\mathrm{p}}{\mathit{H}}_{\mathrm{p}}}$ represents the autocorrelation of the channel gain matrix ${\mathit{H}}_{\mathrm{p}}$—obtained from pilot signals—which calculates the correlation with time-shifted signals. These matrices can be computed as follows:

$${\mathit{R}}_{{\mathit{HH}}_{\mathrm{p}}}=\mathbb{E}({\mathit{HH}}_{\mathrm{p}}^{\mathrm{H}}),{\mathit{R}}_{{\mathit{H}}_{\mathrm{p}}{\mathit{H}}_{\mathrm{p}}}=\mathbb{E}({\mathit{H}}_{\mathrm{p}}{\mathit{H}}_{\mathrm{p}}^{\mathrm{H}}).$$

(6)

As can be seen from (5) and (6), the MMSE method relies on statistical information about the channel. However, in practical environments, obtaining such channel statistical information in advance is challenging, and the MMSE method requires significantly more computations compared to the LS method. As a result, despite its superior performance, the MMSE method may be limited in its applicability to real-time or dynamic environments.

4. Methodology

In this paper, we propose two models, CAMPNet and MSResNet, developed from ReEsNet [17] and Interpolation-ResNet [18], respectively. The CAMPNet model is designed to reflect the importance within channel characteristics by utilizing parallel operations and convolutional attention mechanisms, while MSResNet effectively integrates features extracted from multiple filter scales, enabling more precise representations. The input data for both models consist of extracted pilot signals, with the goal of efficiently reconstructing a channel gain matrix for the transmitted signal based on these inputs.

Figure 2 illustrates the structures of the models from previous studies. Figure 2a illustrates the structure of ReEsNet, which is composed of four ResBlocks and restores the features extracted by the ResBlocks to the original channel size through a transposed convolutional layer. Figure 2b illustrates the structure of Interpolation-ResNet, which is composed of four neural blocks and utilizes an interpolation layer instead of a transposed convolutional layer to restore the features extracted by the neural blocks to the original channel size. Building on these prior models, the proposed CAMPNet and MSResNet aim to further enhance channel estimation performance using pilot data. Detailed descriptions of the design and structural enhancements of the two models are provided in the following subsections.

4.1. CAMPNet

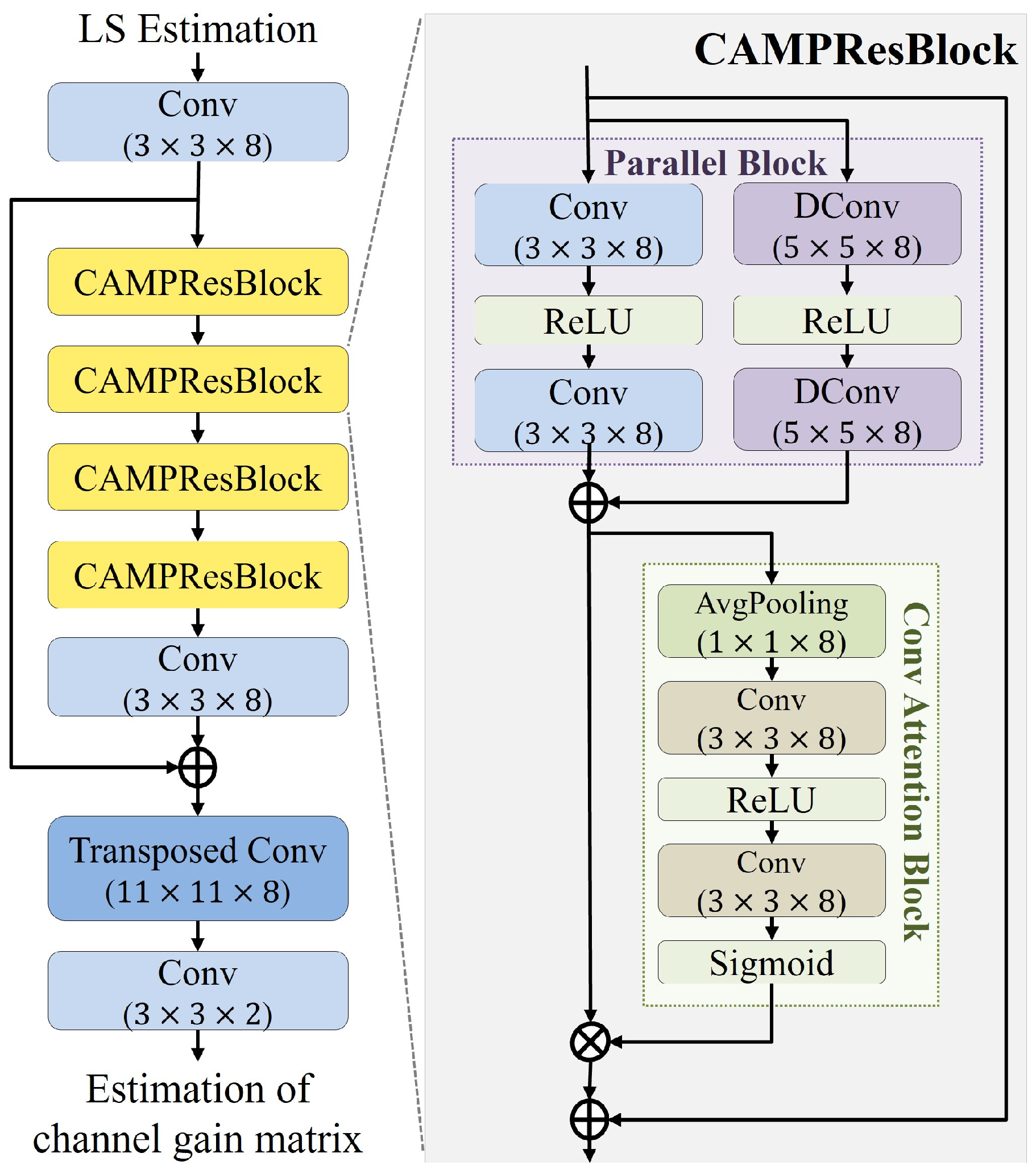
The convolutional attention and multiscale parallel network (CAMPNet) is a model developed based on ReEsNet. Its structure, illustrated in Figure 3, comprises three convolutional layers, four CAMPResBlocks, and one transposed convolutional layer. The CAMPResBlock is a specialized module designed to extract multiscale features through dilated convolutions and efficiently capture channel-specific features by leveraging a convolution-based attention mechanism that highlights the importance of features across channels.

The CAMPResBlock consists of a parallel block and a convolution attention block. The Parallel Block is designed to extract and combine multiscale features by leveraging filters of varying sizes. It employs two standard convolutional layers with filter sizes of $3\times 3$ and two dilated convolutional layers with filter sizes of $5\times 5$, which are arranged in parallel. Dilated convolutions expand the receptive field by spacing filter elements, enabling broader feature extraction without increasing parameters compared to standard convolutions with the same filter size. In this study, the dilation factor in the dilated convolution layers of the parallel block was set to 2, and appropriate padding was applied to maintain the same input and output size. The features extracted from the parallel block are then forwarded to the convolution attention block, which is a convolution-based attention mechanism that emphasizes the importance of specific channels in the feature map. This module uses global average pooling to compress features along the channel axis, computing a $1\times 1\times N_{\mathrm{filters}}$ feature map, and then applies a convolutional layer to determine each channel’s importance. We used $N_{\mathrm{filters}}=8$ for training the model. The pooled features are subsequently forwarded to two convolutional layers, and a sigmoid function is applied to produce a set of importance values for each channel. These importance values are combined with the features extracted from the parallel block via element-wise multiplication, transforming them into a feature map that reflects channel-wise importance. The CAMPResBlock sums its input data and the convolution attention block’s output via a residual connection, stabilizing learning and enhancing CAMPNet’s performance by preserving important features.

The CAMPNet model utilizes the channel gain estimated by the LS method as input data. The LS method provides a simple initial estimation, laying a foundation for refined channel estimation by partially removing noise and reducing the model’s training burden. The LS estimation is passed through the first convolutional layer with a filter size of $3\times 3\times N_{\mathrm{filters}}$, generating an initial feature map. The generated feature map is then processed through four CAMPResBlocks. Within the CAMPResBlocks, features reflecting the importance of each channel are produced, thereby enhancing the representation of significant channel information. The output from the CAMPResBlocks is passed to a second convolutional layer with the same filter size as the first layer, being $3\times 3\times N_{\mathrm{filters}}$. To stabilize the learning process and preserve critical features, the output of this second convolutional layer is residually connected with the output of the first convolutional layer. Afterward, the residual-connected output is forwarded to a transposed convolutional layer with a filter size of $11\times 11\times N_{\mathrm{filters}}$, restoring the data size to match the that of the original channel gain matrix. The restored data are further passed through the third convolutional layer, which produces the final channel estimation result. This result comprises two channels corresponding to the real and imaginary parts of the estimated channel gain matrix. This structure enables CAMPNet to enhance channel estimation accuracy by leveraging parallel blocks and attention mechanisms to extract multiscale features and emphasize crucial channel characteristics.

In summary, the CAMPNet model is an advanced model based on ReEsNet consisting of four specialized blocks for extracting channel features, two convolutional layers, and a transposed convolutional layer for restoring the channel to its original size in a similar manner to ReEsNet. While ReEsNet employs a relatively simple ResBlock structure, consisting of two convolutional layers with a filter size of $3\times 3$ connected via a residual connection, CAMPNet utilizes a CAMPResBlock, which incorporates a parallel convolutional structure with dilated convolutions and an attention mechanism. This design allows CAMPNet to capture channel characteristics more effectively from a multiscale perspective.

4.2. MSResNet

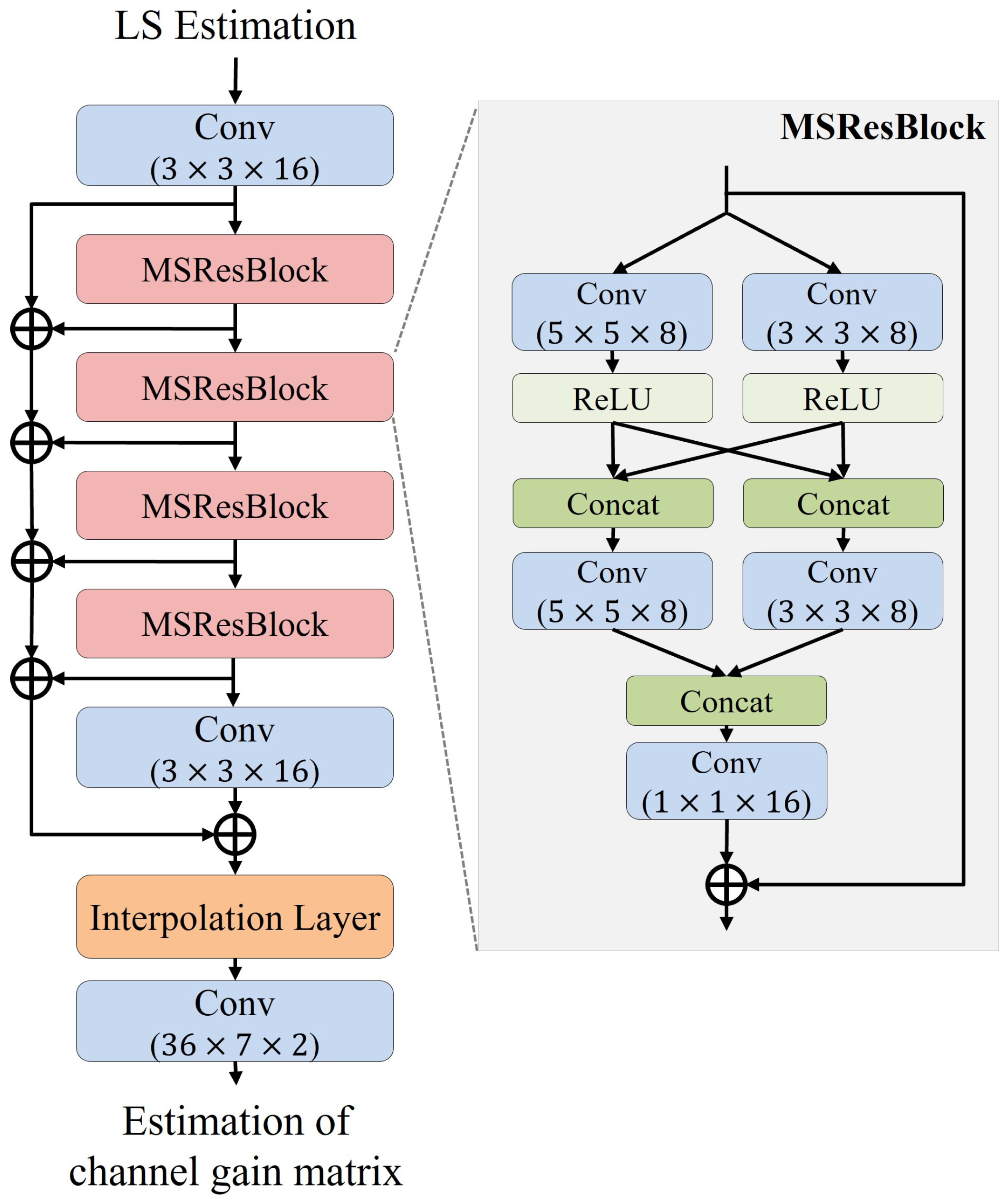
The multiscale residual network (MSResNet) is a model developed based on the structure of Interpolation-ResNet. It utilizes bilinear interpolation instead of a transposed convolutional layer to restore the size of the original channel gain matrix.

The structure of MSResNet is illustrated in Figure 4. MSResNet consists of three convolutional layers, four MSResBlocks, and one interpolation layer. The MSResBlock is a module designed to efficiently extract features across multiple scales by utilizing filters of different sizes and cross-connecting the resulting features. It computes features using convolutional layers of size $3\times 3\times {\displaystyle \frac{N_{\mathrm{filters}}}{2}}$ and $5\times 5\times {\displaystyle \frac{N_{\mathrm{filters}}}{2}}$, and it then cross-connects the outputs from both layers. The number of channels is set to ${\displaystyle \frac{N_{\mathrm{filters}}}{2}}$ to ensure that the total number of channels remains manageable after the cross-connection. The cross-connected features are passed through additional convolutional layers corresponding to each filter size to extract more refined features. Subsequently, all outputs are concatenated and sent to convolutional layers of size $1\times 1\times N_{\mathrm{filters}}$ to fuse multiscale features. Finally, the fused features are combined with the initial input features through a residual connection, producing the final output of the MSResBlock. This structure facilitates multiscale feature extraction and fusion, thereby enhancing the accuracy of channel estimation.

First, when the channel gain matrix calculated through LS estimation is input to the model, it passes through the first convolutional layer to extract initial features. The extracted features pass sequentially through four MSResBlocks, where features from multiscale filters are considered, enabling the extraction of more refined features. The output from the MSResBlocks is forwarded to the second convolutional layer for further feature extraction. Subsequently, the outputs from each MSResBlock and the convolutional layers are summed and sent to the interpolation layer.

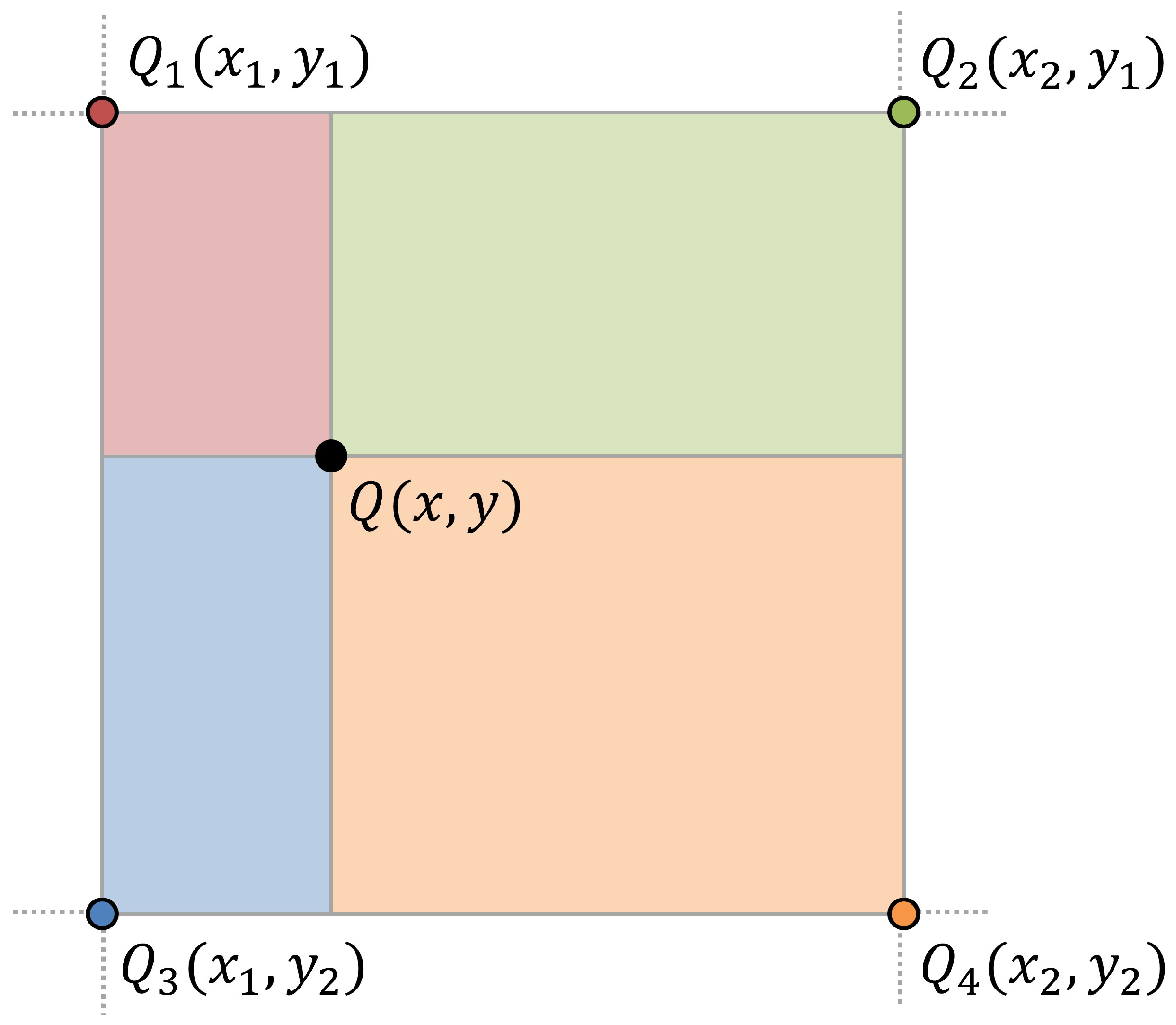
Serving as an alternative to the transposed convolutional layer, the interpolation is conducted through this layer using the following equation:

$$f(Q)={\displaystyle \frac{\left[\begin{array}{cc}{x}_2-x& x-x_1\end{array}\right]\left[\begin{array}{cc}f(Q_1)& f(Q_2)\\ f(Q_3)& f(Q_4)\end{array}\right]\left[\begin{array}{c}{y}_2-y\\ y-y_1\end{array}\right]}{(x_2-x_1)(y_2-y_1)}},$$

(7)

where $x,y$ denote the coordinates of the data point to be interpolated, while $(x_1,y_1),(x_2,y_2)$ represent the coordinates of the neighboring samples. Figure 5 represents a visusalization of binary interpolation. Specifically, $x_1$ and $x_2$ are the coordinates of the two closest samples along the x axis, while $y_1$ and $y_2$ are the coordinates of the two closest samples along the y axis. Accordingly, $Q_1,Q_2,Q_3$, and $Q_4$ represent the neighboring samples surrounding the location to be interpolated. The bilinear interpolation method interpolates the value at the current position $(x,y)$ based on the ratio of the distances to the two surrounding samples. In this way, $f(Q)$ is calculated using the relative distances between $Q_1,Q_2,Q_3,$ and $Q_4$ and the target position, enabling efficient data interpolation without requiring additional trainable parameters. This interpolation method enables the model to restore the features to the original channel gain matrix size without significantly affecting its computational complexity. The features restored to the size of the original channel gain matrix through the interpolation layer are sent to a convolutional layer with a filter size of $36\times 7\times 2$, which outputs the final channel gain matrix of size $N_f\times N_s\times 2$ and is composed of real and imaginary parts. The MSResBlock structure is designed to simultaneously capture fine-grained local features and large-scale global features using multiscaled filters. This approach enables a more accurate interpretation of complex frequency domain information, resulting in enhanced channel estimation accuracy.

In conclusion, MSResNet is a model based on the structure of Interpolation-ResNet and similarly utilizes linear interpolation to restore the original channel size. However, unlike the neural block in Interpolation-ResNet, which consists of two convolutional layers with a filter size of $3\times 3$, MSResNet employs the MSResBlock, which is a structure that extracts features using $3\times 3$ and $5\times 5$ filter sizes and integrates them through cross-connection and fusion. This design enables MSResNet to capture channel characteristics at a wider range of scales.

4.3. Loss Function

Our proposed models take the extracted pilot signals as input and output a channel gain matrix of the same size as the original channel gain matrix. The goal is to minimize the difference between the predicted and the actual channel gain matrix through the model. To achieve this, we use the mean squared error (MSE) as the loss function. The equation for the loss function is as follows:

$$L={\displaystyle \frac{1}{N_f{N}_s}}\sum _{i=1}^{N_f}\sum _{j=1}^{N_s}{\left|\left|{\widehat{\mathbf{H}}}_{ij}-{\mathbf{H}}_{ij}\right|\right|}_2^2,$$

(8)

where $N_f$ denotes the length of the FFT used in the OFDM receiver, and $N_s$ is the number of OFDM symbols in a frame. ${\mathbf{H}}_{ij}$ denotes the actual channel corresponding to the i-th subcarrier and the j-th OFDM symbol, while ${\widehat{\mathbf{H}}}_{ij}$ represents the channel prediction obtained from the model. Using this loss function, the model’s parameters are updated to minimize the discrepancy between the actual channel and the channel predicted by the model. For optimizing the loss function, we employ the Adam optimizer. Detailed hyperparameter settings for model training are provided in the following section.

5. Experiments

In this paper, we focus on the downlink scenario of a single-input single-output (SISO) OFDM system. We compared and analyzed the performance of our proposed models on the propagation channel models: the Extended Pedestrian A (EPA) and the Extended Typical Urban (ETU) channel model of the 3rd Generation Partnership Project (3GPP) [36].

The baseband parameters were configured as follows. Each slot contains one frame consisting of 14 OFDM symbols. Each frame includes 72 subcarriers, with 24 subcarriers designated as pilot subcarriers. The cyclic prefix length was set to 16, the bandwidth was $1.08\mathrm{MHz}$, the carrier frequency was $2.1\mathrm{GHz}$, and the subcarrier spacing was $15\mathrm{kHz}$. The number of pilot symbols per frame was set to 2, with the 1st and 13th OFDM symbols selected as pilot symbols. In the first pilot symbol, the pilot subcarriers begin at the first subcarrier, with a subcarrier spacing of 3. For the second pilot symbol, the pilot subcarriers start at the second subcarrier, maintaining the same subcarrier spacing of 3. These configurations facilitate the efficient allocation of pilot signals, ensuring that sufficient information is available for accurate channel estimation.

The hyperparameter settings for training the proposed models and the baseline models, ReEsNet and Interpolation-ResNet, are summarized in

Table 1. Parameter settings.

Parameter	CAMPNet	ReEsNet [17]
		Interpolation-ResNet [18]
		AttenResNet [33]
		MSResNet
Optimizer	Adam	Adam
Epoch	100	100
Batch size	128	128
Learning rate	0.001	0.001
Learning rate drop period	20	20
Learning rate drop rate	0.5	0.5
L2 regularization	0.001	0.001
Number of filters	8	16

. The experiments were conducted using a single NVIDIA RTX 4090 for training the model utilizing the Deep Learning Toolbox in MATLAB 2024b. All models were trained and evaluated under identical conditions, with the MSE employed as the performance metric. The MSE quantifies the discrepancy between the actual channel and the channel predicted by the model and is defined as follows:

$$\mathrm{MSE}(\widehat{\mathbf{H}},\mathbf{H})={\displaystyle \frac{1}{N_f{N}_s}}\sum _{i=1}^{N_f}\sum _{j=1}^{N_s}{\left|\left|{\widehat{\mathbf{H}}}_{ij}-{\mathbf{H}}_{ij}\right|\right|}_2^2,$$

(9)

where ${\mathbf{H}}_{ij}$ denotes the actual channel corresponding to the i-th subcarrier and the j-th OFDM symbol, while ${\widehat{\mathbf{H}}}_{ij}$ represents the channel prediction obtained from the model. All experimental results in this study were validated by computing the MSE using (9). This method provides an effective means of quantitatively comparing the prediction accuracy of the channel estimation models, enabling a clear assessment of the relative performance of each model.

5.1. EPA Channel Model

We conducted training and testing using data generated from the EPA channel model, which represents a low delay spread environment. In the EPA channel model, the range of path delay is from 0 ns to 410 ns, with relative path power values ranging from $-7\mathrm{dB}$ to $0\mathrm{dB}$. For the experiment, the EPA channel model generated 25,000 training data for each SNR in the range of $0\mathrm{dB}$ to $20\mathrm{dB}$ at intervals of $5\mathrm{dB}$, which were used to train the models. We generated 5000 channel realizations for each SNR at the same intervals within an SNR range of $-5\mathrm{dB}$ to $25\mathrm{dB}$ for testing. The Doppler shift was randomly selected between $0\mathrm{Hz}$ and $97\mathrm{Hz}$, corresponding to moving speeds ranging from $0\mathrm{km}/\mathrm{h}$ to $50\mathrm{km}/\mathrm{h}$. 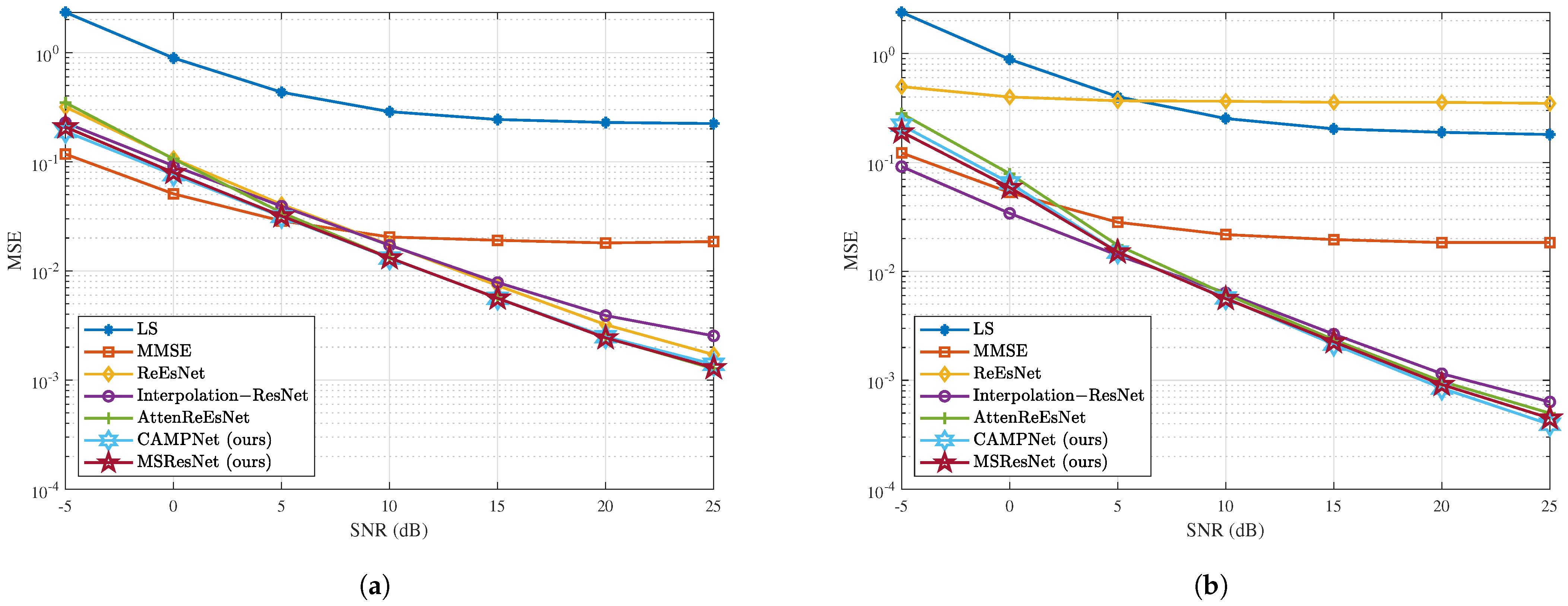Figure 6a demonstrates the experimental results for the EPA channel model. The ReEsNet model demonstrated inferior performance compared to the LS method across the overall SNR range, indicating insufficient channel estimation capability in the EPA channel model. In contrast, although the proposed models, CAMPNet and MSResNet, were slightly inferior to Interpolation-ResNet in the MSE range of $-5\mathrm{dB}$ to $0\mathrm{dB}$, the proposed models outperformed it with SNR values above $5\mathrm{dB}$. Notably, at $25\mathrm{dB}$, CAMPNet achieved approximately a 37.74% reduction in the MSE, while MSResNet achieved a reduction of about 29.11%, demonstrating superior channel estimation performance. The decline in performance at the low-SNR range appears to be due to the increased model complexity. As the model becomes more complex, it better captures the correlation between transmitted and received signals but becomes more vulnerable to channel noise, making it sensitive to distortions. Moreover, in low-SNR environments, the prominence of multipath fading and channel distortion likely exacerbates the model’s susceptibility to such noise. However, both models showed overall performance comparable to AttenReEsNet and achieved significantly better performance than AttenReEsNet in the low-SNR range of $-5\mathrm{dB}$ to $0\mathrm{dB}$. These results validate that the proposed models can leverage multiscale methods and attention mechanisms to perform more effective channel estimation in high-SNR environments.

5.2. ETU Channel Model

We trained and tested our models using data generated from the ETU channel, which is a high delay spread environment. Similar to the experiment in EPA channel, 25,000 training data samples were generated within the SNR range of $0\mathrm{dB}$ to $20\mathrm{dB}$ for training, and 5000 test data samples were generated within the SNR range of $-5\mathrm{dB}$ to $25\mathrm{dB}$ for testing. The maximum Doppler shift was set to $97\mathrm{Hz}$. Figure 6b illustrates the results for the ETU channel model. As illustrated in the figure, MSResNet and CAMPNet consistently outperformed the other channel estimation models across all SNR ranges. Moreover, the performance gap between our proposed models and Interpolation-ResNet widened as the SNR increased. At $25\mathrm{dB}$, MSResNet achieved a 45.13% reduction in the MSE, while CAMPNet recorded a 48.98% reduction compared to Interpolation-ResNet. This validates that the proposed models surpass existing methods in performance, not only in the EPA model with a low delay spread but also in the ETU model with a high delay spread.

5.3. Generalization Capacity

In wireless communication, channel characteristics can vary significantly depending on the time, location, and surrounding conditions. However, training a new channel estimation model for every specific scenario is highly inefficient, making it essential for many deep learning models to be designed to perform well across diverse environments. Therefore, to evaluate the generalization performance of the proposed models, we evaluated our models under conditions where the training and testing channel models differed.

The models trained on the low delay spread EPA channel were tested on the high delay spread ETU channel, and conversely, models trained on the ETU channel were tested on the EPA channel to evaluate their generalization performance. Figure 7 presents the results of these cross-scenario experiments. Figure 7a shows the results of testing the models when trained on the EPA channel model in the ETU channel model. None of the models, including Interpolation-ResNet and AttenReEsNet, performed well in the ETU environment, with the MMSE model showing relatively the best performance. Conversely, Figure 7b illustrates the performance of the models trained on the ETU channel and tested on the EPA channel. The proposed models achieved the lowest MSE, demonstrating superior adaptability in the low delay spread channel compared to the other models. This shows that when generalizing from a high delay spread channel to a low delay spread channel, they outperform existing methods, demonstrating their high potential.

These results indicate that the proposed models have limitations in generalizing from a low delay spread channel to a high delay spread channel. This is likely due to the high delay spread, which involves longer multipath delays and a greater number of multipath components, resulting in a much more complex and dispersed channel response. As a result, models trained on data generated from low delay spread channels with shorter multipath delays are presumed to struggle in accurately capturing the characteristics of such channels.

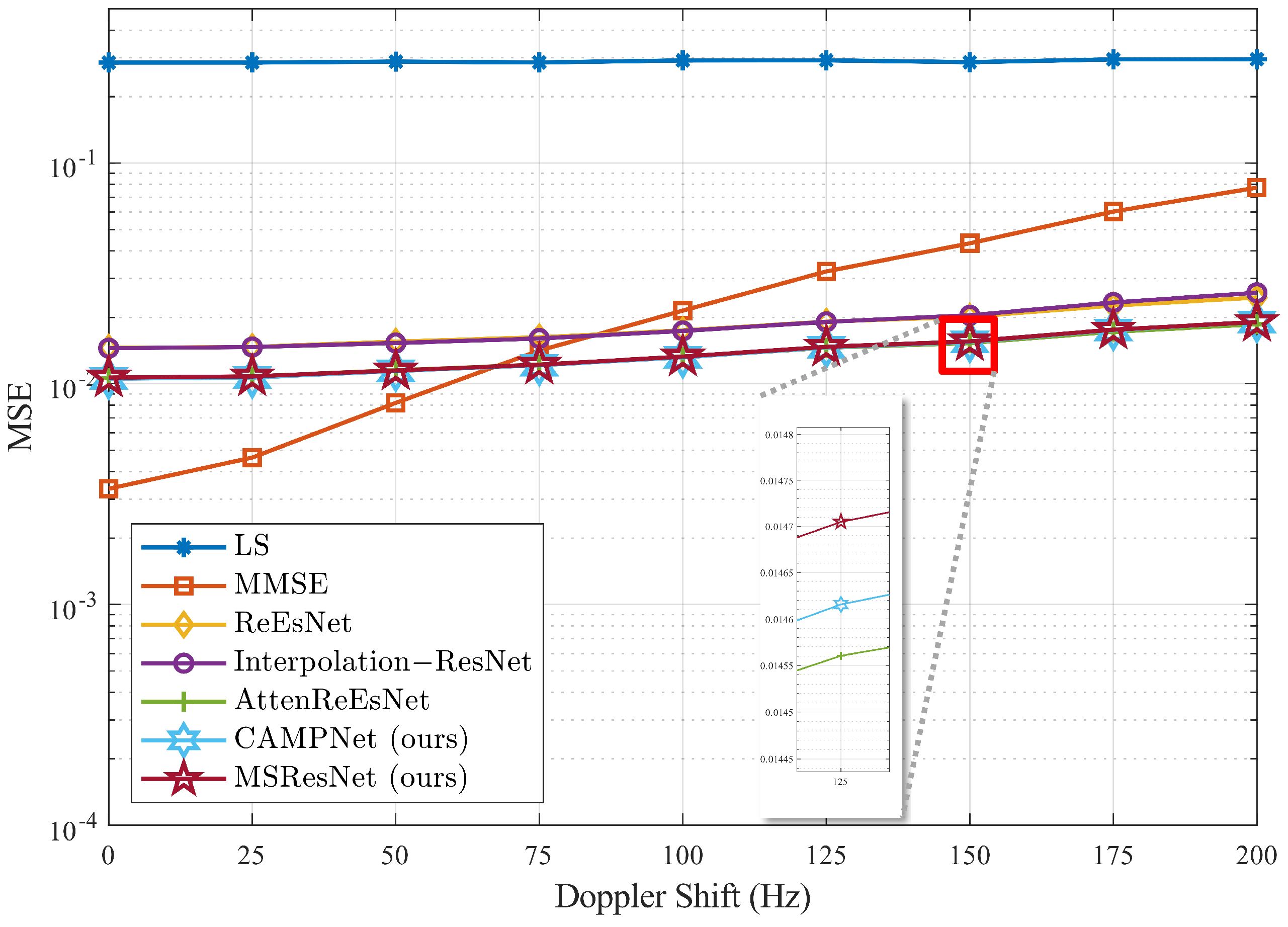
5.4. Various Doppler Shifts

The Doppler shift is a factor that reflects the user’s movement in wireless communication. Maintaining consistent channel estimation performance under varying Doppler shifts is essential, as the model must adapt to changes in user movement. For verify this, we evaluated the robustness of the models trained on the high delay spread ETU channel under varying Doppler shift conditions. The Doppler shift range was set from $0\mathrm{Hz}$ to $200\mathrm{Hz}$ with $25\mathrm{Hz}$ intervals. We tested the models by generating 5000 channel realizations for each Doppler shift, with the SNR fixed at $10\mathrm{dB}$. The results are depicted in Figure 8. As shown, the proposed models, CAMPNet and MSResNet, consistently outperformed the ReEsNet and Interpolation-ResNet across all Doppler shift ranges. Our models achieved up to a 24% reduction in the MSE compared to Interpolation-ResNet, demonstrating their robust performance across various Doppler shift conditions. These results demonstrate that CAMPNet and MSResNet can better adapt to variations in Doppler shifts and reliably perform channel estimation even in fast mobility scenarios.

5.5. Complexity Analysis

We compared the model complexity of the existing methods, including ReEsNet, Interpolation-ResNet, and AttenReEsNet, with the proposed models. The number of learnable parameters of each model is summarized in

Table 2. Comparison of number of learnable parameters and inference time.

Model	Number of Parameters	Inference Time
ReEsNet [17]	23,794	3.54 ms
Interpolation-ResNet [18]	9442	4.29 ms
AttenReEsNet [33]	102,770	9.28 ms
CAMPNet (ours)	30,842	7.21 ms
MSResNet (ours)	46,722	7.05 ms

. Interpolation-ResNet, which utilizes interpolation layers and simple neural blocks, has approximately 60% fewer parameters than ReEsNet. In contrast, AttenReEsNet achieved better performance than Interpolation-ResNet in the high-SNR range but requires more than 10 times the number of parameters. However, even though the performance of our proposed models, CAMPNet and MSResNet, exhibited slightly worse performance than Interpolation-ResNet, they showed superior channel estimation performance to AttenReEsNet while maintaining less than half of the number of leanrable parameters. When comparing the inference time for a single data sample, the proposed models exhibited increased complexity and longer inference times compared to ReEsNet and Interpolation-ResNet. However, they were approximately 2 ms faster than AttenReEsNet. Furthermore, they delivered superior MSE performance at low SNRs and outperformed AttenReEsNet across all SNRs in both the ETU and EPA channel environments. These findings demonstrate that the proposed models strike a balance between performance and efficiency. Overall, these results indicate that the proposed models effectively manage complexity while achieving significant performance improvements.

6. Conclusions

In this paper, we proposed the CAMPNet, which leverages parallel multiscale features and convolutional attention, and the MSResNet, which employs multiscale convolutional structures, to enhance the channel estimation performance. Unlike existing channel estimation methods, our proposed models employ multiscale convolutional operations, allowing them to effectively process both local and global information simultaneously. The CAMPNet improves channel estimation accuracy by emphasizing important features in channels through its parallel blocks and attention mechanisms. The MSResNet incorporates a structure that utilizes two filters of different sizes in parallel and cross-combines their outputs, effectively integrating multiscale information to simultaneously capture both fine-grained details and global features.

The experimental results show that proposed structure significantly improved channel estimation performance compared to existing methods in both the EPA and ETU channel model. Specifically, the proposed models demonstrated up to 48.98% in MSE reduction compared to the existing methods in a high-SNR range. In generalization experiments, the proposed models showed stable performance across diverse channel environments. Additionally, in experiments involving varying Doppler shifts, CAMPNet and MSResNet exhibited robustness, achieving up to 24% lower MSE compared to existing methods. Notably, these models performed effectively even in complex channel conditions, enhancing their applicability in real wireless communication systems. However, as the models became more complex, they demonstrated excellent performance at high-SNR levels but remained sensitive to distortion caused by noise, leading to lower performance at low-SNR levels compared to existing models. Future work could be extended to multiple-input multiple-output (MIMO) environments by generating and training with datasets that account for the number of transmitting and receiving antennas. Additionally, to improve performance not only in environments with greater delay spread but also across a wider range of SNRs, particularly in low-SNR conditions, it is expected that generating data under various channel conditions such as EPA, EVA, and ETU could enhance the diversity of training data. Furthermore, leveraging generalization techniques such as transfer learning and domain adaptation could also contribute to performance improvements.