Highly Robust Active Damping Approach for Grid-Connected Current Feedback Using Phase-Lead Compensation
Abstract
1. Introduction
2. Modeling of the LCL-Type Cascaded H-Bridge SVG System
2.1. Main Circuit Topology
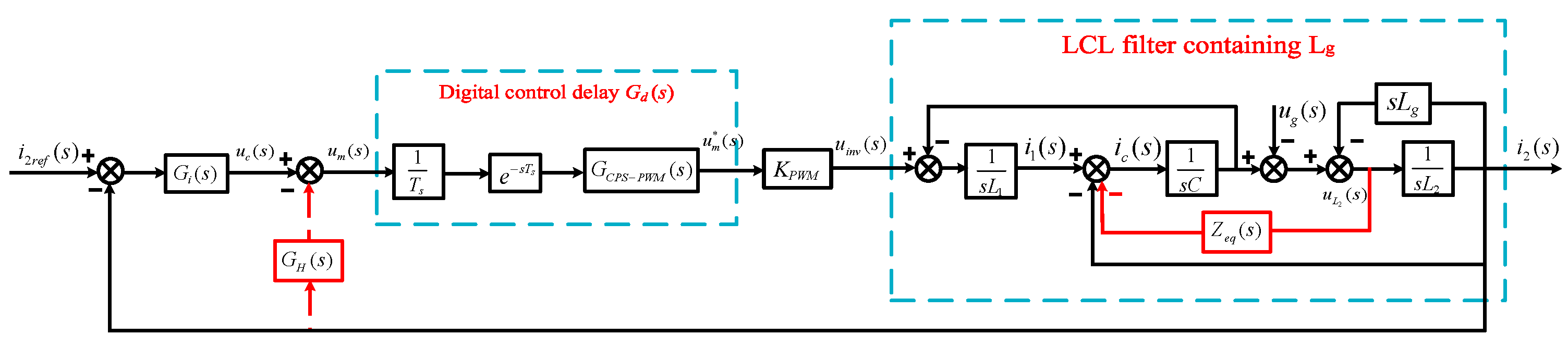
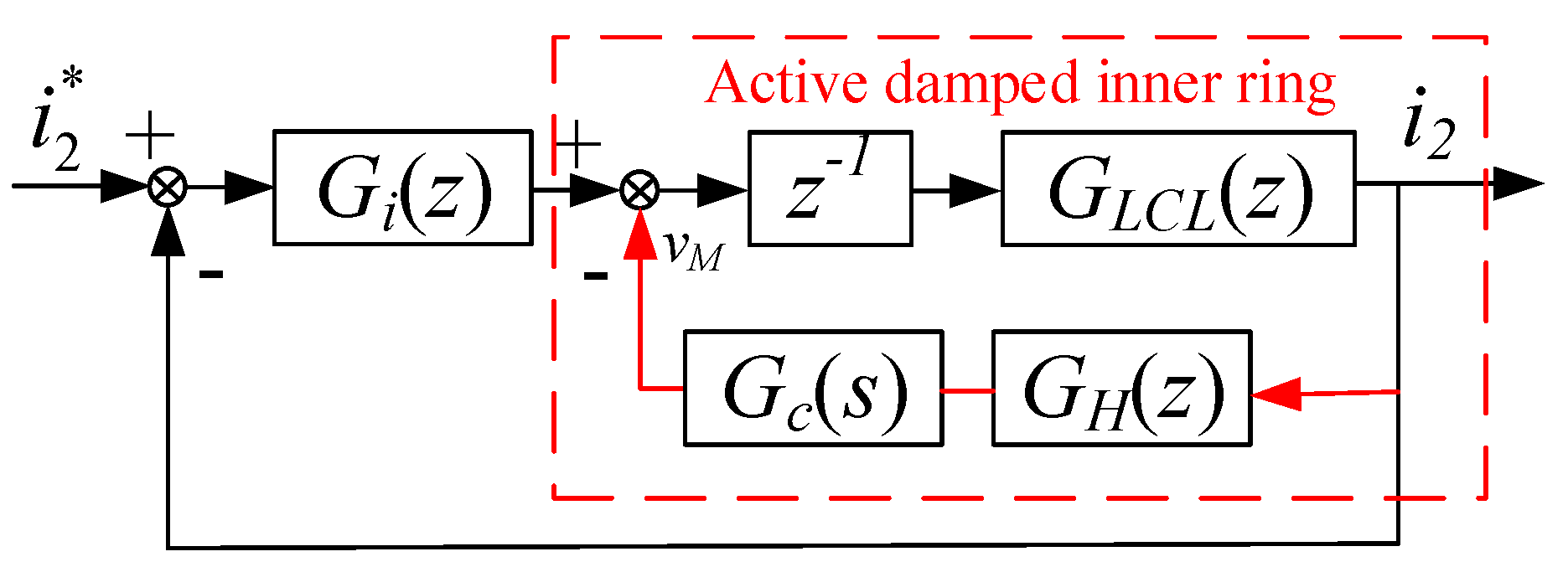
2.2. System Control Framework
3. Impact of Digital Control Delay on Traditional GCFAD
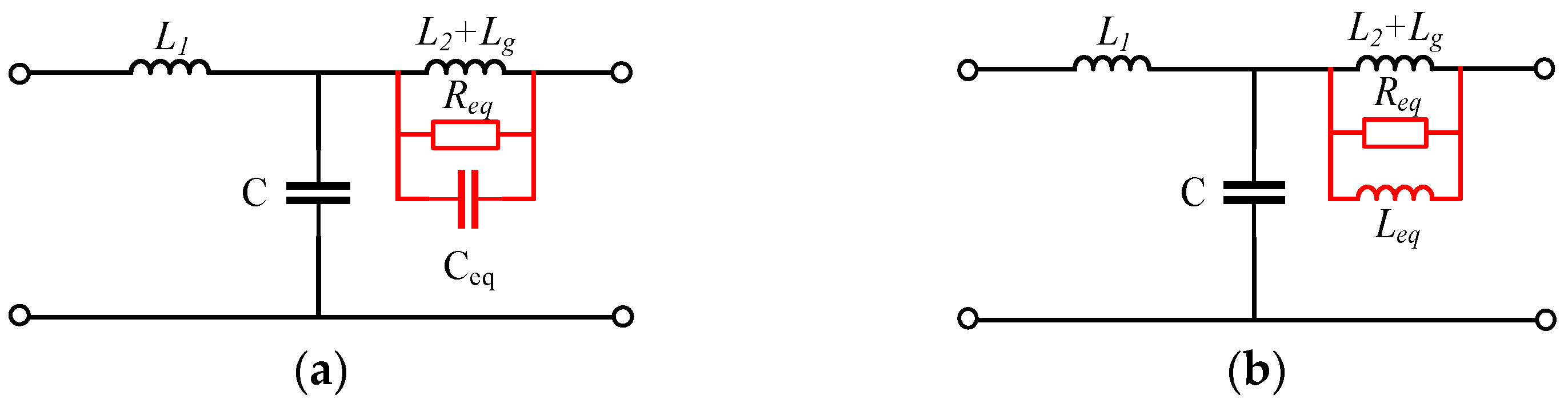
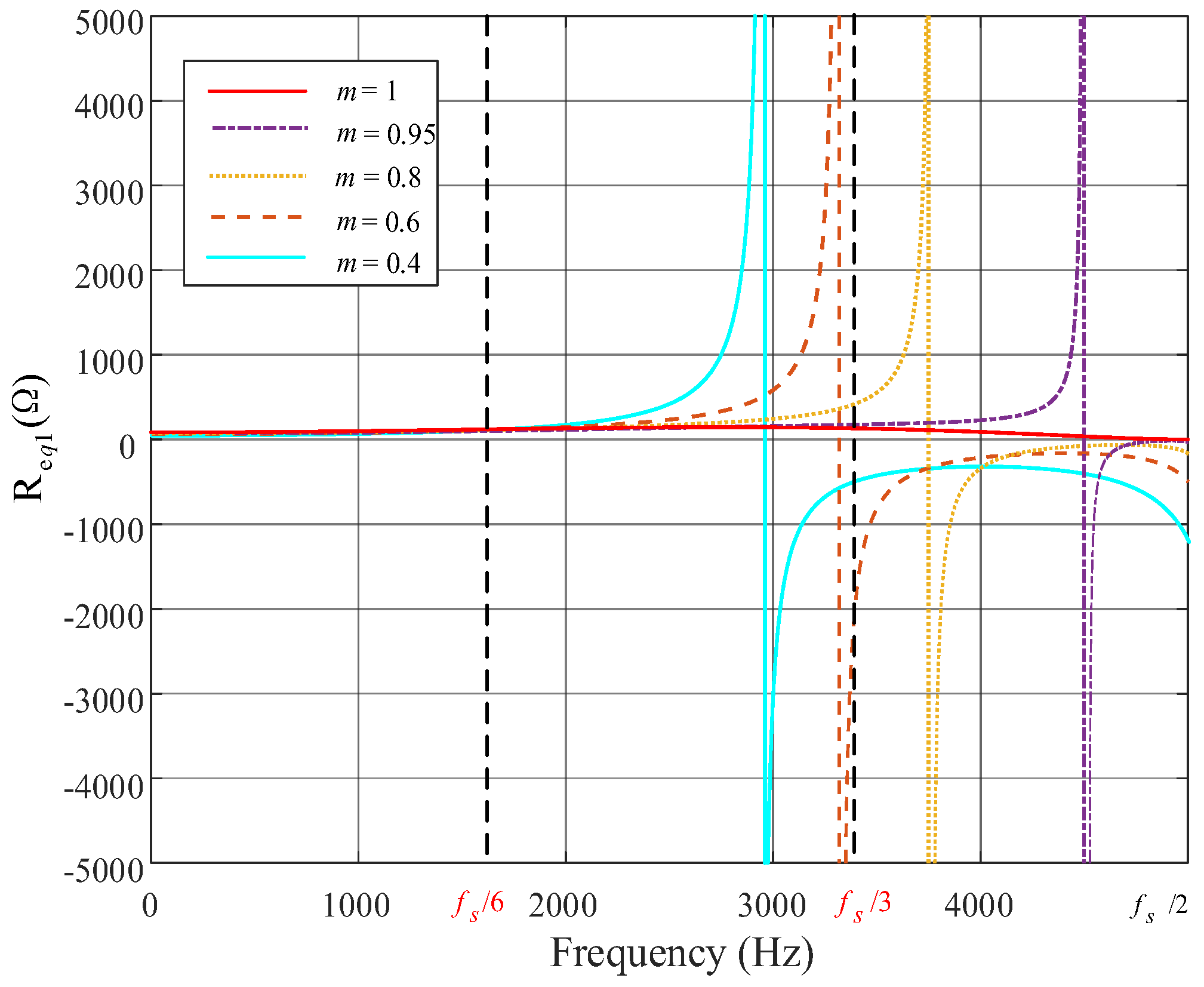
3.1. Virtual Impedance Analysis Under Digital Control
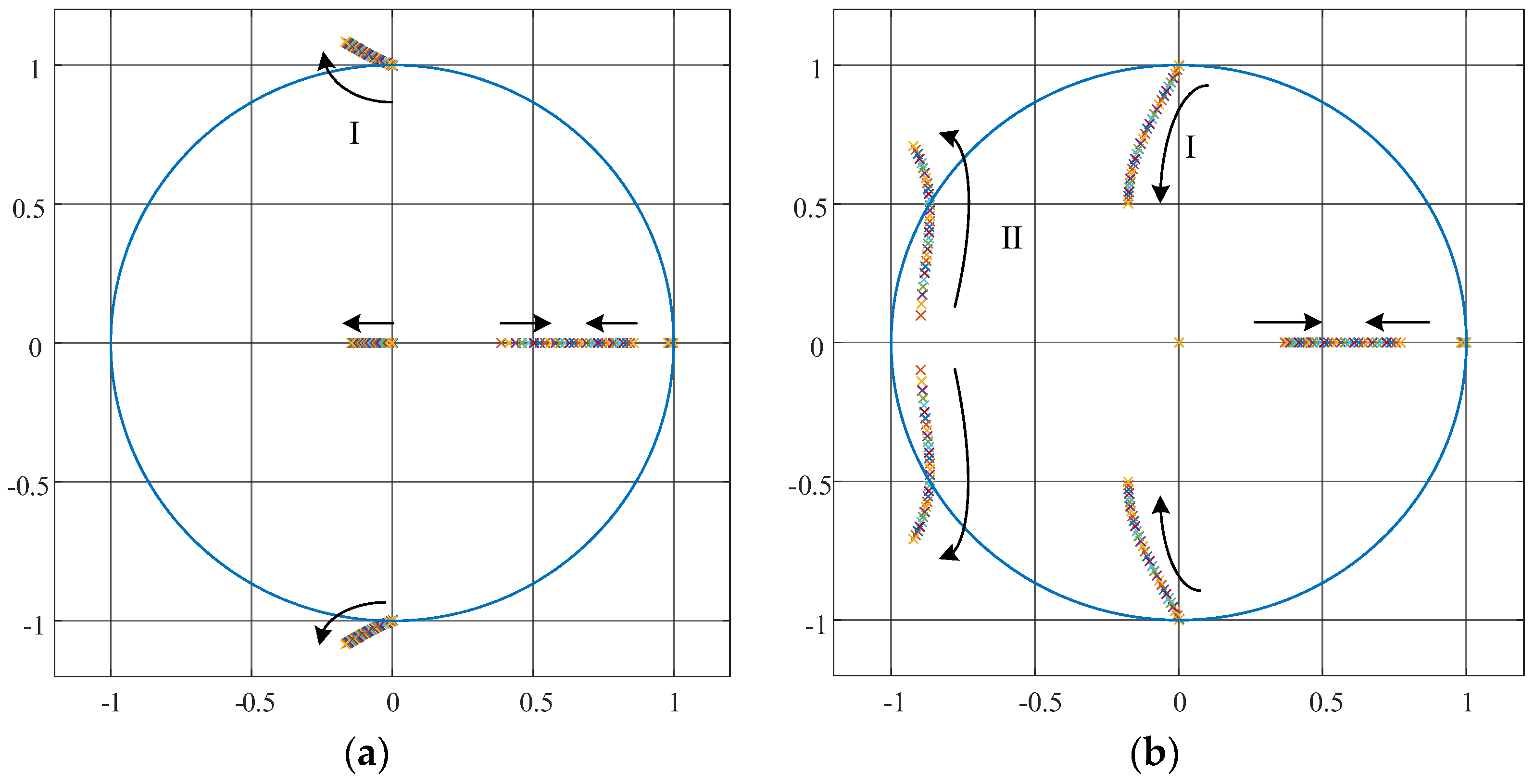
3.2. Stability Verification of the Traditional GCFAD System
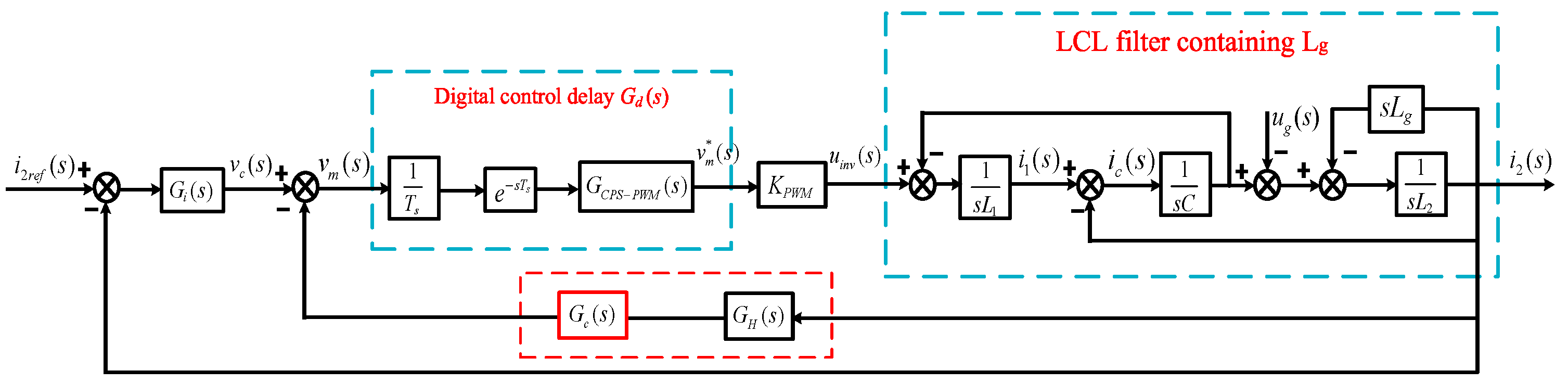
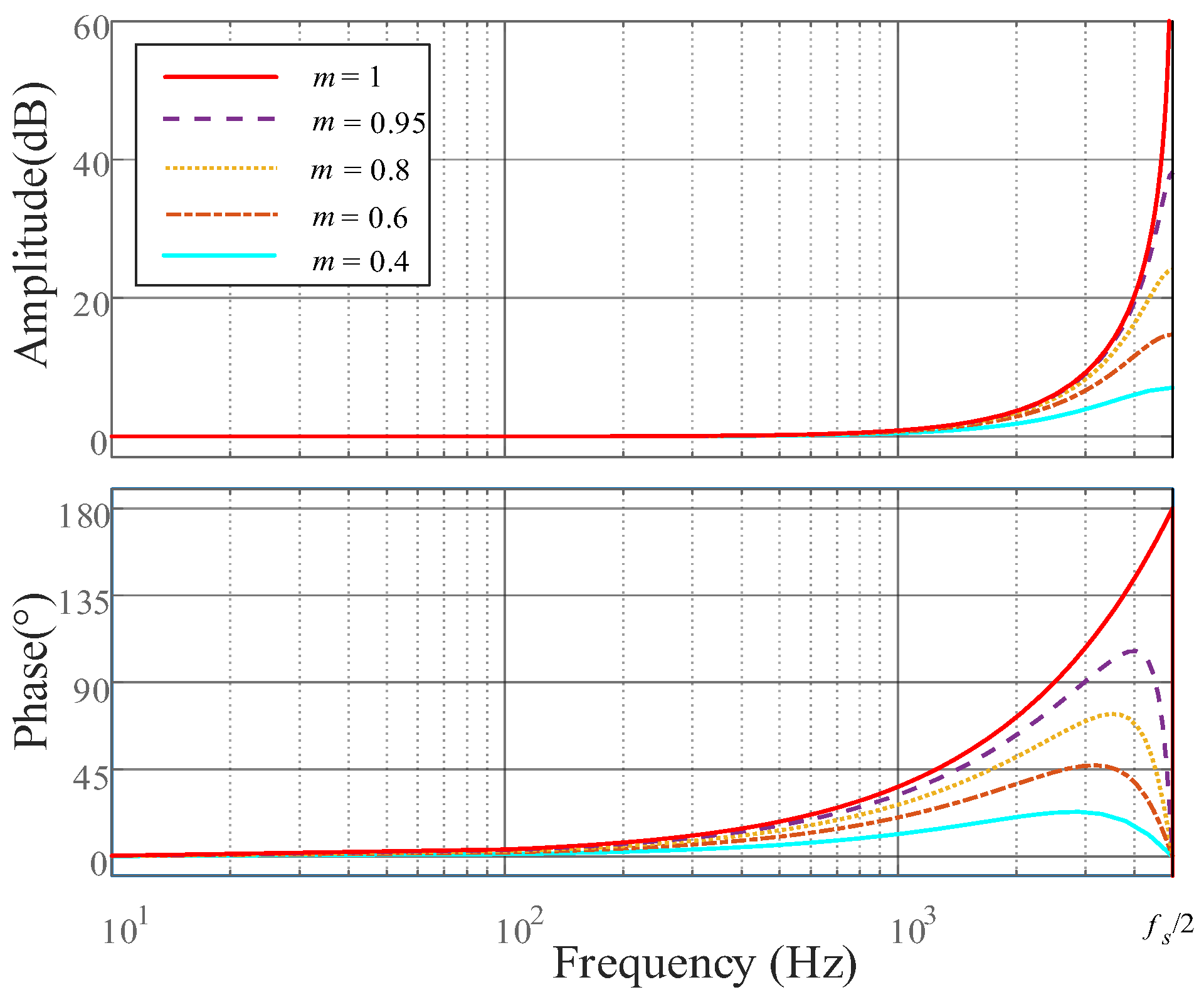
4. Highly Robust GCFAD Strategy Based on Phase-Lead Compensator
4.1. Effective Damping Zone Analysis
4.2. Design and Stability Analysis of GC Current Feedback Coefficient KH
5. Simulation and Verification
6. Conclusions
- (1)
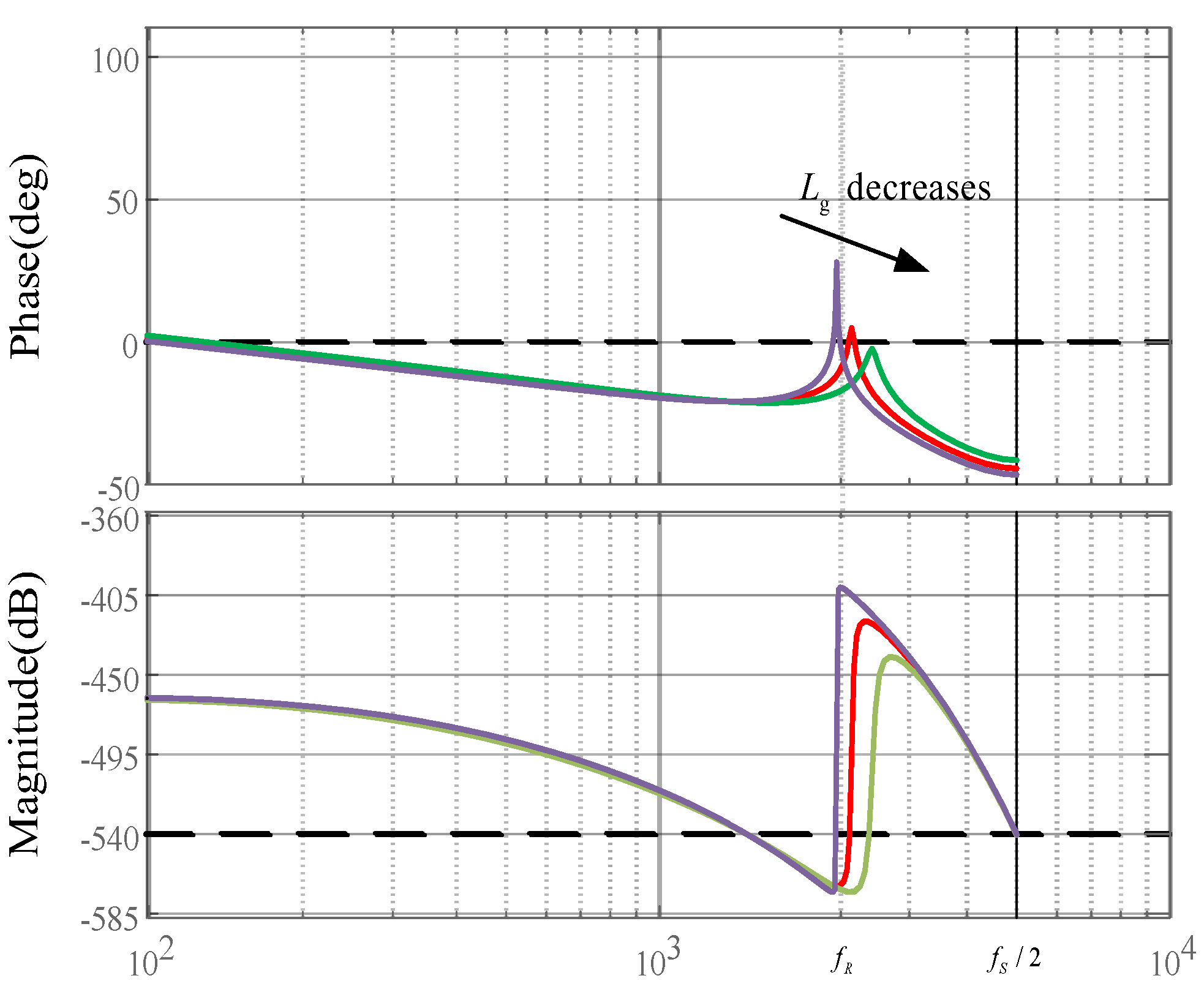
- Affected by the digital control delay, the efficient damping area using the uncompensated GCFAD system is only (0, fR) (fR ∈ (fs/6, fs/3)). In a weak grid environment, the narrower the effective damping range, the poorer the system robustness.
- (2)
- To reduce the adverse effect of the digital control delay, the current work introduces the phase overrun compensation to counteract the control delay. As a result, the system’s efficient damping area is expanded from (0, fR)(fR ∈ (fs/6, fs/3)) to (0, 0.45fs), and the wider effective damping range is more conducive to the LCL filter’s parameter design and the response to the grid impedance variations, thereby improving the system’s stability and robustness.
- (3)
- The stability of the highly robust GCFAD system is rigorously verified, and the optimal active damped feedback link parameters are obtained by combining the polar plots of the closed-loop system. The simulation outcomes confirm the efficiency of the presented approach.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, R.; He, Y.; Liu, J. Research on the unbalanced compensation of delta-connected cascaded h-bridge multilevel SVG. IEEE Trans. Ind. Electron. 2018, 65, 8667–8676. [Google Scholar] [CrossRef]
- Ni, Z.; Narimani, M.; Zargari, N.R. Optimal LCL filter design for a regenerative cascaded h-bridge (CHB) motor drive. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 3038–3043. [Google Scholar]
- Zheng, F.; Wu, W.; Chen, B.; Koutroulis, E. An optimized parameter design method for passivity-based control in a LCL-filtered grid-connected inverter. IEEE Access 2020, 8, 189878–189890. [Google Scholar] [CrossRef]
- Liu, X.; Qi, Y.; Tang, Y.; Guan, Y.; Wang, P.; Blaabjerg, F. Unified active damping control algorithm of inverter for LCL resonance and mechanical torsional vibration suppression. IEEE Trans. Ind. Electron. 2022, 69, 6611–6623. [Google Scholar] [CrossRef]
- Ma, G.; Xie, C.; Li, C.; Zou, J.; Guerrero, J.M. Passivity-based design of passive damping for LCL-type grid-connected inverters to achieve full-frequency passive output admittance. IEEE Trans. Power Electron. 2023, 38, 16048–16060. [Google Scholar] [CrossRef]
- Naresh, P.; Anirudh, C.; Seshadri, V.; Kumar, S. Comparison of passive damping based LCL filter design methods for grid-connected voltage source converters. In Proceedings of the International Conference on Power, Instrumentation, Control and Computing (PICC), Thrissur, India, 17–19 December 2020; pp. 1–6. [Google Scholar]
- Zhao, H.; Wu, W.; Orabi, M.; Koutroulis, E.; Chung, H.S.-H.; Blaabjerg, F. A passive damping design method of three-phase asymmetric-LCL power filter for grid-tied voltage source inverter. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 94–98. [Google Scholar]
- Ji, K.; Pang, H.; He, Z.; Li, Y.; Liu, D.; Tang, G. Active/passive method-based hybrid high-frequency damping design for MMCs. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6086–6098. [Google Scholar] [CrossRef]
- Zhao, N.; Wang, G.; Zhang, R.; Li, B.; Bai, Y.; Xu, D. Inductor current feedback active damping method for reduced DC-link capacitance IPMSM drives. IEEE Trans. Power Electron. 2019, 34, 4558–4568. [Google Scholar] [CrossRef]
- Han, Y.; Li, Z.; Yang, P.; Wang, C.; Xu, L.; Guerrero, J.M. Analysis and design of improved weighted average current control strategy for LCL-type grid-connected inverters. IEEE Trans. Energy Convers. 2017, 32, 941–952. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X.; He, Y.; Pan, D.; Ruan, X. A compensation method to eliminate the impact of time delay on capacitor-current active damping. IEEE Trans. Ind. Electron. 2022, 69, 7512–7516. [Google Scholar] [CrossRef]
- Upadhyay, N.; Padhy, N.P.; Agarwal, P. Grid-current control with inverter-current feedback active damping for LCL grid-connected inverter. IEEE Trans. Indus. Appl. 2024, 60, 1738–1749. [Google Scholar] [CrossRef]
- Pan, D.; Ruan, X.; Wang, X. Direct realization of digital differentiators in discrete domain for active damping of LCL-type grid-connected inverter. IEEE Trans. Power Electron. 2018, 33, 8461–8473. [Google Scholar] [CrossRef]
- He, Y.; Wang, X.; Ruan, X.; Pan, D.; Qin, K. Hybrid active damping combining capacitor current feedback and point of common coupling voltage feedforward for LCL-type grid-connected inverter. IEEE Trans. Power Electron. 2021, 36, 2373–2383. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, Y.; Tu, Y.; Guan, Y.; Shen, K.; Liu, J. Unified active damping strategy based on generalized virtual impedance in LCL-type grid-connected inverter. IEEE Trans. Ind. Electron. 2023, 70, 8129–8139. [Google Scholar] [CrossRef]
- Li, S.; Lin, H. A capacitor-current-feedback positive active damping control strategy for LCL-type grid-connected inverter to achieve high robustness. IEEE Trans. Power Electron. 2022, 37, 6462–6474. [Google Scholar] [CrossRef]
- Xue, C.; Ding, L.; Wu, X.; Li, Y.; Song, W. Model predictive control for grid-connected current-source converter with enhanced robustness and grid-current feedback only. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 5591–5603. [Google Scholar] [CrossRef]
- Kraemer, R.A.S.; Carati, E.G.; Cardoso, R.; da Costa, J.P.; Stein, C.M.O. Virtual state damping for resonance suppression and robustness improvement in LCL-type distributed generation inverters. IEEE Trans. Energy Convers. 2021, 36, 1216–1225. [Google Scholar] [CrossRef]
- Liu, T.; Liu, J.; Liu, Z.; Liu, Z. A study of virtual resistor-based active damping alternatives for LCL resonance in grid-connected voltage source inverters. IEEE Trans. Power Electron. 2020, 35, 247–262. [Google Scholar] [CrossRef]
- Geng, Y.; Qi, Y.; Dong, W.; Deng, R. An active damping method with improved grid current feedback. Proc. CSEE 2018, 38, 5557–5567. (In Chinese) [Google Scholar]
- Wei, X.; Jinsong, K. Stability analysis of LCL type static synchronous compensator for distribution network considering the influence of digital control delay. J. Elect. Eng. 2017, 32, 205–216. (In Chinese) [Google Scholar]
- Lin, Z.; Ruan, X.; Zhang, H.; Wu, L. A generalized real-time computation method with dual-sampling mode to eliminate the computation delay in digitally controlled inverters. IEEE Trans. Power Electron. 2022, 37, 5186–5195. [Google Scholar] [CrossRef]
- Stojić, D.M.; Šekara, T.B. Digital resonant current controller for LCL-filtered inverter based on modified current sampling and delay modeling. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7109–7119. [Google Scholar] [CrossRef]
- Wang, T.; Yao, W.; Li, C.; Yang, H.; Li, W. Aliasing suppression with negligible phase lag for multi-sampled LCL-type grid-tied inverter. IEEE Trans. Power Electron. 2023, 38, 12520–12535. [Google Scholar] [CrossRef]





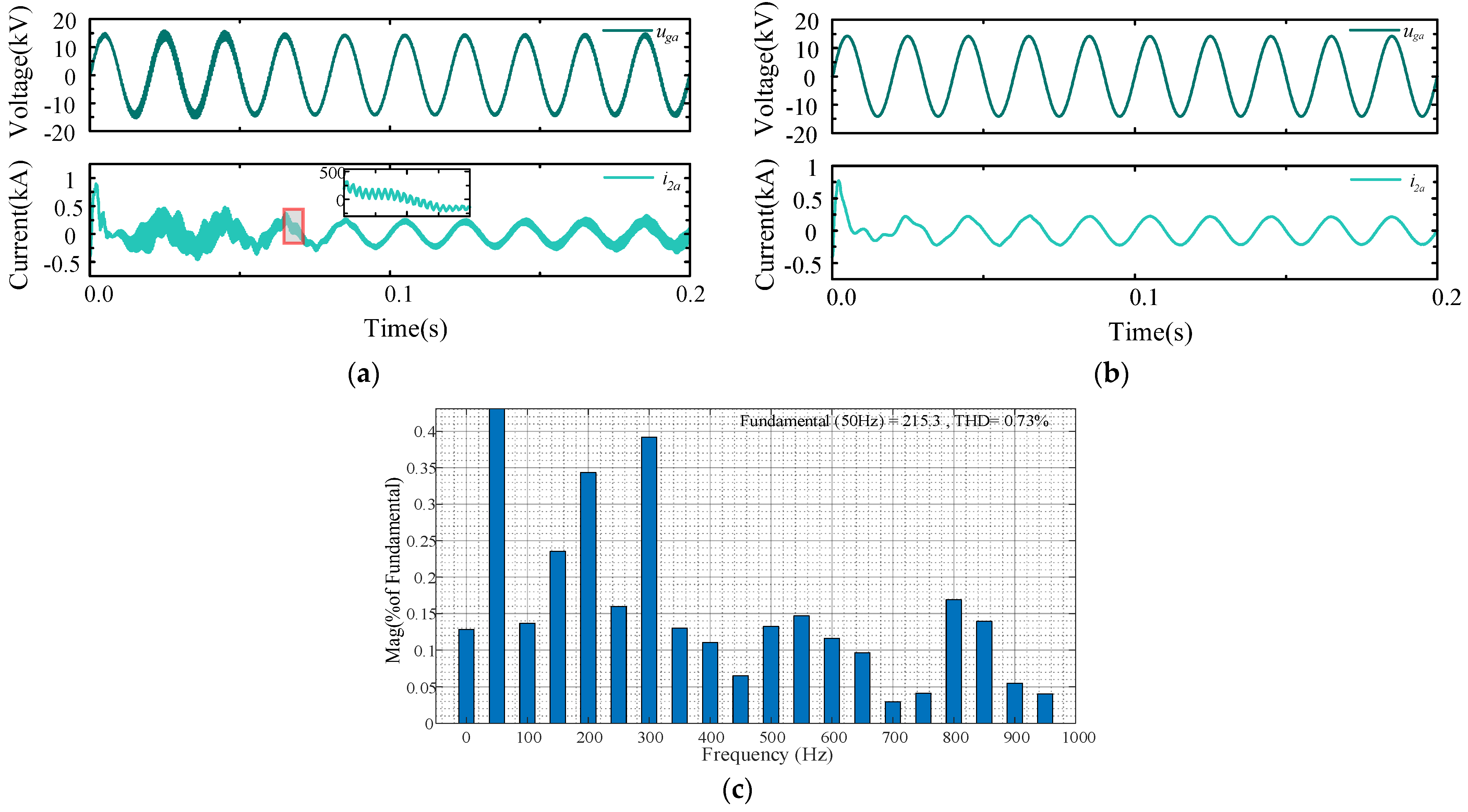
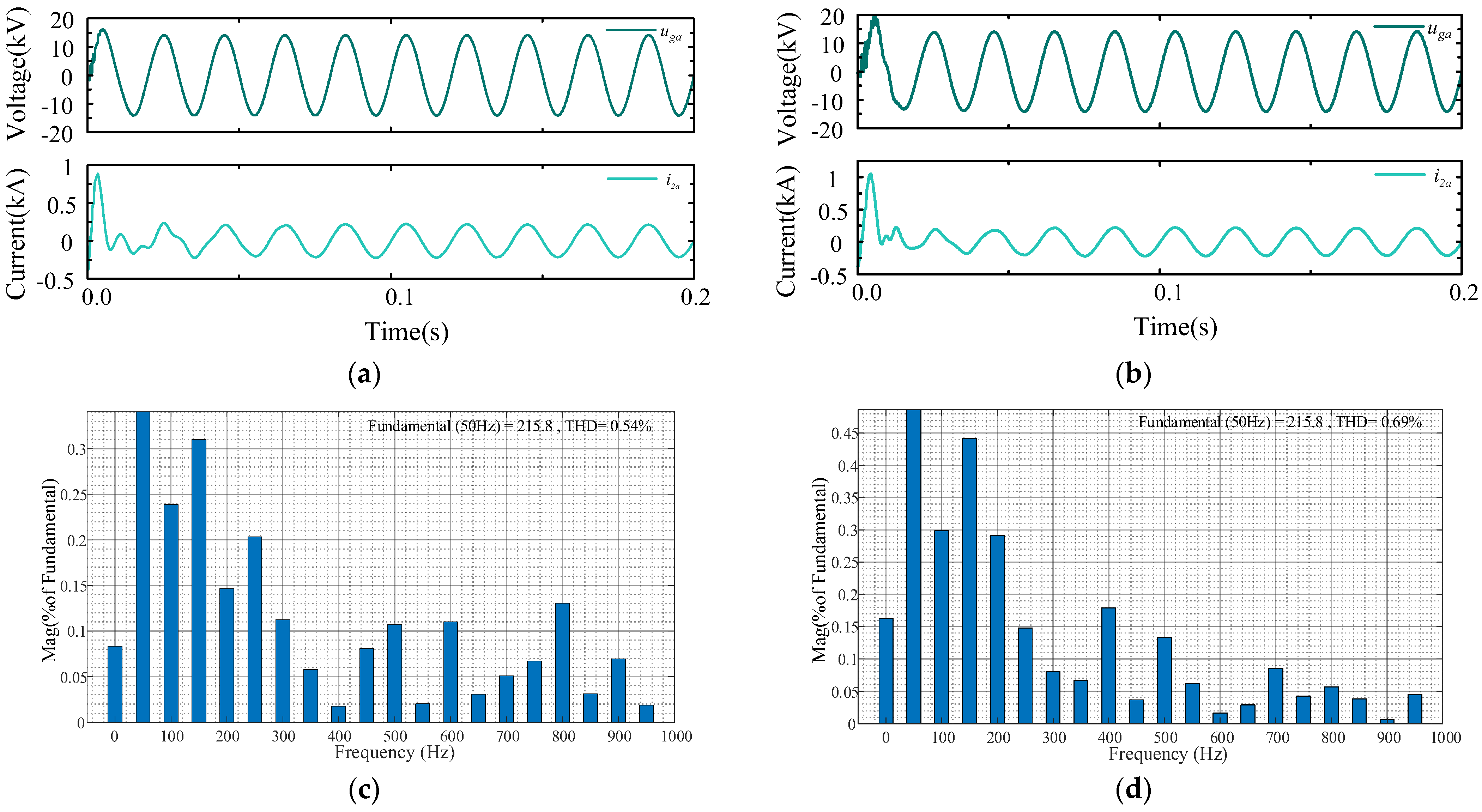
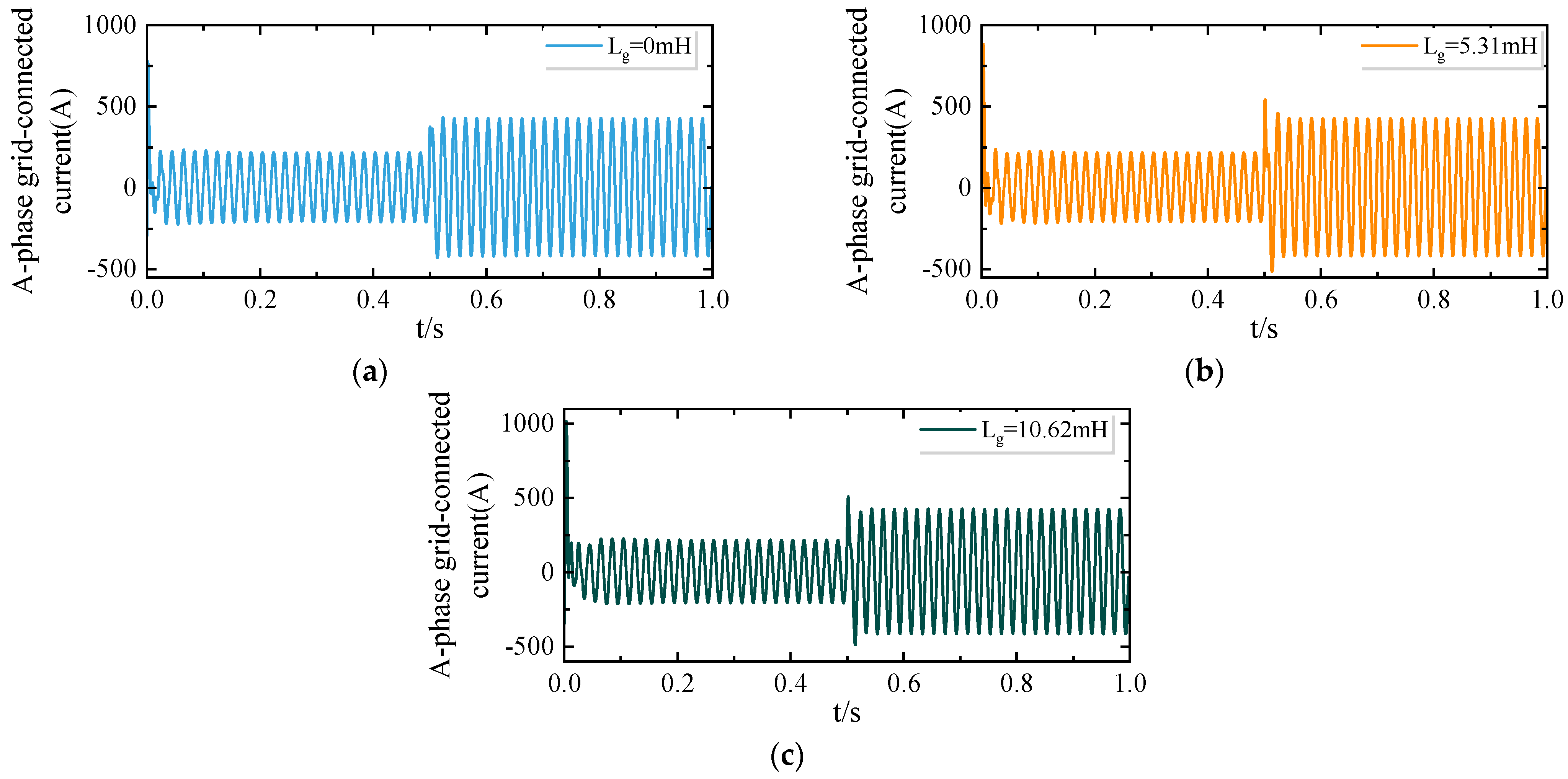
| Parameter | Symbol | Value |
|---|---|---|
| Grid voltage (RMS) | ug | 10,000 V |
| Fundamental frequency | f0 | 50 Hz |
| Rated capacity of the device | S | ±10 Mvar |
| Submodule switching frequency | fSM | 1000 Hz |
| Number of submodules | N | 10 |
| DC input voltage | Udc | 1500 V |
| DC side capacitance | Cdc | 3000 μF |
| Filter capacitance | C | 3.86 μF |
| SVG-side inductance | L1 | 3.5 mH |
| Grid-side inductance | L2 | 1.5 mH |
| Equivalent switching frequency | fsw | 10 kHz |
| Sampling rate | fs | 10 kHz |
| Proportional gain | Kp | 0.316 |
| Integral gain | Ki | 19.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, A.; Tian, Y.; Zhao, H. Highly Robust Active Damping Approach for Grid-Connected Current Feedback Using Phase-Lead Compensation. Electronics 2025, 14, 309. https://doi.org/10.3390/electronics14020309
Guo A, Tian Y, Zhao H. Highly Robust Active Damping Approach for Grid-Connected Current Feedback Using Phase-Lead Compensation. Electronics. 2025; 14(2):309. https://doi.org/10.3390/electronics14020309
Chicago/Turabian StyleGuo, Ang, Yizhi Tian, and Haikun Zhao. 2025. "Highly Robust Active Damping Approach for Grid-Connected Current Feedback Using Phase-Lead Compensation" Electronics 14, no. 2: 309. https://doi.org/10.3390/electronics14020309
APA StyleGuo, A., Tian, Y., & Zhao, H. (2025). Highly Robust Active Damping Approach for Grid-Connected Current Feedback Using Phase-Lead Compensation. Electronics, 14(2), 309. https://doi.org/10.3390/electronics14020309






