KG-PLPPM: A Knowledge Graph-Based Personal Learning Path Planning Method Used in Online Learning
Abstract
1. Introduction
- An ontology is designed to conceptualize related knowledge in online learning. Based on this ontology, a knowledge graph is constructed using data from the open-source dataset MOOCCube.
- A knowledge graph-based personal learning path planning method for online learning is proposed, which consists of a method for evaluating the similarity of knowledge concepts, a method for evaluating the concept mastery degree of the learner, and an algorithm to plan the learning path based on relationships between knowledge concepts and concepts mastery situations. This approach enables the establishment of a learning path that reflects the order of knowledge point acquisition while considering the learner’s current knowledge mastery.
- A series of experiments are conducted across various scenarios. Analysis of the experimental results demonstrates that the proposed method generates learning paths with improved sequencing of knowledge concepts, thereby enhancing learning efficiency.
2. Related Work
2.1. Methods Used in Educational Recommendations
2.2. Methods to Address Learners’ Weaknesses
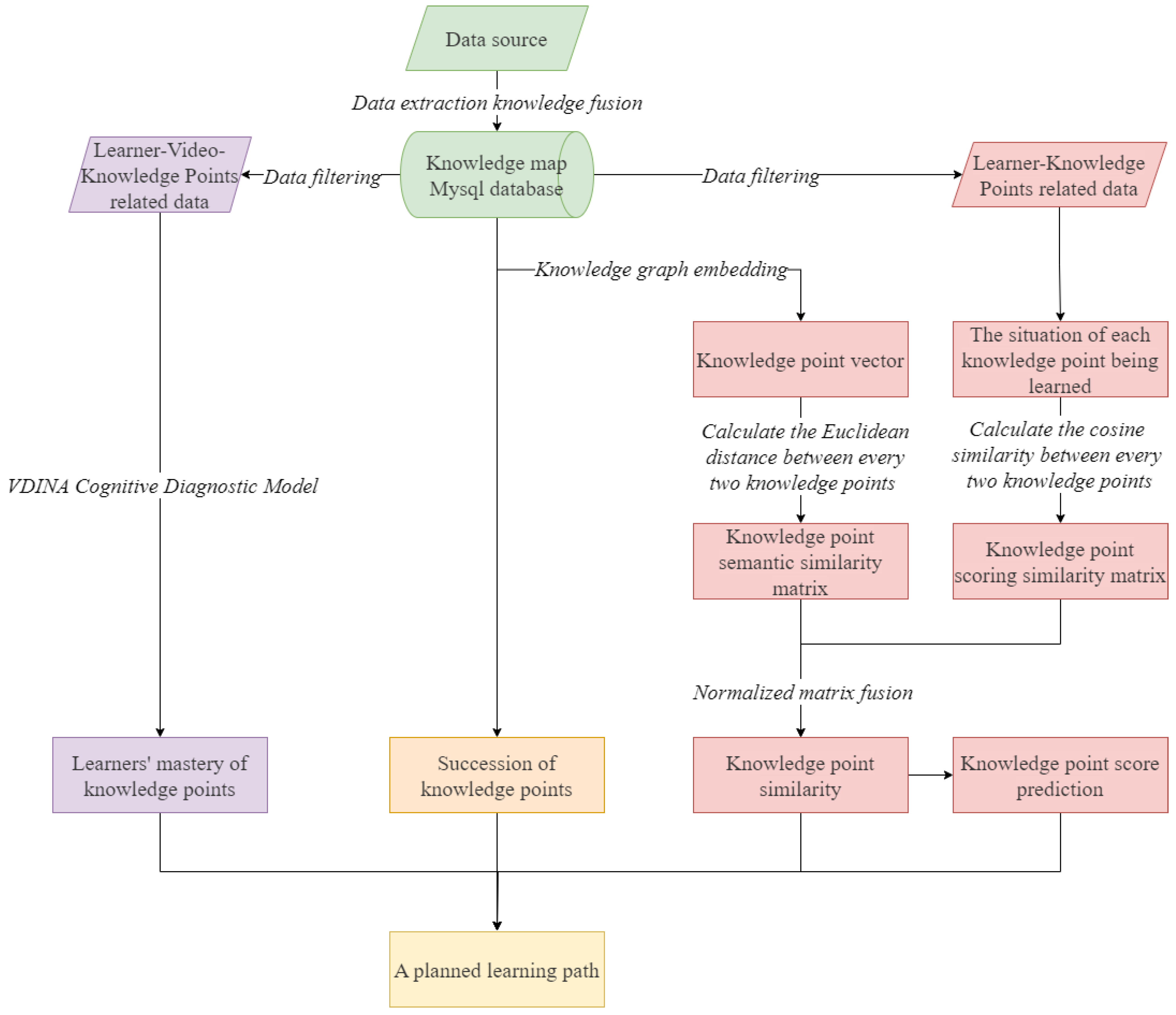
3. Knowledge Graph-Based Personal Learning Path Planning Method
3.1. General Procedure of KG-PLPPM
3.2. Knowledge Graph Construction
3.3. Similarity of Knowledge Concepts Evaluation
3.3.1. The Semantic Similarity of the Knowledge Points
3.3.2. The Score Similarity of the Knowledge Points
3.3.3. Fusion of Two Similarities
3.4. Concepts Mastery Evaluation
3.4.1. Learning Behaviors Modeling
3.4.2. Evaluating Concepts Mastery of a Learner
3.5. Learning Path Planning
- (1)
- For learner and course C, search for all concepts of course C in the knowledge graph, denoted as .
- (2)
- Based on the concept similarity matrix, score predictions are performed for all concepts in . As shown in Equation (12), represents the score prediction of learner on concept . In this equation, represents the concepts contained in all courses learned by learner , signifies the top n concepts with the highest similarity to concept , indicates the similarity between concept and , and denotes whether learner has learned concept or not. Specifically, when the concept has been learned, the value of is 1; otherwise, it is 0. Furthermore, a concept with a higher score is more likely to be learned in the future.
- (3)
- Using the concept mastery vector for learner , calculate the value of each concept of course C, which is the difference between the value of scoring prediction and the value of mastery degree. These values are then sorted in descending order and stored in the set .
- (4)
- Sequentially select a concept from the set as an alternative recommended node, denoting it as _. Additionally, obtain the first-level prior concepts based on the knowledge graph. Using the results from the similarity matrix of knowledge points and the concept mastery vector, select the previous concept that is most similar and weakest, compared with the current alternative recommended concept (_), and denote it as _. If the concept is not already included in the current recommendation path, it should be added; otherwise, repeat step 4 with the next concept in the set .
- (5)
- Set _ (obtained in step 4) as the current extracted alternative recommended concept, and repeat step 4 until there are no previous concepts related to the current concept, or the maximum path length is reached. At this point, the planned path for the current knowledge points (_i) is established, and can be added to the final planned learning path (_).
- (6)
- Return to step 4, and repeat the process for each alternative recommended concept in the set sequentially, until the planned learning path reaches the maximum length.
| Algorithm 1 Personalized learning path recommendation based on knowledge graph |
| Input: |
| Computer domain knowledge graph; |
| A list of learner ’s mastery of each concept ; |
| Collection of concepts ; |
| Course A to be recommended; |
| Concept similarity matrix ; |
| Maximum number of successors ; |
| Maximum path length ; |
| A set of concept sequence relationships ; |
| Output: |
| The learning path recommended for learner . |
| 1. List<Concept> = Collection of concepts of course A; |
| 2. Map<String, Double> = ∅; Calculating learners’ rating predictions for concepts |
| 3. for( in ){ |
| 4. List<Concept> = Top n courses belong to with highest similarity to ; |
| 5. Double a, b; |
| 6. for( in ) |
| 7. if(Learner has learned concepts ) |
| 8. a += ; b += ; |
| 9. .add(, a/b); |
| 10. } |
| 11. //Calculate the set of concepts to be recommended. The higher the level of concepts, the lower the degree of mastery and the higher the interest of learners. |
| 12. Map<Concept, Double> = The value of learner for the concepts of course A (score prediction-mastery level); |
| 13. sort(); // Sort by value from large to small |
| 14. List<Concept> = .key; A collection of concepts for the path to be recommended |
| 15. Recommend a learning path for each concept to be recommended |
| 16. List<Concept> = ∅; //The learning path of each concept to be recommended |
| 17. for( in ){ |
| 18. if(.size > ) break;//End of recommendation |
| 19. List<Concept> = ∅; |
| 20. int = Integer.MIN_VALUE; |
| 21. Concept = ; |
| 22. while( has prior concept && > 0){ |
| 23. String ; |
| 24. for(: Prior concepts of ){ |
| 25. int = (, );//Similarity |
| 26. int = The value of in (1 − u);//Weakness |
| 27. //Record the previous concept with the highest similarity + weakest degree as the next node on the path |
| 28. if( + > ){ |
| 29. = + ; |
| 30. = ; |
| 31. } |
| 32. } |
| 33. .add(); |
| 34. = ; |
| 35. −−; |
| 36. } |
| 37. .add(); //Join learning path of weak |
| 38. } |
| 39. return ; |
4. Experiments
4.1. Experimental Settings and Parameter Settings
4.2. Experiments on Knowledge Sequence Relationships
4.3. Experiments on Learning Efficiency
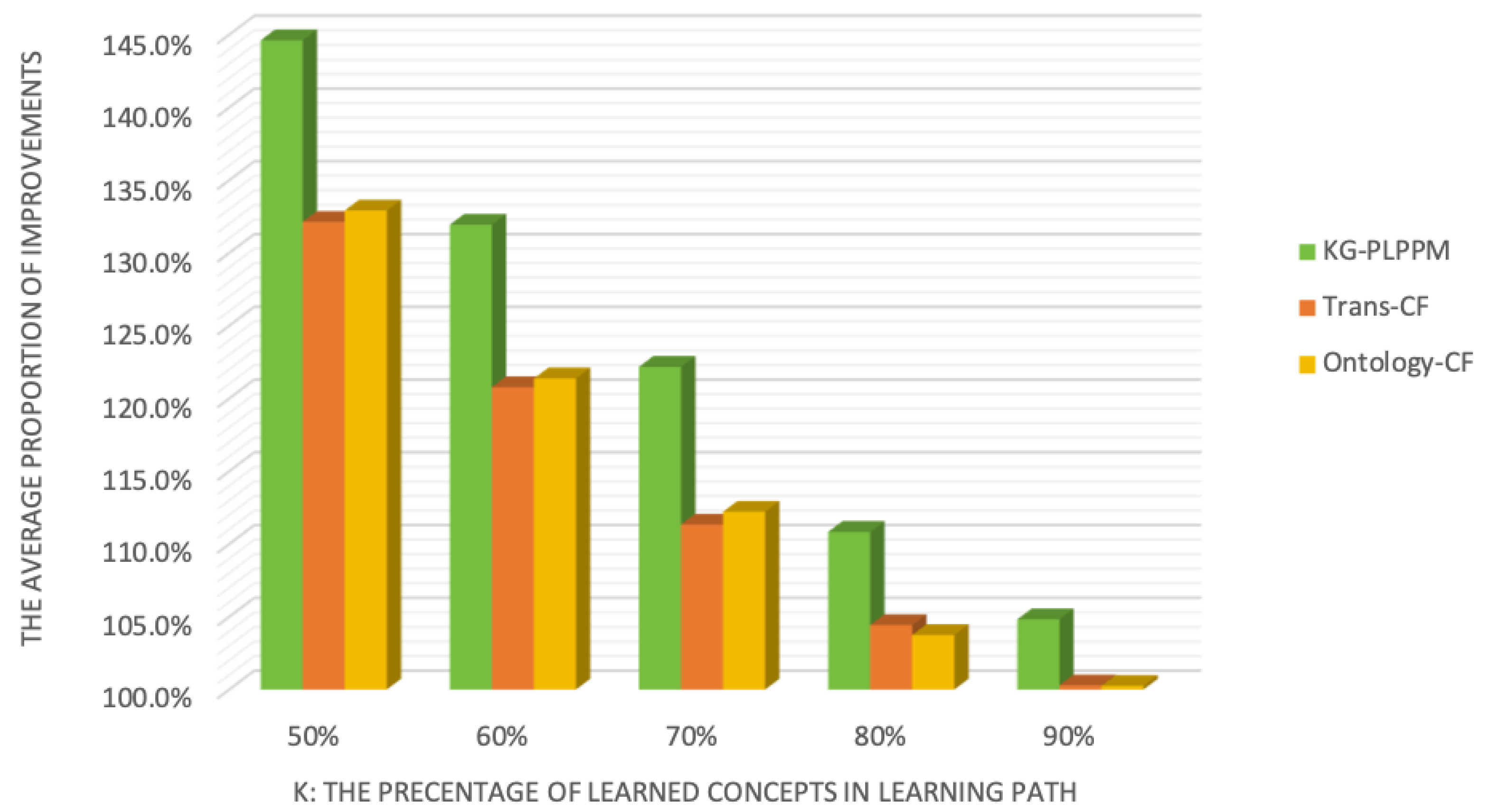
4.3.1. Experiments with Different Percentages of Learned Concepts in the Learning Path
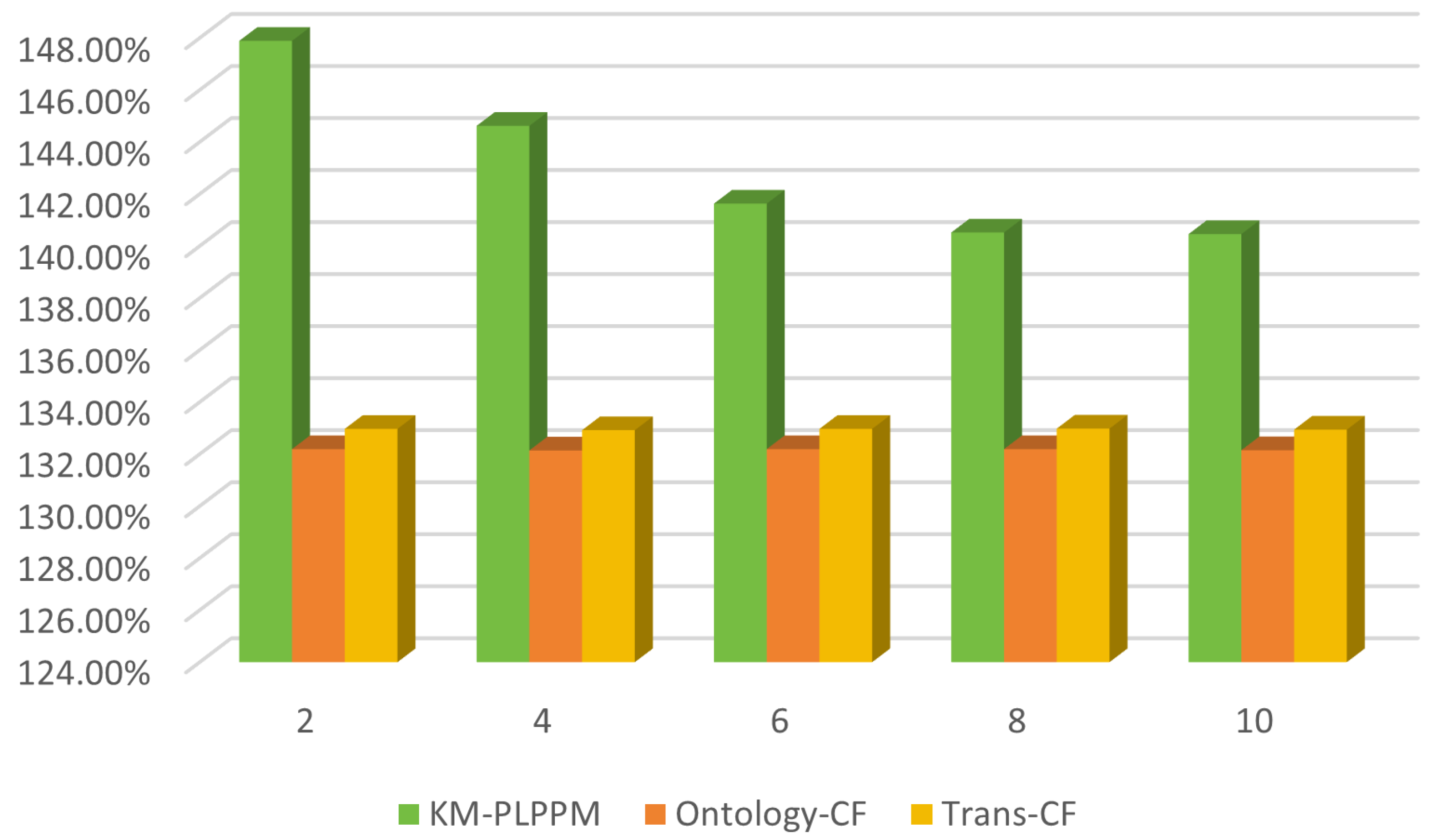
4.3.2. Experiments with a Variety of Learning Path Lengths
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dhawan, S. Online learning: A panacea in the time of COVID-19 crisis. J. Educ. Technol. Syst. 2020, 49, 5–22. [Google Scholar] [CrossRef]
- Conrad, C.; Deng, Q.; Caron, I.; Shkurska, O.; Skerrett, P.; Sundararajan, B. How student perceptions about online learning difficulty influenced their satisfaction during Canada’s Covid-19 response. Br. J. Educ. Technol. 2022, 53, 534–557. [Google Scholar] [CrossRef] [PubMed]
- Warrick, A. Strategies for Reducing Cognitive Overload in the Online Language Learning Classroom. Int. J. Second Foreign Lang. Educ. 2021, 1, 25–37. [Google Scholar] [CrossRef]
- Wang, H.; Fu, W. Personalized learning resource recommendation method based on dynamic collaborative filtering. Mob. Netw. Appl. 2021, 26, 473–487. [Google Scholar] [CrossRef]
- Mbaye, B. Recommender System: Collaborative Filtering of e-Learning Resources. In Proceedings of the International Association for Development of the Information Society, International Association for Development of the Information Society, Madrid, Spain, 4–7 June 2018; pp. 213–217. [Google Scholar]
- Amane, M.; Aissaoui, K.; Berrada, M. ERSDO: E-learning recommender system based on dynamic ontology. Educ. Inf. Technol. 2022, 27, 7549–7561. [Google Scholar] [CrossRef]
- Cheng, S. Research on Learning Path Recommendation Based on MOOC Platform Data in the View of Knowledge Graph. Mod. Inf. Technol. 2022, 6, 169–172. [Google Scholar]
- Yang, Z.; Guiyun, Z. Collaborative filtering recommendation algorithm fuses semantic nearest neighbors based on knowledge graph. In Proceedings of the 2020 Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 14–16 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 470–474. [Google Scholar]
- Raj, N.S.; Renumol, V. An improved adaptive learning path recommendation model driven by real-time learning analytics. J. Comput. Educ. 2024, 11, 121–148. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, Z.; Yu, J.; Zhu, R.; Li, D.; Guo, Q. A learning resource recommendation algorithm based on online learning sequential behavior. Int. J. Wavelets Multiresolution Inf. Process. 2019, 17, 1940001. [Google Scholar] [CrossRef]
- Chen, J.; Fang, H.; Lin, H.; Zheng, H.; Yang, D.; Zhou, X. Personal Learning Recommendation Based on Online Learning Behavior Analysis. Comput. Sci. 2018, 45, 422–426+452. [Google Scholar]
- Tang, C.L.; Liao, J.; Wang, H.C.; Sung, C.Y.; Lin, W.C. Conceptguide: Supporting online video learning with concept map-based recommendation of learning path. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 2757–2768. [Google Scholar]
- Nabizadeh, A.H.; Leal, J.P.; Rafsanjani, H.N.; Shah, R.R. Learning path personalization and recommendation methods: A survey of the state-of-the-art. Expert Syst. Appl. 2020, 159, 113596. [Google Scholar] [CrossRef]
- Urdaneta-Ponte, M.C.; Mendez-Zorrilla, A.; Oleagordia-Ruiz, I. Recommendation systems for education: Systematic review. Electronics 2021, 10, 1611. [Google Scholar] [CrossRef]
- Tahir, S.; Hafeez, Y.; Abbas, M.A.; Nawaz, A.; Hamid, B. Smart learning objects retrieval for E-Learning with contextual recommendation based on collaborative filtering. Educ. Inf. Technol. 2022, 27, 8631–8668. [Google Scholar] [CrossRef]
- Lecue, F. On the role of knowledge graphs in explainable AI. Semant. Web 2020, 11, 41–51. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, M.; Cao, Y.; Jin, W.; Wang, C.; Liu, Y.; Ma, S.; Ren, X. Jointly learning explainable rules for recommendation with knowledge graph. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 1210–1221. [Google Scholar]
- Chen, Z.; Silvestri, F.; Wang, J.; Zhang, Y.; Huang, Z.; Ahn, H.; Tolomei, G. Grease: Generate factual and counterfactual explanations for gnn-based recommendations. arXiv 2022, arXiv:2208.04222. [Google Scholar]
- Chen, Y.; Li, H.; Li, H.; Liu, W.; Wu, Y.; Huang, Q.; Wan, S. An overview of knowledge graph reasoning: Key technologies and applications. J. Sens. Actuator Netw. 2022, 11, 78. [Google Scholar] [CrossRef]
- Chen, P.; Zhu, Y. Recommendation algorithm incorporating representation learning of knowledge graph with matrix factorization. Comput. Eng. Des. 2018, 39, 3137–3142. [Google Scholar]
- Dwivedi, P.; Kant, V.; Bharadwaj, K.K. Learning path recommendation based on modified variable length genetic algorithm. Educ. Inf. Technol. 2018, 23, 819–836. [Google Scholar] [CrossRef]
- Niknam, M.; Thulasiraman, P. LPR: A bio-inspired intelligent learning path recommendation system based on meaningful learning theory. Educ. Inf. Technol. 2020, 25, 3797–3819. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, H.; Zhang, J.; Zhang, Z.; Yuan, P. Design of a Learning Path Recommendation System Based on a Knowledge Graph. Int. J. Inf. Commun. Technol. Educ. 2023, 19, 1–18. [Google Scholar] [CrossRef]
- Ouissem Benmesbah, M.L.; Hafidi, M. An improved constrained learning path adaptation problem based on genetic algorithm. Interact. Learn. Environ. 2023, 31, 3595–3612. [Google Scholar] [CrossRef]
- Lin, L.; Wang, F.; Wang, F. Research on Learning Resource Recommendation Based on Learner Model. In Proceedings of the 2022 5th International Conference on Education Technology Management, Lincoln, UK, 16–18 December 2022; pp. 45–50. [Google Scholar]
- Ali, S.; Hafeez, Y.; Humayun, M.; Jamail, N.S.M.; Aqib, M.; Nawaz, A. Enabling recommendation system architecture in virtualized environment for e-learning. Egypt. Inform. J. 2022, 23, 33–45. [Google Scholar] [CrossRef]
- Li, J. A recommendation model for college English digital teaching resources using collaborative filtering and few-shot learning technology. Comput. Intell. Neurosci. 2022, 2022, 1233057. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, A.; Mishra, D.S.; Kolekar, S.V. Knowledge-based recommendation system using semantic web rules based on Learning styles for MOOCs. Cogent Eng. 2022, 9, 2022568. [Google Scholar] [CrossRef]
- Paulsen, J.; Valdivia, D.S. Examining cognitive diagnostic modeling in classroom assessment conditions. J. Exp. Educ. 2022, 90, 916–933. [Google Scholar] [CrossRef]
- Wanichsan, D.; Panjaburee, P.; Chookaew, S. Enhancing knowledge integration from multiple experts to guiding personalized learning paths for testing and diagnostic systems. Comput. Educ. Artif. Intell. 2021, 2, 100013. [Google Scholar] [CrossRef]
- Yu, J.; Luo, G.; Xiao, T.; Zhong, Q.; Wang, Y.; Feng, W.; Luo, J.; Wang, C.; Hou, L.; Li, J.; et al. MOOCCube: A large-scale data repository for NLP applications in MOOCs. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 3135–3142. [Google Scholar]
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning entity and relation embeddings for knowledge graph completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- De La Torre, J. DINA model and parameter estimation: A didactic. J. Educ. Behav. Stat. 2009, 34, 115–130. [Google Scholar] [CrossRef]



| The Maximum Number of Prior Concepts | Concepts Sequence Degree | ||
|---|---|---|---|
| Trans-C | Ontology-CF | KG-PLPPM | |
| 2 | 0.0044 | 0.0034 | 0.2895 |
| 4 | 0.0044 | 0.0034 | 0.4751 |
| 6 | 0.0044 | 0.0034 | 0.5531 |
| 8 | 0.0044 | 0.0034 | 0.5855 |
| 10 | 0.0044 | 0.0034 | 0.6023 |
| The Percentage of Learned Concepts in Learning Path | The Average Proportion of Improvements | ||
|---|---|---|---|
| KG-PLPPM | Trans-CF | Ontology-CF | |
| 50% | 144.62% | 132.14% | 132.92% |
| 60% | 131.95% | 120.78% | 121.38% |
| 70% | 122.18% | 111.34% | 112.22% |
| 80% | 110.84% | 104.13% | 103.75% |
| 90% | 104.83% | 100.29% | 100.26% |
| The Learning Path Length | The Average Proportion of Learning Efficiency Improvements | ||
|---|---|---|---|
| KG-PLPPM | Trans-CF | Ontology-CF | |
| 2 | 147.89% | 132.19% | 132.97% |
| 4 | 144.62% | 132.14% | 132.92% |
| 6 | 141.63% | 132.19% | 132.97% |
| 8 | 140.52% | 132.19% | 132.98% |
| 10 | 140.46% | 132.15% | 132.94% |
| The Learning Path Length | The Average Proportion of Learning Efficiency Improvements | ||||
|---|---|---|---|---|---|
| 50% | 60% | 70% | 80% | 90% | |
| 2 | 147.89% | 134.12% | 123.38% | 111.46% | 104.75% |
| 4 | 144.62% | 131.95% | 122.18% | 110.84% | 104.83% |
| 6 | 141.63% | 130.12% | 120.96% | 110.21% | 104.86% |
| 8 | 140.52% | 129.77% | 120.42% | 109.98% | 104.94% |
| 10 | 140.46% | 129.69% | 119.96% | 109.92% | 104.97% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, B.; Lin, Y.; Li, Y.; Fang, C.; Li, C.; Wang, X. KG-PLPPM: A Knowledge Graph-Based Personal Learning Path Planning Method Used in Online Learning. Electronics 2025, 14, 255. https://doi.org/10.3390/electronics14020255
Hou B, Lin Y, Li Y, Fang C, Li C, Wang X. KG-PLPPM: A Knowledge Graph-Based Personal Learning Path Planning Method Used in Online Learning. Electronics. 2025; 14(2):255. https://doi.org/10.3390/electronics14020255
Chicago/Turabian StyleHou, Bo, Yishuai Lin, Yuechen Li, Chen Fang, Chuang Li, and Xiaoying Wang. 2025. "KG-PLPPM: A Knowledge Graph-Based Personal Learning Path Planning Method Used in Online Learning" Electronics 14, no. 2: 255. https://doi.org/10.3390/electronics14020255
APA StyleHou, B., Lin, Y., Li, Y., Fang, C., Li, C., & Wang, X. (2025). KG-PLPPM: A Knowledge Graph-Based Personal Learning Path Planning Method Used in Online Learning. Electronics, 14(2), 255. https://doi.org/10.3390/electronics14020255









