Disturbance-Free Switching Control Strategy for Grid-Following/Grid-Forming Modes of Energy Storage Converters
Abstract
1. Introduction
- (1)
- A Novel Constructed-Function-Based VSG Angle-Tracking Technique for Enhanced Synchronization Precision.
- (2)
- A Dual-Channel, State-Latching Architecture for Holistic Disturbance Suppression.
- (3)
- A Non-Intrusive, Communication-Free Strategy for Enhanced Robustness and Practical Deployment.
- (1)
- Intentional Islanding: The system deliberately switches from GFL to GFM mode to form an islanded network and continue supplying power to local critical loads when the main grid requires scheduled maintenance or experiences power quality issues.
- (2)
- Fault Ride-Through and Recovery: Upon a main grid fault, the system must switch to GFM mode to maintain its own stability. After the grid fault is cleared, it must resynchronize and switch back to GFL mode.
- (3)
- Grid Support Services: The system operates in GFM mode to provide active and reactive power support for grid voltage and frequency regulation upon dispatch commands, reverting to GFL mode after the task is completed.
2. Grid-Following/Grid-Forming Converter Modeling and Analysis of Switching Disturbance Mechanism
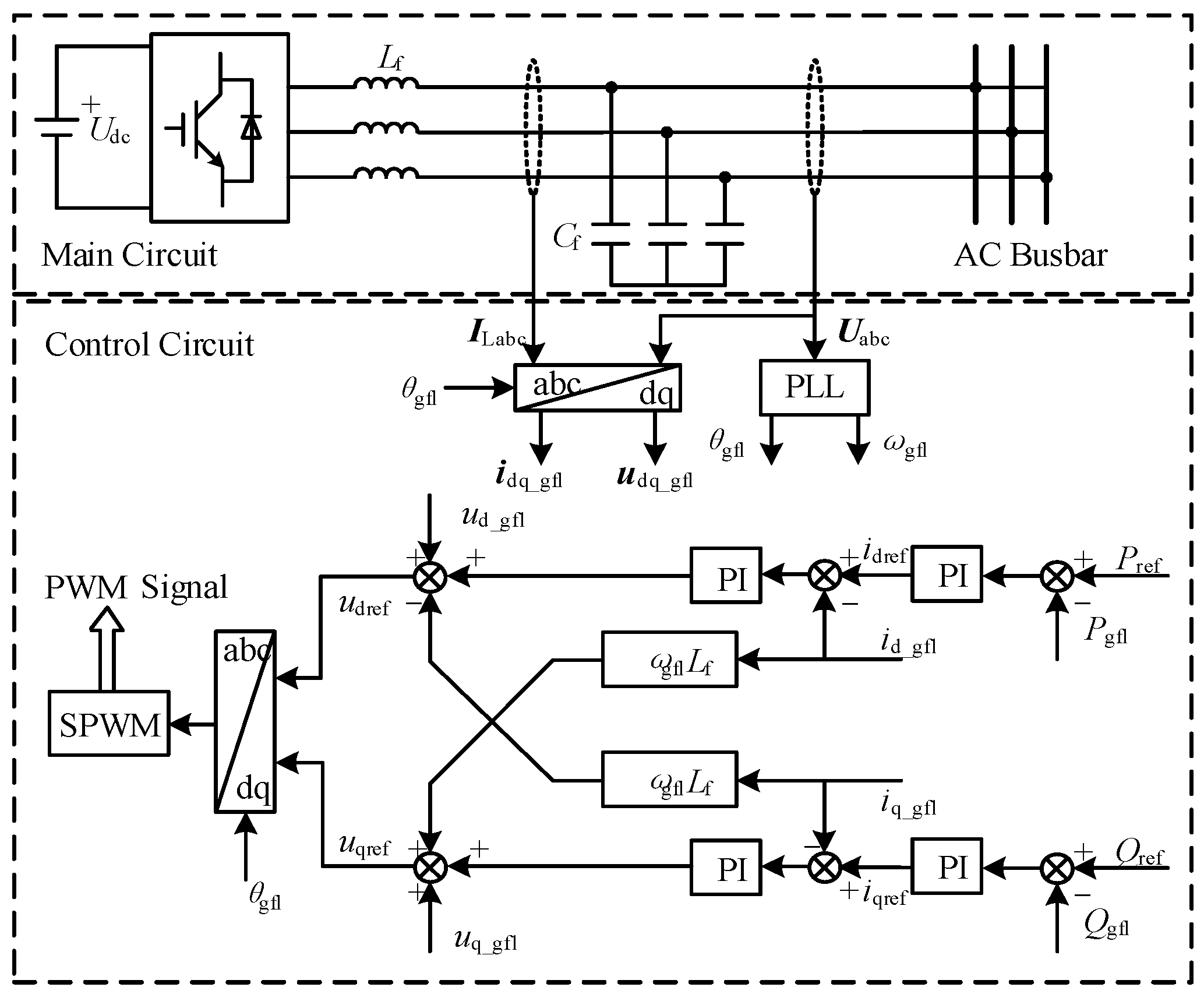
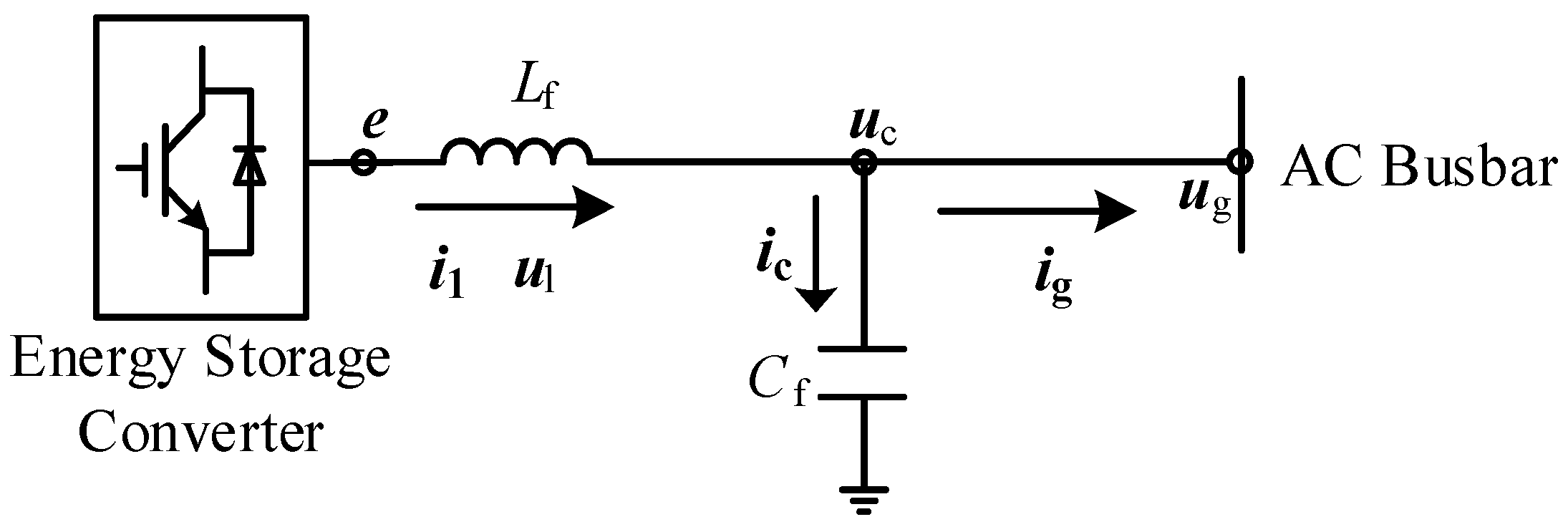
2.1. Dual-Mode Converter System Architecture
2.1.1. Topology of Main Circuit
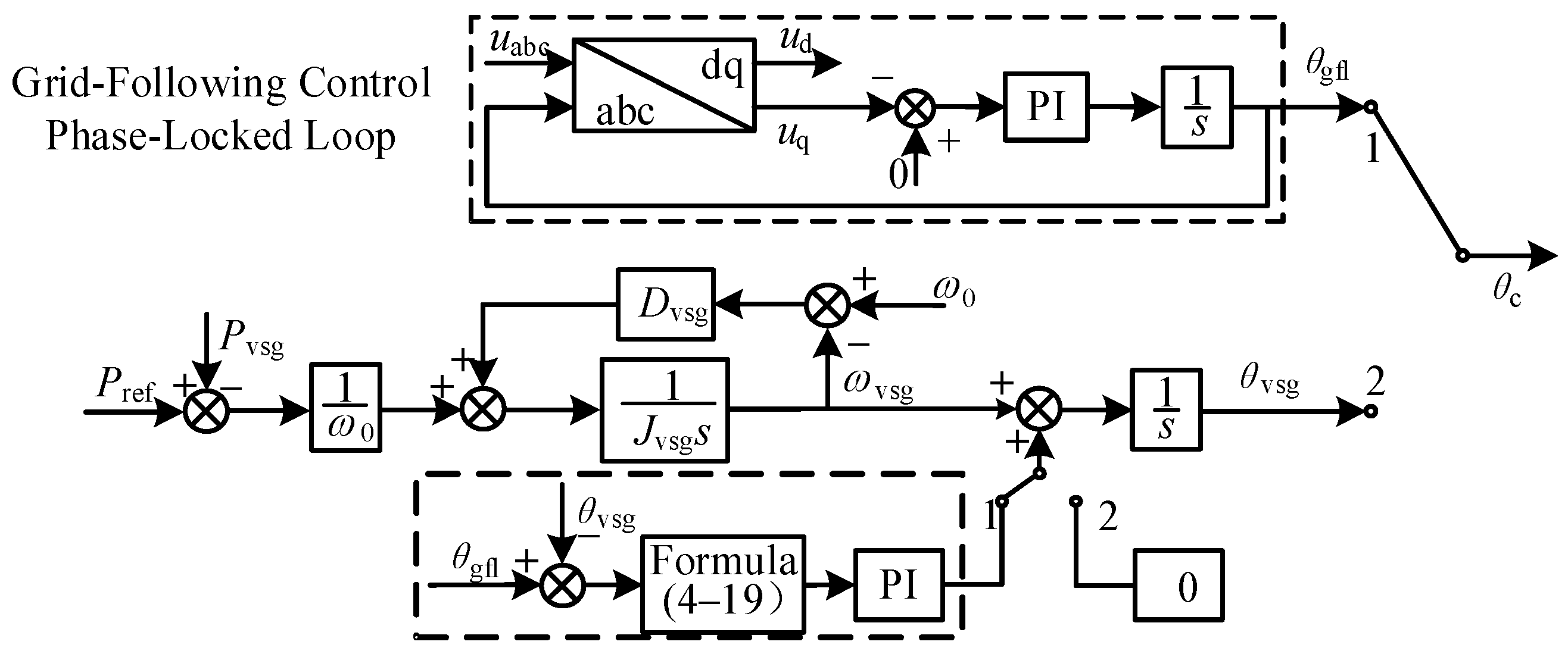
2.1.2. Grid-Following-Type Control Strategy
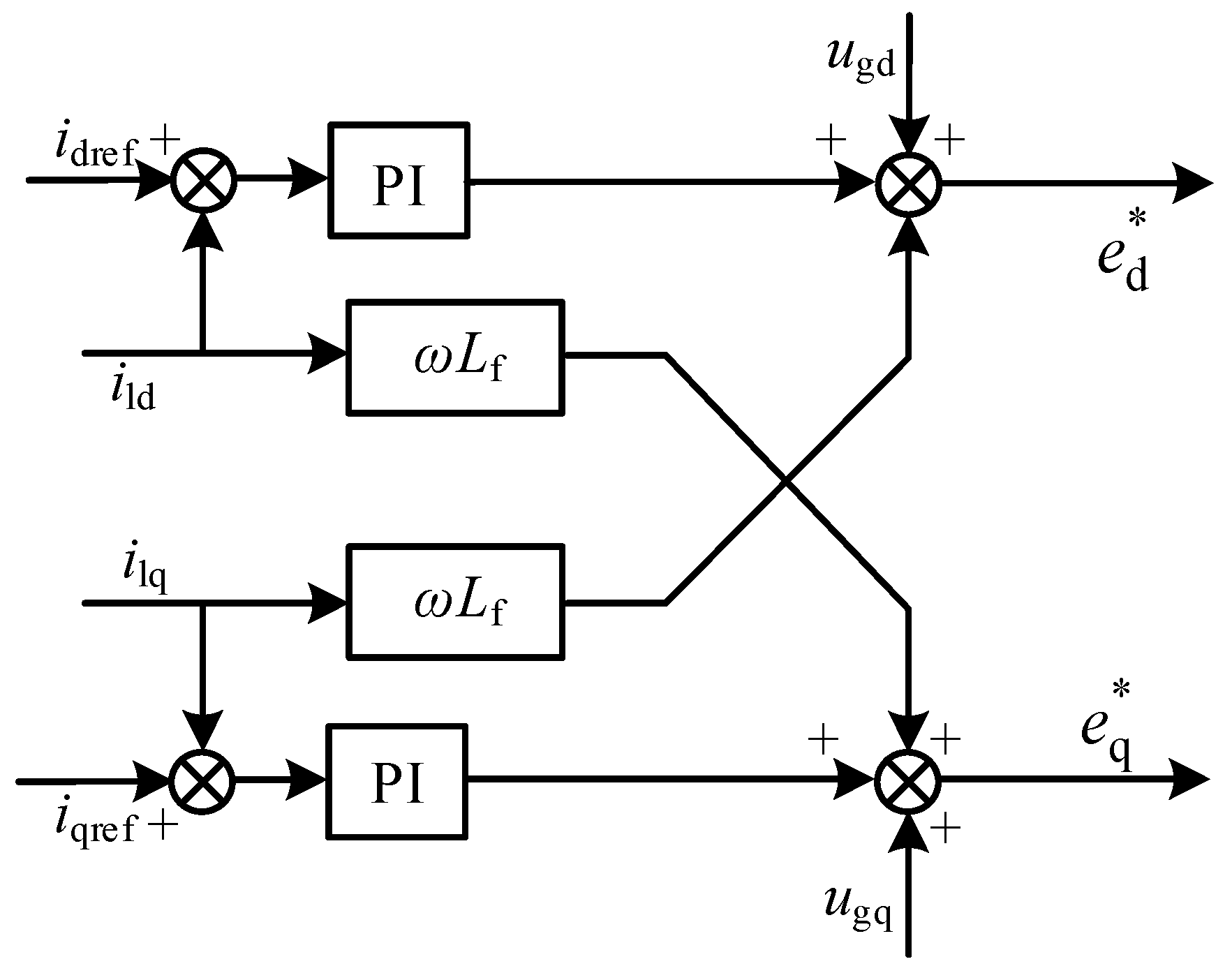
2.1.3. Grid-Forming-Type Control Strategy
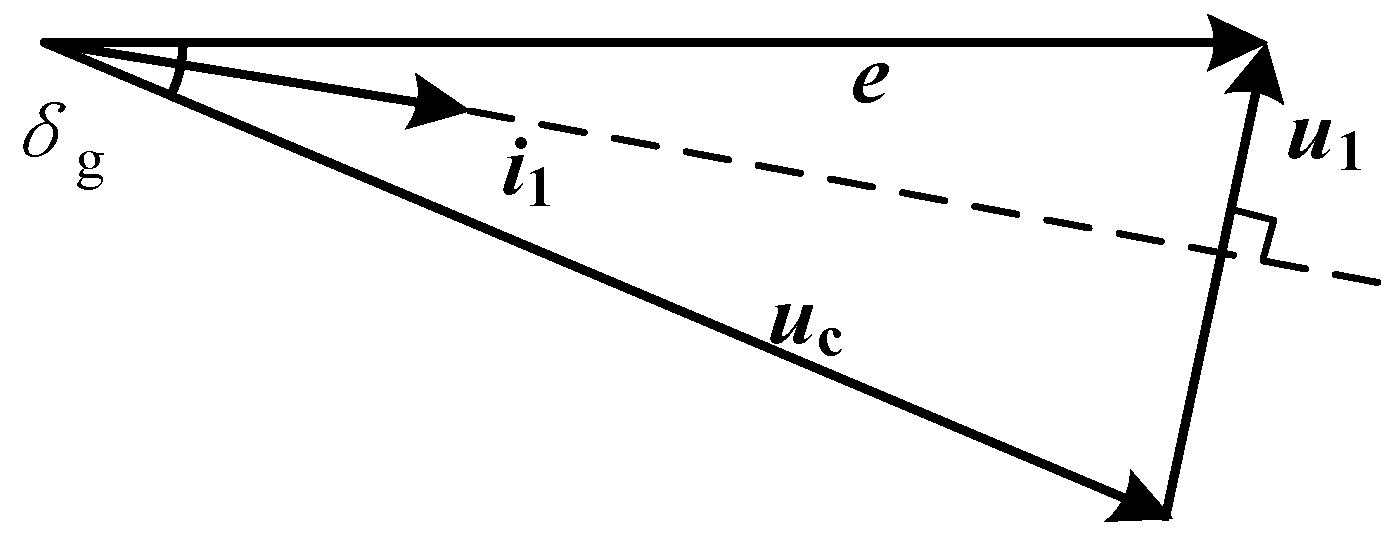
2.2. Mode-Switching Principle and Disturbance-Free Switching Condition
2.3. Analysis of the Mechanism of Transient Disturbances During Switching
2.3.1. Impact of Current Reference Disturbance on Output Power
2.3.2. Impact of Perturbations in Control Angle on Output Power
3. Research on Key Technologies for Seamless Switching
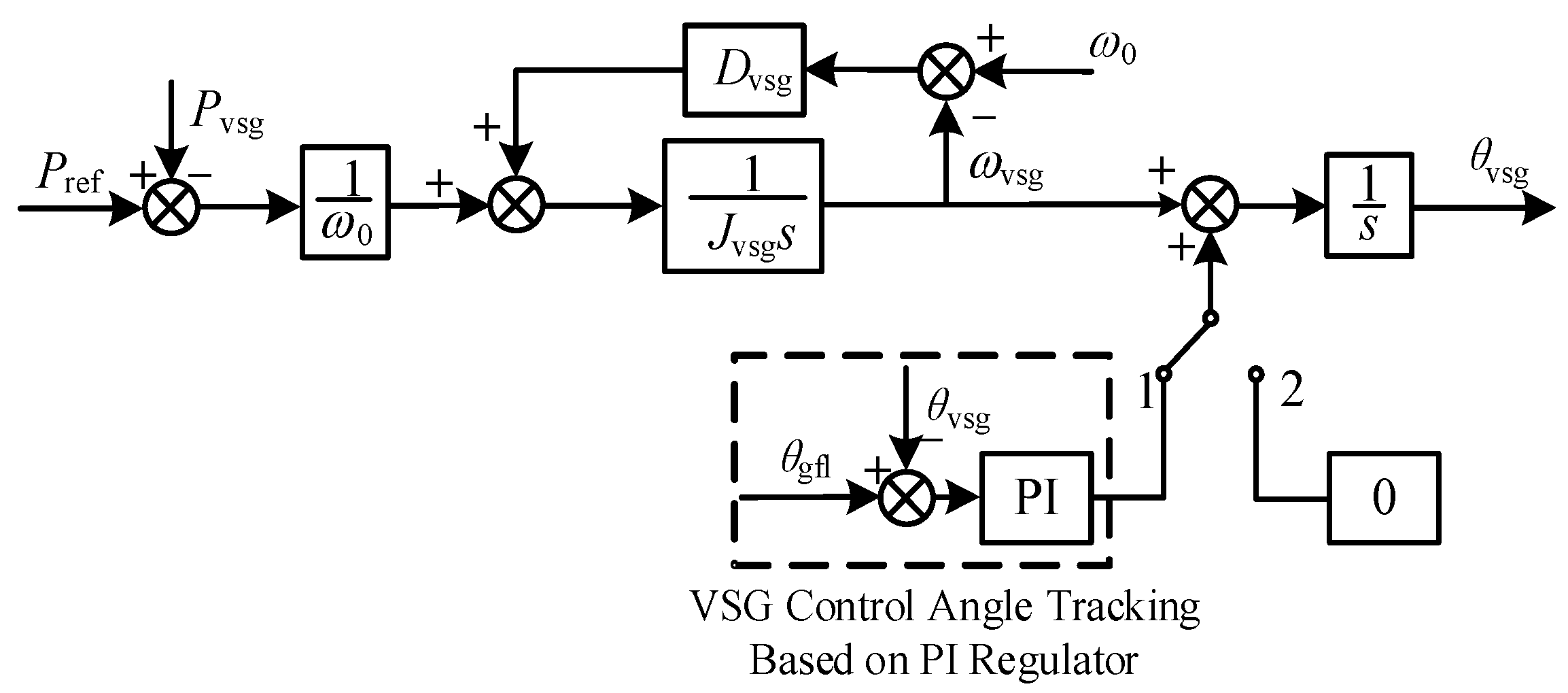
3.1. VSG Angle-Tracking Technology for Mitigating Control Angle Disturbance
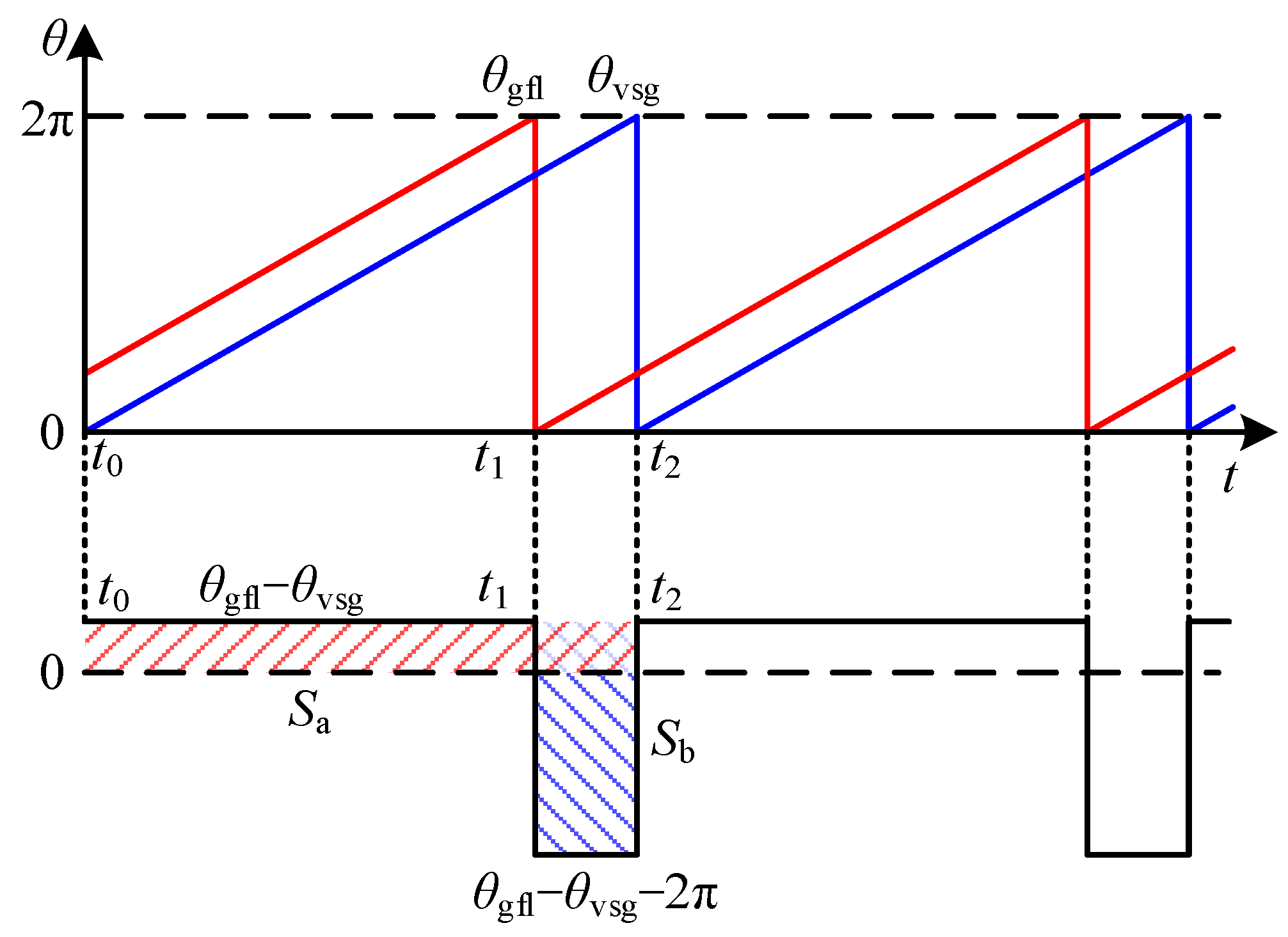
3.1.1. VSG Control Angle-Tracking Technology Based on PI Regulator
- (1)
- If Sa > Sb, meaning the forward-regulation effect of Sa is greater than the reverse-regulation effect of Sb, then Δθ > 0. The control angle difference between the two modes decreases, and the VSG can achieve control angle tracking. However, the reverse-regulation effect of Sb prolongs the adjustment time.
- (2)
- If Sa = Sb, meaning the forward-regulation effect of Sa balances the reverse-regulation effect of Sb, then Δθ = 0. The control angle difference between the two modes remains constant, and the VSG cannot achieve control angle tracking.
- (3)
- If Sa < Sb, meaning the forward-regulation effect of Sa is smaller than the reverse-regulation effect of Sb, then Δθ < 0. The control angle difference between the two modes further increases until the VSG control angle lags by one cycle and becomes equal to that of the grid-following mode. In this case, the VSG can eventually achieve control angle tracking, but the adjustment time is excessively long.
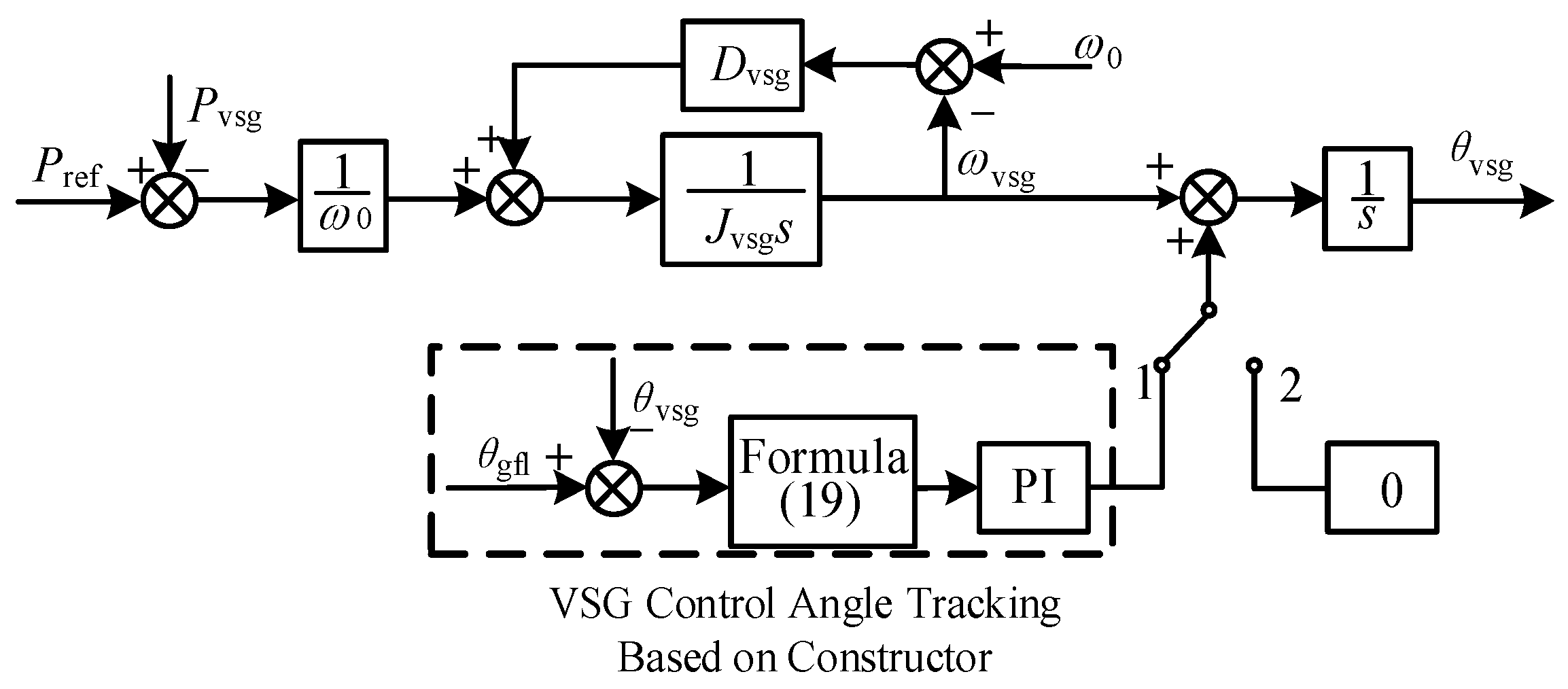
3.1.2. VSG Control Angle-Tracking Technology Based on Constructed Function
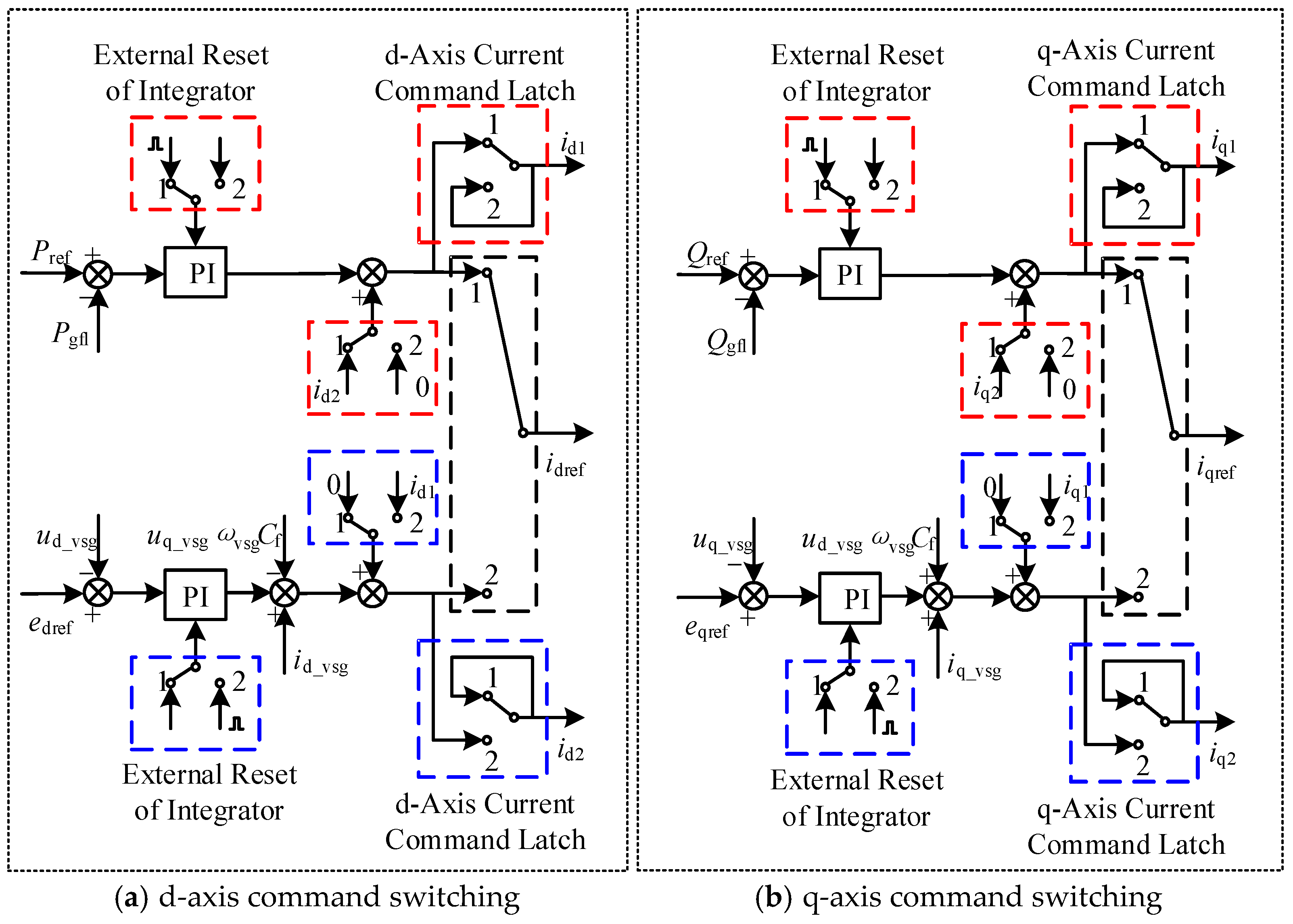
3.2. Disturbance-Free Switching Technology for Control Angle Reference Disturbance
3.3. Current Reference-Disturbance-Free Switching Technology
3.4. Overall Control Algorithm
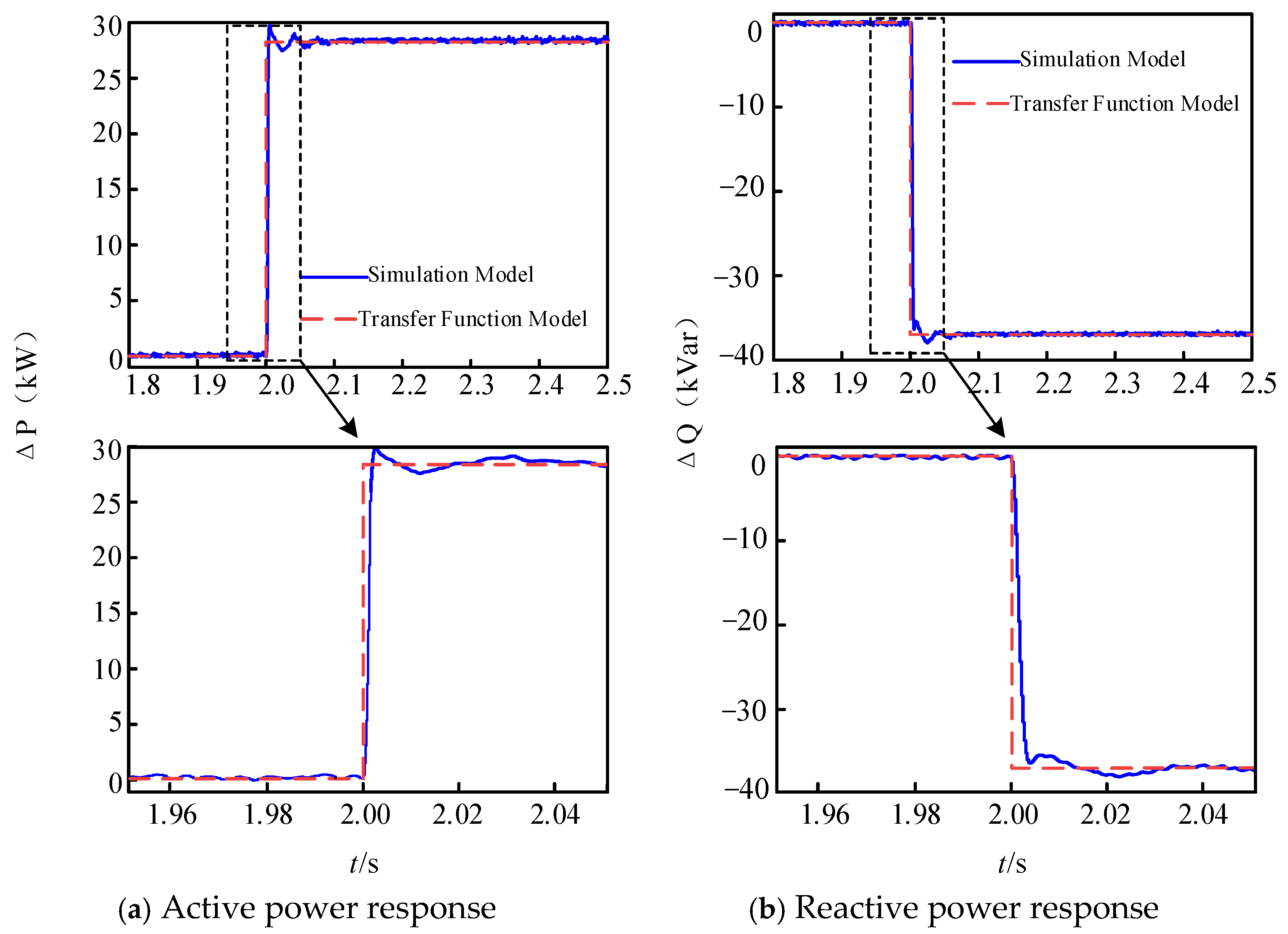
4. Simulation Verification and Result Analysis
4.1. Simulation Model Setup and Parameter Configuration
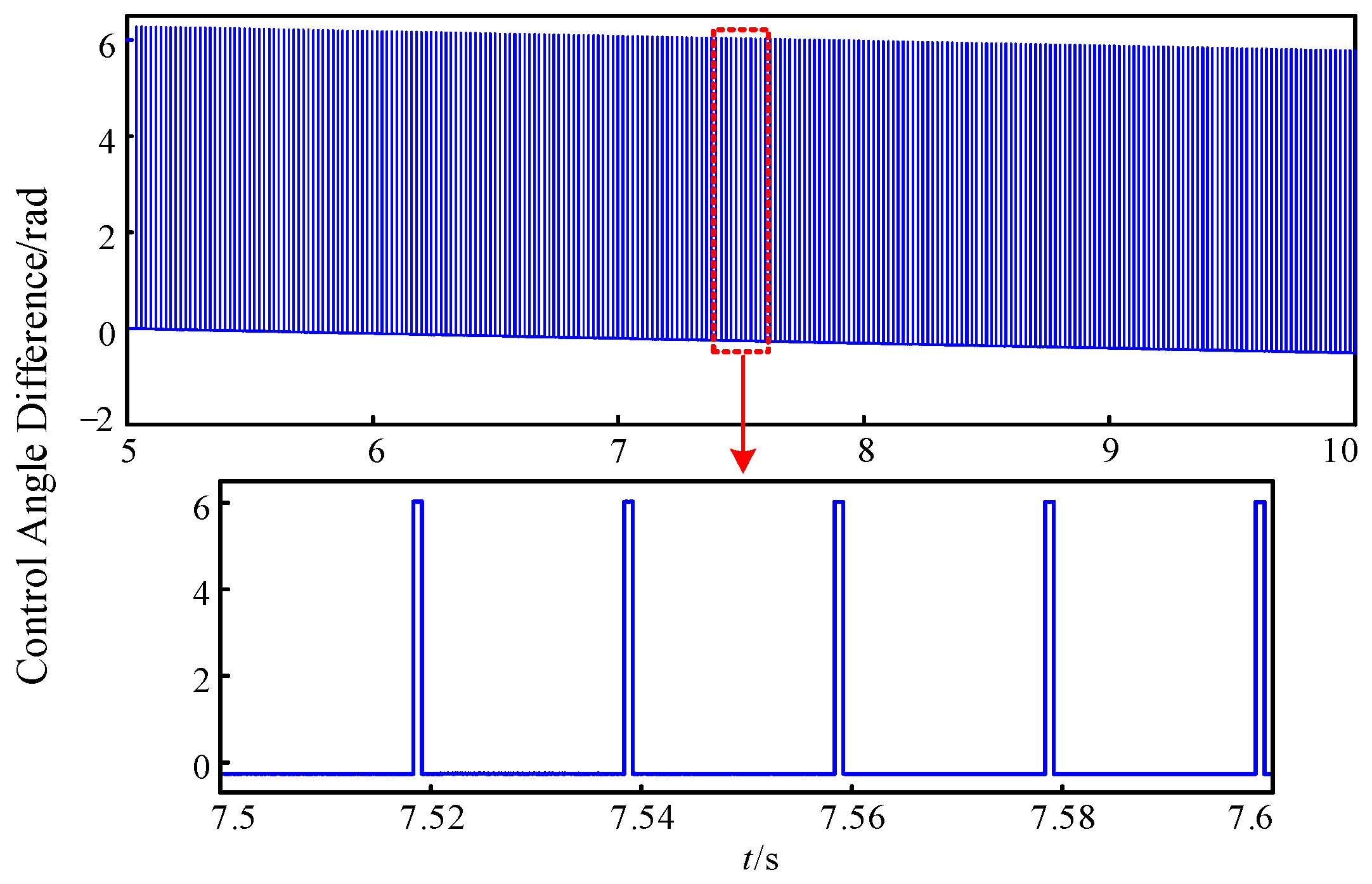
4.2. Validation of Control Angle-Tracking Technology’s Effectiveness
4.2.1. Control Angle-Tracking Strategy Without VSG
4.2.2. PI Regulator-Based VSG Control Angle-Tracking Strategy
4.2.3. Constructed-Function-Based VSG Control Angle-Tracking Strategy
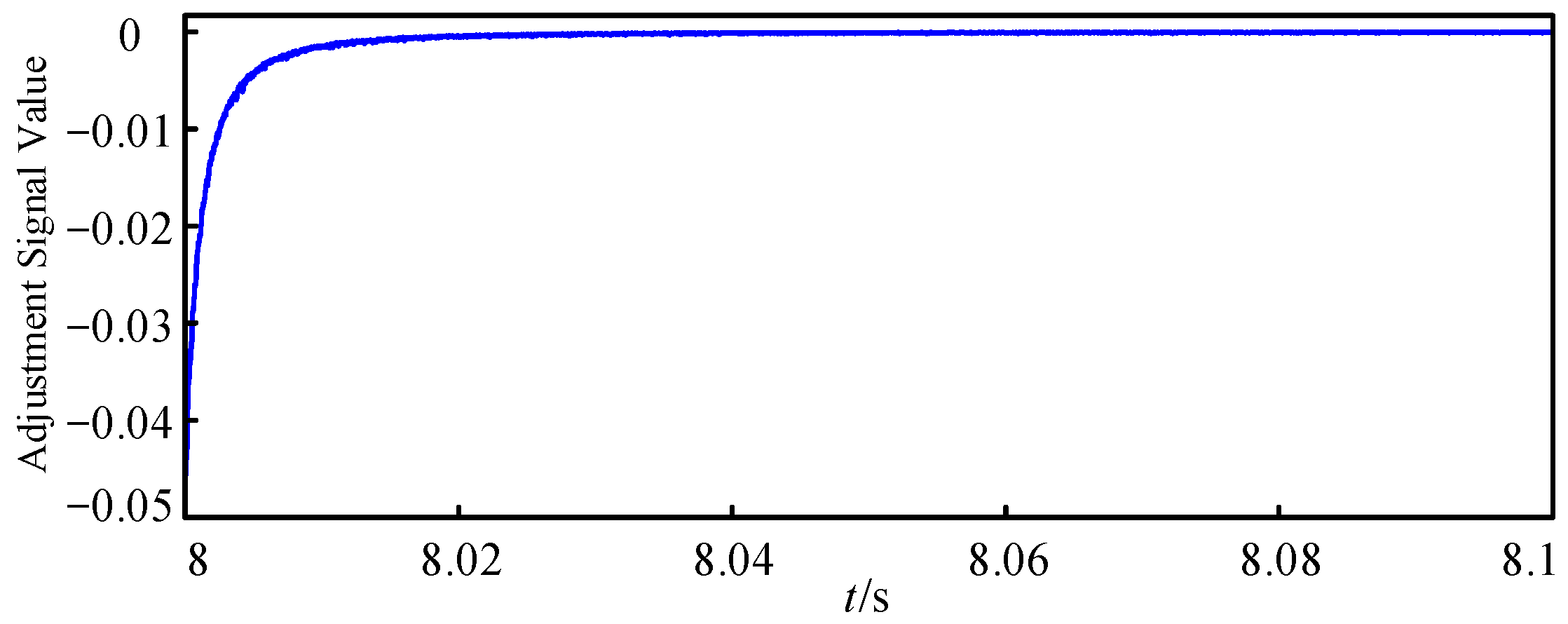
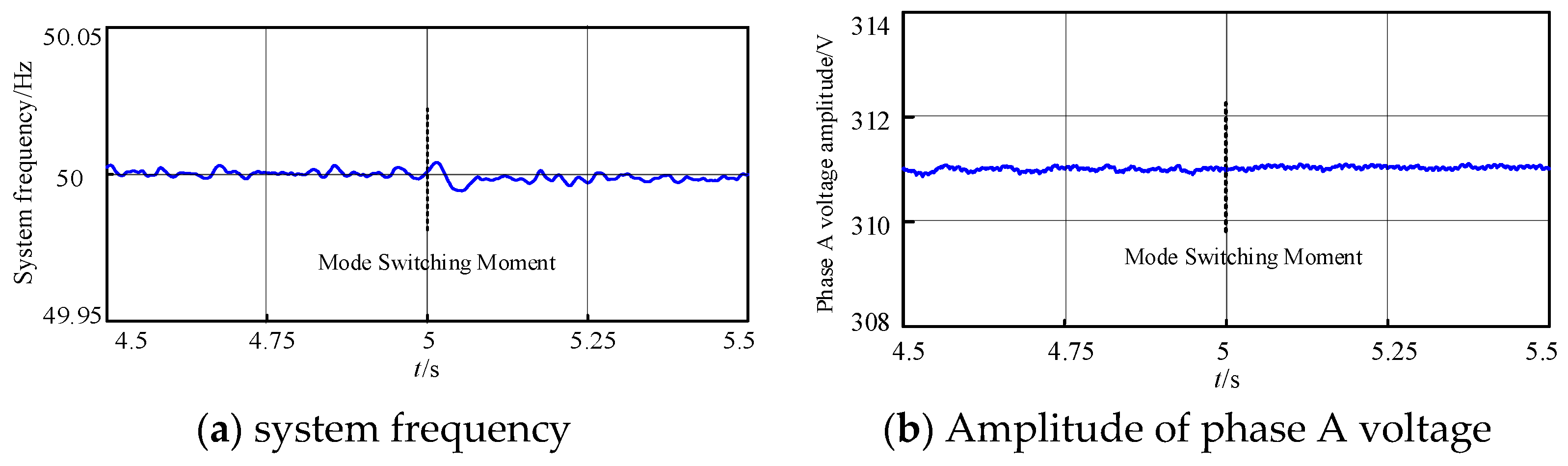
4.3. Performance Validation of the Overall Disturbance-Free Switching Scheme
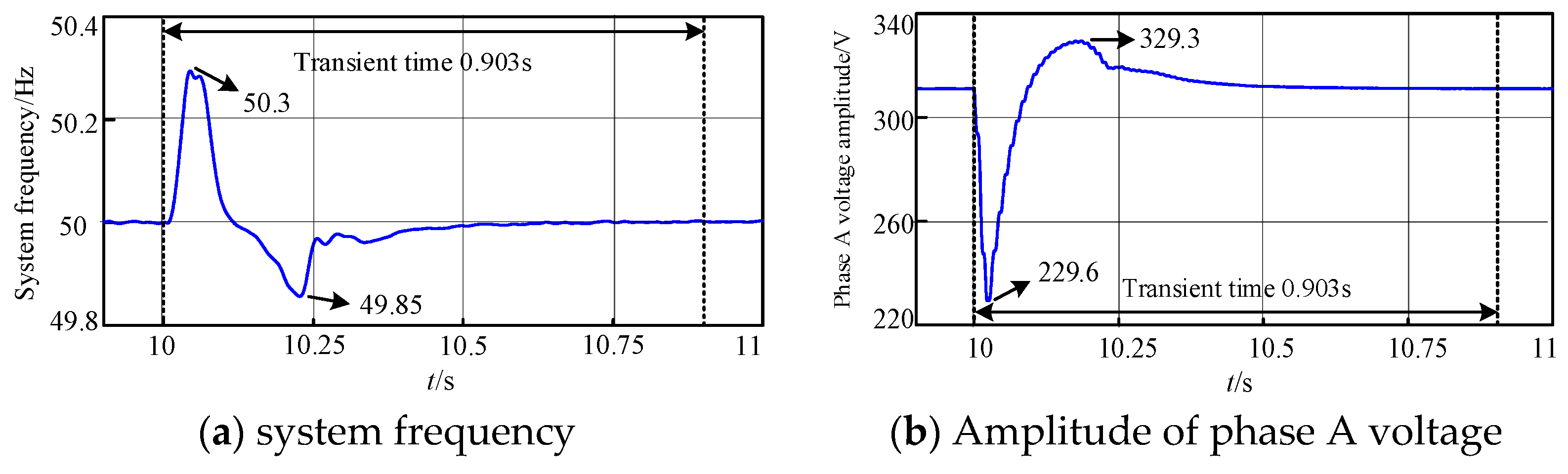
4.3.1. System Response Without Disturbance-Free Switching Strategy
- (1)
- Switching the Dual-Mode Energy Storage Converter from Grid-Forming to Grid-Following Mode
- (2)
- Switching the Dual-Mode Energy Storage Converter from Grid-Following to Grid-Forming Mode
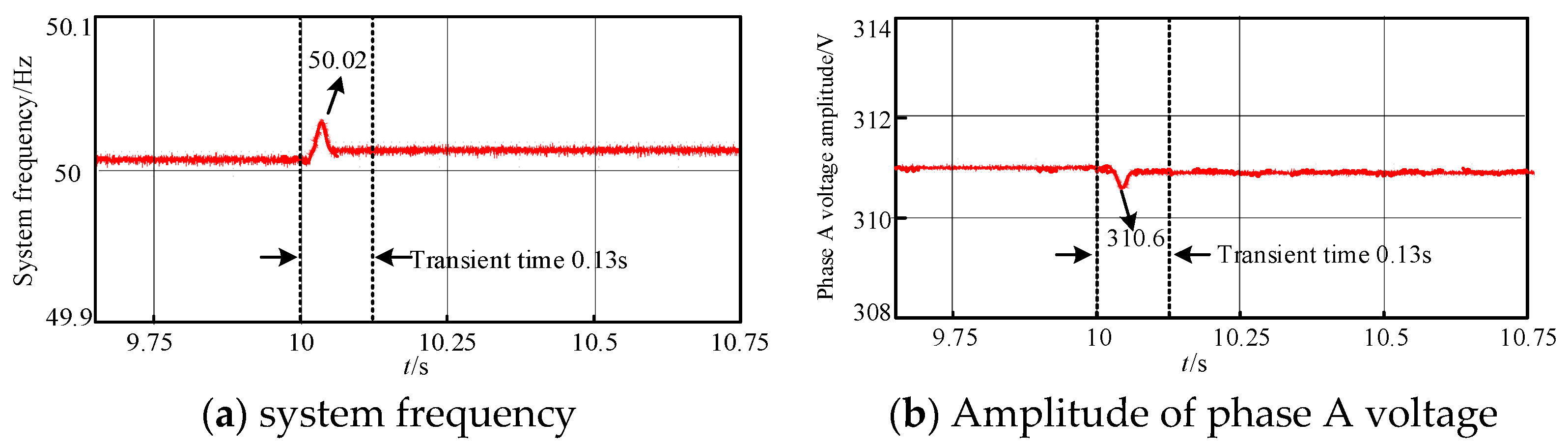
4.3.2. System Response with Disturbance-Free Switching Strategy
4.4. Hardware-in-the-Loop Experimental Validation
4.4.1. Experimental Platform Architecture
- (1)
- Upper Computer: A host PC running MATLAB/Simulink (version R2023a) was used to develop and compile the detailed electromagnetic transient model of the power circuit and the main grid.
- (2)
- Real-Time Simulator (RT-LAB OP4510): Serving as the core for model execution, the simulator is equipped with a powerful Intel Xeon multi-core processor and utilizes the ARTEMIS solver for high-fidelity electrical system simulation. It receives the compiled model from the upper computer and executes it on its real-time processor with a fixed simulation time-step of 50 μs, accurately simulating the dynamic characteristics of the physical plant.
- (3)
- Controller (RTU-BOX): This unit acts as the physical control hardware, with the proposed disturbance-free switching algorithm embedded. Its core is a Texas Instruments TMS320F28335 Digital Signal Processor (DSP). The controller interfaces with the simulator via its analog-to-digital converters (ADCs), acquiring real-time voltage and current signals with 16-bit resolution at a sampling frequency of 10 kHz. Based on these measurements and the embedded algorithm, it calculates and generates PWM modulation signals in real time to achieve closed-loop control of the virtual plant.
- (4)
- Waveform Recorder (Yokogawa DL850E): A high-precision ScopeCorder was employed for the synchronous, high-speed acquisition of electrical quantities (voltages, currents) and internal control signals from both the RT-LAB simulator and the RTU-BOX controller during experiments, enabling detailed post-processing and analysis.
4.4.2. Experimental Scheme and Result Analysis
4.5. Limitations and New Perspectives of Work
- (1)
- Conduct a theoretical stability and convergence analysis: Employ formal methods (e.g., Lyapunov’s direct method) to provide a rigorous mathematical proof of the system’s stability and the convergence of the proposed angle-tracking and current-latching mechanisms.
- (2)
- Quantify the impact of non-ideal conditions: Theoretically analyze and experimentally investigate the specific impact of line impedance and voltage fluctuations on the transient performance of the switching process.
- (3)
- Expand testing to complex microgrid scenarios: Develop more comprehensive simulation and experimental cases to evaluate system performance in realistic environments with high penetration of distributed energy resources, significant load uncertainty, and varied grid strengths to verify coordination capability and robustness.
- (4)
- Investigate multi-converter coordination: Study potential coordination mechanisms between multiple converters employing the proposed strategy to ensure system-wide stability during mode transitions.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Description | Unit |
| GFL | Grid-Following | |
| GFM | Grid-Forming | |
| VSG | Virtual Synchronous Generator | |
| PLL | Phase-Locked Loop | |
| HIL | Hardware-in-the-Loop | |
| DSP | Digital Signal Processor | |
| PWM | Pulse Width Modulation | |
| Po, Qo | Output active and reactive power | kW, kVar |
| Pref, Qref | Reference active and reactive power | kW, kVar |
| idref, iqref | d-axis and q-axis current reference | A |
| ild, ilq | d-axis and q-axis inductor current | A |
| ugd, ugq | d-axis and q-axis grid voltage | V |
| θgfl, θvsg | Control angle of GFL and VSG control | rad |
| δg | Phase-angle difference (θc − θg) | rad |
| ωvsg | Angular frequency reference of VSG | rad/s |
| Lf | Filter inductance | H |
| Cf | Filter capacitance | F |
| Jvsg | Virtual moment of inertia | kg·m2 |
| Dvsg | Damping coefficient | N·m·s·rad−1 |
References
- Wang, W.; Li, G.; He, G.Q. Challenges and Prospects of Renewable Energy Integration Control for New Power Systems. J. New Power Syst. 2023, 1, 145–160. [Google Scholar]
- Min, Y.; Chen, L.; Liu, R. Analysis on characteristics of inertia and inertial response in power system frequency dynamics. Proc. CSEE 2023, 43, 855–868. [Google Scholar]
- He, J.; Wang, C.; Li, C. Typical Problems in Operation and Control of Renewable Energy Industrial Microgrid: Analysis and Solutions. High Volt. Eng. 2024, 51, 3762–3784. [Google Scholar]
- Zhang, Y.; Gao, H.; Zhang, M. Research on frequency response difference of DFIG system controlled by different virtual synchronous generator controls. Trans. China Electrotech. Soc. 2020, 35, 2889–2900. [Google Scholar]
- Liu, H.; Yu, S.; Sun, D. Review of grid-forming converter control technologies and principles. Proc. CSEE 2025, 45, 277–297. [Google Scholar]
- Li, Y.; Ai, C.; Qin, Y. An Overview of Small-disturbance Stability of Grid-forming Convert ers Based on Matching Control. High Volt. Eng. 2025, 51, 774–792. [Google Scholar]
- Gao, B.; Shen, Y.; Song, R. Impedance modeling and sub/super⁃synchronous oscillation stability analysis of virtual synchronous machine controlled modular multilevel converter. Trans. China Electrotech. Soc. 2025, 40, 559–573. [Google Scholar]
- Liu, Y.; Wang, Y.; Peng, Y. Parameter tuning for improving interaction stability of grid-forming converter and power grid. Power Syst. Technol. 2023, 47, 16–27. [Google Scholar]
- Dehghanitafti, H.; Konstantinou, G.; Fletcher, J. Control of distributed photovoltaic inverters for frequency support and system recovery. IEEE Trans. Power Electron. 2022, 37, 4742–4750. [Google Scholar] [CrossRef]
- Chi, Y.; Jiang, B.; Fan, Y.W. Grid-forming converters: Control and behavior of stability. High Volt. Eng. 2025, 51, 1527–1542. [Google Scholar]
- Wang, X.; Ge, J.; Han, L. Theory and practice of grid forming BESS supporting the construction of a new type of power system. Power Syst. Prot. Control 2023, 51, 172–179. [Google Scholar]
- Guo, Z.; Zhang, X.; Li, M. Stability analysis and capacity distribution of multi-paralleled current-controlled inverters and voltage-controlled VSGs grid-connected system. In Proceedings of the 2021 IEEE 12th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Chicago, IL, USA, 28 June–1 July 2021; pp. 1–8. [Google Scholar]
- Cheng, C.; Xie, S.; Zhang, Q. Overview of modeling and stability analysis for single-phase grid connected inverters considering phase-locked loop dynamics. Proc. CSEE 2024, 44, 255–269. [Google Scholar]
- Yue, J.; An, R.; Gao, J. Stability analysis of grid connected inverter based on current positive and negative feedback loop effects under weak grid. Power Syst. Technol. 2023, 47, 2423–2433. [Google Scholar]
- Zhao, Z.; Yang, P.; Zheng, C. Review on dynamic stability research of microgrid. Trans. China Electrotech. Soc. 2017, 32, 111–122. [Google Scholar]
- Hu, Y.; Tian, Z.; Zha, X. Impedance stability analysis and promotion strategy of islanded microgrid dominated by grid connected and grid-following converters. Autom. Electr. Power Syst. 2022, 46, 121–131. [Google Scholar]
- Wang, G.; Pei, W.; Xiong, J. Stability analysis method for hybrid systems of grid-following and grid-forming inverters. Proc. CSEE 2025, 45, 25–38. [Google Scholar]
- Zhan, C.; Wu, H.; Wang, X. Anoverview of stability studies of grid-forming voltage source converters. Proc. CSEE 2023, 43, 2339–2359. [Google Scholar]
- Li, G.; Zhao, L.; Xie, F. Disturbance-free switching control technology for energy storage converters between grid-following and grid-forming modes. Energ. Stor. Sci. Tech. 2025, 14, 2983–2993. [Google Scholar]
- Liang, J.G.; Jin, X.M.; Wu, X.Z. Switching technology between VCS mode and CCS mode for microgrid inverters. Power Syst. Technol. 2014, 38, 830–837. [Google Scholar]
- Yan, X.; Jia, J.; Wang, D. Grid-connected power control and mode-smooth switching of virtual synchronous generators. Autom. Electr. Power Syst. 2018, 42, 91–99. [Google Scholar]
- Wen, C.; Yang, C.; Chen, D. Dual-mode control of the power loop for virtual synchronous energy storage converters. Autom. Electr. Power Syst. 2019, 43, 56–61. [Google Scholar]
- Chen, X.; Wang, Y.C.; Gong, C.Y. Overview of stability research for grid-connected inverters based on impedance analysis method. Proc. CSEE 2018, 38, 2082–2094. [Google Scholar]
- Zhou, Y.Q.; Yao, W.; Zong, Q.H. Optimal configuration method for switchable units of backing/constructing networks in renewable energy plant based on operating short-circuit ratio. Power Syst. Technol. 2024, 48, 1091–1104. [Google Scholar]






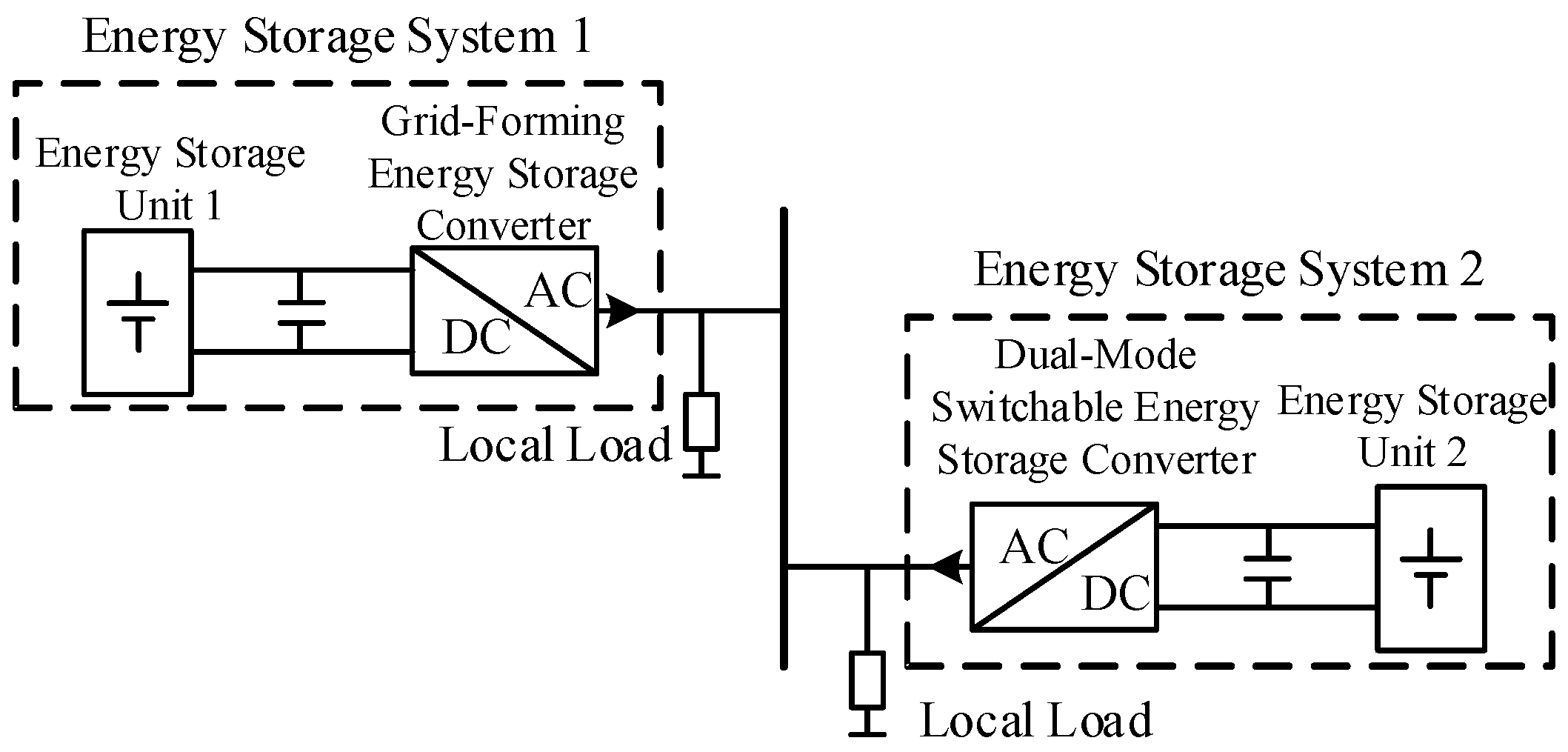





| Type | Parameter | Value |
|---|---|---|
| Energy Storage System 1 | Rated Capacity Sn1/kVA | 600 |
| Rated Line Voltage Un1/V | 380 | |
| Rated Frequency f1/Hz | 50 | |
| Filter Inductance Lf1/mH | 1.5 | |
| Filter Capacitance Cf1/μF | 1 | |
| Damping Coefficient Dvsg1/N·m·s·rad−1 | 203 | |
| Moment of Inertia Jvsg1/kg·m2 | 0.01 | |
| Voltage Outer Loop kup1, kui1 | 5, 20 | |
| Current Inner Loop kip1, kii1 | 500, 2 | |
| Rated Capacity Sn1/kVA | 600 | |
| Energy Storage System 2 | Rated Capacity Sn2/kVA | 600 |
| Rated Line Voltage Un2/V | 380 | |
| Rated Frequency f2/Hz | 50 | |
| Filter Inductance Lf2/mH | 1.5 | |
| Filter Capacitance Cf2/μF | 1 | |
| Damping Coefficient Dvsg2/N·m·s·rad−1 | 203 | |
| Moment of Inertia Jvsg2/kg·m2 | 0.01 | |
| Voltage Outer Loop kup2, kui2 | 5, 20 | |
| Current Inner Loop kip2, kii2 | 500, 2 | |
| Active Power Command P0/kW | 300 | |
| Reactive Power Command Q0/kvar | 0 | |
| Rated Capacity Sn2/kVA | 600 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, G.; Kan, S.; Li, Y.; Zhu, X. Disturbance-Free Switching Control Strategy for Grid-Following/Grid-Forming Modes of Energy Storage Converters. Electronics 2025, 14, 3963. https://doi.org/10.3390/electronics14193963
Jiang G, Kan S, Li Y, Zhu X. Disturbance-Free Switching Control Strategy for Grid-Following/Grid-Forming Modes of Energy Storage Converters. Electronics. 2025; 14(19):3963. https://doi.org/10.3390/electronics14193963
Chicago/Turabian StyleJiang, Geling, Siyu Kan, Yuhang Li, and Xiaorong Zhu. 2025. "Disturbance-Free Switching Control Strategy for Grid-Following/Grid-Forming Modes of Energy Storage Converters" Electronics 14, no. 19: 3963. https://doi.org/10.3390/electronics14193963
APA StyleJiang, G., Kan, S., Li, Y., & Zhu, X. (2025). Disturbance-Free Switching Control Strategy for Grid-Following/Grid-Forming Modes of Energy Storage Converters. Electronics, 14(19), 3963. https://doi.org/10.3390/electronics14193963





