Abstract
The recent demand for 8-bit floating-point (FP) formats is driven by their potential to accelerate domain-specific applications with intensive vector computations (e.g., machine learning, graphics, and data compression). This paper presents the design, implementation, and application of the software model of an 8-bit FP vector arithmetic operation set, compliant with the RISC-V vector instruction set architecture. The model has been developed as an extension of the SoftFloat library and integrated into the RISC-V reference instruction-level simulator Spike, providing the first open-source 8-bit SoftFloat extension for an instruction-set simulator. Based on the SoftFloat library templates for standard FP formats, the proposed extension implements the two widely used 8-bit formats E4M3 and E5M2 in both Open Compute Project (OCP) and IEEE 754 variants. In host-time micro-kernels, FP8 delivers +2–4% more elements per second versus FP32 (across vfadd/vfsub/vfmul) and ≈5% lower RSS; E4M3 and E5M2 perform similarly. Enabling FP8 in Spike increases the stripped binary by ~1.8% (mostly .text). The proposed extension was used to fully verify and correct errors in the vector FP unit design for the eProcessor European project, and continues to be used to verify other 8-bit FP unit implementations.
1. Introduction
Floating-point (FP) arithmetic traditionally relies on high-precision formats such as single precision (32-bit) and double precision (64-bit), which often exceed the precision requirements of many Artificial Intelligence (AI) and machine learning workloads. In fact, half precision (16-bit) formats are widely used during training [1], and even lower-precision formats, particularly 8-bit, can yield significant computational speedups on domain-specific hardware platforms, without substantial loss in accuracy. For instance, Google’s Tensor Processing Units (TPUs) utilize 8-bit precision to enhance the performance of deep learning models [2]. Similarly, NVIDIA GPUs typically support various lower-precision formats [3], including 16-bit FP and 8-bit integer, for optimizing AI workloads. One of NVIDIA’s latest flagship GPUs supports 8-bit floating-point (FP8) formats in its tensor cores [4].
In the microprocessor design scenario, the RISC-V instruction set architecture (ISA) has emerged as a versatile and open-standard platform [5]. In particular, a lot of interest has grown in the vector computing specialized instruction set (RISC-V “V” extension), for both high-performance scientific workloads and AI workloads. The RISC-V vector instructions intrinsically target the execution of highly parallel element-wise computations on vectors, thus potentially benefiting from reduced precision formats to enhance energy and area efficiency.
We introduce an FP8 extension to the SoftFloat library [6], specifically developed for supporting two 8-bit vector FP formats in two different standards—IEEE-like FP8 standard and Open Compute Project (OCP) FP8 standard [7,8]—in the Spike RISC-V reference instruction set simulator [9]. Extending Spike with dual-format FP8 support provides a robust verification platform for evaluating implementations of both standards within RISC-V compliant vector processors.
The extended Spike was integrated into a verification environment employed to verify the 8-bit floating-point support in a RISC-V vector processor design, developed as part of the “eProcessor” project funded by the European Union [10].
Our main contributions are as follows:
- End-to-end FP8 support for Spike: We implement complete FP8 support in SoftFloat—covering E4M3 and E5M2 for both IEEE-like and OCP variants, with full conversion and arithmetic—making it, to our knowledge, the first simulator extension with complete FP8 arithmetic support; we also integrate this into Spike via a new Softfloat_8 backend and minimal frontend changes, making Spike, to our knowledge, the first publicly available RISC-V ISA simulator with complete FP8 arithmetic support.
- Cross-standard numerical analysis: We systematically compare IEEE-like and three OCP configurations (no saturation; saturation on conversion; saturation on conversion and arithmetic) for E4M3/E5M2 on element-wise vector kernels, quantifying typical error, tails, and non-finite behavior, and distilling format/standard guidance.
- Host-time characterization and binary-size impact: Under identical VLEN, we quantify median elements per second and runtime memory footprint (RSS) on vfadd/vfsub/vfmul. FP8 delivers +2–4% more elements per second than FP32 with ≈5% lower RSS; E4M3 ≈ E5M2 in throughput. Enabling FP8 in Spike increases the distribution footprint in the stripped executable by ~1.8% (mostly .text).
While the contribution is a simulator extension rather than an application study, reduced-precision FP8 directly serves domains where an explicit trade-off between performance (throughput, memory/bandwidth) and numerical accuracy must be managed—especially machine learning. Our results quantify that trade-off to inform format and standard choices.
This article is organized as follows: Section 2 reviews existing low-precision floating-point implementations, highlighting their publication status and open-source availability, and adds a concise motivation for FP8 that summarizes performance drivers and machine-learning applications reported in the literature. Section 3 presents the methodology used in implementing the 8-bit SoftFloat library extensions, providing an overview of the function implementations, and reports a numerical study of FP8 arithmetic accuracy (relative error and ULP distributions) across different configurations. Section 4 showcases the verification framework that constitutes the first application case, and reports an analysis of host-time throughput, runtime memory footprint (RSS), and Spike binary-size deltas. Section 5 discusses the broader impact of the work.
2. Motivation, Background, and Related Works
Recent research and industrial practice indicate that FP8 can approach 16-bit accuracy with suitable scaling while improving efficiency; a concise snapshot is reported in Section 2.1. In this section, we focus on formats, standards, and available tools, and we outline the specific gap we address.
Such wide interest in FP8 formats has brought hardware companies to investigate and implement hardware support for FP8. A representative work is the joint article authored by designers at Nvidia, ARM, and Intel [11]. In the article, the same two FP8 formats proposed in our work are discussed. Notably, the E4M3 format (with a 4-bit exponent and a 3-bit mantissa) implemented in their paper does not represent infinities. Instead, it sacrifices infinity representation in favor of a broader dynamic range, which makes it inconsistent with other standard IEEE 754 formats (16-, 32-, and 64-bit). This approach was later standardized by the Open Compute Project in the OCP 8-bit Floating-point Specification [8]. However, the specification only treats these formats as interchange formats, defining their structure and conversion rules but not specifying the associated arithmetic operations. In our model, we implement both this standard and an alternative version of the E4M3 format that aligns with the arithmetic operations and the structure of the other IEEE 754 formats. This allows the format to represent infinities and allows the execution of tests written in high-level languages and cross-compiled for RISC-V architectures without changes in the arithmetic behavior when dealing with infinity values. This compliance also provides programmers with the flexibility to design test benches with ease. Moreover, we also chose to implement arithmetic operations to make the most of the properties of these floating-point formats.
To verify any hardware implementation of FP arithmetic support, the availability of exact software emulation models is crucial. The primary reference for software emulation of FP operations is represented by the SoftFloat library [6], initially developed by John R. Hauser and maintained by the University of California Berkeley’s Architecture Research group. It is a precise and portable software implementation of floating-point arithmetic that adheres to the IEEE 754 standard [7]. Designed to facilitate floating-point operations in environments lacking adequate hardware support, SoftFloat is widely used in both academic and industrial applications to ensure reliable and accurate floating-point computations across different platforms and architectures. The current release supports five binary formats: 16-bit half-precision, 32-bit single-precision, 64-bit double-precision, 80-bit double-extended-precision, and 128-bit quadruple-precision. Support for the 8-bit format is not included in any official release.
Intel has developed an FP8 Emulation Toolkit [12], which enables FP8 format emulation in Python on standard single-precision floating-point Xeon/GPU hardware. It supports both the E5M2 format and the E4M3 format in both its OCP and IEEE-like standards. However, it only supports conversion operations which are necessary for quantizing weights for memory efficiency in machine learning applications, treating the FP8 formats as purely interchange formats. While this toolkit is a valuable resource, it does not support arithmetic operations and it is not designed for integration into an ISA simulator. Moreover, Intel recently released the Advanced Vector Extensions 10.2 Architecture Specification that supports FP8 formats only in their OCP standard version [13]. Again, the formats are treated here as interchange formats as well, and only conversion operations are defined. Similarly, NVIDIA has developed a library for accelerating Transformer models on NVIDIA GPUs [14], utilizing FP8 formats on Hopper and Ada GPUs to enhance performance and reduce memory utilization during training and inference. However, like the Intel toolkit, this library is not intended for integration into an ISA simulator and only uses the formats as interchange formats. Moreover, none of the above target the RISC-V Vector ISA operations.
2.1. The Case for FP8
This subsection summarizes representative evidence for FP8 effectiveness across computer vision, natural language processing, image processing, and LLM training to motivate the dual-format arithmetic support implemented in Spike.
Liu et al. (2022) [15] proposed an adaptive piecewise quantization method that effectively reduces the bias, facilitating the successful quantization of all layers in large-scale Convolutional and Recurrent Neural Network models to 8 bits without accuracy loss. Another notable development in this field is the Hybrid FP8 format from Sun et al. (2019) [16], which employs different precision levels for Neural Network training. They demonstrated the effectiveness of FP8 data in training popular models such as MobileNet and Transformer without significant accuracy loss across a spectrum of applications, including image classification, object detection, and natural language processing. Their research showed a practical difference between the two encodings when contrasting forward and backward passes, with E4M3 being typically better for forward activations on capacity-constrained CNNs/Transformers and E5M2 being advantageous for gradients. Complementing these training-oriented results, Shen et al. (2024) [17] evaluate FP8 post-training quantization across 75 network architectures and report higher workload coverage for FP8 versus INT8 (% vs. %), recommending E4M3 for natural language processing and noting that E3M4 is marginally better for computer vision. From an image-processing perspective, Nesam et al. (2024) [18] report area and power optimizations of 75.2–21.3% and 66.43–20.4%, respectively, when reducing FP16 mantissa bits for pixel pipelines, with quality assessed via PSNR/MSE; Liu et al. (2025) [19] introduce VNDHR, a variational nighttime dehazing framework achieving state-of-the-art perceptual visibility on synthetic and real nighttime hazy images via hybrid regularization. Li et al. (2024) [20] present Mortar-FP8, a software-hardware co-design that converts FP32 weights to FP8 (E4M3) with a dynamic-bias scheme; across classification, detection, video, and image-processing workloads (e.g., super-resolution and style transfer), they report negligible accuracy loss (about %) and up to accelerator speedup (area , power ). On ImageNet, Micikevicius et al. (2022) [11] demonstrated that FP8 training tracks FP16/BF16 across CNN and Transformer families, with deviations typically within run-to-run variation: across 13 models, the median top-1 delta is 0.16 pp (mean 0.21 pp), the worst case is −0.61 pp on MobileNet v2, and ResNet-50 v1.5 shows a slight gain of +0.05 pp. Machine translation results on WMT16 En→De and language modeling perplexity for Transformer-XL/GPT up to 175B parameters similarly follow higher-precision baselines.
Tagliavini et al. (2018) [21] introduced the concept of transprecision computing that allows for fine-grained control over the precision of computations, ensuring that energy efficiency is maximized without compromising the accuracy of results. They introduced new 8-bit and 16-bit floating-point formats to achieve significant reductions in energy consumption and execution time. This approach demonstrates the potential of adopting multiple floating-point types to optimize both hardware and software for ultra-low-power computing applications. In parallel, Lee et al. (2024) [22] systematically quantify the stability–precision trade-off for sub-BF16 LLM training, finding current FP8 schemes more hyperparameter-sensitive and introducing a sharpness-based metric to anticipate divergence. Strengthening this evidence at scale, Fishman et al. (2025) [23] train LLMs with FP8 on datasets up to 2 trillion tokens, identify an instability that emerges only in long runs due to outlier amplification in SwiGLU, and introduce Smooth-SwiGLU to stabilize training. They further quantize both Adam optimizer moments to FP8 and show a 7B model on 256 Intel Gaudi2 accelerators that matches BF16 quality while delivering up to ∼34% higher throughput, underscoring the practical viability of FP8 for large-scale training.
Peng et al. (2023) [24] demonstrated that at LLM scale, pre-training loss curves overlap BF16 and downstream zero-shot quality remains comparable, while end-to-end system savings appear during fine-tuning and alignment. During SFT on H100 GPUs, GPU memory drops from 51.1 GB to 44.0 GB (−14%) and throughput rises from 103 to 131 samples/s (+27%) with essentially unchanged downstream quality; during RLHF, model weights memory falls from 15,082 MB to 10,292 MB (−32%) and optimizer states from 15,116 MB to 5669 MB (−62%), again with comparable AlpacaEval and MT-Bench scores. The SFT snapshot is summarized in Table 1.

Table 1.
Supervised fine-tuning (SFT) on H100: memory, throughput, and downstream quality (from [24]).
Overall, these studies indicate that FP8 reaches 16-bit-level accuracy on standard workloads and delivers material system savings at scale; this motivates first-class FP8 support in toolchains and instruction-set simulators.
3. SoftFloat 8-Bit Extension Implementation
3.1. Supported FP8 Formats
The proposed extension to the SoftFloat library supports two FP8 formats, namely E5M2—featuring 5-bit exponent, 2-bit mantissa, and 1 sign bit—and E4M3—featuring 4-bit exponent, 3-bit mantissa, and 1 sign bit—both in the OCP and in the IEEE-like standard. Both the formats include subnormal number representation. To maintain consistency with the standards, the bias is computed as for both types, where n is the number of bits of the exponent. Therefore, the bias will be for the first type, which has a four-bit exponent, and for the second type, which has a five-bit exponent.
While the IEEE-like FP8 formats adhere strictly to IEEE 754 for encoding infinities and NaNs, raising flags, handling subnormal numbers and rounding modes, the OCP E4M3 variant omits infinities entirely and provides only a single NaN mantissa encoding. Consequently, E4M3 supports just two NaN bit patterns—one positive and one negative—and reclaims the infinity and the other NaN bit patterns to extend its maximum exponent from seven to eight, thereby increasing its dynamic range by one binade (a binade is the set of floating-point values sharing the same exponent).
Another key distinction is the handling of saturation. The OCP standard mandates an optional saturation mode for conversions from wider formats into FP8: on overflow, values clamp to the largest finite representable number rather than producing infinities (or NaNs, in the case of E4M3). However, this requirement applies only to conversions—saturation of arithmetic results is left unspecified. In our implementation, we support both behaviors, allowing users to choose whether saturation applies exclusively to conversions or also to the results of arithmetic operations. Notably, the OCP standard does not require exception handling during these conversions, nor does it require the use of status flags to indicate exceptions, unlike the IEEE format, which mandates exception handling and flag management.
Furthermore, the OCP standard specifies that rounding must be performed using the “round to nearest even” mode. While this is a required implementation for OCP, the specification also allows for the possibility of implementing additional rounding modes, though they are not required by the standard. In our model, we support the “round to nearest even” mode for the OCP formats, while for the IEEE-like formats, we implement all IEEE 754 rounding modes to ensure full compatibility with the standard.
Finally, because the sole NaN encoding in OCP E4M3 () has the mantissa’s most significant bit set, it is inherently a quiet NaN. To enable early error detection and prevent silent propagation, we also provide an option to treat this single NaN as a signaling NaN.

Table 2.
Exponent parameters of the supported FP8 formats.

Table 3.
Value-encoding details of the supported FP8 formats.
3.2. Software Implementation
We extend Spike with FP8 support by introducing a new SoftFloat back-end module (Softfloat_8) and making minimal frontend changes, including a format-selection parameter (E4M3/E5M2), small updates to the RVV FP decode/instruction files to dispatch FP8 elements, and a new instruction (vfcvt.f.f). Figure 1 summarizes the integration.
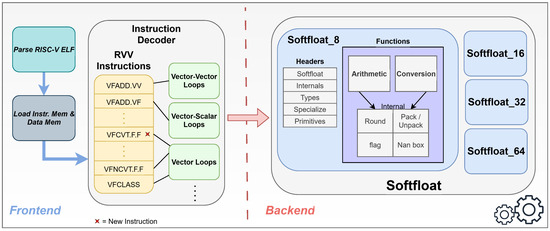
Figure 1.
Spike software architecture with the FP8 back-end (Softfloat_8); frontend modifications include a format-selection parameter, FP8 entries in the RVV decode/instruction files, and a new instruction.
The implementation of the back-end is organized into three parts.
- Headers;
- Arithmetic, conversion, and auxiliary functions;
- Spike integration functions for vector instructions.
Following the template from the SoftFloat library, the header files have been expanded to add all the necessary definitions and function declarations needed for the correct functioning of the library. The headers are organized as follows:
The softfloat.h header contains all the non-internal arithmetic function declarations.
The internals.h header contains internal definitions such as the union type used to map 8-bit variables, together with the definitions of some basic function for the implementations of the arithmetic functions;
The types.h header contains the SoftFloat types declarations, to which new types float8_1_t for E4M3 and float8_2_t for E5M2 have been added.
The specialize.h header contains both the definition of the default NaN values for the newly implemented data types and the declarations of the functions dedicated to handling NaN values.
The softfloat_types.h header contains the macros needed to select the options for the OCP standard formats, as described in Section 3.1. In particular, the macro OFP8_saturate_arith saturates the result of FP8 arithmetic operations and the macro E4M3_isSigNaN transforms the only OCP E4M3 NaN into a signaling one.
Lastly, the primitives.h header defines constants and utility functions that are essential for implementing floating-point operations.
The core functions that use the above headers fall into two categories, as illustrated in Figure 1. The first category comprises the top-level functions invoked by the Spike instruction decoder, encompassing both arithmetic and conversion SoftFloat functions. For both the proposed 8-bit floating-point types E5M2 and E4M3, all the required functions in compliance with the IEEE 754 standard have been implemented, along with an additional function for converting between the two types. Conversion between floating-point types having different precisions is supported via narrowing and widening instructions in the RISC-V instruction set, as well as in the SoftFloat library. In addition to conversion from 8-bit formats to bfloat16 (Brain Floating Point, 16-bit), the newly implemented 8-bit types imply a new conversion operation from E5M2 to E4M3 and vice versa. The existing SoftFloat conversion function templates did not support conversions between formats of the same length, yet, by adapting the existing narrowing and widening functions, we were able to develop the necessary conversion functions while closely adhering to the original template. This new instruction is designated as “vfcvt.f.f”.
The second category of newly defined functions includes common auxiliary routines for floating-point operation support, such as packing and unpacking the FP8 fields, rounding inexact results to the selected round mode, normalization, NaN handling, and flag raising. In the SoftFloat library, a default NaN value is defined for every floating-point data type. To follow the template faithfully, a default NaN value has been implemented for the two FP8 types. The default canonical quiet NaN encoding requires to set the sign bit to `0’, the exponent bits all to `1’, the most significant bit of the mantissa to `1’, and all other bits to `0’. For the E5M2 type the default NaN is and for the E4M3 data type it is for the IEEE-like version and for the OCP version.
As per the IEEE 754 standard for higher precision formats, the arithmetic functions of the SoftFloat extension support the detection of five exceptional conditions (flags), namely inexact, overflow, underflow, divide by zero, and invalid. Flag support is particularly critical in checking the compliance of hardware FP8 unit implementations with existing numerical software applications.
The full list of arithmetic core functions, along with the corresponding RISC-V instructions, is shown in Table 4.

Table 4.
Arithmetic core library functions.
In order to integrate the new SoftFloat extension into the Spike source files, several updates have been implemented.
- The headers and the core function files have been added in the softfloat_8 directory, following a naming convention consistent with their SoftFloat counterparts.
- A template Makefile has been added in the softfloat_8 directory, to specify which files to compile and which headers to include in the software build.
- The float vector instruction files in the directory have been updated to accommodate the new formats.
- The macros in the instruction decode header file have been updated. This header contains macros for instruction decoding and execution, which implement vector loops for single-operand vector instructions, vector–vector and vector–scalar.
- A command-line argument that selects the default FP8 type based on the vector standard element width (vsew) and a bitfield “valtfp” has been added in the Vtype CSR register to distinguish between the two FP8 types. This new CSR was defined as a custom CSR register to avoid using the reserved encoding spaces or bit fields in existing CSRs, avoiding potential conflicts with future ISA spec releases.
3.3. Numerical Evaluation of FP8 Formats and Standards
This section quantifies the numerical behavior of the two FP8 encodings implemented in the simulator (E4M3 with higher mantissa precision, and E5M2 with a wider exponent range) under four standard variants for exceptional values: IEEE-like, OCP without saturation, OCP with saturation on conversion only, and OCP with saturation on both conversion and arithmetic, with the goal of assessing whether FP8 arithmetic is accurate enough for typical element-wise vector kernels. The same input seeds are used for all runs so that the different standards are directly comparable.
The tests of this section are driven by a Python harness that calls the C simulator through a wrapper. The FP32 result serves as ground truth; relative error and ULP distances (=how many representable numbers apart two values are) are measured in FP32 units. For each operation (add, sub, fma) we draw independent operands from three input regimes: (i) Normal, (ii) Uniform, and (iii) signed log-uniform magnitudes spanning decades. The unit-scale cases (Normal and Uniform) probe precision around without activating range effects, which isolates mantissa behavior. The log-uniform case stresses dynamic range: we sample
so with a flat density in . This produces both very small and very large operands, exercising underflow/overflow policies.
We use samples per operation for Normal and Uniform and for log-uniform. The counts are chosen so that reported percentiles are statistically stable and the non-finite rates (NaN/Inf) are well estimated. For an empirical p-quantile, the uncertainty in percentile rank can be bounded by the binomial approximation
With , this gives percentage points at and at . With , the bounds tighten to and points, respectively. For non-finite rates estimated by , the standard error is
so even for moderate incidences (e.g., ) and , we have , yielding a 95% interval. The heavier-tailed log-uniform case therefore uses to stabilize both the P95/P99 on finite samples and the NaN/infinity value (Inf) rates. For FP16/FP32 baselines, we rely on NumPy; for FMA, the baseline is non-fused (multiplication and addition round separately).
For each output and truth y, we compute the absolute relative error
the ULP distance in FP32 units (obtained by ordering FP32 bit patterns so that integer distance equals ULP distance), and the rates of non-finite results (NaN and Inf). Percentiles (median, P95, P99) are computed over finite samples only; non-finite rates are reported separately.
On unit-scale inputs (Normal and Uniform), E4M3 shows about half the median relative error of E5M2 across add, sub, and fma (e.g., ≈0.033 vs. 0.066), with similarly smaller P95 values. In ULP units the medians are also about lower for E4M3 (∼4 · 105 vs. ∼8 · 105). The tails are bounded: P99 in all cases except fma with E5M2 (1.419). FP16 closely tracks FP32 and serves as a reference. Because these unit-scale tests primarily probe precision rather than dynamic range, results are identical across FP8 standards. Table 5 reports Normal; Uniform follows the same pattern.

Table 5.
Normal, FP8 element-wise accuracy vs. FP32 truth (finite cases). Values are median, P95 and P99 of and .
For the range-stress results (log-uniform, decades), the standard used dominates the behaviour. Figure 2 shows the error distributions for fma using the same random seed. A prominent spike at on the horizontal axis (i.e., ) is expected for the E4M3 curve. It arises from trials in which FP8 quantization—either at operand conversion or due to underflow after the operation—produces an output equal to zero, while the FP32 reference is non-zero. By definition this yields , which appears at in the logarithmic plot. The effect is more pronounced for E4M3 because its exponent range is narrower than E5M2. Consistent with this, Table 6 shows that under IEEE-like, E4M3 exhibits NaN and Inf (median ), whereas E5M2 has negligible NaN and 17.4% Inf (median 0.053); OCP (no saturation) removes Inf for E4M3 but yields NaN (median 0.036); adding saturation on conversion reduces non-finites (E4M3 NaN, 0% Inf) at the cost of higher finite error (median ); and saturation on operations and conversion eliminates non-finites entirely (0%/0%) but further increases bias (medians for E4M3 and for E5M2, with P95 near 1).
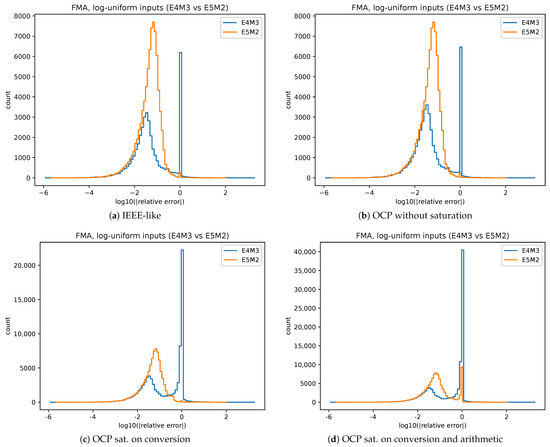
Figure 2.
stephistograms for fma with log-uniform inputs (±5 decades), using the same random seed. Panels: (a) IEEE-like, (b) OCP without saturation, (c) OCP with saturation on conversion only, (d) OCP with saturation on conversion and arithmetic.

Table 6.
Log-uniform ( decades), fma: finite-sample accuracy vs. FP32 truth and non-finite rates.
From these tests, we can see that for data already normalized near unit scale, element-wise FP8 is usable and E4M3 provides lower typical error. For wide-range data, E5M2 is preferable and the choice of the standard is critical: IEEE-like makes overflows explicit through Inf (useful for diagnostics), OCP without saturation suppresses Inf at the cost of NaN propagation for E4M3, and saturation removes non-finite values while introducing bias. If saturation is required, applying it only at conversion reduces bias compared to saturating arithmetic. Overall, this controlled numerical analysis demonstrates that FP8 arithmetic is a viable option for element-wise vector kernels when data are appropriately scaled: typical errors are modest near unit magnitude, and behavior under wide dynamic range and exceptional cases is governed by the format (E4M3 vs. E5M2) and the standard (IEEE-like vs. OCP variants). In addition to numerical viability, FP8’s compact 8-bit representation (4× smaller than FP32 and 2× smaller than FP16) reduces memory footprint and data movement and can increase arithmetic density and effective bandwidth on bandwidth-bound workloads. These practical advantages motivate FP8 as a compelling choice.
4. Application to a Processor Verification Environment and Results
The SoftFloat 8-bit library extension has been employed for the verification of an 8-bit dual-format vector Floating-Point Unit (FPU) in the Vector Processing Unit (VPU) of the eProcessor System-on-Chip [25]. The vector FPU hardware design is based on a totally different scheme than the one used for the software models implemented in the SoftFloat extension, as it converts the input operands to an internal custom 10-bit format and narrows the results back to the desired 8-bit output with appropriate rounding.
The verification methodology employed is sketched in Figure 3. Below, we discuss the steps highlighted in the figure.
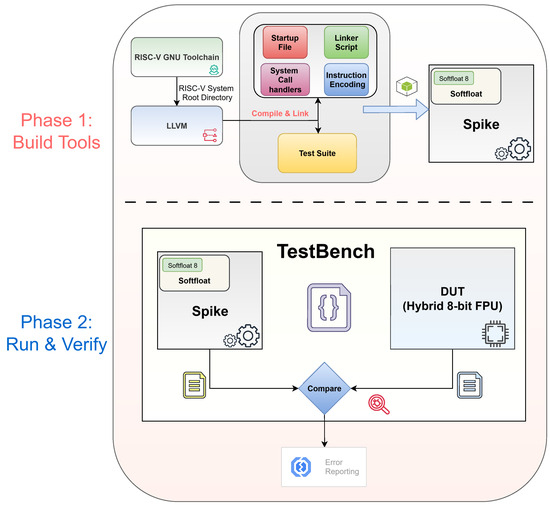
Figure 3.
Two-phase verification methodology with the integrated SoftFloat_8 extension.
- Building RISC-V compiler toolchains: To start, the RISC-V GNU Compiler Collection (GCC) toolchain was built for BareMetal RV64 architectures, which are systems without an operating system. However, GCC does not automatically generate RVV instructions. To overcome this limitation, GCC was used as a bootstrap compiler to build a second toolchain that supports RVV. Specifically, GCC served as the foundation for creating an LLVM-based Clang compiler by providing its system root directory to LLVM. Clang, unlike GCC, supports the RVV extension and uses the GCC system root to locate the required headers, libraries, and RISC-V-specific files needed for compilation.
- Test Suite: A thorough C test was developed with inline RISC-V RVV assembly instructions to test the vector 8-bit floating-point operations. A comprehensive verification of all operations was selected, as it was feasible to test every possible case for each operation and FP8 format in real-time. This approach ensured full coverage, rigorously examining all edge cases and typical scenarios to guarantee the accuracy and reliability of the implementation across all possible inputs and operations. For single-operand operations, the total number of tests per operation is 256. For two-operand operations, the total number of tests per operation is 65,536. For fused multiply–add operations that require three operands, the total number of tests per operation is or 16M.
- Linking for BareMetal: To enable a seamless operation of C programs in a BareMetal RISC-V environment, without the need for deploying a full operating system, a set of files provide macro definitions for handling RISC-V instructions, implementations of basic system call handlers for input/output and memory management, and a linker script that sets up the memory layout for the program. Additionally, the files include assembly code that handles system initialization and startup sequences, ensuring the environment is properly set up for executing C code.
- Test bench: A test bench runs Spike executing the Test Suite with the Device Under Test (DUT) being the hybrid FPU, comparing the output results for all sets of input cases for every operation and testing all rounding modes. Any mismatch is reported back to the user, whether it is a mismatch in the result or in the flag output.
Table 7 lists the FP8 vector instructions implemented in Spike and the input-space coverage exercised by the conformance tests. The “# values” column reports, for each instruction, the cardinality of the operand tuples exhaustively enumerated (unary: 256; binary: 65K; fused ternary: 16M) per rounding mode when applicable.

Table 7.
FP8 vector instructions and corresponding input-space coverage used in verification.
Host-Time Throughput, Memory Footprint, and Binary Size
Beyond functional conformance of the FP8 operations in the verification environment of Figure 3, we also characterize the simulator from a host-time perspective. The goal is to quantify end-to-end throughput (elements per second) and runtime memory footprint (Resident Set Size or RSS) under realistic vector kernels, using the same toolchain and DUT setup. In the following, VLEN denotes the architectural vector register length.
We measure throughput and RSS by running vector micro-kernels that execute vfadd.vv, vfsub.vv, and vfmul.vv over in-memory buffers with no I/O in the hot path. The benchmark sets VLEN = 1024, processes len = 1,048,576 elements per iteration, and repeats for iters = 1000. Each configuration is executed three times and we report medians. Execution is pinned to one core with taskset -c 2. FP8 format is selected at runtime with –vfp8 = 1 (E4M3) and –vfp8 = 2 (E5M2), while the binary is compiled with -DVTYPE = ‘C’ for FP8, -DVTYPE = ‘S’ for FP16, and -DVTYPE = ‘F’ for FP32. To keep the vector configuration identical across types, all runs enable zvl4096b in Spike: –isa = rv64gcv_zvl4096b for FP8/FP32 and –isa = rv64gcv_zvfh_zvl4096b for FP16. The vv instruction variant is used throughout.
Table 8 reports the median elements per second and, for completeness, the retired-instruction count and elapsed time for each operation and type; Table 9 reports the median RSS measured with /usr/bin/time -v. Figure 4 complements the table by plotting elements per second normalized to the FP32 baseline (higher is better), while Figure 5 shows RSS normalized to the FP32 baseline (lower is better).

Table 8.
Host-time throughput with medians over three runs on vfadd.vv, vfsub.vv, and vfmul.vv (VLEN = 1024, len = 1,048,576, iters = 1000); we also report the retired-instruction count and elapsed time.

Table 9.
Runtime memory footprint (RSS, MB; median of three runs) measured with /usr/bin/time -v.
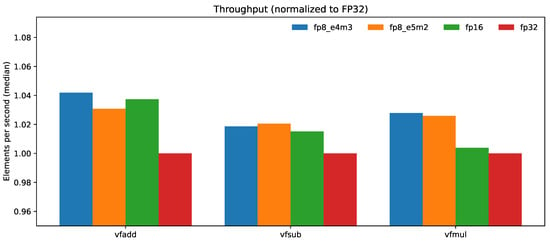
Figure 4.
Throughput normalized to FP32 (elements per second; higher is better) for vfadd.vv, vfsub.vv, and vfmul.vv across FP8 (E4M3/E5M2) and FP16 at identical VLEN (zvl4096b).
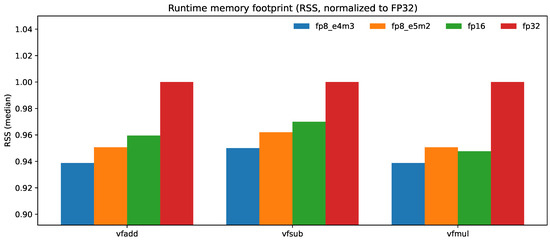
Figure 5.
Runtime memory footprint normalized to FP32 (RSS; lower is better) for vfadd.vv, vfsub.vv, and vfmul.vv.
With identical vector settings, FP8 sustains a small but consistent throughput advantage over FP32 across all three kernels while also using less host memory: (i) FP8 E4M3 is +4.19% (vfadd), +1.87% (vfsub), and +2.79% (vfmul) versus FP32; (ii) FP8 E5M2 is +3.08%, +2.05%, and +2.59% versus FP32, respectively; (iii) FP16 lands between FP32 and FP8 (+3.74%, +1.52%, +0.39% for vfadd, vfsub, vfmul). Median RSS improves by ≈5–6% for FP8 E4M3 (e.g., 9.50 MB vs. 10.12 MB on vfadd/vfmul) and by ≈4–5% for FP8 E5M2; FP16 reduces RSS by ≈3–5% relative to FP32. Finally, E4M3 and E5M2 are within of each other in elements per second across all three ops, indicating that format choice does not materially impact host-time throughput for these memory-resident kernels.
We also report the binary size overhead of enabling FP8 support in Spike. Two simulator binaries are built from the same commit and toolchain: a baseline build without FP8 support and a build with FP8 support enabled. Executable and section sizes are measured with standard tools (ls -l, du -h, size, readelf -S). Table 10 lists the indicators.

Table 10.
Spike binary size with and without FP8 support (stripped executables; MB computed as bytes).
As summarized in Table 10, the stripped on-disk executable grows from 7.618 MB to 7.754 MB (+1.795%), while the code section (.text) increases from 5.602 MB to 5.728 MB (+2.236%). Read-only data (.rodata) rises slightly (+1.588%), and initialized/uninitialized data sections (.data/.bss) are unchanged at the kilobyte level. These deltas are consistent with adding FP8 decode/encode and arithmetic paths primarily to .text, with small lookup/constant additions in .rodata; they do not materially affect global data. For completeness, the unstripped binaries move from 178.13 MB to 179.35 MB (+0.68%), where most of the absolute size is dominated by debug/symbol sections rather than code.
5. Conclusions
The presented integration makes the Spike simulator the first to support arithmetic operations on 8-bit floating-point formats, as well as the first RISC-V simulator to implement 8-bit floating-point operations. The modified simulator has been made available as open-source on GitHub [26], starting as a fork from the master branch of the original Spike repository. The enhanced Spike simulator was also employed to verify the floating-point implementation for an 8-bit FPU developed as part of the eProcessorEuropean project, demonstrating its practical application and robustness.
In addition, we provide a concise numerical study that quantifies FP8 accuracy—reporting relative-error and ULP distributions for E4M3 and E5M2—which confirms conformance to the standards and clarifies edge-case behavior (e.g., subnormals, NaNs). From a host-time perspective, FP8 sustains a small but consistent throughput advantage over FP32 (+2–4% elements per second across vfadd/vfsub/vfmul) while reducing median runtime memory footprint by about 5%; E4M3 and E5M2 perform similarly. Enabling FP8 in Spike incurs a modest distribution footprint increase in the stripped executable (~1.8%), concentrated in .text.
Ultimately, maintaining these enhancements as an open-source resource not only encourages further improvements to the RISC-V simulator but also provides a solid foundation for integrating additional custom extensions in the future. This collaborative environment can significantly streamline the verification process for emerging RISC-V processors, fostering innovation and enabling more efficient hardware development across the community.
Author Contributions
Conceptualization, A.C., A.M. (Antonio Mastrandrea) and M.O.; methodology, A.M. (Andrea Marcelli) and A.M. (Antonio Mastrandrea); software, A.M. (Andrea Marcelli); validation, A.C. and A.M. (Andrea Marcelli); formal analysis, A.C.; investigation, A.M. (Antonio Mastrandrea) and M.B.; resources, M.B. and F.M.; data curation, A.C. and M.B.; writing—original draft preparation, A.M. (Andrea Marcelli) and A.C.; writing—review and editing, M.O. and A.M. (Andrea Marcelli); visualization, A.C., A.M. (Andrea Marcelli) and M.O.; supervision, M.O. and F.M.; project administration, M.O.; funding acquisition, M.O. and F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European High-Performance Computing Joint Undertaking (JU) grant number 956702 “eProcessor” project.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FP | Floating Point |
| FP8 | 8-bit Floating Point |
| AI | Artificial Intelligence |
| TPU | Tensor Processing Unit |
| GPU | Graphics Processing Unit |
| ISA | Instruction Set Architecture |
| OCP | Open Compute Project |
| LLM | Large Language Model |
| E4M3 | 4-bit Exponent, 3-bit Mantissa |
| E5M2 | 5-bit Exponent, 2-bit Mantissa |
| vsew | Vector Standard Element Width |
| GCC | GNU Compiler Collection |
| VPU | Vector Processing Unit |
| FPU | Floating-Point Unit |
| DUT | Device Under Test |
| RSS | Resident Set Size |
| Inf | Infinity Values |
References
- NVIDIA Corporation. Mixed Precision Training. Nvidia.com. Available online: https://docs.nvidia.com/deeplearning/performance/mixed-precision-training/index.html (accessed on 11 January 2025).
- Kaz, S.; Cliff, Y. An In-Depth Look at Google’s First Tensor Processing Unit (TPU). Google.com. Available online: https://cloud.google.com/blog/products/ai-machine-learning/an-in-depth-look-at-googles-first-tensor-processing-unit-tpu (accessed on 11 January 2025).
- Neta, Z.; Hao, W.; Jay, R. Achieving FP32 Accuracy for INT8 Inference Using Quantization Aware Training with NVIDIA TensorRT 2021. Available online: https://developer.nvidia.com/blog/achieving-fp32-accuracy-for-int8-inference-using-quantization-aware-training-with-tensorrt/ (accessed on 11 January 2025).
- Choquette, J. Nvidia hopper h100 gpu: Scaling performance. IEEE Micro 2023, 43, 9–17. [Google Scholar] [CrossRef]
- Andrew, W. RISC-V Unprivileged Specifications. riscv.org. Available online: https://riscv.org/specifications/ratified/ (accessed on 11 January 2025).
- Hauser, J.R. Berkeley SoftFloat 3e. Github.com. Available online: https://github.com/ucb-bar/berkeley-softfloat-3 (accessed on 11 January 2025).
- IEEE Std 754-2019; IEEE Standard for Floating-Point Arithmetic. IEEE Computer Society: Washington, DC, USA, 2019. [CrossRef]
- Micikevicius, P.; Schulte, M. OCP 8-bit Floating Point Specification (OFP8), Revision 1.0; Technical Specification Revision 1.0 (2023-12-01); Open Compute Project: Austin, TX, USA, 2023. [Google Scholar]
- Software, R.V. Spike RISC-V ISA Simulator. Github.com. Available online: https://github.com/riscv-software-src/riscv-isa-sim (accessed on 6 June 2025).
- Quiroga, J.; Roberto Ignacio, G.; Ivan, D.; Henrique, Y.; Asif, A.; Nehir, S.; Óscar, P.; Pérez, V.J.; Mario, R.; Marc, D. Reusable Verification Environment for a RISC-V Vector Accelerator. In Proceedings of the Design and Verification Conference & Exhibition Europe (DVCon Europe) 2022, Munich, Germany, 6–7 December 2022; Accellera Systems Initiative (Accellera): Elk Grove, CA, USA, 2023. [Google Scholar]
- Micikevicius, P.; Stosic, D.; Burgess, N.; Cornea, M.; Dubey, P.; Grisenthwaite, R.; Ha, S.; Heinecke, A.; Judd, P.; Kamalu, J.; et al. Fp8 formats for deep learning. arXiv 2022, arXiv:2209.05433. [Google Scholar] [CrossRef]
- IntelLabs. FP8 Emulation Toolkit. Github.com. Available online: https://github.com/IntelLabs/FP8-Emulation-Toolkit (accessed on 6 June 2025).
- Intel. Intel Advanced Vector Extensions 10.2 (Intel AVX10.2) Architecture Specification, 2025. Version 5.0. Available online: https://www.intel.com/content/www/us/en/content-details/855340/intel-advanced-vector-extensions-10-2-intel-avx10-2-architecture-specification.html (accessed on 9 July 2025).
- NVIDIA. Transformer Engine. Github.com. Available online: https://github.com/NVIDIA/TransformerEngine (accessed on 6 June 2025).
- Liu, C.; Zhang, X.; Zhang, R.; Li, L.; Zhou, S.; Huang, D.; Li, Z.; Du, Z.; Liu, S.; Chen, T. Rethinking the Importance of Quantization Bias, Toward Full Low-Bit Training. IEEE Trans. Image Process. 2022, 31, 7006–7019. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Choi, J.; Chen, C.Y.; Wang, N.; Venkataramani, S.; Srinivasan, V.; Cui, X.; Zhang, W.; Gopalakrishnan, K. Hybrid 8-bit floating point (HFP8) training and inference for deep neural networks. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019. [Google Scholar]
- Shen, H.; Mellempudi, N.; He, X.; Gao, Q.; Wang, C.; Wang, M. Efficient Post-training Quantization with FP8 Formats. In Proceedings of the Machine Learning and Systems, Santa Clara, CA, USA, 13–16 May 2024; Gibbons, P., Pekhimenko, G., Sa, C.D., Eds.; MLSys Proceedings: Indio, CA, USA, 2024; Volume 6, pp. 483–498. [Google Scholar]
- Nesam, J.J.J.; Ganesh, S.S.; Ramachandran, S. Effect of bit-size reduced half-precision floating-point format on image pixel characterization for AI applications. Results Eng. 2024, 24, 103179. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Hu, E.; Wang, A.; Shiri, B.; Lin, W. VNDHR: Variational Single Nighttime Image Dehazing for Enhancing Visibility in Intelligent Transportation Systems via Hybrid Regularization. IEEE Trans. Intell. Transp. Syst. 2025, 26, 10189–10203. [Google Scholar] [CrossRef]
- Li, H.; Lu, H.; Li, X. Mortar-FP8: Morphing the Existing FP32 Infrastructure for High-Performance Deep Learning Acceleration. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2024, 43, 878–891. [Google Scholar] [CrossRef]
- Tagliavini, G.; Mach, S.; Rossi, D.; Marongiu, A.; Benini, L. A transprecision floating-point platform for ultra-low power computing. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 1051–1056. [Google Scholar] [CrossRef]
- Lee, J.; Bae, J.; Kim, B.; Kwon, S.J.; Lee, D. To FP8 and Back Again: Quantifying the Effects of Reducing Precision on LLM Training Stability. CoRR, 2024; in press. [Google Scholar]
- Fishman, M.; Chmiel, B.; Banner, R.; Soudry, D. Scaling FP8 training to trillion-token LLMs. In Proceedings of the Thirteenth International Conference on Learning Representations, Singapore, 24–28 April 2025. [Google Scholar]
- Peng, H.; Kan, W.; Yixuan, W.; Guoshuai, Z.; Yuxiang, Y.; Ze, L.; Yifan, X. Fp8-lm: Training fp8 large language models. arXiv 2023, arXiv:2310.18313. [Google Scholar] [CrossRef]
- eProcessor. eProcessor Website. Available online: https://eprocessor.eu/ (accessed on 6 June 2025).
- Klessydra. Spike RISC-V ISA Simulator with Support for Minifloat. Github.com. Available online: https://github.com/klessydra/spike-with-minifloat-fp8-support (accessed on 20 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).