Boosting Clean-Label Backdoor Attacks on Graph Classification

Abstract

Graph Neural Networks (GNNs) have become a cornerstone for graph classification, yet their vulnerability to backdoor attacks remains a significant security concern. While clean-label attacks provide a stealthier approach by preserving original labels, they tend to be less effective in graph settings compared to traditional dirty-label methods. This performance gap arises from the inherent dominance of rich, benign structural patterns in target-class graphs, which overshadow the injected backdoor trigger during the GNNs’ learning process. We demonstrate that prior strategies, such as adversarial perturbations used in other domains to suppress benign features, fail in graph settings due to the amplification effects of the GNNs’ message-passing mechanism. To address this issue, we propose two strategies aimed at enabling the model to better learn backdoor features. First, we introduce a long-distance trigger injection method, placing trigger nodes at topologically distant locations. This enhances the global propagation of the backdoor signal while interfering with the aggregation of native substructures. Second, we propose a vulnerability-aware sample selection method, which identifies graphs that contribute more to the success of the backdoor attack based on low model confidence or frequent forgetting events. We conduct extensive experiments on benchmark datasets such as NCI1, NCI109, Mutagenicity, and ENZYMES, demonstrating that our approach significantly improves attack success rates (ASRs) while maintaining a low clean accuracy drop (CAD) compared to existing methods. This work offers valuable insights into manipulating the competition between benign and backdoor features in graph-structured data.

1. Introduction

Graph classification plays a fundamental role in numerous real-world applications, including molecular property prediction [1], protein function recognition [2], social network analysis [3], and financial risk control [4]. With the rapid development of GNNs [5,6], graph classification has achieved remarkable progress in terms of both accuracy and scalability. However, this progress is increasingly accompanied by new security risks. Among them, backdoor attacks [7,8,9] have emerged as a particularly insidious threat. By inserting a small number of poisoned samples embedded with predefined triggers into the training set, adversaries can induce the model to misclassify any trigger-containing graph into a target class, without degrading its performance on clean inputs. The highly stealthy and targeted nature of such attacks poses serious challenges to the safe deployment of GNN-based graph classification systems.

Most existing backdoor attacks on graph classification adopt the dirty-label paradigm, where the label of a poisoned sample is forcibly changed to the attacker’s target class. Although this approach typically yields high ASRs, the mismatch between the injected label and the inherent characteristics of the graph introduces an abnormal pattern that tends to be easily identified during data auditing. To enhance stealthiness, recent work has shifted attention to clean-label backdoor attacks [10,11,12], which retain the original labels and thus avoid explicit label inconsistency. However, prior studies have reported that clean-label attacks are generally less effective than dirty-label ones [13,14]. A key reason is that unlike dirty-label attacks, where relabeling provides explicit supervision linking the trigger to the target class, clean-label attacks preserve original labels and thus offer weaker guidance for the model to learn the trigger–label association. In this work, we further investigate this gap and reveal that the suppression of backdoor signals by dominant benign structures is a critical factor underlying the reduced effectiveness of clean-label attacks in graph classification. Following Xu et al. [13], we adopt the Erőos–Rényi (ER) subgraph trigger from [13] as our base trigger design; our goal is to improve its effectiveness under clean-label constraints without changing the trigger type.

To mitigate this competition between benign and malicious patterns, previous work in the vision domain [15] introduced adversarial perturbations to weaken the original features before trigger injection. Inspired by this, we attempted a similar strategy in graph classification by performing a gradient ascent over the adjacency matrix. Contrary to expectations, this approach failed to improve performance and even resulted in negative gains. We hypothesize that the root cause lies in the recursive message-passing mechanism of GNNs: structural perturbations are amplified through repeated aggregation, leading the model to erroneously learn the perturbation as part of the trigger. At inference time, omitting these perturbations renders the trigger incomplete, while retaining them compromises stealthiness.

In light of these challenges, we discard adversarial perturbation and instead aim to disrupt the native feature propagation mechanisms of GNNs. To this end, we introduce a novel trigger injection strategy that departs from prior random selection schemes by deliberately placing trigger nodes at topologically distant locations. This design maximizes the structural dispersion of the trigger, allowing its signals to propagate along diverse paths. Importantly, such dispersed placement not only amplifies the global presence of the backdoor signal, but also interferes with the propagation pathways of benign features, thereby disrupting the aggregation of native substructures. As a result, the model’s reliance on these benign patterns is diminished, while its sensitivity to the injected trigger is enhanced, leading to improved attack effectiveness under clean-label constraints.

Moreover, we observe that existing attacks typically overlook sample-level variability, assuming uniform susceptibility across training graphs. In practice, graph instances exhibit diverse levels of structural complexity and feature expressiveness, affecting their vulnerability to backdoor manipulation. To address this, we further incorporate two vulnerability-aware sample selection strategies: one based on model confidence, which targets graphs with low prediction certainty, and another based on forgetting events, which identifies unstable samples that are frequently misclassified during training. Both approaches isolate “weak” samples that are more likely to be influenced by the trigger, improving the efficiency and success rate of the attack.

Our main contributions are as follows.

• We thoroughly analyze the shortcomings of existing clean-label backdoor attacks on GNNs, identifying the underlying cause as the feature competition between benign graph structures and injected triggers. Additionally, we demonstrate why prior solutions, such as adversarial perturbation, fail in graph classification due to the amplification effects of the GNNs’ message-passing mechanism.
• We introduce a novel long-distance trigger injection strategy, in which trigger nodes are placed at topologically distant locations. This approach disrupts the aggregation of benign substructures and promotes the global propagation of the backdoor signal, improving its effectiveness.
• We propose two vulnerability-aware sample selection strategies to efficiently identify graphs that have a greater impact on the success of the backdoor attack. The first strategy focuses on low model confidence, while the second relies on frequent forgetting events.
• We perform extensive experiments on four widely used benchmark datasets (NCI1, NCI109, Mutagenicity, and ENZYMES). The results demonstrate that our method significantly enhances the ASR in clean-label settings while maintaining a low CAD.

The remainder of this paper is structured as follows. Section 2 provides a review of related work on backdoor attacks in graph classification. Section 3 presents the preliminaries on GNNs and defines the threat model. Section 4 addresses the core challenges of clean-label attacks on graphs, focusing on feature competition and the failure of adversarial perturbation techniques. Section 5 details our proposed strategies for Long-distance Injection and vulnerable sample selection. Section 6 presents experimental results and analysis. Finally, Section 7 concludes the paper.

2. Related Work

2.1. Dirty-Label Backdoor Attacks for Graph Classification

Early studies on backdoor attacks for graph classification primarily adopted the dirty-label paradigm, where the adversary simultaneously injected triggers into training graphs and modified their labels to a target class. Zhang et al. [16] first showed that implanting fixed subgraph structures into a subset of training graphs could induce a GNN to associate these substructures with a target label, enabling targeted misclassification at inference. Subsequent works explored various aspects of trigger design and injection. For example, Xu et al. [17] analyzed the spatial sensitivity of trigger placement and employed GNNExplainer to identify the least important nodes for subgraph trigger injection, although the performance gains were limited. To improve adaptability, Xi et al. [18] proposed generative models to produce structural triggers with a fixed size but diverse topologies, thereby enhancing both variability and evasiveness. Yang et al. [19] introduced perturbation-aware triggers, where meta-gradients derived from adjacency matrices guided structural manipulations. Zheng et al. [20] further investigated motif-level backdoor patterns, systematically analyzing how different semantic substructures influenced attack success rates.

Overall, dirty-label methods in graph classification generally achieve high ASRs. However, label manipulation creates inconsistencies between labels and graph content, which makes such attacks easier to detect. To improve stealth, recent research has shifted toward clean-label settings.

2.2. Clean-Label Backdoor Attacks for Graph Classification

The clean-label paradigm preserves the original labels while injecting triggers, thereby achieving improved evasiveness. Compared with the image domain, this direction remains underexplored in graph classification. Xu et al. [13] employed an Erdős–Rényi (ER) subgraph as a trigger, injecting it into randomly selected nodes of target-class samples, forming the basis for future work. More recently, Meguro et al. [14] proposed a gradient-based clean-label backdoor attack (CLBA) for graphs, leveraging gradient information to guide structural injection or modification without altering labels.

However, existing methods in both dirty-label and clean-label settings have typically assumed that all training samples are equally susceptible to poisoning, overlooking the inherent heterogeneity among graph instances. This oversight results in suboptimal sample efficiency, as it fails to prioritize graphs with greater contribution to backdoor success. Furthermore, although prior dirty-label studies have examined the impact of subgraph trigger injection locations, such strategies have shown limited effectiveness in clean-label scenarios. For example, the LIA (least important node-selecting attack) [17], which we include as a baseline, relies on node importance, whereas our strategy emphasizes global topological dispersion to strengthen trigger propagation. Motif-based approaches [20], on the other hand, aim to identify what kinds of trigger structures are most effective, while our work keeps the ER subgraph fixed and instead focuses on improving its effectiveness through new placement and selection strategies. Motivated by these observations, we adopt the ER subgraph trigger from [13] and focus on studying strategies to improve attack performance.

3. Preliminaries and Problem Definition

3.1. Graph Classification and GNNs

In graph classification, the input is a set of graphs $\mathcal{G}=\{G_1,G_2,\dots ,G_M\}$, where each graph $G=(\mathcal{V},\mathcal{E},X)$ consists of a node set $\mathcal{V}$, an edge set $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$, and a node feature matrix $X={\left[x_v\right]}_{v\in \mathcal{V}}\in {\mathbb{R}}^{\left|\mathcal{V}\right|\times d}$. The objective is to learn a mapping $f:G\to y_G$ that assigns a categorical label $y_G$ to each graph based on both its topological structure and node attributes.

Graph Neural Networks (GNNs) are widely used for this task due to their ability to integrate multi-hop structural dependencies via neighborhood message passing. At the l-th layer, the embedding of node v is updated by aggregating information from its neighbors $\mathcal{N}\left(v\right)$ and combining it with its current representation:

$$h_v^{\left(l\right)}={\mathrm{UPDATE}}^{\left(l\right)}\left(h_v^{(l-1)},{\mathrm{AGG}}^{\left(l\right)}\left(\left\{h_u^{(l-1)}\mid u\in \mathcal{N}\left(v\right)\right\}\right)\right),$$

(1)

where $h_v^{\left(0\right)}=x_v$, and ${\mathrm{AGG}}^{\left(l\right)}(·)$ and ${\mathrm{UPDATE}}^{\left(l\right)}(·)$ denote layer-specific aggregation and update functions.

After L layers of message passing, the final node embeddings $\left\{h_v^{\left(L\right)}\right\}$ are aggregated into a graph-level representation via a readout function:

$$z_G=\mathrm{READOUT}\left(\{h_v^{\left(L\right)}\mid v\in \mathcal{V}\}\right),$$

(2)

where $\mathrm{READOUT}(·)$ is typically implemented as mean, sum, or max pooling. The resulting graph representation $z_G$ is then passed through a classifier (e.g., an MLP) to produce the final prediction. This process follows a local message-passing stage (Equation (1)) followed by a global readout stage (Equation (2)), enabling graph-level inference.

3.2. Problem Definition

3.2.1. Attacker’s Knowledge and Capability

We consider a black-box adversarial setting in which the attacker has no access to the architecture, parameters, gradients, or training procedure of the victim model. However, the attacker can observe the entire clean training dataset, including both the structures and labels of all training graphs. Using this accessible data, the attacker may train a local surrogate model to approximate the victim model’s behavior and guide the design of backdoor triggers. This assumption is consistent with prior studies on graph backdoor attacks [7,13,14,16].

Under the clean-label constraint, the attacker may inject triggers by modifying the structure and/or features of training samples that already belong to the target class, without altering their original labels. This enhances the attack’s evasiveness by preserving label–content consistency.

3.2.2. Attack Objective

Let F denote the backdoored graph classifier trained on a poisoned dataset, $y_t$ the attacker-specified target class, and $g_t$ a predefined trigger. We use $G\oplus g_t$ to represent the structural and/or feature-wise injection of trigger $g_t$ into graph G. The attacker aims to satisfy the following two conditions:

$$\left\{\begin{array}{cc}F(G\oplus g_t)=y_t,\hfill & \forall G\in {\mathcal{D}}_{\mathrm{clean}},\hfill \\ F\left(G\right)=F_o\left(G\right),\hfill & \forall G\in {\mathcal{D}}_{\mathrm{clean}},\hfill \end{array}\right.$$

(3)

where ${\mathcal{D}}_{\mathrm{clean}}$ denotes the clean test distribution and $F_o$ denotes a reference model trained solely on unpoisoned data.

The first condition ensures attack effectiveness: the backdoored model F misclassifies any trigger-containing input as the target label $y_t$, independent of its original class. The second condition ensures attack evasiveness: the model behaves identically to the clean model $F_o$ on benign inputs, thereby avoiding detection.

4. Revisiting Clean-Label Backdoor Attacks in Graph Classification

4.1. Feature Competition: Benign vs. Backdoor Signals

The effectiveness of clean-label backdoor attacks depends on how the model balances attention between benign features and backdoor signals during training. In poisoned samples, both coexist and point to the same label, creating a feature competition. The attack succeeds only when backdoor features become dominant enough to override benign ones.

This phenomenon is especially pronounced in graph classification, where GNNs learn semantically stable local structures such as functional motifs through multi-hop message passing. In clean-label attacks, triggers are injected only into target-class samples without label modification. However, these graphs often contain rich, highly learnable native structures. Small, context-free backdoor subgraphs yield relatively weak signals and are easily ignored by the model.

From an optimization perspective, GNNs minimize overall training loss by exploiting frequently occurring, label-correlated native structures. Since backdoor patterns are rare and semantically ambiguous, the model has little incentive to learn them explicitly. Consequently, their influence is weakened during message passing and fails to form robust representations.

To empirically validate this, we evaluate the impact of trigger size on attack success. Using the NCI1 dataset, we generate ER subgraphs of varying sizes as triggers and inject them into target-class samples under a fixed poisoning rate of 10%. A GCN [21] is trained on the poisoned data, with trigger sizes ranging from 10% to 50% of the average graph size. The results in Figure 1 show that larger triggers yield higher ASRs by increasing the relative proportion of backdoor signals and reducing the influence of native structures. However, overly large triggers disrupt the original topology and cause structural anomalies, compromising stealth.

This experiment reveals a fundamental trade-off: there is an inherent tension between attack efficacy and stealthiness. These findings motivate the search for strategies that enhance the expressiveness of small triggers without noticeably increasing their size, which we pursue in the following sections.

Before introducing our proposed approach, we first revisit an existing technique—adversarial perturbation—that has been effective in other domains, to examine whether it can serve as a viable solution to the feature competition challenge in graph classification.

4.2. Limitations of Adversarial Perturbation in Graph Classification

To address the feature competition challenge, we first explore adversarial perturbation—a technique shown to improve clean-label backdoor attacks in video recognition [15]. The idea is to perturb inputs via gradient ascent before trigger injection, suppressing dominant semantic features so that the model relies more on the trigger during learning.

We adapt this to graphs by applying structural perturbations prior to injection. Node features remain unchanged due to their discrete nature, while edges are flipped to maximize training loss under the true label. We follow the setup in Section 4.1 with the perturbation budget set to 10% of the average number of nodes. During training, we apply perturbations, then inject the trigger. At inference, perturbations are removed.

As shown in Figure 2, this approach significantly reduces the ASR, indicating that it fails to improve performance. We attribute this to a perturbation-as-feature effect: in graphs, each edge flip is a high-impact local change whose influence propagates through message passing. These perturbations are not merely weakening benign patterns, but are themselves learned as salient features. When removed at inference, the learned trigger pattern becomes incomplete, degrading attack success.

To verify this, we retain perturbations at inference. The ASR then recovers and slightly surpasses using the trigger alone, confirming that perturbations become part of the learned backdoor. However, this contradicts the intended use of perturbations as a temporary enhancement mechanism and effectively increases the trigger size, reducing stealth.

In summary, while adversarial perturbation can be effective in continuous domains, its direct transfer to graph classification faces intrinsic challenges. Achieving both high efficacy and stealth in this setting requires designs tailored to the discrete and structural properties of graph data, as will be introduced in Section 5.

5. Strategy Design

Building on our earlier analysis of feature competition in Section 4, we observe that the strong inductive bias of GNNs toward native semantic structures limits the effectiveness of clean-label backdoor attacks. To address this challenge, we propose two complementary strategies that target distinct yet interrelated aspects of the attack: trigger injection and poisoned sample selection. Together, these strategies aim to weaken the dominance of benign structural signals and enhance the expressiveness and impact of backdoor triggers.

5.1. Trigger Injection Strategy

We introduce a Long-distance Trigger Injection strategy to simultaneously amplify the global propagation of backdoor signals and disrupt the aggregation of benign features. The key idea is to select k topologically distant nodes as trigger insertion points. This design achieves two objectives:

1.

Enhancing global backdoor signal coverage: Dispersed trigger nodes propagate their influence along multiple, largely disjoint paths during message passing, creating globally consistent and salient backdoor features.

2.

Disrupting benign feature aggregation: Distant trigger placement increases the likelihood of interfering with multiple semantic substructures, perturbing their propagation pathways and elevating the relative importance of backdoor patterns in the learned representation.

Identifying the exact k mutually farthest nodes is an NP-hard combinatorial optimization problem, requiring exhaustive enumeration of all possible node subsets and pairwise shortest-path distances. To achieve a practical balance between effectiveness and efficiency, we adopt a greedy heuristic with linear-time complexity $O\left(k\right(\left|V\right|+\left|E\right|\left)\right)$, where $\left|V\right|$ and $\left|E\right|$ denote the number of nodes and edges, respectively.

The procedure begins by randomly selecting an initial node $v_1$ with the lowest degree (0-degree nodes are removed in preprocessing). Such low-degree nodes often lie on the periphery of the graph, providing better spatial dispersion. We then iteratively select a node $v_j$ from the remaining pool that maximizes the minimum shortest-path distance to all previously selected nodes $V_{\mathrm{selected}}$:

$$d(v_j,V_{\mathrm{selected}})=\underset{v_i\in V_{\mathrm{selected}}}{min}d(v_j,v_i),$$

(4)

where $d(·,·)$ denotes the shortest-path distance. This process repeats until k nodes are selected, after which the trigger pattern $g_t$ is injected at these locations.

5.2. Vulnerable Sample Selection

Beyond the injection location, the choice of which samples to poison significantly influences backdoor learning. Existing methods often assume uniform vulnerability across training graphs, overlooking the heterogeneity in structural robustness and feature expressiveness. Graphs with rich, stable semantics are generally resistant to backdoor influence, whereas those with ambiguous structures or weakly correlated features—termed vulnerable samples—are more susceptible to manipulation.

We design two strategies to identify such vulnerable samples within the target class under the clean-label constraint: a Confidence-driven method based on static model uncertainty, and a Forgetting-driven method based on dynamic learning instability.

5.2.1. Confidence-Driven Selection

This method leverages the intuition that low-confidence predictions indicate weak or ambiguous benign features. We first train a GCN surrogate model $F_{\mathrm{proxy}}$ on the clean training set, then compute the softmax confidence for each sample in the target class. The $p\%$ of samples with the lowest confidence scores are selected for poisoning, as they are less distinguishable by their native structures and thus more likely to be influenced by the injected trigger.

5.2.2. Forgetting-Driven Selection

The second method draws on the concept of forgetting events [22,23], defined as instances where a sample transitions from being correctly classified to misclassified during training. Formally, let ${\widehat{y}}_t^{\mathrm{epoch}}$ denote the predicted label of sample t at a given training epoch, and $y_t$ its ground-truth label. A forgetting event occurs at epoch e if

$$\mathbb{I}\{{\widehat{y}}_t^{\mathrm{epoch}-1}=y_t\wedge {\widehat{y}}_t^{\mathrm{epoch}}\ne y_t\},$$

(5)

where $\mathbb{I}\{·\}$ denotes the indicator function, returning 1 if the condition is satisfied and 0 otherwise.

The forgetting count of a sample is the total number of such events across training epochs. A high forgetting count suggests that the model struggles to establish a stable decision boundary for that sample, indicating structural or semantic ambiguity.

We train the same GCN surrogate and track forgetting events throughout the training process. The $p\%$ most frequently forgotten samples within the target class are selected for poisoning. Unlike the confidence-based approach, this method captures temporal instability in the learning process, providing a dynamic and fine-grained vulnerability measure.

5.3. Unified Backdoor Injection Procedure

The complete attack pipeline integrates vulnerability-aware sample selection with the long-distance trigger injection strategy. As summarized in Algorithm 1, Stage I identifies vulnerable samples using either the confidence-based or forgetting-based criterion, while Stage II injects the trigger pattern into these selected graphs at topologically distant locations.

Algorithm 1 Backdoor Injection Strategy for Graph Classification

Require:  Clean training set $\mathcal{G}$, target class $y_t$, poisoning rate $p\%$, trigger pattern $g_t$, number of trigger nodes k Ensure:  Poisoned dataset ${\mathcal{G}}^{\mathrm{poisoned}}$   1: Stage I: Vulnerable Sample Selection   2: Train a GCN surrogate model $F_{\mathrm{proxy}}$ on $\mathcal{G}$   3: for each $G\in \mathcal{G}$ with label $y_t$ do   4:    Compute vulnerability score: low confidence or high forgetting count   5: end for   6: Select the $p\%$ most vulnerable samples as ${\mathcal{G}}_{\mathrm{poison}}$   7: Stage II: Long-distance Trigger Injection   8: for each $G\in {\mathcal{G}}_{\mathrm{poison}}$ do   9:    Remove isolated nodes in G to ensure trigger propagation 10:    Initialize $V_{\mathrm{selected}}\leftarrow \left\{v_1\right\}$, where $v_1$ is a random low-degree node 11:    for $j=2$ to k do 12:        For each unselected node $v\notin V_{\mathrm{selected}}$, compute $d_{min}\left(v\right)={min}_{v_i\in V_{\mathrm{selected}}}d(v,v_i)$ 13:        Select $v_j={argmax}_{v\notin V_{\mathrm{selected}}}{d}_{min}\left(v\right)$ 14:        $V_{\mathrm{selected}}\leftarrow V_{\mathrm{selected}}\cup \left\{v_j\right\}$ 15:    end for 16:    Inject trigger $g_t$ into G at $V_{\mathrm{selected}}$ 17: end for 18: return ${\mathcal{G}}^{\mathrm{poisoned}}$

5.4. Complexity Analysis

Before presenting the experimental results, we briefly analyze the computational complexity of our proposed method. Let M denote the number of training graphs, $\overline{\left|V\right|}$ and $\overline{\left|E\right|}$ the average number of nodes and edges per graph, $p\%$ the poisoning rate, k the number of trigger nodes, and num_epochs the number of training epochs.

For the Confidence-driven selection strategy, the main cost comes from training the surrogate GCN on the clean dataset, which requires $O(\mathtt{num}\_\mathtt{epochs}·M·\overline{\left|E\right|})$ time, as message passing is proportional to the number of edges. After training, computing confidence scores for all target-class graphs costs $O(M·\overline{\left|E\right|})$, and selecting the lowest-confidence $p\%·M$ samples costs $O\left(M\right)$.

For the Forgetting-driven selection strategy, the surrogate training cost is the same as in the Confidence-driven method. During training, we additionally track the correctness status and forgetting counts for each sample, which adds $O\left(M\right)$ time and space overhead. Selecting the top $p\%·M$ most-forgotten samples also requires $O\left(M\right)$ time.

For the long-distance trigger injection stage, each poisoned graph undergoes k iterations of farthest-node selection based on shortest-path distance computation, costing $O(\overline{\left|V\right|}+\overline{\left|E\right|})$ per iteration. The total injection cost is $O(p\%·M·k·(\overline{\left|V\right|}+\overline{\left|E\right|}))$, which is small compared to surrogate training.

Overall, in both selection strategies, surrogate model training dominates the total runtime, while the additional costs of vulnerability scoring and trigger injection are minor.

6. Experiments

6.1. Experimental Setup

6.1.1. Datasets

We evaluate our method on four widely used graph classification benchmarks:

• NCI1 and NCI109: Chemical compound datasets where graphs represent molecules, nodes correspond to atoms, and edges correspond to chemical bonds. The classification task is to predict whether a compound is active against specific cancer cells.
• Mutagenicity: A dataset of molecular graphs for predicting mutagenic properties, characterized by larger and more structurally diverse graphs.
• ENZYMES: A bioinformatics dataset containing protein tertiary structures, where the task is to classify each protein into one of six enzyme classes.

The statistics of the datasets are summarized in

Table 1. Statistics of the datasets.

Dataset	Graphs	Classes	Avg. Nodes	Avg. Edges
NCI1	4110	2	29.87	32.30
NCI109	4127	2	29.68	32.13
Mutagenicity	4337	2	30.32	30.77
ENZYMES	600	6	32.63	62.14

.

6.1.2. Evaluation Metrics

We use two metrics to assess both the effectiveness and evasiveness of backdoor attacks:

• ASR (Attack Success Rate): The percentage of poisoned test graphs containing the trigger that are misclassified into the attacker-specified target class. A higher ASR indicates a more effective attack.
• CAD (Clean Accuracy Drop): The absolute decrease in accuracy on clean (non-poisoned) test graphs compared to a clean model. A lower CAD indicates better evasiveness. A negative CAD means the poisoned model slightly outperforms the clean model on benign inputs, which can occur due to regularization effects from injected perturbations.

6.1.3. Baselines

We compare our method against the following baselines, using the same trigger pattern and poisoning rate for fairness:

• Random: Random selection of both samples and trigger node locations.
• LIA (least important node-selecting attack): Trigger nodes are placed on the least important nodes identified by a GNN explainer. Sample selection follows the same vulnerability-aware strategies as our method.
• Degree: Trigger nodes are placed on the lowest-degree nodes to minimize interference with benign patterns. Sample selection follows the same vulnerability-aware strategies as our method.

For all methods, the trigger pattern is an ER subgraph generated with the same parameters, ensuring consistency in trigger structure across experiments.

6.1.4. Parameter Settings

We use a GCN surrogate model to craft backdoor attacks and evaluate them against GCN and GIN target models. Both models have three graph convolution layers, a global mean pooling layer, and a final classifier, with 64 hidden dimensions and a dropout rate of 0.5. Training uses Adam with a learning rate of 0.01 for up to 200 epochs, and early stopping (patience 20, monitored on validation loss). Datasets are split into training/validation/test with an 8:1:1 ratio. Unless otherwise stated, the poisoning rate is 10% and the trigger size k is 5. Each experiment is repeated 10 times using random seeds from 30 to 39, and averages are reported. The ER trigger subgraphs are generated with an edge connection probability of 0.8. Isolated nodes are removed from graphs prior to injection, and mean pooling is used as the READOUT function. All experiments are conducted on an NVIDIA GeForce RTX 4070 Super GPU, and the implementation is based on PyTorch. Baseline clean accuracies are shown in

Table 2. Clean accuracy (%) of GCN and GIN on each dataset before poisoning.

Dataset	GCN	GIN
NCI1	70.41	72.32
NCI109	71.21	73.18
Mutagenicity	77.15	79.61
ENZYMES	35.00	36.67

.

6.2. Overall Performance

We compare our proposed Long-distance Injection (LD) strategy combined with two vulnerability-aware sample selection strategies—Confidence-driven (C) and Forgetting-driven (F)—against all baselines on both GCN and GIN target models. All triggers are ER-generated subgraphs with identical parameters.

As shown in

Table 3. Backdoor attack results on GCN (ASR% ↑/CAD% ↓). The bold values indicate the best performance.

Injection	Selection	NCI1		NCI109		Mutagenicity		ENZYMES
		ASR	CAD	ASR	CAD	ASR	CAD	ASR	CAD
Random	Random	58.84 ± 4.38	0.65 ± 0.94	63.25 ± 4.75	1.25 ± 1.13	47.87 ± 5.22	0.98 ± 1.21	21.53 ± 3.67	0.33 ± 0.72
LIA	C	67.59 ± 3.17	0.28 ± 1.03	78.32 ± 2.89	−0.34 ± 0.87	66.71 ± 4.19	−1.05 ± 1.24	28.36 ± 4.75	1.33 ± 0.90
	F	69.21 ± 2.78	1.21 ± 1.02	74.35 ± 3.67	1.29 ± 1.27	63.52 ± 4.01	1.09 ± 1.08	26.54 ± 4.58	0.67 ± 1.13
Degree	C	67.48 ± 2.36	1.35 ± 1.10	69.89 ± 3.45	1.40 ± 0.82	69.07 ± 2.95	1.22 ± 1.02	26.18 ± 4.91	−0.33 ± 1.34
	F	65.37 ± 3.27	−0.30 ± 0.97	70.34 ± 3.18	−0.83 ± 0.65	68.12 ± 2.74	0.64 ± 0.87	25.69 ± 4.83	1.67 ± 1.59
LD (Ours)	C	82.93 ± 2.04	0.41 ± 1.11	84.88 ± 2.97	−1.45 ± 1.31	86.23 ± 3.62	0.58 ± 1.05	41.36 ± 4.65	0.33 ± 1.62
	F	74.38 ± 3.51	1.03 ± 1.14	78.53 ± 3.11	0.42 ± 1.54	79.69 ± 3.85	1.24 ± 1.47	39.51 ± 4.41	−0.67 ± 1.03

and

Table 4. Backdoor attack results on GIN (ASR% ↑/CAD% ↓). The bold values indicate the best performance.

Injection	Selection	NCI1		NCI109		Mutagenicity		ENZYMES
		ASR	CAD	ASR	CAD	ASR	CAD	ASR	CAD
Random	Random	76.65 ± 4.84	0.82 ± 1.08	75.42 ± 4.21	1.15 ± 0.97	67.50 ± 5.19	−0.25 ± 1.23	36.18 ± 4.62	−1.11 ± 1.58
LIA	C	83.82 ± 3.13	−0.45 ± 1.43	82.02 ± 2.91	−0.50 ± 1.29	78.43 ± 3.34	−0.95 ± 1.36	45.89 ± 3.97	0.56 ± 1.68
	F	83.88 ± 3.27	1.31 ± 1.04	80.19 ± 3.75	1.49 ± 1.19	74.19 ± 4.08	0.88 ± 1.43	41.91 ± 4.23	3.33 ± 1.79
Degree	C	81.53 ± 3.45	1.42 ± 1.02	78.58 ± 3.19	1.52 ± 1.13	73.11 ± 3.91	1.10 ± 0.85	40.56 ± 4.03	4.44 ± 1.65
	F	79.45 ± 4.16	0.65 ± 1.06	79.01 ± 3.71	−1.17 ± 1.35	72.98 ± 3.89	0.23 ± 1.24	39.83 ± 4.49	1.67 ± 1.01
LD (Ours)	C	89.42 ± 1.35	−0.91 ± 1.17	87.91 ± 2.91	1.18 ± 1.03	89.17 ± 2.46	0.73 ± 1.28	64.67 ± 3.78	2.78 ± 1.59
	F	87.63 ± 2.01	1.25 ± 0.96	84.18 ± 3.33	−0.83 ± 1.18	84.05 ± 3.21	1.44 ± 1.14	53.17 ± 3.94	1.67 ± 1.64

, Across all datasets and architectures, the proposed LD injection combined with either C or F selection consistently achieves a higher ASR than all baselines, confirming the advantage of placing triggers at topologically distant locations. The best results are typically obtained with C selection, suggesting that low-confidence target-class samples are more indicative of backdoor vulnerability than those with frequent forgetting events. This also implies that confidence-based ranking can more effectively prioritize samples that amplify the trigger’s influence during training. Between architectures, GIN shows greater vulnerability than GCN, likely due to its stronger ability to capture fine-grained structural dependencies, which facilitates the learning of injected triggers. The CAD remains low in all cases, with occasional negative values indicating no degradation and sometimes a slight improvement in clean accuracy.

6.3. Ablation Studies

To quantify the individual and combined contributions of our two core components—Long-distance Injection (LD) and vulnerability-aware sample selection—we conduct an ablation study on the NCI1 dataset with both GCN and GIN models. Starting from a baseline using Random injection and Random sample selection, we incrementally introduce each component in isolation. Specifically, we replace Random selection with two alternative vulnerability-aware strategies: Confidence-driven (C) and Forgetting-driven (F). We also evaluate the effect of applying the LD injection strategy alone while keeping sample selection Random.

As reported in

Table 5. Ablation study results on NCI1 dataset for GCN and GIN models (ASR% ↑/CAD% ↓). The bold values indicate the best performance.

Method Configuration	GCN		GIN
	ASR	CAD	ASR	CAD
Random Injection + Random Selection (Baseline)	58.84 ± 4.38	0.65 ± 0.94	76.65 ± 4.84	0.82 ± 1.08
Random Injection + Confidence-driven (C) Selection	71.52 ± 2.15	0.88 ± 1.05	82.33 ± 3.52	0.55 ± 1.21
Random Injection + Forgetting-driven (F) Selection	70.46 ± 3.48	1.04 ± 1.12	81.27 ± 3.29	0.42 ± 1.19
LD Injection + Random Selection	75.16 ± 2.58	−0.15 ± 0.99	85.28 ± 3.14	−0.24 ± 1.15
LD Injection + Confidence-driven (C) Selection	82.93 ± 2.04	0.41 ± 1.11	89.42 ± 2.65	−0.91 ± 1.17
LD Injection + Forgetting-driven (F) Selection	81.77 ± 2.11	0.37 ± 1.08	87.65 ± 2.72	−0.83 ± 1.12

, both the C and F selection strategies consistently improve the ASR over the baseline, confirming the advantage of prioritizing vulnerable samples. In this setting, C achieves a slightly higher ASR than F, suggesting that prediction confidence can be a more effective indicator of vulnerability than training instability captured by forgetting events. LD injection alone delivers even larger performance gains, underscoring its central role in enhancing the backdoor effect through topologically dispersed trigger placement. When LD injection is combined with either C or F selection, the ASR reaches its highest values, clearly surpassing all individual variants. These results highlight the strong synergy between the two components and confirm their joint importance in building an effective and stealthy backdoor attack.

6.4. Hyperparameter Sensitivity Analysis

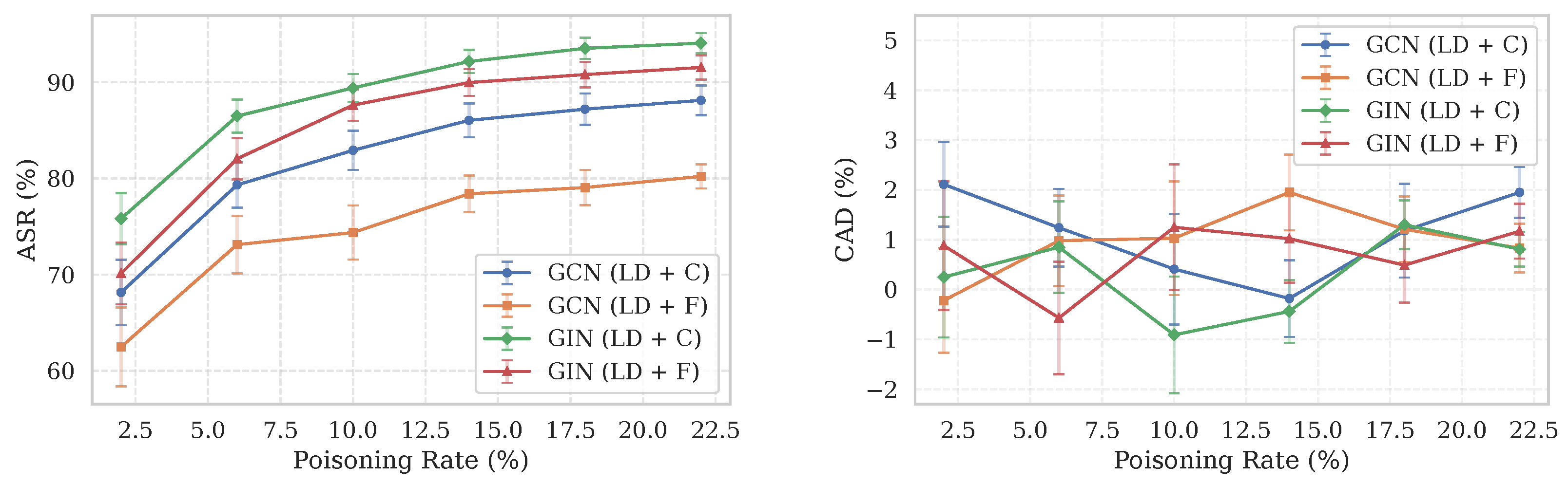
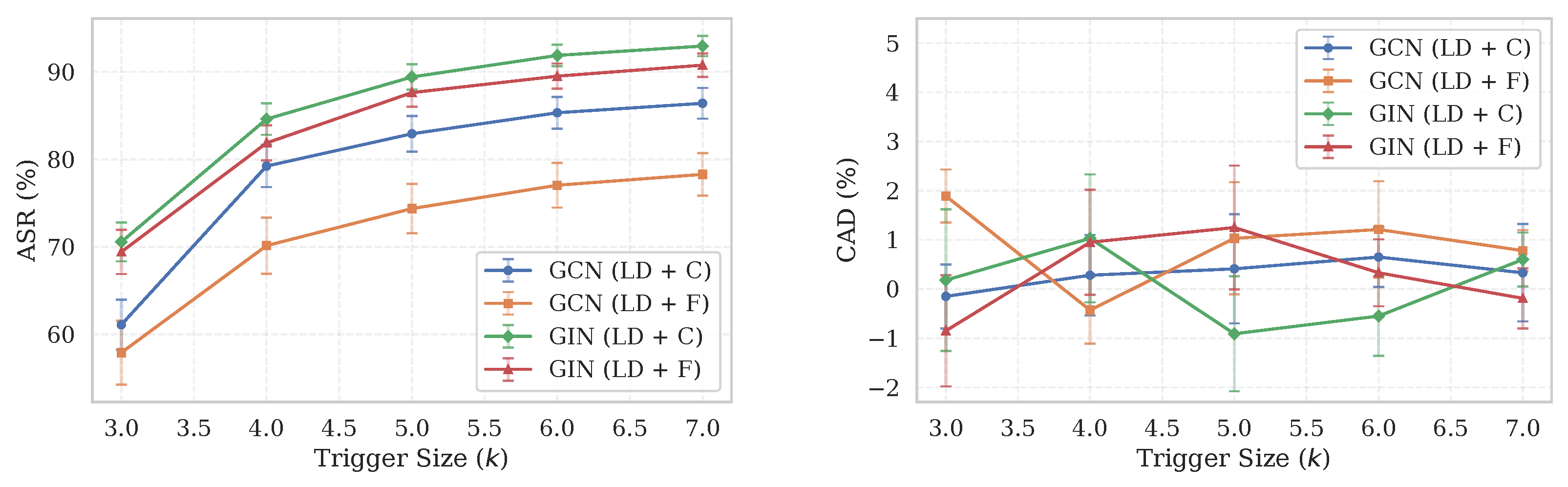
To evaluate the robustness and efficiency of our proposed attack, we perform a sensitivity analysis on the NCI1 dataset, focusing on two key hyperparameters: the poisoning rate and the trigger size (i.e., the number of trigger nodes). We report results for both main configurations, LD + Confidence-driven (C) and LD + Forgetting-driven (F), measuring their impact on the ASR and CAD.

As shown in Figure 3 and Figure 4, the ASR increases rapidly as the poisoning rate and trigger size increase from low values, but the growth rate gradually diminishes, indicating that our attack remains effective even with minimal modifications. In contrast, the CAD shows no clear monotonic trend and remains low and stable across different settings, underscoring the attack’s stealthiness. Similar trends are observed for both GCN and GIN, with the LD + C configuration generally achieving a higher ASR than LD + F.

6.5. Randomized Subsampling (RS) Defense

In a recent survey of trustworthy graph neural networks, Zhang et al. [24] mainly discuss defense methods against adversarial attacks. In contrast, defense strategies specifically designed for backdoor attacks on graphs remain limited. One representative approach in this context is the Randomized Subsampling (RS) defense [16], which has shown effectiveness in certain scenarios [19,25,26]. Following this defense strategy, we generate 20 subsamples for each input graph to make an ensemble prediction, where each subsample retains 80% of the original node pair connections. We measure the attack’s effectiveness by the change in the ASR before and after applying RS, and evaluate its performance overhead by the change in the clean accuracy (CA) of the model.

As shown in

Table 6. Performance of our methods under Randomized Subsampling (RS) defense.

Dataset	Model	Method	CA (%)			ASR (%)
			Before RS	After RS		Before RS	After RS
NCI1	GCN	LD + C	70.41	61.25		82.93 ± 2.04	75.47 ± 1.41
		LD + F				74.38 ± 3.51	66.46 ± 3.82
	GIN	LD + C	72.32	65.69		89.42 ± 2.65	86.23 ± 1.88
		LD + F				87.63 ± 3.01	84.06 ± 2.25
NCI109	GCN	LD + C	71.21	64.16		84.88 ± 2.97	75.17 ± 3.15
		LD + F				78.53 ± 3.11	71.10 ± 3.39
	GIN	LD + C	73.18	63.68		87.91 ± 2.91	84.42 ± 3.01
		LD + F				84.18 ± 3.33	80.47 ± 3.55
Mutagenicity	GCN	LD + C	77.15	73.16		86.23 ± 3.62	82.28 ± 1.87
		LD + F				79.69 ± 3.85	75.17 ± 2.01
	GIN	LD + C	79.61	76.50		89.17 ± 2.46	87.72 ± 2.65
		LD + F				84.05 ± 3.21	82.79 ± 3.42
ENZYMES	GCN	LD + C	35.00	31.67		41.36 ± 4.65	37.78 ± 4.81
		LD + F				39.51 ± 4.41	36.61 ± 4.58
	GIN	LD + C	36.67	33.33		64.67 ± 3.78	62.69 ± 1.85
		LD + F				53.17 ± 3.94	49.38 ± 2.12

, for the GIN model, which consistently achieves a very high initial ASR, the RS defense has a limited mitigating effect, and the attack remains a potent threat. In contrast, RS shows a stronger mitigation effect on the GCN model, resulting in a more noticeable drop in the ASR. Nevertheless, the attack still maintains a considerable success rate on most datasets even after applying RS. Notably, enabling the defense invariably leads to a decrease in CA on the standard test set, highlighting the inherent trade-off between robustness and standard performance. Overall, this experiment suggests that our clean-label backdoor attack, particularly against more expressive models like GIN, remains resilient to existing certified defenses.

6.6. Performance in Dirty-Label Setting

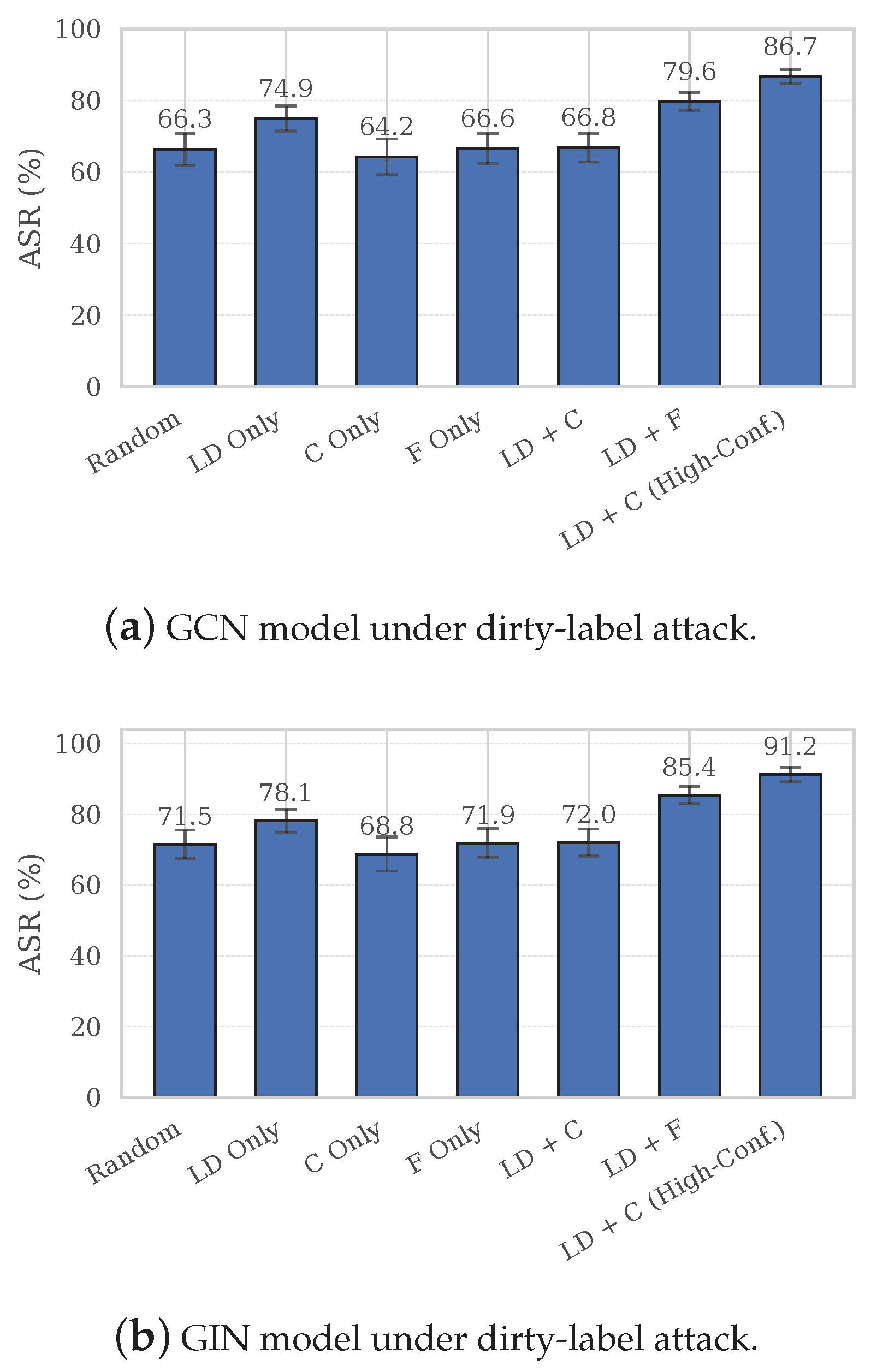
In this section, we investigate whether our optimization framework can be applied to the dirty-label setting. Specifically, we apply our Long-distance Injection (LD) strategy and sample selection mechanism to samples from non-target classes in the training set of the NCI1 dataset. The selected samples are then relabeled, and the resulting poisoned dataset is used to train the GCN and GIN models.

Based on our observations, we further conduct a comparative study on the sample selection mechanism by selecting high-confidence non-target samples as backdoor candidates, instead of the default lowest-confidence selection in the Confidence-driven (C) variant. Since the CAD results are similar to those reported in earlier experiments—with no clear monotonic trend and only minor random fluctuations—we omit them here and present only the ASR results.

As shown in Figure 5, our LD injection strategy remains effective in the dirty-label setting, consistently improving the ASR for both the GCN and GIN models. However, the gain is slightly smaller than in the clean-label setting, likely due to the inherently stronger trigger-learning signal in dirty-label attacks, where the modified label itself provides direct supervision for the backdoor.

Regarding sample selection, the Forgetting-driven (F) variant still yields clear improvements, confirming its applicability beyond the clean-label paradigm. Interestingly, the Confidence-driven (C) variant—when applied to the lowest-confidence samples—leads to performance degradation. We attribute this to the weaker learning signal introduced by relabeling low-confidence samples in the dirty-label setting. In fact, dirty-label attacks can freely choose non-target class samples and relabel them to the target class, so high-confidence samples align better with the new labels and strengthen the trigger–label association. By contrast, clean-label attacks are restricted to target-class samples without relabeling, where low-confidence or unstable ones are more easily influenced by the trigger. To validate this, we conducted a reverse experiment by selecting high-confidence non-target samples as backdoor candidates, which significantly boosts the ASR and achieves the highest performance among all the tested configurations. These findings suggest that, under dirty-label supervision, high-confidence samples are more compatible with effective trigger learning.

7. Conclusions

This paper revisits clean-label backdoor attacks for graph classification through the lens of feature competition between benign structures and injected triggers. We showed why adversarial perturbation, which is effective in continuous domains, fails on graphs: message passing amplifies structural perturbations, causing the model to entangle them with the trigger itself. Building on this insight, we proposed a Long-distance (LD) trigger injection strategy that places ER-generated subgraph triggers at topologically distant locations to strengthen global trigger propagation while disrupting benign feature aggregation. Complementing LD injection, we introduced two vulnerability-aware sample selection mechanisms within the target class, namely Confidence-driven (C) and Forgetting-driven (F), that prioritize samples that are most susceptible to backdoor influence.

Building on these designs, we conducted extensive experiments on four benchmarks (NCI1, NCI109, Mutagenicity, and ENZYMES) with two representative architectures (GCN and GIN). The results show that our method consistently improves the ASR over all baselines while keeping the CAD low. In the clean-label setting, LD+C achieves the best performance, increasing the ASR by 19.83% to 38.36% on GCN and 12.49% to 28.49% on GIN compared with the Random baseline. In the dirty-label setting, evaluated on the NCI1 dataset, LD+C (High-Confidence) achieves the highest gains, with ASR improvements of 20.4% on GCN (from 66.3% to 86.7%) and 19.7% on GIN (from 71.5% to 91.2%). Furthermore, under the Randomized Subsampling defense, the attack strength is largely preserved, especially on the GIN model, where the ASR of LD+C decreases by only 1.45% to 3.49%, indicating resilience to certified defenses.

Taken together, our findings surface the often-overlooked interplay among topology, trigger placement, and sample vulnerability in backdoor design for graphs. Future directions include adaptive defenses tailored to clean-label attacks and extensions to heterogeneous and dynamic graphs.