A Short-Term User-Side Load Forecasting Method Based on the MCPO-VMD-FDFE Decomposition-Enhanced Framework
Abstract
1. Introduction
- A modal decomposition parameter optimization method driven by a multi-dimensional, physically interpretable fitness function is proposed. A fitness function is designed by integrating modal energy entropy, orthogonality, and dominant frequency concentration. Combined with the Crested Porcupine Optimizer with Multidimensional Fitness Function (MCPO), the method jointly optimizes the VMD parameters, significantly improving decomposition quality and physical interpretability.
- A frequency-domain feature enhancement mechanism based on adaptive thresholding and weighted strategies is introduced. Key frequency components are selected using FFT spectral analysis and adaptive thresholding, followed by selective enhancement based on peak significance weighting. This approach effectively strengthens the frequency-domain expressiveness of the modal components.
- An MSCPatchTST model is constructed by integrating a multi-scale convolution module with channel independence. While maintaining the channel independence advantage of PatchTST, the model introduces parallel 1D convolutions at different scales to extract multi-granularity local features. An adaptive fusion mechanism further enhances the model’s ability to capture both local and multi-scale dynamic features of load sequences.
2. Methodology
2.1. MCPO-VMD-FDFE Decomposition-Enhanced Framework
2.1.1. VMD
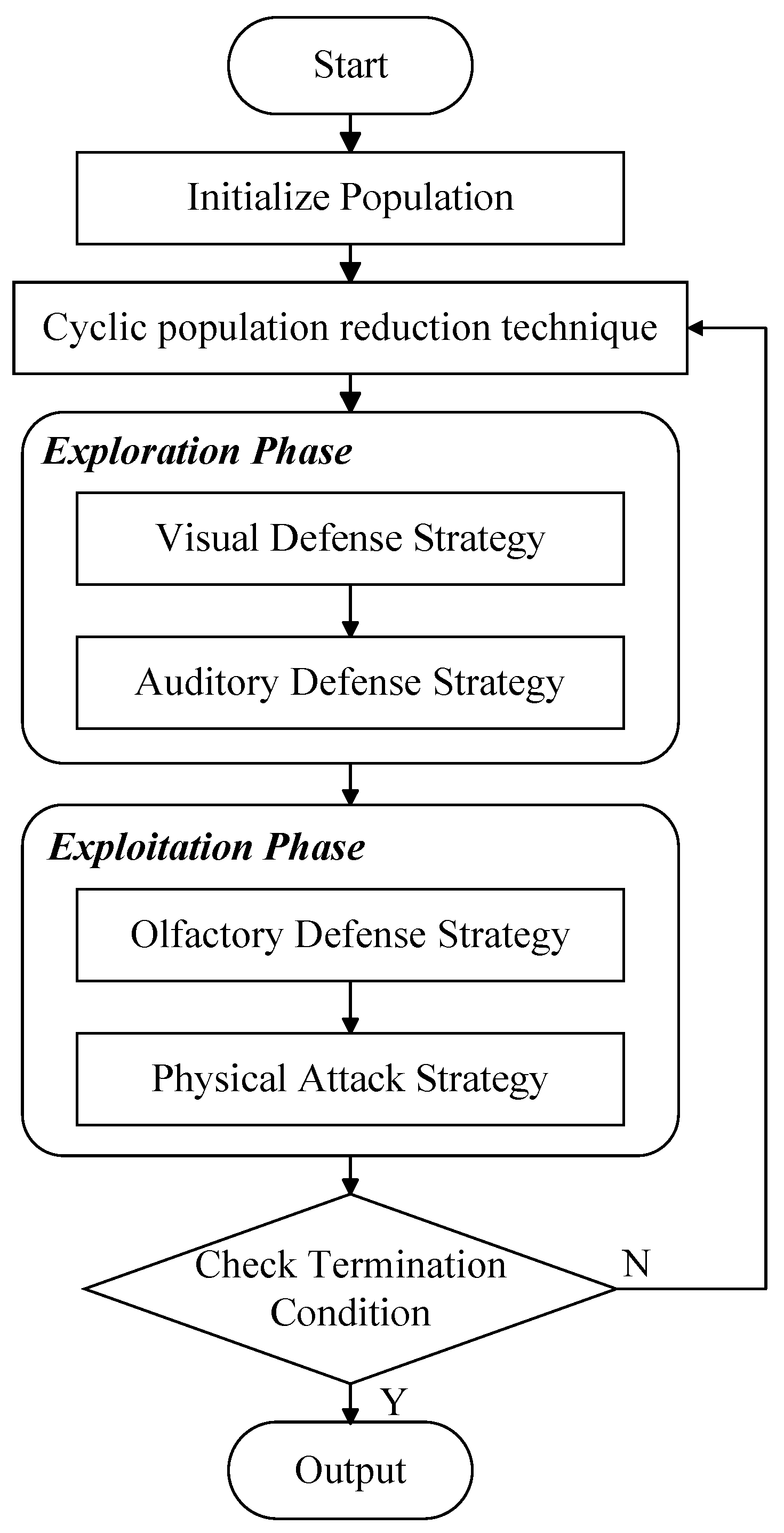
2.1.2. MCPO
2.1.3. Frequency-Domain Feature Enhancement (FDFE)
2.2. MSCPatchTST (PatchTST with Multi-Scale Convolution)
2.2.1. Channel Independence
2.2.2. Patching
2.2.3. Multi-Scale Convolution Module
2.2.4. Transformer Encoder
3. Examples Analysis
3.1. User-Side Load Data
3.2. Model Parameter Settings
3.3. Evaluation Metrics
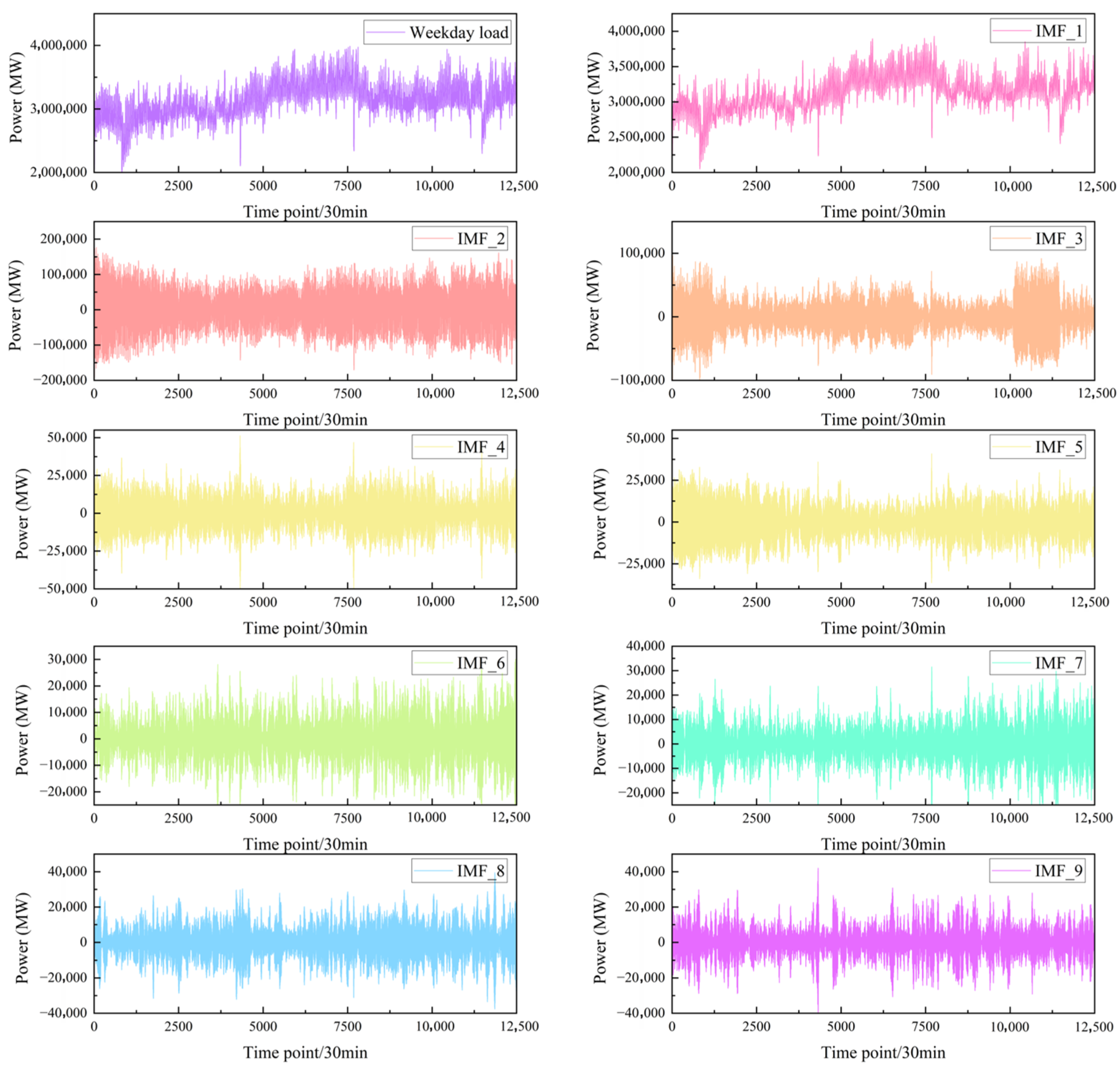
3.4. MCPO-VMD Decomposition Results
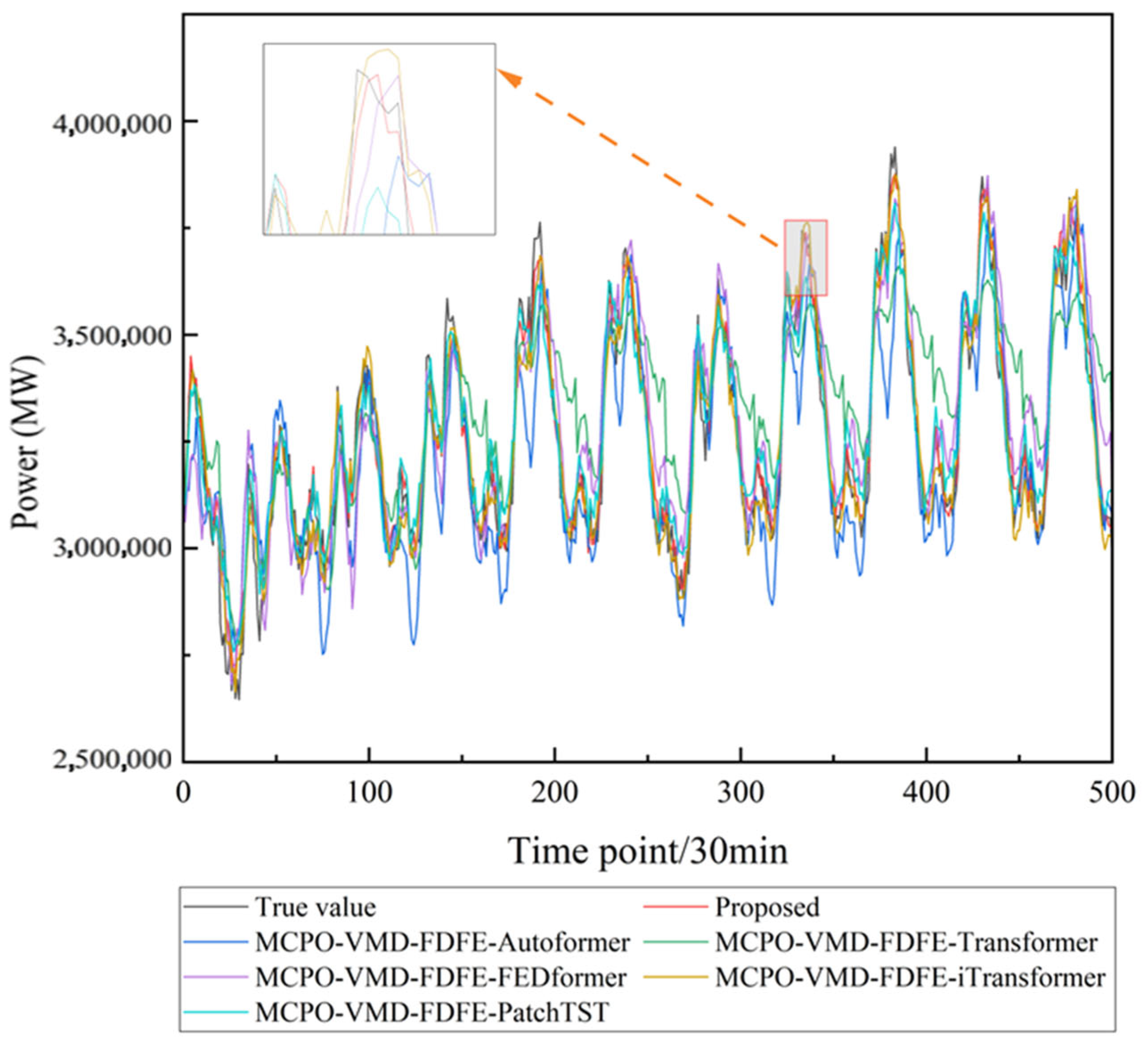
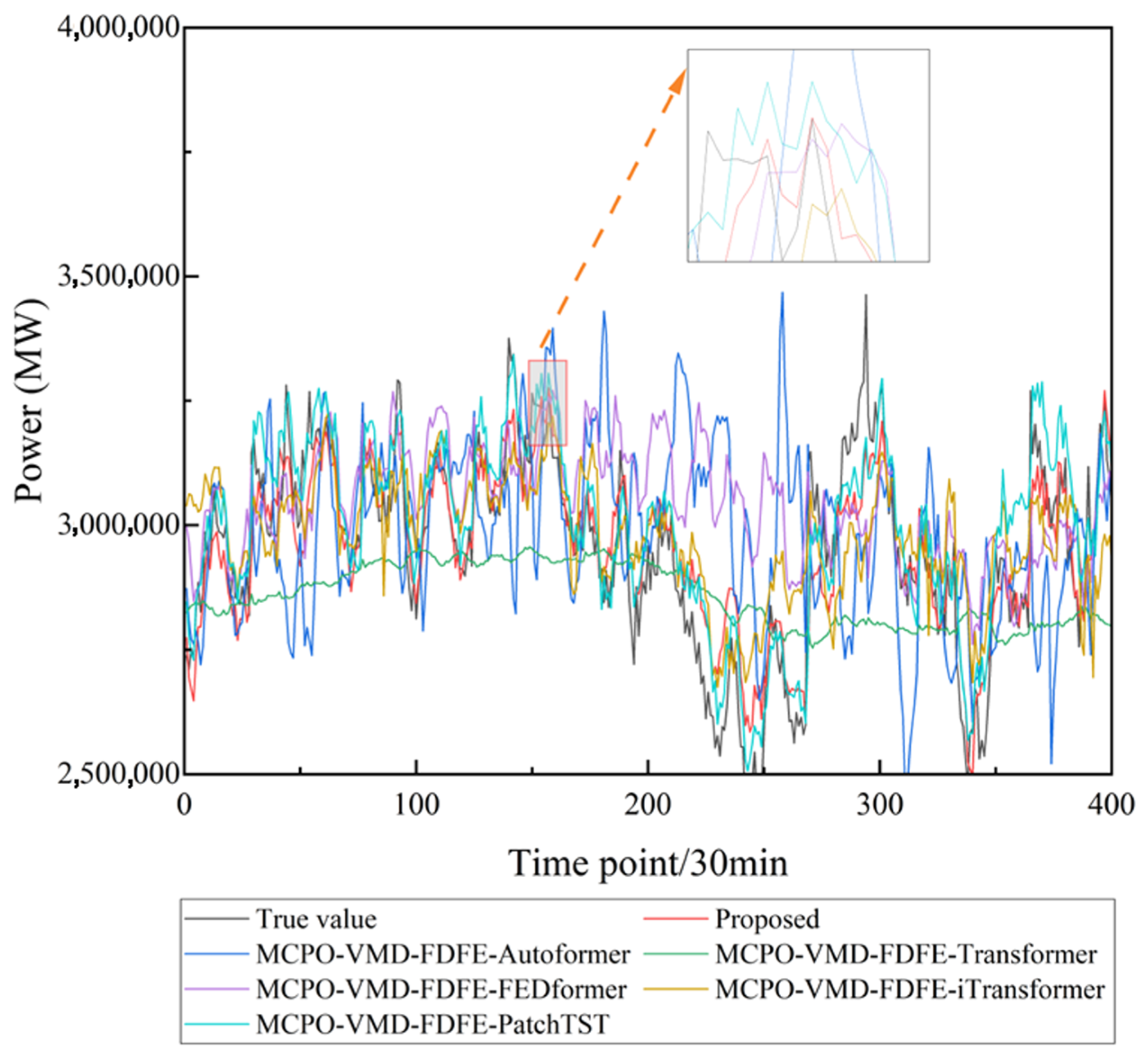
3.5. Ablation Experiment
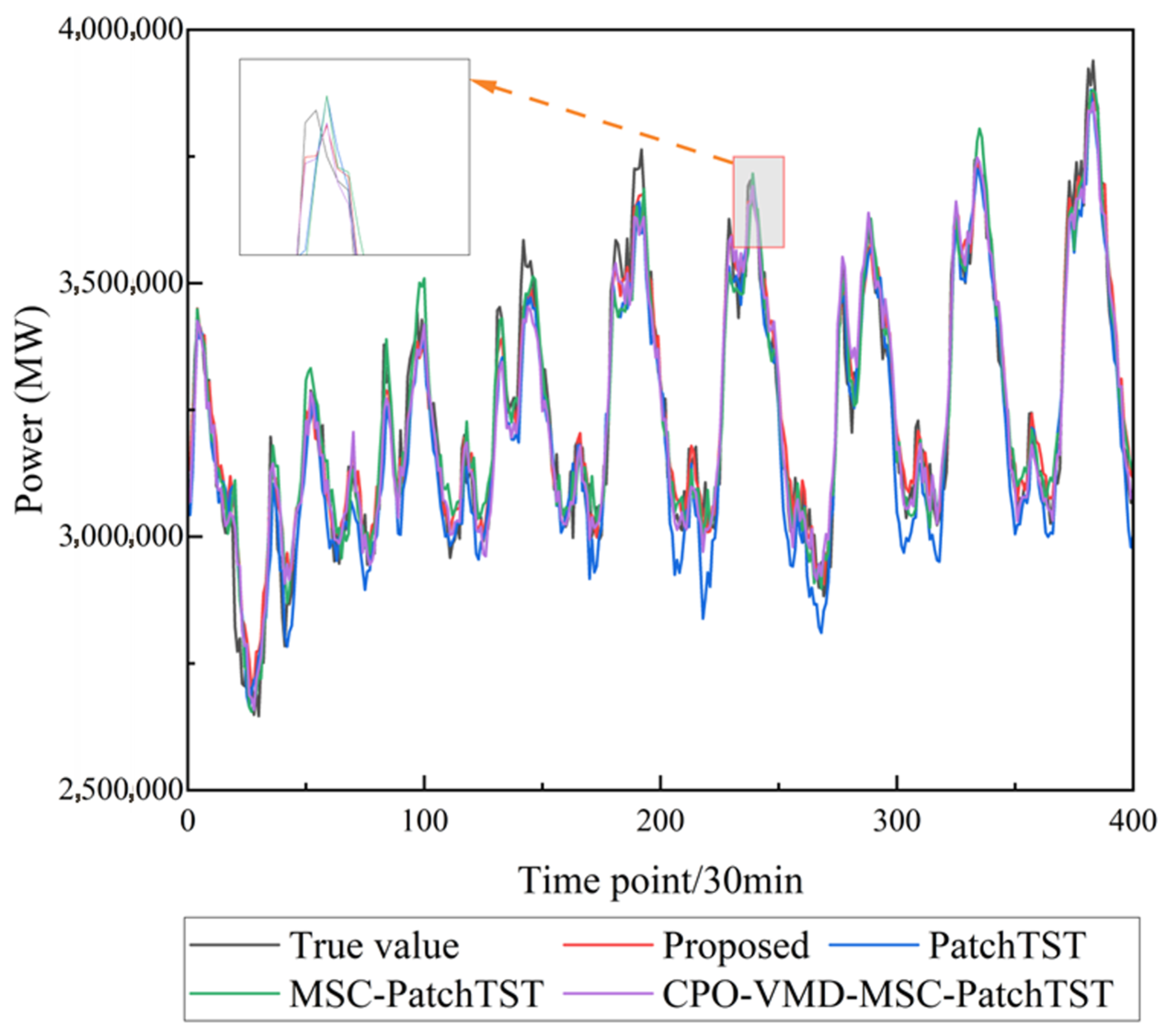
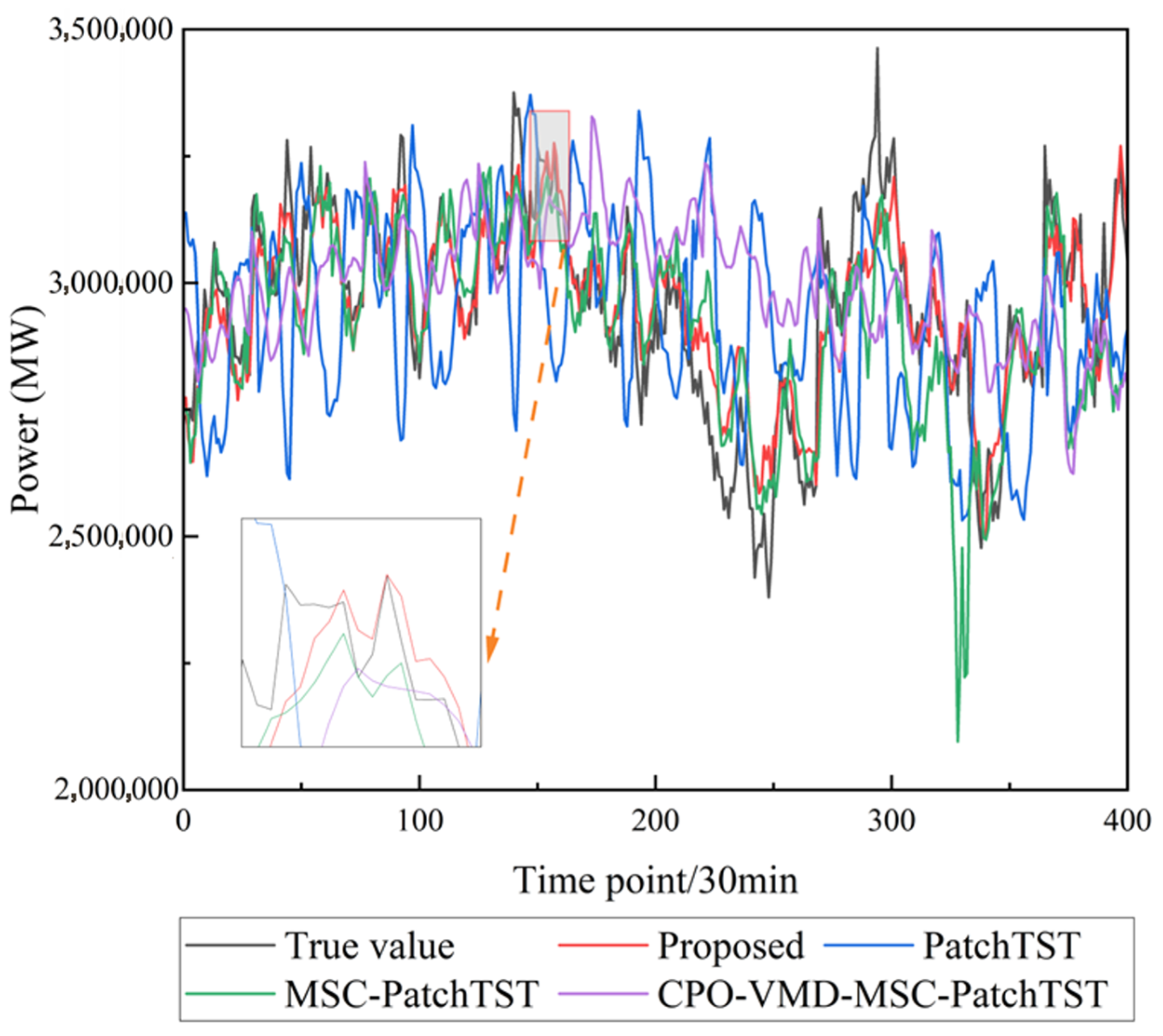
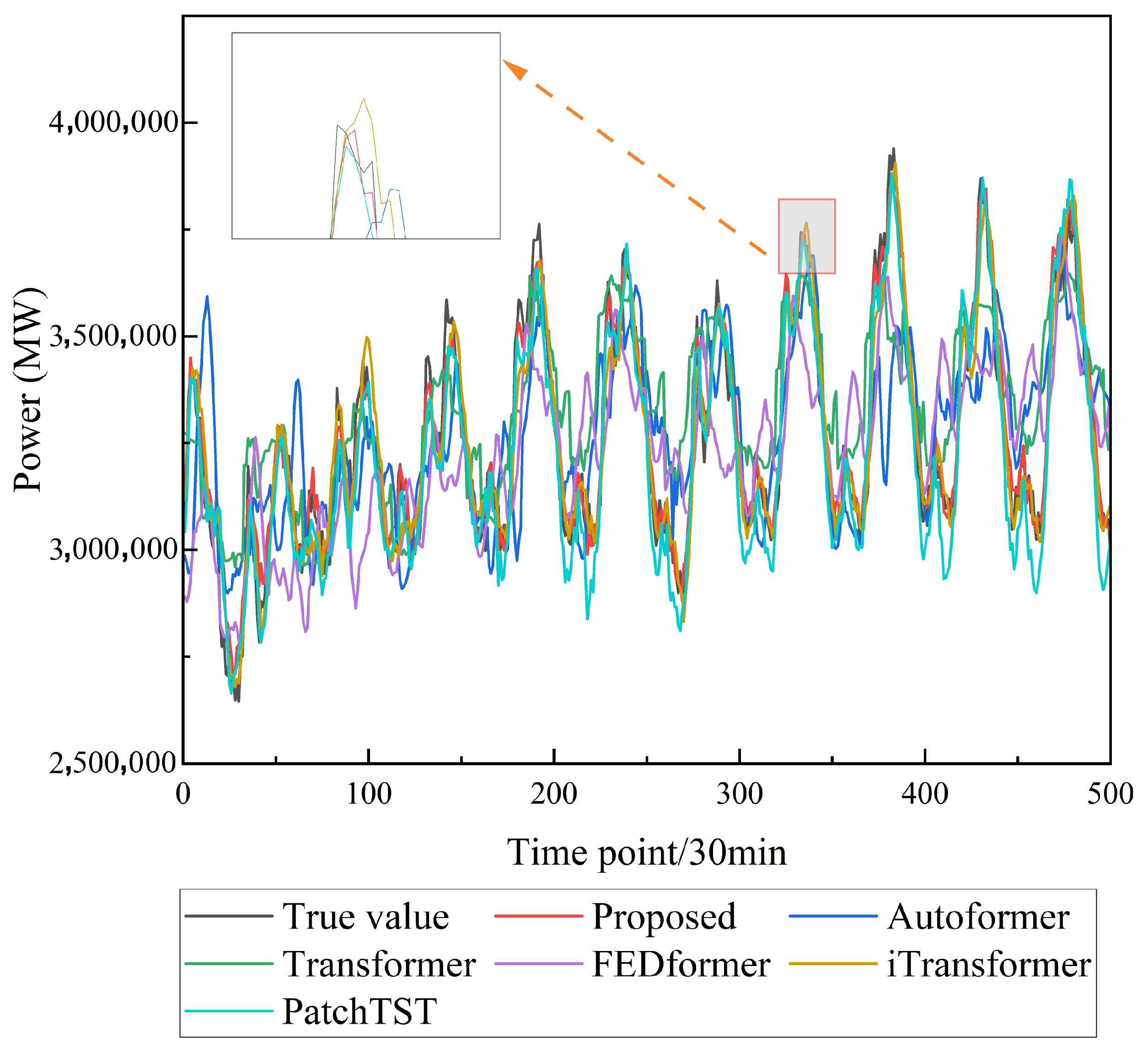
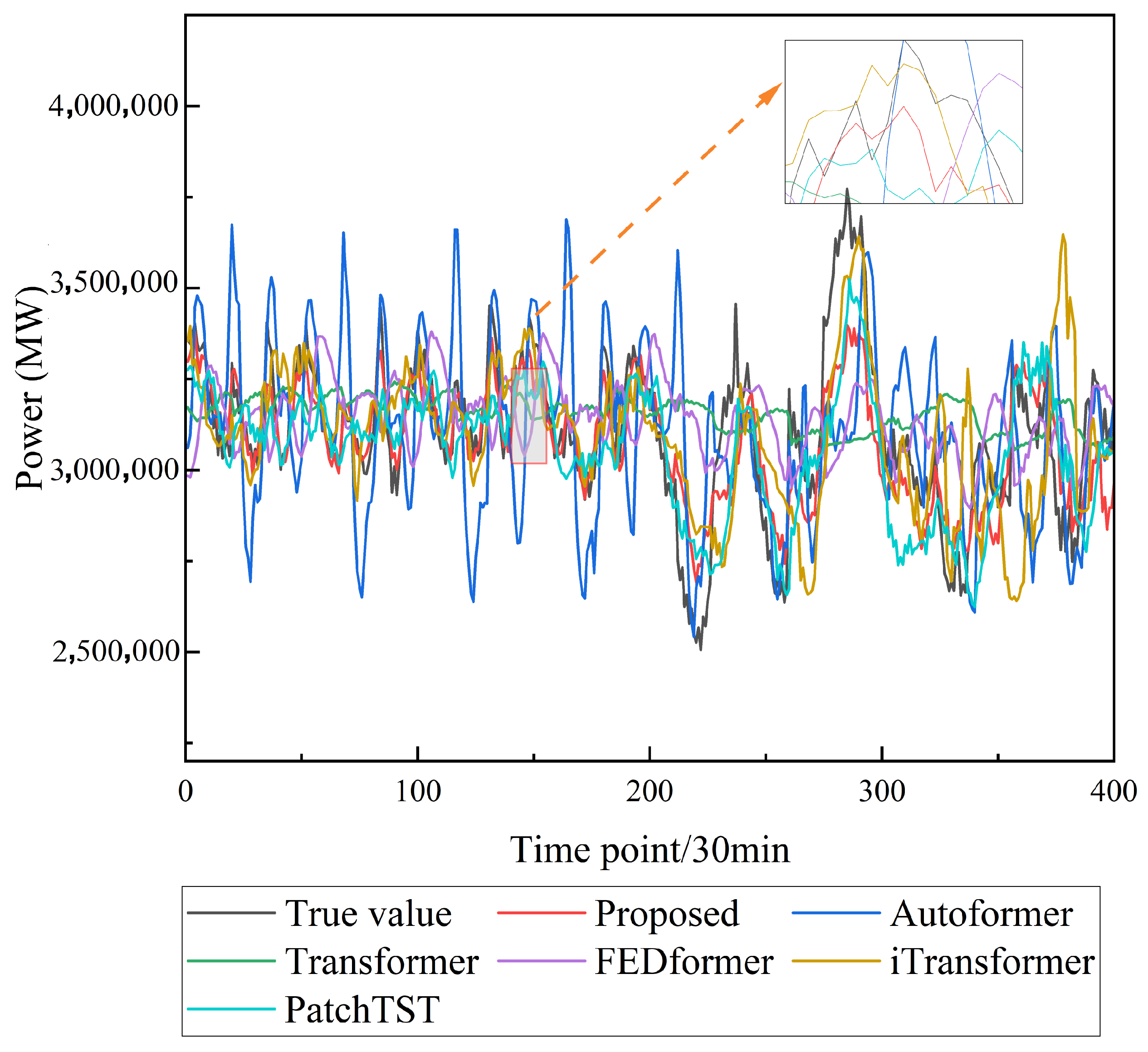
3.6. Comparative Experiment
4. Conclusions
- (1)
- This study proposes a parameter optimization method based on MCPO with a multi-dimensional fitness function, which overcomes the limitations of traditional empirical parameter selection to better match the multi-frequency characteristics of user-side load data. This method enables more effective optimization of key VMD parameters, and ablation studies show that its inclusion leads to average reductions of 26.05%, 28.40%, and 28.52% in RMSE, MAE, and MAPE, respectively, demonstrating its capability in handling non-stationary signals.
- (2)
- A frequency-domain feature enhancement (FDFE) module is designed to highlight key frequency components through adaptive thresholds and weighting strategies. This significantly improves the representational capacity of modal components. Ablation study results indicate that the inclusion of this module leads to average reductions of 30.32%, 32.37%, and 31.84% in RMSE, MAE, and MAPE, respectively, confirming its effectiveness in enhancing the model’s perception of frequency-domain structural features.
- (3)
- The integration of a multi-scale convolution module into the PatchTST model enables the collaborative extraction and adaptive fusion of both local and multi-scale features. This enhances the model’s ability to capture diverse patterns in user-side load data. Ablation study results show that this module contributes to average reductions of 26.05%, 28.40%, and 28.52% in RMSE, MAE, and MAPE, respectively.
- (4)
- The proposed method organically combines the MCPO-VMD decomposition, FDFE, and MSCPatchTST modules into a unified framework. This integrated approach achieves favorable forecasting performance across all three user-side load datasets (weekdays, Saturdays, and Sundays). Experimental results demonstrate that the proposed method consistently outperforms all comparison models, with an overall RMSE reduction of 45.65%, fully validating its effectiveness and stability in user-side load forecasting tasks.
- (5)
- Under the dataset and parameter settings used in this study, the complete workflow from training to prediction can be accomplished within approximately half an hour on a standard computing platform. This indicates that the proposed framework not only achieves high forecasting accuracy but also demonstrates satisfactory computational efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, W.; Chen, Y.; Xiao, C.; Yang, Y.; Yao, J. Design of short-term load forecasting method considering user behavior. Electr. Power Syst. Res. 2024, 234, 110529. [Google Scholar] [CrossRef]
- Zhao, W.; Mu, G.; Zhu, Y.; Xu, L.; Zhang, D.; Huang, H. Research on electric load forecasting and user benefit maximization under demand-side response. Int. J. Swarm Intell. Res. 2023, 14, 1–20. [Google Scholar] [CrossRef]
- Liu, Y.B.; Wu, H.; Liu, T.J.; Yang, Z.Y.; Liu, J.Y.; Li, Q.H. User-Side Net Load Forecasting Algorithm Integrating Empirical Mode Decomposition and Deep Learning. Autom. Electr. Power Syst. 2021, 45, 57–64. [Google Scholar]
- Yan, Q.; Lu, Z.; Liu, H.; He, X.; Zhang, X.; Guo, J. An improved feature-time Transformer encoder-Bi-LSTM for short-term forecasting of user-level integrated energy loads. Energy Build. 2023, 297, 113396. [Google Scholar] [CrossRef]
- Wei, L.; Zhao, J. Hybrid CNN-Multivariate LSTM Model for Accurate Short-Term Electricity Price Forecasting and Energy System Optimization. J. Circuit Syst. Comput. 2025, 34, 2550198. [Google Scholar] [CrossRef]
- Yuqi, J.; An, A.; Lu, Z.; Ping, H.; Xiaomei, L. Short-term load forecasting based on temporal importance analysis and feature extraction. Electr. Power Syst. Res. 2025, 244, 111551. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Huang, X.; Hao, J.; Lei, W.; Wang, Q. Short-term power load forecasting in distribution networks considering human comfort level. Front. Energy Res. 2025, 13, 1514755. [Google Scholar] [CrossRef]
- Ahmad, A.; Xiao, X.; Mo, H.; Dong, D. TFTformer: A novel transformer based model for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2025, 166, 110549. [Google Scholar] [CrossRef]
- Liu, W.; Li, J. Short-term power load forecasting based on genetic algorithm improved VMD-BP. Int. J. Intell. Inf. Technol. 2025, 21, 1–18. [Google Scholar] [CrossRef]
- Zhang, W.; Zhong, A.; Duan, K.; Shao, L. Ultra-short-term user-level load forecasting based on multi-scale component feature learning. Power Syst. Technol. 2024, 48, 2584–2592. [Google Scholar]
- Cao, H.Z.; Wei, B.; Gao, C.; Wu, J.K.; Lei, Z.; Sui, Y.; Chen, Y.B. Short-Term Electric Load Forecasting Method Based on Deep Belief Network. New Type Power Syst. 2025, 3, 111–124. [Google Scholar]
- Chen, C.; Ma, H.R.; Chen, L.J.; Ren, B.W.; Jin, C.; Zhang, T.Y. Multi-Step Short-Term Load Forecasting Method Based on User Group Segmentation. High Volt. Eng. 2023, 49, 4213–4222. [Google Scholar]
- Moudgil, V.; Sadiq, R.; Brar, J.; Hewage, K. Dual-channel encoded bidirectional LSTM for multi-building short-term load forecasting. J. Clean. Prod. 2025, 486, 144555. [Google Scholar] [CrossRef]
- Liu, F.; Wang, X.; Zhao, T.; Zhang, L.; Jiang, M.; Zhang, F. Novel short-term low-voltage load forecasting method based on residual stacking frequency attention network. Electr. Power Syst. Res. 2024, 233, 110534. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, J.; Xiao, G.; He, S.; Deng, K. TransformGraph: A novel short-term electricity net load forecasting model. Energy Rep. 2023, 9, 2705–2717. [Google Scholar] [CrossRef]
- Yazici, I.; Beyca, O.F.; Delen, D. Deep-learning-based short-term electricity load forecasting: A real case application. Eng. Appl. Artif. Intell. 2022, 109, 104645. [Google Scholar] [CrossRef]
- Zhuang, H.; Guo, X.; Shan, D.; Tian, X.; Hou, T. Short-term power load forecasting model based on optimized VMD-BILSTM. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 2029–2033. [Google Scholar] [CrossRef]
- Zhang, Z.; Hong, W.C. Application of variational mode decomposition and chaotic grey wolf optimizer with support vector regression for forecasting electric loads. Knowl. Based Syst. 2021, 228, 107297. [Google Scholar] [CrossRef]
- Yang, W.; Shi, J.; Li, S.; Song, Z.; Zhang, Z.; Chen, Z. A combined deep learning load forecasting model of single household resident user considering multi-time scale electricity consumption behavior. Appl. Energy 2022, 307, 118197. [Google Scholar] [CrossRef]
- Tang, Q.F.; Liu, N.; Zhang, J.H.; Yu, Z.Z.; Zhang, Q.X.; Lei, J.Y. Short-Term Load Forecasting Method for User-Side Microgrids Based on EMD-KELM-EKF and Parameter Optimization. Power Syst. Technol. 2014, 38, 2691–2699. [Google Scholar]
- Zhou, M.; Yu, J.; Wang, M.; Quan, W.; Bian, C. Research on the combined forecasting model of cooling load based on IVMD-WOA-LSSVM. Energy Build. 2024, 317, 114339. [Google Scholar] [CrossRef]
- Li, H.; Tang, Y.; Liu, D. A CrossInformer model based on dual-layer decomposition and interpretability for short-term electricity load forecasting. Alex. Eng. J. 2025, 129, 117–127. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, X.; Niu, D. A new framework for ultra-short-term electricity load forecasting model using IVMD–SGMD two–layer decomposition and INGO–BiLSTM–TPA–TCN. Appl. Soft Comput. 2024, 167, 112311. [Google Scholar] [CrossRef]





| Parameter Name | Parameter Value |
|---|---|
| Seq len | 144 |
| Number of attention heads | 8 |
| Epoch | 100 |
| Batch size | 24 |
| Patience | 10 |
| Dropout | 0.05 |
| Optimizer | Adam |
| Learning rate | 0.001 |
| Activation function | GELU |
| Loss function | MSE |
| Data Type | Method | RMSE | MAE | MAPE% |
|---|---|---|---|---|
| Weekdays | PatchTST | 89,929.68 | 69,955.73 | 2.1973 |
| MSCPatchTST | 76,526.31 | 58,820.48 | 1.8664 | |
| CPO-VMD-MSCPatchTST | 68,999.37 | 50,619.42 | 1.6174 | |
| MCPO-VMD-MSCPatchTST | 67,438.94 | 50,379.3 | 1.6001 | |
| Proposed | 59,131.17 | 44,954.44 | 1.4384 | |
| Saturdays | PatchTST | 158,580.61 | 122,474.26 | 3.926 |
| MSCPatchTST | 145,094.88 | 112,955.72 | 3.6334 | |
| CPO-VMD-MSCPatchTST | 127,526.27 | 96,752.75 | 3.1212 | |
| MCPO-VMD-MSCPatchTST | 126,446.16 | 95,918.71 | 3.0941 | |
| Proposed | 123,069.89 | 93,108.72 | 3.0026 | |
| Sundays | PatchTST | 136,026.05 | 107,074.64 | 3.6329 |
| MSCPatchTST | 111,315.49 | 86,603.41 | 2.9148 | |
| CPO-VMD-MSCPatchTST | 110,783.8 | 89,448.47 | 3.0025 | |
| MCPO-VMD-MSCPatchTST | 90,260.43 | 68,000.33 | 2.2815 | |
| Proposed | 86,655.03 | 64,351.65 | 2.2084 |
| Data Type | Method | RMSE | MAE | MAPE% |
|---|---|---|---|---|
| Weekdays | Autoformer | 202,945.7 | 157,396.15 | 4.9929 |
| Transformer | 188,512.8 | 150,230.16 | 4.7268 | |
| FEDformer | 221,169.5 | 172,782.76 | 5.372 | |
| iTransformer | 78,522.16 | 59,294.69 | 1.8536 | |
| PatchTST | 89,929.68 | 69,955.73 | 2.1973 | |
| Proposed | 76,526.31 | 58,820.48 | 1.8664 | |
| Saturdays | Autoformer | 246,141.07 | 195,330.32 | 6.2523 |
| Transformer | 238,694.39 | 180,513.21 | 5.9675 | |
| FEDformer | 228,628.75 | 181,450.29 | 5.9254 | |
| iTransformer | 204,594.55 | 144,689.18 | 4.7746 | |
| PatchTST | 158,580.61 | 122,474.26 | 3.926 | |
| Proposed | 145,094.88 | 112,955.72 | 3.6334 | |
| Sundays | Autoformer | 272,625.66 | 222,147.36 | 7.6234 |
| Transformer | 219,467.04 | 177,725.57 | 6.0307 | |
| FEDformer | 208,630.76 | 159,150.79 | 5.5775 | |
| iTransformer | 178,165.15 | 130,458.19 | 4.4611 | |
| PatchTST | 136,026.05 | 107,074.64 | 3.6329 | |
| Proposed | 111,315.49 | 86,603.41 | 2.9148 |
| Data Type | Method | RMSE | MAE | MAPE% |
|---|---|---|---|---|
| Weekdays | MCPO-VMD-FDFE-Autoformer | 155,956.6 | 116,683.01 | 3.7178 |
| MCPO-VMD-FDFE-Transformer | 156,730.6 | 127,942.28 | 4.0373 | |
| MCPO-VMD-FDFE-FEDformer | 140,537.6 | 103,701.17 | 3.3195 | |
| MCPO-VMD-FDFE-iTransformer | 65,562.17 | 50,632.98 | 1.5981 | |
| MCPO-VMD-FDFE-PatchTST | 74,270.74 | 57,654.24 | 1.8427 | |
| Proposed | 59,131.17 | 44,954.44 | 1.4384 | |
| Saturdays | MCPO-VMD-FDFE-Autoformer | 239,407.91 | 186,681.7 | 6.1231 |
| MCPO-VMD-FDFE-Transformer | 220,768.05 | 170,794.68 | 5.5672 | |
| MCPO-VMD-FDFE-FEDformer | 204,852.45 | 152,448.84 | 5.0609 | |
| MCPO-VMD-FDFE-iTransformer | 184,007.49 | 133,593.04 | 4.4049 | |
| MCPO-VMD-FDFE-PatchTST | 136,738.68 | 103,215.95 | 3.3602 | |
| Proposed | 123,069.89 | 93,108.72 | 3.0026 | |
| Sundays | MCPO-VMD-FDFE-Autoformer | 243,951.2 | 186,081.62 | 6.4431 |
| MCPO-VMD-FDFE-Transformer | 209,132.61 | 171,928.29 | 5.7637 | |
| MCPO-VMD-FDFE-FEDformer | 200,642.97 | 149,461.14 | 5.2794 | |
| MCPO-VMD-FDFE-iTransformer | 139,269.59 | 110,671.9 | 3.8287 | |
| MCPO-VMD-FDFE-PatchTST | 91,299.71 | 74,078.26 | 2.5305 | |
| Proposed | 86,655.03 | 64,351.65 | 2.2084 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Y.; Shi, J.; Dou, X.; He, Y. A Short-Term User-Side Load Forecasting Method Based on the MCPO-VMD-FDFE Decomposition-Enhanced Framework. Electronics 2025, 14, 3611. https://doi.org/10.3390/electronics14183611
Du Y, Shi J, Dou X, He Y. A Short-Term User-Side Load Forecasting Method Based on the MCPO-VMD-FDFE Decomposition-Enhanced Framework. Electronics. 2025; 14(18):3611. https://doi.org/10.3390/electronics14183611
Chicago/Turabian StyleDu, Yu, Jiaju Shi, Xun Dou, and Yu He. 2025. "A Short-Term User-Side Load Forecasting Method Based on the MCPO-VMD-FDFE Decomposition-Enhanced Framework" Electronics 14, no. 18: 3611. https://doi.org/10.3390/electronics14183611
APA StyleDu, Y., Shi, J., Dou, X., & He, Y. (2025). A Short-Term User-Side Load Forecasting Method Based on the MCPO-VMD-FDFE Decomposition-Enhanced Framework. Electronics, 14(18), 3611. https://doi.org/10.3390/electronics14183611







