Non-Equilibrium Quantum Materials for Electronics
Abstract
1. Introduction
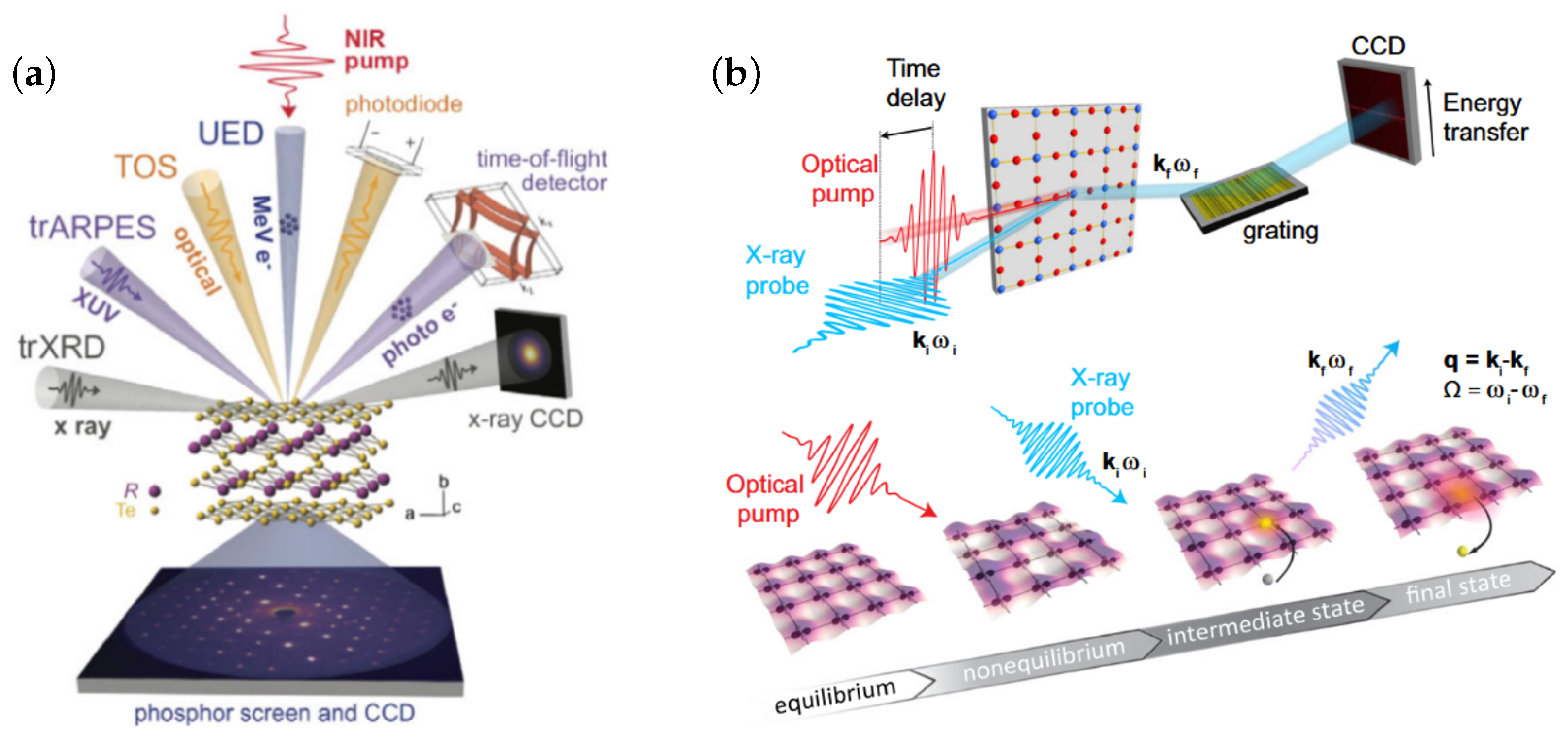
2. Experimental Techniques for Ultrafast Phenomena
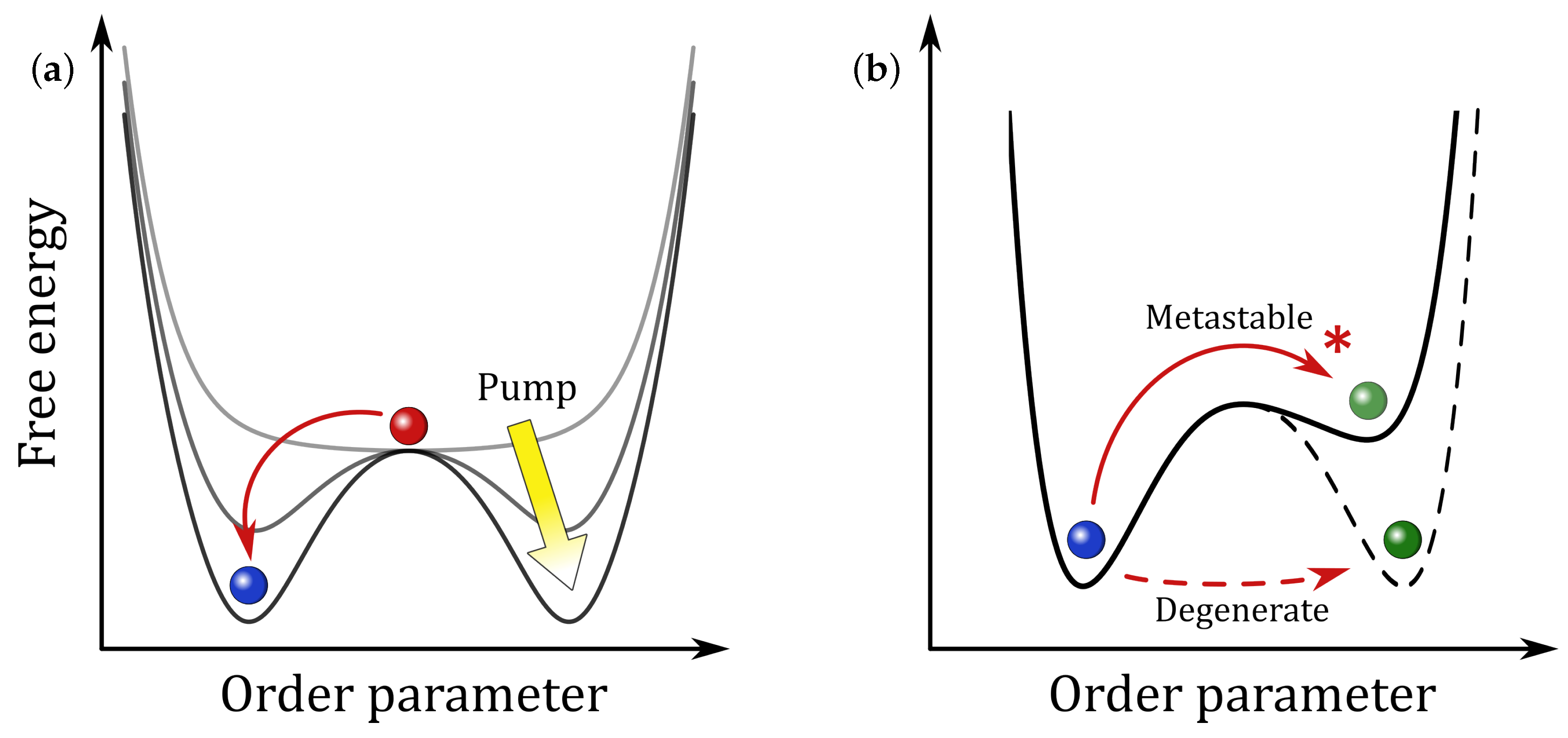
3. Photoinduced Transient Phases
3.1. Photoactive Superconductivity
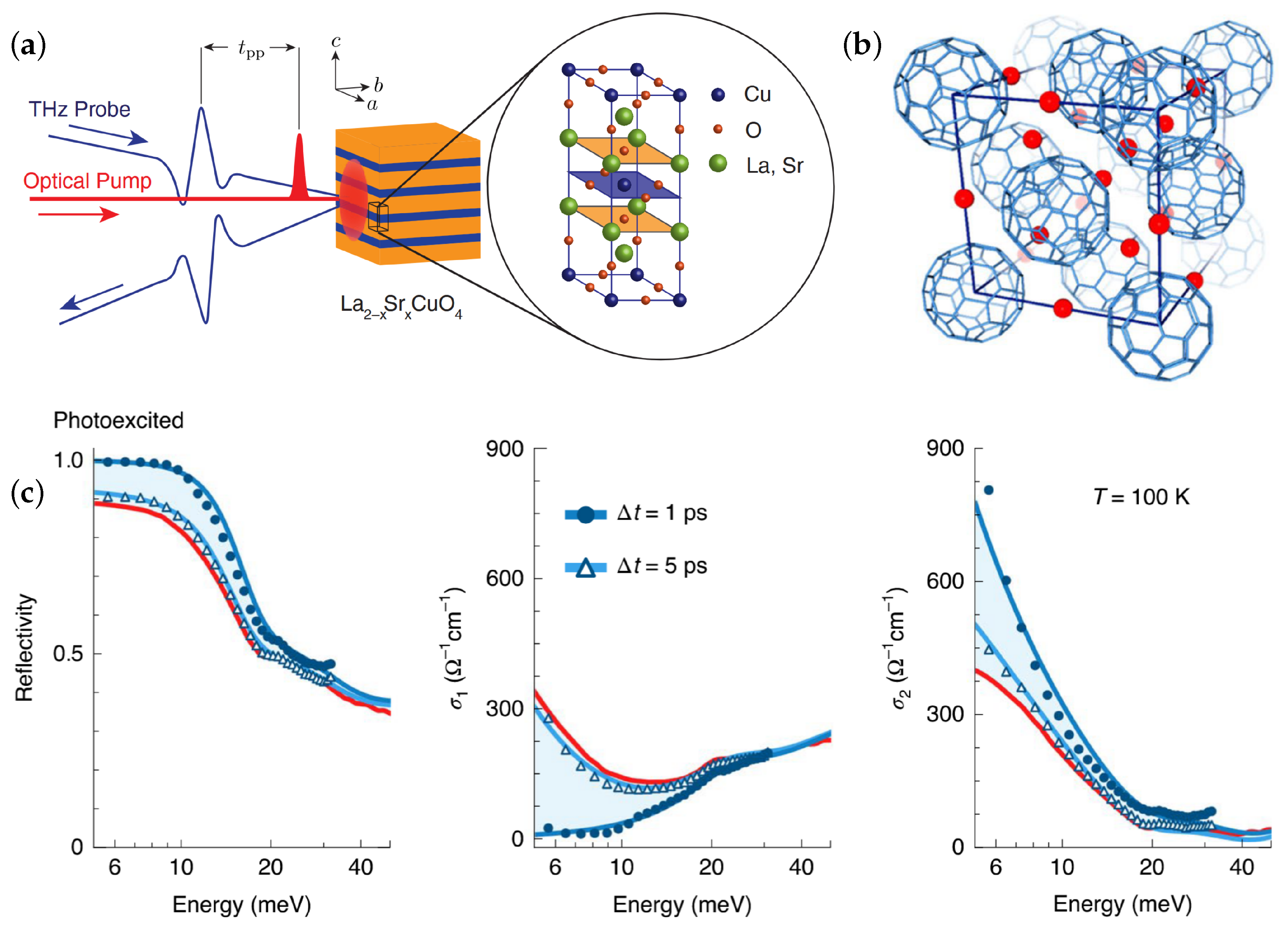
3.1.1. Cuprate Superconductors
3.1.2. Fulleride Superconductors:
3.1.3. Applications
3.2. Metastable Ferroelectricity and Multiferroic Ordering
3.3. Photoinduced Insulator-to-Metal Transition
3.4. More Light-Induced Phases
4. Current-Driven Phases
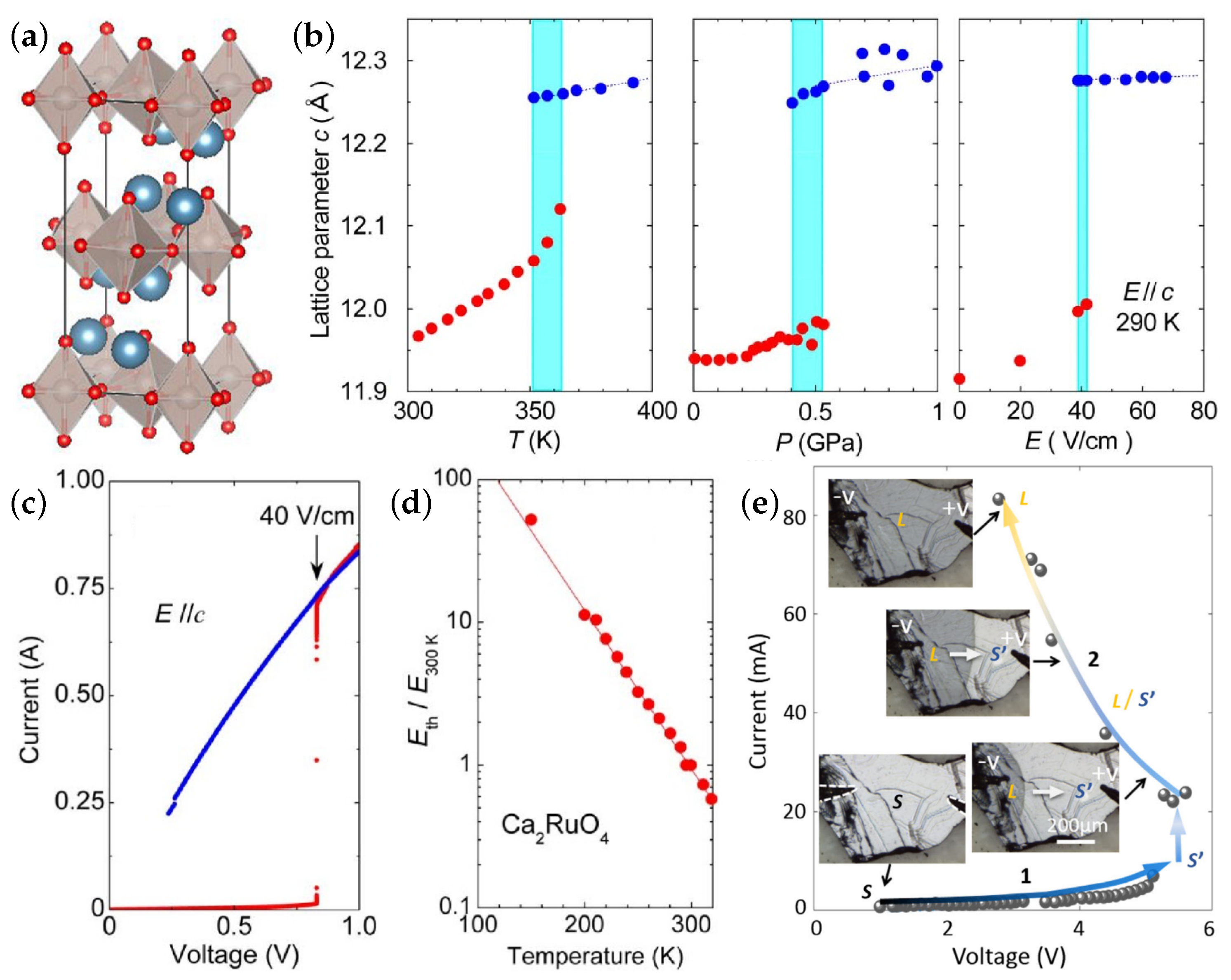
4.1. Current-Driven Insulator-to-Metal Transition in
4.2. Current- and Voltage-Driven Switching in VO2
4.3. Applications in Electronics and Resistive Switching
5. Discussion
Challenges
6. Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CDW | Charge density wave |
| DMFT | Dynamical mean field theory |
| FE | Ferroelectricity |
| IMT | Insulator-to-metal transition |
| IR | Infrared |
| SC | Superconductivity |
| SHG | Second harmonic generation |
| TOS | Time-resolved optical spectroscopy |
| (tr)ARPES | (Time-resolved and) angle-resolved photoemission spectroscopy |
| (tr)RIXS | (Time-resolved) resonant inelastic X-ray scattering |
| trSNOM | Time-resolved scanning near-field optical microscopy |
| (tr)XRD | (Time-resolved) X-ray diffraction |
| UED | Ultrafast electron diffraction |
References
- Basov, D.N.; Averitt, R.D.; Hsieh, D. Towards Properties on Demand in Quantum Materials. Nat. Mater. 2017, 16, 1077–1088. [Google Scholar] [CrossRef] [PubMed]
- de la Torre, A.; Kennes, D.M.; Claassen, M.; Gerber, S.; McIver, J.W.; Sentef, M.A. Colloquium: Nonthermal Pathways to Ultrafast Control in Quantum Materials. Rev. Mod. Phys. 2021, 93, 041002. [Google Scholar] [CrossRef]
- Fausti, D.; Tobey, R.I.; Dean, N.; Kaiser, S.; Dienst, A.; Hoffmann, M.C.; Pyon, S.; Takayama, T.; Takagi, H.; Cavalleri, A. Light-Induced Superconductivity in a Stripe-Ordered Cuprate. Science 2011, 331, 189–191. [Google Scholar] [CrossRef] [PubMed]
- Nicoletti, D.; Casandruc, E.; Laplace, Y.; Khanna, V.; Hunt, C.R.; Kaiser, S.; Dhesi, S.S.; Gu, G.D.; Hill, J.P.; Cavalleri, A. Optically Induced Superconductivity in Striped La2-xBaxCuO4 by Polarization-Selective Excitation in the near Infrared. Phys. Rev. B 2014, 90, 100503. [Google Scholar] [CrossRef]
- Nicoletti, D.; Fu, D.; Mehio, O.; Moore, S.; Disa, A.S.; Gu, G.D.; Cavalleri, A. Magnetic-Field Tuning of Light-Induced Superconductivity in Striped La2−xBaxCuO4. Phys. Rev. Lett. 2018, 121, 267003. [Google Scholar] [CrossRef]
- Först, M.; Tobey, R.I.; Bromberger, H.; Wilkins, S.B.; Khanna, V.; Caviglia, A.D.; Chuang, Y.D.; Lee, W.S.; Schlotter, W.F.; Turner, J.J.; et al. Melting of Charge Stripes in Vibrationally Driven La1.875Ba0.125CuO4: Assessing the Respective Roles of Electronic and Lattice Order in Frustrated Superconductors. Phys. Rev. Lett. 2014, 112, 157002. [Google Scholar] [CrossRef]
- Kaiser, S.; Hunt, C.R.; Nicoletti, D.; Hu, W.; Gierz, I.; Liu, H.Y.; Le Tacon, M.; Loew, T.; Haug, D.; Keimer, B.; et al. Optically Induced Coherent Transport Far above Tc in Underdoped YBa2Cu3O6+δ. Phys. Rev. B 2014, 89, 184516. [Google Scholar] [CrossRef]
- Casandruc, E.; Nicoletti, D.; Rajasekaran, S.; Laplace, Y.; Khanna, V.; Gu, G.D.; Hill, J.P.; Cavalleri, A. Wavelength-Dependent Optical Enhancement of Superconducting Interlayer Coupling in La1.885Ba0.115CuO4. Phys. Rev. B 2015, 91, 174502. [Google Scholar] [CrossRef]
- Khanna, V.; Mankowsky, R.; Petrich, M.; Bromberger, H.; Cavill, S.A.; Möhr-Vorobeva, E.; Nicoletti, D.; Laplace, Y.; Gu, G.D.; Hill, J.P.; et al. Restoring Interlayer Josephson Coupling in La1.885Ba0.115CuO4 by Charge Transfer Melting of Stripe Order. Phys. Rev. B 2016, 93, 224522. [Google Scholar] [CrossRef]
- Hunt, C.R.; Nicoletti, D.; Kaiser, S.; Pröpper, D.; Loew, T.; Porras, J.; Keimer, B.; Cavalleri, A. Dynamical Decoherence of the Light Induced Interlayer Coupling in YBa2Cu3O6+δ. Phys. Rev. B 2016, 94, 224303. [Google Scholar] [CrossRef]
- Zhang, S.J.; Wang, Z.X.; Wu, D.; Liu, Q.M.; Shi, L.Y.; Lin, T.; Li, S.L.; Dai, P.C.; Dong, T.; Wang, N.L. Photoinduced Metastable State with Modulated Josephson Coupling Strengths in Pr0.88LaCe0.12CuO4. Phys. Rev. B 2018, 98, 224507. [Google Scholar] [CrossRef]
- Niwa, H.; Yoshikawa, N.; Tomari, K.; Matsunaga, R.; Song, D.; Eisaki, H.; Shimano, R. Light-Induced Nonequilibrium Response of the Superconducting Cuprate La2-xSrxCuO4. Phys. Rev. B 2019, 100, 104507. [Google Scholar] [CrossRef]
- Cremin, K.A.; Zhang, J.; Homes, C.C.; Gu, G.D.; Sun, Z.; Fogler, M.M.; Millis, A.J.; Basov, D.N.; Averitt, R.D. Photoenhanced Metastable C-Axis Electrodynamics in Stripe-Ordered Cuprate La1.885Ba0.115CuO4. Proc. Natl. Acad. Sci. USA 2019, 116, 19875–19879. [Google Scholar] [CrossRef]
- Zhang, S.J.; Wang, Z.X.; Xiang, H.; Yao, X.; Liu, Q.M.; Shi, L.Y.; Lin, T.; Dong, T.; Wu, D.; Wang, N.L. Photoinduced Nonequilibrium Response in Underdoped YBa2Cu3O6+x Probed by Time-Resolved Terahertz Spectroscopy. Phys. Rev. X 2020, 10, 011056. [Google Scholar] [CrossRef]
- Liu, B.; Först, M.; Fechner, M.; Nicoletti, D.; Porras, J.; Loew, T.; Keimer, B.; Cavalleri, A. Pump Frequency Resonances for Light-Induced Incipient Superconductivity in YBa2Cu3O6.5. Phys. Rev. X 2020, 10, 011053. [Google Scholar] [CrossRef]
- Marciniak, A.; Marcantoni, S.; Giusti, F.; Glerean, F.; Sparapassi, G.; Nova, T.; Cartella, A.; Latini, S.; Valiera, F.; Rubio, A.; et al. Vibrational Coherent Control of Localized d–d Electronic Excitation. Nat. Phys. 2021, 17, 368–373. [Google Scholar] [CrossRef]
- Katsumi, K.; Nishida, M.; Kaiser, S.; Miyasaka, S.; Tajima, S.; Shimano, R. Near-Infrared Light-Induced Superconducting-like State in Underdoped YBa2Cu3Oy Studied by c-Axis Terahertz Third-Harmonic Generation. Phys. Rev. B 2023, 107, 214506. [Google Scholar] [CrossRef]
- Fava, S.; De Vecchi, G.; Jotzu, G.; Buzzi, M.; Gebert, T.; Liu, Y.; Keimer, B.; Cavalleri, A. Magnetic Field Expulsion in Optically Driven YBa2Cu3O6.48. Nature 2024, 632, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Mitrano, M.; Cantaluppi, A.; Nicoletti, D.; Kaiser, S.; Perucchi, A.; Lupi, S.; Di Pietro, P.; Pontiroli, D.; Riccò, M.; Clark, S.R.; et al. Possible Light-Induced Superconductivity in K3C60 at High Temperature. Nature 2016, 530, 461–464. [Google Scholar] [CrossRef]
- Cantaluppi, A.; Buzzi, M.; Jotzu, G.; Nicoletti, D.; Mitrano, M.; Pontiroli, D.; Riccò, M.; Perucchi, A.; Di Pietro, P.; Cavalleri, A. Pressure Tuning of Light-Induced Superconductivity in K3C60. Nat. Phys. 2018, 14, 837–841. [Google Scholar] [CrossRef]
- Budden, M.; Gebert, T.; Buzzi, M.; Jotzu, G.; Wang, E.; Matsuyama, T.; Meier, G.; Laplace, Y.; Pontiroli, D.; Riccò, M.; et al. Evidence for Metastable Photo-Induced Superconductivity in K3C60. Nat. Phys. 2021, 17, 611–618. [Google Scholar] [CrossRef]
- Buzzi, M.; Nicoletti, D.; Fechner, M.; Tancogne-Dejean, N.; Sentef, M.A.; Georges, A.; Biesner, T.; Uykur, E.; Dressel, M.; Henderson, A.; et al. Photomolecular High-Temperature Superconductivity. Phys. Rev. X 2020, 10, 031028. [Google Scholar] [CrossRef]
- Jotzu, G.; Meier, G.; Cantaluppi, A.; Cavalleri, A.; Pontiroli, D.; Riccò, M.; Ardavan, A.; Nam, M.S. Superconducting Fluctuations Observed Far above Tc in the Isotropic Superconductor K3C60. Phys. Rev. X 2023, 13, 021008. [Google Scholar] [CrossRef]
- Wang, E.; Adelinia, J.D.; Chavez-Cervantes, M.; Matsuyama, T.; Fechner, M.; Buzzi, M.; Meier, G.; Cavalleri, A. Superconducting Nonlinear Transport in Optically Driven High-Temperature K3C60. Nat. Commun. 2023, 14, 7233. [Google Scholar] [CrossRef]
- Nova, T.F.; Cartella, A.; Cantaluppi, A.; Först, M.; Bossini, D.; Mikhaylovskiy, R.V.; Kimel, A.V.; Merlin, R.; Cavalleri, A. An Effective Magnetic Field from Optically Driven Phonons. Nat. Phys. 2017, 13, 132–136. [Google Scholar] [CrossRef]
- Mankowsky, R.; von Hoegen, A.; Först, M.; Cavalleri, A. Ultrafast Reversal of the Ferroelectric Polarization. Phys. Rev. Lett. 2017, 118, 197601. [Google Scholar] [CrossRef] [PubMed]
- Nova, T.F.; Disa, A.S.; Fechner, M.; Cavalleri, A. Metastable Ferroelectricity in Optically Strained SrTiO3. Science 2019, 364, 1075–1079. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Qiu, T.; Zhang, J.; Baldini, E.; Lu, J.; Rappe, A.M.; Nelson, K.A. Terahertz Field–Induced Ferroelectricity in Quantum Paraelectric SrTiO3. Science 2019, 364, 1079–1082. [Google Scholar] [CrossRef]
- Disa, A.S.; Fechner, M.; Nova, T.F.; Liu, B.; Först, M.; Prabhakaran, D.; Radaelli, P.G.; Cavalleri, A. Polarizing an Antiferromagnet by Optical Engineering of the Crystal Field. Nat. Phys. 2020, 16, 937–941. [Google Scholar] [CrossRef]
- Shin, D.; Latini, S.; Schäfer, C.; Sato, S.A.; Baldini, E.; De Giovannini, U.; Hübener, H.; Rubio, A. Simulating Terahertz Field-Induced Ferroelectricity in Quantum Paraelectric SrTiO3. Phys. Rev. Lett. 2022, 129, 167401. [Google Scholar] [CrossRef]
- Disa, A.S.; Curtis, J.; Fechner, M.; Liu, A.; von Hoegen, A.; Först, M.; Nova, T.F.; Narang, P.; Maljuk, A.; Boris, A.V.; et al. Photo-Induced High-Temperature Ferromagnetism in YTiO3. Nature 2023, 617, 73–78. [Google Scholar] [CrossRef]
- Zhang, X.; Carbin, T.; Culver, A.B.; Du, K.; Wang, K.; Cheong, S.W.; Roy, R.; Kogar, A. Light-Induced Electronic Polarization in Antiferromagnetic Cr2O3. Nat. Mater. 2024, 23, 790–795. [Google Scholar] [CrossRef]
- Chen, P.; Paillard, C.; Zhao, H.J.; Íñiguez, J.; Bellaiche, L. Deterministic Control of Ferroelectric Polarization by Ultrafast Laser Pulses. Nat. Commun. 2022, 13, 2566. [Google Scholar] [CrossRef] [PubMed]
- Först, M.; Caviglia, A.D.; Scherwitzl, R.; Mankowsky, R.; Zubko, P.; Khanna, V.; Bromberger, H.; Wilkins, S.B.; Chuang, Y.D.; Lee, W.S.; et al. Spatially Resolved Ultrafast Magnetic Dynamics Initiated at a Complex Oxide Heterointerface. Nat. Mater. 2015, 14, 883–888. [Google Scholar] [CrossRef] [PubMed]
- Yasuda, K.; Zalys-Geller, E.; Wang, X.; Bennett, D.; Cheema, S.S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P.; Ashoori, R. Ultrafast High-Endurance Memory Based on Sliding Ferroelectrics. Science 2024, 385, 53–56. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, K.; Yu, J.; Fu, H.; Ding, Z.; Shi, X.; Meng, S. Ultrafast Polarization Switching via Laser-activated Ionic Migration in Ferroelectric CuInP2S6. arXiv 2024, arXiv:2412.09958. [Google Scholar] [CrossRef]
- Lian, C.; Ali, Z.A.; Kwon, H.; Wong, B.M. Indirect but Efficient: Laser-Excited Electrons Can Drive Ultrafast Polarization Switching in Ferroelectric Materials. J. Phys. Chem. Lett. 2019, 10, 3402–3407. [Google Scholar] [CrossRef]
- Bilyk, V.; Mishina, E.; Sherstyuk, N.; Bush, A.; Ovchinnikov, A.; Agranat, M. Transient Polarization Reversal Using an Intense THz Pulse in Silicon-Doped Lead Germanate. Phys. Status Solidi (RRL)–Rapid Res. Lett. 2021, 15, 2000460. [Google Scholar] [CrossRef]
- Zeng, Z.; Först, M.; Fechner, M.; Buzzi, M.; Amuah, E.B.; Putzke, C.; Moll, P.J.W.; Prabhakaran, D.; Radaelli, P.G.; Cavalleri, A. Photo-Induced Chirality in a Nonchiral Crystal. Science 2025, 387, 431–436. [Google Scholar] [CrossRef]
- Zong, A.; Kogar, A.; Bie, Y.Q.; Rohwer, T.; Lee, C.; Baldini, E.; Ergeçen, E.; Yilmaz, M.B.; Freelon, B.; Sie, E.J.; et al. Evidence for Topological Defects in a Photoinduced Phase Transition. Nat. Phys. 2019, 15, 27–31. [Google Scholar] [CrossRef]
- Zong, A.; Dolgirev, P.E.; Kogar, A.; Ergeçen, E.; Yilmaz, M.B.; Bie, Y.Q.; Rohwer, T.; Tung, I.C.; Straquadine, J.; Wang, X.; et al. Dynamical Slowing-Down in an Ultrafast Photoinduced Phase Transition. Phys. Rev. Lett. 2019, 123, 097601. [Google Scholar] [CrossRef]
- Kogar, A.; Zong, A.; Dolgirev, P.E.; Shen, X.; Straquadine, J.; Bie, Y.Q.; Wang, X.; Rohwer, T.; Tung, I.C.; Yang, Y.; et al. Light-Induced Charge Density Wave in LaTe3. Nat. Phys. 2020, 16, 159–163. [Google Scholar] [CrossRef]
- Wandel, S.; Boschini, F.; da Silva Neto, E.H.; Shen, L.; Na, M.X.; Zohar, S.; Wang, Y.; Welch, S.B.; Seaberg, M.H.; Koralek, J.D.; et al. Enhanced Charge Density Wave Coherence in a Light-Quenched, High-Temperature Superconductor. Science 2022, 376, 860–864. [Google Scholar] [CrossRef]
- Cheng, Y.; Zong, A.; Li, J.; Xia, W.; Duan, S.; Zhao, W.; Li, Y.; Qi, F.; Wu, J.; Zhao, L.; et al. Light-Induced Dimension Crossover Dictated by Excitonic Correlations. Nat. Commun. 2022, 13, 963. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Zong, A.; Wu, L.; Meng, Q.; Xia, W.; Qi, F.; Zhu, P.; Zou, X.; Jiang, T.; Guo, Y.; et al. Ultrafast Formation of Topological Defects in a Two-Dimensional Charge Density Wave. Nat. Phys. 2024, 20, 54–60. [Google Scholar] [CrossRef]
- Mori, R.; Takasan, K.; Ai, P.; Ciocys, S.; Kawaguchi, K.; Kondo, T.; Morimoto, T.; Lanzara, A. Possible Evidence of Excitonic Condensation in a Topological Insulator. Proc. Natl. Acad. Sci. USA 2025, 122, e2422667122. [Google Scholar] [CrossRef] [PubMed]
- Morrison, V.R.; Chatelain, R.P.; Tiwari, K.L.; Hendaoui, A.; Bruhács, A.; Chaker, M.; Siwick, B.J. A Photoinduced Metal-like Phase of Monoclinic VO2 Revealed by Ultrafast Electron Diffraction. Science 2014, 346, 445–448. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, A.; Chai, X.; Yang, Y.; Lu, M.; Bai, X.; Chen, Y.; Zhang, Y. An Interesting Functional Phase Change Material VO2: Response to Multivariate Control and Extensive Applications in Optics and Electronics. Adv. Electron. Mater. 2024, 10, 2300699. [Google Scholar] [CrossRef]
- Tao, Z.; Zhou, F.; Han, T.R.T.; Torres, D.; Wang, T.; Sepulveda, N.; Chang, K.; Young, M.; Lunt, R.R.; Ruan, C.Y. The Nature of Photoinduced Phase Transition and Metastable States in Vanadium Dioxide. Sci. Rep. 2016, 6, 38514. [Google Scholar] [CrossRef]
- Xu, C.; Jin, C.; Chen, Z.; Lu, Q.; Cheng, Y.; Zhang, B.; Qi, F.; Chen, J.; Yin, X.; Wang, G.; et al. Transient Dynamics of the Phase Transition in VO2 Revealed by Mega-Electron-Volt Ultrafast Electron Diffraction. Nat. Commun. 2023, 14, 1265. [Google Scholar] [CrossRef]
- Huber, M.A.; Plankl, M.; Eisele, M.; Marvel, R.E.; Sandner, F.; Korn, T.; Schüller, C.; Haglund, R.F., Jr.; Huber, R.; Cocker, T.L. Ultrafast Mid-Infrared Nanoscopy of Strained Vanadium Dioxide Nanobeams. Nano Lett. 2016, 16, 1421–1427. [Google Scholar] [CrossRef]
- Dönges, S.A.; Khatib, O.; O’Callahan, B.T.; Atkin, J.M.; Park, J.H.; Cobden, D.; Raschke, M.B. Ultrafast Nanoimaging of the Photoinduced Phase Transition Dynamics in VO2. Nano Lett. 2016, 16, 3029–3035. [Google Scholar] [CrossRef]
- Sood, A.; Shen, X.; Shi, Y.; Kumar, S.; Park, S.J.; Zajac, M.; Sun, Y.; Chen, L.Q.; Ramanathan, S.; Wang, X.; et al. Universal Phase Dynamics in VO2 Switches Revealed by Ultrafast Operando Diffraction. Science 2021, 373, 352–355. [Google Scholar] [CrossRef]
- Nakamura, F.; Sakaki, M.; Yamanaka, Y.; Tamaru, S.; Suzuki, T.; Maeno, Y. Electric-Field-Induced Metal Maintained by Current of the Mott Insulator Ca2RuO4. Sci. Rep. 2013, 3, 2536. [Google Scholar] [CrossRef]
- Guiot, V.; Cario, L.; Janod, E.; Corraze, B.; Ta Phuoc, V.; Rozenberg, M.; Stoliar, P.; Cren, T.; Roditchev, D. Avalanche Breakdown in GaTa4Se8-xTex Narrow-Gap Mott Insulators. Nat. Commun. 2013, 4, 1722. [Google Scholar] [CrossRef]
- Okazaki, R.; Nishina, Y.; Yasui, Y.; Nakamura, F.; Suzuki, T.; Terasaki, I. Current-Induced Gap Suppression in the Mott Insulator Ca2RuO4. J. Phys. Soc. Jpn. 2013, 82, 103702. [Google Scholar] [CrossRef]
- Curcio, D.; Sanders, C.E.; Chikina, A.; Lund, H.E.; Bianchi, M.; Granata, V.; Cannavacciuolo, M.; Cuono, G.; Autieri, C.; Forte, F.; et al. Current-Driven Insulator-to-Metal Transition without Mott Breakdown in Ca2RuO4. Phys. Rev. B 2023, 108, L161105. [Google Scholar] [CrossRef]
- Suen, C.T.; Marković, I.; Zonno, M.; Heinsdorf, N.; Zhdanovich, S.; Jo, N.H.; Schmid, M.; Hansmann, P.; Puphal, P.; Fürsich, K.; et al. Electronic Response of a Mott Insulator at a Current-Induced Insulator-to-Metal Transition. Nat. Phys. 2024, 20, 1757–1763. [Google Scholar] [CrossRef]
- Bhartiya, V.K.; Hartmann, R.; Forte, F.; Gabriele, F.; Kim, T.; Cuono, G.; Autieri, C.; Fan, S.; Kisslinger, K.; Camino, F.; et al. Evidence of Electronic States Driving Current-Induced Insulator-to-Metal Transition. arXiv 2025, arXiv:2504.17871. [Google Scholar] [CrossRef]
- Zhao, H.; Hu, B.; Ye, F.; Hoffmann, C.; Kimchi, I.; Cao, G. Nonequilibrium Orbital Transitions via Applied Electrical Current in Calcium Ruthenates. Phys. Rev. B 2019, 100, 241104. [Google Scholar] [CrossRef]
- Fukuchi, A.; Katase, T.; Kamiya, T. Room-Temperature Possible Current-Induced Transition in Ca2RuO4 Thin Films Grown Through Intercalation-Like Cation Diffusion in the A2BO4 Ruddlesden–Popper Structure. Small Methods 2024, 8, 2400264. [Google Scholar] [CrossRef]
- Tsurumaki-Fukuchi, A.; Tsubaki, K.; Katase, T.; Kamiya, T.; Arita, M.; Takahashi, Y. Stable and Tunable Current-Induced Phase Transition in Epitaxial Thin Films of Ca2RuO4. ACS Appl. Mater. Interfaces 2020, 12, 28368–28374. [Google Scholar] [CrossRef] [PubMed]
- Avallone, G.; Fermin, R.; Lahabi, K.; Granata, V.; Fittipaldi, R.; Cirillo, C.; Attanasio, C.; Vecchione, A.; Aarts, J. Universal Size-Dependent Nonlinear Charge Transport in Single Crystals of the Mott Insulator Ca2RuO4. npj Quantum Mater. 2021, 6, 91. [Google Scholar] [CrossRef]
- Tsitsishvili, M.; Poletti, D.; Dalmonte, M.; Chiriacò, G. Measurement induced transitions in non-Markovian free fermion ladders. SciPost Phys. Core 2024, 7, 011. [Google Scholar] [CrossRef]
- Muzzi, C.; Tsitsishvili, M.; Chiriacò, G. Entanglement enhancement induced by noise in inhomogeneously monitored systems. Phys. Rev. B 2025, 111, 014312. [Google Scholar] [CrossRef]
- Shi, Y.; Chen, L.Q. Current-Driven Insulator-To-Metal Transition in Strongly Correlated VO2. Phys. Rev. Appl. 2019, 11, 014059. [Google Scholar] [CrossRef]
- Wu, B.; Zimmers, A.; Aubin, H.; Ghosh, R.; Liu, Y.; Lopez, R. Electric-Field-Driven Phase Transition in Vanadium Dioxide. Phys. Rev. B 2011, 84, 241410. [Google Scholar] [CrossRef]
- Orlianges, J.C.; Allegret, O.; Sirjita, E.N.; Masson, A.; Boulle, A.; Théry, V.; Tardif, S.; Micha, J.S.; Crunteanu, A. Electrical Activation of Insulator-to-Metal Transition in Vanadium Dioxide Single-Crystal Nanobeam and Their High-Frequency Switching Performances. J. Appl. Phys. 2024, 136, 064502. [Google Scholar] [CrossRef]
- Ha, S.D.; Zhou, Y.; Fisher, C.J.; Ramanathan, S.; Treadway, J.P. Electrical Switching Dynamics and Broadband Microwave Characteristics of VO2 Radio Frequency Devices. J. Appl. Phys. 2013, 113, 184501. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Z.; Ren, H.; Chen, Y.; Yan, W.; Wang, C.; Li, B.; Jiang, J.; Zou, C. Gate-Controlled VO2 Phase Transition for High-Performance Smart Windows. Sci. Adv. 2019, 5, eaav6815. [Google Scholar] [CrossRef]
- Lee, D.; Chung, B.; Shi, Y.; Kim, G.Y.; Campbell, N.; Xue, F.; Song, K.; Choi, S.Y.; Podkaminer, J.P.; Kim, T.H.; et al. Isostructural Metal-Insulator Transition in VO2. Science 2018, 362, 1037–1040. [Google Scholar] [CrossRef]
- Kim, C.Y.; Slusar, T.; Cho, J.; Kim, H.T. Mott Switching and Structural Transition in the Metal Phase of VO2 Nanodomain. ACS Appl. Electron. Mater. 2021, 3, 605–610. [Google Scholar] [CrossRef]
- Cheng, S.; Navarro, H.; Wang, Z.; Li, X.; Kaur, J.; Pofelski, A.; Meng, Q.; Zhou, C.; Chen, C.; Dean, M.P.M.; et al. Purely Electronic Insulator-Metal Transition in Rutile VO2. Nat. Commun. 2025, 16, 5444. [Google Scholar] [CrossRef]
- Shao, Z.; Cao, X.; Luo, H.; Jin, P. Recent Progress in the Phase-Transition Mechanism and Modulation of Vanadium Dioxide Materials. NPG Asia Materials 2018, 10, 581–605. [Google Scholar] [CrossRef]
- Lee, D.; Lee, J.; Song, K.; Xue, F.; Choi, S.Y.; Ma, Y.; Podkaminer, J.; Liu, D.; Liu, S.C.; Chung, B.; et al. Sharpened VO2 Phase Transition via Controlled Release of Epitaxial Strain. Nano Lett. 2017, 17, 5614–5619. [Google Scholar] [CrossRef]
- Crunteanu, A.; Givernaud, J.; Leroy, J.; Mardivirin, D.; Champeaux, C.; Orlianges, J.C.; Catherinot, A.; Blondy, P. Voltage- and Current-Activated Metal–Insulator Transition in VO2-based Electrical Switches: A Lifetime Operation Analysis. Sci. Technol. Adv. Mater. 2010, 11, 065002. [Google Scholar] [CrossRef]
- Ling, C.; Zhao, Z.; Hu, X.; Li, J.; Zhao, X.; Wang, Z.; Zhao, Y.; Jin, H. W Doping and Voltage Driven Metal–Insulator Transition in VO2 Nano-Films for Smart Switching Devices. ACS Appl. Nano Mater. 2019, 2, 6738–6746. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, X.; Ko, C.; Yang, Z.; Mouli, C.; Ramanathan, S. Voltage-Triggered Ultrafast Phase Transition in Vanadium Dioxide Switches. IEEE Electron Device Lett. 2013, 34, 220–222. [Google Scholar] [CrossRef]
- Zong, A.; Nebgen, B.R.; Lin, S.C.; Spies, J.A.; Zuerch, M. Emerging Ultrafast Techniques for Studying Quantum Materials. Nat. Rev. Mater. 2023, 8, 224–240. [Google Scholar] [CrossRef]
- Mitrano, M.; Wang, Y. Probing Light-Driven Quantum Materials with Ultrafast Resonant Inelastic X-ray Scattering. Commun. Phys. 2020, 3, 184. [Google Scholar] [CrossRef]
- Averitt, R.D.; Taylor, A.J. Ultrafast Optical and Far-Infrared Quasiparticle Dynamics in Correlated Electron Materials. J. Phys. Condens. Matter 2002, 14, R1357. [Google Scholar] [CrossRef]
- Orenstein, J. Ultrafast Spectroscopy of Quantum Materials. Phys. Today 2012, 65, 44–50. [Google Scholar] [CrossRef]
- Cheng, T.K.; Brorson, S.D.; Kazeroonian, A.S.; Moodera, J.S.; Dresselhaus, G.; Dresselhaus, M.S.; Ippen, E.P. Impulsive Excitation of Coherent Phonons Observed in Reflection in Bismuth and Antimony. Appl. Phys. Lett. 1990, 57, 1004–1006. [Google Scholar] [CrossRef]
- Merlin, R. Generating Coherent THz Phonons with Light Pulses. Solid State Commun. 1997, 102, 207–220. [Google Scholar] [CrossRef]
- Taghinejad, M.; Xu, Z.; Lee, K.T.; Lian, T.; Cai, W. Transient Second-Order Nonlinear Media: Breaking the Spatial Symmetry in the Time Domain via Hot-Electron Transfer. Phys. Rev. Lett. 2020, 124, 013901. [Google Scholar] [CrossRef]
- Taghinejad, M.; Xia, C.; Hrton, M.; Lee, K.T.; Kim, A.S.; Li, Q.; Guzelturk, B.; Kalousek, R.; Xu, F.; Cai, W.; et al. Determining Hot-Carrier Transport Dynamics from Terahertz Emission. Science 2023, 382, 299–305. [Google Scholar] [CrossRef]
- Sparapassi, G.; Cavaletto, S.M.; Tollerud, J.; Montanaro, A.; Glerean, F.; Marciniak, A.; Giusti, F.; Mukamel, S.; Fausti, D. Transient Measurement of Phononic States with Covariance-Based Stochastic Spectroscopy. Light. Sci. Appl. 2022, 11, 44. [Google Scholar] [CrossRef]
- Glerean, F.; Rigoni, E.M.; Jarc, G.; Mathengattil, S.Y.; Montanaro, A.; Giusti, F.; Mitrano, M.; Benatti, F.; Fausti, D. Ultrafast Pump-Probe Phase-Randomized Tomography. Light. Sci. Appl. 2025, 14, 115. [Google Scholar] [CrossRef] [PubMed]
- Buzzi, M.; Först, M.; Mankowsky, R.; Cavalleri, A. Probing Dynamics in Quantum Materials with Femtosecond X-rays. Nat. Rev. Mater. 2018, 3, 299–311. [Google Scholar] [CrossRef]
- Cao, Y.; Mazzone, D.G.; Meyers, D.; Hill, J.P.; Liu, X.; Wall, S.; Dean, M.P.M. Ultrafast Dynamics of Spin and Orbital Correlations in Quantum Materials: An Energy- and Momentum-Resolved Perspective. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2019, 377, 20170480. [Google Scholar] [CrossRef] [PubMed]
- Filippetto, D.; Musumeci, P.; Li, R.K.; Siwick, B.J.; Otto, M.R.; Centurion, M.; Nunes, J.P.F. Ultrafast Electron Diffraction: Visualizing Dynamic States of Matter. Rev. Mod. Phys. 2022, 94, 045004. [Google Scholar] [CrossRef]
- Yoshida, S.; Aizawa, Y.; Wang, Z.h.; Oshima, R.; Mera, Y.; Matsuyama, E.; Oigawa, H.; Takeuchi, O.; Shigekawa, H. Probing Ultrafast Spin Dynamics with Optical Pump–Probe Scanning Tunnelling Microscopy. Nat. Nanotechnol. 2014, 9, 588–593. [Google Scholar] [CrossRef]
- Jelic, V.; Iwaszczuk, K.; Nguyen, P.H.; Rathje, C.; Hornig, G.J.; Sharum, H.M.; Hoffman, J.R.; Freeman, M.R.; Hegmann, F.A. Ultrafast Terahertz Control of Extreme Tunnel Currents through Single Atoms on a Silicon Surface. Nat. Phys. 2017, 13, 591–598. [Google Scholar] [CrossRef]
- Yoshida, S.; Arashida, Y.; Hirori, H.; Tachizaki, T.; Taninaka, A.; Ueno, H.; Takeuchi, O.; Shigekawa, H. Terahertz Scanning Tunneling Microscopy for Visualizing Ultrafast Electron Motion in Nanoscale Potential Variations. ACS Photonics 2021, 8, 315–323. [Google Scholar] [CrossRef]
- Garg, M.; Martin-Jimenez, A.; Luo, Y.; Kern, K. Ultrafast Photon-Induced Tunneling Microscopy. ACS Nano 2021, 15, 18071–18084. [Google Scholar] [CrossRef]
- Khusnatdinov, N.N.; Nagle, T.J.; Nunes, G., Jr. Ultrafast Scanning Tunneling Microscopy with 1 Nm Resolution. Appl. Phys. Lett. 2000, 77, 4434–4436. [Google Scholar] [CrossRef]
- López, L.E.P.; Vaitsi, A.; Sleziona, V.; Schulz, F.; Wolf, M.; Müller, M. Atomic-Scale Ultrafast Dynamics of Local Charge Order in a THz-induced Metastable State of 1T-TaS2. arXiv 2025, arXiv:2505.20541. [Google Scholar] [CrossRef]
- Sobota, J.A.; He, Y.; Shen, Z.X. Angle-Resolved Photoemission Studies of Quantum Materials. Rev. Mod. Phys. 2021, 93, 025006. [Google Scholar] [CrossRef]
- Gerber, S.; Yang, S.L.; Zhu, D.; Soifer, H.; Sobota, J.A.; Rebec, S.; Lee, J.J.; Jia, T.; Moritz, B.; Jia, C.; et al. Femtosecond Electron-Phonon Lock-in by Photoemission and x-Ray Free-Electron Laser. Science 2017, 357, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Wegkamp, D.; Herzog, M.; Xian, L.; Gatti, M.; Cudazzo, P.; McGahan, C.L.; Marvel, R.E.; Haglund, R.F.; Rubio, A.; Wolf, M.; et al. Instantaneous Band Gap Collapse in Photoexcited Monoclinic VO2 Due to Photocarrier Doping. Phys. Rev. Lett. 2014, 113, 216401. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Xu, Y.; Ulonska, S.; Robinson, J.S.; Ranitovic, P.; Kaindl, R.A. Bright High-Repetition-Rate Source of Narrowband Extreme-Ultraviolet Harmonics beyond 22 eV. Nat. Commun. 2015, 6, 7459. [Google Scholar] [CrossRef]
- Schmitt, F.; Kirchmann, P.S.; Bovensiepen, U.; Moore, R.G.; Rettig, L.; Krenz, M.; Chu, J.H.; Ru, N.; Perfetti, L.; Lu, D.H.; et al. Transient Electronic Structure and Melting of a Charge Density Wave in TbTe3. Science 2008, 321, 1649–1652. [Google Scholar] [CrossRef] [PubMed]
- Eisele, M.; Cocker, T.L.; Huber, M.A.; Plankl, M.; Viti, L.; Ercolani, D.; Sorba, L.; Vitiello, M.S.; Huber, R. Ultrafast Multi-Terahertz Nano-Spectroscopy with Sub-Cycle Temporal Resolution. Nat. Photonics 2014, 8, 841–845. [Google Scholar] [CrossRef]
- McLeod, A.S.; Wieteska, A.; Chiriaco, G.; Foutty, B.; Wang, Y.; Yuan, Y.; Xue, F.; Gopalan, V.; Chen, L.Q.; Mao, Z.Q.; et al. Nano-Imaging of Strain-Tuned Stripe Textures in a Mott Crystal. npj Quantum Mater. 2021, 6, 46. [Google Scholar] [CrossRef]
- Zhang, J.; McLeod, A.S.; Han, Q.; Chen, X.; Bechtel, H.A.; Yao, Z.; Gilbert Corder, S.N.; Ciavatti, T.; Tao, T.H.; Aronson, M.; et al. Nano-Resolved Current-Induced Insulator-Metal Transition in the Mott Insulator Ca2RuO4. Phys. Rev. X 2019, 9, 011032. [Google Scholar] [CrossRef]
- Ni, G.X.; Wang, L.; Goldflam, M.D.; Wagner, M.; Fei, Z.; McLeod, A.S.; Liu, M.K.; Keilmann, F.; Özyilmaz, B.; Castro Neto, A.H.; et al. Ultrafast Optical Switching of Infrared Plasmon Polaritons in High-Mobility Graphene. Nat. Photonics 2016, 10, 244–247. [Google Scholar] [CrossRef]
- Auston, D.H. Picosecond Optoelectronic Switching and Gating in Silicon. Appl. Phys. Lett. 1975, 26, 101–103. [Google Scholar] [CrossRef]
- McIver, J.W.; Schulte, B.; Stein, F.U.; Matsuyama, T.; Jotzu, G.; Meier, G.; Cavalleri, A. Light-Induced Anomalous Hall Effect in Graphene. Nat. Phys. 2020, 16, 38–41. [Google Scholar] [CrossRef] [PubMed]
- Kennes, D.M.; Wilner, E.Y.; Reichman, D.R.; Millis, A.J. Transient Superconductivity from Electronic Squeezing of Optically Pumped Phonons. Nat. Phys. 2017, 13, 479–483. [Google Scholar] [CrossRef]
- Buzzi, M.; Jotzu, G.; Cavalleri, A.; Cirac, J.I.; Demler, E.A.; Halperin, B.I.; Lukin, M.D.; Shi, T.; Wang, Y.; Podolsky, D. Higgs-Mediated Optical Amplification in a Nonequilibrium Superconductor. Phys. Rev. X 2021, 11, 011055. [Google Scholar] [CrossRef]
- Babadi, M.; Knap, M.; Martin, I.; Refael, G.; Demler, E. Theory of Parametrically Amplified Electron-Phonon Superconductivity. Phys. Rev. B 2017, 96, 014512. [Google Scholar] [CrossRef]
- Murakami, Y.; Golež, D.; Eckstein, M.; Werner, P. Photoinduced Enhancement of Excitonic Order. Phys. Rev. Lett. 2017, 119, 247601. [Google Scholar] [CrossRef]
- Sun, Z.; Millis, A.J. Transient Trapping into Metastable States in Systems with Competing Orders. Phys. Rev. X 2020, 10, 021028. [Google Scholar] [CrossRef]
- Suda, M.; Kato, R.; Yamamoto, H.M. Light-Induced Superconductivity Using a Photoactive Electric Double Layer. Science 2015, 347, 743–746. [Google Scholar] [CrossRef]
- Qiao, G.J.; Zhang, Z.L.; Li, S.W.; Sun, C.P. Controlling Superconducting Transistor by Coherent Light. arXiv 2023, arXiv:2305.04442. [Google Scholar] [CrossRef]
- Peña, V.; Gredig, T.; Santamaria, J.; Schuller, I.K. Interfacially Controlled Transient Photoinduced Superconductivity. Phys. Rev. Lett. 2006, 97, 177005. [Google Scholar] [CrossRef] [PubMed]
- Kazim, S.; Sharma, A.; Yadav, S.; Gajar, B.; Joshi, L.M.; Mishra, M.; Gupta, G.; Husale, S.; Gupta, A.; Sahoo, S.; et al. Light Induced Electron-Phonon Scattering Mediated Resistive Switching in Nanostructured Nb Thin Film Superconductor. Sci. Rep. 2017, 7, 881. [Google Scholar] [CrossRef]
- Prischepa, S.L.; Kushnir, V.N. Phonon Softening in Nanostructured Phonon–Mediated Superconductors (Review). J. Phys. Condens. Matter 2023, 35, 313003. [Google Scholar] [CrossRef]
- Först, M.; Manzoni, C.; Kaiser, S.; Tomioka, Y.; Tokura, Y.; Merlin, R.; Cavalleri, A. Nonlinear Phononics as an Ultrafast Route to Lattice Control. Nat. Phys. 2011, 7, 854–856. [Google Scholar] [CrossRef]
- Nava, A.; Giannetti, C.; Georges, A.; Tosatti, E.; Fabrizio, M. Cooling Quasiparticles in A3C60 Fullerides by Excitonic Mid-Infrared Absorption. Nat. Phys. 2018, 14, 154–159. [Google Scholar] [CrossRef]
- Chiriacò, G.; Millis, A.J.; Aleiner, I.L. Transient Superconductivity without Superconductivity. Phys. Rev. B 2018, 98, 220510. [Google Scholar] [CrossRef]
- Chiriacò, G.; Millis, A.J.; Aleiner, I.L. Negative Absolute Conductivity in Photoexcited Metals. Phys. Rev. B 2020, 101, 041105. [Google Scholar] [CrossRef]
- Dodge, J.S.; Lopez, L.; Sahota, D.G. Optical Saturation Produces Spurious Evidence for Photoinduced Superconductivity in K3C60. Phys. Rev. Lett. 2023, 130, 146002. [Google Scholar] [CrossRef]
- Buzzi, M.; Nicoletti, D.; Rowe, E.; Wang, E.; Cavalleri, A. Comment on arXiv:2210.01114: Optical Saturation Produces Spurious Evidence for Photoinduced Superconductivity in K3C60. arXiv 2023, arXiv:2303.10169. [Google Scholar] [CrossRef]
- Foxen, B.; Mutus, J.Y.; Lucero, E.; Graff, R.; Megrant, A.; Chen, Y.; Quintana, C.; Burkett, B.; Kelly, J.; Jeffrey, E.; et al. Qubit Compatible Superconducting Interconnects. Quantum Sci. Technol. 2017, 3, 014005. [Google Scholar] [CrossRef]
- Jarillo-Herrero, P.; van Dam, J.A.; Kouwenhoven, L.P. Quantum Supercurrent Transistors in Carbon Nanotubes. Nature 2006, 439, 953–956. [Google Scholar] [CrossRef]
- Ando, F.; Miyasaka, Y.; Li, T.; Ishizuka, J.; Arakawa, T.; Shiota, Y.; Moriyama, T.; Yanase, Y.; Ono, T. Observation of Superconducting Diode Effect. Nature 2020, 584, 373–376. [Google Scholar] [CrossRef]
- Karnetzky, C.; Zimmermann, P.; Trummer, C.; Duque Sierra, C.; Wörle, M.; Kienberger, R.; Holleitner, A. Towards Femtosecond On-Chip Electronics Based on Plasmonic Hot Electron Nano-Emitters. Nat. Commun. 2018, 9, 2471. [Google Scholar] [CrossRef]
- Natarajan, C.M.; Tanner, M.G.; Hadfield, R.H. Superconducting Nanowire Single-Photon Detectors: Physics and Applications. Supercond. Sci. Technol. 2012, 25, 063001. [Google Scholar] [CrossRef]
- Eshita, T.; Tamura, T.; Arimoto, Y. 14-Ferroelectric Random Access Memory (FRAM) Devices. In Advances in Non-Volatile Memory and Storage Technology; Nishi, Y., Ed.; Woodhead Publishing: Sawston, UK, 2014; pp. 434–454. [Google Scholar] [CrossRef]
- Scott, J.F.; Paz de Araujo, C.A. Ferroelectric Memories. Science 1989, 246, 1400–1405. [Google Scholar] [CrossRef]
- Salahuddin, S.; Datta, S. Use of Negative Capacitance to Provide Voltage Amplification for Low Power Nanoscale Devices. Nano Lett. 2008, 8, 405–410. [Google Scholar] [CrossRef]
- Müller, J.; Böscke, T.S.; Schröder, U.; Mueller, S.; Bräuhaus, D.; Böttger, U.; Frey, L.; Mikolajick, T. Ferroelectricity in Simple Binary ZrO2 and HfO2. Nano Lett. 2012, 12, 4318–4323. [Google Scholar] [CrossRef]
- Hoffman, J.; Pan, X.; Reiner, J.W.; Walker, F.J.; Han, J.P.; Ahn, C.H.; Ma, T.P. Ferroelectric Field Effect Transistors for Memory Applications. Adv. Mater. 2010, 22, 2957–2961. [Google Scholar] [CrossRef]
- Schmid, S.W.; Pósa, L.; Török, T.N.; Sánta, B.; Pollner, Z.; Molnár, G.; Horst, Y.; Volk, J.; Leuthold, J.; Halbritter, A.; et al. Picosecond Femtojoule Resistive Switching in Nanoscale VO2 Memristors. ACS Nano 2024, 18, 21966–21974. [Google Scholar] [CrossRef]
- Corti, E.; Gotsmann, B.; Moselund, K.; Ionescu, A.M.; Robertson, J.; Karg, S. Scaled Resistively-Coupled VO2 Oscillators for Neuromorphic Computing. Solid-State Electron. 2020, 168, 107729. [Google Scholar] [CrossRef]
- Liu, C.; Tiw, P.J.; Zhang, T.; Wang, Y.; Cai, L.; Yuan, R.; Pan, Z.; Yue, W.; Tao, Y.; Yang, Y. VO2 Memristor-Based Frequency Converter with in-Situ Synthesize and Mix for Wireless Internet-of-Things. Nat. Commun. 2024, 15, 1523. [Google Scholar] [CrossRef] [PubMed]
- Yuan, R.; Tiw, P.J.; Cai, L.; Yang, Z.; Liu, C.; Zhang, T.; Ge, C.; Huang, R.; Yang, Y. A Neuromorphic Physiological Signal Processing System Based on VO2 Memristor for Next-Generation Human-Machine Interface. Nat. Commun. 2023, 14, 3695. [Google Scholar] [CrossRef]
- Li, G.; Xie, D.; Zhong, H.; Zhang, Z.; Fu, X.; Zhou, Q.; Li, Q.; Ni, H.; Wang, J.; Guo, E.j.; et al. Photo-Induced Non-Volatile VO2 Phase Transition for Neuromorphic Ultraviolet Sensors. Nat. Commun. 2022, 13, 1729. [Google Scholar] [CrossRef]
- Kepič, P.; Horák, M.; Kabát, J.; Hájek, M.; Konečná, A.; Šikola, T.; Ligmajer, F. Coexisting Phases of Individual VO2 Nanoparticles for Multilevel Nanoscale Memory. ACS Nano 2025, 19, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- Basak, S.; Sun, Y.; Banguero, M.A.; Salev, P.; Schuller, I.K.; Aigouy, L.; Carlson, E.W.; Zimmers, A. Spatially Distributed Ramp Reversal Memory in VO2. Adv. Electron. Mater. 2023, 9, 2300085. [Google Scholar] [CrossRef]
- Mallick, S.; Chowdhury, D.R. Terahertz Field Driven Active Switching in Vanadium Dioxide-Based Multilayer Metasurfaces. In Proceedings of the 2022 IEEE International Conference on Emerging Electronics (ICEE), Bangalore, India, 11–14 December 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Suzuki, T.; Kubota, Y.; Mitsuishi, N.; Akatsuka, S.; Koga, J.; Sakano, M.; Masubuchi, S.; Tanaka, Y.; Togashi, T.; Ohsumi, H.; et al. Ultrafast Control of the Crystal Structure in a Topological Charge-Density-Wave Material. Phys. Rev. B 2023, 108, 184305. [Google Scholar] [CrossRef]
- Zhou, F.; Williams, J.; Sun, S.; Malliakas, C.D.; Kanatzidis, M.G.; Kemper, A.F.; Ruan, C.Y. Nonequilibrium Dynamics of Spontaneous Symmetry Breaking into a Hidden State of Charge-Density Wave. Nat. Commun. 2021, 12, 566. [Google Scholar] [CrossRef]
- van Kampen, M.; Jozsa, C.; Kohlhepp, J.T.; LeClair, P.; Lagae, L.; de Jonge, W.J.M.; Koopmans, B. All-Optical Probe of Coherent Spin Waves. Phys. Rev. Lett. 2002, 88, 227201. [Google Scholar] [CrossRef] [PubMed]
- Cornelissen, L.J.; Liu, J.; Duine, R.A.; Youssef, J.B.; van Wees, B.J. Long-Distance Transport of Magnon Spin Information in a Magnetic Insulator at Room Temperature. Nat. Phys. 2015, 11, 1022–1026. [Google Scholar] [CrossRef]
- Taghinejad, H.; Yamakawa, K.; Huang, X.; Lyu, Y.; Pritchard Cairns, L.; Husain, S.; Ramesh, R.; Analytis, J.G. Low-Field Regime of Magnon Transport in PLD-Grown YIG Films. Nano Lett. 2025, 25, 6438–6444. [Google Scholar] [CrossRef]
- Safranski, C.; Barsukov, I.; Lee, H.K.; Schneider, T.; Jara, A.A.; Smith, A.; Chang, H.; Lenz, K.; Lindner, J.; Tserkovnyak, Y.; et al. Spin Caloritronic Nano-Oscillator. Nat. Commun. 2017, 8, 117. [Google Scholar] [CrossRef]
- Nikitin, A.A.; Tatsenko, I.Y.; Kostylev, M.P.; Ustinov, A.B. Microwave Magnonic Micro-Oscillator Based on a Nm-Thick YIG Film. J. Appl. Phys. 2024, 135, 123906. [Google Scholar] [CrossRef]
- Lee, J.S.H.; Sutter, T.M.; Karapetrov, G.; Musumeci, P.; Kogar, A. Topological Phase Transition to a Hidden Charge Density Wave Liquid. arXiv 2025, arXiv:2505.04867. [Google Scholar] [CrossRef]
- Merboldt, M.; Schüler, M.; Schmitt, D.; Bange, J.P.; Bennecke, W.; Gadge, K.; Pierz, K.; Schumacher, H.W.; Momeni, D.; Steil, D.; et al. Observation of Floquet States in Graphene. Nat. Phys. 2025, 21, 1093–1099. [Google Scholar] [CrossRef] [PubMed]
- Demidov, V.E.; Urazhdin, S.; Anane, A.; Cros, V.; Demokritov, S.O. Spin–Orbit-Torque Magnonics. J. Appl. Phys. 2020, 127, 170901. [Google Scholar] [CrossRef]
- Fischer, T.; Kewenig, M.; Bozhko, D.A.; Serga, A.A.; Syvorotka, I.I.; Ciubotaru, F.; Adelmann, C.; Hillebrands, B.; Chumak, A.V. Experimental Prototype of a Spin-Wave Majority Gate. Appl. Phys. Lett. 2017, 110, 152401. [Google Scholar] [CrossRef]
- Balynsky, M.; Kozhevnikov, A.; Khivintsev, Y.; Bhowmick, T.; Gutierrez, D.; Chiang, H.; Dudko, G.; Filimonov, Y.; Liu, G.; Jiang, C.; et al. Magnonic Interferometric Switch for Multi-Valued Logic Circuits. J. Appl. Phys. 2017, 121, 024504. [Google Scholar] [CrossRef]
- Imada, M.; Fujimori, A.; Tokura, Y. Metal-Insulator Transitions. Rev. Mod. Phys. 1998, 70, 1039–1263. [Google Scholar] [CrossRef]
- Han, Q.; Millis, A. Lattice Energetics and Correlation-Driven Metal-Insulator Transitions: The Case of Ca2RuO4. Phys. Rev. Lett. 2018, 121, 067601. [Google Scholar] [CrossRef]
- Bertinshaw, J.; Gurung, N.; Jorba, P.; Liu, H.; Schmid, M.; Mantadakis, D.T.; Daghofer, M.; Krautloher, M.; Jain, A.; Ryu, G.H.; et al. Unique Crystal Structure of Ca2RuO4 in the Current Stabilized Semimetallic State. Phys. Rev. Lett. 2019, 123, 137204. [Google Scholar] [CrossRef]
- Tsubaki, K.; Tsurumaki-Fukuchi, A.; Katase, T.; Kamiya, T.; Arita, M.; Takahashi, Y. Dynamics of an Electrically Driven Phase Transition in Ca2RuO4 Thin Films: Nonequilibrium High-Speed Resistive Switching in the Absence of an Abrupt Thermal Transition. Adv. Electron. Mater. 2023, 9, 2201303. [Google Scholar] [CrossRef]
- Mattoni, G.; Yonezawa, S.; Nakamura, F.; Maeno, Y. Role of Local Temperature in the Current-Driven Metal–Insulator Transition of Ca2RuO4. Phys. Rev. Mater. 2020, 4, 114414. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical Mean-Field Theory of Strongly Correlated Fermion Systems and the Limit of Infinite Dimensions. Rev. Mod. Phys. 1996, 68, 13–125. [Google Scholar] [CrossRef]
- Matthies, A.; Li, J.; Eckstein, M. Control of Competing Superconductivity and Charge Order by Nonequilibrium Currents. Phys. Rev. B 2018, 98, 180502. [Google Scholar] [CrossRef]
- Chiriacò, G.; Millis, A.J. Voltage-Induced Metal-Insulator Transition in a One-Dimensional Charge Density Wave. Phys. Rev. B 2018, 98, 205152. [Google Scholar] [CrossRef]
- Chiriacò, G.; Millis, A.J. Polarity Dependent Heating at the Phase Interface in Metal-Insulator Transitions. Phys. Rev. B 2020, 102, 085116. [Google Scholar] [CrossRef]
- Zhou, X.; Jiao, Y.; Li, H. Manipulating the Metal–Insulator Transitions and Thermoelectric Bi-Functionality for Correlated Vanadium Dioxide Pellets. Appl. Phys. Lett. 2024, 125, 032103. [Google Scholar] [CrossRef]
- Bradicich, A.; Yu, Y.; Brown, T.D.; Jardali, F.; Kumar, S.; Williams, R.S.; Shamberger, P.J. Electrically-Driven Metal-Insulator Transitions Emerging from Localizing Current Density and Temperature. Adv. Electron. Mater. 2025, 11, 2400975. [Google Scholar] [CrossRef]
- Kabir, S.; Nirantar, S.; Monshipouri, M.; Low, M.X.; Walia, S.; Sriram, S.; Bhaskaran, M. Device Geometry Insights for Efficient Electrically Driven Insulator-to-Metal Transition in Vanadium Dioxide Thin-Films. Adv. Electron. Mater. 2022, 8, 2100428. [Google Scholar] [CrossRef]
- Cao, X.; Chang, T.; Shao, Z.; Xu, F.; Luo, H.; Jin, P. Challenges and Opportunities toward Real Application of VO2-Based Smart Glazing. Matter 2020, 2, 862–881. [Google Scholar] [CrossRef]
- Cao, R.; Zhang, X.; Liu, S.; Lu, J.; Wang, Y.; Jiang, H.; Yang, Y.; Sun, Y.; Wei, W.; Wang, J.; et al. Compact Artificial Neuron Based on Anti-Ferroelectric Transistor. Nat. Commun. 2022, 13, 7018. [Google Scholar] [CrossRef]
- Christensen, D.V.; Dittmann, R.; Linares-Barranco, B.; Sebastian, A.; Le Gallo, M.; Redaelli, A.; Slesazeck, S.; Mikolajick, T.; Spiga, S.; Menzel, S.; et al. 2022 Roadmap on Neuromorphic Computing and Engineering. Neuromorphic Comput. Eng. 2022, 2, 022501. [Google Scholar] [CrossRef]
- Gao, X.; Roskamp, T.J.; Swoboda, T.; Rosário, C.M.M.; Smink, S.; Muñoz Rojo, M.; Hilgenkamp, H. Multibridge VO2 -Based Resistive Switching Devices in a Two-Terminal Configuration. Adv. Electron. Mater. 2023, 9, 2300304. [Google Scholar] [CrossRef]
- Chiriacò, G. Thermal Purcell effect and cavity-induced renormalization of dissipations. Phys. Rev. B 2024, 110, L161107. [Google Scholar] [CrossRef]

| Phase | Material | Use Case | References |
|---|---|---|---|
| SC | on-chip , Nb nanowires | Superconducting switches and interconnects | [24,117,125,128] |
| Superconducting transistors | [115,126,127] | ||
| IMT | doped | Smart devices | [70,77,167] |
| Resistive Switch | [69,76,77,78,135,170] | ||
| Nanoscale | Memory | [135,140,141] | |
| memristor arrays | Neuromorphic computing | [136,137,138,139] | |
| FE | Ultrafast memory | [27] | |
| hBN | Memory (FeFET) | [35] | |
| Electronic FeRAM | [32] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiriacò, G. Non-Equilibrium Quantum Materials for Electronics. Electronics 2025, 14, 3552. https://doi.org/10.3390/electronics14173552
Chiriacò G. Non-Equilibrium Quantum Materials for Electronics. Electronics. 2025; 14(17):3552. https://doi.org/10.3390/electronics14173552
Chicago/Turabian StyleChiriacò, Giuliano. 2025. "Non-Equilibrium Quantum Materials for Electronics" Electronics 14, no. 17: 3552. https://doi.org/10.3390/electronics14173552
APA StyleChiriacò, G. (2025). Non-Equilibrium Quantum Materials for Electronics. Electronics, 14(17), 3552. https://doi.org/10.3390/electronics14173552








