Hyperspectral Image Classification Using a Spectral-Cube Gated Harmony Network
Abstract
1. Introduction
- We construct a lightweight model integrating a CNN with dynamic gating mechanisms, and propose a Spectral Cooperative Parallel Convolution (SCPC) module to replace the traditional 2D-CNN. SCPC employs a multi-branch interaction mechanism and achieves efficient decoupling-complementarity of spectral–spatial features through a dual-path parallel architecture. Consequently, SCPC reduces the parameter count while enhancing feature discriminability in mixed land-cover boundaries, and effectively addresses the dimensional coupling limitations of traditional single-path methods;
- We design a Dual-Gated Fusion (DGF) module. This module adopts a multi-stage gating aggregation mechanism that decomposes feature processing into local and global branches. The local branch captures neighborhood features through grouped convolution. The global branch establishes long-range spatial correlations through a lightweight attention mechanism. Finally, cross-scale feature complementarity is achieved through adaptive weight fusion, reducing computational overhead while preserving multi-level information;
- SCGHN achieves hierarchical integration of local details and cross-channel contextual information by combining 3D convolution, SCPC and DGF. Therefore, this model significantly enhances the high-level semantic representation capability of HSI while maintaining computational efficiency.
2. Proposed Method
2.1. Architecture of SCGHN Model
2.2. Multimodal Input Preprocessing (MIPP) Module
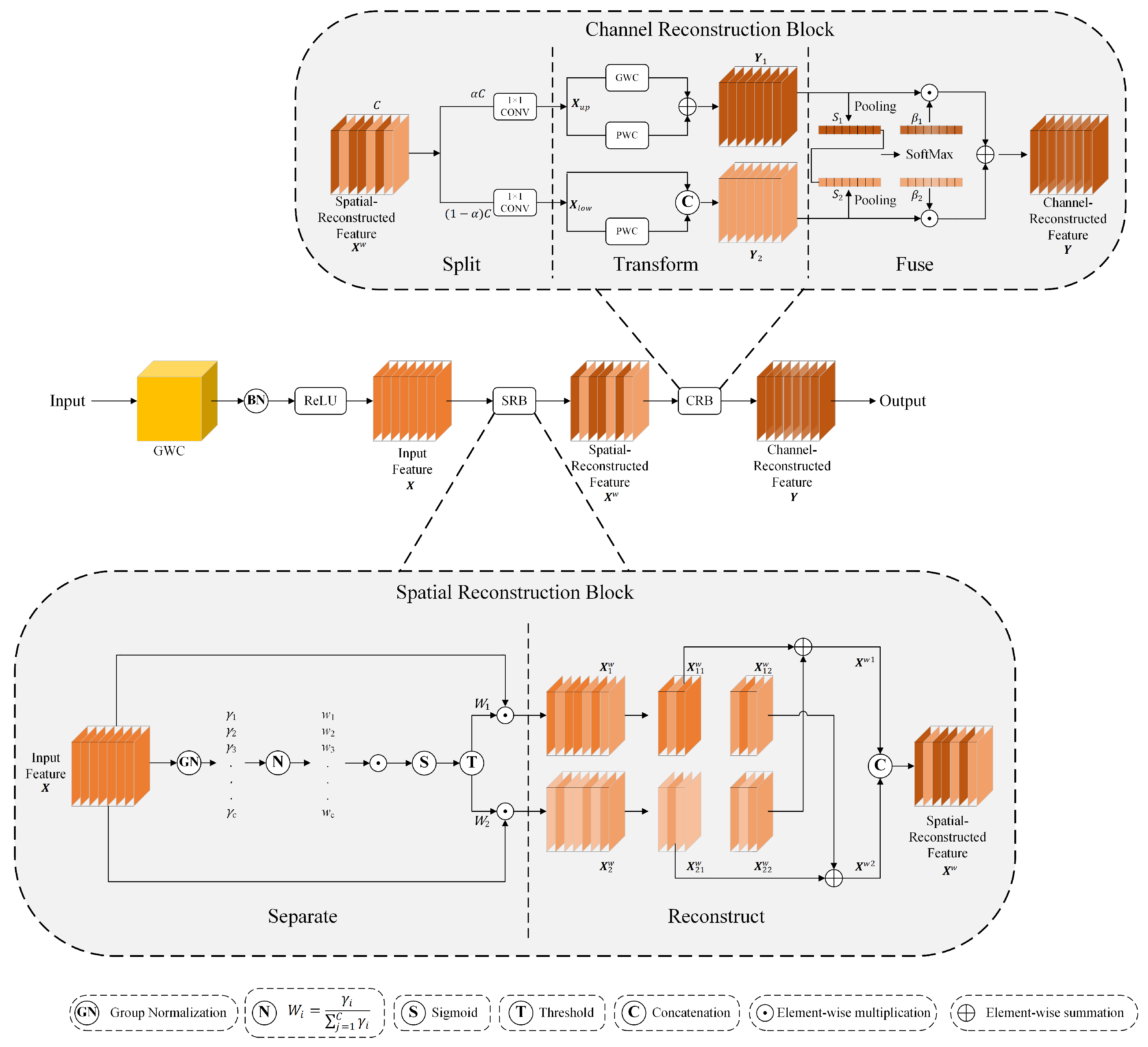
2.3. Spectral Cooperative Parallel Convolution (SCPC) Module
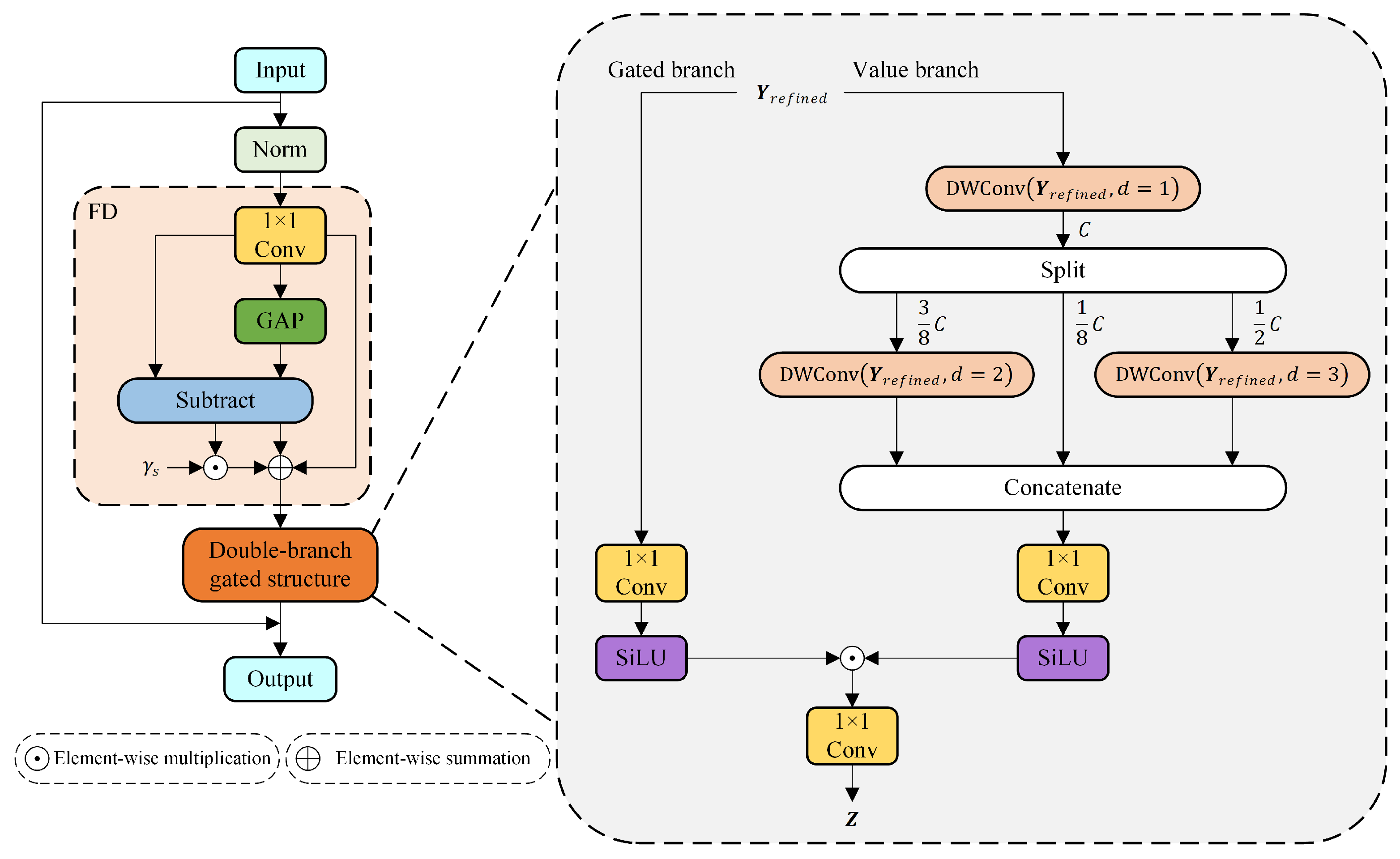
2.4. Dual-Gated Fusion (DGF) Module
3. Experimental Results and Analysis
3.1. Hyperspectral Datasets
3.2. Experimental Setup
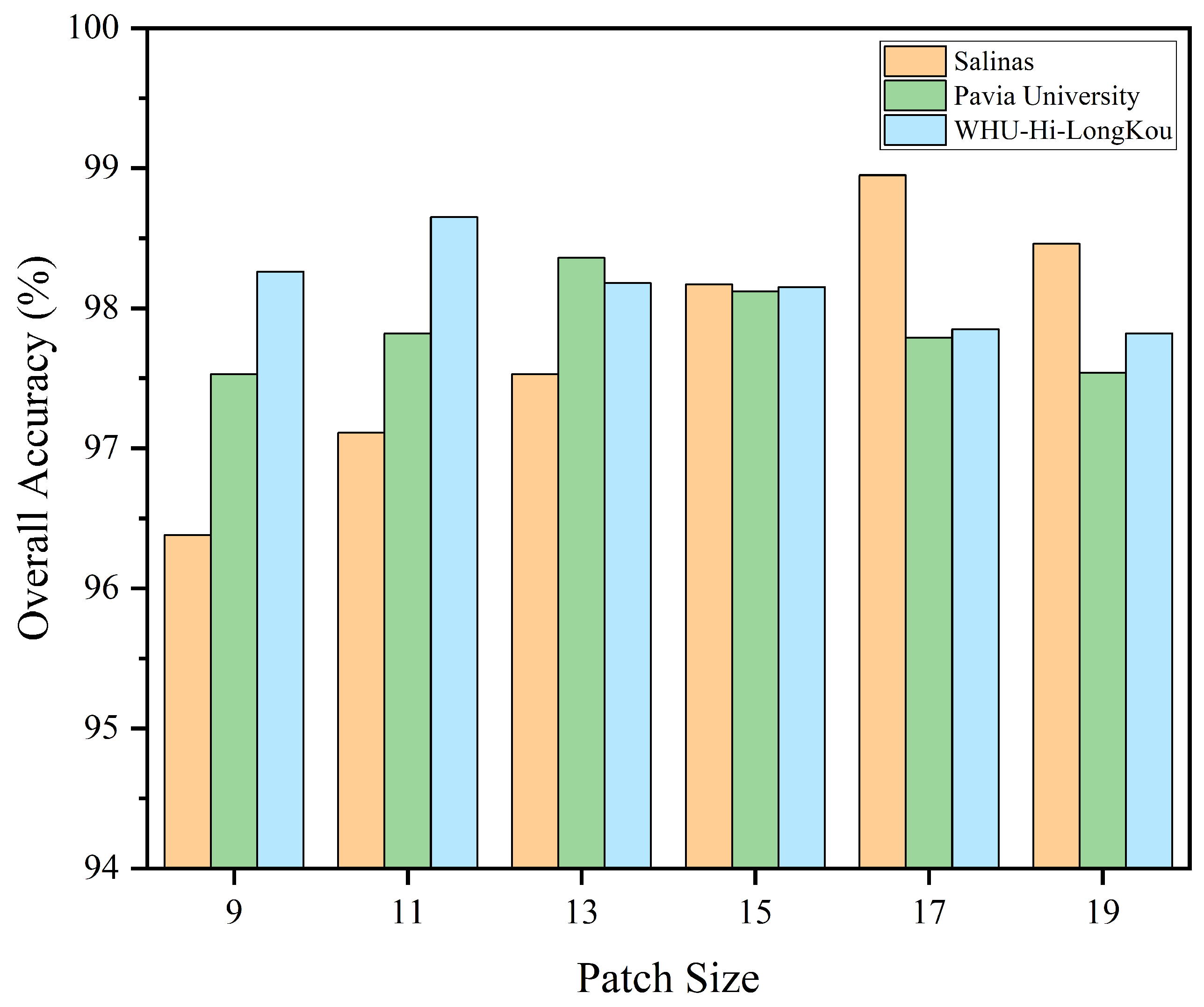
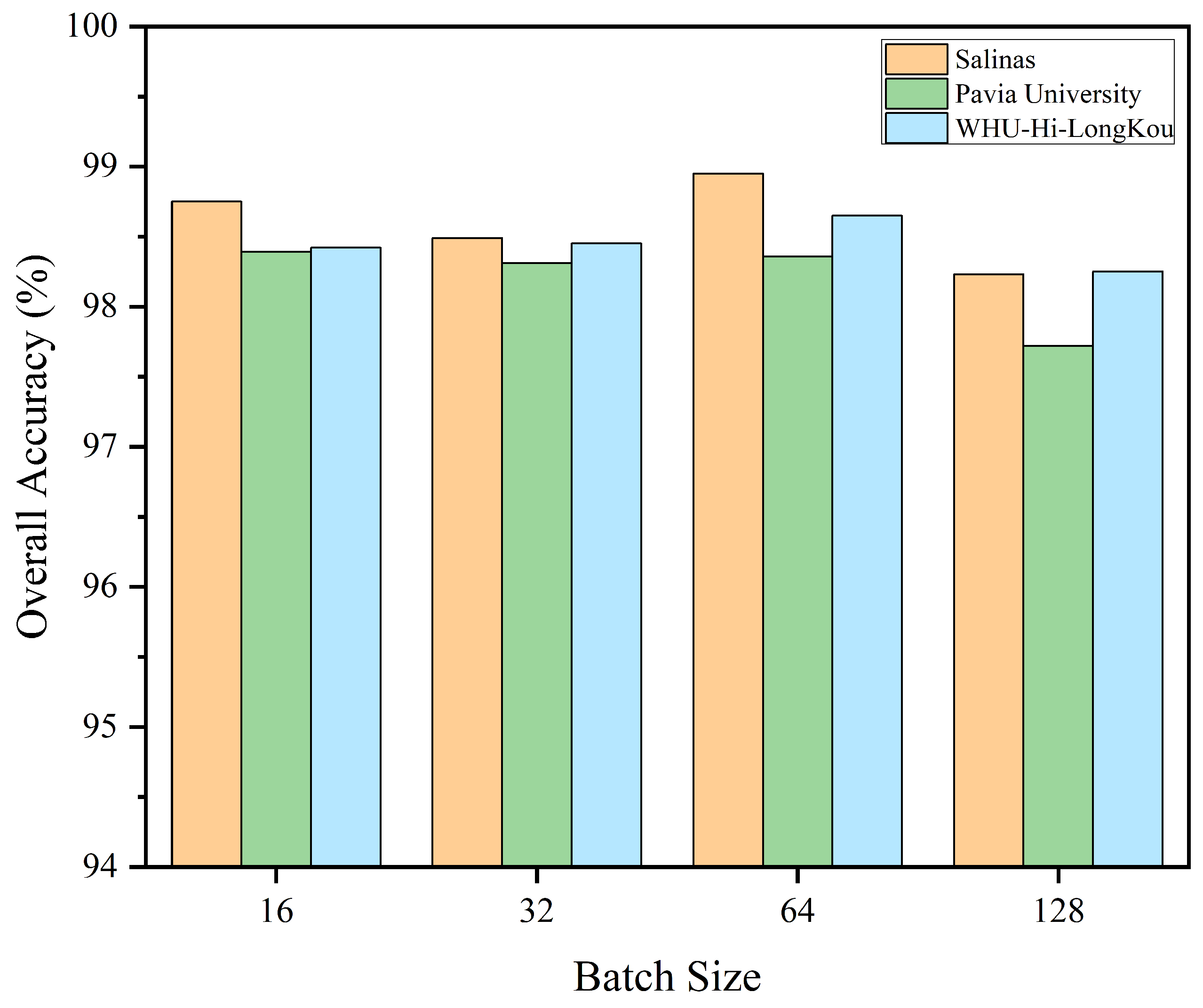
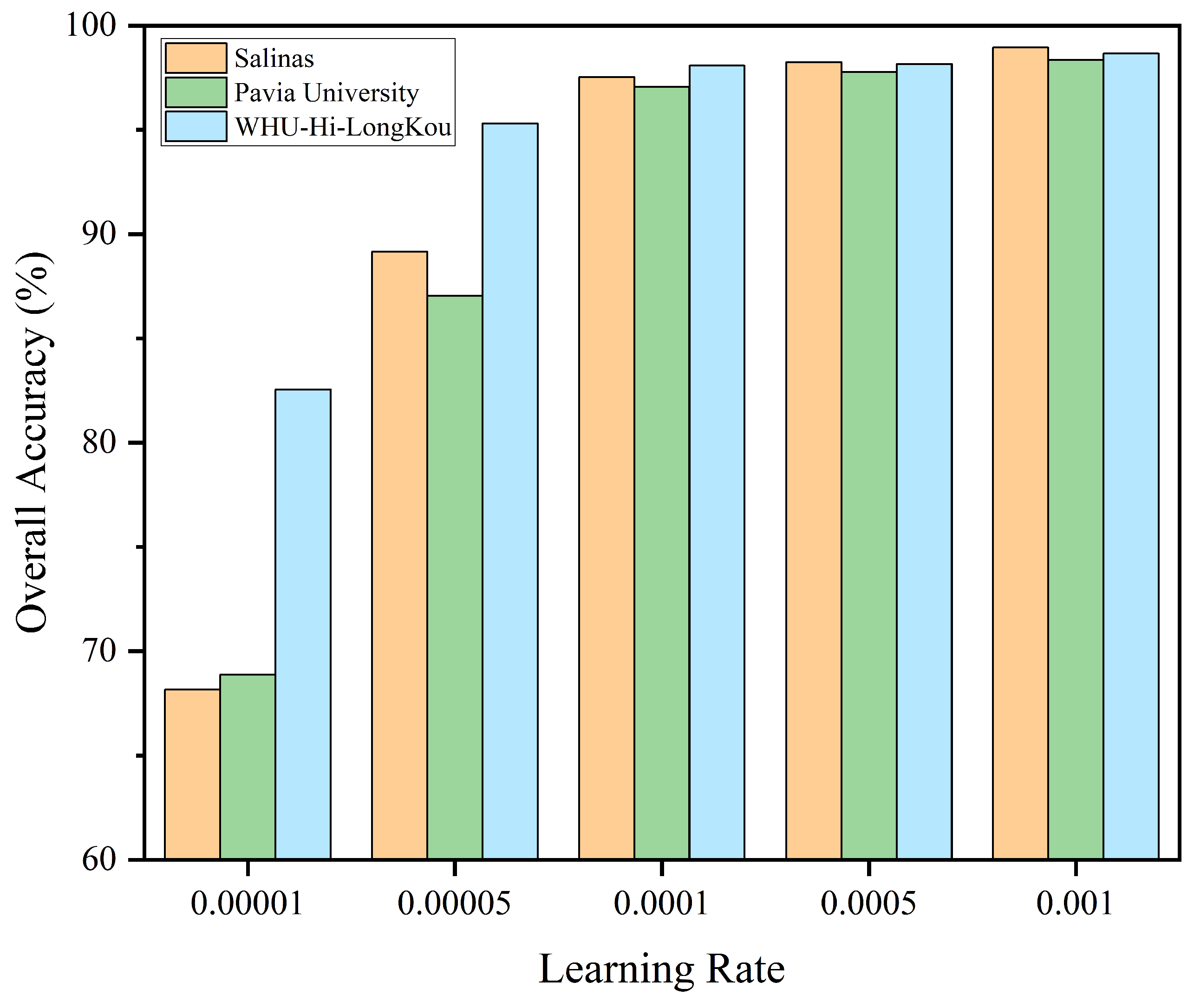
3.3. Analysis on the Settings of Key Parameters
3.4. Ablation Experiments
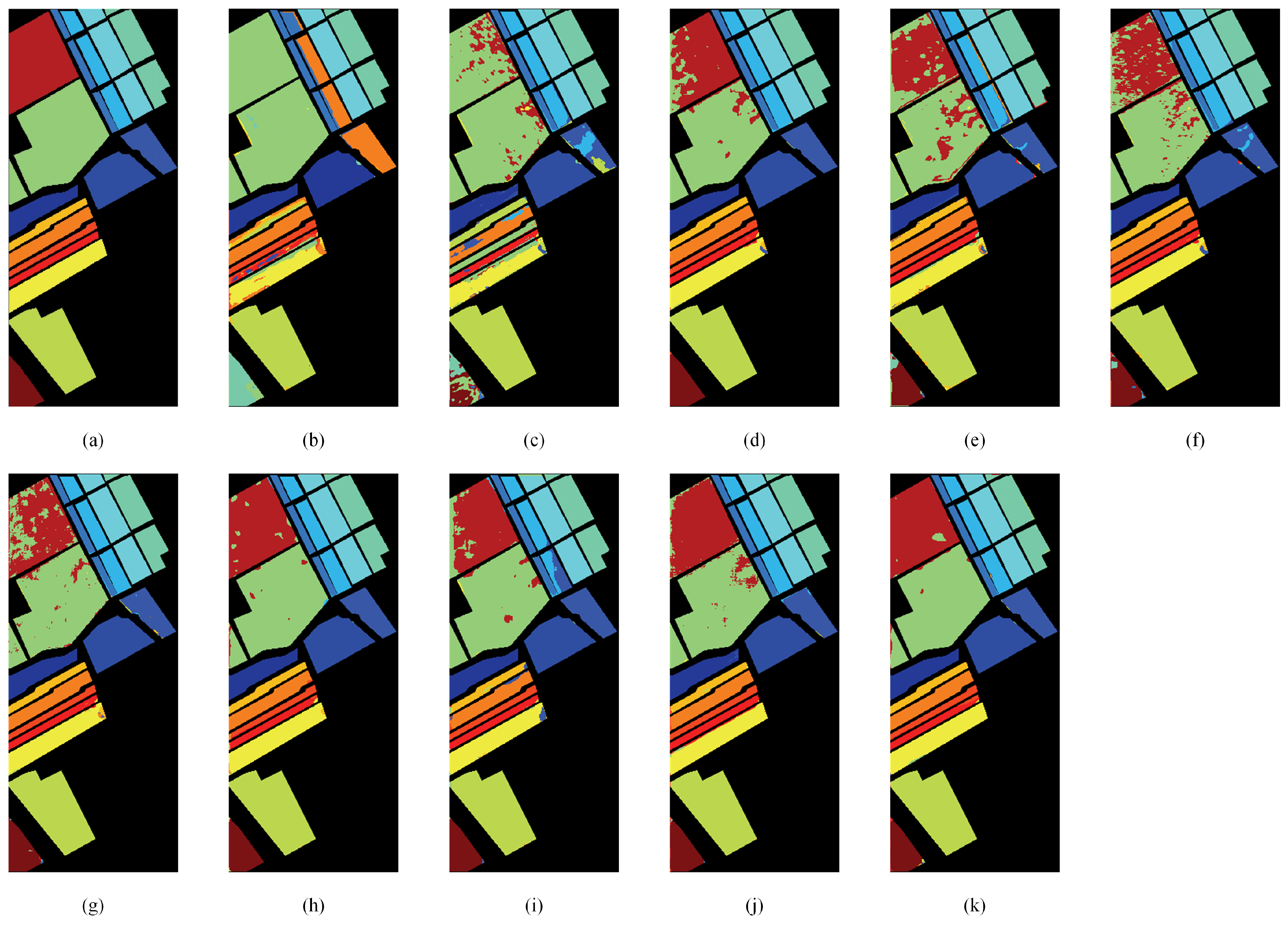
3.5. Comparison with State-of-the-Art Methods
3.6. Analysis on Model Complexity
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HSIC | Hyperspectral image classification |
| HSI | Hyperspectral image |
| SCGHN | Spectral-Cube Gated Harmony Network |
| MIPP | Multimodal Input Preprocessing |
| SCPC | Spectral Cooperative Parallel Convolution |
| DGF | Dual-Gated Fusion |
| LCD | Lightweight Classification Decision |
| SCRConv | Spatial-Channel Reconstruction Convolution |
| SRB | Spatial Reconstruction Block |
| CRB | Channel Reconstruction Block |
| HC32 | 3D–2D Hybrid Convolution |
References
- Yue, J.; Fang, L.; Ghamisi, P.; Xie, W.; Li, J.; Chanussot, J. Optical remote sensing image understanding with weak supervision: Concepts, methods, and perspectives. IEEE Geosci. Remote Sens. Mag. 2022, 10, 250–269. [Google Scholar] [CrossRef]
- Lee, M.A.; Huang, Y.; Yao, H.; Thomson, S.J.; Bruce, L.M. Determining the effects of storage on cotton and soybean leaf samples for hyperspectral analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2562–2570. [Google Scholar] [CrossRef]
- Chi, J.; Crawford, M.M. Spectral unmixing-based crop residue estimation using hyperspectral remote sensing data: A case study at Purdue university. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2531–2539. [Google Scholar] [CrossRef]
- Sahadevan, A.S. Extraction of spatial-spectral homogeneous patches and fractional abundances for field-scale agriculture monitoring using airborne hyperspectral images. Comput. Electron. Agric. 2021, 188, 106325. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of spectral–temporal response surfaces by combining multispectral satellite and hyperspectral UAV imagery for precision agriculture applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Ryan, J.P.; Davis, C.O.; Tufillaro, N.B.; Kudela, R.M.; Gao, B.C. Application of the hyperspectral imager for the coastal ocean to phytoplankton ecology studies in Monterey Bay, CA, USA. Remote Sens. 2014, 6, 1007–1025. [Google Scholar] [CrossRef]
- Brook, A.; Dor, E.B. Quantitative detection of settled dust over green canopy using sparse unmixing of airborne hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 884–897. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Tong, Q.; Sun, X. The Spectral Crust project—Research on new mineral exploration technology. In Proceedings of the 2012 4th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Shanghai, China, 4–7 June 2012. [Google Scholar]
- Lampropoulos, G.A.; Liu, T.; Qian, S.E.; Fei, C. Hyperspectral classification fusion for classifying different military targets. In Proceedings of the IGARSS 2008-2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008. [Google Scholar]
- Ardouin, J.P.; Lévesque, J.; Rea, T.A. A demonstration of hyperspectral image exploitation for military applications. In Proceedings of the 2007 10th International Conference on Information Fusion, Quebec, QC, Canada, 9–12 July 2007. [Google Scholar]
- Yuan, J.; Wang, S.; Wu, C.; Xu, Y. Fine-grained classification of urban functional zones and landscape pattern analysis using hyperspectral satellite imagery: A case study of Wuhan. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3972–3991. [Google Scholar] [CrossRef]
- Zhang, C.; Mou, L.; Shan, S.; Zhang, H.; Qi, Y.; Yu, D.; Zhu, X.; Sun, N.; Zheng, X.; Ma, X. Medical hyperspectral image classification based weakly supervised single-image global learning network. Eng. Appl. Artif. Intell. 2024, 133, 108042. [Google Scholar] [CrossRef]
- Sun, L.; Wu, Z.; Liu, J.; Xiao, L.; Wei, Z. Supervised spectral–spatial hyperspectral image classification with weighted Markov random fields. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1490–1503. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Archibald, R.; Fann, G. Feature selection and classification of hyperspectral images with support vector machines. IEEE Geosci. Remote Sens. Lett. 2007, 4, 674–677. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and spatial classification of hyperspectral data using SVMs and morphological profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef]
- Zhuang, L.; Gao, L.; Ni, L.; Zhang, B. An improved expectation maximization algorithm for hyperspectral image classification. In Proceedings of the 2013 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 26–28 June 2013. [Google Scholar]
- Feng, W.; Bao, W. Weight-based rotation forest for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2167–2171. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Tian, J. Local manifold learning-based k-nearest-neighbor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Cai, R.; Liu, C.; Li, J. Efficient phase-induced gabor cube selection and weighted fusion for hyperspectral image classification. Sci. China Technol. Sci. 2022, 65, 778–792. [Google Scholar] [CrossRef]
- Liang, B.; Liu, C.; Li, J.; Plaza, A.; Bioucas-Dias, J.M. Semisupervised discriminative random field for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12403–12414. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Villa, A.; Benediktsson, J.A.; Chanussot, J.; Bruzzone, L. Classification of hyperspectral images by using extended morphological attribute profiles and independent component analysis. IEEE Geosci. Remote Sens. Lett. 2010, 8, 542–546. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Liu, P.; Li, J.; Wang, L.; He, G. Remote sensing data fusion with generative adversarial networks: State-of-the-art methods and future research directions. IEEE Geosci. Remote Sens. Mag. 2022, 10, 295–328. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Contextual deep CNN based hyperspectral classification. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, T.; Wu, Q.; Li, Y.; Zhong, Q. An implicit transformer-based fusion method for hyperspectral and multispectral remote sensing image. Int. J. Appl. Earth Obs. Geoinf. 2024, 131, 103955. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, K.; Li, M.; Huang, Y.; Yang, G. A Position-Temporal Awareness Transformer for Remote Sensing Change Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3432320. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, X.; Li, S.; Plaza, A. Hyperspectral image classification using groupwise separable convolutional vision transformer network. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3377610. [Google Scholar] [CrossRef]
- Chang, Y.; Liu, Q.; Zhang, Y.; Dong, Y. Unsupervised Multi-view Graph Contrastive Feature Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3431680. [Google Scholar] [CrossRef]
- Wang, M.; Sun, Y.; Xiang, J.; Sun, R.; Zhong, Y. Joint classification of hyperspectral and LiDAR data based on adaptive gating mechanism and learnable transformer. Remote Sens. 2024, 16, 1080. [Google Scholar] [CrossRef]
- Guerri, M.F.; Distante, C.; Spagnolo, P.; Taleb-Ahmed, A. Boosting hyperspectral image classification with Gate-Shift-Fuse mechanisms in a novel CNN-Transformer approach. Comput. Electron. Agric. 2025, 237, 110489. [Google Scholar] [CrossRef]
- Li, S.; Liang, L.; Zhang, S.; Zhang, Y.; Plaza, A.; Wang, X. End-to-end convolutional network and spectral-spatial Transformer architecture for hyperspectral image classification. Remote Sens. 2024, 16, 325. [Google Scholar] [CrossRef]
- Zhong, Y.; Hu, X.; Luo, C.; Wang, X.; Zhao, J.; Zhang, L. WHU-Hi: UAV-borne hyperspectral with high spatial resolution (H2) benchmark datasets and classifier for precise crop identification based on deep convolutional neural network with CRF. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]
- Tang, X.; Yao, Y.; Ma, J.; Zhang, X.; Yang, Y.; Wang, B.; Jiao, L. SpiralMamba: Spatial-Spectral Complementary Mamba with Spatial Spiral Scan for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2025, 63, 3559137. [Google Scholar] [CrossRef]
- Li, L.; Ma, H.; Zhang, X.; Zhao, X.; Lv, M.; Jia, Z. Synthetic aperture radar image change detection based on principal component analysis and two-level clustering. Remote Sens. 2024, 16, 1861. [Google Scholar] [CrossRef]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-D deep learning approach for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Zhang, X.; Shang, S.; Tang, X.; Feng, J.; Jiao, L. Spectral partitioning residual network with spatial attention mechanism for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 3074196. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 3130716. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, T.; Tang, X.; Hu, X.; Peng, Y. CAEVT: Convolutional autoencoder meets lightweight vision transformer for hyperspectral image classification. Sensors 2022, 22, 3902. [Google Scholar] [CrossRef] [PubMed]
- Mei, S.; Song, C.; Ma, M.; Xu, F. Hyperspectral image classification using group-aware hierarchical transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, X.; Peng, Z.; Zhang, T.; Jiao, L. S2Mamba: A spatial-spectral state space model for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2025, 63, 3530993. [Google Scholar] [CrossRef]



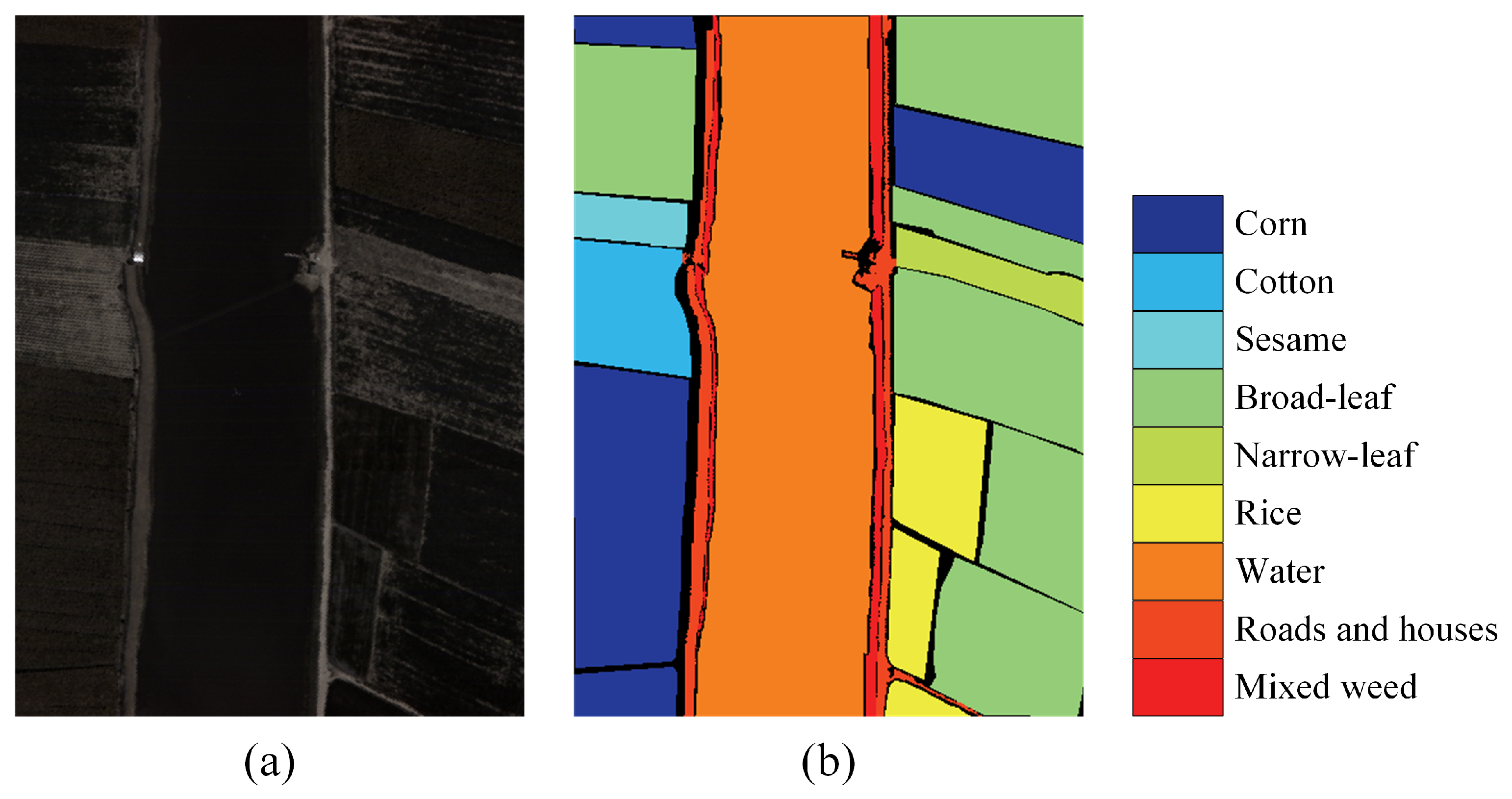


| Class NO. | Land Cover Type | Train Num | Valid Num | Test Num |
|---|---|---|---|---|
| C1 | Brocoli-green-weeds-1 | 10 | 10 | 1989 |
| C2 | Brocoli-green-weeds-2 | 18 | 19 | 3689 |
| C3 | Fallow | 10 | 10 | 1956 |
| C4 | Fallow-rough-plow | 7 | 7 | 1380 |
| C5 | Fallow-smooth | 13 | 14 | 2651 |
| C6 | Stubble | 19 | 20 | 3920 |
| C7 | Celery | 18 | 18 | 3543 |
| C8 | Grapes-untrained | 56 | 57 | 11,158 |
| C9 | Soil-vinyard-develop | 31 | 31 | 6141 |
| C10 | Corn-senesced-green-weeds | 16 | 17 | 3245 |
| C11 | Lettuce-romaine-4wk | 6 | 5 | 1057 |
| C12 | Lettuce-romaine-5wk | 10 | 9 | 1908 |
| C13 | Lettuce-romaine-6wk | 5 | 4 | 907 |
| C14 | Lettuce-romaine-7wk | 6 | 5 | 1059 |
| C15 | Vinyard-untrained | 36 | 36 | 7196 |
| C16 | Vinyard-vertical-trellis | 9 | 9 | 1789 |
| Total | 270 | 271 | 53,588 |
| Class NO. | Land Cover Type | Train Num | Valid Num | Test Num |
|---|---|---|---|---|
| C1 | Asphalt | 66 | 66 | 6499 |
| C2 | Meadows | 186 | 187 | 18,276 |
| C3 | Gravel | 21 | 21 | 2057 |
| C4 | Trees | 30 | 31 | 3003 |
| C5 | Painted metal sheets | 13 | 14 | 1318 |
| C6 | Bare Soil | 50 | 50 | 4929 |
| C7 | Bitumen | 14 | 13 | 1303 |
| C8 | Self-Blocking Bricks | 37 | 37 | 3608 |
| C9 | Shadows | 10 | 9 | 928 |
| Total | 427 | 428 | 41,921 |
| Class NO. | Land Cover Type | Train Num | Valid Num | Test Num |
|---|---|---|---|---|
| C1 | Corn | 69 | 69 | 34,373 |
| C2 | Cotton | 17 | 16 | 8341 |
| C3 | Sesame | 6 | 6 | 3019 |
| C4 | Broad-leaf | 127 | 126 | 62,959 |
| C5 | Narrow-leaf | 8 | 9 | 4134 |
| C6 | Rice | 24 | 23 | 11,807 |
| C7 | Water | 134 | 134 | 66,788 |
| C8 | Roads and houses | 14 | 15 | 7095 |
| C9 | Mixed weed | 10 | 11 | 5208 |
| Total | 409 | 409 | 203,724 |
| Group Nums | Methods | OA (%) | AA(%) | ||
|---|---|---|---|---|---|
| Salinas | 1 | HC32 | |||
| 2 | HC32 + SCPC | ||||
| 3 | HC32 + DGF | ||||
| 4 | SCGHN | ||||
| Pavia University | 1 | HC32 | |||
| 2 | HC32 + SCPC | ||||
| 3 | HC32 + DGF | ||||
| 4 | SCGHN | ||||
| WHU-Hi-LongKou | 1 | HC32 | |||
| 2 | HC32 + SCPC | ||||
| 3 | HC32 + DGF | ||||
| 4 | SCGHN |
| Group Nums | Methods | Parameters/K | FLOPs/M | |
|---|---|---|---|---|
| Salinas | 1 | HC32 | 130.48 | 23.42 |
| 2 | HC32+SCPC | 34.36 | 7.09 | |
| 3 | HC32+DGF | 151.01 | 26.83 | |
| 4 | SCGHN | 54.88 | 10.50 | |
| Pavia University | 1 | HC32 | 130.03 | 11.32 |
| 2 | HC32+SCPC | 33.91 | 3.49 | |
| 3 | HC32+DGF | 150.56 | 12.95 | |
| 4 | SCGHN | 54.44 | 5.12 | |
| WHU-Hi-LongKou | 1 | HC32 | 130.12 | 6.90 |
| 2 | HC32+SCPC | 34.09 | 2.17 | |
| 3 | HC32+DGF | 150.78 | 7.89 | |
| 4 | SCGHN | 54.51 | 3.15 |
| Group Nums | Methods | Train (s) | Test (s) | |
|---|---|---|---|---|
| Salinas | 1 | HC32 | 5.67 | 3.38 |
| 2 | HC32+SCPC | 7.32 | 4.09 | |
| 3 | HC32+DGF | 19.20 | 8.08 | |
| 4 | SCGHN | 8.34 | 4.59 | |
| Pavia University | 1 | HC32 | 7.36 | 4.41 |
| 2 | HC32+SCPC | 8.30 | 5.17 | |
| 3 | HC32+DGF | 9.59 | 5.82 | |
| 4 | SCGHN | 13.85 | 9.68 | |
| WHU-Hi-LongKou | 1 | HC32 | 6.01 | 2.69 |
| 2 | HC32+SCPC | 7.24 | 4.13 | |
| 3 | HC32+DGF | 8.94 | 4.69 | |
| 4 | SCGHN | 10.84 | 6.54 |
| Class | 2DCNN | 3DCNN | SPRN | SpectralFormer | CAEVT | GAHT | SSFTT | GSC-ViT | Mamba | SCGHN |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||||
| 2 | ||||||||||
| 3 | ||||||||||
| 4 | ||||||||||
| 5 | ||||||||||
| 6 | ||||||||||
| 7 | ||||||||||
| 8 | ||||||||||
| 9 | ||||||||||
| 10 | ||||||||||
| 11 | ||||||||||
| 12 | ||||||||||
| 13 | ||||||||||
| 14 | ||||||||||
| 15 | ||||||||||
| 16 | ||||||||||
| OA (%) | ||||||||||
| AA (%) | ||||||||||
| Class | 2DCNN | 3DCNN | SPRN | SpectralFormer | CAEVT | GAHT | SSFTT | GSC-ViT | Mamba | SCGHN |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||||
| 2 | ||||||||||
| 3 | ||||||||||
| 4 | ||||||||||
| 5 | ||||||||||
| 6 | ||||||||||
| 7 | ||||||||||
| 8 | ||||||||||
| 9 | ||||||||||
| OA (%) | ||||||||||
| AA (%) | ||||||||||
| Class | 2DCNN | 3DCNN | SPRN | SpectralFormer | CAEVT | GAHT | SSFTT | GSC-ViT | Mamba | SCGHN |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||||
| 2 | ||||||||||
| 3 | ||||||||||
| 4 | ||||||||||
| 5 | ||||||||||
| 6 | ||||||||||
| 7 | ||||||||||
| 8 | ||||||||||
| 9 | ||||||||||
| OA (%) | ||||||||||
| AA (%) | ||||||||||
| Model | Parameters/K | FLOPs/M | Train Time (s) | Test Time (s) | |
|---|---|---|---|---|---|
| Salinas | 2DCNN | 1718.16 | 57.69 | 33.25 | 8.99 |
| 3DCNN | 261.70 | 137.75 | 14.22 | 7.85 | |
| SPRN | 183.35 | 9.04 | 32.32 | 5.85 | |
| SpectralFormer | 352.40 | 36.43 | 175.26 | 27.80 | |
| CAEVT | 359.95 | 123.02 | 93.57 | 20.95 | |
| GAHT | 972.62 | 47.61 | 44.57 | 8.77 | |
| SSFTT | 148.49 | 11.40 | 7.65 | 3.78 | |
| GSC-ViT | 104.21 | 14.89 | 32.43 | 13.51 | |
| Mamba | 875.97 | 91.56 | 143.61 | 21.78 | |
| SCGHN | 54.88 | 10.50 | 8.34 | 4.59 | |
| Pavia University | 2DCNN | 1484.55 | 34.41 | 43.88 | 13.38 |
| 3DCNN | 225.12 | 91.71 | 18.88 | 12.64 | |
| SPRN | 178.78 | 8.86 | 33.81 | 8.69 | |
| SpectralFormer | 164.39 | 14.44 | 239.14 | 41.84 | |
| CAEVT | 206.09 | 56.35 | 109.21 | 20.88 | |
| GAHT | 927.11 | 45.41 | 54.52 | 13.28 | |
| SSFTT | 148.03 | 11.40 | 11.25 | 7.43 | |
| GSC-ViT | 77.90 | 11.17 | 37.91 | 19.34 | |
| Mamba | 408.73 | 35.92 | 196.09 | 34.31 | |
| SCGHN | 54.44 | 5.12 | 13.85 | 9.68 | |
| WHU-Hi-LongKou | 2DCNN | 1869.32 | 72.89 | 76.19 | 27.61 |
| 3DCNN | 200.98 | 183.22 | 23.66 | 6.90 | |
| SPRN | 184.89 | 9.16 | 46.91 | 13.20 | |
| SpectralFormer | 540.64 | 55.02 | 918.83 | 83.55 | |
| CAEVT | 454.92 | 166.40 | 166.09 | 56.04 | |
| GAHT | 1514.12 | 74.15 | 75.07 | 20.28 | |
| SSFTT | 148.03 | 11.40 | 11.00 | 7.50 | |
| GSC-ViT | 173.06 | 23.07 | 61.09 | 33.96 | |
| Mamba | 1343.89 | 132.76 | 753.44 | 66.51 | |
| SCGHN | 54.50 | 3.15 | 10.84 | 6.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Shen, W.; Zhang, Q. Hyperspectral Image Classification Using a Spectral-Cube Gated Harmony Network. Electronics 2025, 14, 3553. https://doi.org/10.3390/electronics14173553
Li N, Shen W, Zhang Q. Hyperspectral Image Classification Using a Spectral-Cube Gated Harmony Network. Electronics. 2025; 14(17):3553. https://doi.org/10.3390/electronics14173553
Chicago/Turabian StyleLi, Nana, Wentao Shen, and Qiuwen Zhang. 2025. "Hyperspectral Image Classification Using a Spectral-Cube Gated Harmony Network" Electronics 14, no. 17: 3553. https://doi.org/10.3390/electronics14173553
APA StyleLi, N., Shen, W., & Zhang, Q. (2025). Hyperspectral Image Classification Using a Spectral-Cube Gated Harmony Network. Electronics, 14(17), 3553. https://doi.org/10.3390/electronics14173553




