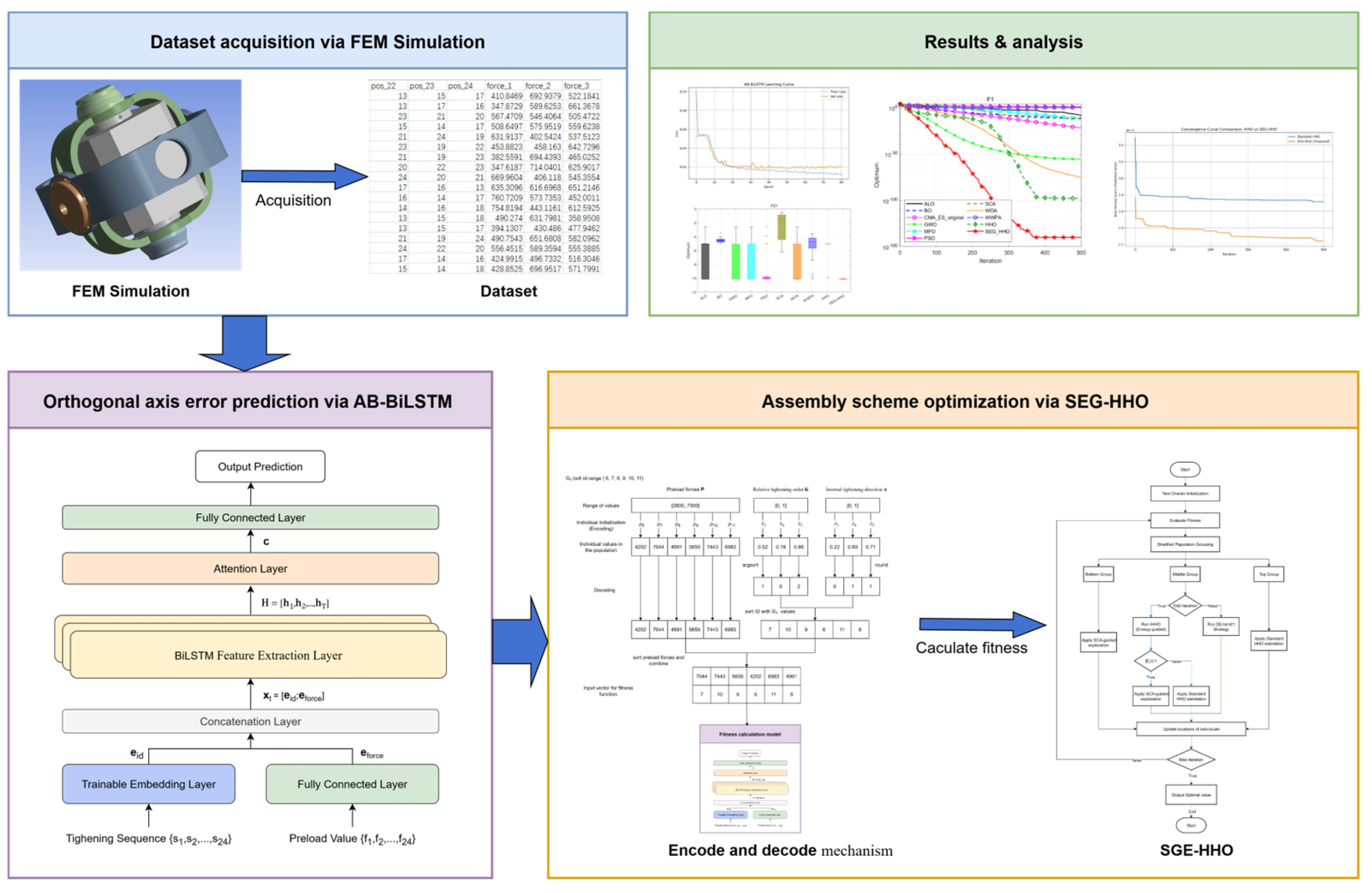
A Sequence-Aware Surrogate-Assisted Optimization Framework for Precision Gyroscope Assembly Based on AB-BiLSTM and SEG-HHO
Abstract
1. Introduction
- (1)
- Integrated Framework for Constrained Assembly Optimization: To address the computational inefficiency of FEM-based simulations and the lack of integration between time-series surrogates and constraint-aware optimization, we propose an end-to-end framework that seamlessly combines FEM data generation, deep learning surrogates, and metaheuristic optimization, enabling efficient handling of sequential dependencies and physical constraints in precision assembly.
- (2)
- High-Efficiency Surrogate Model with Interpretability: Addressing the limitations of traditional surrogate models in capturing sequential dependencies, we developed an AB-BiLSTM model specifically designed for multi-fastener assembly. This model achieves millisecond-level predictions that replace costly finite element method (FEM) evaluations, while incorporating an attention mechanism to enhance interpretability by correlating attention weights with physical phenomena such as preload-induced deformations.
- (3)
- Novel Constraint-Handling Framework and Enhanced Optimizer: To address the critical challenge of incorporating complex physical rules into the optimization loop, we propose two tightly coupled innovations. First, we introduce a constructive encoding–decoding mechanism, a core contribution of our framework that guarantees 100% of candidate solutions are physically feasible by design. This approach fundamentally differs from traditional penalty or repair methods and is pivotal for efficient search. Second, to navigate the resulting complex search space, we developed the SEG-HHO algorithm. Unlike prior HHO improvements that often focus on single-operator enhancements, SEG-HHO implements a novel stratified evolutionary framework that partitions the population into functionally distinct groups, systematically balancing global exploration and local exploitation to improve convergence and maintain solution diversity.
- (4)
- Attention Visualization for Physical Insights: To address the interpretability gap in existing time-series models, we conduct a qualitative-to-quantitative analysis of attention weights, correlating model attention patterns with key assembly steps (e.g., symmetric bolt pairs), thus offering engineers actionable insights into error sources.
2. Related Work
3. Surrogate Modeling for Assembly Error Prediction
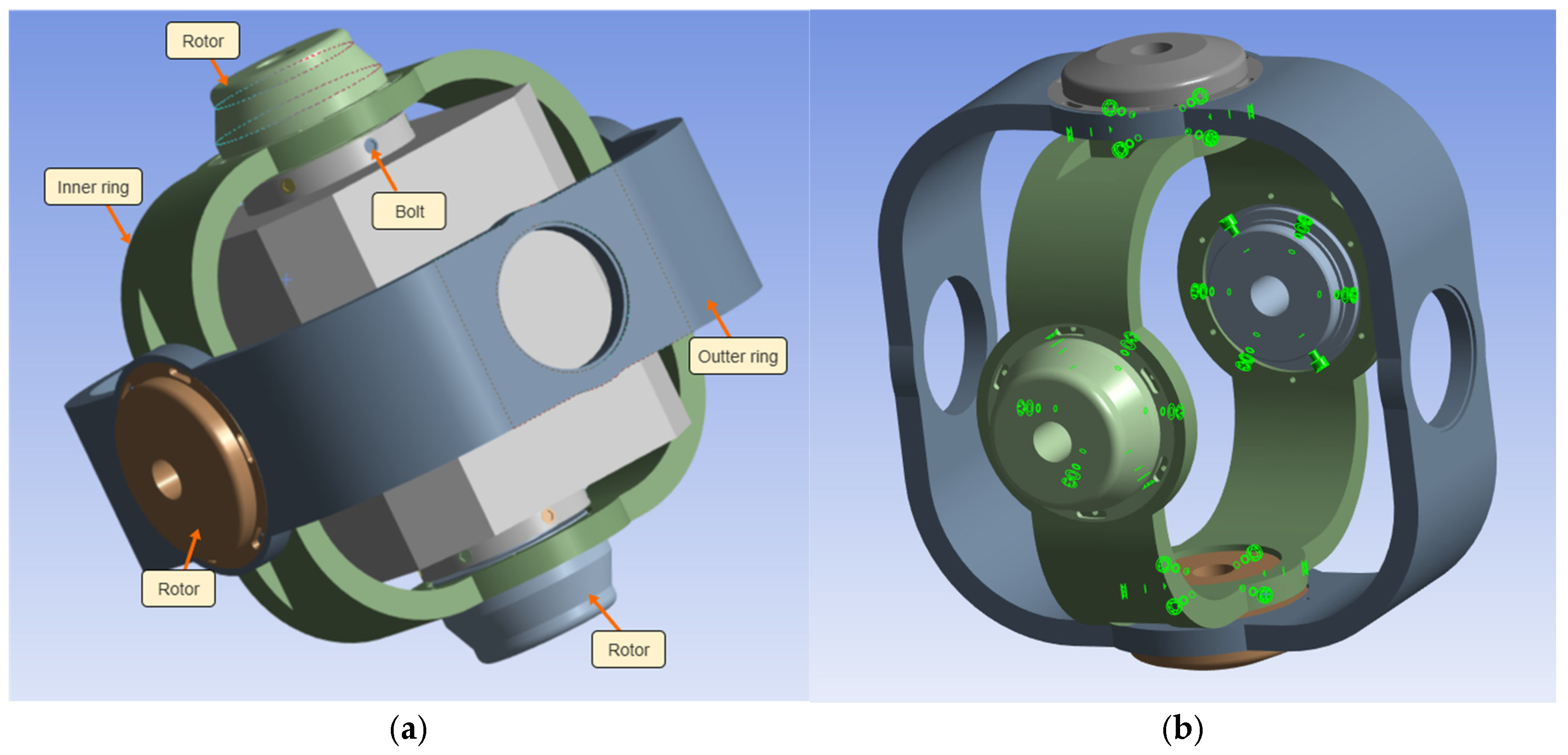
3.1. Dataset Generation via FEM Simulation
3.2. Physical Constraints of the Assembly Process
- (1)
- Grouped Assembly: The 24 bolts are logically divided into four groups, corresponding to the four rotors (inner ring measurement, inner ring drive, outer ring measurement, outer ring drive). During assembly, all bolts within one group must be tightened before proceeding to the next.
- (2)
- Fixed Inter-Group Sequence: The tightening order of the four bolt groups is strictly fixed: first the inner ring measurement rotor, followed by the inner ring drive rotor, then the outer ring measurement rotor, and finally the outer ring drive rotor. This constraint ensures consistency in the macroscopic loading process.
- (3)
- Symmetric Pairing: Within each 6-bolt group, the bolts are paired to form three physically symmetric pairs. Adhering to the principle of symmetry is crucial for ensuring balanced load application and counteracting bending moments.
- (4)
- Adjacent Tightening of Pairs: This is the most critical micro-operational constraint. Within a symmetric pair, the tightening operations for the two bolts must be consecutively adjacent. This action aims to rapidly close the local moment loop, preventing minor component warping due to one-sided forces, which is paramount for controlling the final orthogonal axis error.
3.3. Data Preprocessing and Feature Engineering
3.3.1. Feature Selection
3.3.2. Data Transformation and Normalization
3.4. The Proposed AB-BiLSTM Predictive Model
- (1)
- Input Embedding Layer: Converts the heterogeneous input of each time step (a discrete bolt ID and a continuous preload value) into a unified high-dimensional feature vector.
- (2)
- BiLSTM Feature Extraction Layer: Processes the feature sequence from both forward and backward directions to capture the complete contextual information of each assembly step.
- (3)
- Temporal Attention Layer: Applies weights to the output of the BiLSTM layer to dynamically identify and focus on the “critical steps” that have the greatest impact on the final error.
- (4)
- Output Layer: Integrates the weighted information and regresses the final orthogonal axis error value.
3.4.1. Input Embedding Layer
3.4.2. BiLSTM Feature Extraction Layer
3.4.3. Temporal Attention Mechanism
- Each hidden state is passed through a feedforward attention network to compute an unnormalized attention score :where , , and are trainable parameters, and is the attention dimension.
- The attention weights αt are obtained via a softmax over the attention scores:
- The final context vector is computed as the weighted sum of the hidden states:
3.4.4. Output Layer and Loss Function
4. Process Parameter Optimization via SEG-HHO
4.1. Mathematical Formulation of the Optimization Problem
- Decision Variables
- The tightening sequence vector , where represents the ID of the bolt being operated on at the -th tightening step. is a permutation of the set .
- The preload vector , where represents the final preload value for the bolt with ID .
- Objective Functionmin .
- ConstraintsTo formally describe the assembly constraints detailed in Section 3.2, we first define the bolt groups. The 24 bolts are partitioned into four disjoint sets: , , , and . The decision variables must satisfy the following conditions:
- , for all .
- must satisfy the four process constraints of grouping, group order, symmetry, and adjacency as defined in Section 3.2.
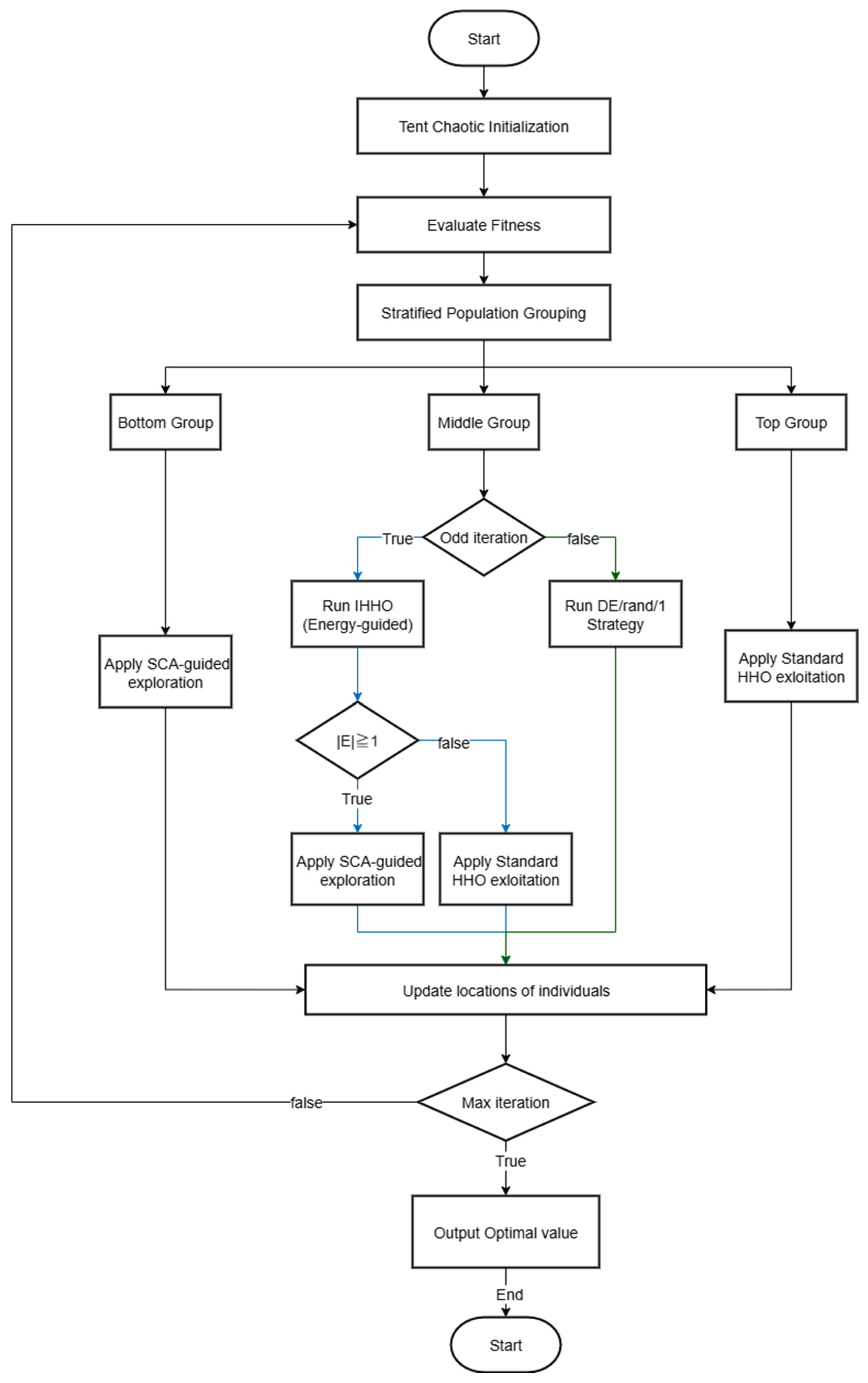
4.2. The Improved Harris Hawks Optimization Algorithm, SEG-HHO
4.2.1. Standard HHO
- Exploration Phase (): In this phase, the hawks widely search for prey, updating their position using one of two strategies based on a random number :where is the current best solution (prey’s location), is a randomly selected hawk, is the average position of the population, and to are random numbers in ; and , respectively, represent the lower and upper bounds of the search space.
- Exploitation Phase (): The hawks besiege the discovered prey. This phase simulates four different attack behaviors based on the energy and the escape probability :
- Soft Besiege: When and , the hawks gradually encircle the prey.where represents the positional difference between the current individual and the prey. represents the random jumping intensity of prey during escape, and is a random number in .
- Hard Besiege: When and , the prey is exhausted, and the hawks tighten their encirclement.
- Soft Besiege with Progressive Rapid Dives: When and , the prey attempts an erratic escape, and the hawks employ dive strategies based on Levy Flight (LF).where represents the individual’s fitness value; is the dimension of the problem; is a random vector; are random numbers within (0,1); is usually set to 1.5; and is a standard gamma function with the following expression: .
- Hard Besiege with Progressive Rapid Dives: When and , the hawks launch a final assault, incorporating Levy Flight in the final encirclement:
4.2.2. The Proposed Stratified and Hybrid Search Strategies
- Bottom Group: Incorporating SCA for Structured Exploration. The exploration mechanism of standard HHO relies on random walks, which can sometimes result in inefficient search paths. To address this, we integrate the core principles of the Sine Cosine Algorithm (SCA) to guide the bottom group. SCA leverages the smooth, periodic oscillations of sine and cosine functions, enabling exploratory individuals to probe the space around the current best solution in a wave-like, more directional manner. Its position is updated as follows:When ,where is a control parameter that linearly decreases from 2 to 0 to balance exploration and exploitation; ,, and are random control parameters for SCA in the ranges , , and respectively. This structured exploration, compared to purely random jumps, more effectively covers promising regions.
- Middle Group: Alternating Hybrid Search with HHO and Differential Evolution (DE). To improve exploration–exploitation balance and enhance population diversity, the middle group adopts an alternating hybrid strategy based on iteration count. Specifically, the algorithm executes HHO during odd-numbered iterations and a DE scheme during even-numbered iterations.In the HHO phase (odd iterations), the algorithm determines its behavior based on the prey’s escaping energy. When the energy is high, the algorithm performs exploration using enhanced strategies inspired by SCA, which enables the search agents to traverse the space more dynamically. When the energy is low, the algorithm switches to the four classical exploitation strategies of HHO, allowing the population to rapidly converge toward the current best solution.In the DE phase (even iterations), the algorithm introduces the “DE/rand/1” mutation and binomial crossover to inject diversity and prevent premature convergence. For each target vector , a mutant vector is generated using:where , , and are distinct random indices from the population and is the mutation scaling factor. This is followed by binomial crossover to produce the trial vector .DE generates new individuals based on the difference vectors between existing population members, which is an extremely effective mechanism for maintaining diversity. By introducing this “perturbation,” we significantly enhance the algorithm’s ability to escape local optima in complex multimodal problems.
- Top Group: Intensifying Local Exploitation to Accelerate Convergence. For the top group, which consists of the fittest individuals, the primary mission is the rapid and precise excavation of promising regions already discovered. Therefore, we retain and intensify the highly efficient hard and soft besiege strategies from the standard HHO. This ensures that the algorithm can leverage the collective intelligence of the population in its final stages to perform a swift refinement of the optimal solution, thereby guaranteeing final convergence accuracy.
| Algorithm 1 The Proposed SEG-HHO Algorithm |
| Input: : Population size : Problem dimension : Maximum number of iterations : Parameters for Differential Evolution : Lower and upper bounds of the search space Output: : The best solution found : The fitness of the best solution using the Tent chaotic map. . . 4: do by fitness in ascending order. into three groups: ). ). ). 11: 12: // Process the Top Group: Intensive Exploitation do 15: end for 16: 17: // Process the Bottom Group: SCA-Enhanced Exploration do 19: // This group exclusively uses the HHO exploration logic ) 21: end for 22: 23: // Process the Middle Group: Alternating Hybrid Search 0 then // Odd Iteration do ) // Includes both SCA_Enhanced_Exploration and exploitation 27: end for 28: else // Even Iteration do ) // DE operates within its own subgroup 31: end for 32: end if 33: 34: // Combine, Evaluate, and Update Global Best . 36: Evaluate the fitness of any newly generated individuals. . 38: end for 39: |
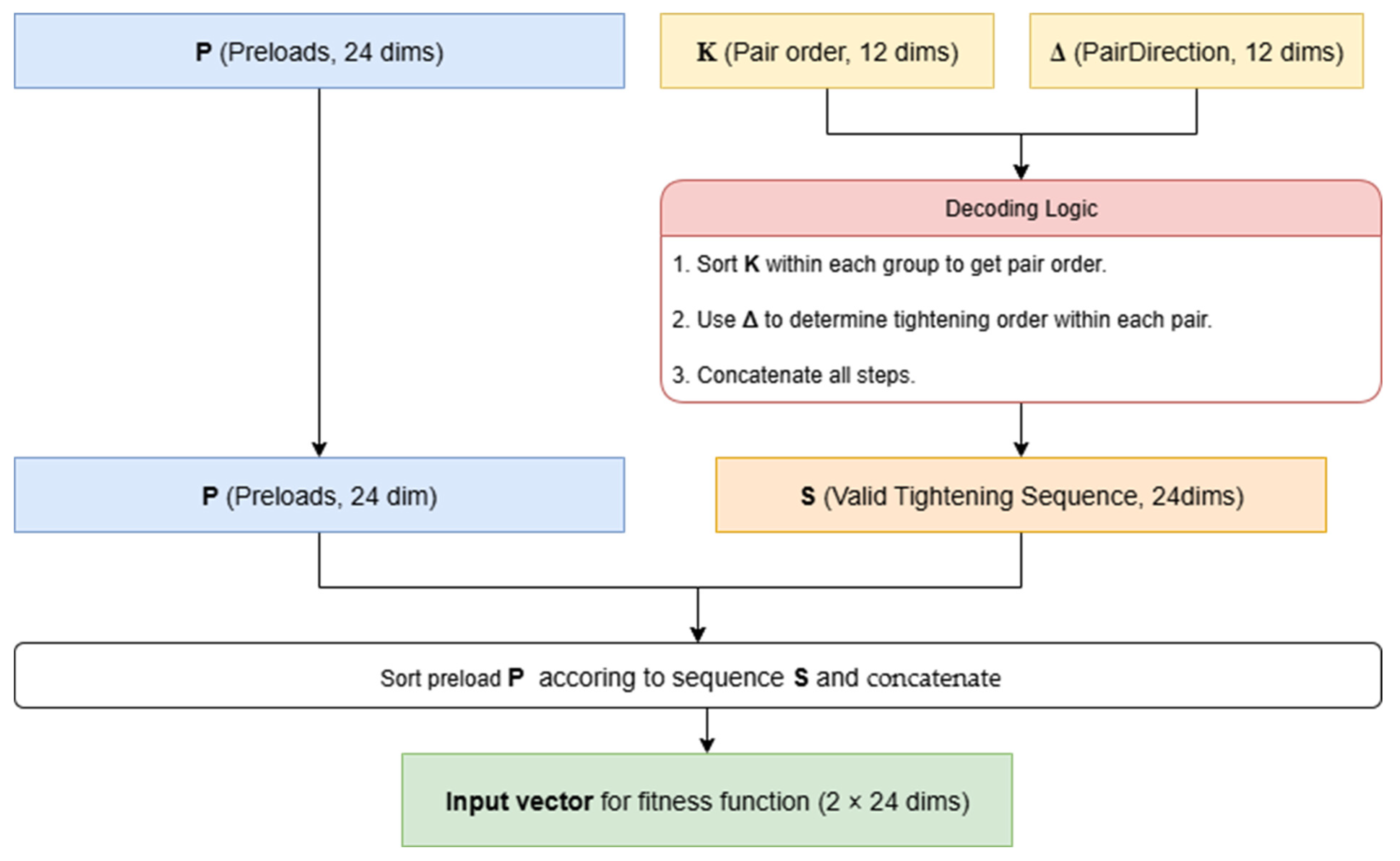
4.3. Encoding and Decoding Mechanism for Assembly Constraints
4.3.1. Definition of the Hybrid Encoding Vector
4.3.2. The Decoding Process
- Preload Decoding: The vector requires no further decoding; its 24 elements directly correspond to the final preload values for the 24 bolts.
- Tightening Sequence Decoding: The generation of the tightening sequence adheres to the predefined assembly constraints and is achieved through a programmatic decoding of the and vectors. The decoding algorithm proceeds according to the fixed group order (), with the following steps:
- For the -th bolt group (), its corresponding sequence-encoding sub-vector and direction-encoding sub-vector are extracted.
- The operation is applied to to determine the tightening order index for the three symmetric pairs within the group.
- The three pairs are processed sequentially according to . For the -th symmetric pair , its corresponding direction-encoding value is queried. If , the tightening order is ; otherwise, it is .
- After executing the decoding for all four groups, a final tightening sequence vector of length 24, which fully satisfies all adjacency and symmetry constraints, is concatenated.
4.3.3. Discussion on the Constraint-Handling Strategy
5. Experiments and Result Analysis
5.1. Experimental Setup
5.1.1. Dataset Overview and Partitioning
5.1.2. Experimental Environment
5.1.3. Performance Metrics
5.2. Performance Evaluation of Predictive Models
5.2.1. Model Selection
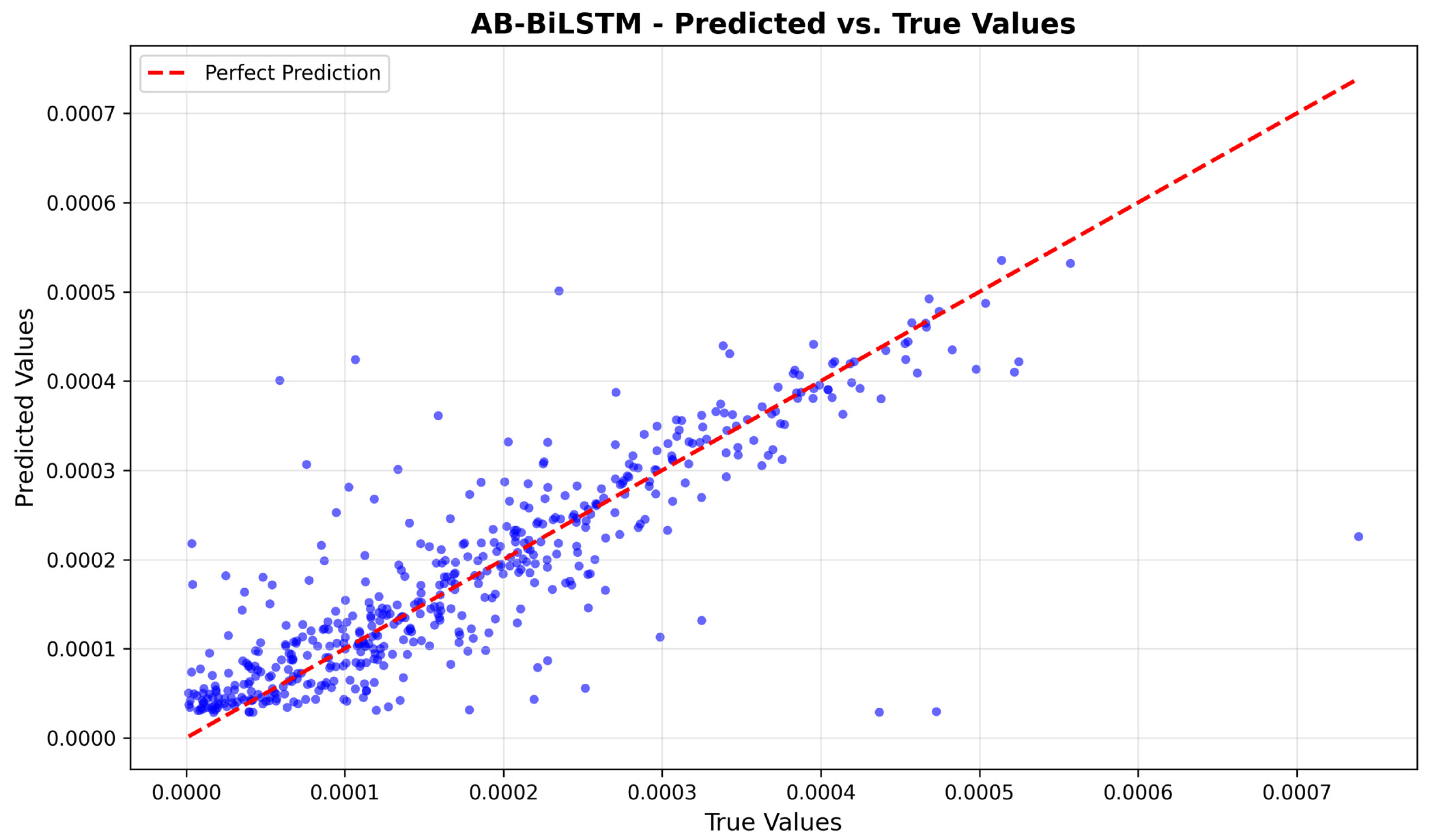
5.2.2. Experiment Results
5.2.3. Analysis of the Attention Mechanism
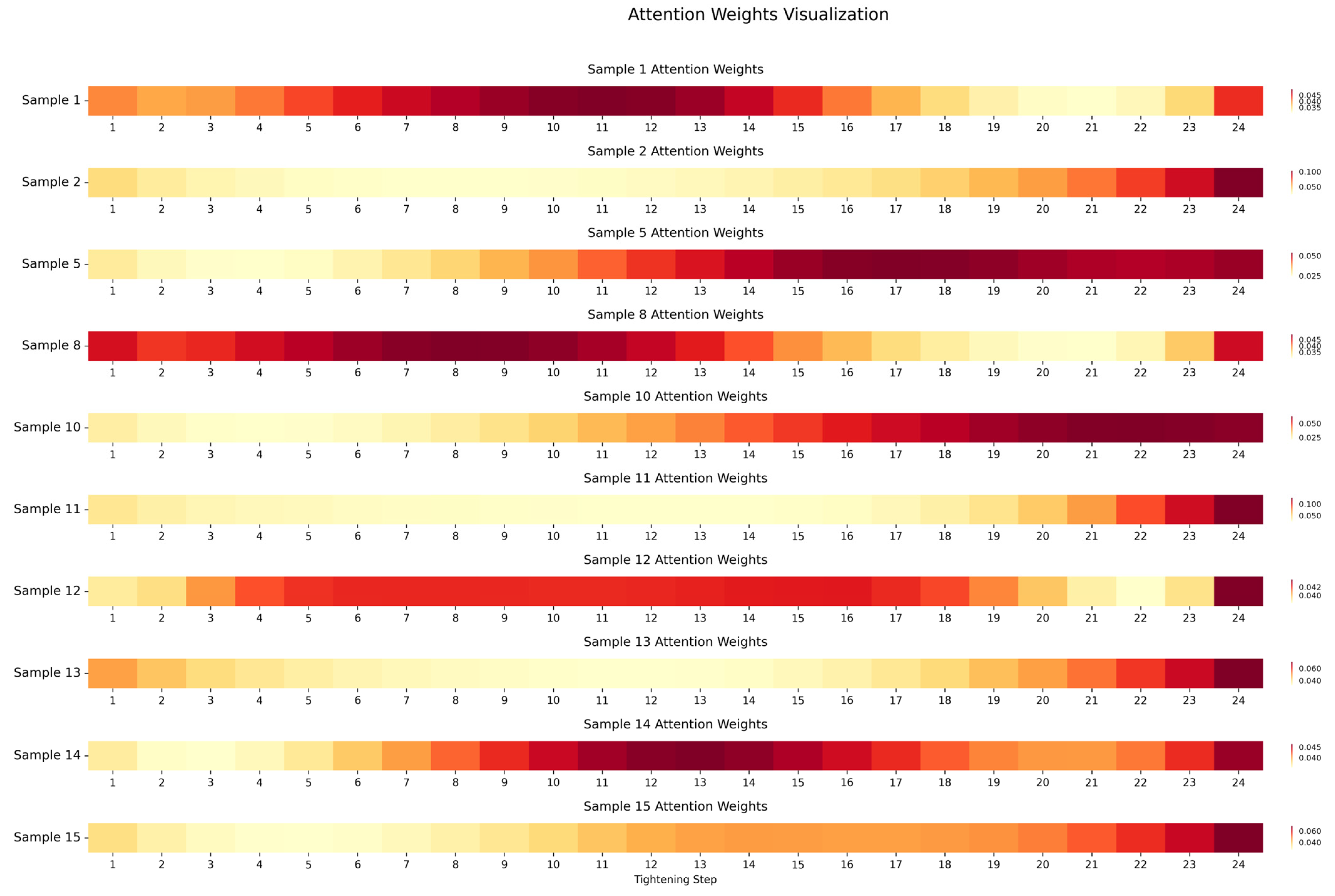
- Global Pattern: A Focus on the “Bookends” of the Process. We first visualized the attention weight heatmaps for ten representative test samples, as shown in Figure 9 (attention_visualization.jpg). The results reveal a consistent global pattern: firstly, the attention weights are significantly concentrated in the final stage of the assembly process (steps 19–24) across most samples (7 of 10), with the final step (step 24) always receiving one of the highest weights across all samples. Secondly, the first step in many samples also receives relatively high attention in early steps, forming a “bookend” pattern of focus. This pattern is highly interpretable from a physical standpoint: the first step establishes the initial baseline for the entire process, while the final few steps “lock in” the ultimate stress state and micro-deformations, making both ends critically influential on the final error.
- 3.
- Structural Knowledge Learning: Capturing the “Rhythm” of Assembly. Given that attention is not merely a response to force values, we hypothesized that it might have learned the inherent structural knowledge of the assembly process, particularly the grouping of bolts. To test this, we statistically analyzed the absolute change in attention (|ΔAttention|) across all test samples, comparing the changes that occur within a bolt group to those at the transition between groups. The box plot in Figure 12 reveals a profound finding: the variance of |ΔAttention| is significantly lower when switching between groups (right box in Figure 12) compared to the changes within a group (left box in Figure 12).This indicates that the model has learned a generalizable and standardized “group-tightening” template or meta-strategy. The smooth transition in attention at group switches suggests the model perceives the process for different component groups as highly consistent. The greater variance within a group implies that the model’s more fine-grained decision-making is focused on assessing the relative importance of the steps inside a single component’s assembly. This discovery confirms that the attention mechanism has learned not only “which steps are important” but, on a deeper level, the very “rhythm” and “modularity” of the assembly task.
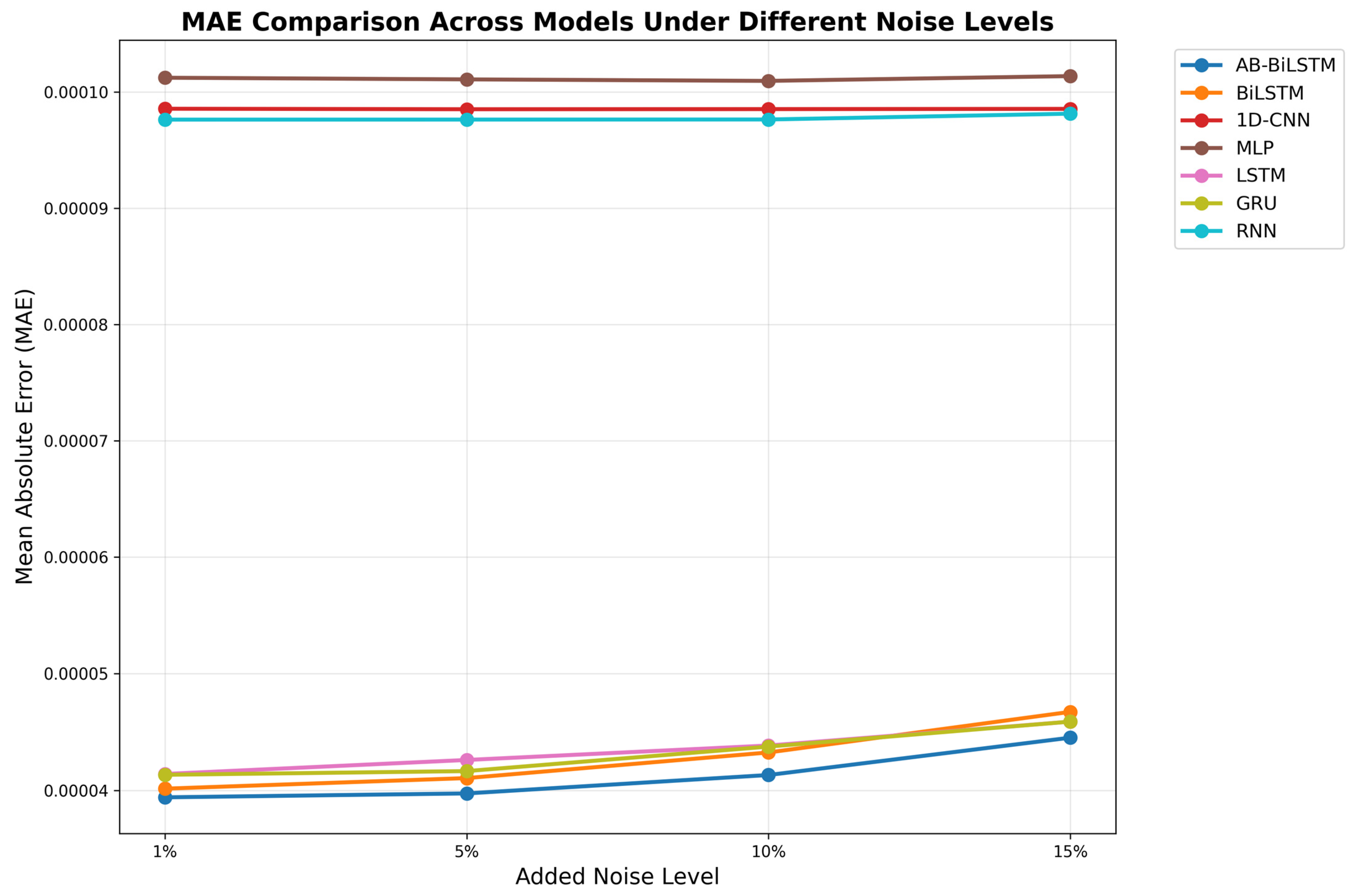
5.2.4. Anti-Noise Robustness Test
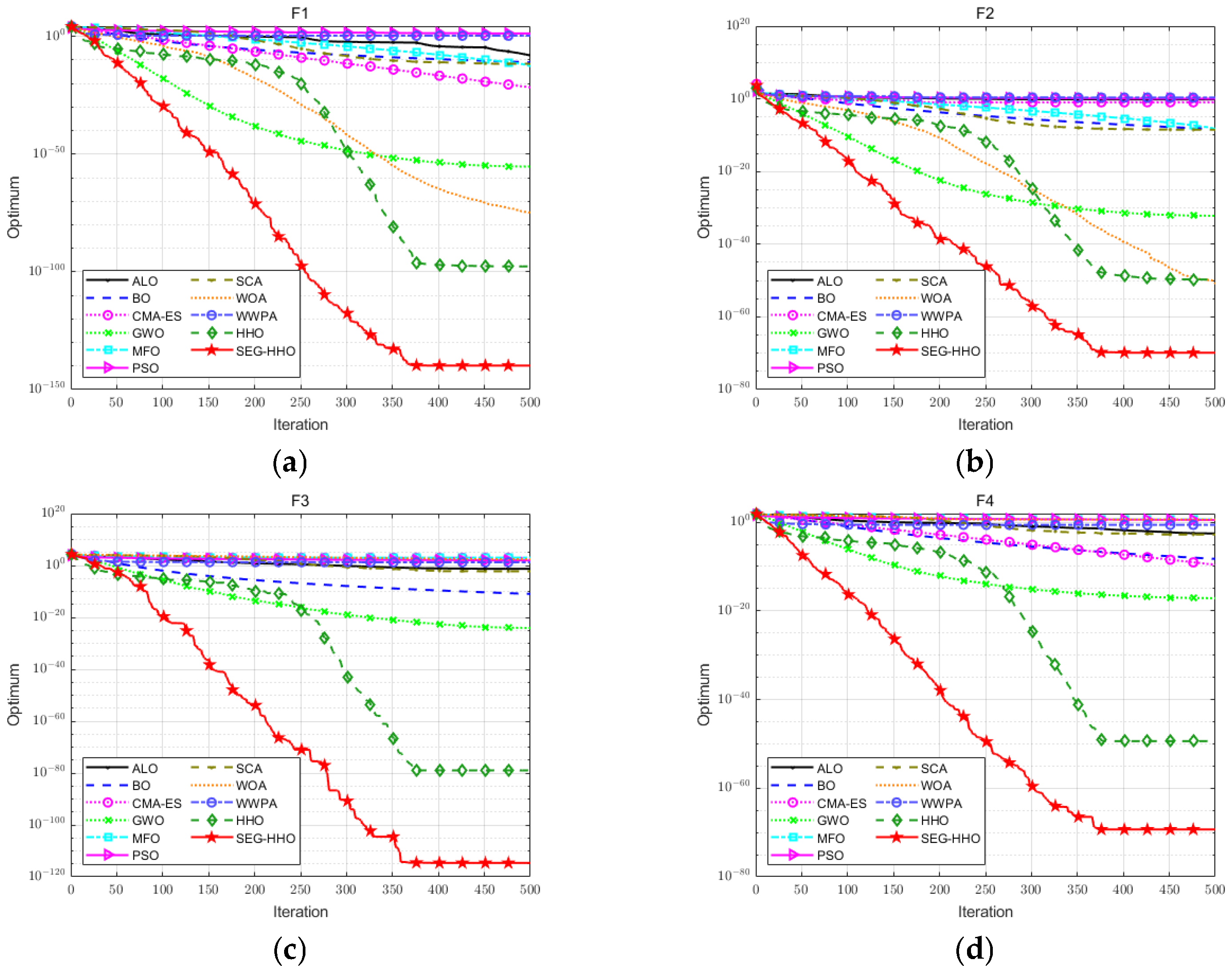
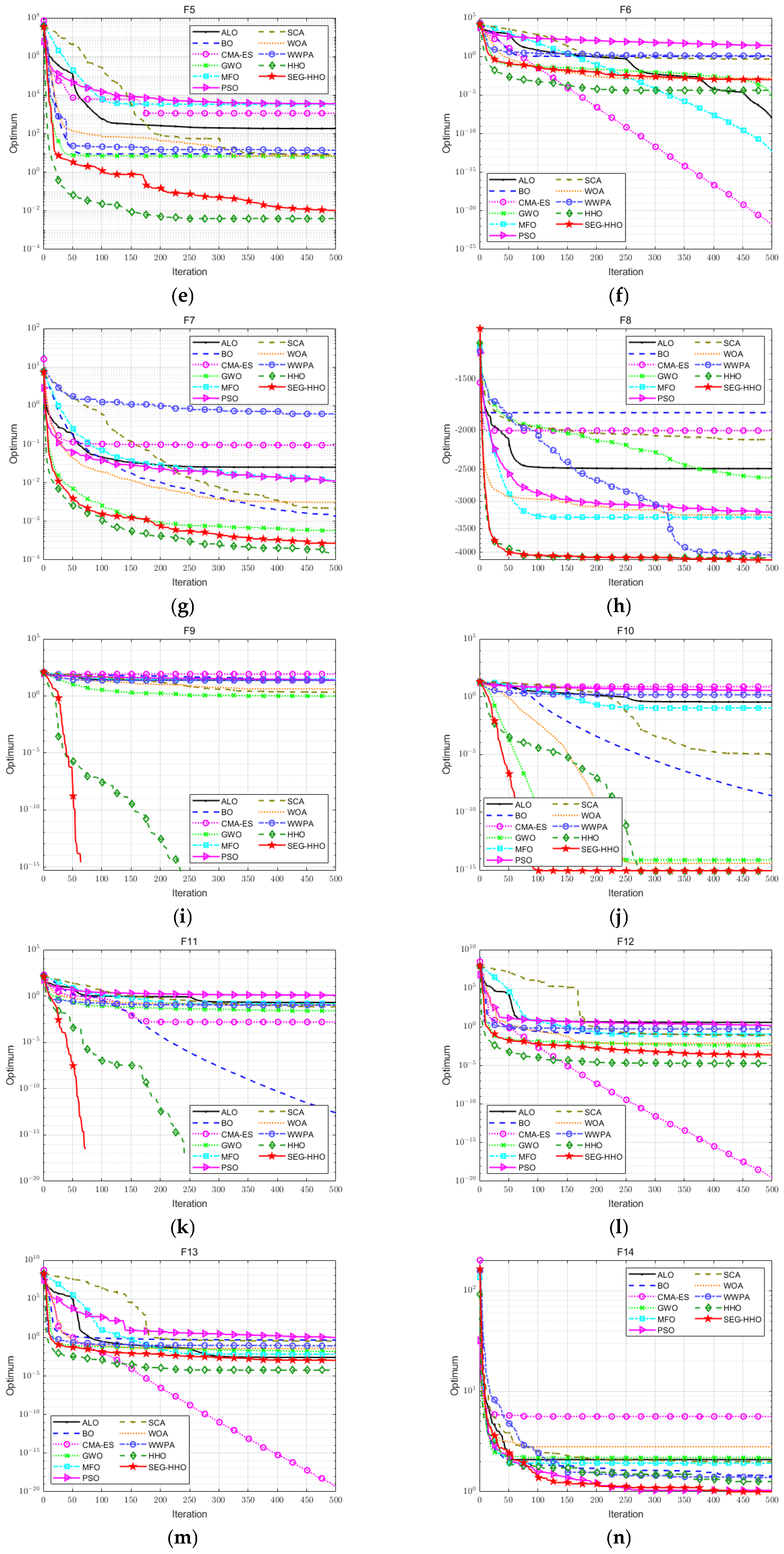
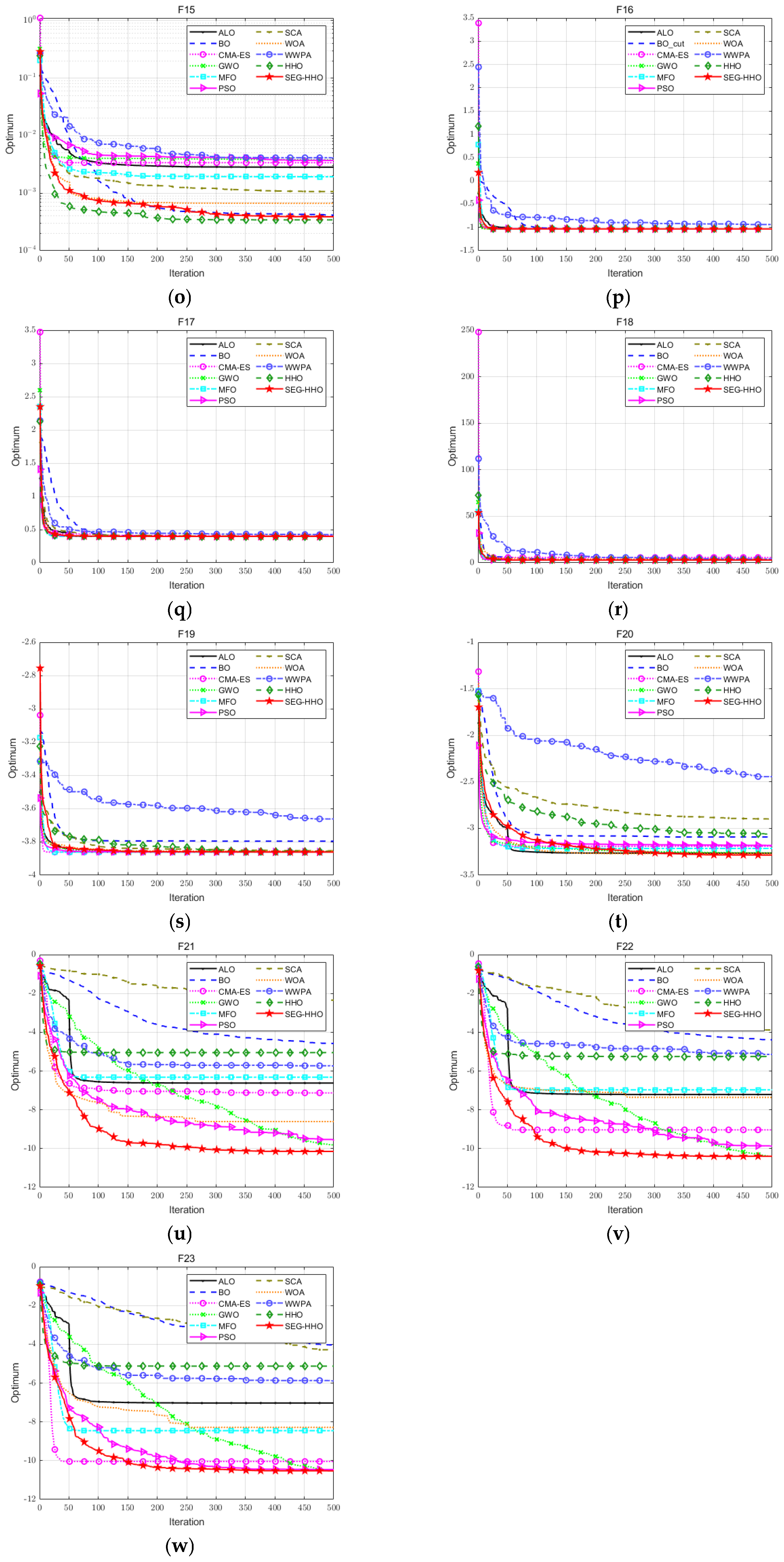
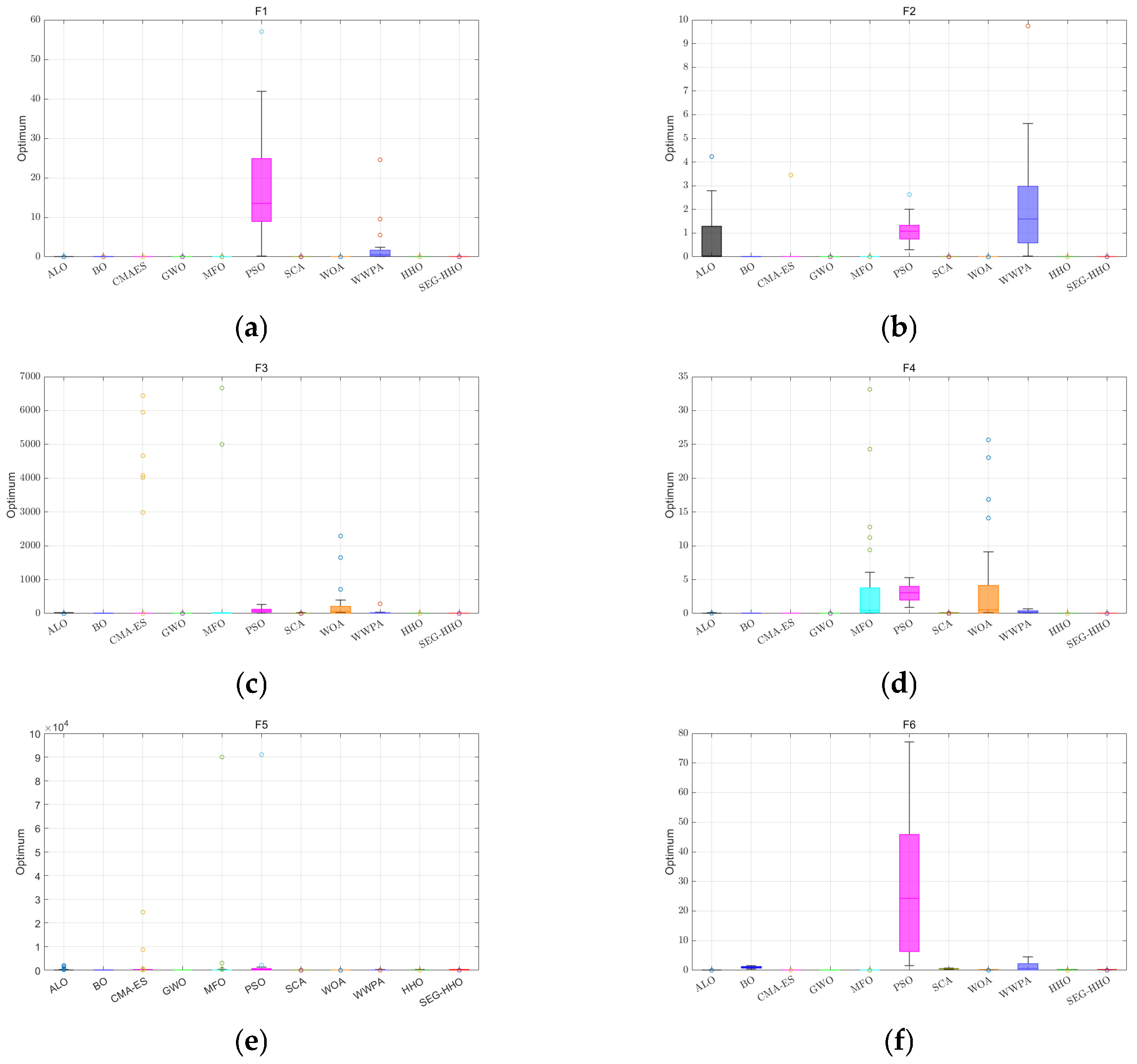
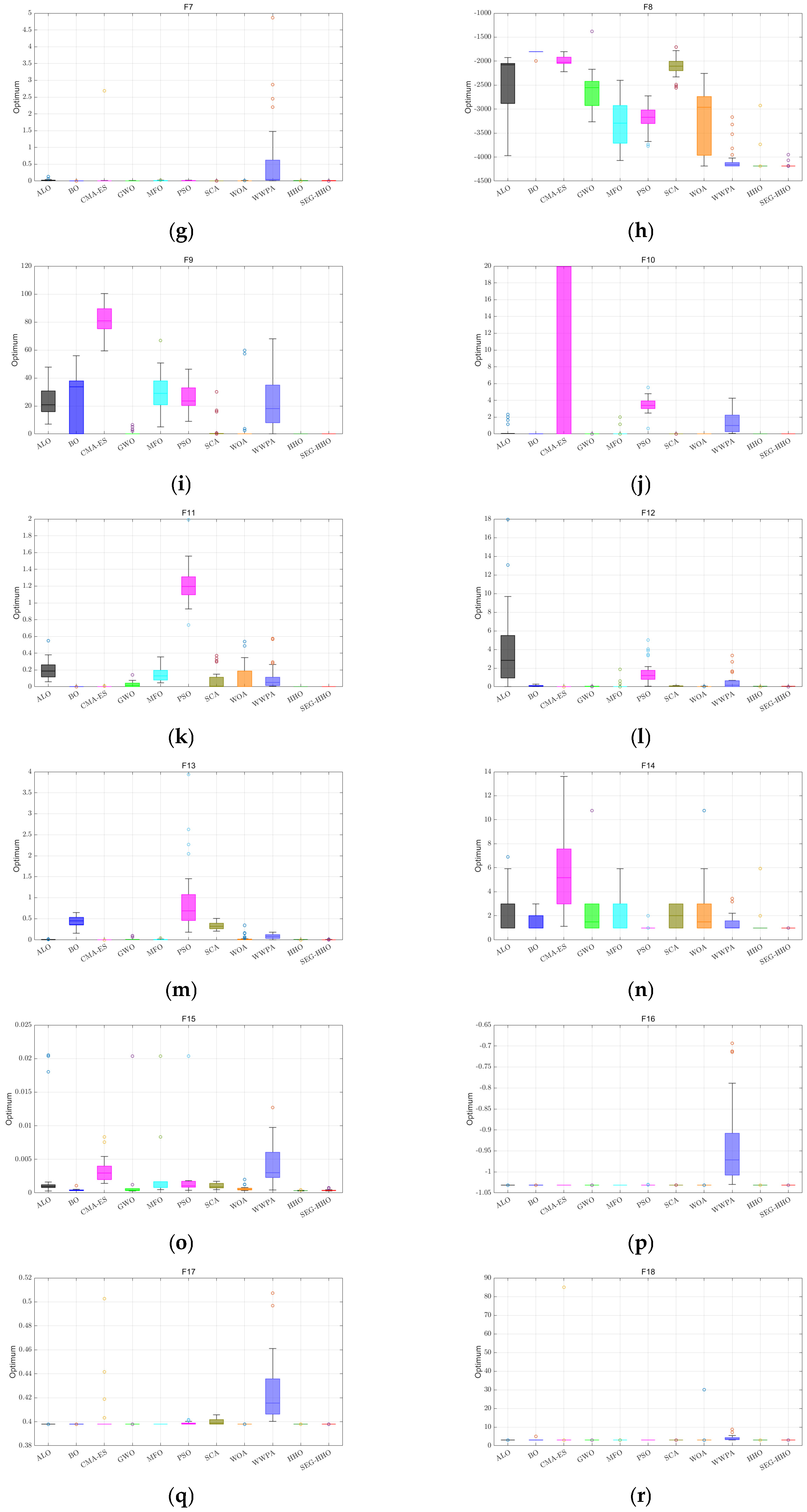
5.3. Performance Verification of Optimization Algorithms
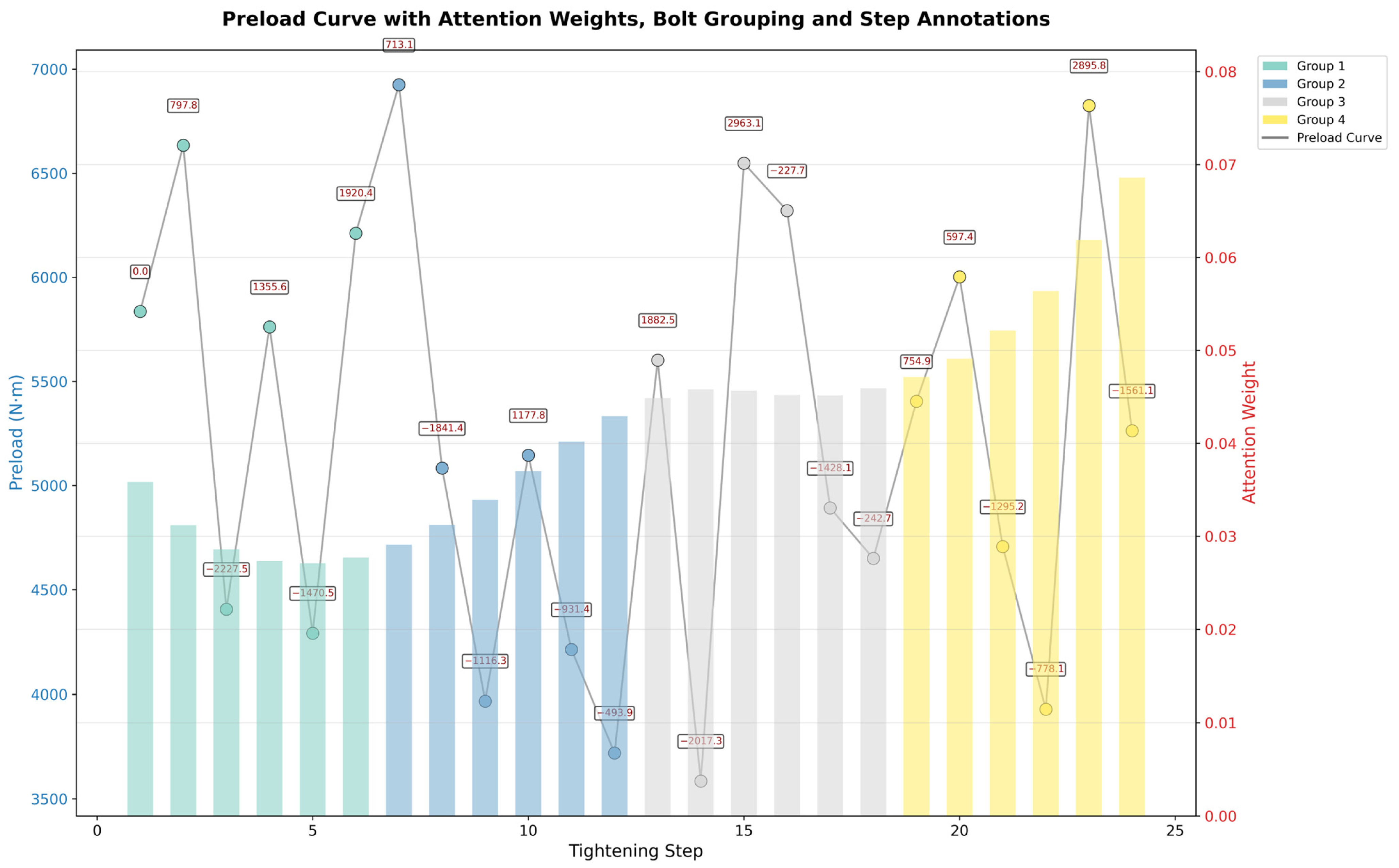
5.4. Analysis of the Optimal Assembly Scheme
6. Discussion
- Simulation-to-Reality Gap: The current study is based entirely on high-fidelity FEM simulation data. This was a deliberate and necessary first step due to the extreme manufacturing cost and low production volume of the specialized gyroscope under study, which makes extensive physical experimentation infeasible at this early stage. This simulation-first approach allowed us to establish a robust proof-of-concept and pre-train a foundational model. The immediate and most critical next step is to bridge the simulation-to-reality gap by incorporating scarce real-world sensor data (e.g., torque readings from instrumented torque wrenches) to fine-tune and calibrate the surrogate model, enhancing its real-world applicability. Future work will also explore the impact of manufacturing tolerances (e.g., rotor coaxiality and hole clearances) and material property variations, which were simplified in the current model.
- Generalizability and Scalability:
- (1)
- The model was validated on a specific 24-bolt gyroscope assembly. To prove broader generalizability, future work should test the framework on diverse bolt configurations and assembly structures, both in simulation and on physical systems (e.g., satellite payload assembly and semiconductor equipment). Beyond the test case, the general design of the framework enhances transferability: the AB-BiLSTM surrogate processes sequential data agnostic to specific patterns, while the SEG-HHO algorithm incorporates an encoding–decoding mechanism that decouples problem-specific constraints (e.g., symmetry and grouping) from the search procedure, enabling adaptation to new constraint types in other domains (e.g., multi-stage tightening, contact uniformity requirements, or tool accessibility constraints in aerospace assembly).
- (2)
- Regarding scalability, the inference time of the AB-BiLSTM model scales linearly with the number of bolts (O(n) complexity) [48], as RNN/LSTM architectures process sequences step-by-step. This suggests efficiency for larger systems, but current experiments are limited to 24 bolts. Scaling to more bolts (e.g., 48) or complex constraints (e.g., dynamic preload interactions) requires further validation of training time growth (potentially quadratic with dataset size expansion [48]) and overfitting risks. While the AB-BiLSTM surrogate scales efficiently, the underlying optimization problem for SEG-HHO faces exponential growth in search space with the number of bolts. To manage this complexity for larger systems, hierarchical optimization or advanced optimizers (e.g., evolutionary algorithms with adaptive operators) will be necessary.
- (3)
- Finally, cross-domain validation remains an open task. A potential roadmap includes the following: (1) within-domain tests on unseen bolt configurations (e.g., varying preload ranges or expanding to 48 bolts); (2) testing domain-specific datasets (e.g., aerospace or semiconductor assemblies); (3) recalibrating physics-based constraints to match new conditions; and (4) collaborating with industrial partners to verify transferability on real production data.
- From Single-Objective to Multi-Objective Optimization: Our current framework minimizes orthogonal axis error as a single objective. In real-world manufacturing, engineers must balance competing objectives such as minimizing error, ensuring uniform stress distribution, reducing assembly time, and minimizing tool wear. A critical future direction is extending the framework to multi-objective optimization. This would require modifying the AB-BiLSTM surrogate to output multiple objectives (e.g., error and stress) and integrating it with optimizer algorithms like NSGA-II or an improved HHO variant. The resulting Pareto front of optimal solutions would enable engineers to make informed, context-aware decisions.
- Path to Industrial Deployment: For practical deployment, this framework could be integrated into Computer-Aided Process Planning (CAPP) systems to generate optimal assembly plans offline. A more advanced implementation would involve creating a near real-time monitoring system on the assembly line. By integrating with IoT sensors on smart tools, the system could continuously feed live data to the AB-BiLSTM model for dynamic calibration, generating context-aware suggestions for process adjustments. This would bridge the gap between simulation predictions and physical execution, enabling iterative refinement of assembly quality.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| FEA | Finite Element Analysis |
| LHS | Latin Hypercube Sampling |
| SVR | Support Vector Regression |
| RSM | Response Surface Methodology |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| MLP | Multi-Layer Perceptron |
| CNN | Convolutional Neural Network |
| AB-BiLSTM | Attention-based Bidirectional Long Short-Term Memory |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| ACO | Ant Colony Optimization |
| ALO | Ant Lion Optimizer |
| HHO | Harris Hawks Optimization |
| LF | Levy Flight |
| DE | Differential Evolution |
| SEG-HHO | Stratified Evolutionary Group-based Harris Hawks Optimization |
| SCA | Sine Cosine Algorithm |
| BO | Bayesian Optimization |
| GWO | Grey Wolf Optimizer |
| MFO | Moth-Flame Optimization |
| WOA | Whale Optimization Algorithm |
| WWPA | Waterwheel Plant Algorithm |
| MSE | Mean Squared Error |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
| R2 | Coefficient of Determination |
| TPE | Tree-structured Parzen Estimator |
| CAPP | Computer-Aided Process Planning |
| IIoT | Industrial Internet of Things |
Appendix A
Appendix A.1
Appendix A.2

Appendix B
| Algorithm | Mean Runtime(s) | Std (s) |
|---|---|---|
| ALO | 1.1273 | 0.0247 |
| BO | 0.1032 | 0.0036 |
| CMA-ES | 0.2100 | 0.0072 |
| GWO | 0.0370 | 0.0020 |
| MFO | 0.0376 | 0.0014 |
| PSO | 0.0599 | 0.0024 |
| SCA | 0.0360 | 0.0021 |
| WOA | 0.0312 | 0.0014 |
| WWPA | 0.0958 | 0.0060 |
| HHO | 0.0830 | 0.0028 |
| SEG-HHO | 0.1534 | 0.0060 |
| Project | Total Execution Time | Average Iteration Time (s) |
|---|---|---|
| FEM simulation | About 3500 h | About 70 h |
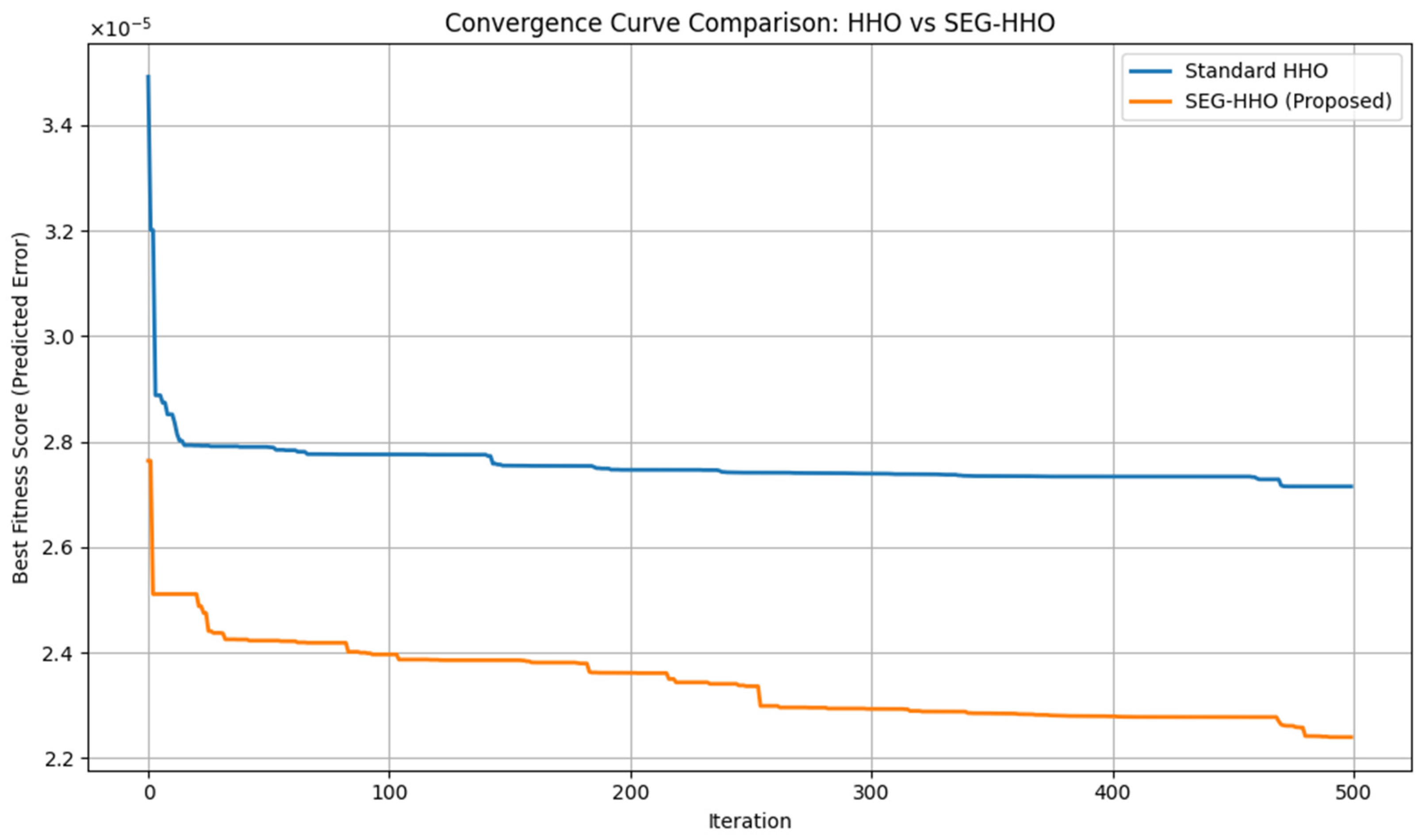
| Surrogate-assisted Standard HHO | 104.9993 s | 0.2099 s |
| Surrogate-assisted SEG-HHO | 91.1565 s | 0.1823 s |
References
- Are Manufacturing Errors Hurting Your Business? Reliability Solutions. Available online: https://reliabilitysolutions.net/articles/the-cost-of-assembly-and-installation-errors/ (accessed on 16 August 2025).
- Shafi, I.; Mazhar, M.F.; Fatima, A.; Alvarez, R.M.; Miró, Y.; Espinosa, J.C.M.; Ashraf, I. Deep Learning-Based Real Time Defect Detection for Optimization of Aircraft Manufacturing and Control Performance. Drones 2023, 7, 31. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.; Han, Y.; Zhang, P.; Zhang, Z.; Zhang, M.; Zhao, G. A Review of Aeroengines’ Bolt Preload Formation Mechanism and Control Technology. Aerospace 2023, 10, 307. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Wang, J.; Cao, R.; Xu, Z. Online O-Ring Stress Prediction and Bolt Tightening Sequence Optimization Method for Solid Rocket Motor Assembly. Machines 2023, 11, 387. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Z.; Song, Y.; Lu, Y.; Feng, Z. Prediction of Multi-Physics Field Distribution on Gas Turbine Endwall Using an Optimized Surrogate Model with Various Deep Learning Frames. Int. J. Numer. Methods Heat Fluid Flow 2023, 34, 2865–2889. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Marino, R. Learning from Survey Propagation: A Neural Network for MAX-E-3-SAT. Mach. Learn. Sci. Technol. 2021, 2, 035032. [Google Scholar] [CrossRef]
- Tatar, E.; Alper, S.E.; Akin, T. Quadrature-Error Compensation and Corresponding Effects on the Performance of Fully Decoupled MEMS Gyroscopes. J. Microelectromech. Syst. 2012, 21, 656–667. [Google Scholar] [CrossRef]
- Grzejda, R. Analysis of the Tightening Process of an Asymmetrical Multi-Bolted Connection. Mach. Dyn. Res. 2016, 39, 25–32. [Google Scholar]
- Wang, Y.; Liu, Y.; Wang, J.; Zhang, J.; Zhu, X.; Xu, Z. Research on Process Planning Method of Aerospace Engine Bolt Tightening Based on Digital Twin. Machines 2022, 10, 1048. [Google Scholar] [CrossRef]
- Shi, M.; Lv, L.; Sun, W.; Song, X. A Multi-Fidelity Surrogate Model Based on Support Vector Regression. Struct. Multidisc. Optim. 2020, 61, 2363–2375. [Google Scholar] [CrossRef]
- Gogu, C.; Passieux, J.-C. Efficient Surrogate Construction by Combining Response Surface Methodology and Reduced Order Modeling. Struct. Multidisc. Optim. 2013, 47, 821–837. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, Z. An Enhanced Kriging Surrogate Modeling Technique for High-Dimensional Problems. Mech. Syst. Signal Process. 2020, 140, 106687. [Google Scholar] [CrossRef]
- Durantin, C.; Rouxel, J.; Désidéri, J.-A.; Glière, A. Multifidelity Surrogate Modeling Based on Radial Basis Functions. Struct. Multidisc. Optim. 2017, 56, 1061–1075. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.-C.; Wu, Z.-M.; Zhu, Y.; Mao, J.-F. Surrogate Modeling of High-Speed Links Based on GNN and RNN for Signal Integrity Applications. IEEE Trans. Microw. Theory Techn. 2023, 71, 3784–3796. [Google Scholar] [CrossRef]
- Xu, L.; Xu, Y.; Wang, K.; Ye, L.; Zhang, W. Two-Stream Bolt Preload Prediction Network Using Hydraulic Pressure and Nut Angle Signals. Eng. Appl. Artif. Intell. 2024, 136, 109029. [Google Scholar] [CrossRef]
- Li, X.; Peng, C.; Zhao, Y.; Xia, X. A Hybrid DSCNN-GRU Based Surrogate Model for Transient Groundwater Flow Prediction. Appl. Sci. 2025, 15, 4576. [Google Scholar] [CrossRef]
- Song, B.; Liu, Y.; Fang, J.; Liu, W.; Zhong, M.; Liu, X. An Optimized CNN-BiLSTM Network for Bearing Fault Diagnosis under Multiple Working Conditions with Limited Training Samples. Neurocomputing 2024, 574, 127284. [Google Scholar] [CrossRef]
- Xie, Y.; Wu, D.; Qiang, Z. A Unifying View for the Mixture Model of Sparse Gaussian Processes. Inf. Sci. 2024, 660, 120124. [Google Scholar] [CrossRef]
- Schweidtmann, A.M.; Bongartz, D.; Grothe, D.; Kerkenhoff, T.; Lin, X.; Najman, J.; Mitsos, A. Deterministic Global Optimization with Gaussian Processes Embedded. Math. Prog. Comp. 2021, 13, 553–581. [Google Scholar] [CrossRef]
- Zhongbo, Y.; Hien, P.L. Pre-Trained Transformer Model as a Surrogate in Multiscale Computational Homogenization Framework for Elastoplastic Composite Materials Subjected to Generic Loading Paths. Comput. Methods Appl. Mech. Eng. 2024, 421, 116745. [Google Scholar] [CrossRef]
- Wan, X.; Liu, K.; Qiu, W.; Kang, Z. An Assembly Sequence Planning Method Based on Multiple Optimal Solutions Genetic Algorithm. Mathematics 2024, 12, 574. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, L.; Wu, D.; Jiang, P.; Bao, J. Assembly Sequence Planning Method for Optimum Assembly Accuracy of Complex Products Based on Modified Teaching–Learning Based Optimization Algorithm. Int. J. Adv. Manuf. Technol. 2023, 126, 1681–1699. [Google Scholar] [CrossRef]
- Malek, N.G.; Eslamlou, A.D.; Peng, Q.; Huang, S. Effective GA Operator for Product Assembly Sequence Planning. Comput.-Aided Des. Appl. 2024, 21, 713–728. [Google Scholar] [CrossRef]
- Zhang, W. Assembly Sequence Intelligent Planning Based on Improved Particle Swarm Optimization Algorithm. Manuf. Technol. 2023, 23, 557–563. [Google Scholar] [CrossRef]
- Ab Rashid, M.F.F.; Tiwari, A.; Hutabarat, W. Integrated Optimization of Mixed-Model Assembly Sequence Planning and Line Balancing Using Multi-Objective Discrete Particle Swarm Optimization. Artif. Intell. Eng. Des. Anal. Manuf. 2019, 33, 332–345. [Google Scholar] [CrossRef]
- Yang, J.; Liu, F.; Dong, Y.; Cao, Y.; Cao, Y. Multiple-Objective Optimization of a Reconfigurable Assembly System via Equipment Selection and Sequence Planning. Comput. Ind. Eng. 2022, 172, 108519. [Google Scholar] [CrossRef]
- Han, Z.; Wang, Y.; Tian, D. Ant Colony Optimization for Assembly Sequence Planning Based on Parameters Optimization. Front. Mech. Eng. 2021, 16, 393–409. [Google Scholar] [CrossRef]
- Tseng, H.-E.; Chang, C.-C.; Lee, S.-C.; Huang, Y.-M. Hybrid Bidirectional Ant Colony Optimization (Hybrid BACO): An Algorithm for Disassembly Sequence Planning. Eng. Appl. Artif. Intell. 2019, 83, 45–56. [Google Scholar] [CrossRef]
- Xing, Y.; Wu, D.; Qu, L. Parallel Disassembly Sequence Planning Using Improved Ant Colony Algorithm. Int. J. Adv. Manuf. Technol. 2021, 113, 2327–2342. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Devan, P.A.M.; Ibrahim, R.; Omar, M.; Bingi, K.; Abdulrab, H. A Novel Hybrid Harris Hawk-Arithmetic Optimization Algorithm for Industrial Wireless Mesh Networks. Sensors 2023, 23, 6224. [Google Scholar] [CrossRef]
- Yagmur, N.; Dag, İ.; Temurtas, H. Classification of Anemia Using Harris Hawks Optimization Method and Multivariate Adaptive Regression Spline. Neural Comput. Appl. 2024, 36, 5653–5672. [Google Scholar] [CrossRef]
- Pavan, G.; Ramesh Babu, A. Enhanced Randomized Harris Hawk Optimization of PI Controller for Power Flow Control in the Microgrid with the PV-Wind-Battery System. Sci. Technol. Energy Transit. 2024, 79, 45. [Google Scholar] [CrossRef]
- Ryalat, M.H.; Dorgham, O.; Tedmori, S.; Al-Rahamneh, Z.; Al-Najdawi, N.; Mirjalili, S. Harris Hawks Optimization for COVID-19 Diagnosis Based on Multi-Threshold Image Segmentation. Neural Comput. Appl. 2023, 35, 6855–6873. [Google Scholar] [CrossRef] [PubMed]
- Akl, D.T.; Saafan, M.M.; Haikal, A.Y.; El-Gendy, E.M. IHHO: An Improved Harris Hawks Optimization Algorithm for Solving Engineering Problems. Neural Comput. Appl. 2024, 36, 12185–12298. [Google Scholar] [CrossRef]
- Ni, J.; Tang, W.C.; Pan, M.; Qiu, X.; Xing, Y. Assembly Sequence Optimization for Minimizing the Riveting Path and Overall Dimensional Error. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 232, 2605–2615. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Yang, Y.; Shen, F. Toward Effective Intrusion Detection Using Log-Cosh Conditional Variational Autoencoder. IEEE Internet Things J. 2021, 8, 6187–6196. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Frazier, P.I. A Tutorial on Bayesian Optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar] [CrossRef]
- Hansen, N. The CMA Evolution Strategy: A Tutorial. arXiv 2016, arXiv:1604.00772. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-Flame Optimization Algorithm: A Novel Nature-Inspired Heuristic Paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle Swarm Optimization Algorithm: An Overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Abdelhamid, A.A.; Towfek, S.K.; Khodadadi, N.; Alhussan, A.A.; Khafaga, D.S.; Eid, M.M.; Ibrahim, A. Waterwheel Plant Algorithm: A Novel Metaheuristic Optimization Method. Processes 2023, 11, 1502. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Benchmarking a Catchment-Aware Long Short-Term MemoryNetwork (LSTM) for Large-Scale Hydrological Modeling. Hydrol. Earth Syst. Sci. Discuss. 2019, 2019, 1–32. [Google Scholar]







| Models | Without Initial Preload | With Initial Preload |
|---|---|---|
| RNN | 0.2925 | 0.1693 |
| LSTM | 0.5651 | −0.0165 |
| BiLSTM | 0.5353 | −0.0311 |
| Component | Description | Data Type/Dimension | Normalization/Encoding |
|---|---|---|---|
| Bolt ID Sequence | Order of bolts tightened in process | Integer, length 24 | Trainable embedding (dim = 32) |
| Preload Sequence | Final preload value for each bolt | Float, length 24 | Z-score normalization |
| Output | Predicted orthogonal axis error | Float, scalar | log(1 + p) + Min–Max normalization |
| Group (Fitness-Based) | Primary Goal (Intuitive Explanation) | Core Mechanism |
|---|---|---|
| Top Group | Deep Exploitation: Quickly refine the best-known solutions. | Standard HHO’s highly efficient “Besiege” strategies. |
| Middle Group | Balanced Search: Adaptively explore new regions while also exploiting promising ones. | Alternating Hybrid Strategy: HHO for exploitation and Differential Evolution (DE) for injecting diversity. |
| Bottom Group | Broad Exploration: Search widely to escape local optima and discover entirely new promising areas. | Sine Cosine Algorithm (SCA) guided the search for structured, wave-like exploration. |
| Algorithm | Core Idea | Exploration Strategy | Exploitation Strategy | Key Contribution in SEG-HHO |
|---|---|---|---|---|
| HHO | Mimics cooperative hunting of hawks. | Hawks track prey based on random perches or average location. | Four “besiege” strategies based on prey energy. | Provides the foundational framework and powerful exploitation operators (used by Top and Middle Groups). |
| DE | Uses vector differences between individuals to create new candidates. | “DE/rand/1” mutation creates diverse trial vectors. | Crossover and selection retain better solutions. | Injects significant population diversity to prevent stagnation (used by Middle Group). |
| SCA | Uses sine/cosine functions to explore/exploit space around the best solution. | Large-amplitude oscillations for global search. | Small-amplitude oscillations for local search. | Provides a structured, directional exploration mechanism, superior to random walks (used by Bottom Group). |
| SEG-HHO | Stratified, multi-strategy co-evolution. | Systematic and layered: SCA for broad search (Bottom); DE for diversity (Middle). | Focused and intensified: Standard HHO for deep exploitation (Top); HHO for refinement (Middle). | Synthesizes the strengths of HHO, DE, and SCA into a cohesive, role-based framework that dynamically balances the search. |
| Hyperparameter | Search Range/Type |
|---|---|
| Batch Size | Categorical [16, 32, 64, 128] |
| Learning Rate | Log-uniform [1e−5, 1e−3] |
| Optimizer | Categorical [Adam, AdamW] |
| Number of Layers | Integer [1, 5] |
| Embedding Dimension | Categorical [16, 32, 64, 128] |
| Hidden Dimension | Categorical [32, 64, 128, 256] |
| Dropout Rate | Categorical [0.0, 0.1, 0.2, 0.3] |
| Value | |
|---|---|
| Batch Size | 16 |
| Learning Rate | 8.8051E−5 |
| Optimizer | AdamW (weight_decay = 1e−4) |
| Num of Layers | 5 |
| Embed Dimension | 32 |
| Hidden Dimension | 256 |
| Dropout Rate | 0.1 |
| Model | Architecture Configuration | Key Hyperparameters |
|---|---|---|
| MLP | Flatten () → Dense (256, ReLU) → Dropout (0.1) → Dense (128, ReLU) → Dropout (0.1) → Dense (1, Softplus) | Neurons: 256 (L1), 128 (L2) Dropout: 0.1 |
| 1D-CNN | Conv1D (256, kernel = 3, ReLU) → Dropout (0.1) → Conv1D (256, kernel = 3, ReLU) → AdaptiveAvgPool1D (1) → Flatten () → Dense (1, Softplus) | Filters: 256 Kernel: 3 Dropout: 0.1 |
| RNN | Embedding (32) → RNN (256, dropout = 0.1) × 5 → Dense (1, Softplus) | Embed Dim: 32 Hidden Dim: 256 Layers: 5 Dropout: 0.1 |
| LSTM | Embedding (32) → LSTM (256, dropout = 0.1) × 5 → Dense (1, Softplus) | Embed Dim: 32 Hidden Dim: 256 Layers: 5 Dropout: 0.1 |
| BiLSTM | Embedding (32) → BiLSTM (256, dropout = 0.1) × 5 → Dense (1, Softplus) | Embed Dim: 32 Hidden Dim: 256 Layers: 5 Dropout: 0.1 |
| Model | MSE | RMSE | MAE | R2 | Latency (ms) | Train Time (s) |
|---|---|---|---|---|---|---|
| AB-BiLSTM | 2.8444E−09 | 5.3333E−05 | 3.5949E−05 | 0.8173 | 1.175323 | 189.8061 |
| BiLSTM | 3.0872E−09 | 5.5562E−05 | 3.7415E−05 | 0.8017 | 1.256722 | 224.274 |
| MLP | 1.5446E−08 | 1.2428E−04 | 9.8472E−05 | 0.0079 | 1.130914 | 55.7333 |
| 1D-CNN | 1.5641E−08 | 1.2506E−04 | 9.8688E−05 | −0.0045 | 1.021677 | 68.3319 |
| RNN | 1.4731E−08 | 1.2137E−04 | 9.5717E−05 | 0.0538 | 1.007865 | 60.1832 |
| LSTM | 2.9932E−09 | 5.4710E−05 | 3.6671E−05 | 0.8077 | 1.357545 | 175.3624 |
| GRU | 2.9833E−09 | 5.4619E−05 | 3.6816E−05 | 0.8083 | 1.362813 | 155.0558 |
| Project | Value |
|---|---|
| ANSYS Average Simulation Time | 14 min/Sample |
| AB-BiLSTM Single Sample Prediction Time | 1.3413 (ms) |
| Total Training Time | 189.8061 (s) |
| Model Accuracy (MAE) | 3.5949E−05 |
| Speedup Ratio | 714,711 |
| AB-BiLSTM | BiLSTM | Improvement | |
|---|---|---|---|
| MSE | 2.8444E−09 | 3.0872E−09 | 8.54% |
| RMSE | 5.3333E−05 | 5.5562E−05 | 4.18% |
| MAE | 3.5949E−05 | 3.7415E−05 | 3.92% |
| R2 | 0.8173 | 0.8017 | 1.95% |
| Noise Level | Model | RMSE | MAE | R2 |
|---|---|---|---|---|
| 1% | AB-BiLSTM | 6.3361E−05 | 3.9414E−05 | 0.7282 |
| BiLSTM | 6.5385E−05 | 4.0155E−05 | 0.7165 | |
| MLP | 1.2535E−04 | 9.8554E−05 | −0.0053 | |
| 1D-CNN | 1.2792E−04 | 1.0122E−04 | −0.0469 | |
| RNN | 1.2701E−04 | 9.7619E−05 | −0.0321 | |
| LSTM | 6.6070E−05 | 4.1412E−05 | 0.7107 | |
| GRU | 6.5368E−05 | 4.1342E−05 | 0.7166 | |
| 5% | AB-BiLSTM | 6.3589E−05 | 3.9748E−05 | 0.7263 |
| BiLSTM | 6.5466E−05 | 4.1059E−05 | 0.7258 | |
| MLP | 1.2779E−04 | 1.0108E−04 | −0.0448 | |
| 1D-CNN | 1.2535E−04 | 9.8513E−05 | −0.0052 | |
| RNN | 1.2699E−04 | 9.7622E−05 | −0.0317 | |
| LSTM | 6.7211E−05 | 4.2610E−05 | 0.7110 | |
| GRU | 6.5344E−05 | 4.1658E−05 | 0.7168 | |
| 10% | AB-BiLSTM | 6.7938E−05 | 4.1324E−05 | 0.7047 |
| BiLSTM | 6.7908E−05 | 4.3254E−05 | 0.7150 | |
| MLP | 1.2775E−04 | 1.0095E−04 | −0.0441 | |
| 1D-CNN | 1.2536E−04 | 9.8523E−05 | −0.0054 | |
| RNN | 1.2699E−04 | 9.7630E−05 | −0.0317 | |
| LSTM | 6.8729E−05 | 4.3845E−05 | 0.6978 | |
| GRU | 6.6685E−05 | 4.3753E−05 | 0.7050 | |
| 15% | AB-BiLSTM | 6.9643E−05 | 4.4518E−05 | 0.6897 |
| BiLSTM | 6.9893E−05 | 4.6727E−05 | 0.6875 | |
| MLP | 1.2816E−04 | 1.0136E−04 | −0.0508 | |
| 1D-CNN | 1.2537E−04 | 9.8543E−05 | −0.0056 | |
| RNN | 1.2737E−04 | 9.8130E−05 | −0.0379 | |
| LSTM | 6.8646E−05 | 4.5889E−05 | 0.6885 | |
| GRU | 6.9545E−05 | 4.5893E−05 | 0.6806 |
| Function | Dimension | Domain | Theoretical Optimum |
|---|---|---|---|
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | −12,569.4 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 2 | 1 | ||
| 4 | 0.00003075 | ||
| 2 | −1.0316285 | ||
| 2 | 0.398 | ||
| 2 | 3 | ||
| 3 | −3.86 | ||
| 6 | −3.32 | ||
| 4 | −10 | ||
| 4 | −10 | ||
| 4 | −10 |
| Function | SEG-HHO | HHO | ALO | BO | CMA-ES | GWO | MFO | PSO | SCA | WOA | WWPA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 4.0221E−139 | 4.3237E−97 | 1.2531E−08 | 1.0253E−11 | 2.1337E−22 | 3.3835E−57 | 4.5905E−13 | 1.7904E+01 | 1.0187E−11 | 5.0654E−75 | 9.6433E−01 |
| Std | 2.1893E−138 | 2.2390E−96 | 1.2114E−08 | 1.3546E−12 | 1.8426E−22 | 9.5492E−57 | 1.2655E−12 | 1.6916E+01 | 4.2301E−11 | 2.7739E−74 | 1.9933 | |
| Min | 1.6133E−171 | 9.5971E−115 | 4.3733E−09 | 7.3048E−12 | 1.3552E−23 | 1.8406E−60 | 3.4952E−15 | 2.5417 | 7.2846E−19 | 9.8147E−92 | 1.4099E−05 | |
| Max | 1.1994E−137 | 1.2279E−95 | 4.9236E−08 | 1.1980E−11 | 7.7019E−22 | 4.9406E−56 | 6.1571E−12 | 7.6199E+01 | 2.2515E−10 | 1.5193E−73 | 9.7573E+00 | |
| Rank | 1 | 2 | 9 | 8 | 5 | 4 | 6 | 11 | 7 | 3 | 10 | |
| F2 | Mean | 1.3457E−73 | 1.8175E−50 | 4.3569E−01 | 4.4464E−09 | 1.1494E−01 | 7.4493E−33 | 6.7998E−09 | 1.8576 | 1.7365E−09 | 1.1527E−50 | 2.1362 |
| Std | 4.4841E−73 | 9.4932E−50 | 8.8104E−01 | 4.1546E−10 | 6.2953E−01 | 1.5590E−32 | 9.5554E−09 | 2.5486 | 3.8080E−09 | 6.2569E−50 | 1.7541 | |
| Min | 8.8058E−88 | 7.5733E−62 | 2.1778E−05 | 3.2226E−09 | 3.6201E−12 | 3.5334E−35 | 4.3657E−10 | 3.6887E−01 | 1.1886E−12 | 5.1848E−59 | 7.0394E−02 | |
| Max | 1.9042E−72 | 5.2069E−49 | 3.2766E+00 | 5.0923E−09 | 3.4481 | 7.9383E−32 | 3.9520E−08 | 1.1626E+01 | 2.0214E−08 | 3.4280E−49 | 5.6360 | |
| Rank | 1 | 3 | 9 | 6 | 8 | 4 | 7 | 10 | 5 | 2 | 11 | |
| F3 | Mean | 2.2224E−113 | 8.3627E−87 | 7.5129E−02 | 1.0715E−11 | 8.5932E+02 | 1.5744E−24 | 7.5142E−02 | 7.3812E+01 | 5.2861E−03 | 2.5802E+02 | 1.8125E+01 |
| Std | 1.2173E−112 | 3.3771E−86 | 2.8736E−01 | 1.4833E−12 | 2.4910E+03 | 4.1683E−24 | 1.1806E−01 | 7.5241E+01 | 2.5573E−02 | 6.0142E+02 | 3.5604E+01 | |
| Min | 3.0890E−163 | 1.5349E−103 | 1.1691E−05 | 6.6643E−12 | 3.3521E−16 | 2.4941E−30 | 3.0860E−04 | 3.4035 | 1.9934E−07 | 2.7756E−01 | 1.9237E−02 | |
| Max | 6.6672E−112 | 1.7628E−85 | 1.5559 | 1.3073E−11 | 1.1638E+04 | 1.9458E−23 | 4.9815E−01 | 3.8305E+02 | 1.4050E−01 | 3.0595E+03 | 1.8765E+02 | |
| Rank | 1 | 2 | 6 | 4 | 11 | 3 | 7 | 9 | 5 | 10 | 8 | |
| F4 | Mean | 1.2864E−70 | 2.5824E−50 | 7.5664E−03 | 5.1141E−09 | 2.4604E−10 | 2.3031E−18 | 2.3634 | 3.1349 | 4.8785E−04 | 5.3139 | 2.8517E−01 |
| Std | 4.1288E−70 | 6.2700E−50 | 2.6260E−02 | 5.6416E−10 | 1.3137E−10 | 4.7874E−18 | 4.7209 | 1.3879 | 7.8757E−04 | 9.8575 | 2.4805E−01 | |
| Min | 2.4386E−88 | 4.7659E−59 | 1.2017E−04 | 3.6044E−09 | 7.4107E−11 | 8.6002E−21 | 2.5910E−03 | 7.9789E−01 | 1.9837E−06 | 4.4480E−03 | 1.5187E−02 | |
| Max | 1.7298E−69 | 3.0726E−49 | 1.4461E−01 | 6.2106E−09 | 5.4165E−10 | 2.4514E−17 | 2.0960E+01 | 6.1695 | 3.5907E−03 | 4.1523E+01 | 9.2019E−01 | |
| Rank | 1 | 2 | 7 | 5 | 4 | 3 | 9 | 10 | 6 | 11 | 8 | |
| F5 | Mean | 1.3699E−02 | 3.6246E−03 | 1.4427E+02 | 8.9375 | 1.1373E+03 | 6.8806 | 2.9057E+02 | 8.7679E+02 | 7.3977 | 1.4575E+01 | 3.4891E+01 |
| Std | 2.0436E−02 | 6.5977E−03 | 3.0888E+02 | 2.2660E−02 | 4.6894E+03 | 6.1221E−01 | 7.5627E+02 | 9.4807E+02 | 3.9958E−01 | 4.2675E+01 | 9.8493E+01 | |
| Min | 1.1309E−04 | 7.3646E−08 | 3.3591E−04 | 8.8810 | 2.8821E−02 | 5.5997 | 5.3872E−01 | 6.5256E+01 | 6.7225 | 6.0650 | 6.3616E−02 | |
| Max | 8.1651E−02 | 2.6413E−02 | 1.4097E+03 | 8.9830 | 2.4505E+04 | 8.0688 | 3.0219E+03 | 3.5664E+03 | 8.7127 | 2.4052E+02 | 5.4888E+02 | |
| Rank | 2 | 1 | 8 | 5 | 11 | 3 | 9 | 10 | 4 | 6 | 7 | |
| F6 | Mean | 7.1125E−04 | 3.9286E−05 | 9.5960E−09 | 1.1660 | 1.8457E−22 | 8.3539E−03 | 2.1482E−13 | 1.9341E+01 | 4.4334E−01 | 1.1771E−03 | 1.5115 |
| Std | 1.0798E−03 | 4.8862E−05 | 7.3957E−09 | 3.6229E−01 | 1.8178E−22 | 4.5738E−02 | 3.4699E−13 | 2.0632E+01 | 1.2892E−01 | 1.8088E−03 | 2.7255 | |
| Min | 2.7693E−06 | 2.1451E−08 | 1.4970E−09 | 6.0281E−01 | 2.2973E−23 | 1.3786E−06 | 1.6529E−16 | 6.5394E−01 | 1.3759E−01 | 1.6681E−04 | 6.4583E−04 | |
| Max | 4.8326E−03 | 1.8459E−04 | 3.2171E−08 | 1.9152 | 7.1981E−22 | 2.5052E−01 | 1.3355E−12 | 9.3079E+01 | 7.9438E−01 | 9.3304E−03 | 1.1056E+01 | |
| Rank | 5 | 4 | 3 | 9 | 1 | 7 | 2 | 11 | 8 | 6 | 10 | |
| F7 | Mean | 2.4234E−04 | 1.3449E−04 | 2.5568E−02 | 1.3099E−03 | 9.4317E−02 | 6.4183E−04 | 1.0582E−02 | 1.2460E−02 | 3.3207E−03 | 4.1173E−03 | 5.5540E−01 |
| Std | 2.1518E−04 | 1.1525E−04 | 1.5359E−02 | 5.6530E−04 | 4.8975E−01 | 4.0287E−04 | 5.7722E−03 | 8.3088E−03 | 3.0142E−03 | 4.7981E−03 | 1.0855 | |
| Min | 2.1300E−05 | 6.7575E−06 | 5.9484E−03 | 3.7901E−04 | 1.9734E−03 | 1.7332E−04 | 2.5292E−03 | 1.4248E−03 | 8.3565E−05 | 4.2644E−05 | 7.4487E−03 | |
| Max | 4.2719E−04 | 5.2581E−04 | 6.4417E−02 | 2.4076E−03 | 2.6873 | 1.8263E−03 | 2.5607E−02 | 3.6523E−02 | 1.2389E−02 | 1.8394E−02 | 5.1779 | |
| Rank | 2 | 1 | 9 | 4 | 10 | 3 | 7 | 8 | 5 | 6 | 11 | |
| F8 | Mean | −4.1898E+03 | −4.1337E+03 | −2.4084E+03 | −2.1373E+03 | −2.0065E+03 | −2.7073E+03 | −3.2070E+03 | −3.0933E+03 | −2.1513E+03 | −3.3437E+03 | −4.1179E+03 |
| Std | 7.7913E−02 | 2.1435E+02 | 5.6280E+02 | 2.5236E+02 | 1.0598E+02 | 3.9449E+02 | 3.3510E+02 | 3.0495E+02 | 1.7189E+02 | 5.9841E+02 | 9.7660E+01 | |
| Min | −4.1898E+03 | −4.1898E+03 | −4.1898E+03 | −1.7517E+03 | −2.2205E+03 | −3.9528E+03 | −3.8345E+03 | −3.7059E+03 | −2.5033E+03 | −4.1897E+03 | −4.1897E+03 | |
| Max | −4.1895E+03 | −3.2607E+03 | −1.8059E+03 | −2.6788E+03 | −1.8059E+03 | −1.7848E+03 | −2.5226E+03 | −2.5019E+03 | −1.8031E+03 | −2.2658E+03 | −3.8155E+03 | |
| Rank | 1 | 2 | 8 | 10 | 11 | 7 | 5 | 6 | 9 | 4 | 3 | |
| F9 | Mean | 0.0000 | 0.0000 | 2.1193E+01 | 2.5615E+01 | 8.1279E+01 | 1.0194 | 2.4883E+01 | 2.2596E+01 | 3.5449E−01 | 4.6969E−01 | 2.5361E+01 |
| Std | 0.0000 | 0.0000 | 9.2015 | 1.9668E+01 | 1.0483E+01 | 1.7340 | 1.3398E+01 | 7.5508 | 1.4250 | 2.5726 | 2.1420E+01 | |
| Min | 0.0000 | 0.0000 | 5.9698 | 0.0000 | 5.9464E+01 | 0.0000 | 5.9698 | 6.4443 | 0.0000 | 0.0000 | 3.4409 | |
| Max | 0.0000 | 0.0000 | 4.1788E+01 | 5.1699E+01 | 1.0049E+02 | 4.5936 | 5.0814E+01 | 4.1797E+01 | 7.6396 | 1.4091E+01 | 1.0022E+02 | |
| Rank | 1.5 | 1.5 | 6 | 10 | 11 | 5 | 8 | 7 | 3 | 4 | 9 | |
| F10 | Mean | 8.8818E−16 | 8.8818E−16 | 1.1556E−01 | 2.2528E−09 | 7.2736E+00 | 7.9936E−15 | 9.3379E−02 | 3.5630 | 2.5722E−02 | 4.6777E−15 | 2.1494 |
| Std | 0.0000 | 0.0000 | 3.5245E−01 | 9.6568E−10 | 9.7253E+00 | 2.2853E−15 | 3.6117E−01 | 8.3052E−01 | 1.4087E−01 | 2.2726E−15 | 1.5578 | |
| Min | 8.8818E−16 | 8.8818E−16 | 1.8640E−05 | 8.2867E−10 | 4.4702E−12 | 4.4409E−15 | 1.6146E−08 | 1.8003 | 4.6100E−10 | 8.8818E−16 | 1.9373E−02 | |
| Max | 8.8818E−16 | 8.8818E−16 | 1.1551 | 4.7654E−09 | 1.9955E+01 | 1.5099E−14 | 1.6462 | 5.2139 | 7.7157E−01 | 7.9936E−15 | 4.5925 | |
| Rank | 1.5 | 1.5 | 8 | 5 | 11 | 4 | 7 | 10 | 6 | 3 | 9 | |
| F11 | Mean | 0.0000 | 0.0000 | 1.7695E−01 | 1.7097E−13 | 1.5612E−03 | 1.8052E−02 | 1.5688E−01 | 1.2383 | 1.3477E−01 | 4.9390E−02 | 1.4376E−01 |
| Std | 0.0000 | 0.0000 | 1.0286E−01 | 9.9430E−14 | 3.2032E−03 | 2.5002E−02 | 1.2108E−01 | 2.8534E−01 | 2.0162E−01 | 1.2370E−01 | 2.0097E−01 | |
| Min | 0.0000 | 0.0000 | 3.9459E−02 | 5.3957E−14 | 0.0000 | 0.0000 | 2.9555E−02 | 6.8737E−01 | 4.6629E−15 | 0.0000 | 1.1735E−04 | |
| Max | 0.0000 | 0.0000 | 4.9965E−01 | 5.0770E−13 | 9.8573E−03 | 9.5327E−02 | 6.3256E−01 | 2.0188 | 7.8036E−01 | 4.8854E−01 | 7.5767E−01 | |
| Rank | 1.5 | 1.5 | 10 | 3 | 4 | 5 | 9 | 11 | 7 | 6 | 8 | |
| F12 | Mean | 1.6329E−04 | 2.3626E−05 | 3.0189 | 1.2885E−01 | 3.0273E−20 | 6.4181E−03 | 2.3710E−01 | 1.5398 | 9.9768E−02 | 8.0953E−03 | 6.6295E−01 |
| Std | 2.0591E−04 | 3.8893E−05 | 2.9063 | 8.6162E−02 | 4.6130E−20 | 1.1701E−02 | 7.4049E−01 | 1.4066 | 4.1493E−02 | 1.1521E−02 | 9.1868E−01 | |
| Min | 3.2988E−08 | 8.9026E−08 | 1.3255E−08 | 2.4600E−02 | 8.6676E−22 | 3.2591E−07 | 2.2052E−16 | 7.1929E−02 | 3.3306E−02 | 1.8571E−04 | 2.1025E−03 | |
| Max | 9.0597E−04 | 2.1115E−04 | 9.4435E+00 | 3.3026E−01 | 1.9621E−19 | 3.9660E−02 | 3.6897 | 6.2637 | 1.7897E−01 | 4.0584E−02 | 3.2552 | |
| Rank | 3 | 2 | 11 | 7 | 1 | 4 | 8 | 10 | 6 | 5 | 9 | |
| F13 | Mean | 1.3790E−03 | 8.6393E−05 | 1.7998E−03 | 4.1957E−01 | 4.8367E−20 | 2.3475E−02 | 4.7612E−03 | 1.4157 | 3.4762E−01 | 2.5076E−02 | 1.2071E−01 |
| Std | 2.4770E−03 | 1.9683E−04 | 4.9380E−03 | 1.7401E−01 | 7.5554E−20 | 4.3276E−02 | 8.9788E−03 | 1.2985 | 8.8778E−02 | 3.1795E−02 | 1.4885E−01 | |
| Min | 1.3859E−05 | 1.3577E−07 | 2.3292E−09 | 1.5318E−01 | 1.5840E−21 | 2.9422E−06 | 4.3275E−16 | 1.3607E−01 | 1.6382E−01 | 4.3244E−04 | 1.5739E−03 | |
| Max | 1.2234E−02 | 8.7306E−04 | 2.1027E−02 | 7.8560E−01 | 3.0408E−19 | 1.0476E−01 | 4.3949E−02 | 5.2993 | 5.0547E−01 | 1.0903E−01 | 6.5415E−01 | |
| Rank | 3 | 2 | 4 | 10 | 1 | 6 | 5 | 11 | 9 | 7 | 8 | |
| F14 | Mean | 9.9800E−01 | 1.5156 | 2.1861 | 1.3808 | 5.6075 | 6.9591 | 2.9717 | 9.9842E−01 | 1.7240 | 3.0226 | 1.6062 |
| Std | 5.7011E−10 | 1.2596 | 1.4746 | 5.8174E−01 | 3.4400 | 4.6046 | 2.3075 | 1.4717E−03 | 1.8861 | 3.5889 | 1.4332 | |
| Min | 9.9800E−01 | 9.9800E−01 | 9.9800E−01 | 9.9800E−01 | 1.1420 | 9.9800E−01 | 9.9800E−01 | 9.9800E−01 | 9.9800E−01 | 9.9800E−01 | 9.9800E−01 | |
| Max | 9.9800E−01 | 5.9288 | 6.9033 | 3.1916 | 1.3619E+01 | 1.2671E+01 | 8.8408 | 1.0053 | 1.0763E+01 | 1.0763E+01 | 6.9155 | |
| Rank | 1 | 4 | 7 | 3 | 10 | 11 | 8 | 2 | 6 | 9 | 5 | |
| F15 | Mean | 4.5043E−04 | 4.5478E−04 | 2.1646E−03 | 4.3284E−04 | 3.3546E−03 | 3.1136E−03 | 1.5957E−03 | 6.3656E−03 | 9.0330E−04 | 6.3855E−04 | 4.5102E−03 |
| Std | 2.6430E−04 | 3.1606E−04 | 5.0239E−03 | 1.2105E−04 | 3.2217E−03 | 6.8860E−03 | 3.5600E−03 | 8.5956E−03 | 3.3178E−04 | 3.8501E−04 | 2.6013E−03 | |
| Min | 3.1107E−04 | 3.0775E−04 | 3.5349E−04 | 3.2073E−04 | 1.2444E−03 | 3.0756E−04 | 5.7500E−04 | 5.8275E−04 | 3.5141E−04 | 3.0750E−04 | 6.5236E−04 | |
| Max | 1.4880E−03 | 1.4592E−03 | 2.0885E−02 | 8.4493E−04 | 1.7946E−02 | 2.0363E−02 | 2.0363E−02 | 2.0371E−02 | 1.5359E−03 | 1.8719E−03 | 1.0673E−02 | |
| Rank | 2 | 3 | 7 | 1 | 9 | 8 | 6 | 11 | 5 | 4 | 10 | |
| F16 | Mean | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0315 | −1.0316 | −1.0316 | −9.1372E−01 |
| Std | 1.3115E−09 | 3.9422E−09 | 1.7408E−13 | 2.2544E−06 | 6.7752E−16 | 1.7814E−08 | 6.7752E−16 | 1.7847E−04 | 3.9793E−05 | 7.3095E−10 | 8.7428E−02 | |
| Min | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0151 | |
| Max | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0308 | −1.0315 | −1.0316 | −6.6497E−01 | |
| Rank | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 10 | 5 | 5 | 11 | |
| F17 | Mean | 3.9789E−01 | 3.9789E−01 | 3.9789E−01 | 4.0133E−01 | 4.0372E−01 | 3.9789E−01 | 3.9789E−01 | 3.9911E−01 | 4.0019E−01 | 3.9790E−01 | 4.2217E−01 |
| Std | 1.1558E−05 | 2.1284E−05 | 1.3221E−13 | 1.0291E−02 | 2.0633E−02 | 4.0530E−06 | 0.0000 | 2.0462E−03 | 2.2699E−03 | 1.8988E−05 | 2.1706E−02 | |
| Min | 3.9789E−01 | 3.9789E−01 | 3.9789E−01 | 3.9792E−01 | 3.9789E−01 | 3.9789E−01 | 3.9789E−01 | 3.9790E−01 | 3.9807E−01 | 3.9789E−01 | 3.9883E−01 | |
| Max | 3.9795E−01 | 3.9798E−01 | 3.9789E−01 | 4.5511E−01 | 5.0270E−01 | 3.9790E−01 | 3.9789E−01 | 4.0639E−01 | 4.0767E−01 | 3.9796E−01 | 4.7649E−01 | |
| Rank | 3 | 5 | 1.5 | 9 | 10 | 4 | 1.5 | 7 | 8 | 6 | 11 | |
| F18 | Mean | 3.0000 | 3.0000 | 3.0000 | 3.2091 | 5.7331 | 3.0000 | 3.0000 | 3.0088 | 3.0001 | 3.9006 | 4.1195 |
| Std | 1.9351E−07 | 3.7305E−07 | 4.9870E−13 | 5.3784E−01 | 1.4970E+01 | 5.3590E−05 | 1.2148E−15 | 1.1239E−02 | 2.0373E−04 | 4.9325 | 8.6770E−01 | |
| Min | 3.0000 | 3.0000 | 3.0000 | 3.0004 | 3.0000 | 3.0000 | 3.0000 | 3.0003 | 3.0000 | 3.0000 | 3.0674 | |
| Max | 3.0000 | 3.0000 | 3.0000 | 5.9236 | 8.4992E+01 | 3.0002 | 3.0000 | 3.0416 | 3.0010 | 3.0016E+01 | 6.1939 | |
| Rank | 3.5 | 3.5 | 1.5 | 8 | 11 | 5 | 1.5 | 7 | 6 | 9 | 10 | |
| F19 | Mean | −3.8628 | −3.8594 | −3.8628 | −3.7976 | −3.8628 | −3.8616 | −3.8628 | −3.8618 | −3.8528 | −3.8518 | −3.6951 |
| Std | 7.0773E−05 | 3.3573E−03 | 7.6683E−13 | 5.6929E−02 | 2.7101E−15 | 2.4787E−03 | 2.7101E−15 | 1.9228E−03 | 2.6319E−03 | 1.2384E−02 | 1.0024E−01 | |
| Min | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8576 | −3.8621 | −3.8404 | |
| Max | −3.8624 | −3.8476 | −3.8628 | −3.6714 | −3.8628 | −3.8549 | −3.8628 | −3.8548 | −3.8437 | −3.8138 | −3.4705 | |
| Rank | 4 | 7 | 2 | 10 | 2 | 6 | 2 | 5 | 8 | 9 | 11 | |
| F20 | Mean | −3.2886 | −3.0837 | −3.2701 | −3.0421 | −3.1923 | −3.2612 | −3.2284 | −3.2379 | −2.9662 | −3.2073 | −2.3642 |
| Std | 6.3050E−02 | 1.2127E−01 | 6.0326E−02 | 1.7531E−01 | 2.8053E−01 | 7.4955E−02 | 5.3868E−02 | 1.0683E−01 | 1.9522E−01 | 1.1681E−01 | 3.1541E−01 | |
| Min | −3.3220 | −3.3088 | −3.3220 | −3.3175 | −3.3220 | −3.3220 | −3.3220 | −3.3140 | −3.1538 | −3.3217 | −3.1143 | |
| Max | −3.1196 | −2.8477 | −3.1981 | −2.6698 | −1.9084 | −3.0816 | −3.1376 | −2.8946 | −2.2364 | −3.0092 | −1.7193 | |
| Rank | 1 | 8 | 2 | 9 | 7 | 3 | 5 | 4 | 10 | 6 | 11 | |
| F21 | Mean | −1.0136E+01 | −5.2134 | −6.3718 | −4.5390 | −7.1262 | −8.6158 | −7.1338 | −9.2629 | −2.6131 | −8.5277 | −5.3737 |
| Std | 3.3253E−02 | 8.8795E−01 | 3.0741 | 3.0250E−01 | 3.1973 | 2.6461 | 3.1867 | 2.0800 | 1.9487 | 2.5277 | 1.7623 | |
| Min | −1.0153E+01 | −9.9147 | −1.0153E+01 | −4.9442 | −1.0153E+01 | −1.0153E+01 | −1.0153E+01 | −1.0140E+01 | −6.2452 | −1.0151E+01 | −1.0081E+01 | |
| Max | −1.0002E+01 | −5.0282 | −2.6305 | −3.5246 | −2.6305 | −2.6301 | −2.6305 | −2.6038 | −4.9652E−01 | −2.6298 | −3.5762 | |
| Rank | 1 | 9 | 7 | 10 | 6 | 3 | 5 | 2 | 11 | 4 | 8 | |
| F22 | Mean | −1.0398E+01 | −5.2393 | −6.7556 | −4.2772 | −9.0340E+00 | −1.0185E+01 | −6.5457 | −1.0268E+01 | −3.2287 | −7.0900 | −5.7023 |
| Std | 5.9680E−03 | 8.5907E−01 | 3.5373 | 4.0367E−01 | 2.8140E+00 | 1.1856 | 3.5539 | 1.9469E−01 | 2.0636 | 3.0621 | 1.9896 | |
| Min | −1.0403E+01 | −9.7876 | −1.0403E+01 | −4.8239 | −1.0403E+01 | −1.0403E+01 | −1.0403E+01 | −1.0400E+01 | −9.2492 | −1.0401E+01 | −1.0198E+01 | |
| Max | −1.0382E+01 | −5.0599 | −1.8376 | −3.3661 | −2.7519 | −3.9070 | −1.8376 | −9.5134 | −5.2104E−01 | −1.8374 | −3.7635 | |
| Rank | 1 | 9 | 6 | 10 | 4 | 3 | 7 | 2 | 11 | 5 | 8 | |
| F23 | Mean | −1.0529E+01 | −4.8521 | −5.7379 | −4.2550 | −1.0043E+01 | −1.0084E+01 | −7.7387 | −1.0233E+01 | −3.4865 | −6.9959 | −5.8250 |
| Std | 9.5381E−03 | 8.3014E−01 | 3.3166 | 1.0075 | 1.8878 | 1.7514 | 3.5573 | 1.0586 | 1.4188 | 3.5046E+00 | 1.7594 | |
| Min | −1.0536E+01 | −5.1284 | −1.0536E+01 | −7.5831 | −1.0536E+01 | −1.0536E+01 | −1.0536E+01 | −1.0536E+01 | −5.0160 | −1.0536E+01 | −1.0141E+01 | |
| Max | −1.0496E+01 | −2.3986 | −1.8595 | −2.3182 | −2.4273 | −2.4217 | −1.6766 | −4.6748 | −9.4350E−01 | −1.6756 | −3.2967 | |
| Rank | 1 | 9 | 8 | 10 | 4 | 3 | 5 | 2 | 11 | 6 | 7 | |
| Average Rank | 2.0435 | 3.8261 | 6.3043 | 7.0000 | 6.8261 | 4.7391 | 5.8696 | 7.6522 | 7.0000 | 5.9130 | 8.8261 | |
| Total Rank | 1 | 2 | 6 | 8.5 | 7 | 3 | 4 | 10 | 8.5 | 5 | 11 |
| Tightening Step | Bolt ID to Tighten | Optimal Preload (N) |
|---|---|---|
| 1 | 1 | 3922.0301 |
| 2 | 4 | 6018.8798 |
| 3 | 3 | 4227.532 |
| 4 | 0 | 3936.155 |
| 5 | 2 | 7498.363 |
| 6 | 5 | 3974.7681 |
| 7 | 6 | 5928.3233 |
| 8 | 9 | 5408.6954 |
| 9 | 11 | 6107.7574 |
| 10 | 8 | 4014.669 |
| 11 | 7 | 6215.32 |
| 12 | 10 | 5646.2751 |
| 13 | 13 | 4208.5797 |
| 14 | 16 | 3977.4113 |
| 15 | 17 | 7092.6078 |
| 16 | 14 | 6096.561 |
| 17 | 12 | 5722.6305 |
| 18 | 15 | 3957.5649 |
| 19 | 21 | 5594.9603 |
| 20 | 18 | 7500 |
| 21 | 23 | 7365.7369 |
| 22 | 20 | 4090.1051 |
| 23 | 19 | 7498.3514 |
| 24 | 22 | 7320.901 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, D.; Jian, Y.; Yang, H. A Sequence-Aware Surrogate-Assisted Optimization Framework for Precision Gyroscope Assembly Based on AB-BiLSTM and SEG-HHO. Electronics 2025, 14, 3470. https://doi.org/10.3390/electronics14173470
Lin D, Jian Y, Yang H. A Sequence-Aware Surrogate-Assisted Optimization Framework for Precision Gyroscope Assembly Based on AB-BiLSTM and SEG-HHO. Electronics. 2025; 14(17):3470. https://doi.org/10.3390/electronics14173470
Chicago/Turabian StyleLin, Donghuang, Yongbo Jian, and Haigen Yang. 2025. "A Sequence-Aware Surrogate-Assisted Optimization Framework for Precision Gyroscope Assembly Based on AB-BiLSTM and SEG-HHO" Electronics 14, no. 17: 3470. https://doi.org/10.3390/electronics14173470
APA StyleLin, D., Jian, Y., & Yang, H. (2025). A Sequence-Aware Surrogate-Assisted Optimization Framework for Precision Gyroscope Assembly Based on AB-BiLSTM and SEG-HHO. Electronics, 14(17), 3470. https://doi.org/10.3390/electronics14173470






