Multi-Radar Track Fusion Method Based on Parallel Track Fusion Model

Abstract

With the development of multi-sensor collaborative detection technology, radar track fusion has become a key means to improve target tracking accuracy. Traditional fusion methods based on Kalman filtering and weighted averaging have the problem of insufficient adaptability in complex environments. This paper proposes an end-to-end deep learning track fusion method, which achieves high-precision track reconstruction through residual extraction and parallel network fusion, providing a new end-to-end method for track fusion. The method combines the attention mechanism and the long short-term memory network in parallel and optimizes the computational complexity. Through the uncertainty weighting mechanism, the fusion weight is dynamically adjusted according to the reliability of the track features. Experimental results show that the mean absolute error of fusion accuracy of this method is 79% lower than the Kalman filter algorithm and about 87% lower than the mainstream deep learning model, providing an effective way for multi-radar track fusion in complex scenarios.

1. Introduction

Modern radar systems face challenges from complex electromagnetic environments and multi-target interference. Track estimation from a single sensor often suffers from insufficient accuracy and poor robustness. Track fusion can effectively improve the accuracy and reliability of target state estimation by integrating multi-sensor data. It is a core technology in military reconnaissance, intelligent transportation, and other fields.

As the core area of multi-sensor information fusion, track fusion technology aims to achieve high-precision joint estimation of the state of moving targets by collaboratively processing distributed sensor data. Linear weighted fusion methods, such as variance weighting and convex combination fusion, only use single-time position information and have low accuracy. Kalman filter fusion achieves dynamic updates through state estimation, but it has a strong dependence on motion models and noise parameters, and its performance degrades significantly when the model mismatches. Deep learning technology can establish a direct mapping from raw sensor data to fused track data, breaking through the limitations of traditional methods that rely on staged processing. Optimal fusion of multisource information can be achieved through end-to-end global optimization.

The progression of multi-radar track fusion methodologies has been shaped by persistent challenges in complex operational environments. Early linear fusion techniques, such as variance weighting and convex combination, relied exclusively on instantaneous position data, leading to significant accuracy degradation during target maneuvers due to their neglect of temporal dynamics [1]. This limitation spurred the development of Kalman filter-based approaches, where Kumar et al. interacting multiple model (IMM) filter enabled asynchronous fusion of radar and identification of friend or foe (IFF) data, substantially reducing maneuvering target position errors [2]. However, these model-driven methods maintained stringent dependencies on predefined motion patterns and noise parameters, causing performance collapse under model mismatch [3].

Subsequent innovations focused on sequential processing frameworks to enhance adaptability. Bu et al. combined IMM with unscented Kalman filters (UKF) to compensate for spatiotemporal biases under nearly coordinated turn (NCT) and nearly constant acceleration (NCA) models [3], while Zhang et al. avoided covariance matrix inversions through information filtering for equivalent centralized fusion [4]. Though the improved robustness, scalability issues persisted in distributed networks. Gayraud et al. addressed this through track graph construction using space-time discretization, processing asynchronous covariance via random maximum consensus [5]. Crucially, Dunham et al. revealed the fundamental trade-off between system-level fusion and point track fusion, that is, higher position accuracy and better velocity estimation [6], highlighting the need for context-aware architectures.

The shift toward complex systems yielded specialized solutions. Xia et al. unified active/passive radar data through measurement dimension expansion [7], while Li et al. Newton difference field fusion eliminated non-uniform errors in joint array domains [8]. For dynamic weighting, Qiao et al. comprehensive adaptive weighted data fusion (CAWDF) incorporated historical relationships to suppress outliers [9], and Zhang et al. asynchronous fusion based on track quality with multiple model (AFTQMM) allocated weights via multi-model track quality [10]. By fusing multi-period local tracks with time correlation, the mean square error of the fused track is lower than that of the local track [11]. Yet these methods struggled with real-time reliability shifts during interference, as fixed heuristics could not adapt to sudden sensor degradation.

Breakthroughs in deep learning have enabled new approaches. Yun et al. fully convolutional network avoided parameter explosion through differential loss weighting [12], while Li et al. cloud-edge collaborative architecture combined offline training with online updates [13]. Chen et al. deep learning track fusion algorithm bypassed traditional correlation assumptions for over-the-horizon radar (OTHR) fusion [14], and He et al. hybrid consensus strategy improved multi-target tracking through decentralized node estimation [15]. However, these approaches revealed three unresolved deficiencies: sequential spatiotemporal processing neglected feature synergy [12], static fusion weights ignored real-time confidence fluctuations [16], and multitask optimization imbalances persisted [13]. For radar networks, Wu et al. accelerated correlation via multithreading optimization [17], and Gao et al. optimized power combinations to extend detection ranges [18]. Despite these advances, the field’s core limitations remain: inadequate parallel spatiotemporal integration, inability to dynamically weight features based on live reliability, and unresolved conflicts in multitasking optimization deficiencies that require fundamentally new architectural approaches.

In order to solve the problem of insufficient spatiotemporal fusion, that is, the sequential processing of spatial and temporal features ignores their interdependence, and the static fusion strategy cannot be dynamically adjusted according to the changes in physical features, this paper proposes an end-to-end track fusion method with parallel fusion of time and space. This method enhances track features through a fully connected neural network and extracts features using a parallel attention mechanism and a long short-term memory network. Through selection of adaptive feature weights, it reconstructs high-precision fused tracks. The main contributions are as follows:

• This study presents a series of data normalization methods, processing data based on different input physical features separately. Track data are segmented, rectified, and normalized using a z-score transformation. Sensor-specific physical properties are preserved by integrating a feature group enhancement layer and a temporal embedding mechanism.
• The parallel track fusion model (PTFM) is based on a spatiotemporal-aware parallel fusion architecture, combines an attention mechanism for adaptive feature calibration, and uses a gated long short-term memory network for long-term temporal dependency modeling, effectively improving the fusion accuracy of target positions.
• The model features an adaptive multitask loss mechanism that dynamically balances optimization conflicts among estimation tasks such as position, velocity, and heading. Uncertainty weights focus on high-confidence features, significantly improving fusion robustness and reducing error propagation in complex scenarios.

Verification on the multisource track segment association dataset shows that the proposed method outperforms existing traditional method and deep learning models in core metrics. The core metrics include position root mean square error (RMSE), mean absolute error (MAE), variance, etc. This method provides a technical method for intelligent collaborative sensing technology in distributed radar networks.

2. Multi-Radar Track Fusion Model

2.1. End-to-End Track Fusion Problem Description

Multi-sensor track fusion involves fusing track information from multiple sensors on the same target to obtain a more accurate, continuous, and robust target track estimate. This problem can be formalized as a state estimation problem: given a sequence of observations from a heterogeneous sensor system at discrete time steps, estimate the target’s true track. Within the framework of deep learning, we consider an end-to-end fusion approach. This method directly learns the mapping function from the original multi-sensor time series data to the optimal fusion track, realizes global optimization learning from input to output, and outputs the final target track.

Suppose we have $\mathit{M}$ sensors, each of which outputs an observation vector at time step $\mathit{t}$. For the sensor $\mathit{m}$, its time series is

$${\mathit{X}}_m={\left[{\mathit{x}}_m^{\left(1\right)},{\mathit{x}}_m^{\left(2\right)},\dots ,{\mathit{x}}_m^{\left(T\right)}\right]}^T\in {\mathbb{R}}^{T\times D_m},$$

(1)

where $\mathit{T}$ is the time step length and $D_m$ is the dimension of the sensor $\mathit{m}$’s observation vector, usually including position, velocity, heading, etc. For example, a typical observation vector can be ${\mathit{x}}_m^{\left(t\right)}=[ \mathit{x}, \mathit{y}, \mathit{v}, \mathit{\theta } {]}^T$. The fused target track sequence is

$$\mathit{Y}={\left[{\mathit{y}}^{\left(1\right)},{\mathit{y}}^{\left(2\right)},\dots ,{\mathit{y}}^{\left(T\right)}\right]}^T\in {\mathbb{R}}^{T\times D_y},$$

(2)

where $D_y$ is the output dimension, usually corresponding to the position, speed, and heading in the input, such as four dimensions: longitude, latitude, speed, and heading angle.

Our goal is to learn a mapping function $\mathcal{F}$ that maps a multi-sensor input sequence to a target track sequence:

$$\mathit{Y}=\mathcal{F}\left({\mathit{X}}_1,{\mathit{X}}_2,\dots ,{\mathit{X}}_M;\mathit{\Theta }\right),$$

(3)

where $\mathit{\Theta }$ is the parameter of the mapping function and the weights of the deep learning model. Therefore, we propose the parallel track fusion model (PTFM), which achieves the optimal fusion of multisource information through end-to-end global optimization.

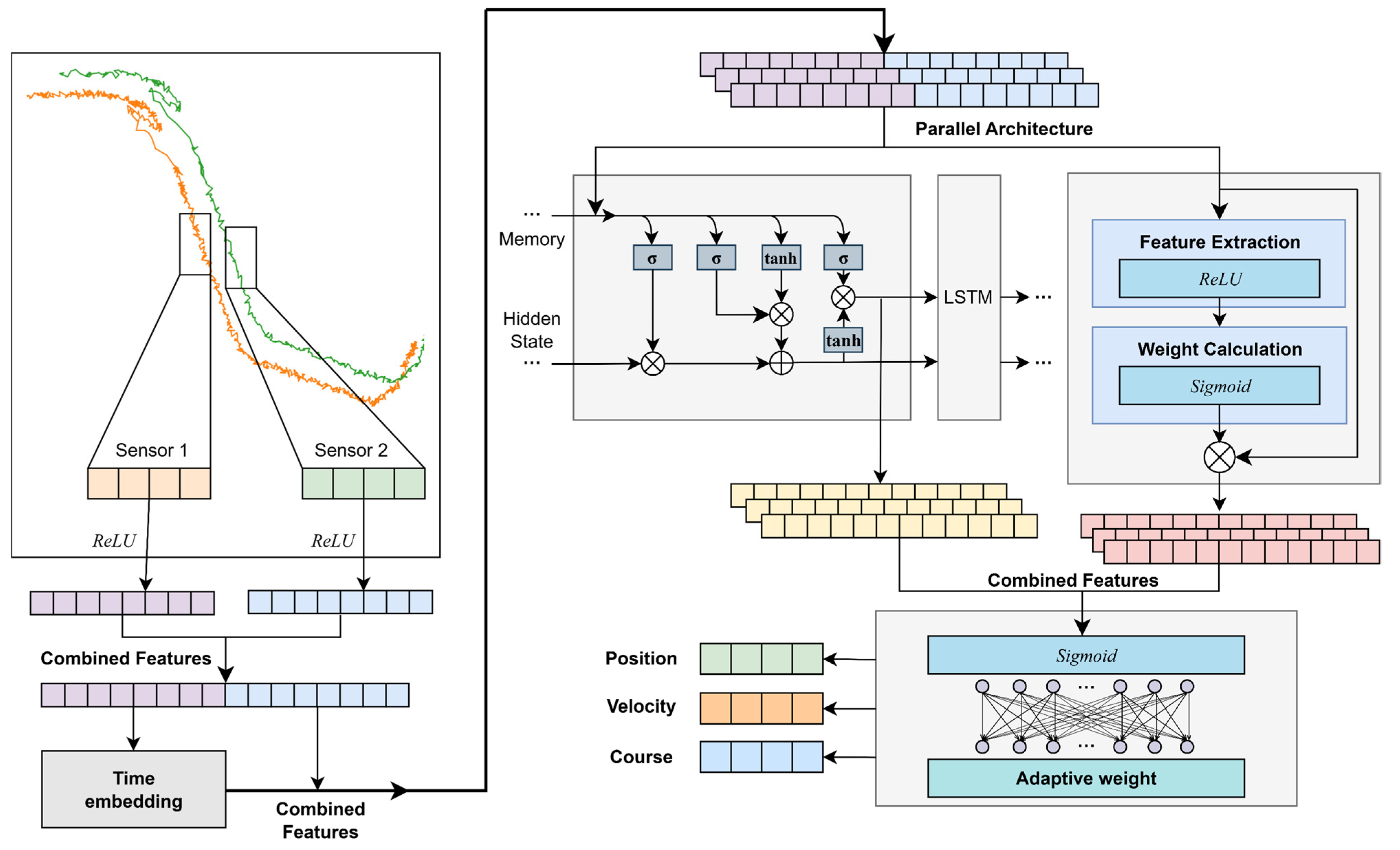
2.2. Overall Framework Design

The core challenge of multi-radar track fusion is to solve the spatiotemporal asynchrony, feature heterogeneity, and robustness problems of heterogeneous sensor data in complex scenarios. The parallel track fusion model builds on time-step alignment and track correlation, employing a core model parallel architecture to achieve high-precision multi-radar track fusion through feature enhancement, spatiotemporal collaboration, dynamic optimization, and multitask output processing. The innovation of this architecture is reflected in three aspects. First, it preserves the physical characteristics of different radars through physical perception. Second, it integrates an attention mechanism with a gated long short-term memory (LSTM) network to address the problem of extracting spatiotemporal features from asynchronous data. Third, it designs an adaptive multitask loss function to dynamically balance the optimization conflicts among position, velocity, and heading estimation.

The input of PTFM is the time series observation tensor $\mathit{X}\in {\mathbb{R}}^{N\times T\times 8}$ of the dual radar sensors, where N is the number of samples, T is the fixed time step, and the feature dimension includes the longitude and latitude, speed, and heading of the two radar sources. Each radar contributes four-dimensional features, totaling eight dimensions. The output layer generates a fused track $\mathit{Y}\in {\mathbb{R}}^{N\times T\times 4}$, which contains the fused longitude and latitude, speed, and heading. The overall framework is shown in Figure 1.

First, the sensor data is segmented, and the input tensor is decoupled into independent data subsets of sensor 1 and sensor 2 according to the radar source to avoid mutual interference of heterogeneous features. The bidirectional data is nonlinearly mapped through an independent fully connected network to achieve bidirectional feature data enhancement and retain the feature distribution patterns of different radar sensors. Triangular periodic coding is used to generate time embedding vectors so the model can separate and process the spatial position changes and time evolution laws caused by target movement. The importance of spatial features is dynamically adjusted through the attention weighting mechanism, and the gated LSTM is combined to capture the timing dependency to achieve the coordinated fusion of spatiotemporal features. Finally, the adaptive weight learning is combined to balance the multitask loss to generate position, speed, and heading fusion.

2.3. Data Preprocessing Module

Data preprocessing is fundamental to track fusion. Its core goal is to eliminate format differences in heterogeneous sensor input data through three-dimensional tensor reshaping and standardization. To eliminate time-step misalignment between the input sensor data and the true track data, the track segment clipping method utilizes a multidimensional track data preprocessing algorithm [19].

Different sensors have varying data collection rates and latencies, leading to inconsistent track timestamps and observation counts. To overcome this, a preprocessing pipeline ensures temporal alignment and data uniformity. First, the shared time coverage between sensors is determined by finding their earliest common start and latest common end timestamp. Next, for a data point from sensor A at time $\mathit{t}$, a time window is defined around $\mathit{t}$. Sensor B’s data falling within this window is averaged, aligning its value to $\mathit{t}$. The algorithm then segments the aligned tracks into sequential, standardized time windows defined by window size. At the same time, the real track data is aligned to the same timestamp using interpolation method. This process mitigates sensor timing differences, creates standardized temporal windows, computes inter-sensor disparities within them, and normalizes the data for downstream analysis or model training.

PTFM preprocessing includes dimensionality correction, sensor data separation, and linear normalization, providing high-quality input for subsequent feature extraction. Sensor stream separation is used to extract multidimensional observations from different sensors as input streams, and the true value of real data is used as the target stream to form a physically isolated supervision topology. In the process of mathematically modeling the standardization process, given a three-dimensional data tensor $\mathit{X}\in {\mathbb{R}}^{N\times T\times 4}$, where $\mathit{N}$ represents the number of samples and $\mathit{T}$ represents the time step. Each feature dimension $\mathit{f}\in \{\mathrm{1,2},\mathrm{3,4}\}$ is independently normalized. Reshape the 3D feature slices into a 2D matrix ${\mathit{M}}_f$:

$${\mathit{M}}_f=\left[\begin{array}{ccc}{x}_{\mathrm{1,1},f}& \dots & x_{1,T,f}\\ ⋮& \ddots & ⋮\\ x_{N,1,f}& \dots & x_{N,T,f}\end{array}\right]\in {\mathbb{R}}^{N\times T}.$$

(4)

Calculate the mean and standard deviation of the feature matrix:

$${\mu }_f={\displaystyle \frac{1}{N·T}}\sum _{i=1}^N\sum _{j=1}^T{x}_{i,j,f},$$

(5)

$${\sigma }_f=\sqrt{{\displaystyle \frac{1}{N·T}}\sum _{i=1}^N\sum _{j=1}^T{\left(x_{i,j,f}-{\mu }_f\right)}^2}.$$

(6)

$x_{i,j,f}$ represents the value of the feature of the $\mathit{f}$th dimension in the $\mathit{j}$th time step in the $\mathit{i}$th sample. ${\mu }_f$ and ${\sigma }_f$ are the mean and standard deviation of the feature matrix, respectively. The preprocessing uses a standardized z-score transformation to eliminate the dimensional effect. The transformation formula is $\mathcal{Z}:{\tilde{x}}_{i,j,f}=(x_{i,j,f}-{\mu }_f)/{\sigma }_f$. At the same time, the parameters are saved to achieve a strictly reversible mapping ${\mathcal{Z}}^{-1}:x_{i,j,f}={\sigma }_f·{\tilde{x}}_{i,j,f}+{\mu }_f$, guarantees the stability of the reverse mapping, and ensures that the prediction results can be reverse-mapped to the geographic coordinate system to avoid information distortion.

2.4. Feature Enhancement Layer

The goal of the feature enhancement layer is to improve the representation ability of the original radar data through nonlinear transformation while retaining the physical property differences of the sensors. The data of each sensor passes through an independent two-layer fully connected network. The first layer uses the $\mathit{R}\mathit{e}\mathit{L}\mathit{U}$ activation function to map the original 4-dimensional features, namely latitude, longitude, speed, and heading, to a 32-dimensional space. The second layer uses the ReLU activation function again to map the 32-dimensional feature vector to a 64-dimensional space. The purpose is to increase the expressiveness of each sensor data so subsequent fusion can be based on richer features. The whole process realizes a hierarchical transformation from original low-dimensional features to high-dimensional abstract representations. Suppose the input data of sensor $\mathit{i}$ is $s^{\left(i\right)}\in {\mathbb{R}}^{T\times 4}$, where $\mathit{T}$ is the sequence length and $h^{\left(i\right)}$ represents the feature vector of sensor $\mathit{i}$ after being mapped by the activation function:

$$h_1^{\left(i\right)}=\mathit{ReLU}\left(s^{\left(i\right)}{W}_1^{\left(i\right)}+b_1^{\left(i\right)}\right), W_1^{\left(i\right)}\in {\mathbb{R}}^{4\times 32},b_1^{\left(i\right)}\in {\mathbb{R}}^{32},$$

(7)

$$h_2^{\left(i\right)}=\mathit{ReLU}\left({h_1}^{\left(i\right)}{W}_2^{\left(i\right)}+b_2^{\left(i\right)}\right), W_2^{\left(i\right)}\in {\mathbb{R}}^{32\times 64},b_2^{\left(i\right)}\in {\mathbb{R}}^{64}.$$

(8)

The two enhanced features are concatenated in the last dimension:

$$h_{\mathit{combined} }=\left[h_2^{\left(1\right)},h_2^{\left(2\right)}\right]\in {\mathbb{R}}^{T\times 128}.$$

(9)

2.5. Time Embedding Mechanism

Asynchrony is one of the core problems of multi-radar fusion. Therefore, the track data in the model is a uniform time-sampling sequence after preprocessing, and the original delay of the sensor has been corrected in the preprocessing stage. At the same time, LSTM itself has the ability to remember the time sequence, but it is difficult to accurately identify the absolute position information. Therefore, the time embedding part uses all-zero delay as a position encoding technique so each row in the embedding matrix corresponds to a different position rather than using real delay embedding. The encoding method is as follows:

$$\left\{\begin{array}{c}\mathit{PE}(t,2i)=\mathit{sin}\left({\displaystyle \frac{t}{10000^{2i/d}}}\right)\\ \mathit{PE}(t,2i+1)=\mathit{cos}\left({\displaystyle \frac{t}{10000^{(2i+1)/d}}}\right)\end{array}\right.,$$

(10)

$\mathit{t}$ is the time step index, $\mathit{i}$ is the dimension index, and $\mathit{d}=16$ is the embedding dimension. This design makes the embedding vectors of different time steps distinguishable through the frequency attenuation mechanism while retaining a certain periodicity so the model can separate and process the spatial position changes and time evolution laws caused by the movement of the target. Its core value is to inject absolute time-step position information into the model while improving the spatiotemporal modeling capability with minimal computational cost.

The enhanced 64-dimensional sensor features are spliced with the 16-dimensional time embedding vector in the channel dimension to form a fusion tensor with a dimension of T × 144. This operation deeply binds the time information with the spatial features so the model can use the information of the time dimension and the space dimension for track inference at the same time. In a variety of motion scenarios, the spliced features can more accurately capture the correlation between time delay and position change and improve the accuracy of fusion.

2.6. Parallel Fusion Core

The parallel fusion core is a key module of PTFM. Through the synergy of the attention weighting mechanism and gated LSTM, dynamic calibration of spatial features and long-term modeling of time dependence are achieved. This module contains four subunits, attention feature calibration, gated LSTM time series modeling, parallel fusion, and residual connection.

2.6.1. Attention Weighting Mechanism

The reliability of different radars in complex scenarios varies dynamically. The role of this attention mechanism is to dynamically select features, give greater weights to important features, and suppress unimportant features. Since the output dimension is the same as the input dimension, it is feature-by-feature attention, that is, a weight is given to each feature at each time step. Let the input feature tensor be $X\in {\mathbb{R}}^{B\times T\times D},$ where $\mathit{B}$ is the batch size, $\mathit{T}$ is the time series length, and $\mathit{D}$ is the fusion features’ dimension. Its mathematical transformation follows a dual-mapping relationship, and the first layer is a high-dimensional nonlinear projection:

$$\mathit{H}=\mathit{ReLU}\left(\mathit{X}{\mathit{W}}_1+{\mathit{b}}_1\right),$$

(11)

where ${\mathit{W}}_1\in {\mathbb{R}}^{\mathit{D}\times 128}$, ${\mathit{b}}_1\in {\mathbb{R}}^{128}$, the nonlinear dimensionality increase transformation of the input features, is realized through the 128-dimensional latent space activation, and the cross-sensor interaction features are extracted. The second level is dimensional adaptive gating:

$$\mathit{A}=\mathit{\sigma }\left(\mathit{H}{\mathit{W}}_2+{\mathit{b}}_2\right),$$

(12)

where ${\mathit{W}}_2\in {\mathbb{R}}^{128\times \mathit{D}}$, ${\mathit{b}}_2\in {\mathbb{R}}^{\mathit{D}}$, the Sigmoid activation function $\mathit{\sigma }(\mathit{z})={\left(1+e^{-z}\right)}^{-1}$, is used to generate the $\mathit{D}$-dimensional space-gating vector $\mathit{A}$ of [0, 1], satisfying ${\mathit{X}}_{\mathit{attended} }=\mathit{X}\odot \mathit{A}$, where ⊙ represents the Hadamard product and ${\mathit{X}}_{\mathit{attended}}$ represents the output feature tensor.

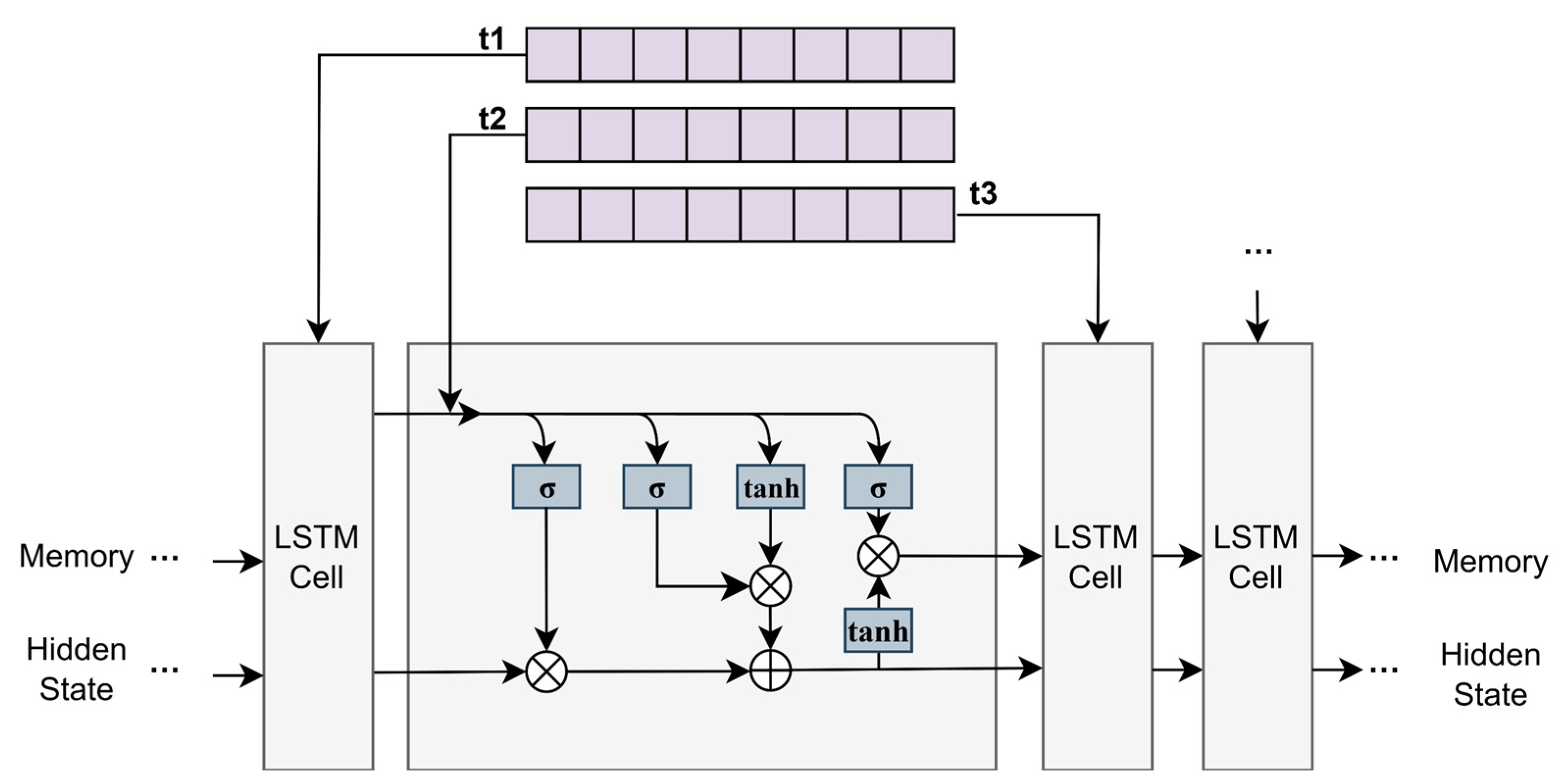
2.6.2. LSTM Time Series Modeling

The long short-term memory network (LSTM) solves the gradient vanishing problem of traditional RNN through the gating mechanism and is suitable for capturing the long-range dependency of the track. The LSTM time series model framework is shown in Figure 2.

The LSTM design of PTFM adopts an orthogonal initialization strategy and contains 64 memory units, and the cell state update equation is

$${\mathit{C}}_t={\mathit{f}}_t\odot {\mathit{C}}_{t-1}+{\mathit{i}}_t\odot \mathit{tanh}\left({\mathit{W}}_c·\left[{\mathit{h}}_{t-1},{\mathit{x}}_t\right]\right),$$

(13)

where the forget gate is ${\mathit{f}}_t$; the input gate is ${\mathit{i}}_t$, which respectively control the fusion ratio of the historical state and the current input; ${\mathit{W}}_c$ is the weight matrix; ${\mathit{h}}_{t-1}$ is the hidden state of the previous time step; and ${\mathit{x}}_t$ is the current input feature. L2 regularization is introduced, and $\mathit{\lambda }=10^{-4}$ is taken to constrain the norm of the weight matrix to reduce the risk of gradient vanishing. In the 50-step ship track prediction, the long-range dependency modeling error of LSTM is further reduced.

2.6.3. Gated Parallel Fusion and Residual Connection

To achieve the coordinated optimization of spatiotemporal features, PTFM innovatively adopts a dual-branch parallel fusion architecture. The temporal feature branch uses LSTM to output 64-dimensional temporal features ${\mathit{H}}_{\mathit{LSTM}}\in {\mathbb{R}}^{T\times 64}$ to capture the temporal evolution of target motion, while the spatial feature branch uses the 144-dimensional spatial features ${\mathit{X}}_{\mathit{attended} }\in {\mathbb{R}}^{\mathrm{T}\times 144}$ after attention weighting to retain the spatial correlation of the sensor.

The dual-path features are spliced into a 208-dimensional tensor along the channel dimension, and feature selection is achieved through the gating function:

$$\mathit{G}=\mathit{\sigma }\left({\mathit{W}}_g·\left[{\mathit{H}}_{\mathit{LSTM}},{\mathit{X}}_{\mathit{attended}}\right]\right),$$

(14)

where $\mathit{\sigma }$ is the Sigmoid function, ${\mathit{W}}_g$ is the gating weight matrix, and $\mathit{G}\in [0, 1{]}^{T\times 208}$ is the gating coefficient. The fusion result is

$$\mathit{O}=\mathit{G}\odot \left[{\mathit{H}}_{\mathit{LSTM}},{\mathit{X}}_{\mathit{attended}}\right].$$

(15)

In order to avoid information loss in the deep network, the residual connection is introduced: ${\mathit{O}}_{\mathrm{final} }=\mathit{O}+{\mathit{W}}_r·{\mathit{X}}_{\mathit{attended}}$, where ${\mathit{W}}_r$ is the linear projection matrix. The ablation experiment confirms that this design improves the fusion accuracy of dense target scenes and verifies the effectiveness of spatiotemporal feature complementarity.

2.7. Adaptive Weights and Multi-Task Output Layer

One of the core innovations of this study is the proposal of an adaptive multitask loss mechanism based on uncertainty modeling. The adaptive weight branch converts the input into a three-dimensional normalized weight coefficient through a fully connected layer and a Softmax activation function. This coefficient is used to dynamically adjust the loss contribution weight of each subtask during multitask learning, thereby achieving an adaptive balance between tasks and preventing low-quality features from contaminating the core feature prediction through a shared layer. The core breakthrough of this module is that there is no need to preset feature validity priors. The output dimension is expanded to seven dimensions, of which the newly added three dimensions are weight parameters. The output of the model at time step $\mathit{t}$ includes three predicted values of position, velocity, and heading and the corresponding weight vector ${\mathit{w}}_{\mathit{t}}=\left[{\mathit{w}}_{\mathit{p}}^{\left(\mathit{t}\right)},{\mathit{w}}_{\mathit{v}}^{\left(\mathit{t}\right)},{\mathit{w}}_{\mathit{\theta }}^{\left(\mathit{t}\right)}\right]\in {\mathbb{R}}^3$, which is generated by the terminal Softmax layer:

$${\mathit{w}}_t=\mathrm{softmax}\left({\mathit{z}}_t\right)=\left[{\displaystyle \frac{e^{z_p^{\left(t\right)}}}{\sum e^{z_t}}},{\displaystyle \frac{e^{z_v^{\left(t\right)}}}{\sum e^{z_t}}},{\displaystyle \frac{e^{z_{\theta }^{\left(t\right)}}}{\sum e^{z_t}}}\right],$$

(16)

where ${\mathit{z}}_t$ is the linear projection output of the 128-dimensional fusion feature. The model dynamically balances the position, speed, and heading losses through the coefficients learned by the adaptive weight layer:

$$\mathcal{L}={\displaystyle \frac{1}{\mathit{exp}\left({\sigma }_p\right)}}{\mathcal{L}}_{\mathit{pos} }+{\displaystyle \frac{1}{\mathit{exp}\left({\sigma }_v\right)}}{\mathcal{L}}_{\mathit{vel} }+{\displaystyle \frac{1}{\mathit{exp}\left({\sigma }_c\right)}}{\mathcal{L}}_{\mathit{course} }+{\sigma }_p+{\sigma }_v+{\sigma }_c,$$

(17)

$${\mathcal{L}}_{\mathit{pos} }={\displaystyle \frac{1}{T}}\sum _{t=1}^T{‖{\mathit{p}}_t^{\mathit{true} }-{\mathit{p}}_t^{\mathit{pred}}‖}_2^2,$$

(18)

$${\mathcal{L}}_{\mathit{vel} }={\displaystyle \frac{1}{T}}\sum _{t=1}^T{\left(v_t^{\mathit{true} }-v_t^{\mathit{pred}}\right)}^2,$$

(19)

$${\mathcal{L}}_{\mathit{course} }={\displaystyle \frac{1}{T}}\sum _{t=1}^{T}min\left(\left|{\theta }_t^{\mathit{true} }-{\theta }_t^{\mathit{pred}}\right|,360-\left|{\theta }_t^{\mathit{true} }-{\theta }_t^{\mathit{pred}}\right|\right),$$

(20)

among them, ${\mathcal{L}}_{\mathit{pos}}$ is the Euclidean distance loss of position, ${\mathcal{L}}_{\mathit{vel}}$ is the mean square error loss of speed, and ${\mathcal{L}}_{\mathit{course}}$ is the periodic loss of heading.

The dynamic weight parameters ${\sigma }_p$, ${\sigma }_v$, ${\sigma }_{\theta }$ are calculated using sequential averaging:

$${\sigma }_p={\displaystyle \frac{1}{T}}\sum _{t=1}^{T}ln\sum \left({\displaystyle \frac{1}{w_p^{\left(t\right)}+ϵ}}\right).$$

(21)

This design results in a negative correlation between ${\sigma }_p$ and the weight ${\mathit{w}}_{\mathit{p}}^{\left(\mathit{t}\right)}$ when the confidence level of the position prediction is high, ${\mathit{w}}_{\mathit{p}}^{\left(\mathit{t}\right)}$ increases, and ${\sigma }_p$ decreases accordingly, thereby increasing the contribution of the position loss term ${\mathcal{L}}_{\mathit{pos}}$ to the total loss. During backpropagation, the gradient of the loss function with respect to each weight parameter is

$${\displaystyle \frac{\partial \mathcal{L}}{\partial {\sigma }_p}}=-{\displaystyle \frac{{\mathcal{L}}_{\mathit{pos}}}{\mathit{exp}\left({\sigma }_p\right)}}+1,$$

(22)

$${\displaystyle \frac{\partial \mathcal{L}}{\partial w_p^{\left(t\right)}}}={\displaystyle \frac{1}{T}}·{\displaystyle \frac{\partial \mathcal{L}}{\partial {\sigma }_p}}·{\displaystyle \frac{-1}{w_p^{\left(t\right)}+ϵ}}.$$

(23)

In the process of training based on experimental data, the position weight is further increased, and the speed and heading weight are relatively low, which meets the actual needs of position accuracy priority in target tracking.

The goal of the multitask output layer is to simultaneously optimize the estimation accuracy of position, speed, and heading and solve the conflict of multi-objective optimization and the problem of low data quality of some input features. This layer adopts a decoupled output structure and an adaptive loss mechanism. The output layer of the model is designed as a multi-output architecture. The position estimation branch maps the feature into a 2D latitude and longitude coordinate output representing the geographic location through a fully connected layer and a linear activation function. The speed and heading estimation branch compresses the input into scalar outputs representing 1D instantaneous speed and heading, respectively, through a fully connected layer and a linear activation function.

3. Experiment and Result Analysis

3.1. Experimental Settings

3.1.1. Experimental Data Design

This study uses the multisource track association dataset (MTAD) for model validation [20]. The dataset covers multiple high-confidence simulation scenarios. The experimental data contains more than 18,000 sets of associated track segments, with a training set to validation set ratio of 3:2. Each set of track segment contains one track of data measured by two radar sensors and one AIS real track data. The fusion task involves challenging conditions, such as target maneuvering behavior, sensor noise interference, and complex system errors. The example diagram of sensor tracks and actual tracks is shown in Figure 3. Subfigures a, b, and c represent three examples of track scenarios. As can be seen from the example tracks, the initial radar detection tracks have large errors and sensor noise.

In the calculation process of the indicator evaluation part, the model is trained using standardized data with a mean of 0 and a standard deviation of 1. Therefore, when calculating results such as geographic distance error, it is calculated on the original data after denormalization, and the Haversine formula is used to calculate the actual geographic distance. Only after denormalization do these values have clear physical meanings, while the mean absolute error value in the training graph is the mean absolute error of the standardized data, which is independent of the original feature scale. Therefore, the values in the training graph are mainly used to present the training process, while the values in the evaluation table are used to objectively compare the performance of models and methods.

3.1.2. Training Parameter Configuration

To enhance experimental reproducibility, this section systematically describes the hyperparameter configuration and optimization strategy for model training. The model is implemented in TensorFlow 2.15 using the Adam optimizer. The initial learning rate is set to 0.001, and weight parameters are dynamically adjusted. The learning rate is adaptively decayed using a callback function: if the validation loss does not improve for 10 consecutive training epochs, the learning rate is decayed to 0.5 times the current value, with a lower threshold of ${10}^{-6}$. The training batch size is fixed at 32, the maximum number of epochs is set to 150, and an early stopping mechanism is implemented to prevent overfitting. This mechanism intelligently terminates training by continuously monitoring the validation set loss trend. If the validation loss does not show a downward trend for 20 consecutive training epochs, the training process is automatically terminated, and the model weights corresponding to the lowest validation loss are automatically restored. Regarding the regularization strategy, L2 weight regularization is introduced in the LSTM layer with a coefficient of $\mathit{\lambda }=10^{-4}$, and weight initialization uses an orthogonal initialization method. During training, the validation set position MAE, velocity MAE, and heading MAE metrics are monitored in real time, and the trends of key metrics are visualized using convergence curves.

3.2. Comparative Experiments

The comparative methods cover classic signal processing algorithms and cutting-edge deep learning models, including four traditional methods: weighted fusion (WF), Kalman filter (KF), convex combination fusion (CCF), covariance intersection fusion (CIF), and long short-term memory network (LSTM), Transformer, and fully connected models (Dense) based on deep learning. In terms of the evaluation system, the track association performance is quantitatively analyzed through three core indicators: position root mean square error (RMSE), mean absolute error (MAE), and variance.

The experimental results clearly show that the parallel fusion model proposed in this study shows comprehensive advantages in the track prediction task. As shown in

Table 1. Performance comparison of different methods.

	PTFM	WAF	KF	CCF	CIF	LSTM	Transformer	Dense
RMSE (km)	2.6180	10.576	10.667	10.597	10.561	4.6811	4.5797	7.6242
MAE (km)	0.3542	1.4244	1.6672	1.5786	1.2918	2.4953	3.1070	2.2228
Variance (km2)	6.7284	109.83	111.01	109.81	109.86	15.687	11.320	53.187

, this method is significantly better than various comparative methods in the three core indicators of root mean square error, mean absolute error, and variance. This breakthrough performance is attributed to the innovative design of the model architecture. The attention mechanism and the long short-term memory network parallel processing structure are constructed; key feature focus and time-dependent modeling are taken into account. A gated fusion mechanism and residual connection are used to optimize the information integration process.

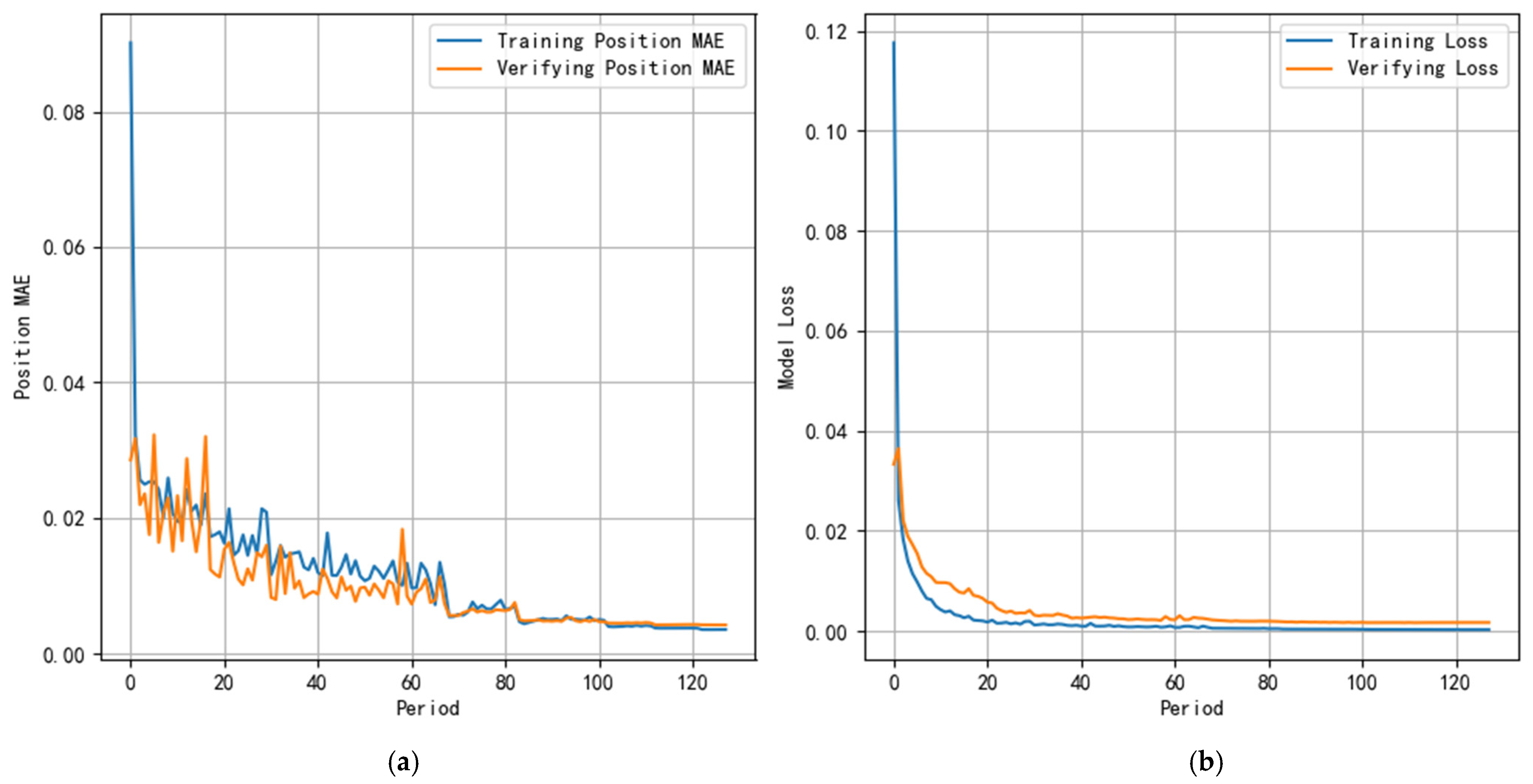
The PTFM method is significantly better than the traditional method and the single deep learning method in terms of position estimation accuracy, especially in complicated scenarios. The RMSE of the PTFM method is 32.7% lower than that of KF, indicating that it has a stronger generalization ability for complex motion patterns. The change in the mean absolute error of the position during training is shown in Figure 4a, and the model training loss is shown in Figure 4b. The vertical axis of the figure is a dimensionless indicator value used to measure model error or performance.

It is worth paying special attention to the outstanding performance of the mean absolute error, which is 72.4% lower than the optimal traditional method and 85.7% lower than the 2.4953 of the mainstream deep learning model. The parallel structure effectively leverages the complementary capabilities of the two mechanisms. The attention layer dynamically focuses on key track nodes, while the LSTM branch strengthens the modeling of long-term dependencies across the continuous track dynamics. This design overcomes the inherent limitations of single models. The LSTM model alone, due to its lack of feature focus, results in an MAE as high as 2.4953 km, a 604% degradation compared to PTFM. The Transformer model, on the other hand, suffers from a MAE of 3.1070 km due to the dilution of local details by global attention, a 778% degradation compared to PTFM. At the same time, the low level of prediction variance of 9.2169 verifies the stable performance of the gated fusion structure, which is 91.8% lower than the traditional method and 82.7% lower than the densely connected model.

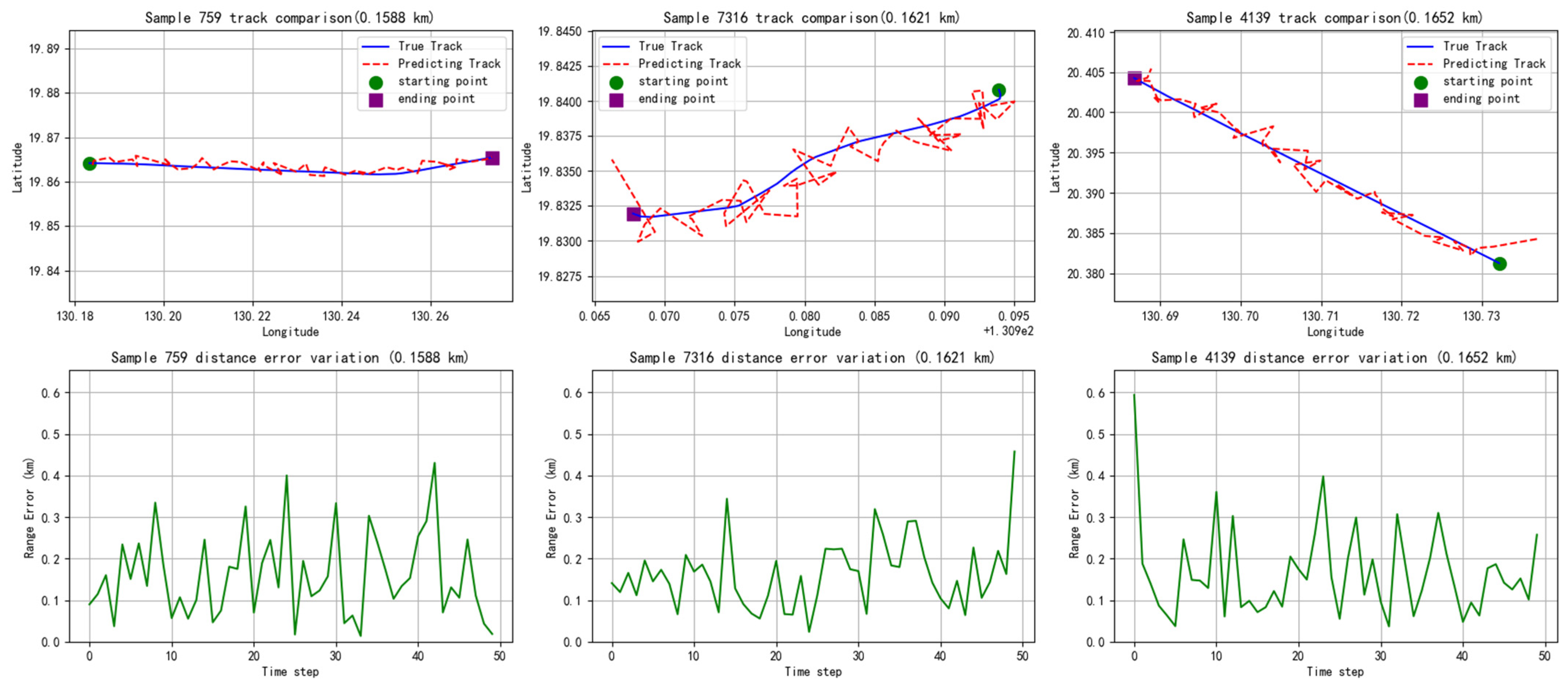
In the data processing stage, standardized preprocessing ensures the scale consistency of multisource sensor inputs, and serialization processing completely retains the dynamic characteristics of the track. In the experiment, the performance of traditional filtering methods is limited by the linear assumption, such as the root mean square error of Kalman filtering is 10.667; although the mainstream time series model is better than the traditional method in root mean square error, it still has a significant gap with this method in key indicators due to the lack of a dedicated module for multisensor fusion. The comparison between the predicted track and the actual track and the change of the distance range error with the track point are shown in Figure 5.

The PTFM model achieves a root mean square error of 33.3% higher than the closest comparison method through multitask collaborative prediction of the position decoding layer, speed decoding layer, and heading decoding layer. Experimental data proves that in complex track prediction scenarios, the parallel fusion architecture has an advantage over the serial processing mode. Its attention weighting mechanism can effectively deal with sensor noise interference, and the gated fusion design significantly improves feature utilization.

3.3. Feature Weight Comparison Experiment

This experiment deeply analyzes the performance difference of the adaptive weight module in multitask fusion. The experimental data reveal the significant optimization effect of this mechanism on position estimation and the complex trade-off relationship between other tasks. The results of the feature weight experiment are shown in

Table 2. Comparison of different feature output performance.

	Model	Position (km)	Velocity (m/s)	Course (°)
MAE	Base	1.1136	1.1998	21.873
	Adaptive	0.3542	2.6786	86.130
RMSE	Base	4.0714	9.0650	44.969
	Adaptive	2.6180	12.931	97.654

.

The adaptive weight mechanism shows excellent performance in the position prediction task. The fixed weight model has a position MAE of 1.1136 km and an RMSE of 4.0714 km, while the adaptive weight model significantly reduces the MAE to 0.3542 km, a decrease of 68.2%, and the RMSE to 2.6180 km, a decrease of 35.7%. This breakthrough improvement stems from the synergistic mechanism of multitask feature fusion and loss adaptation in the model architecture: in the feature fusion stage, the position, speed, and heading features interact in multidimensional space; the adaptive weight layer dynamically adjusts the task loss contribution through the learned probability distribution so the position feature obtains a higher gradient priority in the back propagation. Experiments have shown that this mechanism can effectively strengthen the spatiotemporal correlation modeling of high-credibility input features in the dataset.

While improving the position accuracy, the adaptive weight module causes the performance of the speed and heading tasks to decline. The speed MAE increased from 1.1998 to 2.6786, and the RMSE increased from 9.0650 to 12.931. The heading MAE increased from 21.873° to 86.130°, and the RMSE increased from 44.969° to 97.654°. The results show that there is a coupling between the optimization of the position task and the speed and heading estimation. When the weight of the position task increases, the speed and heading weights decay relatively, making it difficult for their feature extraction layers to obtain sufficient gradient updates. At the same time, it reflects the model’s ability to select high-precision features. It can effectively select features with high accuracy and strong stability in multidimensional input features, thereby enhancing the utilization of effective data.

Experimental data further demonstrates that, even in scenarios where input feature validity is unknown, this module can dynamically filter key features, achieving global interference rejection by actively sacrificing secondary features. In complex multi-radar collaborative detection scenarios, the reliability and noise level of sensor data vary dynamically, leading to inherent optimization conflicts between position, velocity, and heading estimation tasks. Traditional fusion methods assign fixed weights to various features and are unable to adapt to environmental variations such as electromagnetic interference and target maneuvers. While the PTFM model significantly improves position accuracy, it also increases velocity and heading errors. The root cause lies in gradient competition in multitask optimization: when the model prioritizes high-confidence position features through the attention mechanism, gradient updates for velocity and heading tasks are relatively insufficient, automatically recognizing the signal-to-noise ratio advantage of position information.

In engineering practice, position data is typically more stable than velocity and heading data. In applications such as military reconnaissance, position accuracy often holds greater tactical value, and velocity and heading data can be directly calculated from position data. Weight decay for velocity and heading tasks essentially cuts off noise propagation paths, preventing low-quality features from contaminating the core position prediction through shared layers. The core breakthrough of this module lies in the absence of a predefined feature validity prior. In fixed-weight models, sensor confidence weights must be preassigned, but this static assignment struggles to cope with dynamic interference. The adaptive model addresses this dilemma through end-to-end training. When the training and validation datasets have advantages in other feature dimensions, the model automatically prioritizes optimization based on the input data’s signal-to-noise ratio, selecting the most advantageous features for fusion judgment while suppressing the propagation of low-quality features.

3.4. Parallel Architecture Comparison Experiment

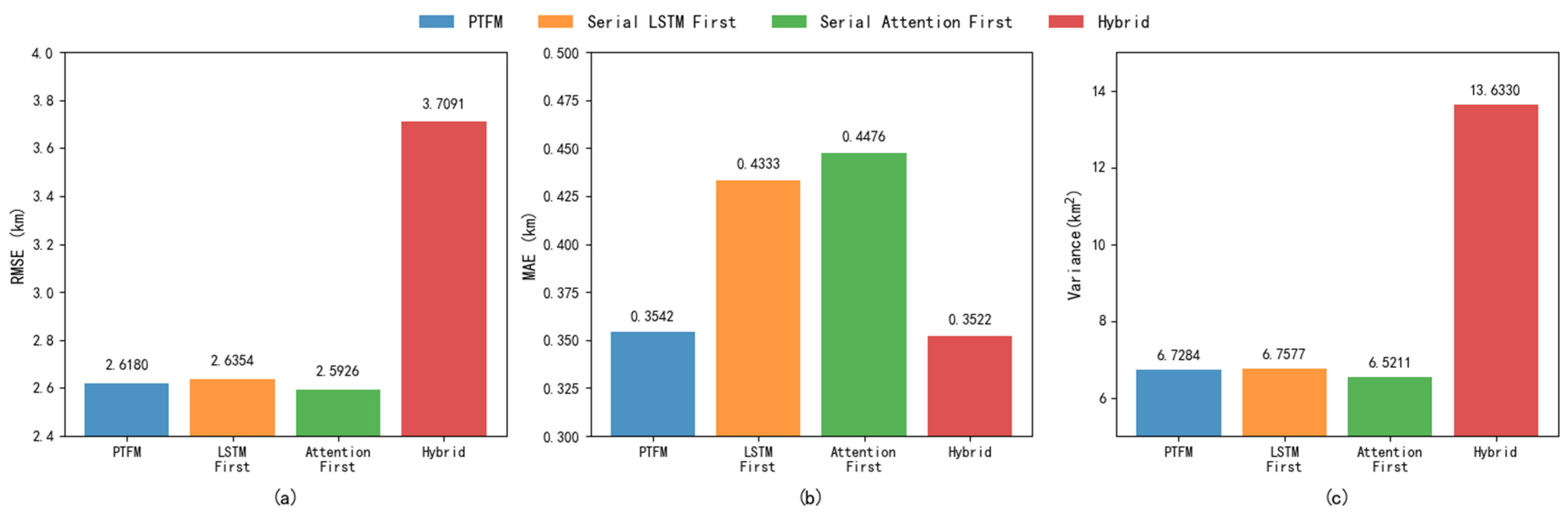
To verify the superiority of PTFM’s parallel architecture over its sequential counterpart, we conducted comparative experiments using a rigorous controlled experimental methodology, constructing four different deep learning fusion architectures for performance comparison. These experiments compared the PTFM’s parallel architecture, a sequential LSTM–attention architecture, a sequential attention–LSTM architecture, and an ungated hybrid parallel architecture. This experimental design ensured that performance differences were solely due to the architecture itself rather than external factors. The detailed results of the comparative experiments are presented in

Table 3. Performance comparison of different architectures.

	PTFM	Serial LSTM First	Serial Attention First	Hybrid
RMSE (km)	2.6180	2.6354	2.5926	3.7091
MAE (km)	0.3542	0.4333	0.4476	0.3522
Variance (km2)	6.7284	6.7577	6.5211	13.633

and Figure 6. The subfigures a, b and c represent the experimental results of RMSE, MAE and Variance respectively.

To address the dimensionality mismatch inherent in the sequential architecture, a dimensional adapter layer was introduced. This layer, through a parameter matrix and mathematical transformations, enables bidirectional conversion between 144-dimensional and 64-dimensional models. The adapter layer was activated only in the corresponding architecture, minimizing the impact of parameter differences on experimental results.

The experimental results showed that the different fusion architectures exhibited significant performance differences in the track prediction task. Based on error metrics, the attention-first sequential architecture achieved the best RMSE (RMSE) of 2.5926 km and a variance of 6.5211, demonstrating its superiority in overall prediction accuracy and stability. Notably, while the parallel fusion without gating architecture achieved the lowest MAE of 0.3522 km, its variance of 13.6332 was significantly higher than the other architectures, indicating significant prediction volatility. This demonstrates that PTFM effectively controls extreme errors while maintaining high prediction accuracy. The PTFM architecture achieved optimal performance, with an RMSE of 2.6180 km and a MAE of 0.3542 km, while maintaining a low variance of 6.7284. This demonstrates that its parallel fusion mechanism and gating strategy effectively coordinate the spatiotemporal feature extraction process, maintaining both prediction accuracy and output stability. The core advantage of the gating mechanism lies in its ability to dynamically adjust the contributions of different feature streams, enabling adaptive optimization of feature selection through learnable weight parameters. This design avoids the inconsistency associated with simple feature concatenation in parallel fusion without gating architectures and overcomes the error accumulation inherent in serial architectures. This performance advantage may stem from the model’s decoupling of sensor spatiotemporal characteristics and the optimized integration of heterogeneous data from multiple sources through the adaptive weighting mechanism.

3.5. Different Number of Track Points

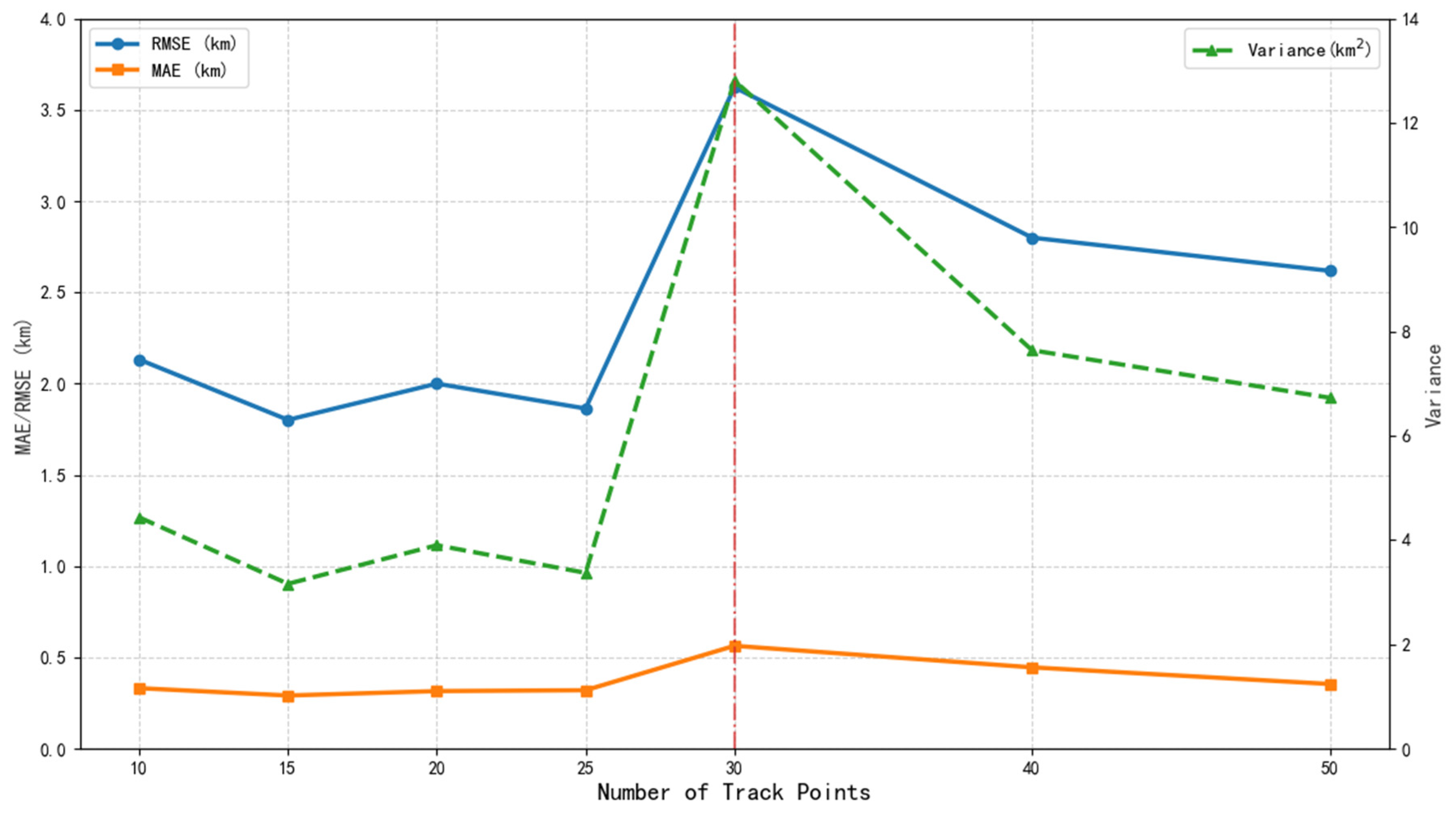
This section discusses the performance under different numbers of track points for a systematic analysis. The experimental results reveal the sensitivity of the model to track length and the efficiency boundary of key components, as shown in

Table 4. Performance comparison of different track points.

	10	15	20	25	30	40	50
RMSE (km)	2.1320	1.8014	1.9999	1.8636	3.6236	2.7997	2.6180
MAE (km)	0.3313	0.2910	0.3152	0.3200	0.5633	0.4453	0.3542
Variance (km2)	4.4357	3.1604	3.9004	3.3706	12.813	7.6400	6.7284

. The model performance changes with the data of the track points, as shown in Figure 7.

When the number of track points is between 10 and 25, the model shows relatively stable fusion accuracy. The RMSE fluctuates between 1.8014 and 2.1320, and the MAE is stable in the range of 0.2910 to 0.3200, indicating that the model has a strong ability to extract spatiotemporal features of short sequences. This advantage is mainly attributed to the synergy of the dual-branch parallel architecture. The sensor’s feature enhancement layer extracts sensor-specific features separately through the fully connected layer, while the LSTM time series modeling layer effectively captures local time series dependencies. At the same time, the attention mechanism branch optimizes the feature fusion process through dynamic weight allocation, and its output and the splicing of LSTM features significantly improve the ability to represent key information of short sequences.

When the number of track points increases to 30, there is a significant performance degradation: RMSE jumps to 3.6236, an increase of 94.4% compared with 25 points; MAE reaches 0.5633, an increase of 76.0%; and the variance surges to 12.813. This phenomenon exposes the limitations of the model in dealing with medium time series dependencies. Although the LSTM layer is designed to retain complete sequence information, the fixed-length time series modeling capability may face the risk of gradient diffusion under long sequences. It is worth noting that the time embedding layer uses static sine and cosine encoding and lacks the ability to adaptively adjust the sequence length, which may lead to insufficient representation of time information in medium sequences. In addition, the feature interaction of the gated fusion mechanism in high-dimensional space may introduce noise accumulation effects.

When the number of track points continues to increase to 40 or 50, the model shows a certain degree of self-regulation ability. RMSE drops to 2.6180, MAE drops to 0.3542, and variance converges to 6.7284. The local recovery of performance benefits from the synergy of the adaptive loss weight mechanism and the residual connection structure. The former alleviates the conflict problem of multi-objective optimization by dynamically balancing the loss weights of various input features; the latter suppresses the degradation of deep networks through cross-layer connections. However, the variance index is still significantly higher than that of short sequences, indicating that uncertainty propagation under long sequences still has influence.

3.6. Ablation Experiment

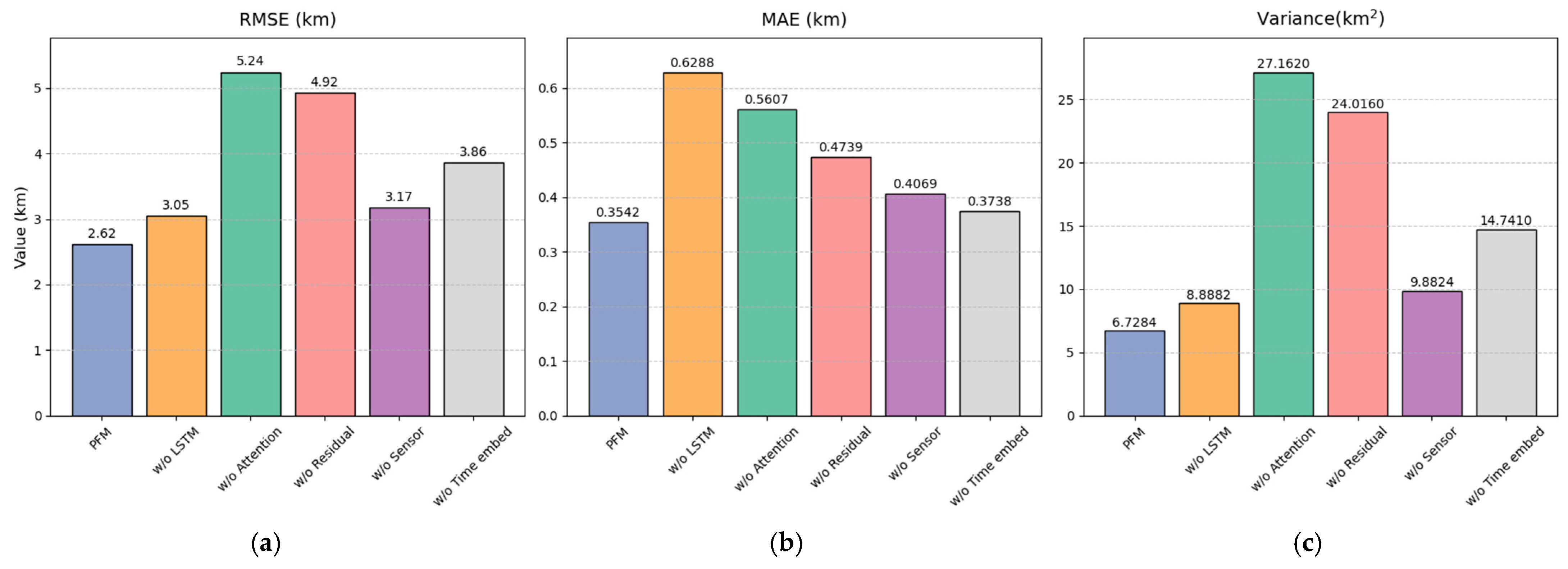
In order to verify the effectiveness of each module, an ablation experiment is conducted. The ablation experiment results systematically reveal the functional contribution of each module of the model. The complete model performs best in terms of RMSE, MAE, and variance, verifying the effectiveness of the overall architecture design. The comparison of different ablation experiment results is shown in

Table 5. Comparison of different ablation experiment results.

	PTFM	w/o LSTM	w/o Attention	w/o Residual	w/o Sensor Enhance	w/o Time Embedding
RMSE (km)	2.6180	3.0469	5.2418	4.9235	3.1698	3.8576
MAE (km)	0.3542	0.6288	0.5607	0.4739	0.4069	0.3738
Variance (km2)	6.7284	8.8882	27.162	24.016	9.8824	14.741

, where w/o denotes the ablation of specified component from the complete PTFM architecture. The model performance of different ablation experiments is shown in Figure 8. The subfigures a, b and c represent the experimental results of RMSE, MAE and Variance respectively.

When the LSTM module is removed, the RMSE increases to 3.0469, an increase of 16.4%; the MAE increases to 0.6288, an increase of 77.6%; and the variance expands to 8.8882. This phenomenon stems from the key modeling ability of the LSTM layer for time series dependence. Its orthogonally initialized 64-unit network retains the complete sequence information through configuration. The model after ablation loses the ability to characterize the continuous state of the track, resulting in a significant degradation in the performance of time dimension feature extraction.

The removal of the attention module caused the most severe performance degradation, with RMSE rising to 5.2418 and variance increasing to 27.162, both of which were significantly higher than the base model. This result confirms the dual value of the attention branch, the dynamic weights generated by its 128-dimensional attention layer not only achieve differentiated fusion of sensor features, but, more importantly, fix the dimensional alignment problem after splicing the temporal embedding and sensor features. After ablation, the model cannot adaptively focus on key features, resulting in a significant increase in noise sensitivity, which is particularly evident in the abnormal increase in the variance index.

The ablation of residual connections caused a decrease in model stability, with the variance index rising to 24.016. Its cross-module connection effectively alleviates the vanishing gradient, and the residual path allows deep features to be directly transmitted back to the operation node, ensuring the efficiency of backpropagation. The lack of this mechanism makes it difficult for the optimization process to converge, and the RMSE deteriorates to 4.9235.

The influence of the temporal embedding module is reflected in the temporal alignment dimension. After removal, the RMSE increased to 3.8576, an increase of 47.3%, verifying the role of sine and cosine position encoding. Although zero-delay embedding is used in the experiment, its fixed encoding mode still provides sequence position priors and enhances the perception of the temporal dimension. The ablation of the sensor enhancement layer increases the MAE to 0.4069, reflecting the necessity of the dual-path Dense layer to upgrade the feature dimension of the original sensor data. Through dual-sensor branch processing, the model improves the representation compatibility of heterogeneous sensor data.

The above conclusions show that LSTM and temporal attention constitute the core feature extraction framework, the residual mechanism ensures the optimization stability, and temporal embedding and sensor enhancement, respectively, enhance the position sensitivity and data compatibility. The modules work together to achieve a balance between accuracy and robustness in the track fusion task.

3.7. Computational Efficiency and Real-Time Experiments

To comprehensively evaluate the computational efficiency and real-time performance of the PTFM framework, we conducted a series of benchmark tests. These experiments compared PTFM with traditional Kalman filtering and LSTM models across multiple performance metrics, providing a deep understanding of the PTFM framework’s computational characteristics. The experimental platform is based on a laptop computer with Windows system, 24 physical CPU cores, 32 logical CPU cores, 31.63 GB total memory, and NVIDIA GeForce RTX 4070 Laptop GPU. The indicators compared in the experiment are cold start time, average delay, maximum delay, CPU usage, and memory usage. The performance analysis results, shown in

Table 6. Comparison of computational efficiency and real-time performance of different methods.

	Cold Start (ms)	Avg Latency (ms)	Max Latency (ms)	CPU Usage (%)	Mem Usage (MB)
PTFM	35.34	44.35	117.66	158.38	601.89
Kalman	42.42	31.68	42.91	105.76	602.28
LSTM	41.93	39.73	43.82	127.90	603.61

, demonstrate competitive overall performance in terms of computational efficiency and real-time performance.

PTFM achieved the best cold start performance, with a cold start time of 35.34 ms, the shortest among the three models. This demonstrates PTFM’s high efficiency in model initialization and initial inference preparation, which is crucial for real-time applications requiring fast response times. However, in terms of average latency during the continuous inference phase, PTFM’s 44.35 ms was slightly higher than the Kalman filter’s 31.68 ms, but better than the LSTM’s 39.73 ms. This result reflects PTFM’s balanced approach between computational complexity and accuracy. However, from the perspective of latency stability, PTFM has some shortcomings, and its maximum latency needs further improvement. PTFM’s peak latency of 117.66 ms is significantly higher than the other two methods, suggesting potential performance fluctuations under extreme conditions.

In terms of resource usage, in the experimental configuration of 24 cores and 32 threads, the PTFM framework’s CPU utilization of 158.38% demonstrates relatively low CPU consumption and computational pressure. This indicates that the PTFM framework only utilized the computing resources of approximately 1.58 logical cores during operation, or only 4.95% of the total CPU capacity of the system’s 32 logical cores. This reflects the computational efficiency of the PTFM framework’s algorithmic design and demonstrates that it can complete track fusion tasks with relatively few computational resources. Compared to the Kalman and LSTM methods, its CPU utilization, while relatively high, is still adequate. Memory usage shows that all three methods have peak memory usage of around 600 MB, with no significant difference, indicating that memory requirements primarily stem from the underlying framework and data processing pipeline rather than the model itself.

Combining these results, the PTFM framework achieves reasonable computational efficiency through high CPU utilization while maintaining a relatively reasonable memory footprint. Its advantage in cold start makes it suitable for application scenarios that require fast initialization, while its lack of latency stability suggests that further optimization of the computational graph structure or the introduction of a dynamic scheduling mechanism may be necessary. Compared with traditional Kalman filtering and LSTM, PTFM has a certain gap in average latency, but this gap may be exchanged for performance advantages when dealing with complex nonlinear problems.

4. Conclusions

This paper proposes a radar track fusion method based on parallel fusion model of deep learning. Through model-driven residual extraction, the attention mechanism and LSTM parallel processing simultaneously capture key spatiotemporal features and long-term dependencies, solving the single-dimensional defects of the LSTM model and the local information loss of the Transformer. Through the coordinated optimization of various modules, high-precision track fusion in complex scenarios is achieved. Experimental results show that this method is significantly better than traditional algorithms in fusion accuracy and motion pattern generalization ability, providing a new solution for radar track fusion technology. Future research will further explore the application of graph neural networks in multi-sensor spatiotemporal correlation modeling to improve the real time and robustness of the system.