Efficient Private Information Retrieval Scheme with Dynamic Database

Abstract

Private information retrieval (PIR) is a typical application scenario of encrypted computing, which allows users to retrieve data from a database by providing only an encrypted index. In an academic research scenario, multiple parties may entrust their data to a third party and require collaborative retrieval. However, due to competitive relationships and mutual distrust between these parties, they do not share public–private keys, making single-key mechanisms inadequate for meeting actual privacy requirements. In this case, based on the multi-key fully homomorphic encryption (MKFHE) algorithm, we construct an efficient PIR scheme with an access permission verification mechanism and dynamic database. Specifically, we design an MKFHE algorithm to protect multi-user privacy information. The vector–matrix multiplication optimization algorithm is adopted to improve computational efficiency, the expand algorithm is used to reduce user communication traffic, and homomorphic multiplication with ciphertext chunking is used to avoid excessive noise caused by direct ciphertext multiplication. Experiments based on the SEAL library show that by transferring part of the computational pressure to the offline stage, the online query response efficiency of our scheme is improved by about 7.69%, and the online computational efficiency of vector–matrix multiplication is improved by about 19.7%.

1. Introduction

In an open environment, researchers mainly rely on two cryptographic primitives, searchable encryption [1] and private information retrieval (PIR) [2], to meet the requirements for the private retrieval of encrypted data in a multi-source data framework. Searchable encryption technology supports users to perform flexible retrieval based on keywords by double encryption of the data and its keyword index. However, its core goal is to hide the search mode and data semantics, and it usually requires the data to be stored in ciphertext on the server side. In contrast, the design of a PIR protocol is more flexible. Users only need to encrypt the query index and send it to the server, the server data (which can be plaintext or ciphertext) are all involved in the encrypted calculation, and the ciphertext result is returned to the user, which prevents the server from inferring the specific location of the queried data and thus protects user data privacy. This feature endows PIR with distinct advantages for privacy preservation in multi-source data scenarios.

Fully homomorphic encryption (FHE) [3] enables arbitrary operation on ciphertext data without decryption, and the final result is also ciphertext, thus realizing data privacy protection in the process of calculating and using index and database data, which provides a more suitable idea for a PIR protocol. In 2009, Gentry [3] first constructed the PIR protocol based on the fully homomorphic encryption scheme in his doctoral dissertation, achieving sublinear communication complexity. Since then, PIR schemes based on fully homomorphic encryption have been developed rapidly. Each scheme weighs three indicators (request size, response size and server computing overhead) and develops a wide range of fast PIR methods. It is worth noting that for each user’s query, all the data in the database need to participate in the operation to generate the corresponding response. If any data does not participate in the operation in this process, it means that the user’s query target is not in it, and information leakage has occurred.

The PIR protocol based on fully homomorphic encryption can effectively protect the index information while preventing the server from obtaining the retrieval data and retrieval range. However, in real application scenarios, multi-source data often serves multiple independent users who do not trust each other, so the protocol should not only ensure the privacy and security of information retrieval but also meet the privacy requirements of data between participating users. Therefore, a PIR scheme using a multi-key fully homomorphic encryption (MKFHE) [4] algorithm is considered. This kind of scheme permits the collaborative computation of multiple data owners without disclosing the private information of each participant, which makes the scheme more suitable for real-world scenarios and has stronger practicability and broader application potential.

1.1. Related Work

Private information retrieval (PIR) technology has been evolving around two core goals of “preserving query privacy” and “reducing communication overhead” since it was proposed by Chor et al. [2] in 1995. Early schemes achieved privacy protection through information theoretic or computational complexity assumptions, but were limited by linear communication costs. With the breakthrough development of homomorphic encryption, PIR gradually evolved toward cryptography-based optimization approaches. In 2009, Gentry [3] proposed the first fully homomorphic encryption scheme, which brought a paradigm innovation for PIR. The PIR protocol based on the fully homomorphic encryption constructed by Gentry broke through the sublinear communication complexity for the first time, starting the practical exploration stage of the secret state retrieval. After that, fully homomorphic encryption and PIR schemes based on it began to develop rapidly.

In the research into PIR schemes based on fully homomorphic encryption, structural coding and ciphertext operation optimization are the key technical breakthroughs. In 2016, Melchor et al.’s XPIR [5] achieved a minute-level response on million-scale databases for the first time by using multidimensional vector encoding and ring learning with errors (RLWEs) [6] secret state operation. However, the size of the query increases linearly with the size of the database, which exposes the bottleneck of communication efficiency. SealPIR [7] proposed by Angel in 2018 introduced polynomial compression technology to compress the query size to 1/27 of XPIR, but at the cost of response size expansion and server computational complexity increase. To solve this problem, OnionPIR [8] by Mughees et al. in 2021 innovatively used RGSW [9] outer product operation to compress the response ciphertext expansion ratio from 100 times to 4.2 times; however, at the same time, it increases the client initialization time and the server memory bandwidth pressure, and the state dependence of the protocol also limits its dynamic update ability. Subsequent studies such as FastPIR [10] and SPIRAL [11] protocol families further try ciphertext rotation and hybrid encryption schemes, but it is always difficult to achieve the global optimum among request size, response size, and computational overhead, which highlights the inherent contradiction of efficiency balance in single-server architecture. There is still much room for the optimal design of PIR schemes based on fully homomorphic encryption.

At the same time, representing an important breakthrough in the field of cryptography, the multi-key homomorphic encryption (MKFHE) scheme aims to solve the problem of private computation with multi-party participation, and provides new possibilities for the design of PIR protocols for multi-user collaborative scenarios. The core goal of MKFHE is to allow multiple parties to directly perform joint operations on ciphertexts encrypted with independent keys, while ensuring that only the authorized party can decrypt the results. Since the LTV12 scheme [4] was proposed in 2012, MKFHE has formed four major technical routes of the NTRU type [4], GSW type [12], BGV type [13], and TFHE type [14], based on different mathematical assumptions and ciphertext operation mechanisms. Specifically, NTRU-type schemes rely on polynomial ring operations to achieve efficient key expansion, GSW schemes support low noise accumulation through approximate eigenvector methods, BGV schemes significantly reduce computational overhead while maintaining computational depth, and TFHE schemes focus on fast Boolean operation optimization. These characteristics theoretically enable it to support multi-user independent PIR scenarios. However, the complete scheme design of PIR based on MKFHE is still facing challenges, and there are some problems to be solved:

• Computational complexity and key management. The computational complexity of multi-key fully homomorphic encryption algorithm is high, especially in the process of encryption, decryption and homomorphic operation, resulting in large computational overhead and significant time consumption. Key management also becomes more complex because efficient key distribution, storage, and update mechanisms are required to prevent private key compromise or misuse with each party holding an independent key. In addition, improper key management may lead to degraded communication efficiency and increased system overhead.
• PIR protocol optimization and communication overhead. In the PIR protocol of MKFHE, balancing the request size, response size, and server computational overhead is an important challenge. Large response size will increase the burden of network transmission, while excessive computing overhead may affect the system efficiency. More importantly, the communication overhead and latency caused by frequent encrypted data exchange may put pressure on the real-time performance and scalability of the system.
• Privacy protection and user trust. Although MKFHE can effectively protect privacy, ensuring comprehensive protection of all participants’ data privacy in multi-party scenarios remains challenging. Since parties usually do not trust each other, how to enhance user trust and avoid man-in-the-middle attacks or data leakage through reasonable authentication and data sharing protocols has become a key issue in the design of the scheme.

1.2. Our Contributions

In this paper, an optimization scheme of PIR based on multi-key fully homomorphic encryption is proposed, which supports the dynamic update of the database. With the background of secure access to massive data in the environment of multiple data sources, the security architecture and attack protection method of private information retrieval are designed. The specific contributions are as follows:

• This paper provides theoretical methods and technical solutions for private information retrieval of multi-source data. An MKFHE method constructed by normalized public keys is used to reduce the amount of communication and simplify the calculation process. The distributed decryption technology is used to mitigate single-point-of-failure risks and effectively protect the private information of each participant.
• In the design of the PIR scheme, the expand algorithm is used to further reduce the communication overhead, and the optimization method of vector–matrix multiplication is used to improve the online calculation efficiency of the scheme. The response generation efficiency is improved by 1.95–7.69%, and the online calculation efficiency of the vector–matrix multiplication is improved by 19.7%. In addition, the scheme also adopted homomorphic ciphertext multiplication with ciphertext chunking to avoid direct ciphertext multiplication, thereby reducing noise accumulation.
• The PIR scheme proposed in this paper can hide access and retrieval information well and has an access permission verification mechanism. It supports dynamic database and multi-user collaborative retrieval while protecting user data privacy, so as to enhance the practicability and flexibility of the method.

2. Preliminaries

2.1. Basic Notation

In this paper, a represents a vector, and $\mathit{a}\left[i\right]$ represents the $i$-th element of the vector $\mathit{a}$. $x\leftarrow A$ indicates that x is uniformly sampled from the probability distribution or set A. The polynomial ring is denoted as $R=Z\left(x\right)/x^n+1$, with $\chi$ being the error distribution on R. Let λ be the security parameter, L be the circuit depth, and K is the upper limit on the number of parties. The integer $n$ is chosen as $n(\lambda )$, the noise distribution over R is $\mathit{\chi }=\chi (\lambda , K, L)$, and the $q=poly(n)$ is the ciphertext modulus. $O(·)$ represents the asymptotic upper bound of the performance of the algorithm as the input size grows.

2.2. RLWE, Gadget Vector, and Smudging Lemma

RLWE, proposed by Lyubashevsky [6] as the ring-based variant of learning with errors (LWE) [15], constitutes a computationally hard lattice problem. Let security parameter $\lambda$ define system parameters: prime modulus $q=q\left(\lambda \right)\ge 2;$ polynomial $f\left(x\right)=x^n+1$ with $n=n (\lambda )$ being a power of 2; quotient ring $R=Z\left(x\right)/x^n+1;$ and error probability distribution $\chi$ over $R$. The RLWE problems are defined as follows:

Search Problem: Given $\rho$ pairs ($a_i{,b}_i)$ where $a_i\leftarrow R_q, e_i\leftarrow \chi$, and $b_i=a_i·s+e_i$, recover secret $s\leftarrow R_q$.

Decisional Problem: Distinguish between $\rho$ RLWE samples ($a_i{, b}_i=a_i·s+e_i)$ and $\rho$ uniform random pairs ($a_i{, b}_i)\leftarrow R_q\times R_q$.

The gadget vector $\mathit{g}=\left(g_0, g_1, \dots , g_{d-1}\right)\in Z^d$ and its associated decomposition function $g^{-1}(·)$ were proposed by Micciancio [16] in 2012. This function maps any element $\theta \in R_q$ (where $R_q$ is a polynomial ring modulo $q$) to a vector $\mathit{u}=(u_0, u_1, \dots , u_{d-1})\in R^d$, such that $\theta ={\sum }_{i=0}^{d-1}{g}_i·u_{i}mod q$. The gadget vector is typically designed as a geometric sequence (e.g., $g_i=b^i$ for a base $b$).

Smudging lemma [17] is a key tool in cryptography for analyzing sensitive information masked by noise. If we add a “sufficiently wide” (magnitude much larger than $B$) independent noise $Y$ to a random variable $X$ with bounded values (magnitude at most $B$), the distribution of $X+Y$ will be statistically indistishable from the distribution of pure noise $Y$.

In other words, let $e_1\in [-{ B}_1, { B}_1]$ be a bounded integer, and $e_2\in [-{ B}_2, { B}_2]$ be uniformly sampled. If $B_1/{ B}_2=\mathrm{negl}(\lambda )$ (where $\mathrm{negl}(\lambda )$ is a negligible function of the security parameter $\lambda$), then the distribution of $e_1{+e}_2$ is statistically indistinguishable from that of $e_2$.

2.3. Key Switching and Rotation

Key switching is a technique used to transform a ciphertext that is encrypted under one key to another key. This is particularly useful in homomorphic encryption schemes, where performing multiple operations on encrypted data may result in a ciphertext that becomes increasingly noisy and difficult to decrypt. Key switching helps mitigate this problem by allowing the ciphertext to be re-encrypted under a new key that is more suitable for further operations.

The specific algorithm for key switching is as follows:

• ${SwitchKeyGen(k}_1\in R_q^n,{sk}_2=(1,s_2)\in R_q^2)$
  Calculate the length $\beta =⌊\mathit{log}q⌋+1$ of the elements in $R_q$, and select $n\beta$ RLWE instances $\left(-a_i{s}_2+e_i,a_i\right),i=1,2,\dots ,n\mathsf{\beta }$. Computing ${\mathit{s}}^{\mathbf{\prime }}=\mathrm{P}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}2\left({sk}_1\right)\in R_q^{n\mathsf{\beta }}$, and then output switch-key ${\tau }_{{sk}_1\to {sk}_2,i}=\left(-a_i{s}_2+e_i+{\mathit{s}}^{\mathbf{\prime }}\left[\mathit{i}\right],a_i\right)$.
• $SwitchKey({\mathit{\tau }}_{{sk}_1\to {sk}_2},c\in R_q^n)$
  A bit decomposition ${\mathit{c}}^{\mathbf{\prime }}=\mathrm{B}\mathrm{i}\mathrm{t}\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\left(\mathit{c}\right)\in R_q^{n\mathsf{\beta }}$ is performed on the ciphertext, get key switching result ${\mathit{c}}^{\mathbf{″}}\mathbf{=}{\mathbf{\sum }}_{\mathit{i}\mathbf{=}\mathbf{1}}^{\mathit{n}\mathsf{\beta }}{\mathit{c}}^{\mathbf{\prime }}[\mathit{i}]\mathbf{\cdot }{\mathit{\tau }}_{{sk}_1\to {sk}_2,i}$.
  where the $\mathrm{B}\mathrm{i}\mathrm{t}\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}(·)$ and $\mathrm{P}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}2(·)$ functions are defined as follows:

For a vector $\mathit{v}\in Z_q^n$, define $\mathrm{B}\mathrm{i}\mathrm{t}\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}(\mathit{v})$ as the binary decomposition of each component of $\mathit{v}$. Let $\beta =⌊\mathit{log}q⌋+1$, then $\mathrm{B}\mathrm{i}\mathrm{t}\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\left(\mathit{v}\right)=({\mathit{v}}_{0, 0}, \dots , {\mathit{v}}_{0, \beta -1}, \dots , {\mathit{v}}_{n-1, 0}, \dots , {\mathit{v}}_{n-1, \beta -1})\in {\{0, 1\}}^{n·\beta }$, where ${\mathit{v}}_{i, j}\in \{0, 1\}$ and ${\mathit{v}}_i={\sum }_{j=0}^{\beta -1}{2}^j·{\mathit{v}}_{i, j} \mathrm{mod} q$.

For a vector $\mathit{w}\in Z_q^n$, define $\mathrm{P}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}2\left(\mathit{w}\right)$ as: $\mathrm{P}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{f}2\left(\mathit{w}\right)=(2^0·{\mathit{w}}_0,2^1·{\mathit{w}}_0,\dots ,2^{\beta -1}·{\mathit{w}}_0,\dots ,2^0·{\mathit{w}}_{n-1},\dots ,2^{\beta -1}·{\mathit{w}}_{n-1}\in Z_q^{n·\beta }$. This ensures the inner product invariance: $⟨BitDecomp\left(\mathit{v}\right),Powersof2\left(\mathit{w}\right)⟩=⟨v,w⟩\mathrm{mod}q$.

Rotation refers to cyclically shifting the slots of a ciphertext in single instruction, multiple data (SIMD)-style homomorphic encryption. It allows permuting encrypted data for parallel processing.

For a ciphertext $\mathit{c}\mathit{t}$ encoding a vector $(m_0, m_1, \dots , m_{n-1})$, a rotation by $k$ positions uses a Galois key ${\mathit{G}\mathit{K}}_{\mathit{k}}$. The rotated ciphertext $\mathit{c}\mathit{t}\mathbf{\prime }$ satisfies $\mathit{c}{\mathit{t}}^{\mathbf{\prime }}\approx \mathit{E}\mathit{n}\mathit{c}((m_k, m_{k+1}, \dots , m_{n-1},m_0, \dots , m_{k-1}))$. Implemented via automorphism $x\mapsto x^{5^k}$ in polynomial rings. ($x^{5^k}$ is chosen because when $n=2^m$, 5 is a primitive root of modulo $2n$, that is, $5^k \mathrm{mod} 2n$ can cover all odd numbers, thus generating different cyclic shift steps).

2.4. Private Information Retrieval

A typical single-server PIR scheme usually includes two entities, the user and the database server, as shown in Figure 1.

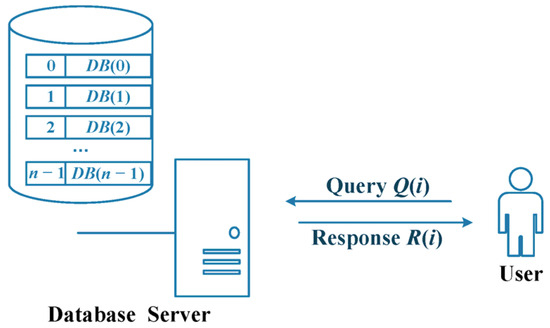
Figure 1. Typical PIR model.

The database (DB) server is used to store and process the data, $\mathit{D}\mathit{B}=\left\{\left(i, \mathit{D}\mathit{B}\left[i\right]\right)\right|0\le i\le n-1\}$ with a total of $n$ entries. To simplify the PIR protocol discussed later, we assume that the value of each item $\mathit{D}\mathit{B}\left[i\right]$ is a positive integer and not just a bit. In addition, after the query user makes a PIR query using unbounded computation, the server will provide the PIR response to the query user.

Users can directly make PIR queries to the DB server and obtain the desired results from the DB server. At the same time, the user does not want to reveal the query value $i$ to the DB server when requesting the corresponding data $DB\left[i\right]$ from the DB and hopes that the communication of the PIR is efficient.

Formally, the single-server PIR protocol consists of the following three phases:

• Query generation phase $\left(Q\left(i\right)\leftarrow QG\left(i\right)\right)$: Taking index $i$ as input, the user sends query $Q(i)$ to the server;
• Response generation phase $(R(i)\leftarrow RG(Q\left(i\right), \mathit{D}\mathit{B}))$: Using the query $Q(i)$ and the database DB, the server returns a response $R(i)$ to the user;
• Response retrieval phase $(DB[i]\leftarrow RR(R(i)))$: After receiving the response $R(i)$, the user outputs the data $DB\left[i\right]$ corresponding to index $i$.

A single-server PIR protocol is correct if for any database DB of size $n$, any index $i$ is $0\le i\le n-1$, $\mathit{D}\mathit{B}\left[i\right]=RR(\mathit{D}\mathit{B}, i, Q(i), R(i)$ holds, where $Q\left(i\right)=QG\left(i\right), R(i)=RG(Q(i), DB)$.

In the security model, the DB server is honest but curious and has no collusion with any other third party. In other words, the DB server will faithfully follow the protocol; however, it is curious about the value of the user’s query. Note that if the DB server is compromised by some attacker, the compromised DB server may launch other active attacks and return a response with errors to unauthenticated users. However, since we focus on communication efficient PIR protocols for users in this paper, active attacks from compromised DB servers are beyond the main scope of this work, although it is not difficult to apply some verifiable techniques to address these attacks.

3. Building Blocks

In this paper, the PIR scheme involves the optimization technique of vector–matrix multiplication, which improves the online calculation efficiency by extracting the diagonal vector of the matrix and rotating the ciphertext in the offline stage of the server. The expand algorithm is used to reduce user communication traffic, while the ciphertext chunk algorithm is used to effectively reduce the noise accumulation in the calculation process. The MKFHE scheme is also optimized to meet the requirements of multi-user privacy protection in PIR scenarios. The purpose of this section is to explain these important components in detail.

3.1. Optimization Methods for Vector-Matrix Multiplication

Some HE schemes based on the RLWE assumption use the structure of the Galois group to implement the rotation operation of the plaintext slot, denoted by $\mathrm{R}\mathrm{o}\mathrm{t}(\mathrm{c}\mathrm{t};\mathcal{l})$, which transforms the ciphertext $ct$ of $\mathit{m}=\left(m_0, \dots , m_{n-1}\right)\in \mathcal{M}={\mathcal{R}}^n$ into the ciphertext of $\rho (\mathit{m};\mathcal{l}):=(m_{\mathcal{l}}, \dots , m_{n-1}, m_0, \dots , m_{\mathcal{l}-1})$ where $\mathcal{l}$ denotes the step size of the rotation, which can be positive or negative, and the rotation $(-\mathcal{l})$ is the same as $(n-\mathcal{l})$.

Specifically, the optimized approach for vector–matrix multiplication [18] uses an algorithm for computing arbitrary linear transformations on encrypted vectors, which can be represented by combining rotation and constant multiplication operations. For some matrix $U\in {\mathcal{R}}^{n\times n}$, define its $\mathcal{l}$-th diagonal vector ${\mathit{u}}_{\mathcal{l}}=(U_{0, \mathcal{l}}, U_{1, \mathcal{l}+1}, \dots , U_{n-\mathcal{l}-1, n-1}, U_{n-\mathcal{l}, 0}, \dots , U_{n-1, \mathcal{l}-1})\in {\mathcal{R}}^n$, where $0\le \mathcal{l}<n$. The vector and matrix product $\mathit{m}·U$ can be expressed as the sum of component multiplications of the diagonal vector of the matrix and the rotated vector, i.e.,

$$\mathit{m}·U=\sum _{\mathbf{0}\le \mathcal{l}<\mathit{n}}\left(\rho \left(\mathit{m};\mathcal{l}\right)\odot u_{\mathcal{l}}\right)$$

where ⊙ denotes the component multiplication between vectors.

Given a matrix $U\in {\mathrm{R}}^{n\times n}$ and a ciphertext $ct$ of a vector m, the following homomorphic linear transformation algorithm (Algorithm 1) describes how to compute the ciphertext of the desired vector $\mathit{m}·U$.

Algorithm 1. Homomorphic linear transformation algorithm: $\mathrm{L}\mathrm{i}\mathrm{n}\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}(ct;U)$

Input: plaintext matrix U, ciphertext vector $ct$. Output: ciphertext vector $c{t}^{\prime }$. Find $\mathcal{l}$ diagonal vectors of U, ${\mathit{u}}_{\mathcal{l}}=(U_{0,\mathcal{l}},U_{1,\mathcal{l}+1},\dots ,U_{n-\mathcal{l}-1,n-1},U_{n-\mathcal{l},0},\dots ,U_{n-1,\mathcal{l}-1}).$ ${ct}^{\prime }\leftarrow \mathrm{C}\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}(ct;u_0))$. Execute ${ct}^{\prime }\leftarrow \mathrm{A}\mathrm{d}\mathrm{d}({ct}^{\prime }, \mathrm{C}\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}(\mathrm{R}\mathrm{o}\mathrm{t}(ct;\mathcal{l});u_{\mathcal{l}})) \mathrm{for} \mathcal{l}=1 \mathrm{to} n-1$. Return ${ct}^{\prime }$.

When vector matrix multiplication is directly calculated, each column of the matrix requires $n$ plaintext multiplications and $n-1$ additions, totaling $O(n^2)$ multiplications and $O(n^2)$ additions, that is, the complexity is asymptotically $O(n^2)$ multiplications. As shown in the state linear transformation algorithm, the computational cost of vector and matrix multiplication mainly consists of $n$ constant multiplications and $n-1$ rotation operations. Note that rotation often requires a key transformation, which makes it more expensive to compute than addition or constant multiplication. Therefore, we can conclude that the operation complexity of the optimization method is asymptotically $O(n)$ rotations.

3.2. Expand Algorithm

The expand algorithm (Algorithm 2) [7] requires a special homomorphic operation $\mathrm{S}\mathrm{u}\mathrm{b}(\mathit{c}\mathit{t},k)$: Firstly, suppose we have a ciphertext pair $\mathit{c}\mathit{t}=({ct}_0(x),{ct}_1(x))$, replace $x$ by $x^k$, and transform into a new ciphertext $\mathit{c}{\mathit{t}}^{\prime }=({ct}_0(x^k),{ct}_1(x^k))$, then the decryption key corresponding to the new ciphertext is changed to $s(x^k)$. For consistency, we use the key transformation algorithm to process the ciphertext $\mathit{c}{\mathit{t}}^{\prime }$, and obtain the ciphertext $\mathit{c}\mathit{t}″$ with decryption key $s(x)$. At this time, the ciphertext $\mathit{c}\mathit{t}″$ becomes the encryption of the message $m(x^k)$.

Algorithm 2. Expand algorithm: $(c_0,c_1,\dots ,c_{n-1})\leftarrow \mathrm{Expand}(query,n)$

Input: $query=\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}(x^{idx})$, the size of the database n. Output: a set of ciphertexts $\mathit{c}=(c_0,c_1,\dots ,c_{n-1})$. Find a minimum $m=2^l \mathrm{such} \mathrm{that} m\ge n.$ Initialize a ciphertext vector $\mathit{ciphertexts}=\left[query\right]$ with the query. As the algorithm runs, the number of elements in the ciphertexts vector increases. For j = 0, 1,…, l − 1 iteration loop runs: (1) For $k=0,1,\dots ,2^j-1$ iteration loop runs: $$\begin{gathered} c_0\leftarrow \mathit{ciphertexts}\left[k\right] \\ {c}_1\leftarrow c_0·x^{-2^j} \\ {c\prime }_k\leftarrow c_0+\mathrm{Sub}(c_0,N/2^j+1) \\ {c\prime }_{k+2^j}\leftarrow c_1+\mathrm{Sub}(c_1,N/2^j+1) \end{gathered}$$ (2) When the inner iteration is finished, set $\mathit{ciphertexts}\leftarrow [{c^{\prime }}_0,{c^{\prime }}_1,\dots ,{c^{\prime }}_{2^{j+1}-1}]$ and proceed to the next outer iteration. $inverse\leftarrow m^{-1}mod t.$ For $j=0,1,\dots ,n-1, \mathrm{set} c_j=inverse·\mathit{ciphertexts}\left[j\right].$

The expand algorithm constructs a ciphertext vector from a single query index by performing $O(n)$ lightweight homomorphic operations, including homomorphic addition, homomorphic substitution, and monomial multiplication. This generates a sparse encrypted vector where only the target position contains $\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}(1)$ (others are $\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}(0)$), ready for subsequent computations. (The details of the encryption algorithm MKFHE.Enc are given in the subsequent MKFHE scheme.)

3.3. Ciphertext Chunking Algorithm

The ciphertext chunking algorithm can effectively reduce the noise accumulation in the calculation process, which is divided into two parts: the homomorphic ciphertext multiplication with ciphertext chunking (Algorithm 3) and the homomorphic ciphertext decryption with ciphertext chunking (Algorithm 4).

In the process of using the ciphertext chunking algorithm, it is usually necessary to first perform homomorphic ciphertext multiplication with ciphertext chunking ${\mathit{c}}_{cMult}\leftarrow \mathrm{c}\mathrm{h}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{s}\mathrm{H}\mathrm{E}\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}(c_0,c_1,F)$. It has two processes in turn, ciphertext chunking and plain-ciphertext multiplication, as shown in the following:

Algorithm 3. Homomorphic ciphertext multiplication with ciphertext chunking: ${\mathit{c}}_{cMult}\leftarrow \mathrm{c}\mathrm{h}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{s}\mathrm{H}\mathrm{E}\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}(c_0,c_1,F)$

Input: two homomorphic encrypted ciphertexts $c_0,c_1$ with block size F. Output: 2F ciphertexts ${\mathit{c}}_{cMult}=\left(c_{cMult,0},c_{cMult,1},\dots ,c_{cMult,2F-1}\right)$. Ciphertext chunking: Let $w={\displaystyle \frac{⌈logq⌉}{F}}$, the ciphertext c0 is divided into F chunks in 2w base decomposition. It satisfies that $c_0=c_{0,0}+2^w{c}_{0,1}+\cdots +2^{\left(F-1\right)w}{c}_{0,F-1}mod q$. Note: According to the BFV ciphertext form, we know that each small block contains 2 ring elements $c_{0,i}=(c_{0,i,0},c_{0,i,1}),i=0,1,\dots ,F-1$ Plain-ciphertext multiplication: $c_{0,i}=(c_{0,i,0},c_{0,i,1}),i=0,1,\dots ,F-1$ is taken as the plaintext multiplied with the ciphertext c1 to obtain a ciphertext vector ${\mathit{c}}_{cMult}=\left(c_{cMult,0},c_{cMult,1},\dots ,c_{cMult,2F-1}\right)$, where ${\mathit{c}}_{cMult,2i}=c_{0,i,0}{c}_1,{\mathit{c}}_{cMult,2i+1}=c_{0,i,1}{c}_1,i=1,2,\dots ,F-1$

The $\mathrm{c}\mathrm{h}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{s}\mathrm{H}\mathrm{E}\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}$ algorithm divides the ciphertext with large coefficient into F ciphertext chunks with small coefficient, and each ciphertext chunk is regarded as plaintext, so as to perform plaintext multiplication operation. Then in order to decrypt ${\mathit{c}}_{cMult}$ to get $m_0{m}_1$, it needs to be decrypted twice, that is, sequentially execute decryption, reconstruction, and decryption again. This process is called homomorphic ciphertext decryption with ciphertext chunking: $m\leftarrow \mathrm{c}\mathrm{h}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{s}\mathrm{D}\mathrm{e}\mathrm{c}(sk,{\mathit{c}}_{cMult})$, and the specific algorithm is as follows. (The details of the decryption algorithm MKFHE.Dec are given in the subsequent MKFHE scheme).

Algorithm 4. Homomorphic ciphertext decryption with ciphertext chunking: $m_{cMult}\leftarrow \mathrm{c}\mathrm{h}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{s}\mathrm{D}\mathrm{e}\mathrm{c}(sk,{\mathit{c}}_{cMult})$

Input: a set of ciphertexts ${\mathit{c}}_{cMult}=(c_{cMult,0},c_{cMult,1},\dots ,c_{cMult,2F-1})$ generated by the $chunksHEMult$ algorithm. Output: decryption yields message $m\in R_t$. Chunk decryption: Decrypt each ciphertext ${\mathit{c}}_{cMult}, m_{cMult,i}=\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{D}\mathrm{e}\mathrm{c}\left(sk,c_{cMult,i}\right),i=0,1,\dots ,2F-1$. Reconstruction: Compute ${ct}_0={\sum }_{i=0}^{F-1}{2}^{i·w}{m}_{cMult,2i} mod q,{ct}_1={\sum }_{i=0}^{F-1}{2}^{i·w}{m}_{cMult,2i+1} mod q$, and then form a new ciphertext $ct=\left({ct}_0,{ct}_1\right)$. Decryption: $m_{cMult}=\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{D}\mathrm{e}\mathrm{c}\left(sk,ct\right)$.

Through this homomorphic ciphertext multiplication with ciphertext chunking, the ciphertext multiplication calculation in the PIR scheme is optimized, and the noise accumulation in the process is reduced. The decryption process is further recovered and reconstructed to ensure that the PIR scheme can obtain the correct output after complex calculations in the ciphertext state.

3.4. MKFHE Scheme

There are two types of multi-key schemes in the existing MKFHE algorithm. One is that each participant encrypts data with different public keys and then converts the ciphertext under the same key by key conversion method. The other is to convert each party’s key into a normalized public key and then encrypt and perform homomorphic operations. The latter is more convenient, efficient, and easy to calculate when solving the problem that the ciphertext encrypted with different keys cannot be directly homomorphic operation. At the same time, the MKFHE algorithm also has two different decryption methods. Sequential decryption starts from the first participant and sequentially transmits the decryption results to continue the decryption, which is simple but has great single-point-of-failure risks. Distributed decryption is that each participant calculates part of the decryption results independently, and then the final results are collected to complete the decryption together. It effectively safeguards the privacy of each participant’s private key, greatly mitigates single-point-of-failure risks, while demonstrating superior efficiency and strong scalability.

Our MKFHE scheme consists of five algorithms: initialization algorithm MKFHE.setup, key generation algorithm MKFHE.KeyGen, encryption algorithm MKFHE.enc, homomorphic operation algorithm MKFHE.Eval, and decryption algorithm MKFHE.dec. MKFHE.Setup sets the system parameters to construct the framework of multi-party homomorphic encryption. MKFHE.KeyGen generates public and private key pairs and computation keys for each party (i.e., the query user). These public keys are transformed into normalized public keys by performing specific operations (e.g., sum) on the public keys of all parties, so that the ciphertext size is reduced and independent of the number of parties. MKFHE.Eval provides homomorphic addition (EvalADD) and homomorphic multiplication (EvalMult) operations on ciphertexts. It performs specified homomorphic operations on two input ciphertexts to obtain the operation result ciphertext. MKFHE.Dec adopts a distributed decryption method.

The specific BFV-MKFHE scheme is given as follows:

• $MKFHE.\mathrm{S}\mathrm{e}\mathrm{t}\mathrm{u}\mathrm{p}\left(1^{\lambda },1^k,1^l\right)$
  The security parameter $\lambda$ is input, and the upper limit of the participant size $K$, the plaintext domain $R_t$, and the circuit depth $L$ are set. The integer $n=n(\lambda )$ is selected, the polynomial ring $R=Z\left(x\right)/x^n+1$ is denoted, the noise distribution $\mathit{\chi }=\mathit{\chi }(\lambda ,K,L)$ is defined, and the ciphertext modulus $q=\mathrm{p}\mathrm{l}\mathrm{o}\mathrm{y}\left(n\right)$ and the special modulus $p$ satisfying $p>q$ are selected.
• $MKFHE.KeyGen(\eta \in \left[k\right])$
  The key is generated for the $\eta$-th party, $l=L,\dots ,0$.

  (a) 

  The private key generation: select $s_{l, \eta }$ uniformly from $R_q$, the private key of the $\eta$-th party is denoted as ${\mathit{s}\mathit{k}}_{\mathit{l},\mathit{\eta }}=(1, { s}_{l, \eta })$.

  (b) 

  Public key generation: Select $a_{l, \eta }$ uniformly in $R_q$, randomly sample noise $e_{l, \eta }$ from $\chi$, the public key of the $\eta$-th party is denoted as ${\mathit{p}\mathit{k}}_{\mathit{l},\mathit{\eta }}=\left({\left[-\left(a_{l, \eta }{s}_{l, \eta }+e_{l, \eta }\right)\right]}_q, a_{l, \eta }\right)=\left(b_{l, \eta }, a_{l, \eta }\right)\in R_q^2$.

  (c) 

  Normalized public key: Compute ${\mathit{p}\mathit{k}}_{\mathit{l}}={\sum }_{\eta =1}^k{\mathit{p}\mathit{k}}_{\mathit{l},\mathit{\eta }}=\left({\sum }_{\eta =1}^k{b}_{l, \eta }, {\sum }_{\eta =1}^k{a}_{l, \eta }\right)=\left(b_l, a_l\right)$ as the uniform public key used for encryption.

  (d) 

  Computing key generation: select $a_l, r_l, d_{l, 1}$ uniformly from $R_q$, randomly sample noise $e_{l, 1}, e_{l, 2}$ from $\chi$, computing $d_{l, 0}=-s_l·d_{l, 1}+e_{l, 1}+r_l·g(\mathrm{m}\mathrm{o}\mathrm{d} q),d_{l, 2}=r_l·a_l+e_{l, 2}+s_l·g(\mathrm{m}\mathrm{o}\mathrm{d} q)$, construct the computation key ${\mathit{D}}_{\mathit{l}}=\left[d_{l, 0}\right|d_{l, 1}\left|d_{l, 2}\right]\in R_q^3$, where $\mathit{g}=\left(g_i\right)\in Z^d$ is the tool vector.

• $MKFHE.\mathrm{E}\mathrm{n}\mathrm{c}({pk}_l,{pt}_{\eta })$
  The plaintext ${pt}_{\eta }\in R_t$ is encrypted using the normalized public key ${\mathit{p}\mathit{k}}_{\mathit{l}}$. $\mathrm{\mu }$ is uniformly selected from $R_2$, and the noise $e_l,{e\prime }_l\leftarrow \chi$ is randomly sampled. Generating ciphertext ${\mathit{c}\mathit{t}}_{\mathit{l},\mathit{\eta }}=\left(c_0,c_1\right)=({\left[⌊{\displaystyle \frac{q}{t}}{pt}_{\eta }⌉+b_l\mathrm{\mu }+e_l\right]}_q,{[a_l\mathrm{\mu }+{e\prime }_l]}_q)\in R_q^2$, where $⌊·⌉$ means approximate rounding.
• $\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{v}\mathrm{a}\mathrm{l}({\mathit{c}\mathit{t}}_{\mathbf{1}},{\mathit{c}\mathit{t}}_{\mathbf{2}},\left({\mathit{D}}_{\mathit{l}},b_l\right))$
  The computation key is input, and the ciphertext ${\mathit{c}\mathit{t}}_{\mathbf{1}},{\mathit{c}\mathit{t}}_{\mathbf{2}}\in R_q^2$ is performed via homomorphic operation, including homomorphic addition EvalADD and homomorphic multiplication EvalMult.

  (a) 

  EvalADD: ${\mathit{c}\mathit{t}}_3\leftarrow {[{ct}_1+{ct}_2]}_q=({\left[c_{1,0}+c_{2,0}\right]}_q,{\left[c_{1,1}+c_{2,1}\right]}_q)\in R_q^2$.

  (b) 

  EvalMult: ${\mathit{c}{\mathit{t}}^{\prime }}_{\mathbf{3}}\leftarrow {\left[⌊{{\displaystyle \frac{t}{q}}(ct}_1\otimes {ct}_2)⌉\right]}_q=({\left[⌊{{\displaystyle \frac{t}{q}}c}_{1,0}{c}_{2,0}⌉\right]}_q,{\left[⌊{{\displaystyle \frac{t}{q}}c}_{1,0}{c}_{2,1}⌉\right]}_q,{\left[⌊{{\displaystyle \frac{t}{q}}c}_{1,1}{c}_{2,0}⌉\right]}_q,{\left[⌊{{\displaystyle \frac{t}{q}}c}_{1,1}{c}_{2,1}⌉\right]}_q)\in R_q^4$. Then, the modulus improved relinearization algorithm [19] MR-Relin $(\mathit{c}\mathit{t},\left({\mathit{D}}_{\mathit{l}},b_l\right))$ is invoked to obtain the ciphertext ${\mathit{c}\mathit{t}}_3\in R_q^2$.

  The MR-Relin algorithm (Algorithm 5) is described in detail as follows:

Algorithm 5. Relinearization algorithm for modulus improvement: MR-Relin$\left(\mathit{c}\mathit{t}, \left({\mathit{D}}_{\mathit{l}}, { b}_l\right)\right)$

Input: a ciphertext $\mathit{c}\mathit{t}=({{ c}_{0, 0}, { c}_{0, 1}, c}_{1, 0}, { c}_{1, 1})\in R_q^4$ after ⊗ operation, combination key $\left({\mathit{D}}_{\mathit{l}}, { b}_l\right)$ of the computing key and the public key. Output: ciphertext $\mathit{c}\mathit{t}\mathbf{\prime }=({ c^{\prime }}_0, {c^{\prime }}_1)\in R_q^2$. Let ${c\prime }_0, {c\prime }_1, {c″}_0, {c″}_1\leftarrow 0$. ${c^{″}}_{1, 1}\leftarrow ⟨g^{-1}\left(c_{1, 1}\right), b_l⟩\left(mod pq\right)$ ${c\prime }_{1, 1}\leftarrow ⌊p^{-1}·{c^{″}}_{1, 1}⌉$ ${(c^{″}}_0, {c^{″}}_1)\leftarrow {(c″}_0, {c″}_1)+g^{-1}\left({c\prime }_{1, 1}\right)\left[d_{l, 0}{|d}_{l, 1}\right](\mathrm{mod} pq)$ ${c″}_1\leftarrow {c\prime }_1+⟨g^{-1}\left(c_{1, 1}\right), d_{l, 2}⟩(\mathrm{m}\mathrm{o}\mathrm{d} pq)$ Calculate ${c\prime }_0\leftarrow c_{0, 0}+\lfloor p^{-1}·{c″}_0\rceil (\mathrm{m}\mathrm{o}\mathrm{d} q)$ ${c\prime }_1\leftarrow c_{0, 1}+c_{1, 0}\lfloor p^{-1}·{c″}_1\rceil (\mathrm{m}\mathrm{o}\mathrm{d} q)$

• Where $g^{-1}(·)$ is the bit decomposition function, which can transform an element $\theta \in R_q$ into a vector $\mathit{u}=(u_0, u_1, \dots , u_{d-1})\in R^d$, and satisfy the $\theta ={\sum }_{i=0}^{d-1}{g}_i·u_i mod q$.

• $MKFHE.Dec({\mathit{c}\mathit{t}}_{\mathit{l}}, {\mathit{s}\mathit{k}}_{\mathit{l},\mathit{\eta }})$
  Multi-party cooperation to achieve distributed decryption.

  (a) 

  Each party randomly samples the noise $e_{\eta }\leftarrow \varphi$ (the noise selection satisfies the Smudging lemma) and uses its own private key to calculate the partial decryption result $m_{\eta }^{*}={[{\mathit{c}\mathit{t}}_{\mathit{l}}{·\mathit{s}\mathit{k}}_{\mathit{l},\mathit{\eta }}+e_{\eta }]}_q$.

  (b) 

  The partial decryption results are summed up to obtain the final decryption result $m^{*}={[\lfloor {\displaystyle \frac{q}{t}}{\sum }_{\eta =1}^k{m}_{\eta }^{*}\rfloor ]}_t$.

Next, we prove the correctness and security of this MKFHE scheme.

3.4.1. Correctness

The correctness of this scheme is determined by the properties of the basic BFV [20] algorithm and the relinearization algorithm. A vector $\mathit{c}\mathit{t}=(c_0, c_1)\in R_q^2$ is obtained by encrypting the plaintext $m\in R_t$ with multi-key BFV. Under the private key $sk=(1, s)$, the vector satisfies $⟨\mathit{c}\mathit{t},\mathit{s}\mathit{k}⟩\approx ⌊{\displaystyle \frac{t}{q}}⌉m (\mathrm{m}\mathrm{o}\mathrm{d} q)$, so the decryption algorithm can correctly recover $m$. If ${ct}_1$ and ${ct}_1$ are the encryption of $m_1$ and $m_2$ with respect to the private key $sk=(1, s)$, then their scaled tensor product $\mathit{c}\mathit{t}={\left[⌊{ {\displaystyle \frac{t}{q}}(ct}_1\otimes {ct}_2)⌉\right]}_q$ such that $⟨ct, sk\otimes sk⟩\approx ⌊{\displaystyle \frac{t}{q}}⌉·m_1{m}_2 (\mathrm{m}\mathrm{o}\mathrm{d} q)$, similar to the general BFV scheme, the relinearization algorithm can finally output $\mathit{c}\mathit{t}\mathbf{\prime }$, which satisfies $⟨\mathit{c}\mathit{t}\mathbf{\prime },sk\otimes sk⟩\approx ⌊{\displaystyle \frac{t}{q}}⌉·m_1{m}_2 (\mathrm{m}\mathrm{o}\mathrm{d} q)$. Therefore, it only needs to prove the correctness of the relinearization algorithm used in the scheme. The proof is as follows:

In the MR-Relin$\left(\mathit{c}\mathit{t},\left({\mathit{D}}_{\mathit{l}},b_l\right)\right)$ algorithm, by calculating $c_{i,j}=⟨{\mathit{g}}^{-\mathbf{1}}\left(c_{i,j}\right),b_j⟩,0\le i,j\le 1$, then adding ${\mathit{g}}^{-\mathbf{1}}\left({c\prime }_{i,j}·[d_{i,0},d_{i,1}]\right)$ and $⟨{\mathit{g}}^{-\mathbf{1}}\left(c_{i,j}\right),d_{i,2}⟩$, we can obtain $({c\prime }_0,{c\prime }_i)$ and ${c\prime }_j$. Notice that $g^{-1}\left({c\prime }_{i,j}·[d_{i,0},d_{i,1}]\right)·\left(1,s_i\right)\approx r_i·{c^{\prime }}_{i,j}\left(\mathrm{m}\mathrm{o}\mathrm{d} q\right)$, $⟨g^{-1}\left(c_{i,j}\right),d_{i,2}⟩·s\approx ⟨g^{-1}\left(c_{i,j}\right)-r_i{b}_j+s^2·g⟩=-r_i·{c^{\prime }}_{i,j}+c_{i,j}·s^2(\mathrm{m}\mathrm{o}\mathrm{d} q)$.

According to the definition of $\mathit{c}\mathit{t}\mathbf{\prime }$, the following can be obtained:

$$\begin{array}{c}⟨\mathit{c}{\mathit{t}}^{\prime },sk⟩={c^{\prime }}_0+{c^{\prime }}_1·s\hfill \\ =c_{0,0}+\left(c_{0,0}+c_{0,1}+2c_{1,0}\right)\mathrm{s}+{\mathit{g}}^{-\mathbf{1}}\left({c^{\prime }}_{1,1}·\left[d_{1,0},d_{1,1}\right]\right)·\left(1,\mathrm{s}\right)+⟨{\mathit{g}}^{-\mathbf{1}}\left(c_{1,1}\right),d_{1,2}⟩·\mathrm{s}\left(mod q\right)\hfill \\ \approx c_{0,0}+\left(c_{0,0}+c_{0,1}+2c_{1,0}\right)s_1+\left(c_{1,1}\right)·s^2\hfill \\ =⟨\mathit{c}\mathit{t},sk\otimes sk⟩\left(mod q\right)\hfill \end{array}$$

The correctness of the relinearization algorithm can be proved by the above derivation. The MKFHE scheme meets the correctness requirements as a whole, and can correctly recover the corresponding plaintext after encryption, homomorphic operation, and distributed decryption, which is suitable for encrypted state computing scenarios that require multi-party cooperation.

3.4.2. Security

Based on the RLWE assumption and Smudging lemma, we strictly prove the security of the MKFHE scheme from three dimensions of encryption semantic security, multi-user scenario security, and distributed decryption privacy as follows.

(1)

IND-CPA security based on RLWE.

The indistinguishability under chosen plaintext attack (IND-CPA) security of the scheme directly reduces to the hardness of the RLWE problem. For individual players, the public key ${\mathit{p}\mathit{k}}_{\mathit{l},\mathit{\eta }}=\left(b_{l, \eta }, a_{l, \eta }\right)$ of the structure to meet $b_{l, \eta }=-a_{l, \eta }{s}_{l, \eta }-e_{l, \eta } \mathrm{m}\mathrm{o}\mathrm{d} q$, where $a_{l, \eta }\leftarrow R_q$ is the uniform random polynomial $e_{l, \eta }\leftarrow \chi$ is the small noise. According to the RLWE hypothesis, the attacker cannot distinguish the public key $\left(b_{l, \eta }, a_{l, \eta }\right)$ and uniform random sample $\left(b_{l, \eta }, u\right)$, which $u\leftarrow R_q$. Furthermore, the ciphertext generated by the encryption process can be regarded as a linear combination of RLWE samples in ${\mathit{c}\mathit{t}}_{\mathit{l},\mathit{\eta }}=\left(c_0, c_1\right)$ in which $c_0={\left[⌊{\displaystyle \frac{q}{t}}{pt}_{\eta }⌉+b_l\mu +e_l\right]}_q$ and $c_1={[a_l\mu +{e\prime }_l]}_q$. Since the attacker cannot distinguish RLWE samples from random values, it cannot infer any information about the plaintext ${pt}_{\eta }$ from the ciphertext, which satisfies IND-CPA security.

(2)

Key security in multi-user scenarios.

In a multi-user scenario, even if the attacker obtains the public keys of all parties ${\left\{{\mathit{p}\mathit{k}}_{\mathit{l},\mathit{\eta }}\right\}}_{\eta =1}^k$, he cannot recover the private key $s_{l, \eta }$ of any party. In particular, the unified public key ${\mathit{p}\mathit{k}}_{\mathit{l}}={\sum }_{\eta =1}^k{\mathit{p}\mathit{k}}_{\mathit{l},\mathit{\eta }}=\left(b_l, a_l\right)$ is a linear combination of the multiple independent RLWE samples. Due to the linearity of the RLWE problem, the attacker cannot separate the private key component $s_{l, \eta }$ or the noise $e_{l, \eta }$ of a single party from the unified public key. Even if the attacker obtains $k-1$ private keys through the side channel, the remaining private keys are still protected by RLWEs, because the decryption requires the joint operation of all participants. Therefore, the scheme still maintains the confidentiality of the key in the multi-user scenario.

(3)

Privacy protection for distributed decryption.

In the process of distributed decryption, each participant outputs a partial decryption result $m_{\eta }^{*}={[{\mathit{c}\mathit{t}}_{\mathit{l}}{·\mathit{s}\mathit{k}}_{\mathit{l},\mathit{\eta }}+e_{\eta }]}_q$, where $e_{\eta }\leftarrow \varphi$ is the Smudging noise added actively. According to the Smudging Lemma, when the magnitude of the Smudging noise is much larger than the magnitude of the noise in the private key of the participant or the noise generated during encryption, the distribution of $e_{\eta }$ will mask the statistical characteristics of these noises. In this case, the partial decryption result $m_{\eta }^{*}$ is statistically indistinguishable from the distribution containing only Smudging noise, hence ensuring that the information of the participant’s private key $s_{l, \eta }$ and the public key noise $e_{l, \eta }$ is not leaked.

In conclusion, the proposed MKFHE scheme meets the security requirements and is suitable for multi-party collaborative dense state computing scenarios.

4. PIR Scheme

Based on the building blocks presented before, this section presents an efficient PIR scheme with a dynamic database. The design of the scheme aims to improve the performance of the secret computing scheme, reduce the resource consumption in data processing process in the multi-source data environment by optimizing the calculation and communication mechanism, and ensure that the efficient query of private information can be completed without decryption.

4.1. System Model

In this model, a user requests data in the database by sending an encrypted query, the database server computes the response in secret state after receiving the query, and then the user jointly decrypts the final query result. The model achieves efficient information retrieval under the premise of protecting multi-user data privacy and prevents unauthorized access and leakage. The system model diagram is shown in Figure 2, and the detailed descriptions are as follows:

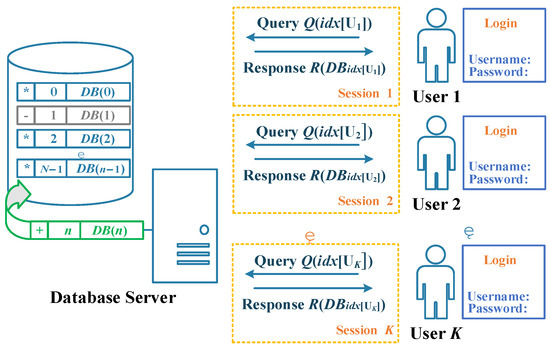
Figure 2. System model.

• Database (DB) Server: A DB server is a computer or system dedicated to storing, managing, and providing database services. Its main responsibility is to handle database management system (DBMS) requests and provide services such as data storage, retrieval, and update for clients (such as applications, users). The database server has powerful functions in computing and storage. In this method, the database is denoted $\mathit{D}\mathit{B}=\left\{\left(i,\mathit{D}\mathit{B}\left[i\right]\right)\right|0\le i\le n-1\}$, and there are $n$ entries stored. After the query user makes a query using unbounded computation, the DB server will provide the response to the query user.

In addition, this method supports the dynamic update of the database. It only needs to mark the data ${DB}_{r,c}$ stored in row $r$ and column $c$ of the original database matrix on the database side with the label of storage status “+, −, *”. Use (${DB}_{r,c}$, +), (${DB}_{r,c}$, −), (${DB}_{r,c}$, *) to indicate that the status of the current database side element ${DB}_{r,c}$ is newly appended, deprecated, or remains unchanged, respectively. Since the new label only presents the status information of the corresponding data of the location without specific data values, it can be disclosed to users who meet the access restrictions, so that they can conveniently store the status labels according to this group and issue queries.

• User: The client or entity that initiates a data query expects to retrieve specific information from the database without letting the database service provider know the data content of the query. The main goal of users is to ensure query privacy, that is, to obtain data while preserving their own privacy. In this method, multiple query users $(1\le j\le K)$ do not collude, and users who pass the access permission verification (that is, their username and password are correct when they login) can directly query the DB server and obtain the expected results from the DB server. At the same time, the user does not want to reveal the index value $idx$ of the query to the DB server when requesting the corresponding data $DB\left[j\right]$ from the DB.

4.2. Security Model

The security model of the private information retrieval scheme in this paper is that the user and the database (DB) server are semi-honest, that is, the user and the DB server are honest-but-curious, and there is no collusion between the DB server and any other third party. Specifically, the user and the database server will faithfully follow the protocol and perform corresponding operations, performing encryption, decryption, calculation, and other tasks within the scope specified by the protocol to ensure the normal operation of the system. However, although they perform the operations in the protocol honestly, they may still try to obtain more information than the data they need by analyzing the ciphertext or query information during the execution out of curiosity.

Under this model, the database server cannot decrypt the ciphertext data and access its content, but it can observe the user’s query request and the response data returned by it. Nonetheless, the database server cannot infer a specific query target from it or leak sensitive information related to other users. This is crucial to protect user privacy, because the server’s “curiosity” will not lead to any leakage of private data. At the same time, users may also be curious about other users’ query results and hope to obtain other users’ query values by some means. However, according to the design of this scheme, users can only access the ciphertext data that they are authorized to use, and they will not expose or obtain the query content of other users during the query process. Therefore, under this security model, although the participants in the system may be curious about the behavior and data of other parties, data privacy is always guaranteed due to the strong privacy protection mechanism.

4.3. Specific PIR Scheme

According to the private information retrieval system model, the MKFHE scheme, and related algorithms and optimizations previously proposed on the basis of specific requirements, the following detailed description of the private information retrieval scheme based on multi-key fully homomorphic encryption is given. The PIR scheme ensures data privacy and security, improves computational efficiency, and supports efficient private information retrieval. The implementation of the scheme includes the following five stages, and the flow chart is shown in Figure 3.

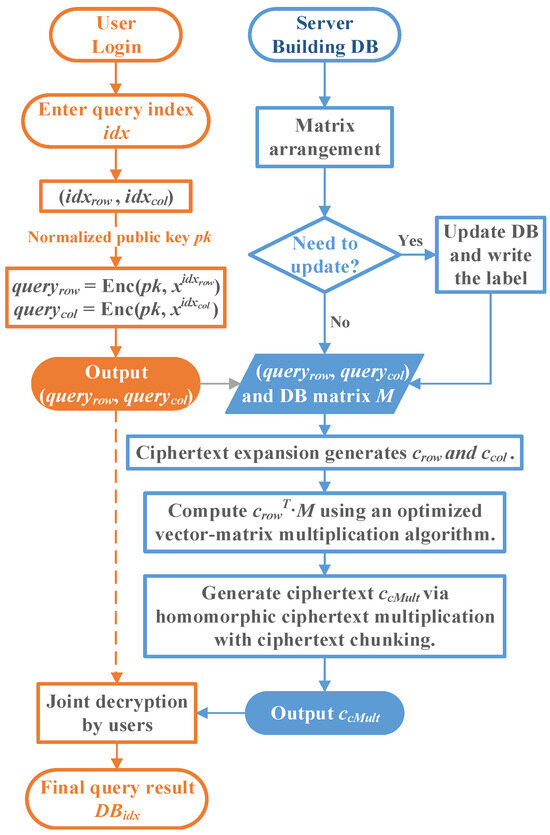
Figure 3. Flowchart of the specific PIR scheme.

(1)

Database construction and access permission verification.

(a)

Database construction and matrix orchestration

Construct a database $DB$ of size $n$. Let each record in the database be ${DB}_i,i=0,1,\dots ,n-1$. Using the database matrix arrangement method, the database of $n$ elements is arranged into a $\sqrt{n}\times \sqrt{n}$ matrix $M$:

$$M=\left[\begin{array}{ccc}{DB}_{0,0}& {DB}_{0,1}& \begin{array}{cc}\cdots & {DB}_{0,\sqrt{n}-1}\end{array}\\ {DB}_{1,0}& {DB}_{1,1}& \begin{array}{cc}\cdots & {DB}_{1,\sqrt{n}-1}\end{array}\\ \begin{array}{c}⋮\\ {DB}_{\sqrt{n}-1,0}\end{array}& \begin{array}{c}⋮\\ {DB}_{\sqrt{n}-1,1}\end{array}& \begin{array}{c}\begin{array}{cc}\ddots & ⋮\end{array}\\ \begin{array}{cc}\cdots & {DB}_{\sqrt{n}-1,\sqrt{n}-1}\end{array}\end{array}\end{array}\right]$$

(b)

Verification of access permission

When users use the system for the first time, they should register by selecting a unique username and setting a strong password (such as containing upper and lower case letters, numbers, and special characters). The user password is processed by hash algorithms (such as bcrypt, SHA-256, etc.). The username and the processed user password are stored in the database.

When logging in, the user enters the username and password in the login screen. The system queries the database to find a record that matches the entered username and obtains the stored password hash value. Then, the password entered by the user is hashed using the same hash algorithm and compared with the hash value stored in the database. If the two match, authentication was successful. Otherwise, the login fails.

Once authentication is complete, the system will create a user session (e.g., generating a session ID) and provide access rights. In the system, user permissions are usually controlled by access control lists (ACL).

(2)

Dynamic database update.

(a)

Determine if the database needs to be updated dynamically

Determine whether it is necessary to support the dynamic update of the database. If necessary, add a set of storage status labels “+,−, *”, indicating the newly appended, deprecated, and remains unchanged of the corresponding location data, respectively. That is, for the element ${\mathrm{D}\mathrm{B}}_{\mathrm{r},\mathrm{c}}$ stored in column $\mathrm{c}$ of row $\mathrm{r}$ of the current database matrix, (${\mathrm{D}\mathrm{B}}_{\mathrm{r},\mathrm{c}}$, +), (${\mathrm{D}\mathrm{B}}_{\mathrm{r},\mathrm{c}}$, −), and (${\mathrm{D}\mathrm{B}}_{\mathrm{r},\mathrm{c}}$, *) are used to denote the status of this element as newly appended, deprecated, or remains unchanged data on the database side, respectively.

(b)

Update the database

When the database needs to add new data, the server will put the new elements into the end of the original database in sequence, and mark the storage status label “+”, that is, (${\mathrm{D}\mathrm{B}}_{\mathrm{r},\mathrm{c}}$, +). When certain data in the database needs to be deleted, the database server will change the storage state label to “−”, marking the data as invalid, that is, (${\mathrm{D}\mathrm{B}}_{\mathrm{r},\mathrm{c}}$, −). The data in other database locations remain unchanged in (${\mathrm{D}\mathrm{B}}_{\mathrm{r},\mathrm{c}}$, *) state.

(c)

Store state labels publicly

A set of updated labels of the database is exposed to users who pass the access permission verification, and it is convenient for users to store state labels according to this group and issue queries.

(3)

Initialization and user query.

(a)

System initialization

The system calls the key generation algorithm MKFHE.Setup, sets the security parameters, the number of participating users $(\mathrm{K}\ge 1)$ and other parameters, generates different public and private key pairs for each user, generates the calculation key, and finally obtains the normalized public key $\mathit{p}\mathit{k}$ and then makes it publicly available.

(b)

The user sends a query to the server

The j-th user ${\mathrm{U}}_{\mathrm{j}}\left(\mathrm{j}\in \left[1,\mathrm{K}\right]\right)$ enters the query index $\mathrm{i}\mathrm{d}\mathrm{x}\in \left\{0,1,\dots ,\mathrm{n}-1\right\}$, that is, user ${\mathrm{U}}_{\mathrm{j}}$ expects to query the $\mathrm{i}\mathrm{d}\mathrm{x}$-th record in the database. Then, user ${\mathrm{U}}_{\mathrm{j}}$ transforms the index $\mathrm{i}\mathrm{d}\mathrm{x}$ into $\left({\mathrm{i}\mathrm{d}\mathrm{x}}_0,{\mathrm{i}\mathrm{d}\mathrm{x}}_1\right)$, which locates the position of the expected query element in the database orchestration matrix M in the form of row and column coordinates, where ${\mathrm{i}\mathrm{d}\mathrm{x}}_0=⌈{\displaystyle \frac{\mathrm{i}\mathrm{d}\mathrm{x}}{\sqrt{\mathrm{n}}}}⌉-1$, ${\mathrm{i}\mathrm{d}\mathrm{x}}_1=\mathrm{i}\mathrm{d}\mathrm{x}-{\mathrm{i}\mathrm{d}\mathrm{x}}_0\sqrt{\mathrm{n}}$. Finally, user ${\mathrm{U}}_{\mathrm{j}}$ uses $\mathit{p}\mathit{k}$ to generate encryption ${\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}}_{\mathit{j}}=\left({\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{r}\mathrm{y}}_{\mathrm{r}\mathrm{o}\mathrm{w}},{\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{r}\mathrm{y}}_{\mathrm{c}\mathrm{o}\mathrm{l}}\right)$, where ${\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{r}\mathrm{y}}_{\mathrm{r}\mathrm{o}\mathrm{w}}=\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}(\mathrm{p}\mathrm{k},{\mathrm{x}}^{{\mathrm{i}\mathrm{d}\mathrm{x}}_0})$, ${\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{r}\mathrm{y}}_{\mathrm{c}\mathrm{o}\mathrm{l}}=\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}\left(\mathrm{p}\mathrm{k},{\mathrm{x}}^{{\mathrm{i}\mathrm{d}\mathrm{x}}_1}\right)$, which is sent to the DB server.

(4)

DB server calculation and response.

(a)

DB server computes the user query

The DB server first receives the encrypted ${\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}}_{\mathit{j}}$ from user $U_j$ and runs the expand algorithm (Algorithm 2) to expand the encrypted query ${\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}}_{\mathit{j}}$ into two ciphertext vectors: $c_{row}=\left(c_{row,0},c_{row,1},\dots ,c_{row,\sqrt{n}}\right)\leftarrow Expand\left({query}_{row},\sqrt{n}\right)$, $c_{col}=\left(c_{col,0},c_{col,1},\dots ,c_{col,\sqrt{n}}\right)\leftarrow Expand({query}_{col},\sqrt{n})$. Subsequently, the DB server calls the homomorphic addition MKFHE.EvalADD and the homomorphic multiplication MKFHE.EvalMult to compute the ciphertext row vector $\mathit{v}={\mathit{c}}_{row}^{T}M={(v_0,v_1,\dots ,v_{\sqrt{n}-1})}^T$, where $v_k={\sum }_{i=0}^{\sqrt{n}-1}{c}_{row,i}{DB}_{i,k},k=0,1,\dots ,\sqrt{n}-1$. This process can use the optimization method of vector–matrix multiplication to improve operation efficiency (Algorithm 1). Finally, the DB server uses homomorphic ciphertext multiplication based on ciphertext chunking (Algorithm 3) to calculate ${\mathit{c}}_{cMult,k}\leftarrow chunksHEMult\left(v_k,c_{col,k},F\right),k=0,1,\dots ,\sqrt{n}-1$, and then uses homomorphic addition to sum ${\mathit{c}}_{cMult}={\sum }_{k=0}^{\sqrt{n}-1}{\mathit{c}}_{cMult,k}$, where ${\mathit{c}}_{cMult}$ contains 2F ciphertexts $\left(c_{cMult,0},c_{cMult,1},\dots ,c_{cMult,2F-1}\right)$.

(b)

DB Server Response

The DB server responds to the user query by returning the ciphertext ${\mathit{c}}_{cMult}$ to the user.

(5)

The user obtains the final query result.

(a)

Multiple users jointly decrypt the response to obtain the final query result

The user receives the query ciphertext result ${\mathit{c}}_{cMult}$ returned by the server, uses the homomorphic ciphertext decryption algorithm based on ciphertext chunking (Algorithm 4), jointly decrypts the response, and computes the final message output $m_{cMult}\leftarrow chunksDec(sk,{\mathit{c}}_{cMult})$. That is, the final query result (database data ${DB}_{idx}$ corresponding to index $idx$).

4.4. Correctness and Security Analysis of Our PIR Scheme

4.4.1. Correctness

The correctness of the proposed PIR scheme relies on the core features of the MKFHE algorithm and the scheme combined with the dynamic update mechanism of the database to ensure that users could accurately retrieve the target entries in the database. This is verified in stages:

(1)

Correctness of database matrix choreography

The database of size $n$ is arranged as a $\sqrt{n}\times \sqrt{n}$ matrix $M$, and each element $M_{r, c}$ corresponds to the database data ${DB}_{r·\sqrt{n}+c}$. The user query index $idx\in [0, n-1]$ is transformed into the row and column coordinates $\left({idx}_0,{idx}_1\right)$, which satisfies ${idx}_0=⌈{\displaystyle \frac{idx}{\sqrt{n}}}⌉-1,{idx}_1=idx-{idx}_0\sqrt{n}$, ensures that each $idx$ is uniquely mapped to the matrix position $M_{{idx}_0, {idx}_1}$, and traverses and covers all database elements.

(2)

Correctness of database dynamic update

When the database is dynamically updated, the system clearly identifies the validity of the data through the public status labels “+, -, *”. Before issuing a query, the client first accesses these tags to determine whether the target entry is valid or not and to avoid sending an invalid operation to the server. This mechanism not only reduces the computational burden of the server but also enables the client to sense the changes in the data state in real time, so that it can dynamically adjust the query strategy and only request the valid data. When the server updates the database, the index mapping of the original matrix structure is maintained by synchronously updating the data and labels, so that the user can still accurately locate the target position through the original index.

(3)

Correctness of encrypted query generation

User $U_j$ generates encrypted query ${\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}}_{\mathit{j}}=\left({query}_{row},{query}_{col}\right)=(\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}\left(pk, x^{{idx}_0}\right), \mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}\left(pk,x^{{idx}_1}\right))$. The row and column indexes are encoded in the form of polynomials $x^{{idx}_0}$ and $x^{{idx}_1}$ to ensure that the server can locate the target element through homomorphic operation. The correctness of homomorphic encryption depends on the correctness of MKFHE scheme.

(4)

Correctness of query expansion expand and matrix operations

After receiving the encrypted query, the database server expands the encrypted query into row vector $c_{row}$ and column vector $c_{col}$, so that it is encrypted “1” only in the position of the target row ${idx}_0$ and column ${idx}_1$, and the rest are encrypted “0”, which ensures that the homomorphic multiplication and addition operation only extracts the target element. Then perform matrix operations, through homomorphism by arithmetic ciphertext row vector $\mathit{v}={\mathit{c}}_{row}^{T}M={(v_0, v_1, \dots , v_{\sqrt{n}-1})}^T$, including $v_k={\sum }_{i=0}^{\sqrt{n}-1}{c}_{row,i}{DB}_{i,k},k=0,1,\dots ,\sqrt{n}-1$. Since $v_k={\sum }_{i=0}^{\sqrt{n}-1}{c}_{row,i}{DB}_{i,k},k=0,1,\dots ,\sqrt{n}-1$ is only nonzero in row ${idx}_0$, the result $\mathit{v}$ corresponds to row ${idx}_0$ of the matrix $M$. Then use the homomorphic ciphertext multiplication based on ciphertext blocks to calculate ${\mathit{c}}_{cMult,k}\leftarrow \mathrm{c}\mathrm{h}\mathrm{u}\mathrm{n}\mathrm{k}\mathrm{s}\mathrm{H}\mathrm{E}\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\left(v_k,c_{col,k},F\right)$ and use homomorphic addition to sum ${\mathit{c}}_{cMult}={\sum }_{k=0}^{\sqrt{n}-1}{\mathit{c}}_{cMult,k}$. Since $c_{col}$ is nonzero only in the ${idx}_1$ column, the final result ${\mathit{c}}_{cMult}$ corresponds to $M_{{idx}_0, {idx}_1}={DB}_{idx}$. The correctness of the procedure involving homomorphic addition and multiplication depends on the correctness of the MKFHE scheme.

(5)

Correctness of distributed decryption

After receiving the response ciphertext ${\mathit{c}}_{cMult}$, the client decrypts the response jointly using a homomorphic ciphertext decryption algorithm chunksDec based on ciphertext chunking. The correctness of the decryption result depends on the correctness of the chunksDec decryption algorithm and reconstruction (the correctness of the ciphertext chunking algorithm is verified by the code in Section 5.3). The correctness of the involved homomorphic addition and multiplication and decryption depends on the correctness of the MKFHE scheme, and the MKFHE parameter ensures that the total noise amplitude is less than $q/(2t)$ to avoid decryption errors.

In summary, depending on the correctness of the MKFHE scheme, the proposed scheme supports the dynamic update of the database while strictly guaranteeing the correctness of the query results. The client avoids invalid queries through tags and finally recovers the target data through distributed decryption, while the server responds to valid requests accurately through homomorphic operation. The design achieves efficient and scalable private information retrieval under the premise of protecting user privacy.

4.4.2. Security

We rigorously prove that the designed PIR scheme is secure against the attacker $\mathcal{A}=\{User,Server\}$. A probabilistic polynomial-time simulator ${\mathcal{S}}^{Server}$ is constructed to play the role of DB server in interacting with the user, and it is proved that the user cannot distinguish between the real view and the ideal view computationally, thereby ensuring the security of the PIR scheme. Here are the detailed proof steps:

(1)

Define the true perspective and the ideal perspective

• Real perspective: The view of the user interacting with a real database server. The user sends an encrypted $\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}$ with index $\mathrm{i}\mathrm{d}\mathrm{x}$, and the DB server returns the query result ciphertext ${\mathit{c}}_{cMult}$. After receiving ${\mathit{c}}_{cMult}$, the user jointly decrypts it to obtain ${DB}_{idx}$.
• Ideal perspective: The view of the user interacting with the simulator ${\mathcal{S}}^{Server}$. The user sends an encrypted $\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}$ of index $idx$, and the simulator ${\mathcal{S}}^{Server}$ returns the ciphertext ${\mathit{c}\prime }_{cMult}$ corresponding to ${DB}_{idx\prime }$ to the user. After receiving the ciphertext ${\mathit{c}\prime }_{cMult}$, the user decrypts it to obtain ${DB}_{idx\prime }$.

(2)

Construct the simulator ${\mathcal{S}}^{Server}$

• Receive the query: The simulator ${\mathcal{S}}^{Server}$ receives the $\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}$ sent by the user.
• Generate the ciphertext: The simulator ${\mathcal{S}}^{Server}$ generates an encrypted query $\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}\mathbf{\prime }$ which is computationally indistinguible with the real query $\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}$, that is, $\mathit{Q}\mathit{u}\mathit{e}\mathit{r}{\mathit{y}}^{\mathbf{\prime }}=(\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}\left(pk,x^{{idx}_0\prime }\right),\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}\left(pk,x^{{idx}_1\prime }\right))$, where $\left({idx}_0\prime ,{idx}_1\prime \right)$ is the index corresponding to ${\mathrm{D}\mathrm{B}}_{\mathrm{i}\mathrm{d}\mathrm{x}\prime }$. The simulator ${\mathcal{S}}^{Server}$ continues to perform the operations of the DB server Query and response phase on $\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}\prime$ to obtain the ciphertext ${\mathit{c}\prime }_{cMult}$.
• Return the ciphertext: The simulator ${\mathcal{S}}^{Server}$ returns ${\mathit{c}\prime }_{cMult}$ to the user.

(3)

Prove the indistinguishability

We need to show that the real and ideal views of the user are computationally indistinguishable. Specifically, we need to show that the following two distributions are computationally indistinguishable.

Real distribution: The distribution of user interactions with real DB servers, that is, $(Query, {\mathit{c}}_{cMult}, {DB}_{idx})$.

Ideal distribution: The distribution of user interactions with the simulator ${\mathcal{S}}^{Server}$, that is, $(Query, {\mathit{c}\mathbf{\prime }}_{cMult}, {DB\prime }_{idx})$.

• Indistinguishability of ciphertext: According to the security assumption of the MKFHE encryption scheme (the BFV-MKFHE scheme in this paper is IND-CPA secure), $\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}$ and $\mathit{Q}\mathit{u}\mathit{e}\mathit{r}{\mathit{y}}^{\mathbf{\prime }}=(\mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}\left(pk,x^{{idx}_0\prime }\right), \mathrm{M}\mathrm{K}\mathrm{F}\mathrm{H}\mathrm{E}.\mathrm{E}\mathrm{n}\mathrm{c}\left(pk,x^{{idx}_1\prime }\right))$ are computationally indistinguishable, that is, c_cMult and Query^’ are also computationally indistinguishable by the same operation. That is, for any probabilistic polynomial-time distinguisher D, there exists a negligible function $\epsilon (\lambda )$ such that:

  $$\mid Pr\left[D\left({\mathit{c}}_{cMult}\right)=1\right]-Pr[D({\mathit{c}\mathbf{\prime }}_{cMult})=1]\mid \le \epsilon (\lambda )$$
• Indistinguishability of viewpoints: Since ciphertexts ${\mathit{c}}_{cMult}$ and ${\mathit{c}\mathbf{\prime }}_{cMult}$ are computationally indistinguishable, the user’s true view $(Query,{\mathit{c}}_{cMult},{DB}_{idx})$ and ideal view $(Query,{\mathit{c}\mathbf{\prime }}_{cMult},{DB\prime }_{idx})$ are also computationally indistinguishable.

(4)

Security conclusion

• On the side of user: The user can only obtain the ${DB}_{idx}$ from the database server, but not any other information in the database. Since ${\mathit{c}}_{cMult}$ and ${\mathit{c}\mathbf{\prime }}_{cMult}$ are indistinguishable, the user cannot infer other information about the database from the ciphertext. Then, we can assert that the user cannot learn anything about the data from the database server except ${DB}_{idx}$, which means that the single-server PIR protocol is secure against the database server and leaks no other information.
• On the side of database server: The database server only receives the user’s query $\mathit{Q}\mathit{u}\mathit{e}\mathit{r}\mathit{y}$ and cannot infer the user’s concrete query index $idx$. Therefore, the database server cannot obtain the user’s private information.

In summary, since the simulator ${\mathcal{S}}^{Server}$ is able to generate ciphertexts that are computationally indistinguishable from the ciphertexts returned by the real server, and the user cannot distinguish between the ideal and the real perspective, the following can be concluded: the PIR scheme designed in this paper is secure against the attacker $\mathcal{A}=\{User,Server\}$, which can effectively protect the user’s access information and retrieval information, and prevent the database server from leaking other information.

4.5. Remark

Inspired by the new private information retrieval scheme proposed by Luo et al. in 2024 [21], this section further explores a transferable optimization method, which encodes a single column of the database matrix into a polynomial ring structure and utilizes the algebraic properties of the automorphism transformation to reduce computational complexity and enhance computational efficiency.

(1)

Technical implementation.

(a)

Database matrix encoding

First, each column of the database matrix is encoded as a polynomial in the polynomial ring $R_q=Z_q\left[x\right]/(x^n+1)$, that is, for the database matrix $DB\in Z_p^{n\times n}$, its $j$-th column is encoded as $t_j\left(x\right)={DB}_{0, j}+{DB}_{1, j}x+\cdots +{DB}_{n-1, j}{x}^{\left(n-1\right)}$. When the database server generates the response, $t_j\left(x\right)$ can be directly multiplied with the RLWE ciphertext in the user’s query.

(b)

Shift optimization for rotation

In the polynomial ring $R_q$, given a polynomial ${a\left(x\right)=a}_0+a_{1}x+\cdots +a_{N-1}{x}^{N-1}$, the rotation operation $\mathrm{R}\mathrm{o}\mathrm{t}\left(a\left(x\right), k\right)$ can be cyclically shifted by the automorphism transformation $x\mapsto x^{5^k}$, i.e., $\mathrm{R}\mathrm{o}\mathrm{t}\left(a\left(x\right), k\right)=a_0+a_1{x}^{5^k}+\cdots +a_{N-1}{(x^{5^k})}^{N-1}\in R_q$. In fact, an automorphism transformation on its coefficient form is equivalent to a permutation on its corresponding number theoretic transform (NTT) form [22]. That is, two NTT representations with different rotation steps $\mathrm{N}\mathrm{T}\mathrm{T}(a(x^{5^i})$ and $\mathrm{N}\mathrm{T}\mathrm{T}(a(x^{5^j})$ have the same elements, and they are just a permutation of each other. Therefore, $\mathrm{N}\mathrm{T}\mathrm{T}(a(x^{5^k})$ can be obtained by performing NTT only once for all rotation steps $k$, instead of multiple times. This feature enables ciphertext rotation operation to be completed directly by the shift instruction in memory without complex multiplication. Combined with basis decomposition commutativity $(g^{-1}(a\left(x^{5^k}\right))=g^{-1}\left(a\right)\left(x^{5^k}\right))$, rotation operation can be decomposed into two phases: preprocessing and online replacement. In the preprocessing phase, all forms of automorphism $\mathrm{N}\mathrm{T}\mathrm{T}(g^{-1}\left(a\right)\left(x^{5^k}\right))$ of $g^{-1}\left(a\right)$ are computed and stored; in the online phase, the preprocessed NTT representation is called directly to complete the cyclic shift by memory replacement.

(2)

Application in the PIR Scheme.

(a)

Query generation phase

When the user generates a query, it needs to specify the target index $(u,w)$. When constructing the RLWE ciphertext, the RLWE ciphertext $\mathrm{R}\mathrm{L}\mathrm{W}\mathrm{E}({\mathrm{N}\mathrm{T}\mathrm{T}}^{-1}(u)$ encrypting the one-hot vector $u$ is generated, where $u$ is the vector whose $u$-th bit is 1. When constructing RGSW ciphertext, the RGSW ciphertext encrypting $x^{-w}$ is generated. The polynomial encoding enables query construction with only one polynomial encryption and does not need to deal with complex two-dimensional index logic.

(b)

Response generation phase

The server utilizes the preprocessed matrix $M$ and the query ciphertext for efficient computation. Firstly, $\mathrm{B}\mathrm{S}\mathrm{G}\mathrm{S}(M, \mathrm{R}\mathrm{L}\mathrm{W}\mathrm{E}({\mathrm{N}\mathrm{T}\mathrm{T}}^{-1}(u)))\to \mathrm{R}\mathrm{L}\mathrm{W}\mathrm{E}({\mathrm{N}\mathrm{T}\mathrm{T}}^{-1}(M·u)))$ is calculated by the baby-step giant-step strategy, and the matrix–vector multiplication $M·u$ is decomposed into multiple lightweight shifts and point multiplications. In the baby-step, all displacement copies of $\mathrm{R}\mathrm{o}\mathrm{t}(ct,k)$ are precomputed, and the preprocessed basis decomposition results are multiplexed. The giant-step combines the displacement results and generates the final response $\mathrm{R}\mathrm{L}\mathrm{W}\mathrm{E}({\mathrm{N}\mathrm{T}\mathrm{T}}^{-1}(M·u))$ by key switching. Then the outer product of the RGSW ciphertext and RLWE ciphertext is used to extract the target element ${DB}_{u, w}$. The frequency domain point multiplication and automorphism permutation reduce the response generation complexity from $O(n^2)$ to $O(n \mathrm{l}\mathrm{o}\mathrm{g}n)$.

(c)

Response retrieval phase

When the client decrypts the final LWE ciphertext, it obtains ${DB}_{u,w}$ through the standard LWE decryption process without additional inverse polynomial transformation. The preprocessing and frequency domain computation are completely completed by the server, and the decryption complexity of the client is the same as that of plaintext retrieval.

(3)

Performance improvement analysis.

As shown in Table 1.

Table 1. Performance improvement analysis.

	Complexity of Traditional Methods	Complexity of Our Method	Complexity of Luo’s Method
Database encoding	$O\left(n\right)$	$O(n)$	$O(\sqrt{n})$
Matrix–vector multiplication	$O\left(n\right)$	$O(\sqrt{n})$	$O(\sqrt{n})$
Rotation operation (online single time)	/	$O\left(\sqrt{n}\right)$	$O(1)$
Key switching (online single time)	/	$\mathit{O}\left(\sqrt{\mathit{n}}\right)$	$\mathit{O}(\mathbf{1})$

5. Performance Analysis

In this section, we mainly analyze the performance of the PIR scheme designed in this paper, focusing on the evaluation of computational efficiency, communication overhead, scalability, and other aspects, and compare it with the existing SealPIR [7], as shown in Table 2. Through sufficient theoretical analysis and experimental verification, the PIR scheme proposed in this paper shows significant advantages in many aspects.

Table 2. Comparison of PIR schemes.

	SealPIR [7]	Ours
Homomorphic encryption scheme	BFV	BFV-MKFHE
Dynamic database	×	√
Vector–matrix Multiplication optimization	×	√
Programmed exposition of ciphertext blocking algorithm	×	√

5.1. Optimized MKFHE and Dynamic Database

In our PIR scheme, based on the multi-user scenario, considering that each query user is independent of each other, a BGV-type [13] multi-key fully homomorphic encryption scheme is used to ensure the private information security of users and improve the overall security of the system. The optimized MKFHE scheme used in the PIR scheme in this paper effectively reduces the noise, and by using the same public key, reduces the calculation key size and ciphertext size while saving the homomorphic multiplication time. The comparative analysis between the proposed MKFHE scheme and other BGV-type multi-key homomorphic encryption schemes is shown in Table 3.

Table 3. Comparison of BGV-type MKFHE schemes.

	LZY19 [23]	CDKS19 [24]	YZLL23 [19]	Ours
Computing key size	$O(k^{3}n)$	$O(kn)$	$O(kn)$	$O(n)$
Ciphertext size	$O(kn)$	$O(kn)$	$O(kn)$	$O(n)$
Multiplication complexity	$O(k^{3}n)$	$O(k^{2}n)$	$O(k^{2}n)$	$O(n)$
Multiplication noise	$\mathit{O}({\mathit{k}}^{\mathbf{2}}{\mathit{n}}^{\mathbf{4}}{\mathit{B}}^{\mathbf{2}})$	$\mathit{O}({\mathit{k}}^{\mathbf{2}}{\mathit{n}}^{\mathbf{3}}{\mathit{B}}^{\mathbf{2}})$	$\mathit{O}({\displaystyle \frac{\mathbf{1}}{\mathit{p}}}{\mathit{k}}^{\mathbf{2}}{\mathit{n}}^{\mathbf{3}}{\mathit{B}}^{\mathbf{2}})$	$\mathit{O}({\displaystyle \frac{\mathbf{1}}{\mathit{p}}}{\mathit{n}}^{\mathbf{3}}{\mathit{B}}^{\mathbf{2}})$

Compared with the existing SealPIR scheme [7] which only uses a single BFV scheme, the proposed PIR scheme is obviously more suitable for real-world scenarios with multi-party participation and has significant application advantages. Our scheme also supports the dynamic updating of the database, allowing the database to dynamically add or delete data during the operation of the scheme to adapt to the requirements of frequent data changes in real scenarios. It has strong flexibility and applicability and is of great significance in practical applications.

5.2. Vector-Matrix Multiplication Optimization

Compared with SealPIR, this paper introduces an optimization algorithm of vector–matrix multiplication, which significantly improves the computational efficiency. The detailed analysis is as follows:

Computational complexity: The optimization method mainly consists of $n-1$ additions, $n$ multiplications (corresponding to CMult operations), and $n-1$ rotations (corresponding to Rot operations). Since the rotation operation involves key conversion, the computational cost is high, and the total complexity is asymptotically $O(n)$ rotations.

Optimization effect:

In order to test the performance of the optimization method, our experimental platform uses a computer with normal performance, Intel Core i5-8250U CPU 1.60 GHz, running Ubuntu 20.04 64-bit Linux operating system through a virtual machine environment, and equipped with 24 GB memory and 8-core processor. In the experiment, we use the open source encryption library SEAL 4.0.0 to simulate the PIR scheme with the optimized algorithm of vector–matrix multiplication designed in this paper and compare it with the existing SealPIR scheme. The experiment uses the BFV encryption algorithm in the SEAL library to encrypt the user’s query index and decrypt the final result. To ensure classical security of 128 bits, we set the polynomial modulus $N$ to 4096, the size of the coefficient modulus $q$ to 109$(36+36+37)$, and the plaintext modulus $t$ to 20 bits. The database sizes selected in the experiment are $16 \mathrm{M}\mathrm{B}\left(2^{16}\times 256 \mathrm{B}\right), 64 \mathrm{M}\mathrm{B}\left(2^{18}\times 256 \mathrm{B}\right), 256 \mathrm{M}\mathrm{B}\left(2^{20}\times 256 \mathrm{B}\right),$ and $1 \mathrm{G}\mathrm{B} (2^{22}\times 256 \mathrm{B})$, that is, the size of a single database data item is set to 256 B, and the dimension of the database matrix is set to 2.

It should be mentioned that our experimental results are based on the mean of 50 runs of the program. (Some of the values are shown in Table 4). At the same time, in order to compare and study the efficiency improvement of the PIR scheme after the optimization method of embedding vector–matrix multiplication, the following “Our scheme” does not implement multi-key encryption, database dynamic update, and other functions.

Table 4. Partial running results of the PIR scheme.

Database Scale	Phase		SealPIR	Our Scheme
${\mathbf{2}}^{\mathbf{16}}\times \mathbf{256} \mathbf{B}$ $\mathbf{16} \mathbf{M}\mathbf{B}$	Preprocessing		1162 ms	1288 ms
	Response generation	online	771 ms	756 ms
		offline	/	197 ms
${\mathbf{2}}^{\mathbf{18}}\times \mathbf{256} \mathbf{B}$ $\mathbf{64} \mathbf{M}\mathbf{B}$	Preprocessing		4211 ms	4648 ms
	Response generation	online	1804 ms	1745 ms
		offline	/	309 ms
${\mathbf{2}}^{\mathbf{20}}\times \mathbf{256} \mathbf{B}$ $\mathbf{256} \mathbf{M}\mathbf{B}$	Preprocessing		14,443 ms	14,977 ms
	Response generation	online	6049 ms	5727 ms
		offline	/	616 ms
${\mathbf{2}}^{\mathbf{22}}\times \mathbf{256} \mathbf{B}$ $\mathbf{1} \mathbf{G}\mathbf{B}$	Preprocessing		85,921 ms	86,814 ms
	Response generation	online	23,195 ms	21,411 ms
		offline	/	1252 ms

Our experimental results show that the time of query generation, query serialization and deserialization, and response decryption are all between 1 and 7 ms, which is short, and there is no difference between the schemes, that is, the addition of the optimization method of vector matrix multiplication has no effect on these times, and the unified analysis is as follows.

The generation time of the client query is about 3 ms, which is short because the query operation only needs to encrypt the index once. Its computational complexity is limited by lightweight polynomial multiplication and a small choice of plaintext modulus, which indicates that the client resource consumption is low and suitable for edge device deployment. The difference between the query serialization time of 6–7 ms and the deserialization time of 1–2 ms reflects the overhead characteristics of data format conversion, that is, the client needs to convert the ciphertext structure into the network transmission format, which involves the modulo number aligned byte stream encapsulation of the polynomial coefficients, while the server can quickly restore the ciphertext pair in microseconds with the efficient memory mapping mechanism. The decryption of the client takes about 4 ms, and the low time consumption highlights the advantage of asymmetric computing, that is, the decryption only needs to restore the polynomial coefficients of a single ciphertext and does not need to consider the complex noise constraints, so that the terminal device can quickly obtain the plaintext results.

However, the addition of the optimization method of vector–matrix multiplication undoubtedly has a certain impact on the preprocessing time of PIR scheme. The comparison diagram of the preprocessing time of PIR scheme drawn from the data is shown in Figure 4.

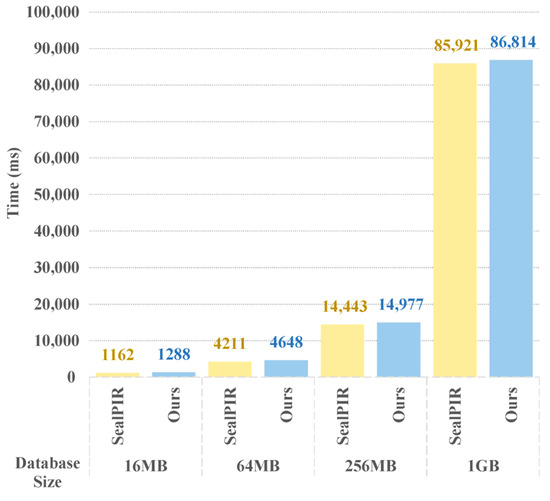
Figure 4. Comparison of preprocessing time of PIR scheme.

The preprocessing time of the PIR scheme is relatively long, mainly because the server needs to complete the core operations such as homomorphic encryption coding and key generation of the database in the startup phase. The initialization process of the database involves dividing the original data into blocks and encoding them into polynomial structures. This step needs to optimize the computational efficiency by number theoretic transformation (NTT), and its complexity is positively related to the scale of the data. At the same time, the generation of the Galois key needs to construct multiple rotation keys according to the degree of the polynomial ring to support the replacement operation of the ciphertext slot. The computational overhead of such key generation increases significantly with the increase in the degree of the polynomial ring. Figure 4 shows that the average time of the proposed scheme in this operation is about 126–893 ms more than SealPIR, which is mainly used for the diagonal extraction of the database matrix. However, this operation takes very little time in the whole preprocessing stage, and can be implemented offline, so it has little impact on the overall performance of the scheme.

The response generation time on the server side is the main performance bottleneck of the scheme, and the core load of the scheme comes from the homomorphic multiplication and addition operation and the noise management mechanism. In SealPIR, the server needs to perform slot-by-slot multiplication and accumulation of the encoded database polynomials and query ciphertext. Although the NTT acceleration of polynomial multiplication reduces the complexity to $O(n\mathrm{l}\mathrm{o}\mathrm{g}n)$, the calculation still requires high computing power support.

As shown in Figure 5, the optimization algorithm of vector–matrix multiplication introduced in the proposed scheme may increase the total average time of this operation to a certain extent, mainly because the additional ciphertext rotation operation is introduced to support a more flexible slot access pattern. Ciphertext rotation realizes slot cyclic shift through Galois key, and its computational complexity is related to polynomial degree and rotation step size. A single rotation can take several milliseconds, and the overall time may be prolonged after accumulation. However, the ciphertext rotation operation can be completely processed offline by the server, and the tree reduction (butterfly network) optimization method can be used, so that only $O(log m)$ Galois rotation operations are needed to generate $m$ rotated ciphertexts, which reduces the online computation time by about 15–1784 ms and improves the efficiency by about 1.95% to 7.69%. This trade-off strategy not only shifts the pressure of real-time computing to offline processing but also imposes higher demands for server storage resources.

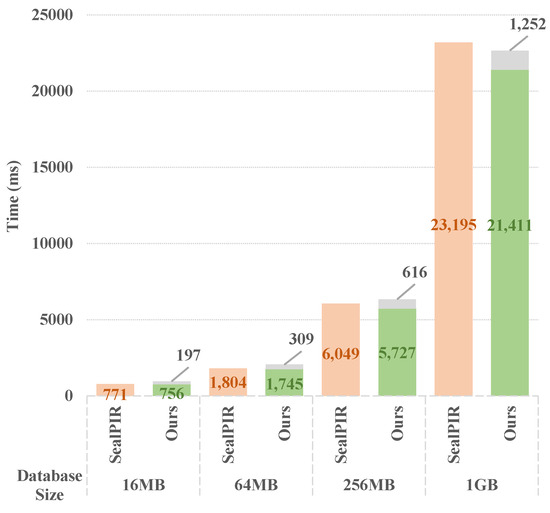
Figure 5. Comparison of server response generation time in PIR scheme.

Among them, the core idea of using a butterfly network (similar to tree reduction) optimization method to further reduce the ciphertext rotation time is as follows: First, all rotation steps can be expressed in binary form (such as $2^0, 2^1, \dots , 2^{\mathit{log}m-1}$), the server can precalculate the Galois key corresponding to these rotation steps, that is, the rotation key with step $2^i$ is stored through GaloisKeys. When performing the rotation operation, the server does not need to calculate the ciphertext rotation independently for each rotation step but unrolls the rotation operation layer by layer by way of hierarchical expansion. Starting from the lowest layer (step size $2^0$), the rotation of larger steps is applied layer by layer, and each layer operation reuses the result of the previous layer to generate a new copy of the ciphertext by strided combination. In this way, the number of rotations required is significantly reduced, thus further improving the efficiency of rotation operations.

In order to further explore the vector–matrix multiplication optimization module, we selected a database size of $2^{20}$ integers, and performed 50 tests without optimizing the ciphertext rotation operation (i.e., directly multiplying the vector and the matrix), taking the average and obtaining the following results, as shown in Figure 6. The direct method takes 1.03256 s and the online calculation time of the optimized method is 0.82915 s (the total time is 5.36311 s, including 0.12583 s for diagonal extraction and encoding and 4.40813 s for ciphertext rotation), which is 0.20341 s shorter and the performance is improved by about 19.7%.

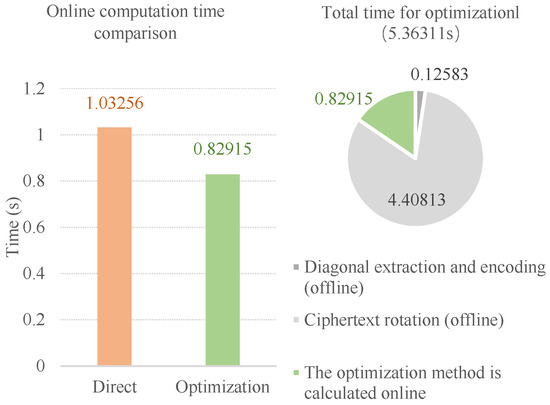
Figure 6. Test results of vector–matrix multiplication optimization.

5.3. Program Verification of Ciphertext Chunking Algorithm

In the design of the PIR scheme, the matrix of the database leads to the operation of ciphertext multiplied by ciphertext. In order to ensure the correctness of the whole protocol, the parameter of the homomorphic encryption scheme needs to be set large, which reduces the computational efficiency. In order to solve this problem, the scheme adopted the homomorphic ciphertext multiplication based on ciphertext block, and the ciphertext ${\mathit{c}}_{cMult}$ generated by this special homomorphic ciphertext multiplication must also go through a special homomorphic decryption to recover the final result. In this paper, the specific operation steps of the ciphertext blocking algorithm (Section 3.3) are given in detail, and its correctness is verified by code implementation. The detailed analysis is as follows:

The experimental platform of Intel Core i5-8250U 1.60 GHz CPU, 8 GB memory, Windows 10 operating system, Python 3.12.6 implementation on VScode platform is used to verify the correctness. The parameters are set as polynomial modulus degree $n=2048$, coefficient modulus $q=1152921504606830593 \left(\mathit{log}q=60\right)$, plaintext modulus $t=2^{23}$, and special modulus $p=1532495540865823528131582195248413530532739854796537858$, the average $\mu =0$, noise $\sigma =1.6$, chunk size $F=10 (F\ge 6.4)$, weight $w=6 (w={\displaystyle \frac{⌈logq⌉}{F}})$.

The experimental results show that the direct method directly multiplies the two ciphertexts in 5.81 s, and the decryption time is 0.07 s. In the ciphertext chunking algorithm, the ciphertext chunking time is 0.02 s, the plaintext multiplication time is 70.90 s, and the decryption time is 0.66 s. The correctness verification results show that the corresponding plaintext of the recovered data can be decrypted correctly after the homomorphic ciphertext multiplication and decryption operation based on the ciphertext chunking algorithm.

This part of the code uses the most basic BFV scheme and does not use any other encryption libraries or optimizations, so it takes a long time to build, but it can still be used for qualitative analysis and algorithm correctness verification. Therefore, the above results can verify well the correctness of the ciphertext chunking algorithm given in this paper. At the same time, it can also be seen that running the homomorphic ciphertext multiplication and decryption based on ciphertext chunking requires more time (about ten times) than the direct multiplication and decryption of two ciphertexts, and there is significant room for improvement in computational efficiency.

Through the performance analysis of four parts of the optimized BFV-MKFHE scheme, supporting database dynamic update, vector–matrix multiplication optimization algorithm, and program verification of ciphertext chunking algorithm, it can be seen that the PIR scheme designed in this paper demonstrates significant advantages in terms of computational efficiency, communication overhead, and scalability. In particular, the introduction of the vector–matrix multiplication optimization algorithm improves the online calculation efficiency of server vector–matrix multiplication by about 19.7%. The performance analysis results show that the proposed scheme can effectively support the requirements of private information retrieval, optimize the design scheme, improve computational efficiency, and be more suitable for practical application scenarios.

6. Conclusions

In this paper, an efficient private information retrieval scheme with dynamic database is proposed, which aims to study the design of a private information retrieval scheme under a multi-data source framework based on multi-key fully homomorphic encryption algorithm. The scheme focuses on improving the computational efficiency and scalability of private information retrieval. The improved MKFHE algorithm is used to generate encrypted queries with a lower length from different clients, the vector–matrix multiplication optimization method is embedded to improve the computational efficiency of response phase, and the expand algorithm and ciphertext chunking algorithm are used to further reduce communication traffic and noise, respectively. The scheme also adds a user access permission verification mechanism to avoid unauthorized users from accessing the system. At the same time, it supports the dynamic update of the database, which enhances the flexibility and practicability of the scheme. In the future, the scheme can further integrate technical points such as NTT preprocessing and automorphism shift optimization, and deeply explore the potential of hardware acceleration, so as to promote the evolution of privacy information retrieval to lower latency and higher throughput.