Small-Signal Modeling of Asymmetric PWM Control Based Series Resonant Converter
Abstract
1. Introduction
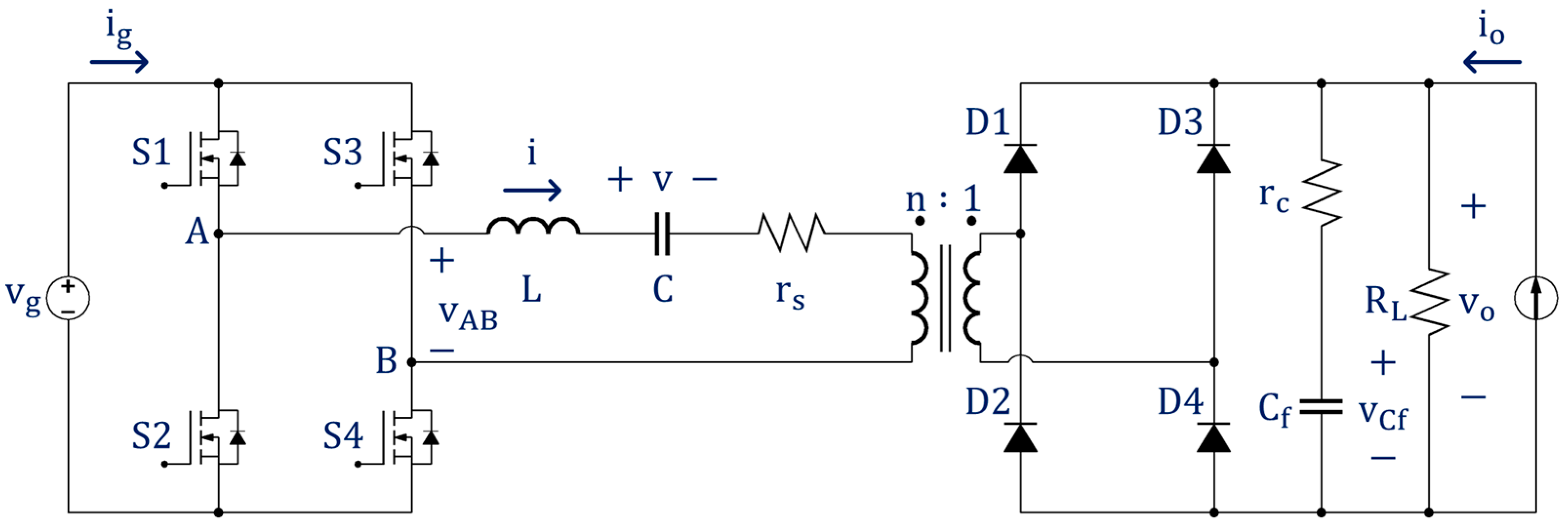
2. Small Signal Modeling
2.1. Nonlinear State Equation
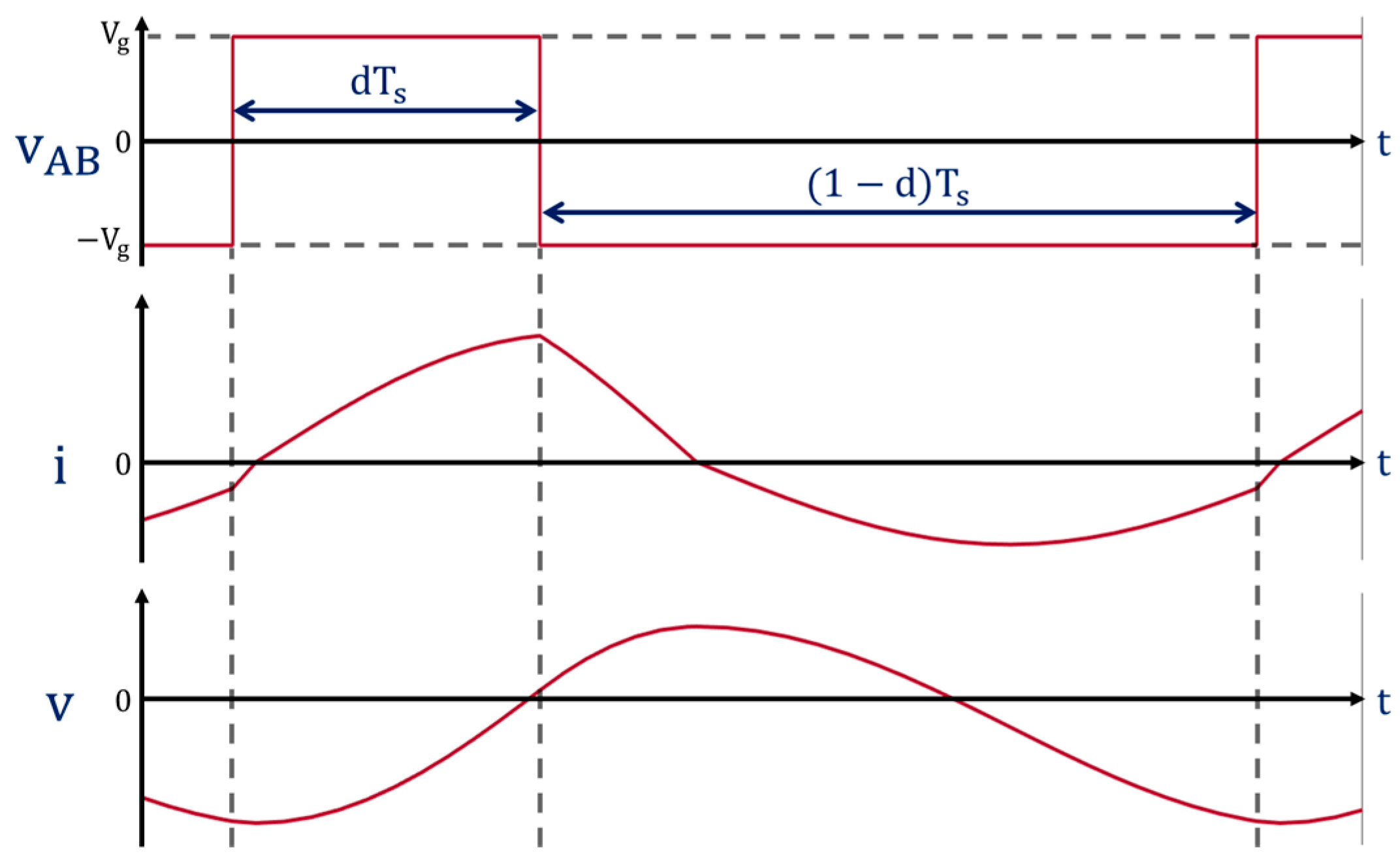
2.2. Harmonic Approximation
2.3. Extended Describing Function
2.4. Harmonic Balance
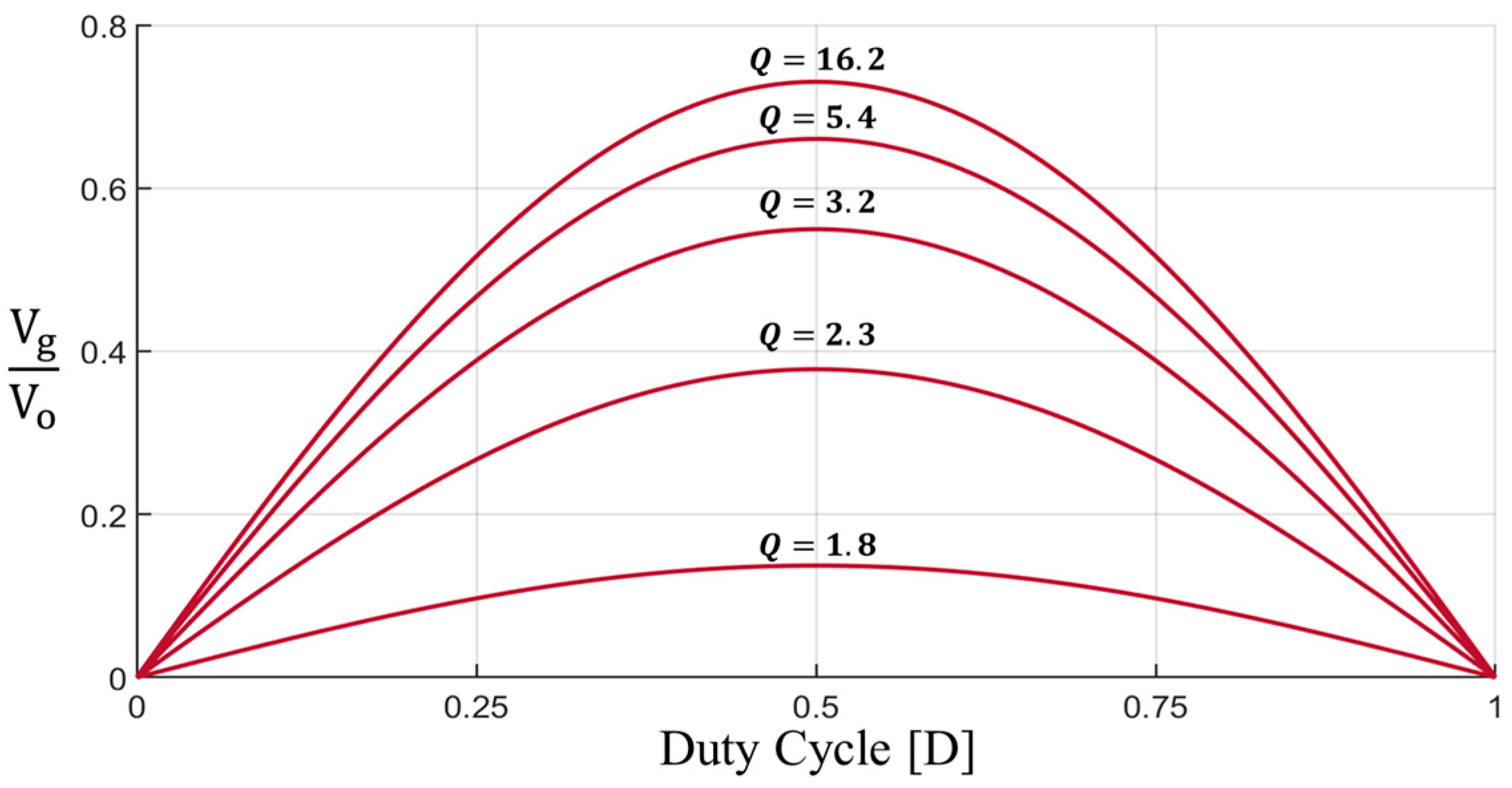
2.5. Steady-State Solution
2.6. Perturbation and Linearization
3. Simulation and Experimental Results
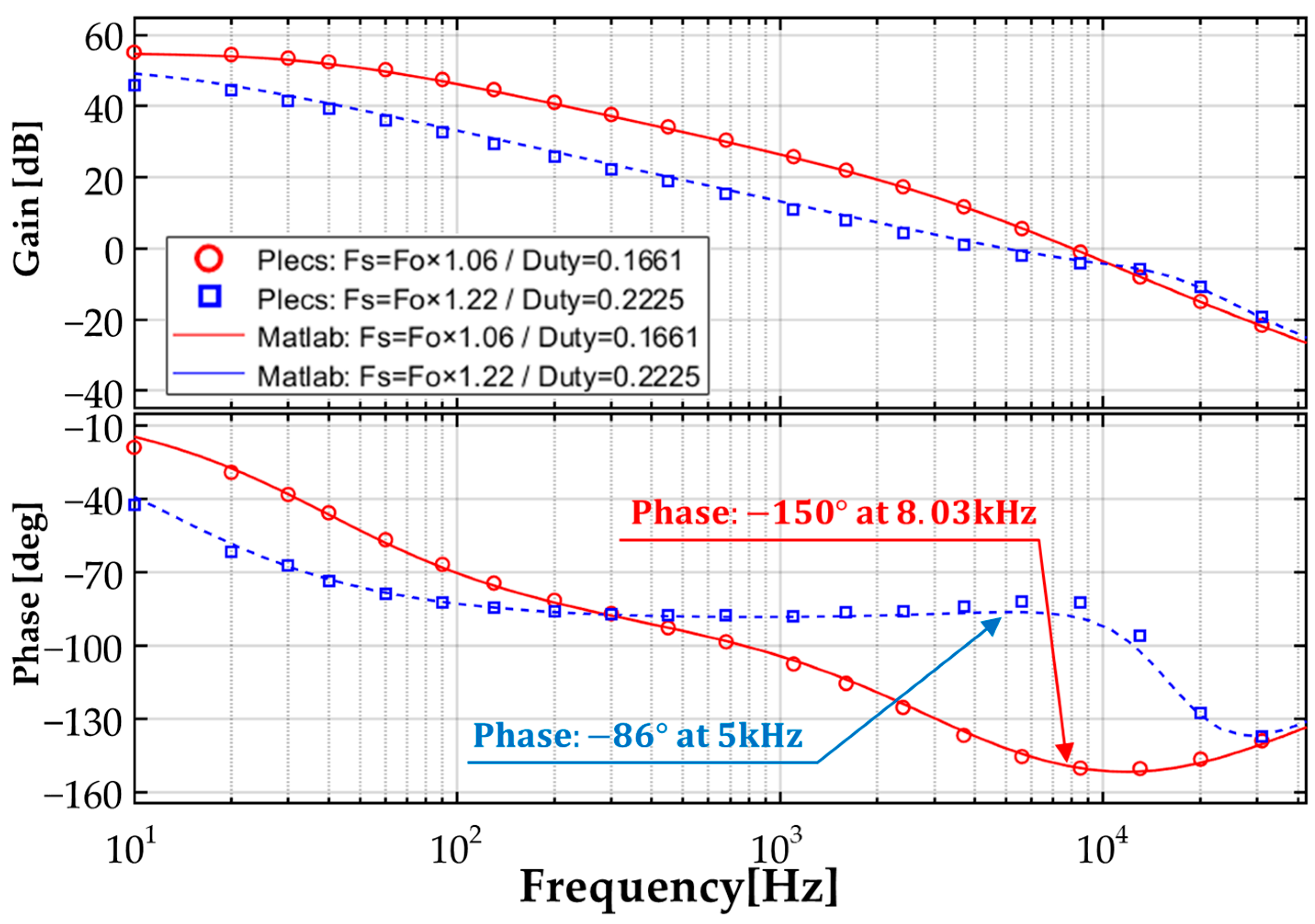
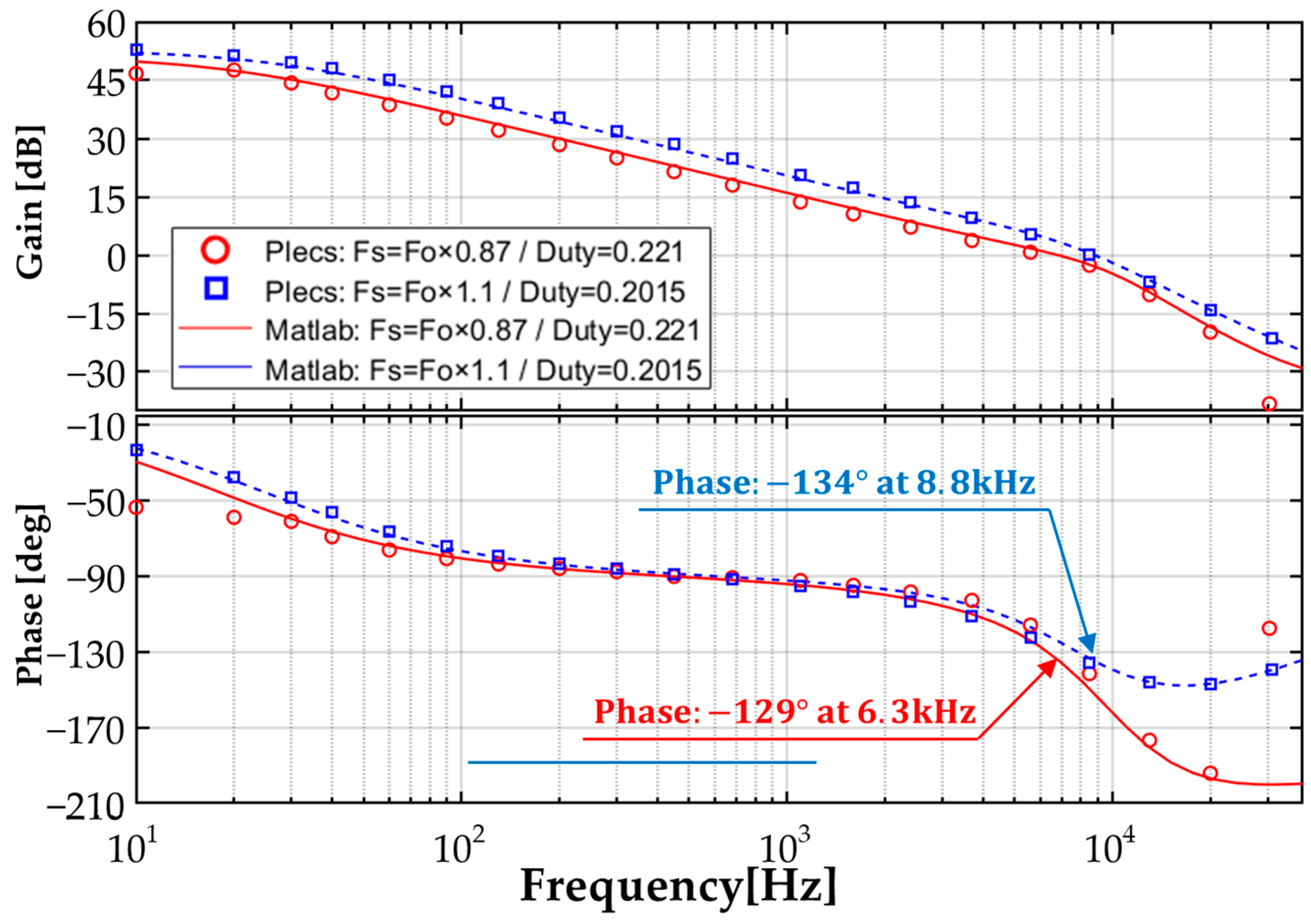
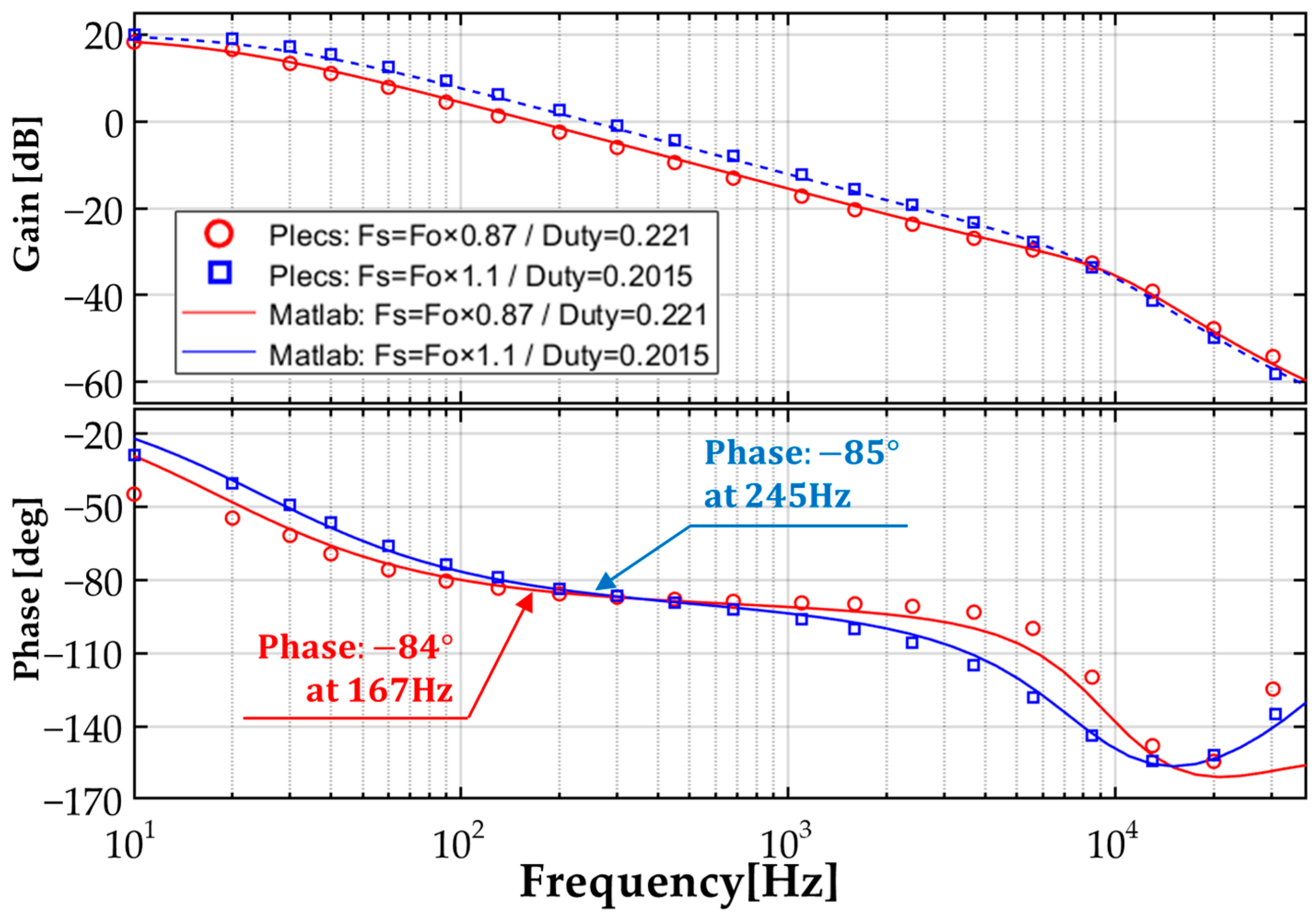
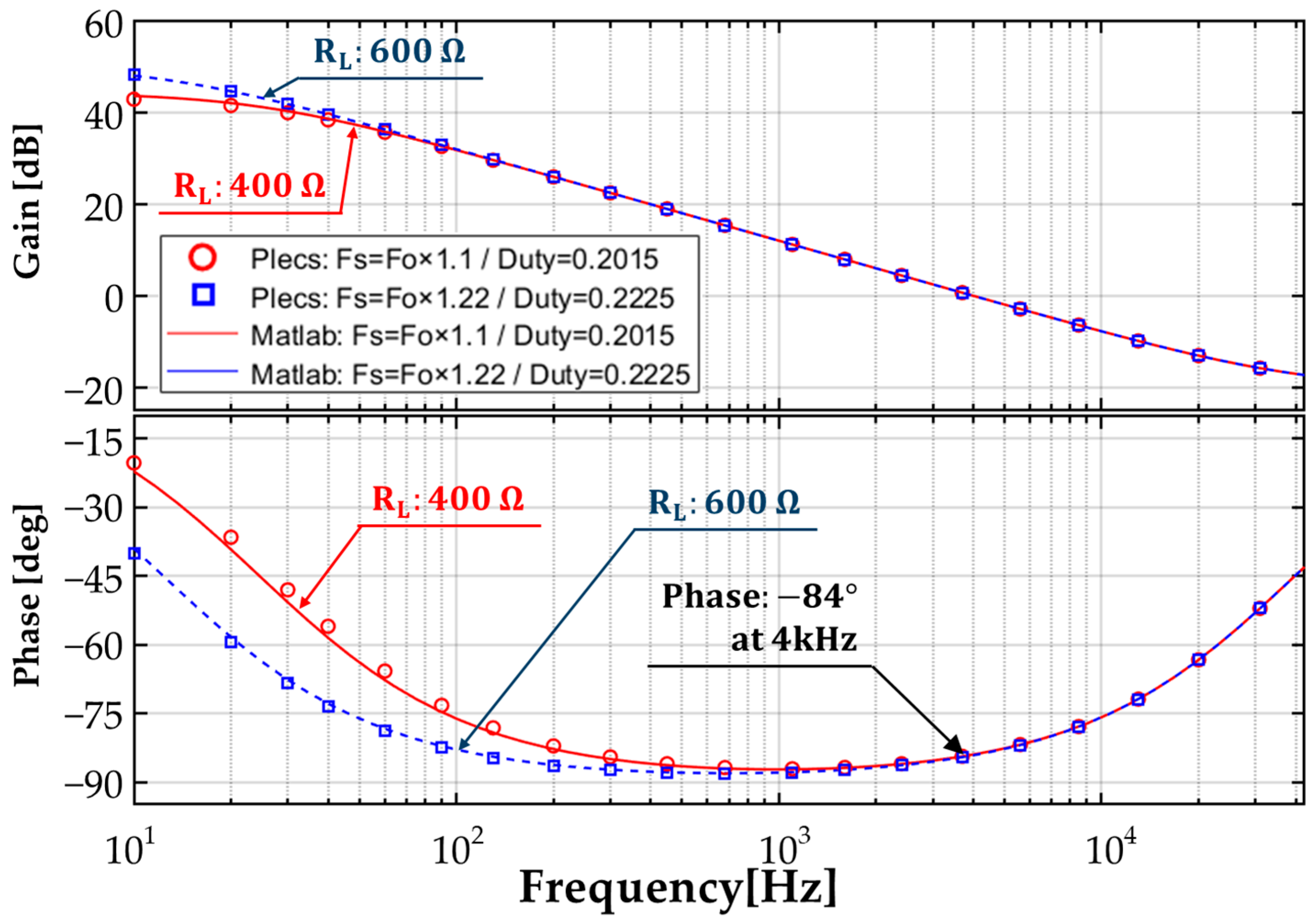
3.1. Simulation Results
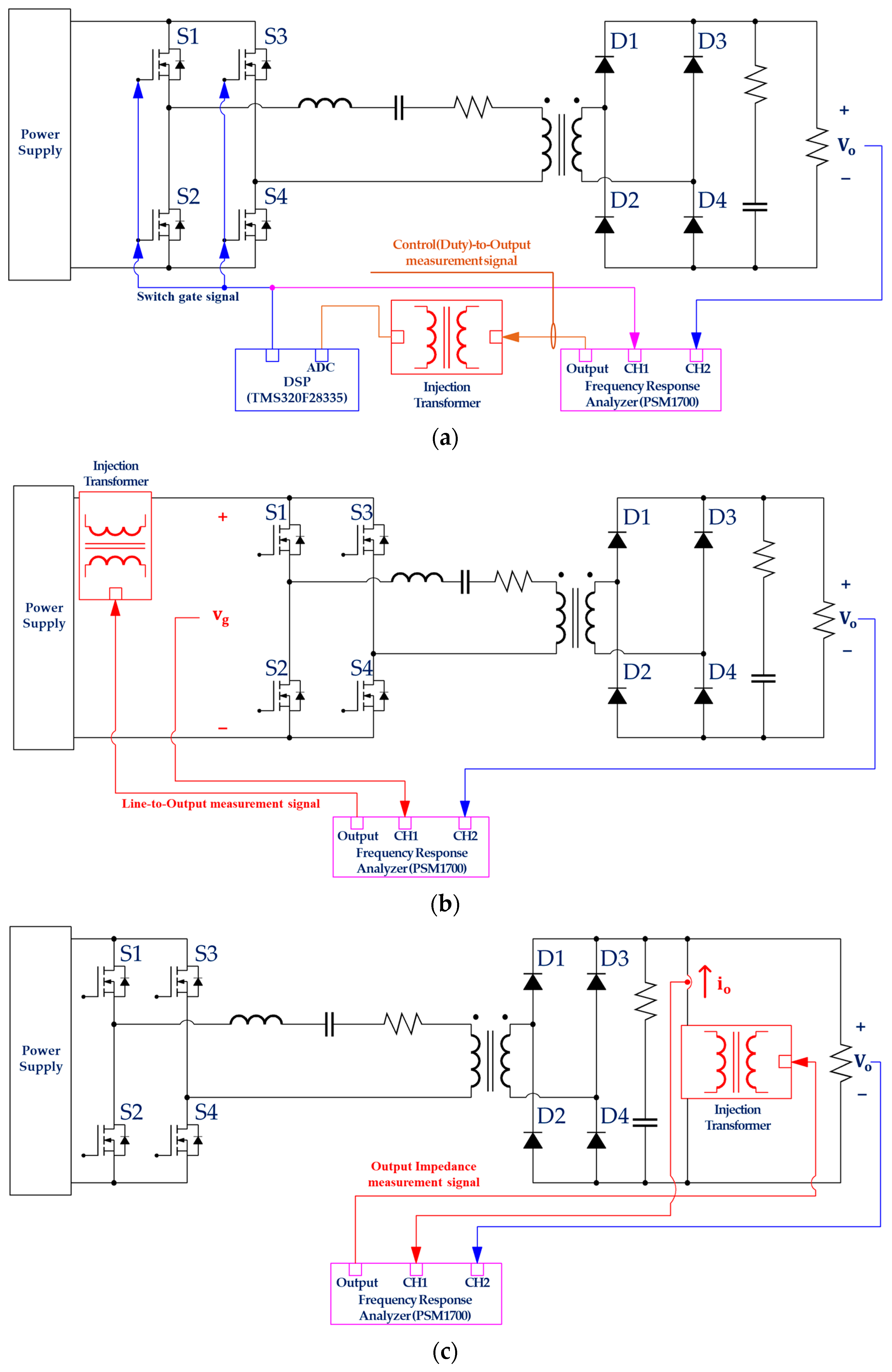
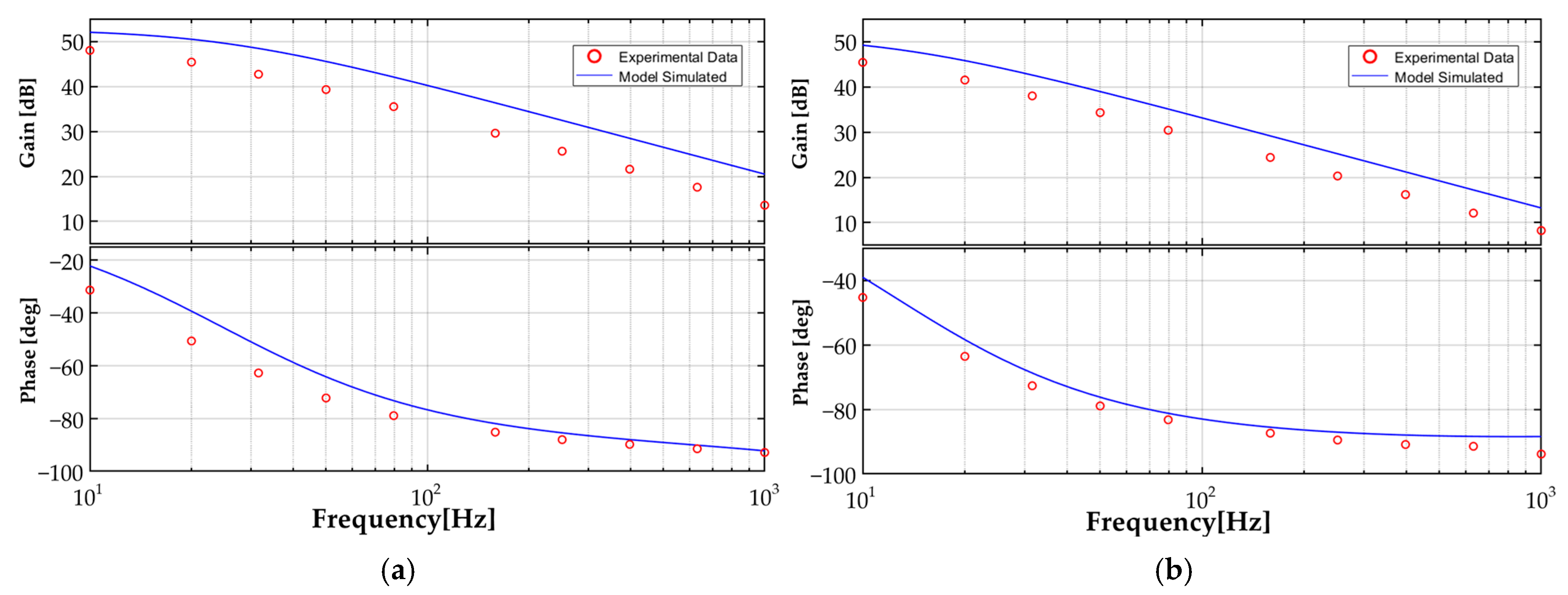
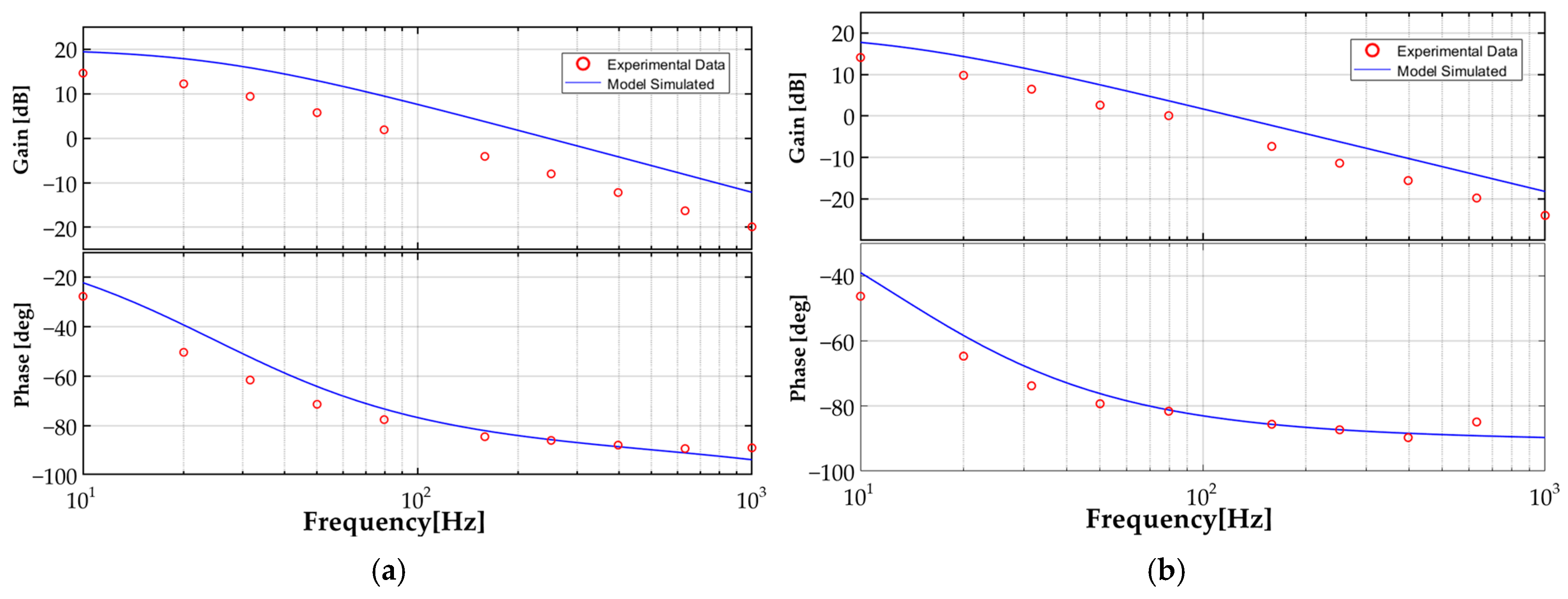
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, J.-W.; Barbosa, P. PWM-Controlled Series Resonant Converter for Universal Electric Vehicle Charger. IEEE Trans. Power Electron. 2021, 12, 13578–13588. [Google Scholar] [CrossRef]
- Dao, N.D.; Lee, D.-C.; Phan, Q.D. High-Efficiency SiC-Based Isolated Three-Port DC/DC Converters for Hybrid Charging Stations. IEEE Trans. Power Electron. 2020, 10, 10455–10465. [Google Scholar] [CrossRef]
- Kwon, Y.D.; Freijedo, F.D.; Wijekoon, T.; Liserre, M. Series Resonant Converter-Based Full-Bridge DC–DC Partial Power Converter for Solar PV. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 2, 1719–1729. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, H.; Al-Durra, A.; Qin, Z.; Blaabjerg, F. A Structure-Reconfigurable Series Resonant DC–DC Converter with Wide-Input and Configurable-Output Voltages. IEEE Trans. Ind. Electron. 2019, 2, 1752–1764. [Google Scholar] [CrossRef]
- Lee, K.-J. Steady-State Analysis of Asymmetrical Pulse-Width-Modulated Series Resonant Converter for Light Load Condition. Electronics 2025, 14, 63. [Google Scholar] [CrossRef]
- Jain, P.K.; St-Martin, A.; Edwards, G. Asymmetrical pulse-width-modulated resonant DC/DC converter topologies. IEEE Trans. Power Electron. 1996, 3, 413–422. [Google Scholar] [CrossRef]
- Ryu, S.-H.; Kim, D.-H.; Kim, M.-J.; Kim, J.-S.; Lee, B.-K. Adjustable Frequency–Duty-Cycle Hybrid Control Strategy for Full-Bridge Series Resonant Converters in Electric Vehicle Chargers. IEEE Trans. Ind. Electron. 2014, 10, 5354–5362. [Google Scholar]
- Park, H.-P.; Kim, M.; Jung, J.-H. Bidirectional Current-Fed CLLC Resonant Converter Employing Asymmetric PWM. IEEE Trans. Energy Conver. 2021, 4, 3167–3177. [Google Scholar] [CrossRef]
- Chen, G.; Chen, Z.; Chen, Y.; Feng, C.; Zhu, X. Asymmetric Phase-Shift Modulation Strategy of DAB Converters for Improved Light-Load Efficiency. IEEE Trans. Power Electron. 2022, 8, 9104–9113. [Google Scholar] [CrossRef]
- Mahdavifard, M.; Mazloum, N.; Zahin, F.; KhakparvarYazdi, A.; Abasian, A.; Khajehoddin, S.A. An Asymmetrical DAB Converter Modulation and Control Systems to Extend the ZVS Range and Improve Efficiency. IEEE Trans. Power Electron. 2022, 10, 12774–12792. [Google Scholar] [CrossRef]
- Pont, N.C.D.; Bandeira, D.G.; Lazzarin, T.B.; Barbi, I. A ZVS APWM Half-Bridge Parallel Resonant DC–DC Converter with Capacitive Output. IEEE Trans. Power Electron. 2019, 7, 5231–5241. [Google Scholar] [CrossRef]
- Awasthi, A.; Bagawade, S.; Kumar, A.; Jain, P. Time-Domain Analysis of APWM-Frequency Modulated Low-Q LLC Resonant Converter for Wide Input and Load Range Applications. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 1334–1340. [Google Scholar]
- Guo, Z.; Zhu, Y.; Sha, D. Zero-Voltage-Switching Asymmetrical PWM Full-Bridge DC–DC Converter with Reduced Circulating Current. IEEE Trans. Ind. Electron. 2021, 5, 3840–3853. [Google Scholar] [CrossRef]
- Yang, E.X.; Lee, F.C.; Jovanovic, M.M. Small-signal modeling of series and parallel resonant converters. In Proceedings of the APEC ‘92 Seventh Annual Applied Power Electronics Conference and Exposition, Boston, MA, USA, 23–27 February 1992; pp. 785–792. [Google Scholar]
- Chang, C.-H.; Chang, E.-C.; Cheng, C.-A.; Cheng, H.-L.; Lin, S.-C. Small Signal Modeling of LLC Resonant Converters Based on Extended Describing Function. In Proceedings of the 2012 International Symposium on Computer, Consumer and Control, Taichung, Taiwan, 4–6 June 2012; pp. 365–368. [Google Scholar]
- Tian, S.; Lee, F.C.; Li, Q. Equivalent Circuit Modeling of LLC Resonant Converter. IEEE Trans. Power Electron. 2020, 8, 8833–8845. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, N.; Wang, X.; Wang, F.; Liu, M. A Small-Signal Modeling Method for Bidirectional CLLC Resonant Converter. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, G.-M.; Lee, K.-J. Small-Signal Modeling of Asymmetric PWM Control Based Series Resonant Converter. Electronics 2025, 14, 3394. https://doi.org/10.3390/electronics14173394
Park G-M, Lee K-J. Small-Signal Modeling of Asymmetric PWM Control Based Series Resonant Converter. Electronics. 2025; 14(17):3394. https://doi.org/10.3390/electronics14173394
Chicago/Turabian StylePark, Gwang-Min, and Kui-Jun Lee. 2025. "Small-Signal Modeling of Asymmetric PWM Control Based Series Resonant Converter" Electronics 14, no. 17: 3394. https://doi.org/10.3390/electronics14173394
APA StylePark, G.-M., & Lee, K.-J. (2025). Small-Signal Modeling of Asymmetric PWM Control Based Series Resonant Converter. Electronics, 14(17), 3394. https://doi.org/10.3390/electronics14173394









