Enhancing Agent-Based Negotiation Strategies via Transfer Learning
Abstract
1. Introduction
- TLNAgent is among the first to apply transfer learning in reinforcement learning to negotiation scenarios, systematically identifying critical challenges in cross-task transfer within negotiation frameworks.
- To address these challenges, this study introduces a detection method to determine whether to activate the transfer module. Leveraging its adaptation model, TLNAgent preliminarily assesses the helpfulness of source policies and selects which source policies to transfer, ensuring that task-relevant knowledge is prioritized.
- A Gaussian Mixture Model-Universal Background Model (GMM-UBM) is incorporated to dynamically determine the weighting factors for source policies during knowledge transfer. Additionally, the transfer module employs a lateral connection architecture, which demonstrates efficiency and effectiveness in scenarios involving diverse opponents and domains.
- Empirical validation of the proposed strategy includes comparative evaluations against multiple baselines under corresponding experimental settings. Further, ablation studies are conducted to isolate the contributions of individual components, while game-theoretic analyses are employed to ground the approach in theory.
2. Related Work
2.1. Deep Reinforcement Learning
2.2. Transfer Learning in RL
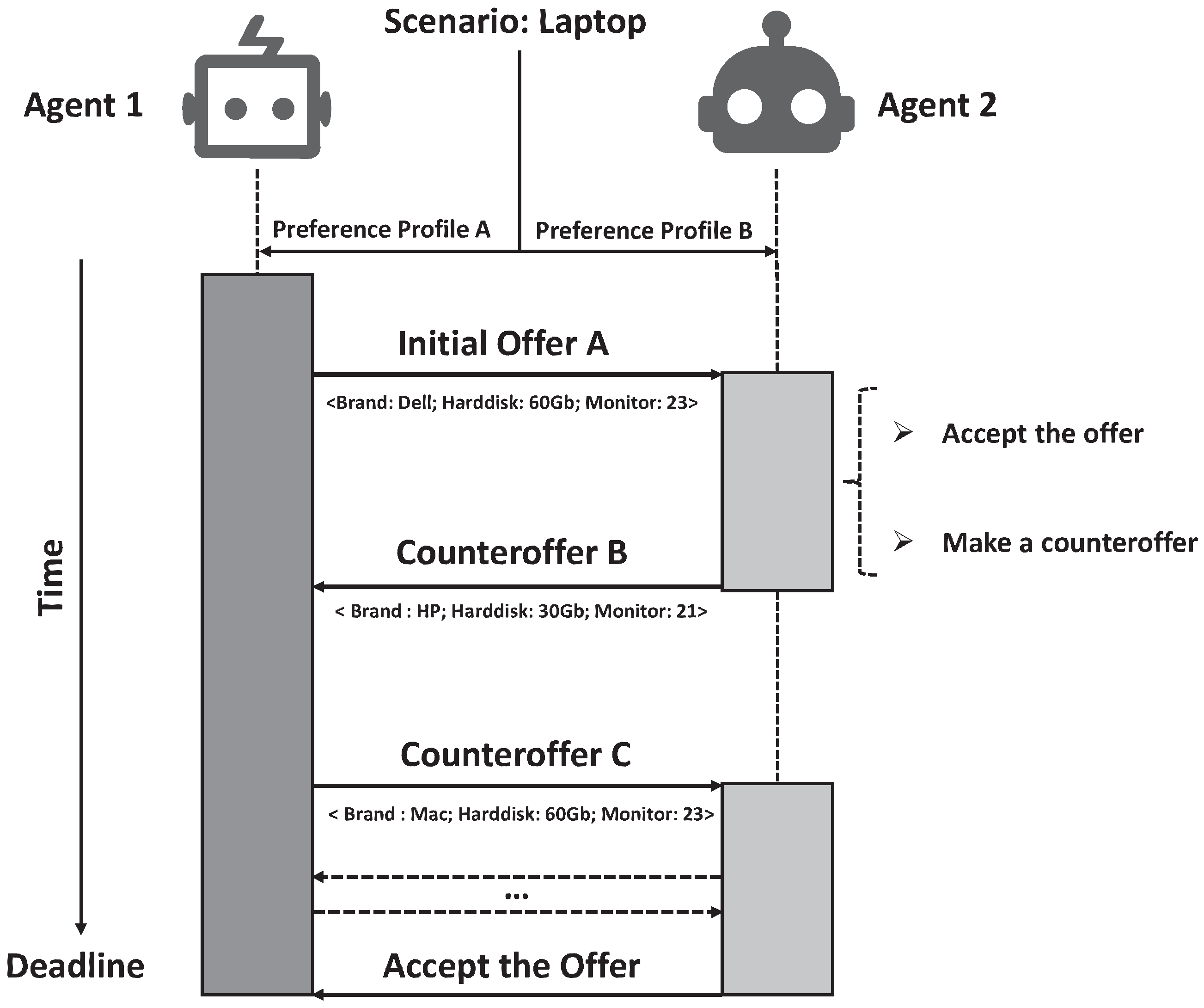
3. Negotiation Settings
3.1. Negotiation Domain
3.2. Negotiation Protocol
3.3. Negotiation Profiles
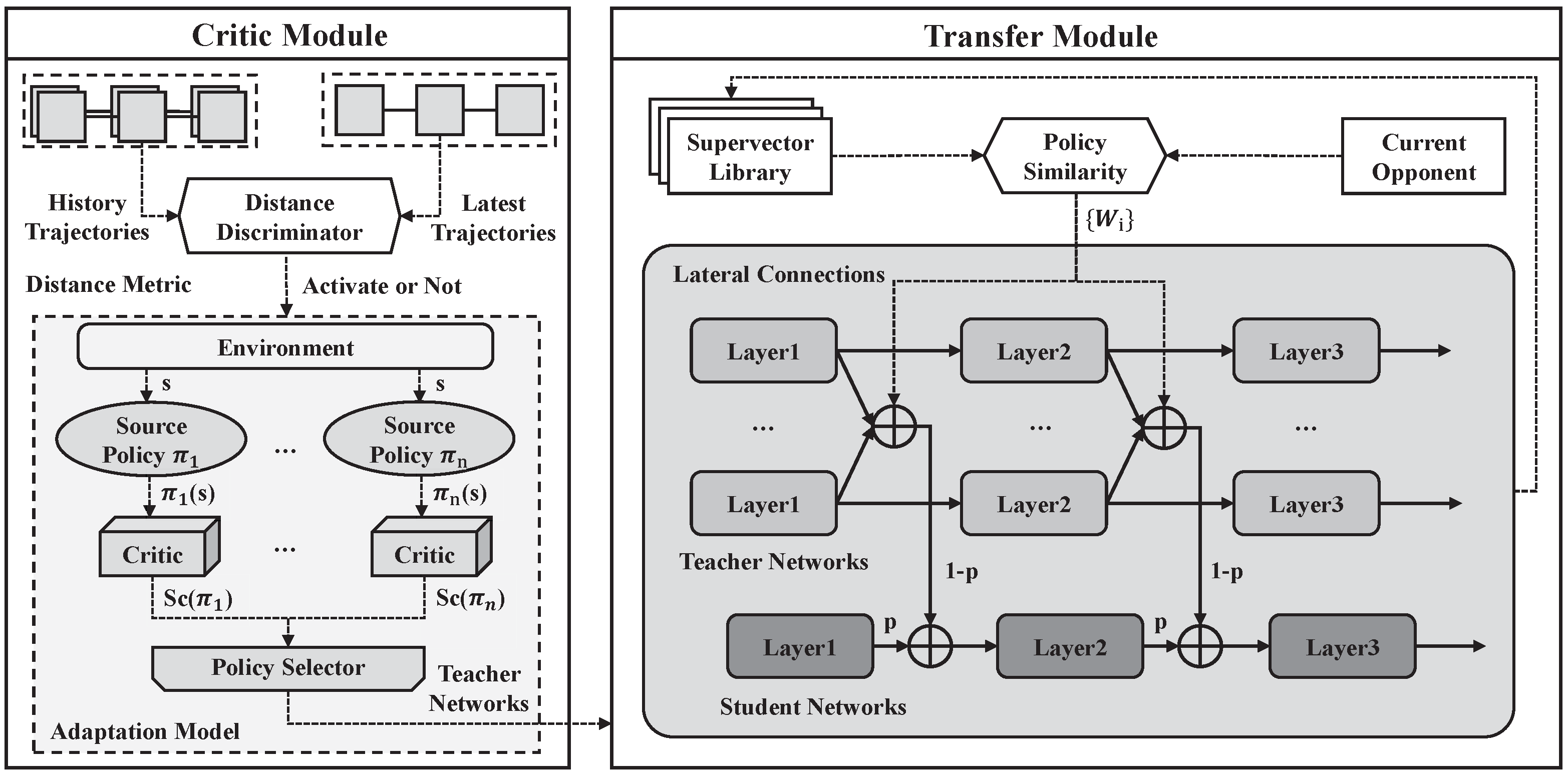
4. Transfer Learning-Based Negotiating Agent
4.1. Framework Overview
| Algorithm 1: TLNAgent |
 |
4.2. Negotiation Module
4.3. Critic Module
| Algorithm 2: Critic module |
 |
4.3.1. Distance Discriminator
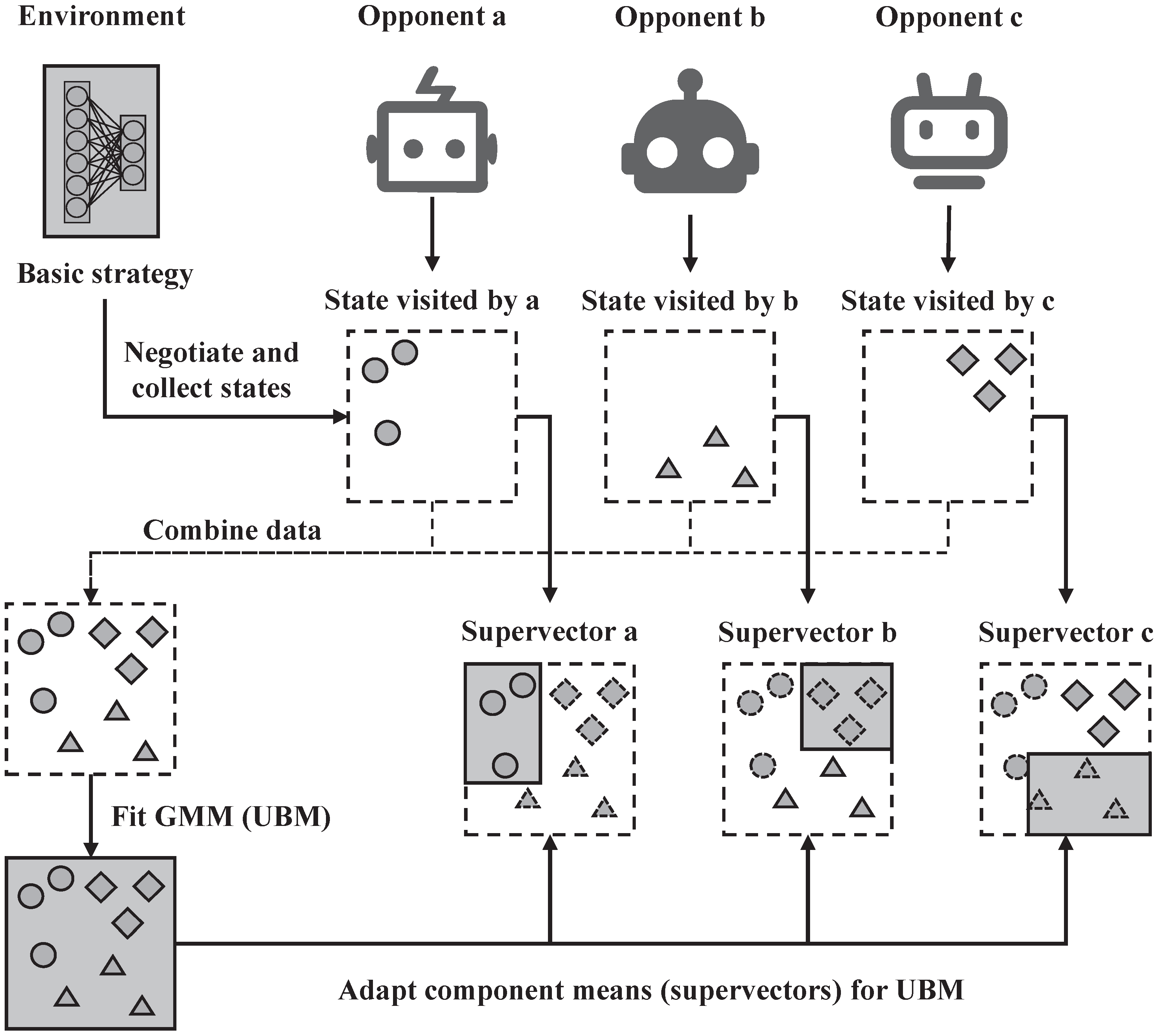
4.3.2. Adaptation Model
4.4. Transfer Module
4.4.1. Weight Assignment
| Algorithm 3: Transfer Module |
|
4.4.2. Knowledge Transfer
5. Experiments
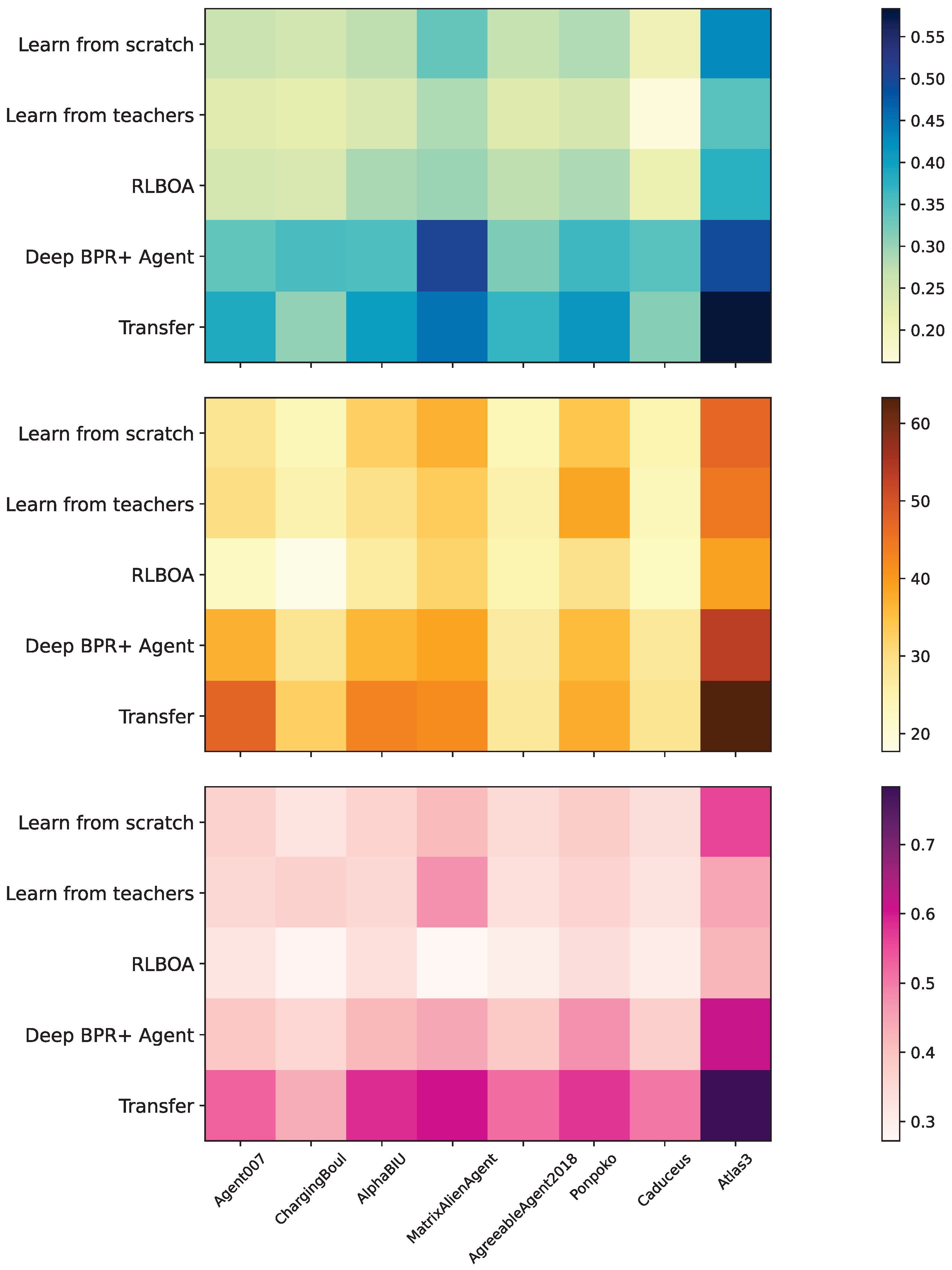
5.1. Performance of New Opponent Learning
- Initial Utility Benchmark: The average reward during the initial stages of negotiation.
- Accumulated Utility Benchmark: The accumulated utility obtained by the agent in the first 100 sessions.
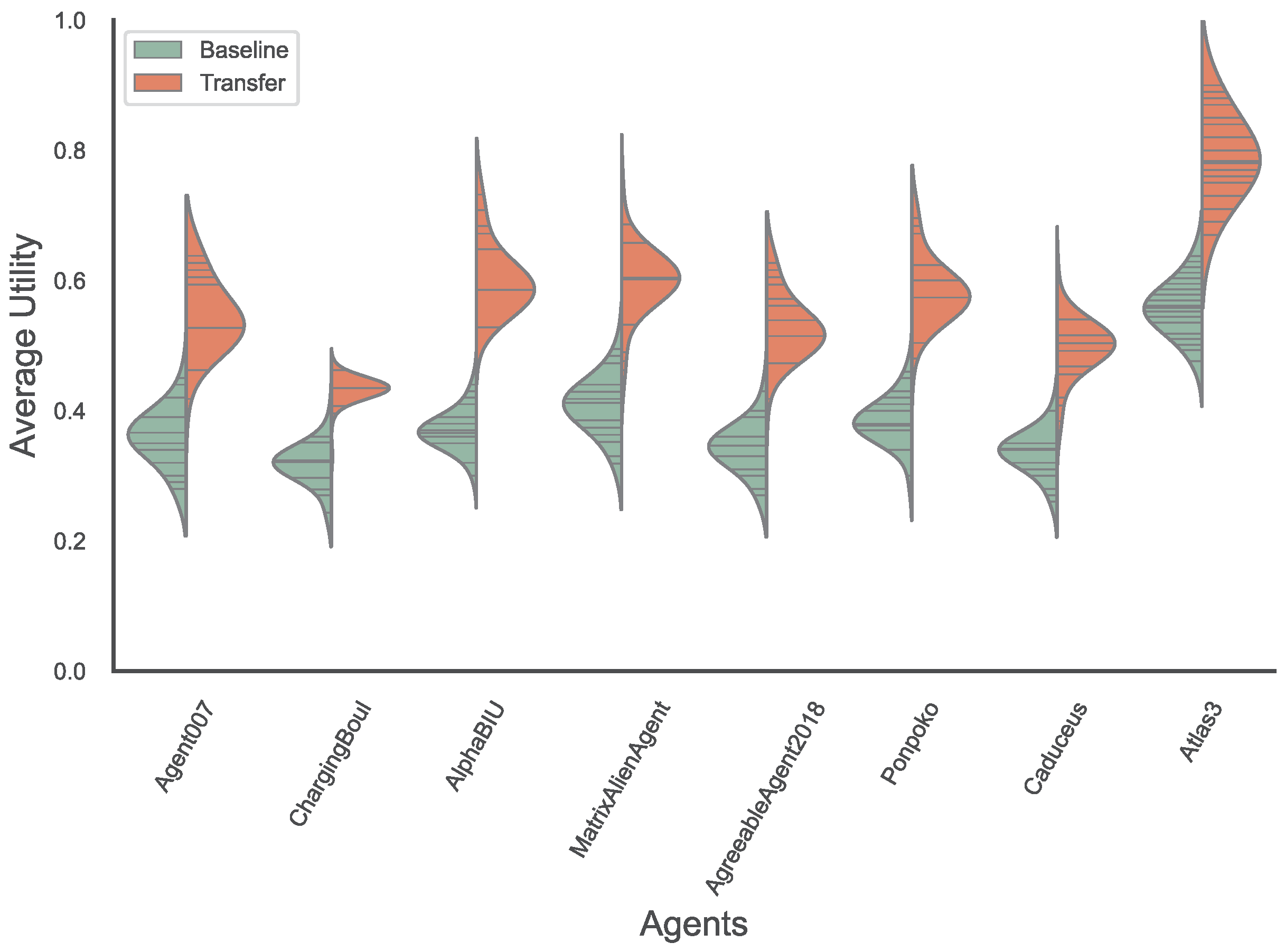
- Average Utility Benchmark: The mean utility obtained by the agent negotiating with an opponent over all fifty domains.
5.1.1. Initial Utility Performance
5.1.2. Accumulated Utility Performance
5.1.3. Average Utility Performance
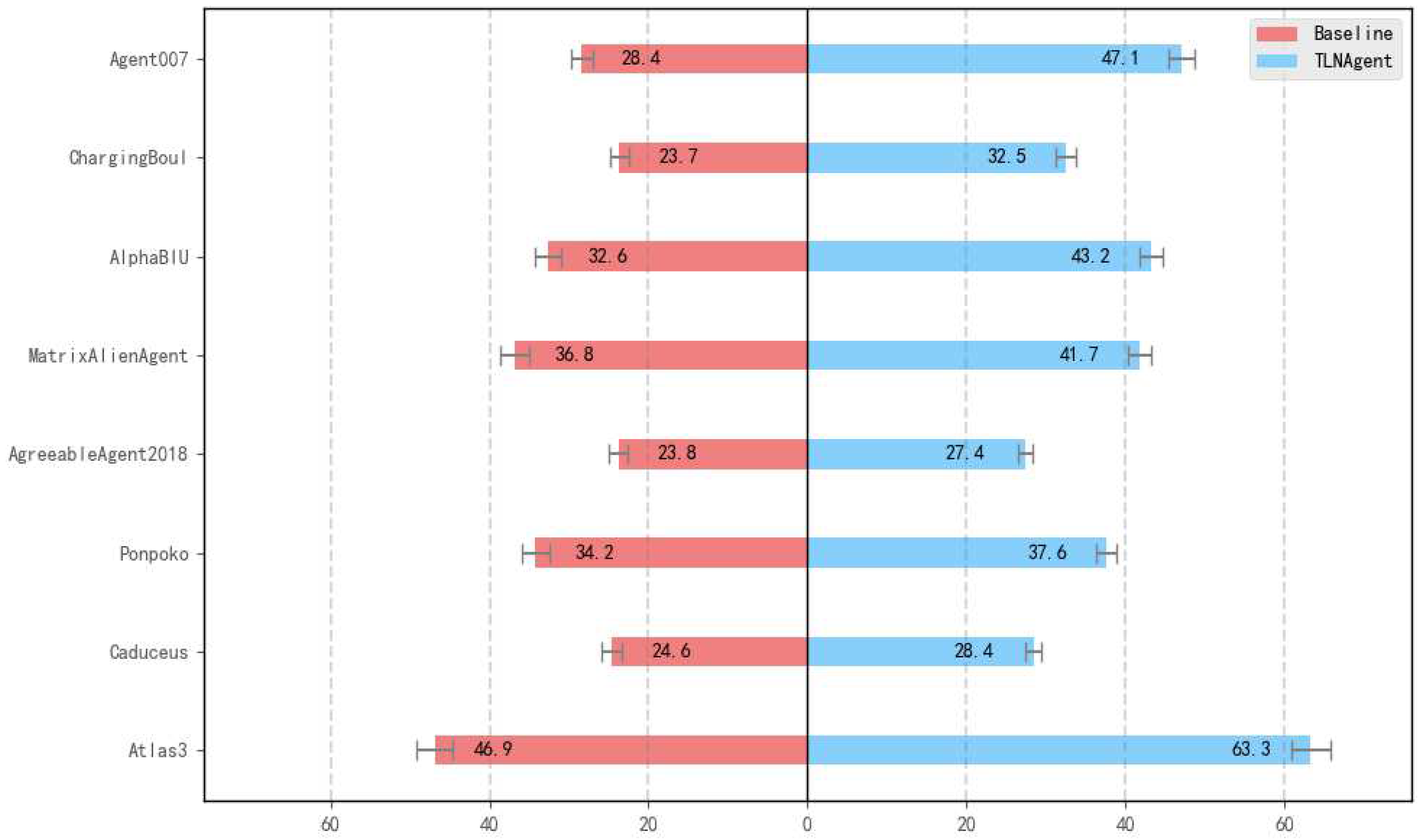
5.2. Performance Against ANAC-Winning Agents
- Average Utility Benchmark: The mean utility obtained by agent when negotiating with every other agent on all domains D, where A and D denote all of the agents and all of the domains used in the tournament, respectively.
- Agreement Rate Benchmark: The rate of agreement achieved between the agent and all others throughout the tournament.
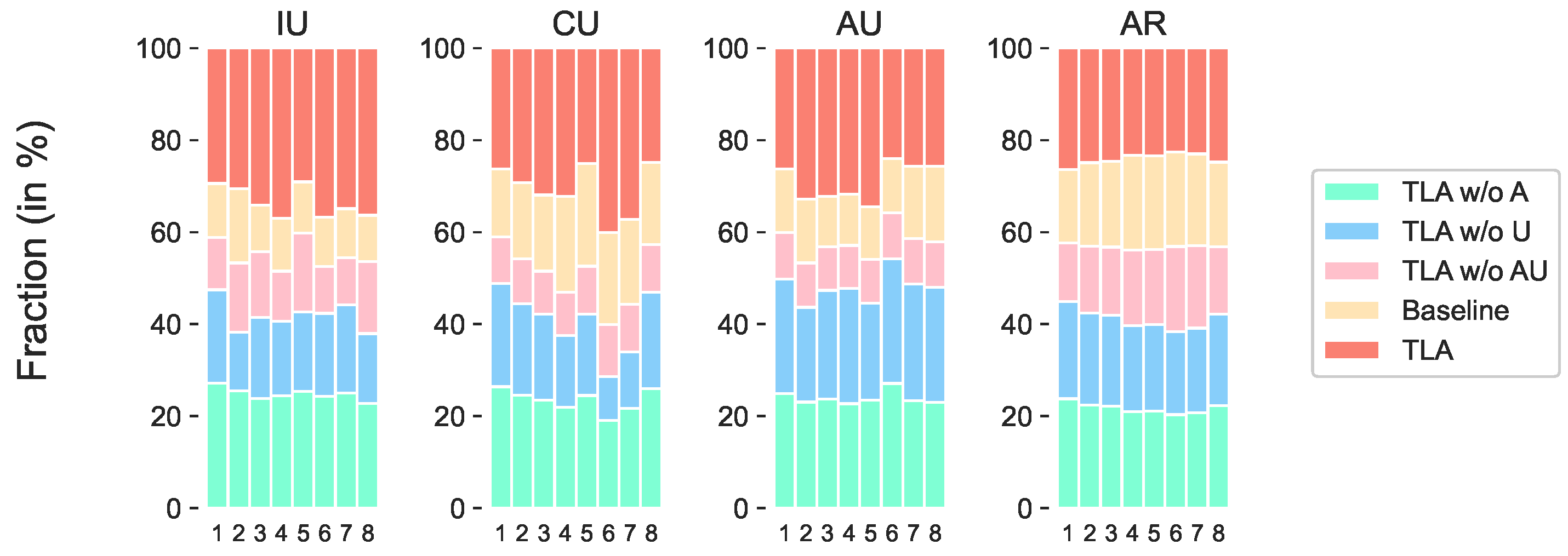
5.3. Ablation Studies
- : Updates the negotiation strategy without the adaptation model.
- : Updates the negotiation strategy without the UBMs.
- : Updates the negotiation strategy without the adaptation model or the UBMs.
5.4. Sensitivity Analysis
5.4.1. Performance with Fixed Thresholds
5.4.2. Learned Dynamic Threshold
5.5. Computational Overhead
5.6. Empirical Game-Theoretic Analysis
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Varotto, L.; Fabris, M.; Michieletto, G.; Cenedese, A. Visual sensor network stimulation model identification via Gaussian mixture model and deep embedded features. Eng. Appl. Artif. Intell. 2022, 114, 105096. [Google Scholar] [CrossRef]
- Luzolo, P.H.; Elrawashdeh, Z.; Tchappi, I.; Galland, S.; Outay, F. Combining Multi-Agent Systems and Artificial Intelligence of Things: Technical challenges and gains. Internet Things 2024, 28, 101364. [Google Scholar] [CrossRef]
- Chen, S.; Semenov, I.; Zhang, F.; Yang, Y.; Geng, J.; Feng, X.; Meng, Q.; Lei, K. An effective framework for predicting drug-drug interactions based on molecular substructures and knowledge graph neural network. Comput. Biol. Med. 2024, 169, 107900. [Google Scholar] [CrossRef]
- Li, F.; Wang, D.; Li, Y.; Shen, Y.; Pedrycz, W.; Wang, P.; Wang, Y.; Zhang, W. Stacked fuzzy envelope consistency imbalanced ensemble classification method. Expert Syst. Appl. 2025, 265, 126033. [Google Scholar] [CrossRef]
- He, H.; Chen, D.; Balakrishnan, A.; Liang, P. Decoupling Strategy and Generation in Negotiation Dialogues. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; Riloff, E., Chiang, D., Hockenmaier, J., Tsujii, J., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; pp. 2333–2343. [Google Scholar] [CrossRef]
- Yang, R.; Chen, J.; Narasimhan, K. Improving Dialog Systems for Negotiation with Personality Modeling. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing, ACL/IJCNLP 2021, Virtual Event, 1–6 August 2021; Volume 1. [Google Scholar]
- Luo, X.; Li, Y.; Huang, Q.; Zhan, J. A survey of automated negotiation: Human factor, learning, and application. Comput. Sci. Rev. 2024, 54, 100683. [Google Scholar] [CrossRef]
- Priya, P.; Chigrupaatii, R.; Firdaus, M.; Ekbal, A. GENTEEL-NEGOTIATOR: LLM-Enhanced Mixture-of-Expert-Based Reinforcement Learning Approach for Polite Negotiation Dialogue. In Proceedings of the AAAI-25, Sponsored by the Association for the Advancement of Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Walsh, T., Shah, J., Kolter, Z., Eds.; AAAI Press: Washington, DC, USA, 2025; pp. 25010–25018. [Google Scholar] [CrossRef]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef] [PubMed]
- Ye, D.; Chen, G.; Zhang, W.; Chen, S.; Yuan, B.; Liu, B.; Chen, J.; Liu, Z.; Qiu, F.; Yu, H.; et al. Towards Playing Full MOBA Games with Deep Reinforcement Learning. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Yang, T.; Hao, J.; Meng, Z.; Zhang, C.; Zheng, Y.; Zheng, Z. Towards Efficient Detection and Optimal Response against Sophisticated Opponents. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, ijcai.org, Macao, 10–16 August 2019; pp. 623–629. [Google Scholar]
- Bagga, P.; Paoletti, N.; Alrayes, B.; Stathis, K. A Deep Reinforcement Learning Approach to Concurrent Bilateral Negotiation. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI-20, Yokohama, Japan, 11–17 July 2020; pp. 297–303. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, 2–4 May 2016; Conference Track Proceedings. 2016. [Google Scholar]
- Chang, H.C.H. Multi-issue negotiation with deep reinforcement learning. Knowl.-Based Syst. 2021, 211, 106544. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Q.; You, H.; Yang, T.; Hao, J. Transfer Learning based Agent for Automated Negotiation. In Proceedings of the 2023 International Conference on Autonomous Agents and Multiagent Systems, AAMAS 2023, London, UK, 29 May–2 June 2023; ACM: New York, NY, USA, 2023; pp. 2895–2898. [Google Scholar]
- Chen, S.; Zhao, J.; Zhao, K.; Weiss, G.; Zhang, F.; Su, R.; Dong, Y.; Li, D.; Lei, K. ANOTO: Improving Automated Negotiation via Offline-to-Online Reinforcement Learning. In Proceedings of the 23rd International Conference on Autonomous Agents and Multiagent Systems, AAMAS 2024, Auckland, New Zealand, 6–10 May 2024; Dastani, M., Sichman, J.S., Alechina, N., Dignum, V., Eds.; International Foundation for Autonomous Agents and Multiagent Systems/ACM: New York, NY, USA, 2024; pp. 2195–2197. [Google Scholar]
- Bakker, J.; Hammond, A.; Bloembergen, D.; Baarslag, T. RLBOA: A modular reinforcement learning framework for autonomous negotiating agents. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Montreal, QC, Canada, 13–17 May 2019; pp. 260–268. [Google Scholar]
- Chen, L.; Dong, H.; Han, Q.; Cui, G. Bilateral Multi-issue Parallel Negotiation Model Based on Reinforcement Learning. In Proceedings of the Intelligent Data Engineering and Automated Learning—IDEAL 2013—14th International Conference, IDEAL 2013, Hefei, China, 20–23 October 2013; Proceedings. Yin, H., Tang, K., Gao, Y., Klawonn, F., Lee, M., Weise, T., Li, B., Yao, X., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2013; Volume 8206, pp. 40–48. [Google Scholar]
- Tesauro, G.; Kephart, J.O. Pricing in Agent Economies Using Multi-Agent Q-Learning. Auton. Agents Multi-Agent Syst. 2002, 5, 289–304. [Google Scholar] [CrossRef]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M.A. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.A.; Fidjeland, A.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Lin, L.J. Self-Improving Reactive Agents Based On Reinforcement Learning, Planning and Teaching. Mach. Learn. 1992, 8, 293–321. [Google Scholar] [CrossRef]
- Bagga, P.; Paoletti, N.; Stathis, K. Learnable Strategies for Bilateral Agent Negotiation over Multiple Issues. arXiv 2020, arXiv:2009.08302. [Google Scholar]
- Chang, H.C.H. Multi-Issue Bargaining With Deep Reinforcement Learning. arXiv 2020, arXiv:2002.07788. [Google Scholar] [CrossRef]
- Razeghi, Y.; Yavuz, C.O.B.; Aydogan, R. Deep reinforcement learning for acceptance strategy in bilateral negotiations. Turk. J. Electr. Eng. Comput. Sci. 2020, 28, 1824–1840. [Google Scholar] [CrossRef]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; PMLR: Cambridge, MA, USA, 2015; pp. 1889–1897. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Higa, R.; Fujita, K.; Takahashi, T.; Shimizu, T.; Nakadai, S. Reward-based negotiating agent strategies. Proc. AAAI Conf. Artif. Intell. 2023, 37, 11569–11577. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft Actor-Critic Algorithms and Applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning; PMLR: Cambridge, MA, USA, 2018; pp. 1861–1870. [Google Scholar]
- Sengupta, A.; Mohammad, Y.; Nakadai, S. An Autonomous Negotiating Agent Framework with Reinforcement Learning Based Strategies and Adaptive Strategy Switching Mechanism. In Proceedings of the 20th International Conference on Autonomous Agents and MultiAgent Systems, AAMAS ’21, Virtual Event, 3–7 May 2021; pp. 1163–1172. [Google Scholar]
- Wu, L.; Chen, S.; Gao, X.; Zheng, Y.; Hao, J. Detecting and Learning Against Unknown Opponents for Automated Negotiations. In Proceedings of the PRICAI 2021: Trends in Artificial Intelligence, Hanoi, Vietnam, 8–12 November 2021; Pham, D.N., Theeramunkong, T., Governatori, G., Liu, F., Eds.; Springer: Cham, Switzerland, 2021; pp. 17–31. [Google Scholar]
- Arslan, F.; Aydogan, R. Actor-critic reinforcement learning for bidding in bilateral negotiation. Turk. J. Electr. Eng. Comput. Sci. 2022, 30, 1695–1714. [Google Scholar] [CrossRef]
- Taylor, M.E.; Stone, P. Transfer Learning for Reinforcement Learning Domains: A Survey. J. Mach. Learn. Res. 2009, 10, 1633–1685. [Google Scholar]
- Zhu, Z.; Lin, K.; Jain, A.K.; Zhou, J. Transfer Learning in Deep Reinforcement Learning: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13344–13362. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Wang, W.; Tang, H.; Hao, J.; Meng, Z.; Mao, H.; Li, D.; Liu, W.; Chen, Y.; Hu, Y.; et al. An Efficient Transfer Learning Framework for Multiagent Reinforcement Learning. Adv. Neural Inf. Process. Syst. 2021, 34, 17037–17048. [Google Scholar]
- Rusu, A.A.; Colmenarejo, S.G.; Gülçehre, Ç.; Desjardins, G.; Kirkpatrick, J.; Pascanu, R.; Mnih, V.; Kavukcuoglu, K.; Hadsell, R. Policy Distillation. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, Puerto Rico, 2–4 May 2016; Conference Track Proceedings. Bengio, Y., LeCun, Y., Eds.; 2016. [Google Scholar]
- Parisotto, E.; Ba, L.J.; Salakhutdinov, R. Actor-Mimic: Deep Multitask and Transfer Reinforcement Learning. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Schmitt, S.; Hudson, J.J.; Zídek, A.; Osindero, S.; Doersch, C.; Czarnecki, W.M.; Leibo, J.Z.; Küttler, H.; Zisserman, A.; Simonyan, K.; et al. Kickstarting Deep Reinforcement Learning. arXiv 2018, arXiv:1803.03835. [Google Scholar] [CrossRef]
- Fernández, F.; Veloso, M.M. Probabilistic policy reuse in a reinforcement learning agent. In Proceedings of the 5th International Joint Conference on Autonomous Agents and Multiagent Systems, Hakodate, Japan, 8–12 May 2006. [Google Scholar]
- Li, S.; Zhang, C. An Optimal Online Method of Selecting Source Policies for Reinforcement Learning. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-18), the 30th Innovative Applications of Artificial Intelligence (IAAI-18), and the 8th AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-18), New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Liu, I.; Peng, J.; Schwing, A.G. Knowledge Flow: Improve Upon Your Teachers. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Yang, T.; Hao, J.; Meng, Z.; Zhang, Z.; Hu, Y.; Chen, Y.; Fan, C.; Wang, W.; Liu, W.; Wang, Z.; et al. Efficient Deep Reinforcement Learning via Adaptive Policy Transfer. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 11–17 July 2020. [Google Scholar]
- Tao, Y.; Genc, S.; Chung, J.; Sun, T.; Mallya, S. REPAINT: Knowledge Transfer in Deep Reinforcement Learning. In Proceedings of the 38th International Conference on Machine Learning, Virtual Event, 18–24 July 2021. [Google Scholar]
- You, H.; Yang, T.; Zheng, Y.; Hao, J.; Taylor, M.E. Cross-domain adaptive transfer reinforcement learning based on state-action correspondence. In Proceedings of the Uncertainty in Artificial Intelligence, Proceedings of the Thirty-Eighth Conference on Uncertainty in Artificial Intelligence, Eindhoven, The Netherlands, 1–5 August 2022. [Google Scholar]
- Aydoğan, R.; Festen, D.; Hindriks, K.V.; Jonker, C.M. Alternating Offers Protocols for Multilateral Negotiation. In Modern Approaches to Agent-based Complex Automated Negotiation; Fujita, K., Bai, Q., Ito, T., Zhang, M., Hadfi, R., Ren, F., Aydoğan, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 153–167. [Google Scholar]
- Ramdas, A.; Trillos, N.G.; Cuturi, M. On Wasserstein Two-Sample Testing and Related Families of Nonparametric Tests. Entropy 2017, 19, 47. [Google Scholar] [CrossRef]
- Geary, D.N.; Mclachlan, G.J.; Basford, K.E. Mixture Models: Inference and Applications to Clustering. J. R. Stat. Soc. Ser. A (Stat. Soc.) 1989, 152, 126. [Google Scholar] [CrossRef]
- Kinnunen, T.; Li, H. An overview of text-independent speaker recognition: From features to supervectors. Speech Commun. 2010, 52, 12–40. [Google Scholar] [CrossRef]
- Reynolds, D.A.; Quatieri, T.F.; Dunn, R.B. Speaker Verification Using Adapted Gaussian Mixture Models. Digit. Signal Process. 2000, 10, 19–41. [Google Scholar] [CrossRef]
- Campbell, W.; Sturim, D.; Reynolds, D. Support vector machines using GMM supervectors for speaker verification. IEEE Signal Process. Lett. 2006, 13, 308–311. [Google Scholar] [CrossRef]
- Wan, M.; Gangwani, T.; Peng, J. Mutual Information Based Knowledge Transfer Under State-Action Dimension Mismatch. In Proceedings of the Thirty-Sixth Conference on Uncertainty in Artificial Intelligence, Virtual Online, 3–6 August 2020. [Google Scholar]
- Jonker, C.; Aydogan, R.; Baarslag, T.; Fujita, K.; Ito, T.; Hindriks, K. Automated negotiating agents competition (ANAC). In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Jordan, P.R.; Kiekintveld, C.; Wellman, M.P. Empirical game-theoretic analysis of the TAC supply chain game. In Proceedings of the Sixth International Joint Conference on Automomous Agents and Multi-Agent Systems, Honolulu, HI, USA, 14–18 May 2007; pp. 1188–1195. [Google Scholar]
- Williams, C.; Robu, V.; Gerding, E.; Jennings, N. Using Gaussian Processes to Optimise Concession in Complex Negotiations against Unknown Opponents. In Proceedings of the 22nd Internatioanl Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 432–438. [Google Scholar]

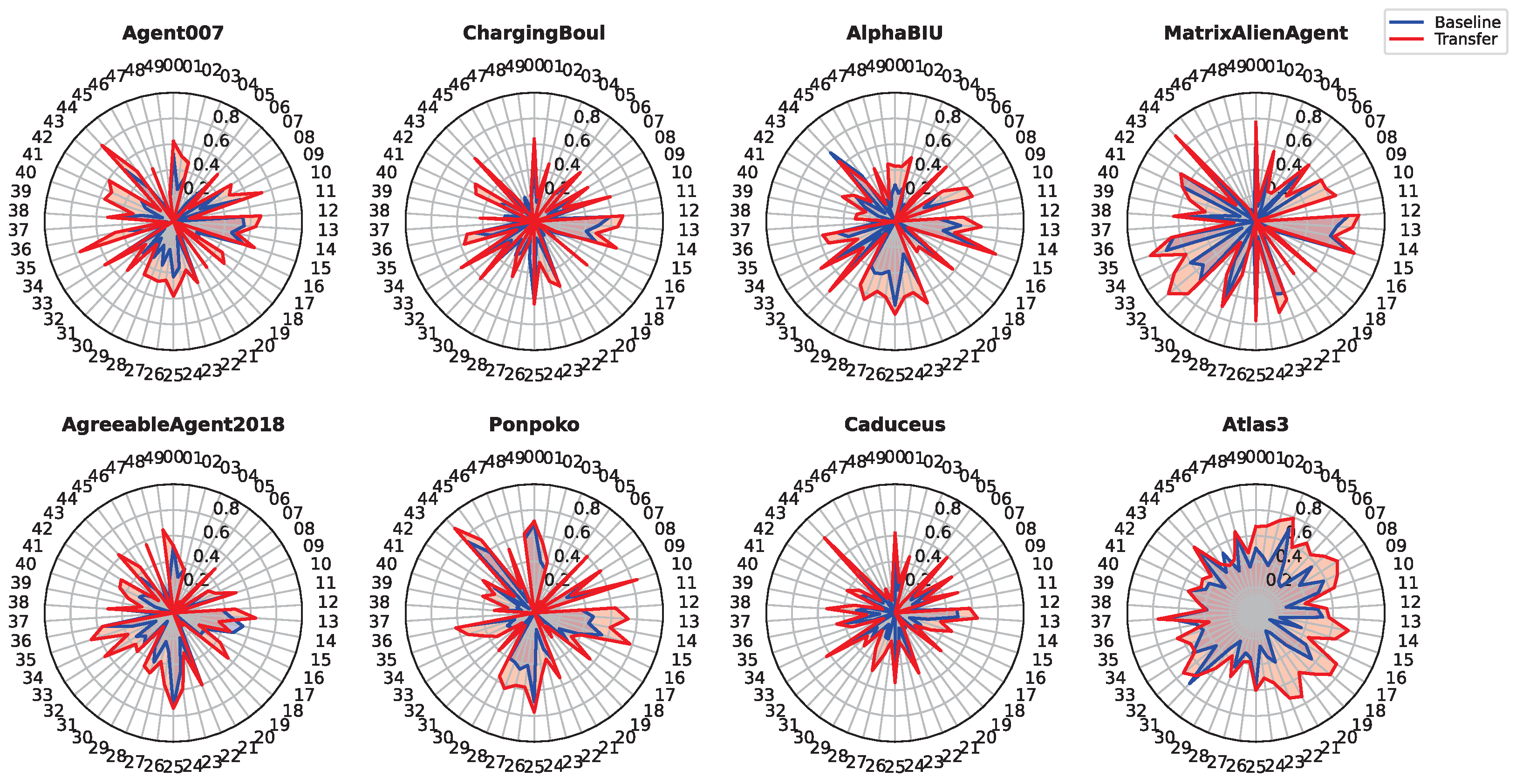



| Agent | Avg. Utility | 95% Confidence Interval | Avg. Agreement Rate | 95% Confidence Interval | ||
|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | Lower Bound | Upper Bound | |||
| AgreeableAgent2018 | 0.467 | 0.444 | 0.490 | 0.79 | 0.78 | 0.80 |
| Agent36 | 0.331 | 0.314 | 0.347 | 0.51 | 0.49 | 0.53 |
| PonPoko | 0.335 | 0.318 | 0.351 | 0.55 | 0.53 | 0.57 |
| CaduceusDC16 | 0.315 | 0.299 | 0.331 | 0.77 | 0.75 | 0.79 |
| Caduceus | 0.383 | 0.364 | 0.402 | 0.44 | 0.43 | 0.45 |
| YXAgent | 0.321 | 0.305 | 0.337 | 0.53 | 0.51 | 0.55 |
| Atlas3 | 0.571 | 0.542 | 0.600 | 0.82 | 0.81 | 0.83 |
| ParsAgent | 0.375 | 0.356 | 0.394 | 0.47 | 0.45 | 0.49 |
| AlphaBIU | 0.550 | 0.523 | 0.578 | 0.64 | 0.62 | 0.66 |
| MatrixAlienAgent | 0.452 | 0.426 | 0.475 | 0.59 | 0.57 | 0.61 |
| Agent007 | 0.629 | 0.598 | 0.660 | 0.57 | 0.55 | 0.59 |
| ChargingBoul | 0.566 | 0.538 | 0.594 | 0.57 | 0.56 | 0.58 |
| MiCRO | 0.588 | 0.559 | 0.617 | 0.42 | 0.39 | 0.45 |
| TLAgent | 0.648 | 0.616 | 0.680 | 0.88 | 0.86 | 0.90 |
| Threshold s | Transfer Activation Rate (%) | Average Utility | Agreement Rate (%) |
|---|---|---|---|
| 0.2 | 78 ± 0.02 | 0.592 ± 0.02 | 82 ± 0.02 |
| 0.3 (Original) | 45 ± 0.02 | 0.648 ± 0.02 | 88 ± 0.02 |
| 0.4 | 22 ± 0.02 | 0.561 ± 0.02 | 75 ± 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Weiss, G. Enhancing Agent-Based Negotiation Strategies via Transfer Learning. Electronics 2025, 14, 3391. https://doi.org/10.3390/electronics14173391
Chen S, Weiss G. Enhancing Agent-Based Negotiation Strategies via Transfer Learning. Electronics. 2025; 14(17):3391. https://doi.org/10.3390/electronics14173391
Chicago/Turabian StyleChen, Siqi, and Gerhard Weiss. 2025. "Enhancing Agent-Based Negotiation Strategies via Transfer Learning" Electronics 14, no. 17: 3391. https://doi.org/10.3390/electronics14173391
APA StyleChen, S., & Weiss, G. (2025). Enhancing Agent-Based Negotiation Strategies via Transfer Learning. Electronics, 14(17), 3391. https://doi.org/10.3390/electronics14173391






