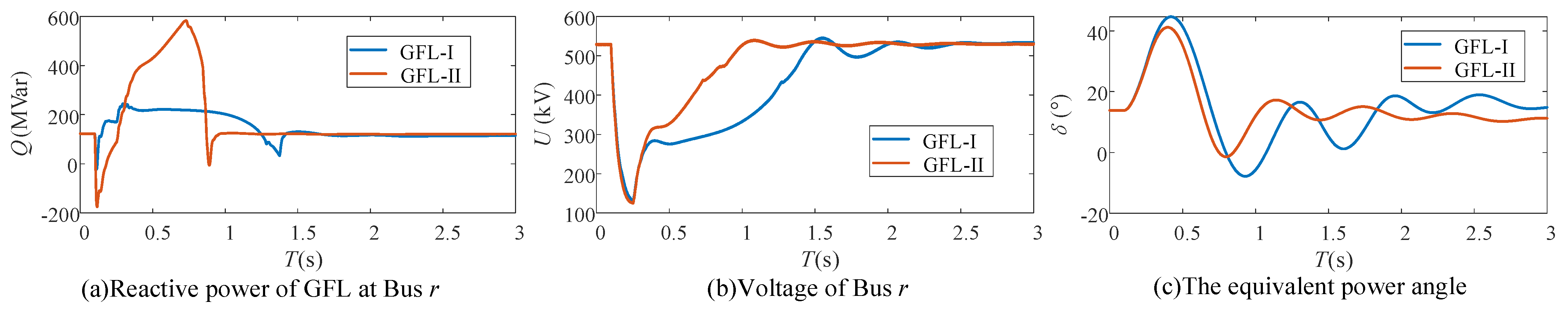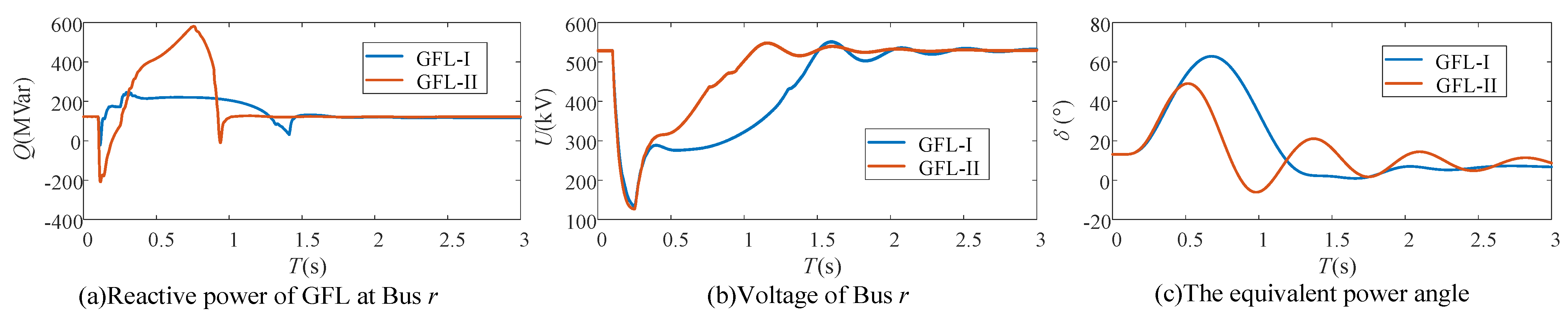Transient Synchronous Stability Analysis and Control Improvement for Power Systems with Grid-Following Converters

Abstract

Amid the global transition towards sustainable energy, the increasing integration of power sources equipped with grid-following (GFL) voltage source converters (VSCs) into power systems has significantly impacted transient synchronous stability. How to analyze the transient synchronous mechanism of power systems with GFL and how to fully utilize GFL to enhance the transient synchronous stability are critical challenges. Therefore, based on the extended equal area criterion (EEAC), the influence mechanism of the transient voltage stability on the transient synchronous stability of multi-machine power systems is analyzed. Furthermore, an explicit power angle equation is derived, incorporating the distribution location and active power characteristics of GFL, to explain their impact on the transient synchronous stability between synchronous generators (SGs). Inspired by the above insights, an improved control strategy of GFL is proposed for transient stability enhancement. The proposed strategy can effectively accelerate the voltage recovery speed and enhance the transient synchronous stability under different coherence grouping scenarios. Finally, the correctness of the mechanism analysis and the effectiveness of the proposed control strategy are validated on the simplified system of a real power grid using the PSCAD platform.

1. Introduction

With global energy transformation, renewable energy sources such as wind and photovoltaic power are accounting for an increasingly significant proportion of power grids [1]. In scenarios involving long-distance transmission of renewable energy, the application of flexible high-voltage direct current (HVDC) technology has become increasingly prevalent [2]. Both renewable energy systems and flexible HVDC systems are interconnected to power grids through voltage source converters (VSCs). Consequently, the proportion of VSC-based interfaces in modern power systems continues to rise substantially [3]. Unlike synchronous generators (SGs), the dynamic behavior of VSCs is predominantly governed by their control algorithms [4].

Currently, grid-following (GFL) control remains the predominant approach for VSCs in practical engineering applications [5]. GFL converters utilize phase-locked loops (PLLs) to synchronize with the power grid, essentially operating as controllable AC current sources [6,7]. Due to their technological maturity and fast power response characteristics [8], GFL converters have been widely adopted in real-world projects. However, as the penetration level of GFL converters in power systems continues to increase, their impact on the transient synchronous stability of power systems has become non-negligible. Therefore, many scholars have studied the transient synchronous stability for power systems with GFL.

In [9,10,11,12], the influence of GFL on the transient synchronous stability is analyzed. In [9,10], the impact of the GFL penetration rate on the transient synchronous stability of a one-machine infinite bus (OMIB) system is analyzed based on the equal area criterion (EAC). Given that practical power systems exhibit multi-machine configurations with complex network topology, the authors of [11,12] address the gap in OMIB-based studies through multi-machine system analysis. In [11], an analysis method of optimal GFL proportion is proposed. The study in [12] shows that the effects of GFL on the transient synchronous stability are determined by several factors, including the selection of the SGs used to balance GFL, the reactive power control mode of GFL, and GFL penetration level. The above studies explored the impact of the GFL penetration rate on the transient synchronous stability when GFLs are concentrated at a single location. However, since GFLs are widely distributed across different locations in actual systems, it is essential to investigate how the active power characteristics of GFLs at different positions affect transient synchronous stability. In addition, the influence mechanism of the transient voltage stability on the transient synchronous stability of multi-machine power systems has not been examined.

Furthermore, considerable progress has been made in GFL control strategies for enhancing transient synchronous stability.

The studies of [13,14,15,16,17] focus on the control strategies of GFL to enhance the transient synchronous stability. In [13,14], the control strategy is designed based on time–domain simulation results and the transient synchronous stability is improved by increasing the reactive power injection from GFL into the system. In contrast, the GFL control strategies in [15,16,17] are based on theoretical analysis. Literature [15] designed a post-fault active power control strategy for GFL to reduce the unbalanced power of nearby SGs. Literature [16] proposed a coordinating scheme of DFIG post-fault active power and the unit tripping control. Nevertheless, these studies did not consider the applicability of control strategies across different coherence grouping scenarios and the differentiated control of GFLs at various locations. To overcome the limitations, the authors of [17] present a Wide Area Control (WAC) strategy based on a nonlinear optimal control algorithm using Reinforcement Learning (RL) and Neural Networks (NNs). The proposed WAC strategy can allocate appropriate control signals to wind farms at different locations and is applicable to various coherence grouping scenarios. However, the interpretability and generalization capability of neural network methods may struggle to meet the needs of actual power grids.

To address the above limitations, the influence mechanism of the transient voltage stability on the transient synchronous stability is analyzed in this paper. In addition, the influence mechanism of the distribution location and active power characteristics of GFL on the synchronous stability between SGs is revealed. Based on theoretical analysis, an improved GFL control strategy is proposed. The correctness of the mechanism analysis and the effectiveness of the proposed control strategy are validated through electromagnetic transient (EMT) simulations on a simplified system of an actual large power grid.

The main contributions of the paper include:

(1) Based on the extended equal area criterion (EEAC), the influence mechanism of the transient voltage stability on the transient synchronous stability of multi-machine power systems is analyzed. Research demonstrates that the slower voltage recovery dynamics increase the acceleration area while reducing the maximum deceleration area, thereby deteriorating the synchronous stability.

(2) Based on EEAC, an explicit power angle equation that accounts for the distribution location and active power characteristics of GFL is derived, and the influence mechanism of the distribution location and active power characteristics of GFL on the transient synchronous stability between SGs can be explained. Research demonstrates that the transient synchronous stability between SGs can be improved by decreasing the active power of the GFL near the leading SG cluster and increasing the active power of the GFL near the lagging SG cluster.

(3) Inspired by the above insights, an improved GFL control strategy is proposed. Through improved q-axis current control, the transient voltage stability is enhanced, thereby improving the transient synchronous stability. Through improved d-axis current control, the transient synchronous stability under different coherence grouping scenarios is enhanced by differentiated control of GFLs at various locations. A comparative analysis between the enhanced GFL control strategy proposed in this work and previously reported GFL control strategies is presented in

Table 1. A comparative analysis between the enhanced GFL control strategy proposed in this work and previously reported GFL control strategies.

	Supported by Mechanistic Analysis	Applicability Across Different Coherence Grouping Scenarios	Dataset-Independent
[13,14]	No	No	Yes
[15,16]	Yes	No	Yes
[17]	Yes	Yes	No
This paper	Yes	Yes	Yes

.

The rest of the paper is organized as follows: Section 2 introduces the classical GFL control. The mechanism analysis of the transient synchronous stability is discussed in Section 3. Based on the mechanism of Section 3, Section 4 proposes an improved GFL control strategy. Section 5 validates the correctness of the mechanism analysis and the effectiveness of the proposed control strategy through case studies. Finally, Section 6 summarizes the main conclusions.

2. Modeling of GFL

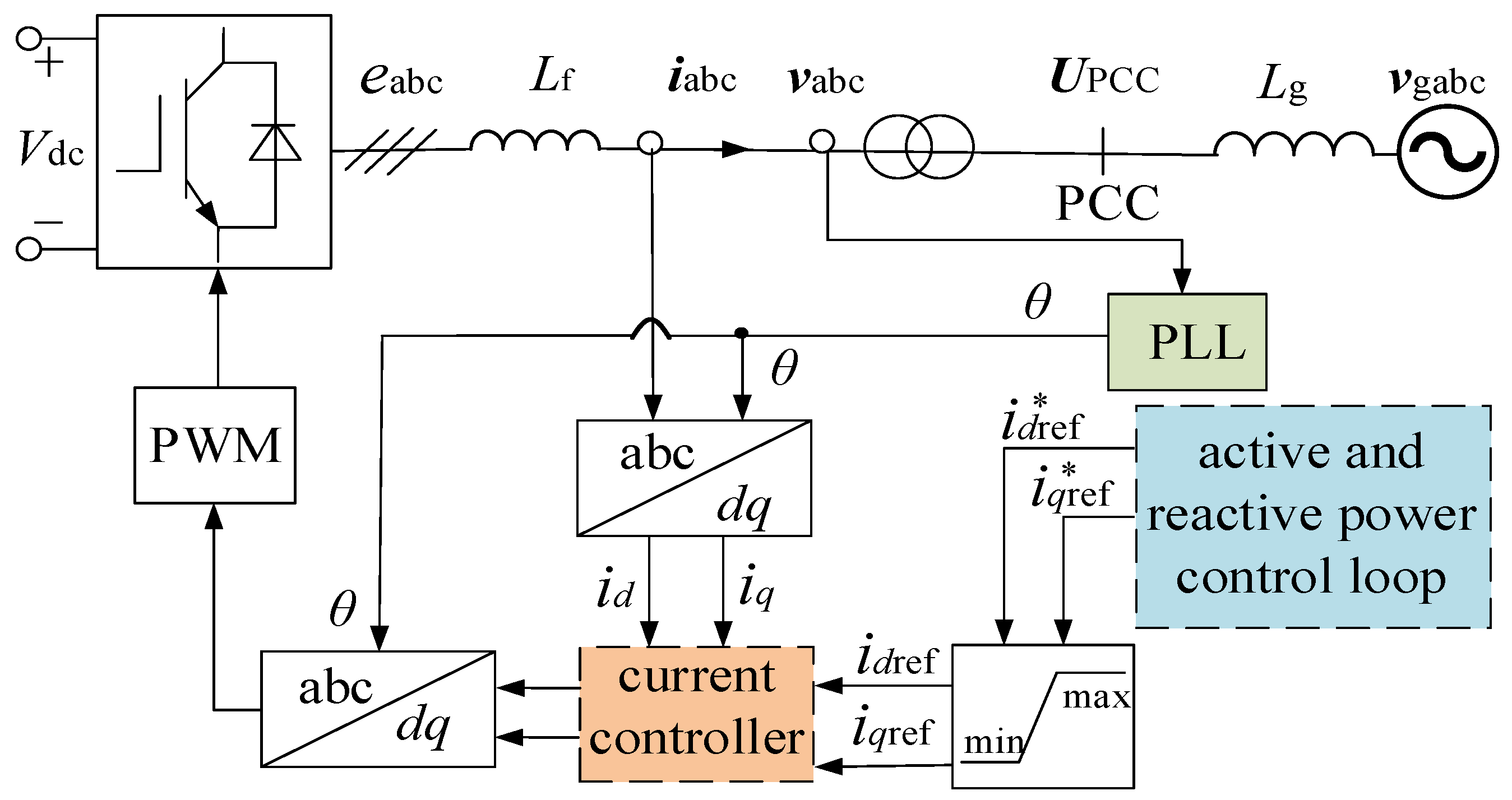
The classical control structure of GFL is shown in Figure 1 [6].

PCC in Figure 1 means the point of common coupling (PCC) of GFL. GFL uses constant active power control and constant AC voltage control when there is no fault.

The classic GFL control strategy during the low-voltage ride-through is [18]

(1) The expression of i_qref:

$$\left\{\begin{array}{c}{i}_{q\mathrm{ref}}=-1.5\left(0.9-U_{\mathrm{PCC}}\right),0.2<U_{\mathrm{PCC}}<0.9\\ i_{q\mathrm{ref}}=-1,U_{\mathrm{PCC}}\le 0.2\end{array}\right.$$

(1)

The upper and lower limits of i_qref are i_max and −i_max. U_PCC is the voltage amplitude of PCC in Figure 1.

(2) The expression of i_dref:

i_dref is generated based on the constant active power control as (2). The upper and lower limits of i_dref are (i_max² − i_qref²)^0.5 and −(i_max² − i_qref²)^0.5.

The expression of the active power control loop is

$$i_{d\mathrm{ref}}=k_{\mathrm{p}}(P_{\mathrm{ref}}-P_{\mathrm{e}})+k_{\mathrm{i}}{\displaystyle \int (P_{\mathrm{ref}}-P_{\mathrm{e}})}dt$$

(2)

where P_ref and P_e are the command value and actual value of active power. k_p and k_i are the proportional and integral coefficients of PI controller.

GFL can be equivalent to an admittance. Its expression is [11]

$$y_{\mathrm{GFL}}=-g_{\mathrm{GFL}}+\mathrm{j}{b}_{\mathrm{GFL}}=-{\displaystyle \frac{P_{\mathrm{GFL}}}{U_{\mathrm{PCC}}^2}}+\mathrm{j}{\displaystyle \frac{Q_{\mathrm{GFL}}}{U_{\mathrm{PCC}}^2}}$$

(3)

where g_GFL and b_GFL are the equivalent conductance and equivalent susceptance of GFL. P_GFL and Q_GFL are the active power and reactive power of GFL.

3. Mechanism Analysis

In this section, the influence mechanism of the transient voltage stability on the synchronous stability will be analyzed. In addition, the influence mechanism of the distribution location and active power characteristics of GFL on the synchronous stability between SGs will be revealed.

3.1. The Influence Mechanism of the Transient Voltage Stability on the Synchronous Stability

According to EEAC [12], all SGs in the power grid can be divided into two clusters including the leading SG cluster and the lagging SG cluster. For the convenience of expression, the leading cluster is called Cluster S and the lagging cluster is called Cluster R. The swing equations of Cluster S and Cluster R are:

$$\left\{\begin{array}{c}{M}_S{\displaystyle \frac{{\mathrm{d}}^2{\delta }_S}{d{t}^2}}=P_{\mathrm{m}.S}-P_{\mathrm{e}.S}\\ M_R{\displaystyle \frac{{\mathrm{d}}^2{\delta }_R}{\mathrm{d}{t}^2}}=P_{\mathrm{m}.R}-P_{\mathrm{e}.R}\end{array}\right.$$

(4)

where M_S and M_R are, respectively, the inertia coefficients of Cluster S and Cluster R. δ_S and δ_R are, respectively, the rotor angles of Cluster S and Cluster R. P_m.S and P_m.R are, respectively, the total mechanical power of Cluster S and Cluster R. P_e.S and P_e.R are, respectively, the total electromagnetic power of Cluster S and Cluster R.

Further, the swing equations of the two machine groups can be rewritten as the swing equation of the equivalent single-machine infinite system based on EEAC. Therefore, (4) can be written as:

$$M_{SR}{\displaystyle \frac{{\mathrm{d}}^2{\delta }_{SR}}{\mathrm{d}{t}^2}}=P_{\mathrm{m}.SR}-P_{\mathrm{e}.SR}$$

(5)

where

$${\delta }_{SR}={\delta }_S-{\delta }_R$$

(6)

$$M_{SR}={\displaystyle \frac{M_S{M}_R}{M_{\mathrm{T}}}}$$

(7)

$$M_{\mathrm{T}}=M_S+M_R$$

(8)

$$P_{\mathrm{m}.SR}=\left(M_R{P}_{\mathrm{m}.S}-M_S{P}_{\mathrm{m}.R}\right)/M_{\mathrm{T}}$$

(9)

$$P_{\mathrm{e}.SR}={\displaystyle \frac{M_R{P}_{\mathrm{e}.S}-M_S{P}_{\mathrm{e}.R}}{M_{\mathrm{T}}}}=P_{\mathrm{C}}+P_{\max }\sin \left({\delta }_{SR}-\gamma \right)$$

(10)

$$\left\{\begin{array}{c}{P}_{\mathrm{C}}={\displaystyle \frac{M_R}{M_{\mathrm{T}}}}{\displaystyle {\displaystyle \sum }_{i\in S}}{\displaystyle {\displaystyle \sum }_{m\in S}}{E}_i{E}_m{G}_{im}-{\displaystyle \frac{M_S}{M_{\mathrm{T}}}}{\displaystyle {\displaystyle \sum }_{j\in R}}{\displaystyle {\displaystyle \sum }_{n\in R}}{E}_j{E}_n{G}_{jn}\\ P_{\max }=\sqrt{C^2+D^2}\\ C={\displaystyle \frac{M_R-M_S}{M_{\mathrm{T}}}}{\displaystyle {\displaystyle \sum }_{i\in S}}{\displaystyle {\displaystyle \sum }_{j\in R}}{E}_i{E}_j{G}_{ij}\\ D={\displaystyle {\displaystyle \sum }_{i\in R}}{\displaystyle {\displaystyle \sum }_{j\in S}}{E}_i{E}_j{B}_{ij}\\ \gamma =-arctan{\displaystyle \frac{C}{D}}\end{array}\right.$$

(11)

M_SR, δ_SR, P_m.SR, and P_e.SR are, respectively, the inertia coefficient, rotor angle, mechanical power, and electromagnetic power of the equivalent single-machine infinite bus system. G_ij + jB_ij is the mutual admittance between node i and node j. E_i is the internal potential of the i-th SG of Cluster S. E_j is the internal potential of the j-th SG of Cluster R.

Based on (5), Figure 2 can be obtained.

In Figure 2, U represents the port voltage of SG and U₁ < U₂ < 1 p.u. P_m.SR/M_SR is the mechanical power of the equivalent single-machine infinite bus system. Curves 1, 2, and 3 correspond to the P-δ curves at different voltage levels. Figure 2a assumes that the voltage can quickly recover from U₁ to 1 p.u. after the fault is removed. In contrast, Figure 2b assumes that the voltage first returns from U₁ to U₂ and then to 1 p.u.

For Figure 2a: In a normal steady state, the operating point is a. When an AC short circuit fault occurs and the voltage’s magnitude drops to U₁, the operating point moves to point b. Since P_m.SR/M_SR > P_e.SR/M_SR, the operating point accelerates along Curve 2 from point b to point c. Assume that the fault is cleared when δ_SR = δ_c and the voltage can quickly recover from U₁ to 1p.u. Then, the operating point moves to d. Since P_m.SR/M_SR < P_e.SR/M_SR, the operating point decelerates along Curve 1. If the acceleration area S₁ is greater than the maximum deceleration area S_dmax, δ_SR will continue to increase along Curve 1 and the system will lose its transient synchronous stability. If S₁ < S_dmax, δ_SR can move to point a and the system is stable in transient synchronization.

For Figure 2b: Similar to Figure 2a, the trajectory of the operating point under an AC fault is a-b-c. Assume that the fault is cleared when δ_SR = δ_c. In addition, the voltage recovery process does not follow a direct transition from U₁ to 1 p.u., but rather requires first restoring from U₁ to U₂ and then to 1 p.u. Therefore, the operating point moves from c to d. Since P_m.SR/M_SR > P_e.SR/M_SR, the operating point accelerates along Curve 3 from point d to point e. As the voltage returns from U₂ to 1 p.u., the operating point also moves from e to f. Since P_m.SR/M_SR < P_e.SR/M_SR, the operating point decelerates along Curve 1. If the acceleration area (S₁ + S₂) is greater than the maximum deceleration area S′_dmax, δ_SR will continue to increase along Curve 1 and the system will lose its transient synchronous stability. If (S₁ + S₂) < S′_dmax, δ_SR can move to point a and the system is stable in transient synchronization.

From the above analysis, it can be seen that as the voltage recovery speed slows down, the acceleration area increases and the maximum deceleration area decreases, which negatively impacts the transient synchronous stability of the system.

3.2. The Influence Mechanism of the Distribution Location and Active Power Characteristics of GFL on the Synchronous Stability Between SGs

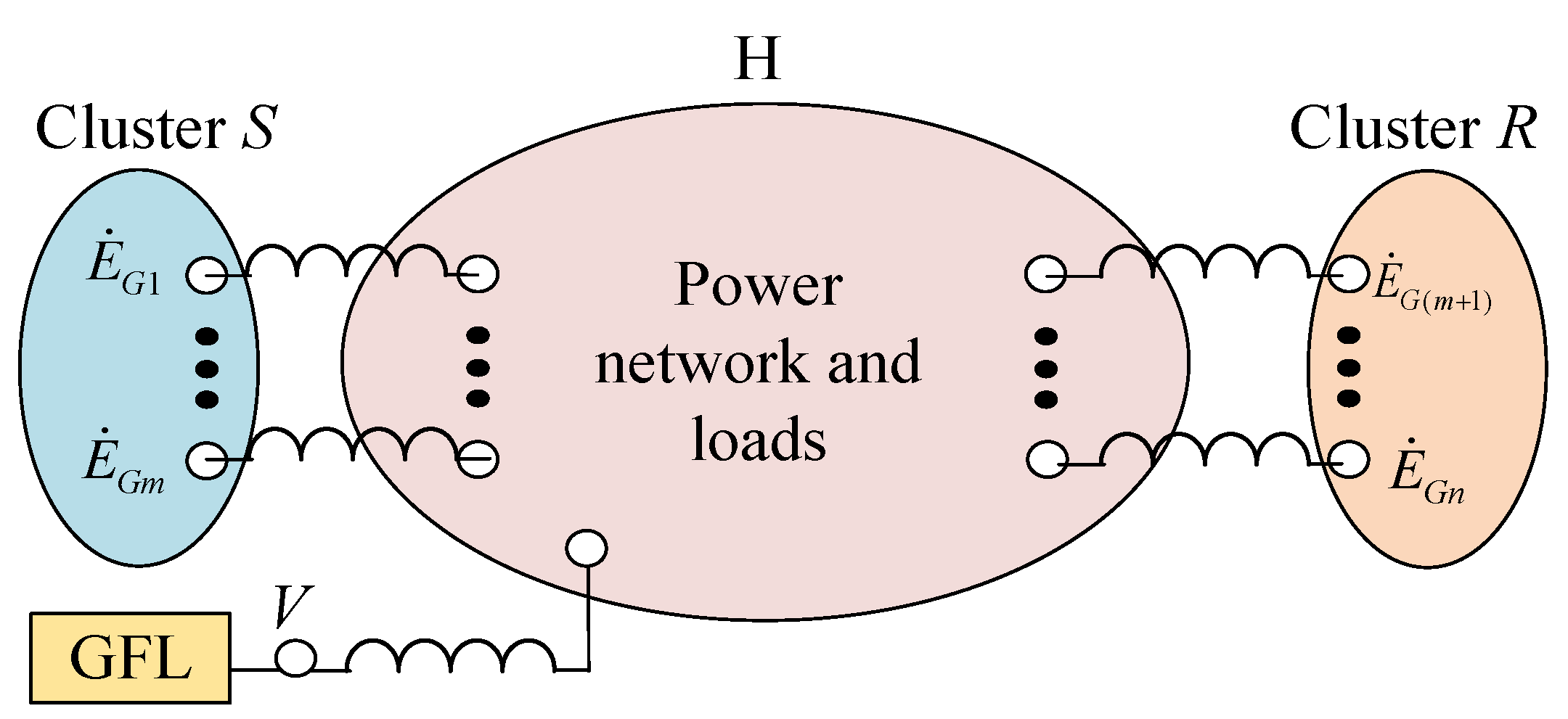
Suppose that GFL is connected to the power grid and the PCC of GFL is near Cluster S. The diagram of the power grid with GFL is shown in Figure 3, which contains four types of nodes: the internal potential nodes within the SGs of Cluster S and Cluster R, the PCC of GFL, and the ordinary nodes of the power network and loads.

Based on Figure 3, only the internal potential nodes of the S-side SGs, the internal potential nodes of the R-side SGs, and the PCC of GFL are retained while the ordinary nodes are eliminated. Then, the network equation can be written as

$$\left[\begin{array}{c}{\dot{\mathit{I}}}_V\\ {\dot{\mathit{I}}}_S\\ {\dot{\mathit{I}}}_R\end{array}\right]=\left[\begin{array}{ccc}{\mathit{Y}}_{VV}& {\mathit{Y}}_{VS}& 0\\ {\mathit{Y}}_{SV}& {\mathit{Y}}_{SS}& {\mathit{Y}}_{SR}\\ 0& {\mathit{Y}}_{RS}& {\mathit{Y}}_{RR}\end{array}\right]\left[\begin{array}{c}{\dot{\mathit{U}}}_V\\ {\dot{\mathit{E}}}_S\\ {\dot{\mathit{E}}}_R\end{array}\right]$$

(12)

${\left[{\dot{I}}_V{\dot{I}}_S{\dot{I}}_R\right]}^{\mathrm{T}}$ is the injection current vector. ${\left[{\dot{U}}_V{\dot{E}}_S{\dot{E}}_R\right]}^{\mathrm{T}}$ is the voltage vector. Since the PCC of GFL is near Cluster S, Y_VR ≈ 0.

Eliminate the PCC of GFL, then

$$\left[\begin{array}{c}{\dot{\mathit{I}}}_S+\mathsf{\Delta }{\dot{\mathit{I}}}_V\\ {\dot{\mathit{I}}}_R\end{array}\right]=\left[\begin{array}{cc}{\mathit{Y}}_{SS}& {\mathit{Y}}_{SR}\\ {\mathit{Y}}_{RS}& {\mathit{Y}}_{RR}\end{array}\right]\left[\begin{array}{c}{\dot{\mathit{E}}}_S\\ {\dot{\mathit{E}}}_R\end{array}\right]$$

(13)

The injection current of GFL is shifted to the potential nodes of Cluster S, and the increased injection current of the potential nodes of Cluster S becomes:

$$\mathsf{\Delta }{\dot{I}}_{Vi}=Y_{iV}{Y_{VV}}^{-1}{\dot{I}}_V=k_{iS}{\dot{I}}_V=k_{iS}{\displaystyle \frac{P_{VS}+\mathrm{j}{Q}_{VS}}{U_{VS}}},i\in S$$

(14)

where k_iS is the load displacement coefficient corresponding to the GFL near Cluster S. P_VS and Q_VS are the active power and reactive power of the GFL near Cluster S. U_VS is the PCC voltage of the GFL near Cluster S. i is the number of a certain SG of Cluster S.

If GFL is equivalent to an admittance according to (3), ${\dot{I}}_V=0$ and (13) become:

$$\left[\begin{array}{c}{\dot{\mathit{I}}}_S\\ {\dot{\mathit{I}}}_R\end{array}\right]=\left[\begin{array}{cc}{\mathit{Y}}_{SS}^{\prime }& {\mathit{Y}}_{SR}\\ {\mathit{Y}}_{RS}& {\mathit{Y}}_{RR}\end{array}\right]\left[\begin{array}{c}{\dot{\mathit{E}}}_S\\ {\dot{\mathit{E}}}_R\end{array}\right]$$

(15)

where

$$\left\{\begin{array}{c}{Y}_{ii}^{\prime }=\left(G_{ii}+\mathrm{j}{B}_{ii}\right)+\left(\Delta G_i+\mathrm{j}\Delta B_i\right)=Y_{ii}+\Delta Y_i,i\in S\\ \Delta Y_i=\mathsf{\Delta }{\dot{I}}_{Vi}/{\dot{E}}_i=\Delta G_i+\mathrm{j}\Delta B_i,i\in S\end{array}\right.$$

(16)

From (15) and (16), it can be seen that the access of GFL only changes the self-admittance of Cluster S.

Then, according to (14), (16), and [19], we can get:

$$\mathsf{\Delta }{G}_i=k_{iS}{P}_{VS}/\left(E_i{U}_{VS}\right),i\in S$$

(17)

where E_i is the internal potential of the i-th SG of Cluster S. Since GFL emits active power to the grid, ΔG_i < 0 and k_iS < 0.

Based on (9), (10), (11), (16), and (17), the access of GFL and the change in Y_ii (i ∈ S) do not affect P_m.SR, P_max, and γ but affect P_C. P_C becomes

$$\begin{array}{c}{P}_{\mathrm{C}}={\displaystyle \frac{M_R}{M_{\mathrm{T}}}}{\displaystyle {\displaystyle \sum }_{i\in S}}{\displaystyle {\displaystyle \sum }_{m\in S}}{E}_i{E}_m{G}_{im}-{\displaystyle \frac{M_S}{M_{\mathrm{T}}}}{\displaystyle {\displaystyle \sum }_{j\in R}}{\displaystyle {\displaystyle \sum }_{n\in R}}{E}_j{E}_n{G}_{jn}\\ +{\displaystyle \frac{M_R}{M_{\mathrm{T}}}}{\displaystyle {\displaystyle \sum }_{i\in S}}{k}_{iS}{P}_{VS}{E}_i/\left(U_{VS}\right)\end{array}$$

(18)

Similarly, if the PCC of GFL is near Cluster R, P_C becomes

$$\begin{array}{c}{P}_{\mathrm{C}}={\displaystyle \frac{M_R}{M_{\mathrm{T}}}}{\displaystyle {\displaystyle \sum }_{i\in S}}{\displaystyle {\displaystyle \sum }_{m\in S}}{E}_i{E}_m{G}_{im}-{\displaystyle \frac{M_S}{M_{\mathrm{T}}}}{\displaystyle {\displaystyle \sum }_{j\in R}}{\displaystyle {\displaystyle \sum }_{n\in R}}{E}_j{E}_n{G}_{jn}\\ -{\displaystyle \frac{M_S}{M_{\mathrm{T}}}}{\displaystyle {\displaystyle \sum }_{j\in R}}{k}_{jR}{P}_{VR}{E}_j/\left(U_{VR}\right)\end{array}$$

(19)

where k_jR is the load displacement coefficient corresponding to the GFL near Cluster R. P_VR is the active power of the GFL near Cluster R. U_VR is the PCC voltage of the GFL near Cluster R.

According to (5), (10), (18), and (19), decreasing the active power of the GFL near Cluster S or increasing the active power of the GFL near Cluster R will make P_C and P_e.SR increase, which can reduce the acceleration area and increase the maximum deceleration area according to Figure 2a, thereby improving the transient synchronous stability.

4. Improved Control Strategy

In this section, based on the analysis in Section 3, an improved control strategy of GFL is proposed to enhance the transient synchronous stability. Specifically, the enhanced control strategy comprises two key components: improved d-axis current control and q-axis current control.

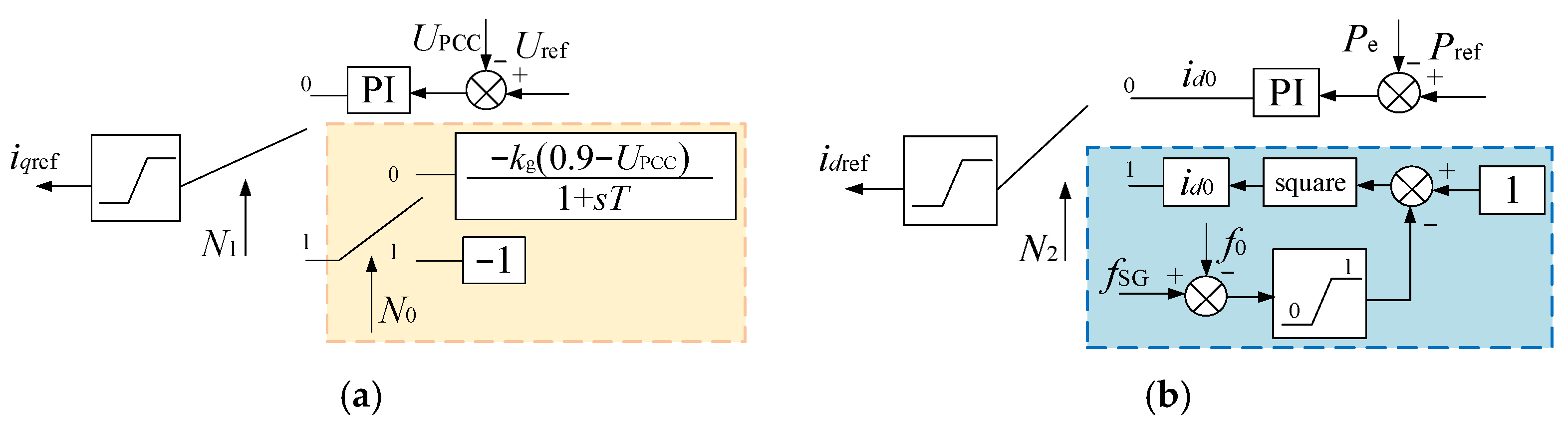
4.1. i_qref

According to Figure 2, the transient synchronous stability can be enhanced by accelerating the voltage recovery speed. Therefore, it is necessary to adjust the q-axis current command to enhance the reactive power support capability of GFL.

i_qref can be designed as

$$\left\{\begin{array}{c}{i}_{q\mathrm{ref}}={\displaystyle \frac{-k_{\mathrm{g}}\left(0.9-U_{\mathrm{PCC}}\right)}{1+sT}},0.2<U_{\mathrm{PCC}}<0.9\\ i_{q\mathrm{ref}}=-1,U_{\mathrm{PCC}}\le 0.2\end{array}\right.$$

(20)

where k_g is the amplification factor of the voltage difference and k_g > 1.5. U_PCC is the voltage of PCC in Figure 1. T is the time constant of the first-order filter.

By increasing k_g, |i_qref| of (20) is greater than that of (1), and the reactive power support capability of the GFL under (20) is stronger than that under (1).

However, increasing k_g will introduce oscillations. Therefore, a first-order filter needs to be added.

In addition, considering that increasing k_g reduces the regulation range of the d-axis current, which is not conducive to the subsequent use of the d-axis current to improve the transient synchronous stability, the first-order filter can slow down the increase speed of |i_qref|, thereby allowing sufficient regulation space for the d-axis current.

4.2. i_dref

According to Figure 2, (18) and (19), decreasing P_VS or increasing P_VR can enhance the synchronous stability between SGs. However, the results of coherent clustering may vary in the actual power grid. Therefore, how to determine the d-axis current control strategy of GFL in different locations without obtaining the homology clustering result in advance?

This paper proposes that the higher the frequency of the SG near the GFL, the smaller the active power of the GFL should be. Clearly, this perspective aligns with the mechanism analysis in Section 3 and does not involve the recognition of coherence grouping. Therefore, i_dref can be designed as

$$\left\{\begin{array}{c}{i}_{d\mathrm{ref}}=i_{d0}=k_{\mathrm{p}}(P_{\mathrm{ref}}-P_{\mathrm{e}})+k_{\mathrm{i}}{\displaystyle \int (P_{\mathrm{ref}}-P_{\mathrm{e}})}dt,U_{\mathrm{PCC}}>0.7\\ i_{d\mathrm{ref}}=i_{d0}{[1-\left(f_{\mathrm{SG}}-f_0\right)]}^2,\left(f_{\mathrm{SG}}-f_0\right)\in [0,1],U_{\mathrm{PCC}}\le 0.7\end{array}\right.$$

(21)

where P_ref and P_e are the command value and actual value of active power. k_p and k_i are the proportional and integral coefficients of the PI controller. U_PCC is the voltage of PCC in Figure 1. f_SG is the frequency of the SG near the GFL. SG transmits f_SG to the nearby GFL through wired or wireless communication. f₀ = 50 Hz. The upper and lower limits of i_dref are (i_max² − i_qref²)^0.5 and −(i_max² − i_qref²)^0.5.

The GFL calculates the i_dref according to (21). Since the frequency of the leading SG cluster is greater than that of the lagging SG cluster, the i_dref of the GFL near the leading SG cluster is less than that of the GFL near the lagging SG cluster based on (21), which is equivalent to decreasing the active power of the GFL near the leading SG cluster and increasing the active power of the GFL near the lagging SG cluster. Therefore, based on the analysis conclusion in Section 3.2, it can be seen that (21) can enhance the synchronous stability.

It should be noted that the proposed improvement control strategy of the d-axis current relies on advanced low-latency communication technologies.

The proposed GFL control strategy ((20) and (21)) is shown in Figure 4.

When U_PCC ≤ 0.2, N₀ = 1, otherwise N₀ = 0. When U_PCC < 0.9, N₁ = 1, otherwise N₁ = 0. When U_PCC ≤ 0.7, N₂ = 1, otherwise N₂ = 0.

5. Case Studies

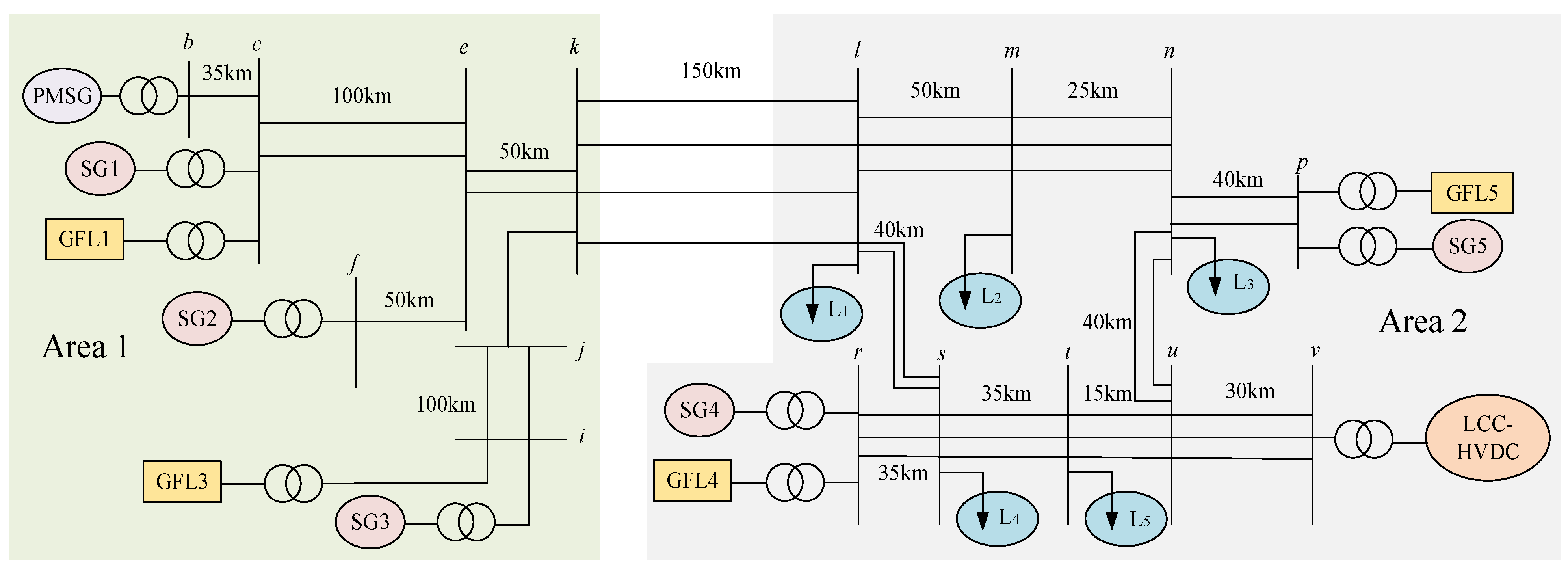
The system in Figure 5 is the simulation system of this paper. The simulation is based on a PSCAD platform.

Area 1 is the power sending area and Area 2 is the load center. L₁, L₂, L₃, L₄, and L₅ represent the loads, which consist of a 70% constant impedance and 30% induction motor. SG adopts the static excitation system ST1A model and the prime mover governor model TGOV1 in PSCAD. For more details of this system, refer to [20] and Appendix A. For GFL, P_ref = 0.8 p.u., U_ref = 1.03 p.u., K_pll = 50, T_pll = 0.01 s, i_max = 1.0 p.u., T = 0.1 s, k_g = 10, k_p = 0, k_i = 33.3.

In Figure 5, the benchmark scenario is as follows:

The numbers for SG1, SG2, SG3, SG4, and SG5 are 4, 4, 3, 4, and 4. Each SG has a rated capacity of 360 MVA. The active power of each SG is 288 MW. The active power of GFL at Bus p, the line commutated converter based high voltage DC (LCC-HVDC), and the permanent magnet synchronous generator (PMSG) are 576 MW, 3000 MW, and 70 MW. There is no GFL at c, i, r.

Based on the benchmark scenario, Scenarios 1 and 2 are designed as

Table 2. The operation scenarios.

Number	Setting of Power Sources
1	The number of SG1-SG5 are 2, 4, 1, 2, 4. The active power of the GFLs on Buses c, i, r, and p is all 576 MW.
2	Based on Scenario 1, the inertia of SG5 is doubled.

.

There are two purposes for designing Scenarios 1 and 2:

(1) Simulate different coherent clustering situations to verify the applicability of the proposed control strategy in different scenarios.

(2) Simulate more severe power angle oscillation scenarios to validate the effectiveness of the proposed control strategy.

Further, three control modes are set to verify the effectiveness of the proposed GFL control strategy in this paper.

To study the transient synchronous stability, a three-phase fault occurs on the n side of one of the mn lines at 0.1 s, and the faulty line is removed at 0.25 s. The fault ground resistance is 7 Ω.

5.1. The Influence of the Transient Voltage Stability on the Synchronous Stability

To simulate different levels of transient voltage stability, under Scenario 1 and Scenario 2, simulations are conducted based on GFL-I and GFL-II of

Table 3. Three different control modes of GFL.

Number	Control Mode
I	(1) + (2)
II	(2) + (20)
III	(20) + (21)

. The simulation results are shown in Figure 6 and Figure 7. In addition, three control modes of Table 3 are set to verify the effectiveness of the proposed GFL control strategy in this paper.

In Figure 6 and Figure 7, the equivalent power angle is the power angle of the equivalent single-machine infinite system based on EEAC and can characterize the synchronous stability of a multi-machine system. The definition of the equivalent power angle is

$$\delta ={\displaystyle \frac{{\displaystyle {\displaystyle \sum _{i\in S}}{M}_i}{\delta }_i}{{\displaystyle {\displaystyle \sum _{i\in S}}{M}_i}}}-{\displaystyle \frac{{\displaystyle {\displaystyle \sum _{j\in R}}{M}_j}{\delta }_j}{{\displaystyle {\displaystyle \sum _{j\in R}}{M}_j}}}$$

(22)

where S and R represent the leading SG cluster and the lagging SG cluster. M_i and δ_i are the inertia coefficient and rotor angle of the i-th SG in the leading SG cluster. M_j and δ_j are the inertia coefficient and rotor angle of the j-th SG in the lagging SG cluster.

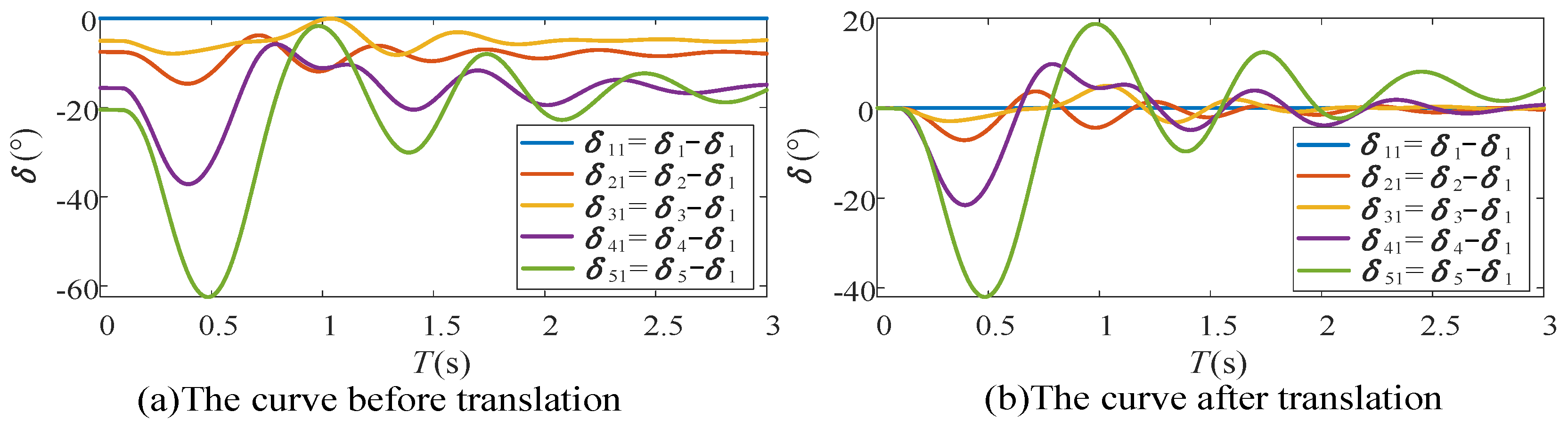
To determine the leading and lagging SG clusters, Figure 8a and Figure 9a show the power angle difference curves of each SG and SG1 in Scenarios 1 and 2, respectively. δ₁ represents the power angle of SG1 in Figure 5. Similarly, δ₂, δ₃, δ₄, and δ₅ correspond to the power angle of SG2, SG3, SG4, and SG5 in Figure 5. To clearly observe the results of homology clustering, the curves in Figure 8a and Figure 9a are shifted so that the pre-fault power angle difference of each curve is 0, and the curves in Figure 8b and Figure 9b can be obtained.

Based on Figure 8b, under Scenario 1, SG1, SG2, and SG3 belong to the leading SG cluster while SG4 and SG5 belong to the lagging SG cluster. Based on Figure 9b, under Scenario 2, SG1, SG2, SG3, and SG4 belong to the leading SG cluster while SG5 belongs to the lagging SG cluster. Therefore, based on the homology clustering results and (22), the equivalent power angle curves of Figure 6 and Figure 7 can be obtained.

From Figure 6 and Figure 7, it can be observed that:

(1) Based on (b) and (c), the slower the voltage recovery speed is, the worse is the transient synchronous stability.

(2) Based on (a), (b), and (c), the proposed q-axis current control can effectively enhance the reactive power support capability of GFL, thereby improving the transient voltage stability and the transient synchronous stability.

These phenomena are consistent with the analysis of Section 3.1 and Section 4.1.

5.2. The Effectiveness of the Proposed GFL Control Strategy

The previous analysis of 5.1 has already validated that the proposed q-axis control strategy of (20) can enhance the transient voltage stability, thereby improving the transient synchronous stability. Next, it is necessary to verify the enhancing effect of the proposed d-axis control strategy of (21) on the synchronous stability based on the comparative simulations of GFL-II and GFL-III.

Under Scenario 1, simulations are conducted based on GFL-II and GFL-III. The simulation results are shown in Figure 10.

From Figure 10, it can be observed that:

(1) Based on (b), SG1 is the leading SG cluster and SG4 is the lagging SG cluster.

(2) Under the proposed d-axis current control strategy, the reduction in active power of GFL1 is greater than that of GFL4, which means that compared to SG4, the first-swing acceleration of SG1 is more strongly suppressed, as shown in (c), (d), (e), and (f). Therefore, the equivalent power angle and the power angle difference between SG1 and SG4 become smaller as shown in (a) and (b), and the synchronous stability is enhanced.

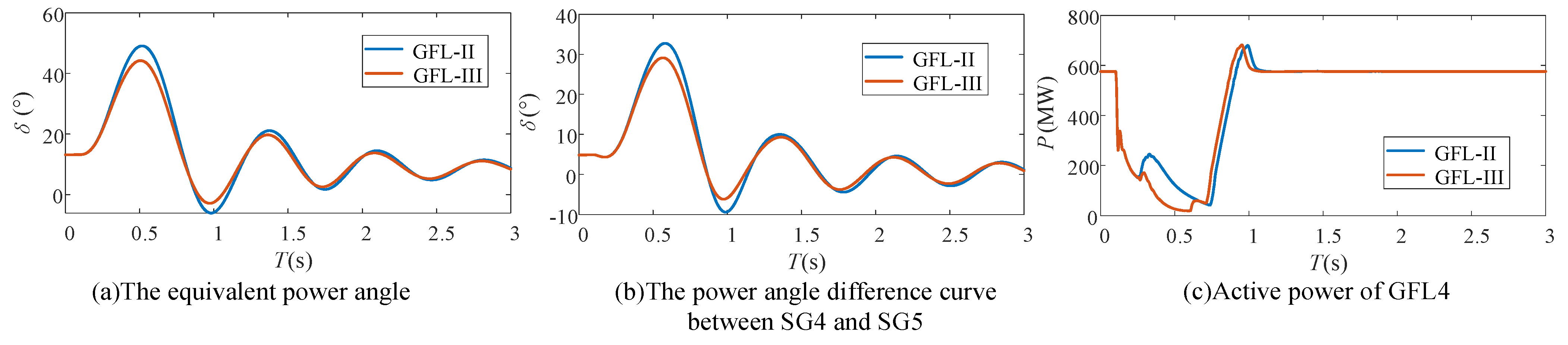
To verify the effectiveness of the proposed GFL control strategy under different coherence groupings, Scenario 2 is introduced for further simulation.

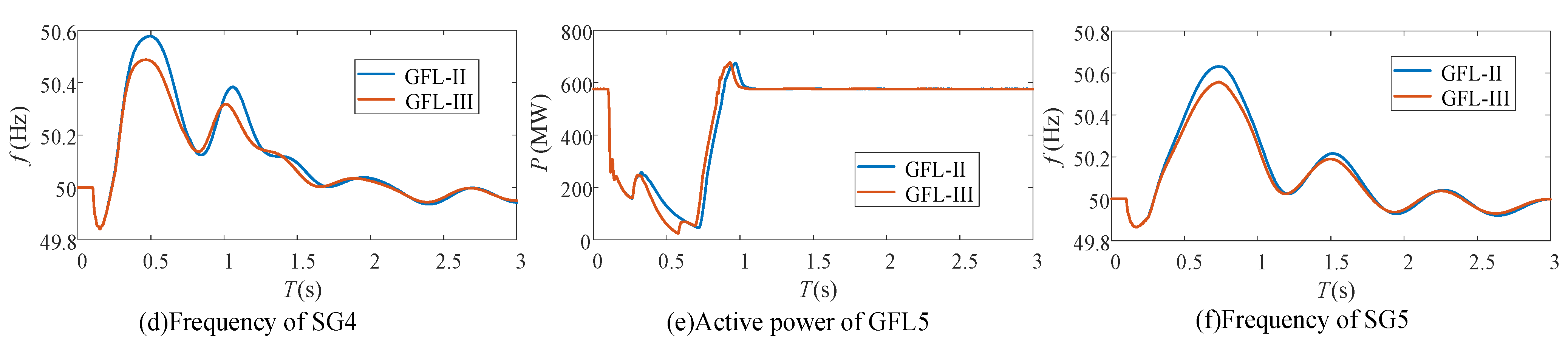
Under Scenario 2, simulations are conducted based on GFL-II and GFL-III. The simulation results are shown in Figure 11.

From Figure 11, it can be observed that:

(1) Based on (b), SG4 is the leading SG cluster and SG5 is the lagging SG cluster.

(2) Under the proposed d-axis current control strategy, the reduction in active power of GFL4 is greater than that of GFL5, which means that compared to SG5, the first-swing acceleration of SG4 is more strongly suppressed, as shown in (c), (d), (e), and (f). Therefore, the equivalent power angle and the power angle difference between SG4 and SG5 becomes smaller as shown in (a) and (b), and the synchronous stability is enhanced.

These phenomena are consistent with the analysis of Section 3.2 and Section 4.2.

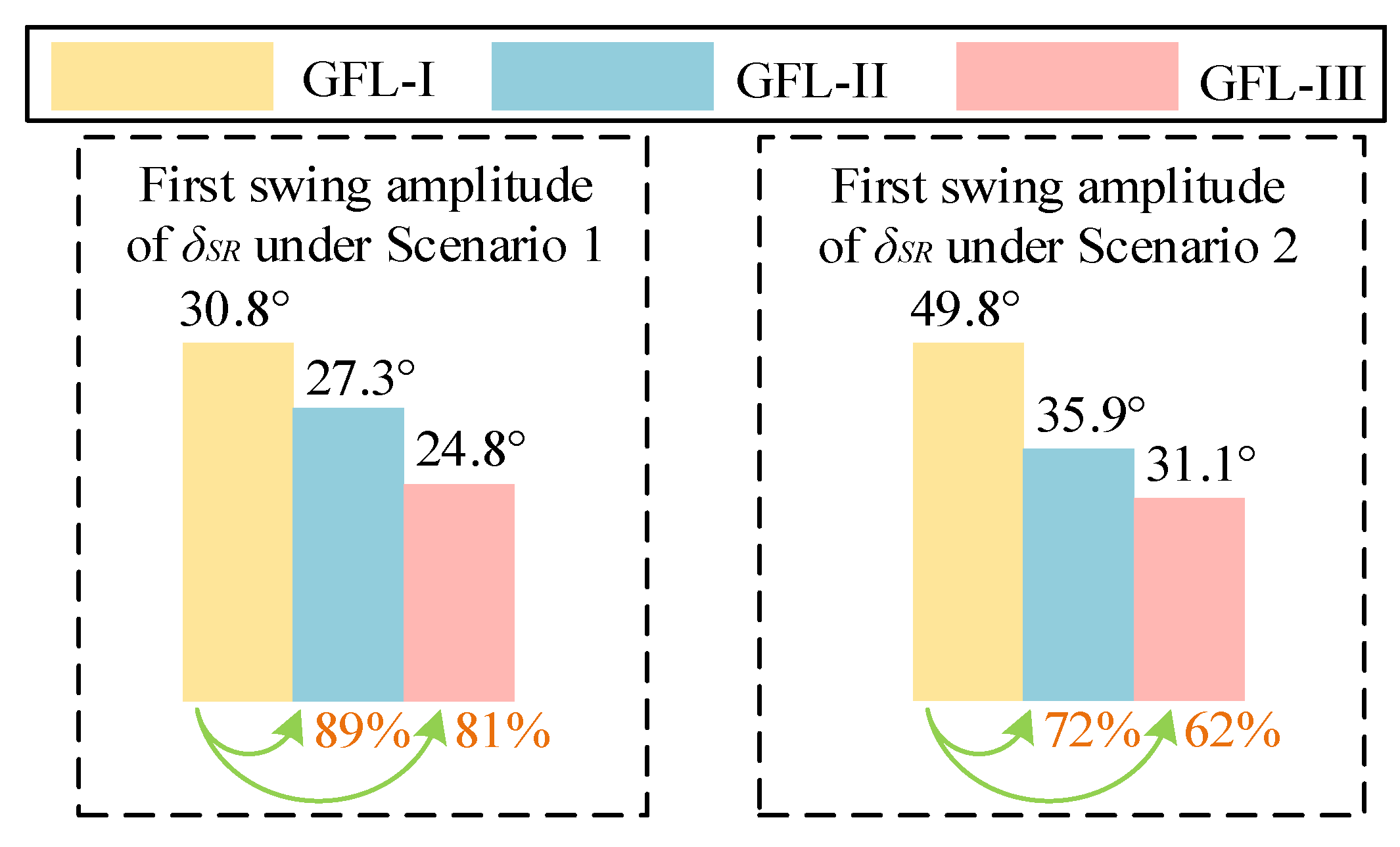
To more intuitively and quantitatively demonstrate the improvement effect of the GFL control strategy proposed in this paper on the synchronous stability, the first swing amplitude of the equivalent power angle under different scenarios and GFL control modes are shown in Figure 12.

From Figure 12, it can be observed that:

(1) Under the proposed q-axis current control strategy, the first swing amplitude of δ_SR has decreased by 11% and 28% in Scenarios 1 and 2. This demonstrates that under the proposed q-axis current control strategy, the equivalent power angle oscillation in multi-machine systems is reduced, thereby enhancing the transient synchronous stability.

(2) Under the complete improved control strategy of GFL, the first swing amplitude of δ_SR has decreased by 19% and 38% in Scenarios 1 and 2, which means that the proposed improved GFL control strategy effectively reduces equivalent power angle oscillations in multi-machine systems and enhances the transient synchronous stability.

6. Conclusions

In this paper, the influence mechanism of the transient voltage stability on the synchronous stability of multi-machine power systems is analyzed. The influence mechanism of the distribution location and active power characteristics of GFL on the synchronous stability between SGs is revealed. Based on the mechanism analysis, an improved GFL control strategy is proposed for transient stability enhancement. The conclusions are as follows:

(1) The slower voltage recovery dynamics increase the acceleration area while reducing the maximum deceleration area, thereby deteriorating the synchronous stability.

(2) The transient synchronous stability between SGs can be improved by decreasing the active power of the GFL near the leading SG cluster and increasing the active power of the GFL near the lagging SG cluster.

(3) Through improved q-axis current control of GFL, the transient voltage stability is enhanced, thereby improving the transient synchronous stability.

(4) Through improved d-axis current control of GFL, the transient synchronous stability between SGs under different coherence grouping scenarios is enhanced by differentiated control of GFLs at various locations.