Prediction Model of Offshore Wind Power Based on Multi-Level Attention Mechanism and Multi-Source Data Fusion
Abstract
1. Introduction
- A short-term wind power prediction model, MAM-BiGRU, with the multimodal fusion of the multi-layer attention mechanism (MAM) and the bidirectional gating unit (BiGRU) is proposed.
- A dual spatial attention mechanism (DSAM) module is constructed to realize the effective fusion of complex multidimensional data.
- A BiGRU module based on the temporal attention mechanism (TAM) is constructed to capture the significant features of multivariate wind power time series changes.
- Multiple wind meteorological features, such as the power, wind speed, temperature, wind direction, humidity, and barometric pressure, are considered in the modeling.
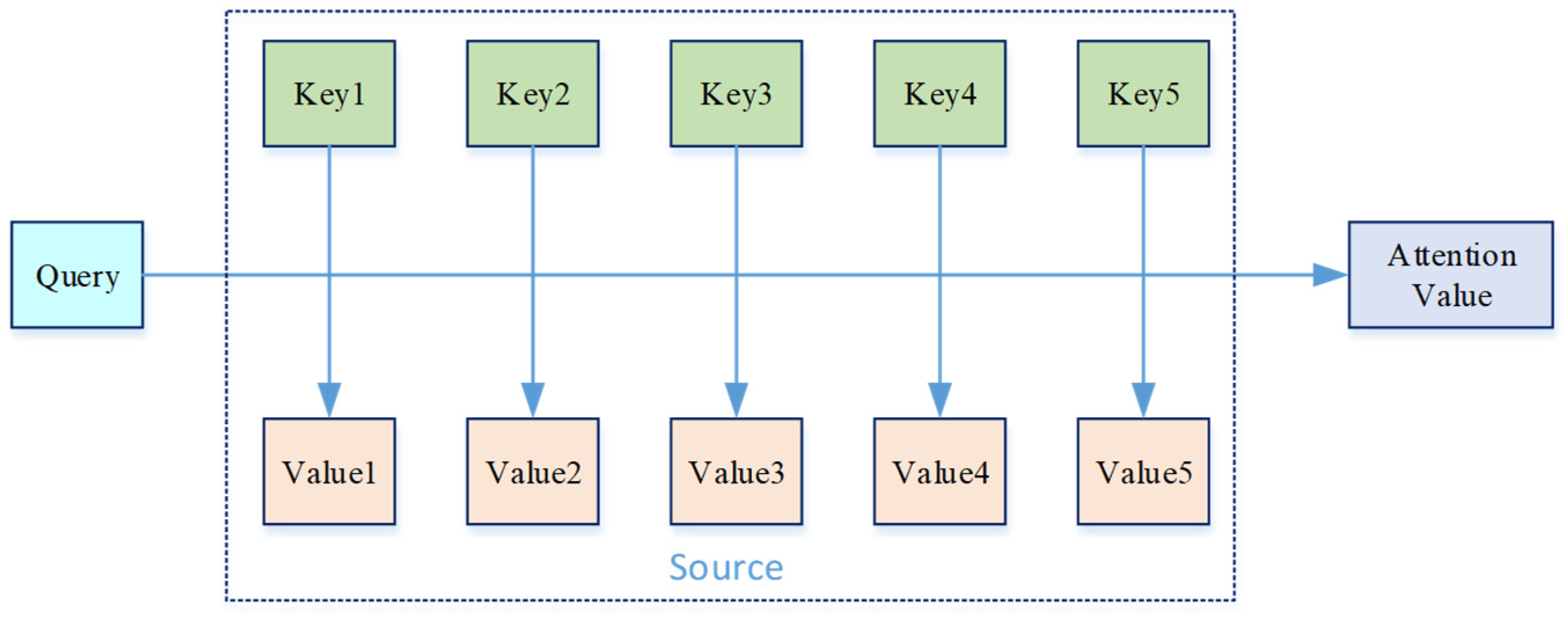
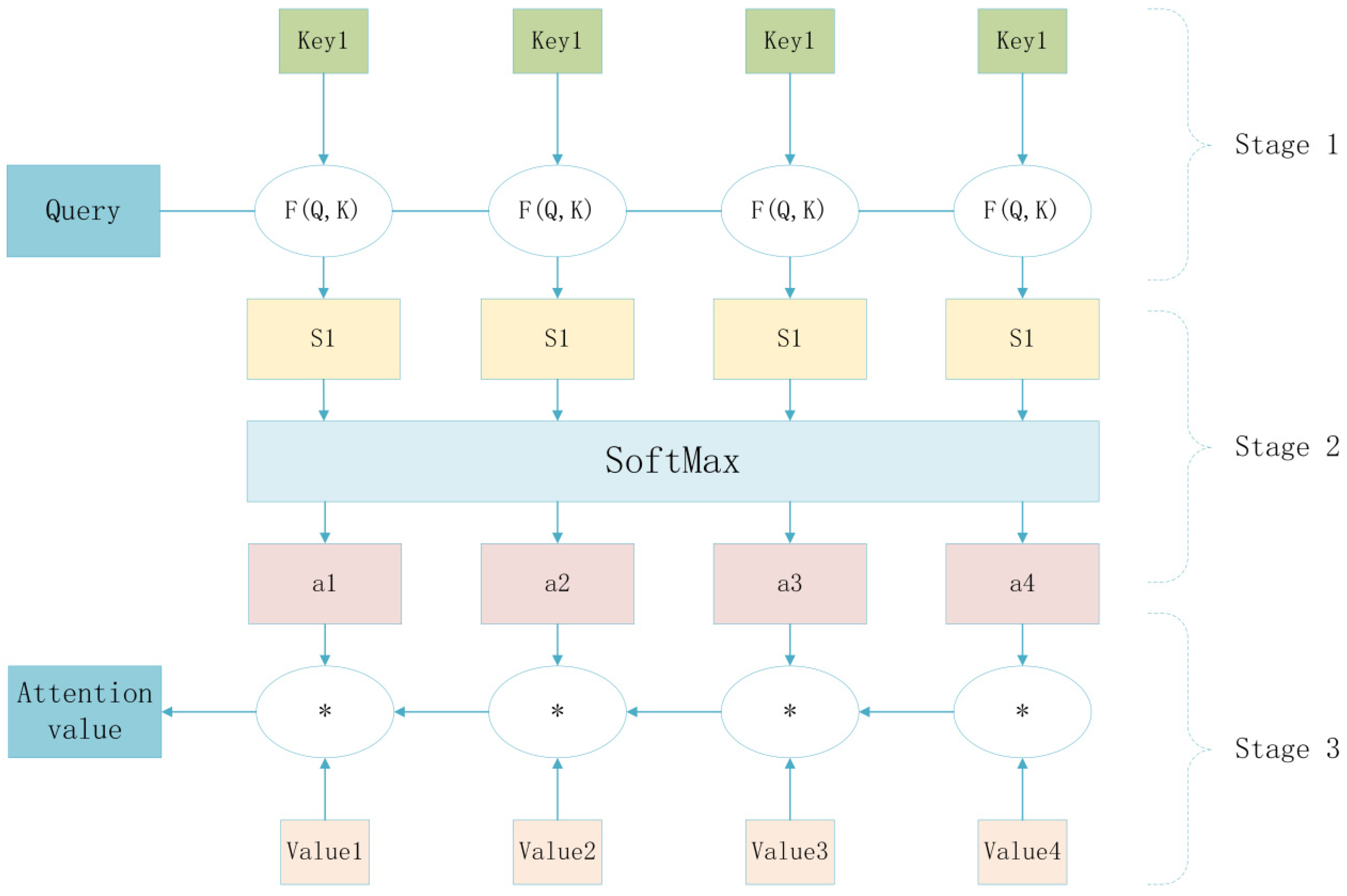
2. Attention Mechanism Algorithmic Foundations
3. Short-Term Wind Power Prediction Model with Multi-Layer Attention
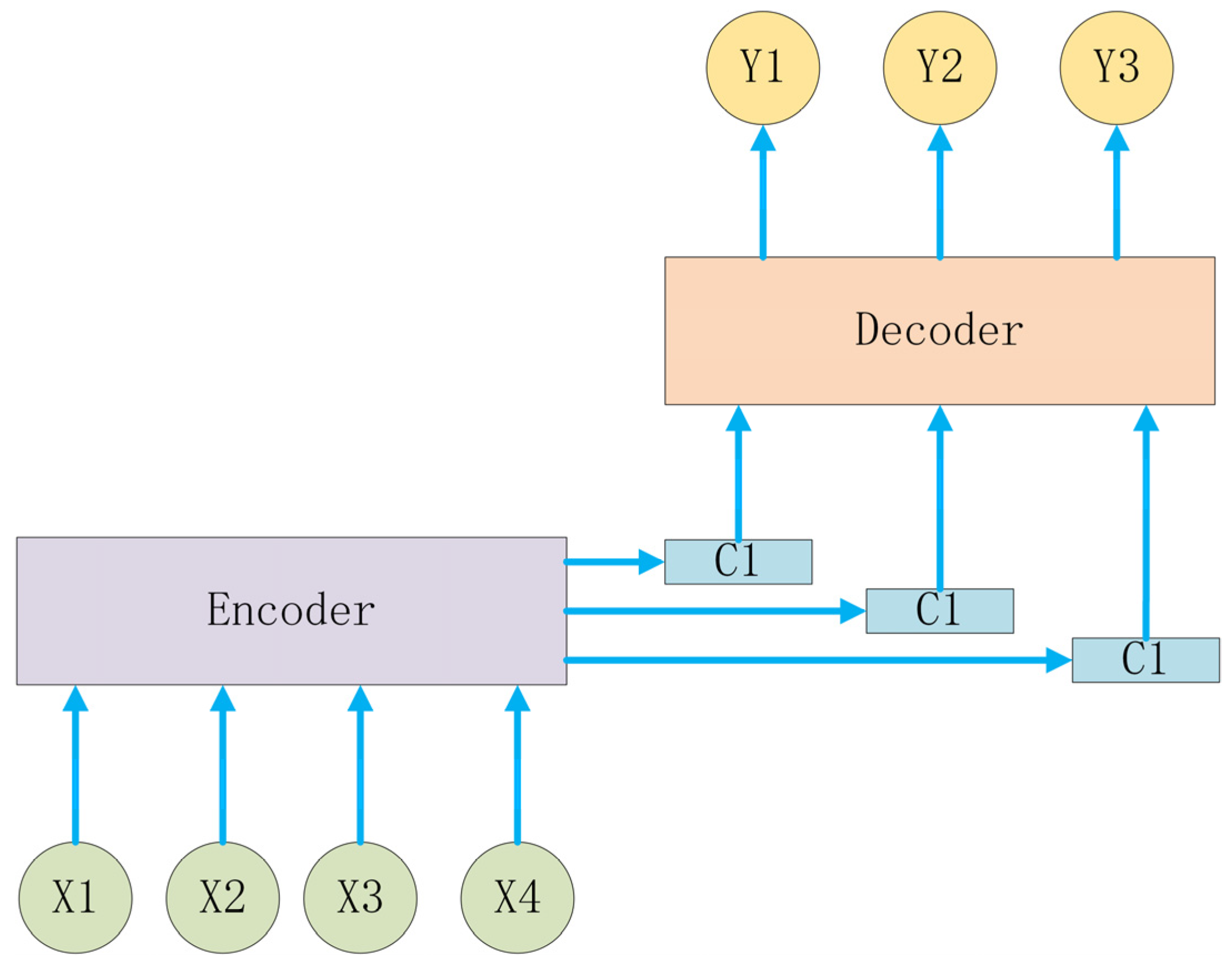
3.1. A Description of the Multimodal Fusion Wind Power Prediction Problem
3.2. Aerodynamic Characteristics and Mechanical Performance Analysis of Inflatable Savonius Wind Turbines
3.3. The General Framework of the Model
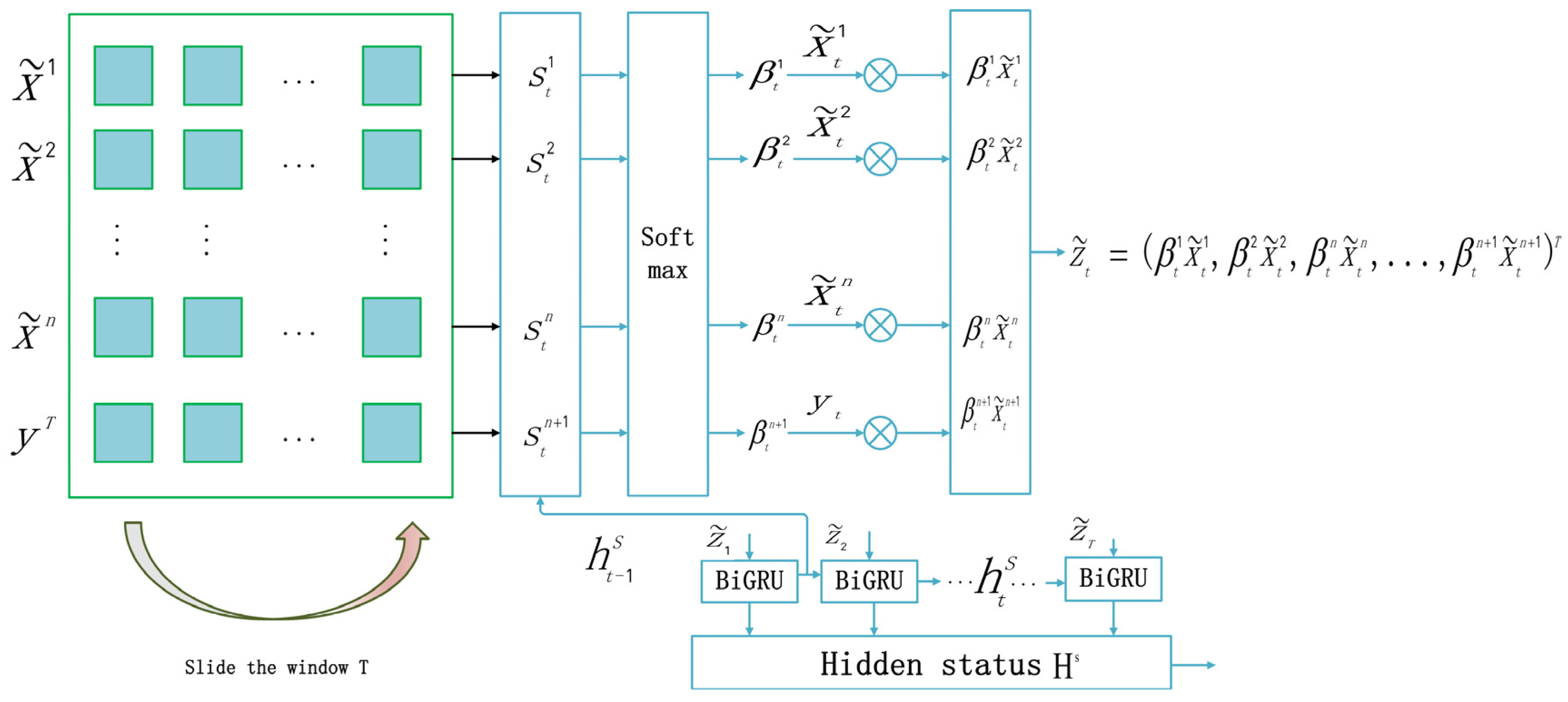
3.3.1. Hierarchical Struacture
- (1)
- First layer of spatial attention mechanism SAM1
- (2)
- Second-level spatial attention mechanism SAM2
3.3.2. Time Attention TAM-BiGRU
4. Experimental Tests and Analysis of Results
4.1. Experimental Design
4.2. Experimental Results
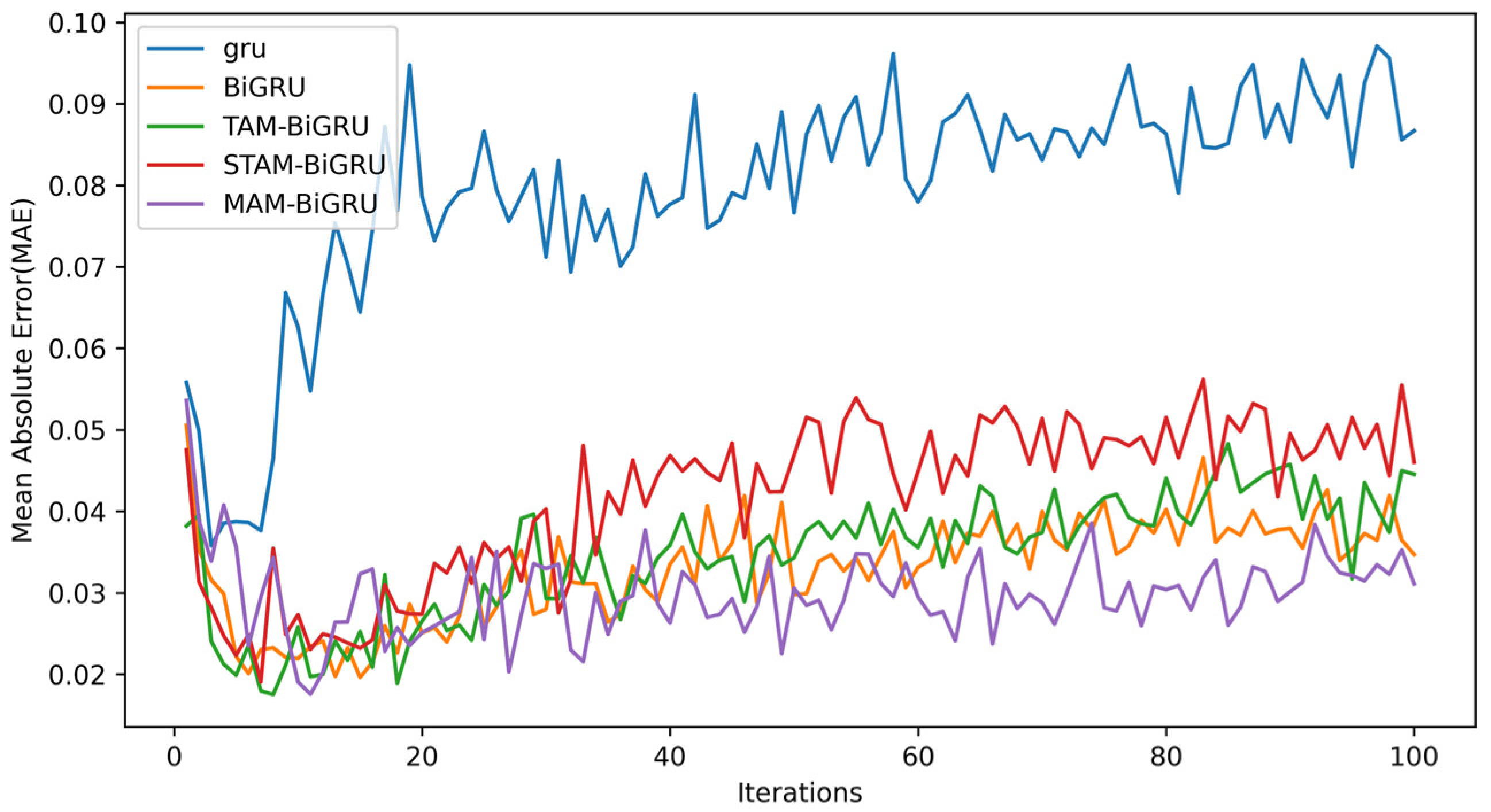
4.2.1. Loss Function Training Iteration Plot
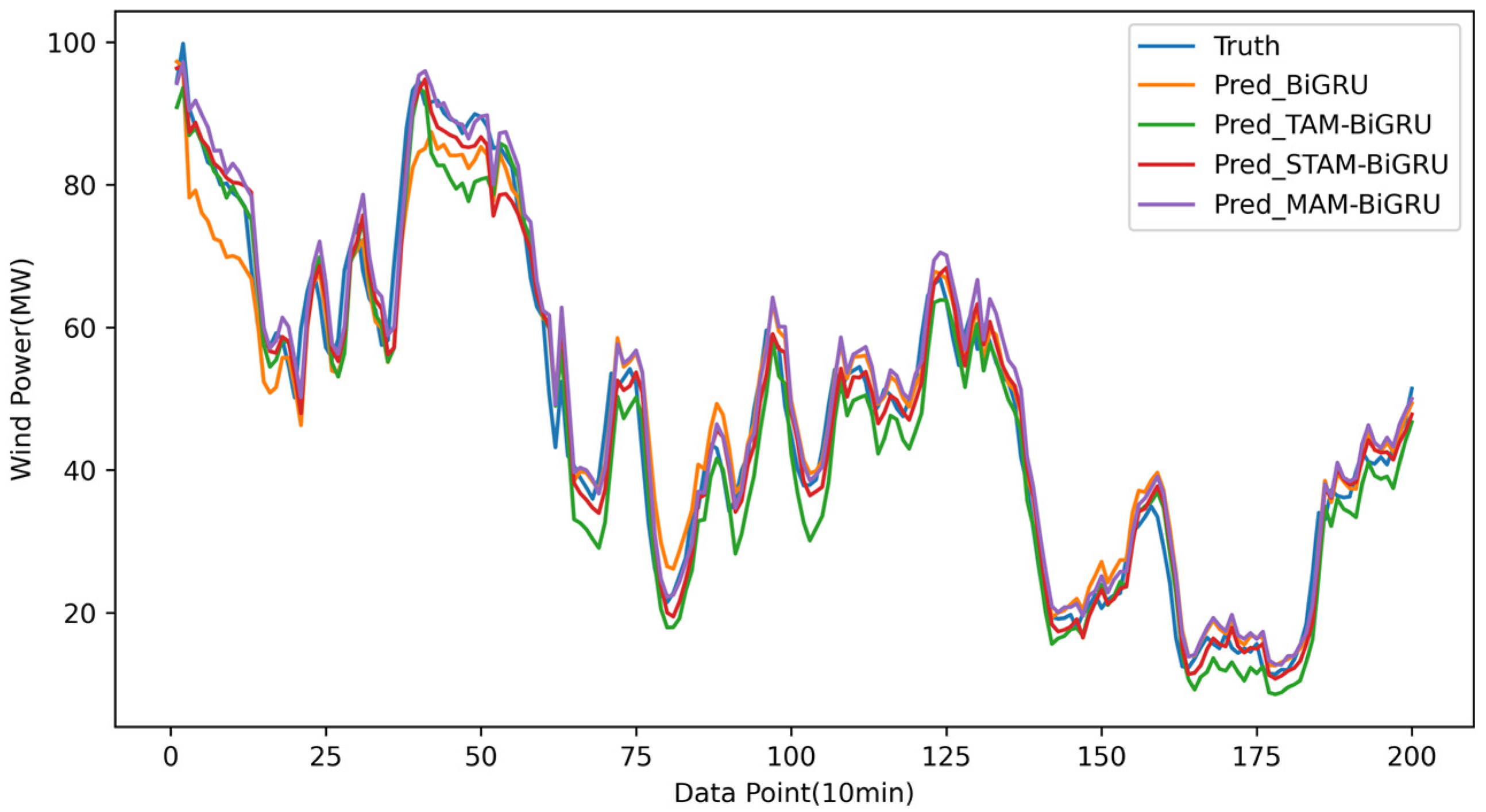
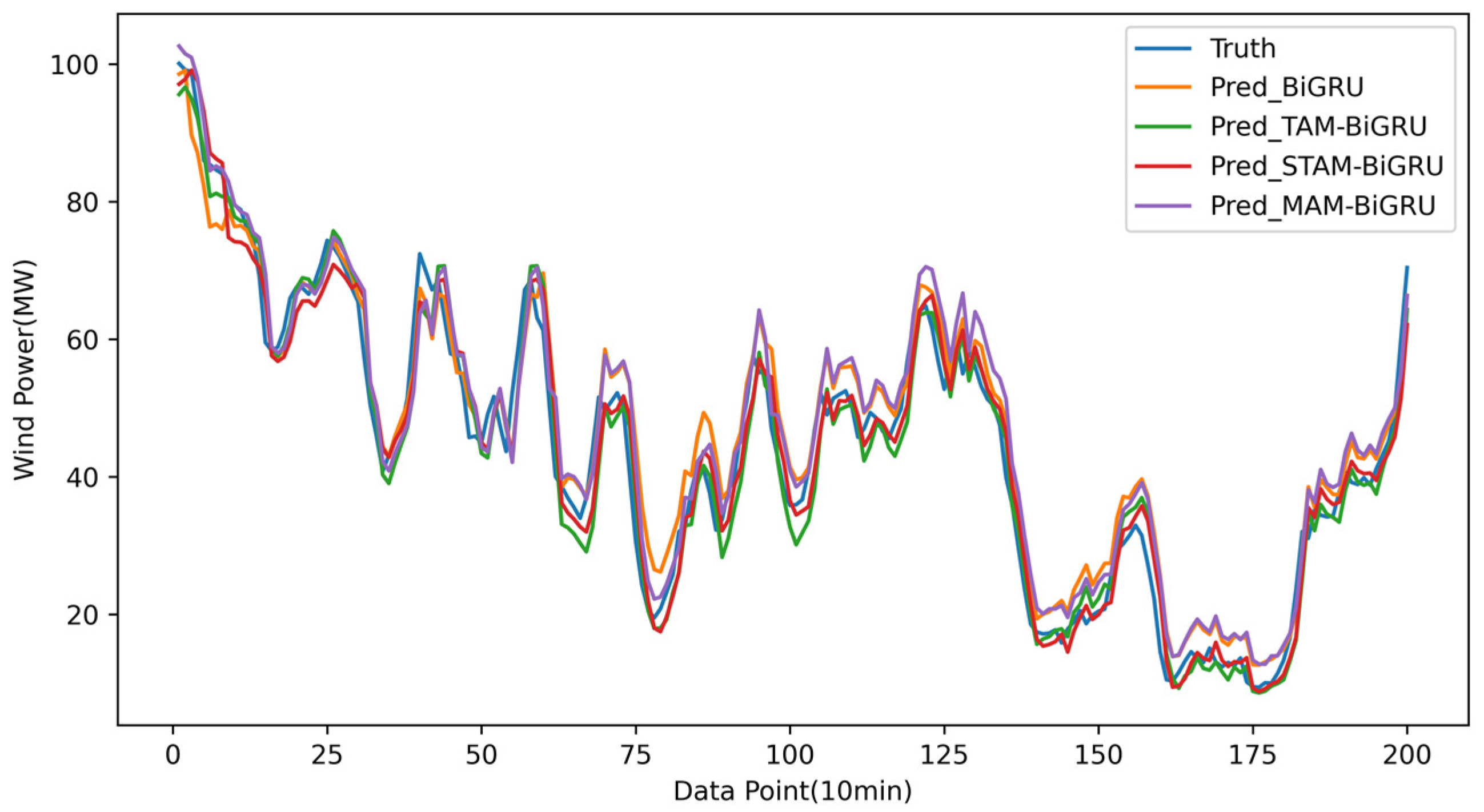
4.2.2. Plots of the Results of the Over-the-Top Multi-Step Prediction
4.2.3. Comparison Table of Prediction Accuracy of Models
- Attention models are generally better: Models incorporating attention (MAM-BiGRU, STAM-BiGRU, TAM-BiGRU) consistently outperform vanilla GRU and BiGRU networks.
- Temporal attention is effective but insufficient: While the TAM-BiGRU effectively captures long-term dependencies—yielding a higher accuracy than the GRU/BiGRU—it still neglects spatial interactions among input variables.
- Limitations of single-layer spatio-temporal attention: The STAM-BiGRU improves short-term forecasts but degrades markedly over multi-step horizons, as its single spatial attention layer cannot fully model complex inter-variable relationships and is vulnerable to irrelevant feature noise.
- Advantages of multi-layer spatio-temporal attention: The proposed MAM-BiGRU, with its stacked spatial and temporal attention modules, more comprehensively extracts multimodal features, preserves critical dependencies between the target and auxiliary sequences, and achieves the highest accuracy and stability in short-term multi-step predictions under complex offshore conditions.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Attention Mechanism |
| NWP | Numerical Weather Prediction |
| AR | Autoregressive |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| BPNN | Backpropagation Neural Network |
| ELM | Extreme Learning Machine |
| WPD | Wavelet Packet Decomposition |
| LSTM | Long Short-Term Memory Network |
| CNN | Convolutional Neural Network |
| ARMA | Autoregressive Moving Average |
| DWT | Discrete Wavelet Transform |
| EEMD | Ensemble Empirical Mode |
| BA | Bi-Attention Mechanism |
| CSO | Crisscross Optimization Algorithm |
| MAM | Multi-Layer Attention Mechanism |
| BiGRU | Bidirectional Gating Recurrent Unit |
| DSAM | Dual Spatial Attention Mechanism |
| TAM | Temporal Attention Mechanism |
| RNN | Recurrent Neural Network |
| GRU | Gating Recurrent Unit |
| STAM | Spatio-Temporal Attention Mechanism |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| MSTAM | Multi-Layer Spatio-Temporal Attention Mechanism |
References
- Desalegn, B.; Gebeyehu, D.; Tamrat, B.; Tadiwose, T.; Lata, A. Onshore versus offshore wind power trends and recent study practices in modeling of wind turbines’ life-cycle impact assessments. Clean. Eng. Technol. 2023, 17, 100691. [Google Scholar] [CrossRef]
- Global Wind Energy Council. Global Wind Energy Council Report 2019. 2020. Available online: http://arxiv.org/abs/1704.02971 (accessed on 26 July 2025).
- Abdel-Aty, A.-H.; Nisar, K.S.; Alharbi, W.R.; Owyed, S.; Alsharif, M.H. Boosting wind turbine performance with advanced smart power prediction: Employing a hybrid AR–MA–LSTM technique. Alex. Eng. J. 2024, 96, 58–71. [Google Scholar] [CrossRef]
- de Castro, M.; Salvador, S.; Gómez-Gesteira, M.; Costoya, X.; Carvalho, D.; Sanz-Larruga, F.J.; Gimeno, L. Europe, China and the United States: Three different approaches to the development of offshore wind energy. Renew. Sustain. Energy Rev. 2019, 109, 55–70. [Google Scholar] [CrossRef]
- Lu, S.; Gao, Z.; Xu, Q.; Jiang, C.; Zhang, A.; Wang, X. Class-imbalance privacy-preserving federated learning for decentralized fault diagnosis with biometric authentication. IEEE Trans. Ind. Inform. 2022, 18, 9101–9111. [Google Scholar] [CrossRef]
- Li, M.; Jiang, X.; Carroll, J.; Negenborn, R.R. A multi-objective maintenance strategy optimization framework for offshore wind farms considering uncertainty. Appl. Energy 2022, 321, 119284. [Google Scholar] [CrossRef]
- Choi, Y.; Park, S.; Choi, J.; Lee, G.; Lee, M. Evaluating offshore wind power potential in the context of climate change and technological advancement: Insights from Republic of Korea. Renew. Sustain. Energy Rev. 2023, 183, 113497. [Google Scholar] [CrossRef]
- Hanifi, S.; Liu, X.; Lin, Z.; Lotfian, S. A critical review of wind power forecasting methods—Past, present and future. Energies 2020, 13, 3764. [Google Scholar] [CrossRef]
- Zhang, W.; He, Y.; Yang, S. A multi-step probability density prediction model based on Gaussian approximation of quantiles for offshore wind power. Renew. Energy 2023, 202, 992–1011. [Google Scholar] [CrossRef]
- Wu, Z.; Xia, X.; Xiao, L.; Liu, Y. Combined model with secondary decomposition-model selection and sample selection for multi-step wind power forecasting. Appl. Energy 2020, 261, 114345. [Google Scholar] [CrossRef]
- Poggi, P.; Muselli, M.; Notton, G.; Cristofari, C.; Louche, A. Forecasting and simulating wind speed in Corsica by using an auto-regressive model. Energy Convers. Manag. 2003, 44, 3177–3196. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Liang, X.; Li, Y. Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks. Appl. Energy 2015, 157, 183–194. [Google Scholar] [CrossRef]
- Rahimilarki, R.; Gao, Z.; Zhang, A.; Binns, R.R. Robust neural network fault estimation approach for nonlinear dynamic systems with applications to wind turbine systems. IEEE Trans. Ind. Inform. 2019, 15, 6302–6312. [Google Scholar] [CrossRef]
- Yan, L.; Hu, P.; Li, C.; Yao, Y.; Xing, L.; Lei, F.; Zhu, N. The performance prediction of ground source heat pump system based on monitoring data and data mining technology. Energy Build. 2016, 127, 1085–1095. [Google Scholar] [CrossRef]
- Zhao, Y.; Ye, L.; Li, Z.; Song, X.; Lang, Y.; Su, J. A novel bidirectional mechanism based on time series model for wind power forecasting. Appl. Energy 2016, 177, 793–803. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, J. A hybrid forecasting approach applied in wind speed forecasting based on a data processing strategy and an optimized artificial intelligence algorithm. Energy 2018, 160, 87–100. [Google Scholar] [CrossRef]
- Lu, P.; Ye, L.; Zhao, Y.; Dai, B.; Pei, M.; Li, Z. Feature extraction of meteorological factors for wind power prediction based on variable weight combined method. Renew. Energy 2021, 179, 1925–1939. [Google Scholar] [CrossRef]
- Chen, H. Cluster-based ensemble learning for wind power modeling from meteorological wind data. Renew. Sustain. Energy Rev. 2022, 167, 112652. [Google Scholar] [CrossRef]
- Liu, H.; Yang, L.; Zhang, B.; Zhang, Z. A two-channel deep network based model for improving ultra-short-term prediction of wind power via utilizing multi-source data. Energy 2023, 283, 128510. [Google Scholar] [CrossRef]
- Hanifi, S.; Zare-Behtash, H.; Cammarano, A.; Lotfian, S. Offshore wind power forecasting based on WPD and optimised deep learning methods. Renew. Energy 2023, 218, 119241. [Google Scholar] [CrossRef]
- Qin, Y.; Song, D.; Chen, H.; Cheng, W.; Jiang, G.; Cottrell, G. A dual-stage attention-based recurrent neural network for time series prediction. arXiv 2017, arXiv:1704.02971. [Google Scholar]
- Meng, A.; Chen, S.; Ou, Z.; Ding, W.; Zhou, H.; Fan, J.; Yin, H. A hybrid deep learning architecture for wind power prediction based on bi-attention mechanism and crisscross optimization. Energy 2022, 238, 121795. [Google Scholar] [CrossRef]
- Wang, X.; Cai, X.; Li, Z. Ultra-short-term wind power forecasting method based on a cross LOF preprocessing algorithm and an attention mechanism. Power Syst. Prot. Control. 2020, 48, 92–99. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. Paper No. 1409.0473. [Google Scholar]
- Shi, Y.; Meng, J.; Wang, J. Seq2seq model with RNN attention for abstractive summarization. In Proceedings of the 2019 International Conference on Computational Linguistics & Intelligent Text Processing, Santa Fe, NM, USA, 10–16 April 2019. [Google Scholar]
- Yin, R.; Zhang, Y.; Zhou, X.; Wang, L.; Li, Q.; Chen, S. Time series computational prediction of vaccines for Influenza A H3N2 with recurrent neural networks. J. Bioinform. Comput. Biol. 2020, 18, 1023–1039. [Google Scholar] [CrossRef]
- Lin, J.; Wang, Y.; Yu, H.; Jian, L. Conceptual design of inflatable Savonius wind turbine and performance investigation of varying thickness and arc angle of blade. In Proceedings of the 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2), Hangzhou, China, 15–18 December 2023; pp. 1370–1376. [Google Scholar]




| Parameter Symbol | Parameter Value |
|---|---|
| Input Dimension | 96 * 6 |
| Time Steps | 96 |
| BiGRU Layer Length | 64 |
| BiGRU Activation Function | Relu |
| Attention Dimension | 3 |
| Batch Size | 64 |
| Learning Rate | 0.0001 |
| Epoch | 100 |
| Dropout Prob | 0.3 |
| Predicted Step Size | GRU | BiGRU | TAM-BiGRU | STAM-BiGRU | MAM-BiGRU |
|---|---|---|---|---|---|
| Step 1 (15 min) | 0.0258 | 0.0253 | 0.0240 | 0.0237 | 0.0216 |
| Step 3 (45 min) | 0.0316 | 0.0310 | 0.0294 | 0.0290 | 0.0265 |
| Step 5 (75 min) | 0.0568 | 0.0557 | 0.0529 | 0.0521 | 0.0475 |
| Step 8 (2 h) | 0.0791 | 0.0775 | 0.0736 | 0.0725 | 0.0659 |
| Step 16 (4 h) | 0.0834 | 0.0817 | 0.0776 | 0.0765 | 0.0692 |
| Step 32 (8 h) | 0.0905 | 0.0887 | 0.0843 | 0.0830 | 0.0757 |
| Step 48 (12 h) | 0.0920 | 0.0902 | 0.0857 | 0.0844 | 0.0766 |
| Step 96 (24 h) | 0.1121 | 0.1099 | 0.1044 | 0.1023 | 0.0932 |
| Predicted Step Size | GRU | BiGRU | TAM-BiGRU | STAM-BiGRU | MAM-BiGRU |
|---|---|---|---|---|---|
| Step 1 (15 min) | 0.0315 | 0.0309 | 0.0293 | 0.0289 | 0.0264 |
| Step 3 (45 min) | 0.0376 | 0.0368 | 0.0350 | 0.0345 | 0.0315 |
| Step 5 (75 min) | 0.0623 | 0.0611 | 0.0580 | 0.0571 | 0.0520 |
| Step 8 (2 h) | 0.0756 | 0.0741 | 0.0704 | 0.0693 | 0.0629 |
| Step 16 (4 h) | 0.0829 | 0.0812 | 0.0796 | 0.0785 | 0.0697 |
| Step 32 (8 h) | 0.0960 | 0.0941 | 0.0894 | 0.0880 | 0.0803 |
| Step 48 (12 h) | 0.1176 | 0.1152 | 0.1095 | 0.1078 | 0.0979 |
| Step 96 (24 h) | 0.1392 | 0.1364 | 0.1296 | 0.1252 | 0.1168 |
| Predicted Step Size | MAE | RMSE | ||||
|---|---|---|---|---|---|---|
| GRU | BiGRU | MAM-BiGRU | GRU | BiGRU | MAM-BiGRU | |
| Step 1 (15 min) | 0.0254 | 0.0248 | 0.0238 | 0.0320 | 0.0307 | 0.0261 |
| Step 3 (45 min) | 0.0313 | 0.0306 | 0.0292 | 0.0373 | 0.0370 | 0.0312 |
| Step 5 (75 min) | 0.0573 | 0.0554 | 0.0534 | 0.0628 | 0.0609 | 0.0518 |
| Step 8 (2 h) | 0.0789 | 0.0780 | 0.0733 | 0.0761 | 0.0739 | 0.0635 |
| Step 16 (4 h) | 0.0839 | 0.0815 | 0.0782 | 0.0826 | 0.0817 | 0.0694 |
| Step 32 (8 h) | 0.0901 | 0.0893 | 0.0848 | 0.0965 | 0.0938 | 0.0807 |
| Step 48 (12 h) | 0.0926 | 0.0899 | 0.0854 | 0.01172 | 0.1158 | 0.0975 |
| Step 96 (24 h) | 0.1118 | 0.1105 | 0.1041 | 0.1398 | 0.1361 | 0.1173 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Lin, Y.; Li, S.; Gao, X. Prediction Model of Offshore Wind Power Based on Multi-Level Attention Mechanism and Multi-Source Data Fusion. Electronics 2025, 14, 3183. https://doi.org/10.3390/electronics14163183
Xu Y, Lin Y, Li S, Gao X. Prediction Model of Offshore Wind Power Based on Multi-Level Attention Mechanism and Multi-Source Data Fusion. Electronics. 2025; 14(16):3183. https://doi.org/10.3390/electronics14163183
Chicago/Turabian StyleXu, Yuanyuan, Yixin Lin, Shuhao Li, and Xiutao Gao. 2025. "Prediction Model of Offshore Wind Power Based on Multi-Level Attention Mechanism and Multi-Source Data Fusion" Electronics 14, no. 16: 3183. https://doi.org/10.3390/electronics14163183
APA StyleXu, Y., Lin, Y., Li, S., & Gao, X. (2025). Prediction Model of Offshore Wind Power Based on Multi-Level Attention Mechanism and Multi-Source Data Fusion. Electronics, 14(16), 3183. https://doi.org/10.3390/electronics14163183





