Dependent Task Graph Offloading Model Based on Deep Reinforcement Learning in Mobile Edge Computing
Abstract
1. Introduction
- Unlike most existing MEC works, which focus on isolated task offloading assignments, we propose a low-complexity dynamic multi-task offloading framework. In order to adjust to dynamic offloading circumstances, this framework dynamically allocates computing resources according to the number of tasks and their dependencies.
- We formulate the offloading decision-making problem for DAG-based tasks as a Markov Decision Process (MDP), incorporating a carefully designed state–action space and reward function. To solve this, we develop a dependent task graph offloading model—APPGM. This model leverages an attention-based network to model extended dependencies among task inputs and translate task representations into offloading decisions. Notably, the model can learn near-optimal offloading strategies without relying on expert knowledge.
- In order to enhance the effectiveness of the attention module, we employ a GRU (Gated Recurrent Unit)-driven RNN (Recurrent Neural Network) model trained with clipped surrogate loss functions combined with first-order approximation techniques. This training approach leads to enhanced comprehensive profits () of the offloading system.
- We conduct extensive simulation experiments using synthetic DAGs to evaluate the performance of our proposed method. The results are compared against advanced heuristic baselines, demonstrating the superior effectiveness of our approach.
2. Related Works
2.1. Heuristic Algorithm-Based Task Offloading
2.2. DRL-Based Task Offloading
3. System Model and Problem Formulation
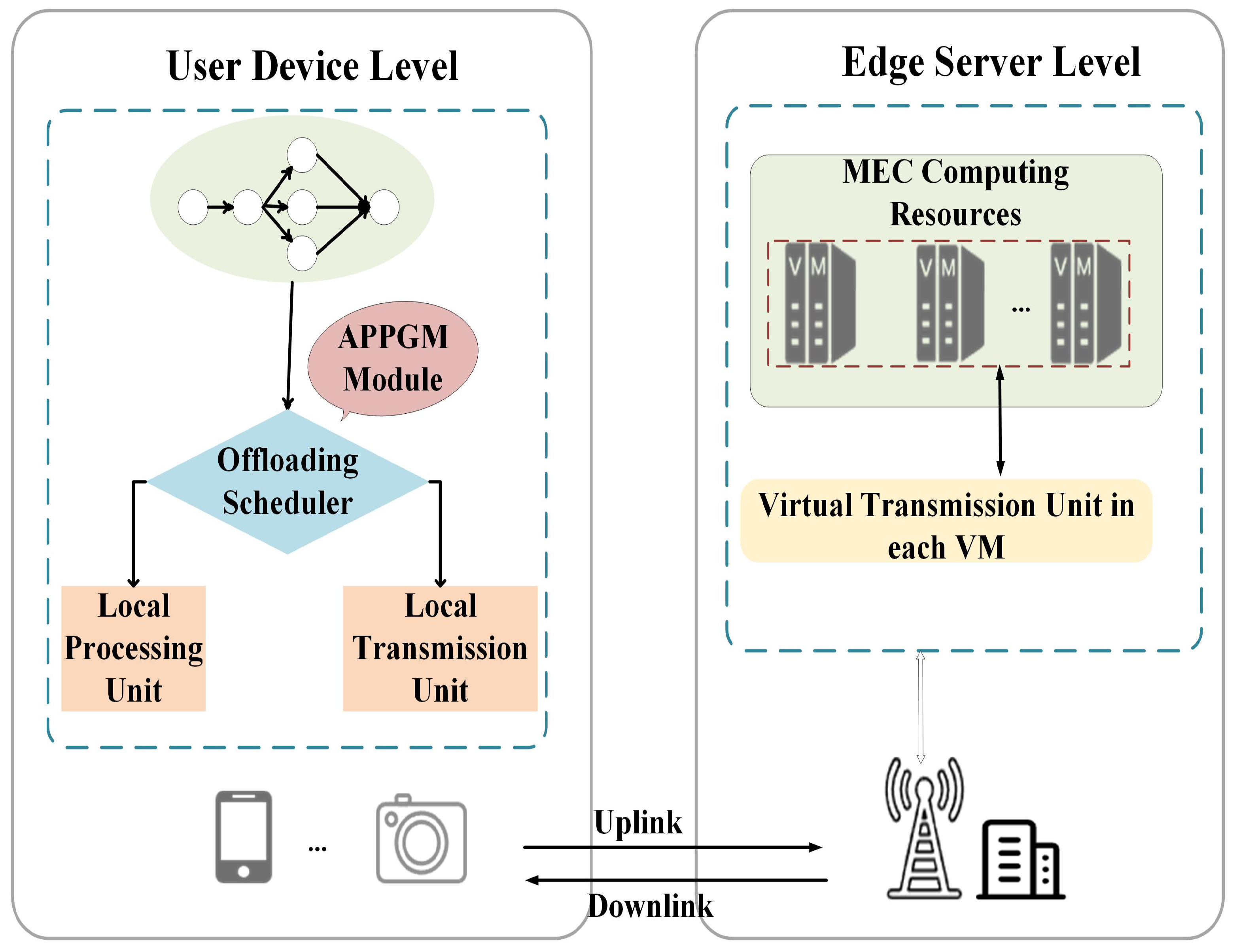
3.1. System Architecture Overview
3.2. Latency Model
3.2.1. Local Execution
3.2.2. Offloaded Execution
3.3. Energy Consumption Model
3.3.1. Local Execution
3.3.2. Offloaded Execution
3.4. Optimization Objective
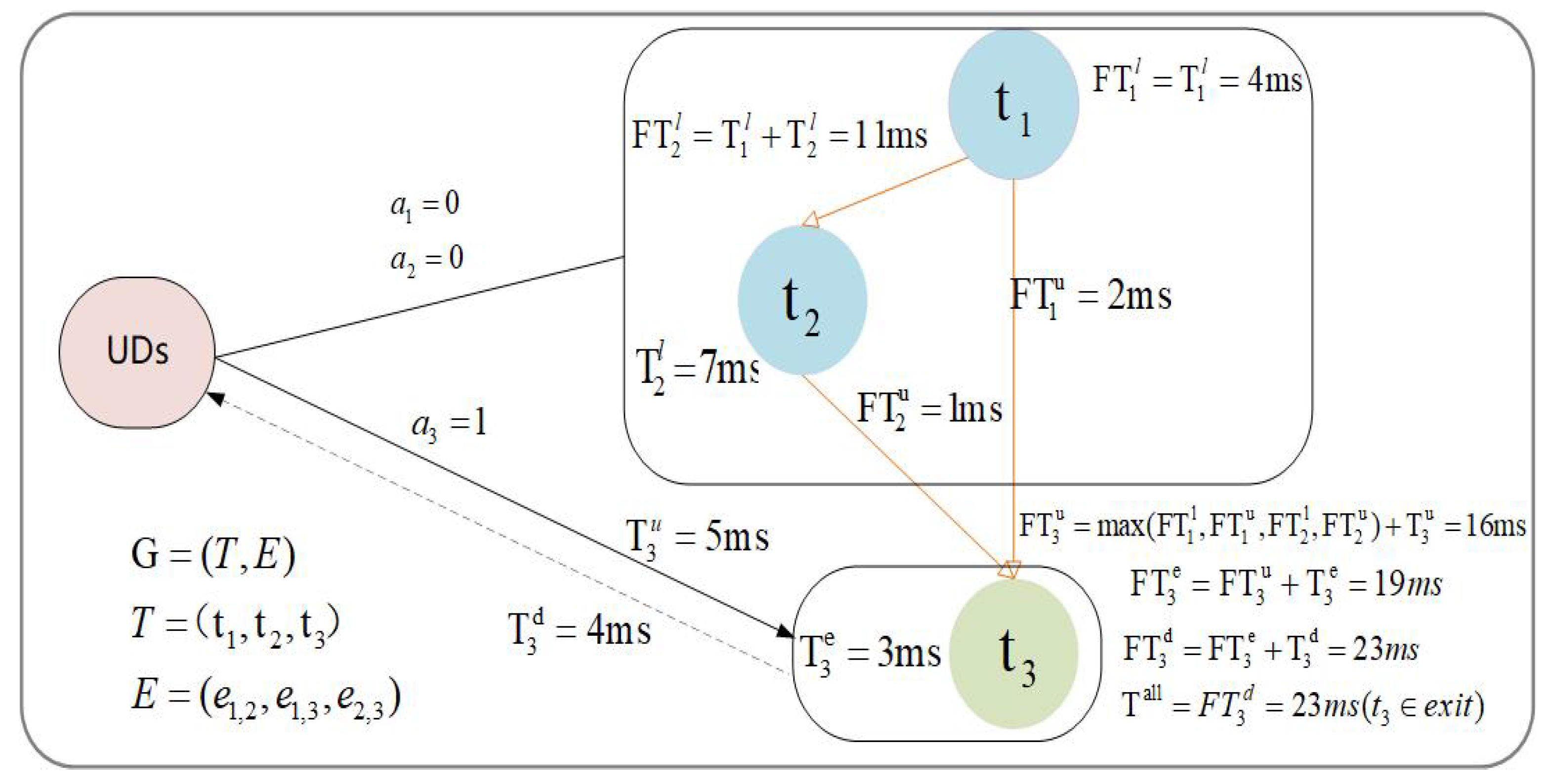
3.5. Task Topological Sorting Model
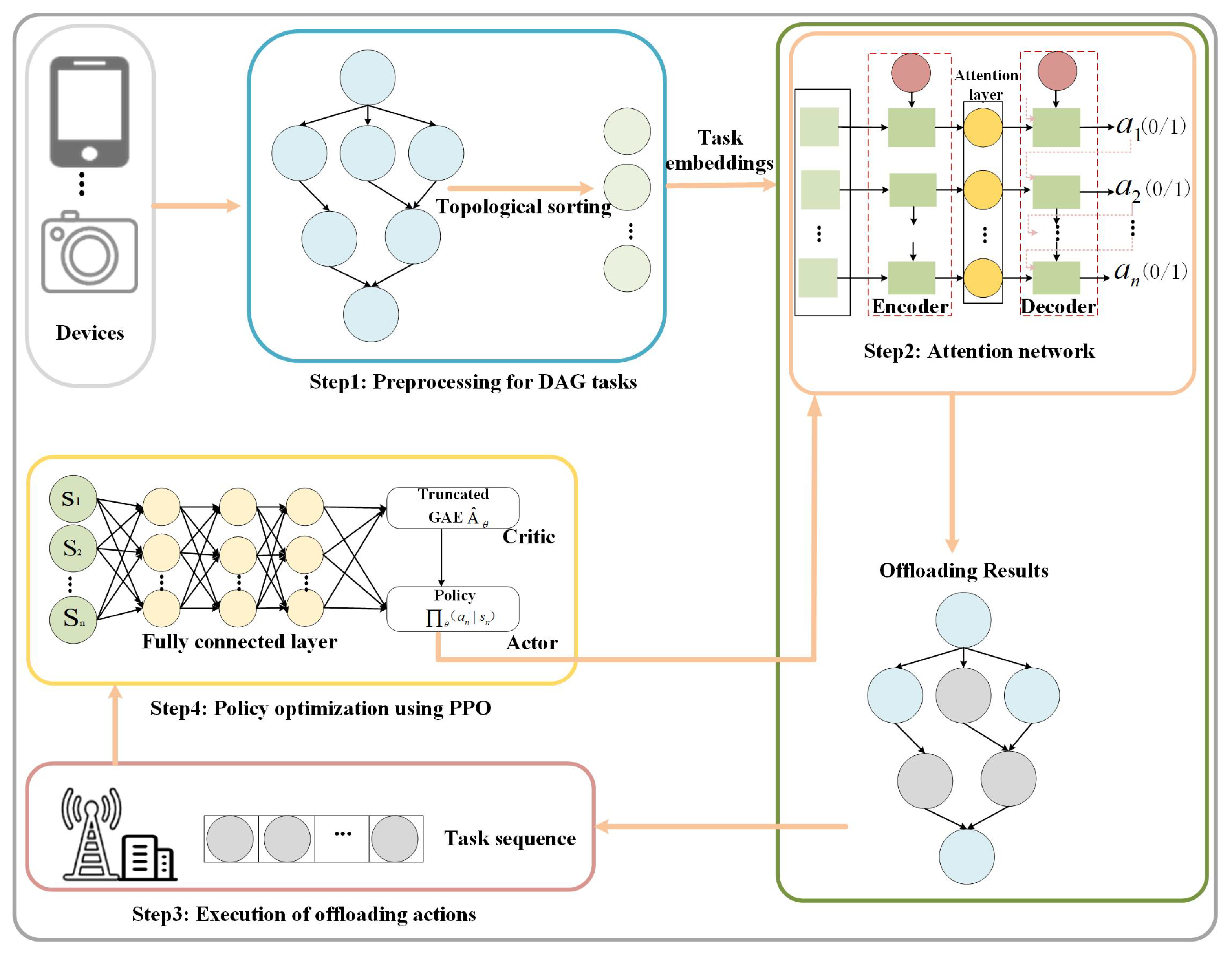
4. Attention-Based Proximal Policy Optimization for Task Graph Offloading Model (APPGM)
4.1. Construction of MDP
- (1)
- State Space
- (2)
- Action Space
- (3)
- Reward Function
4.2. The APPGM Module Design
- (1)
- The Attention Mechanism Network for APPGM
- (2)
- The Training Process of the APPGM
5. Simulation Results and Discussion
5.1. Simulation Settings and Hyperparameter Details
- Greedy Algorithm: Offloads the task to the location (local or edge) that yields a better combined benefit based on immediate comparison.
- HEFT Algorithm: A heuristic static DAG scheduling algorithm based on the earliest finish time strategy.
- Round Robin (RR): Tasks in the DAG are alternately assigned between local processing and edge computing.
- Random Strategy: Each task node is randomly allocated to either local execution or edge computing, while ensuring dependency constraints are respected.
5.2. Results Analysis
5.2.1. Impact of Weight Preference
5.2.2. Impact of Transmission Rate
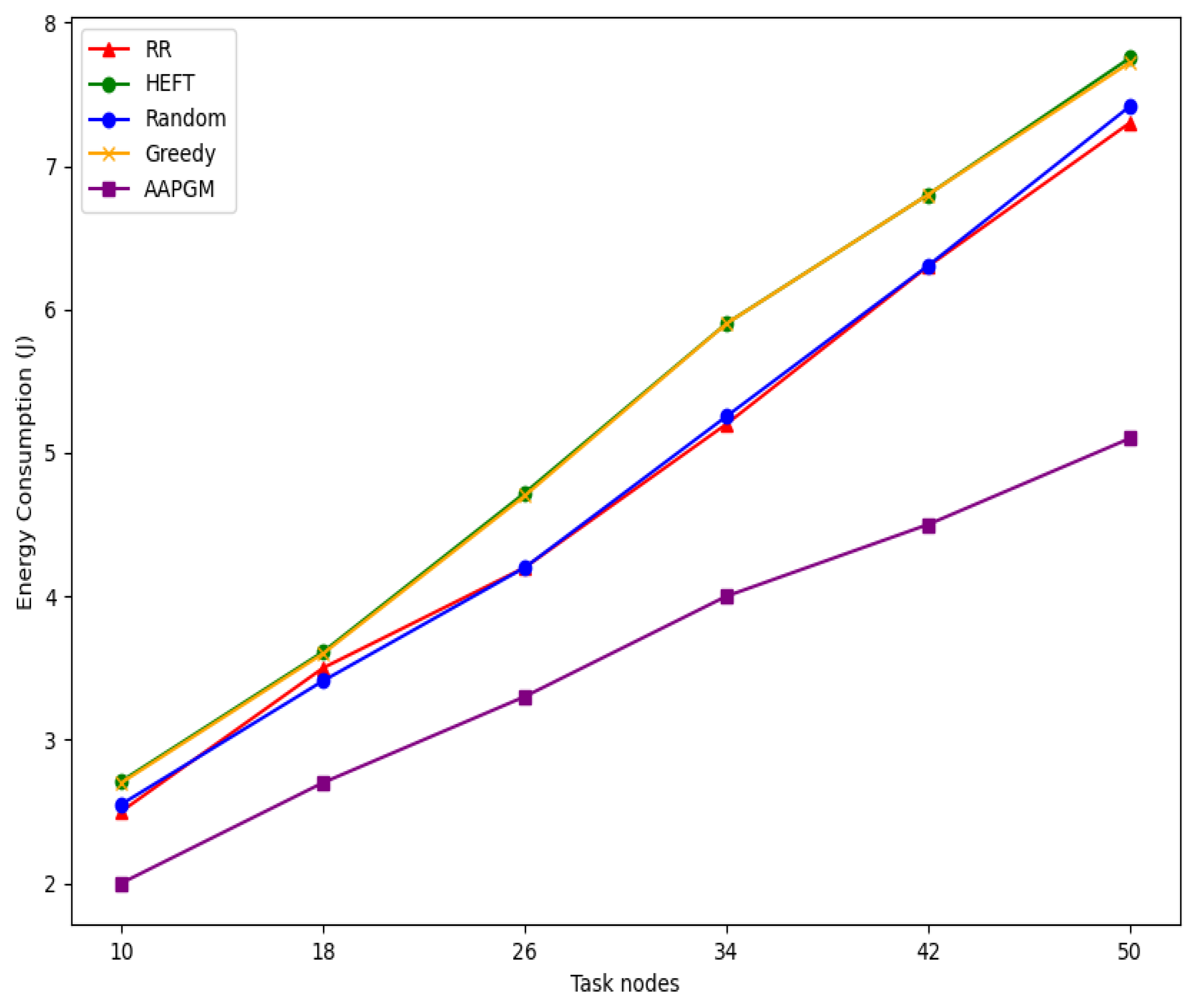
5.2.3. Impact of Task Node Scale
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bai, T.; Pan, C.; Deng, Y.; Elkashlan, M.; Nallanathan, A.; Hanzo, L. Latency Minimization for Intelligent Reflecting Surface Aided Mobile Edge Computing. IEEE J. Sel. Areas Commun. 2020, 38, 2666–2682. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J.; Min, G.; Zhan, W.; Zomaya, A.Y.; Georgalas, N. Dependent Task Offloading for Edge Computing Based on Deep Reinforcement Learning. IEEE Trans. Comput. 2022, 71, 2449–2461. [Google Scholar] [CrossRef]
- Sun, Z.; Mo, Y.; Yu, C. Graph-Reinforcement-Learning-Based Task Offloading for Multiaccess Edge Computing. IEEE Internet Things J. 2023, 10, 3138–3150. [Google Scholar] [CrossRef]
- Sabella, D.; Sukhomlinov, V.; Trang, L.; Kekki, S.; Paglierani, P.; Rossbach, R. Developing Software for Multi-Access Edge Computing; ETSI White Paper No. 20; ETSI: Sophia Antipolis, France, 2019. [Google Scholar]
- Masoud, A.; Haider, A.; Khoshvaght, P.; Soleimanian, F.; Moghaddasi, K.; Rajabi, S. Optimizing Task Offloading with Metaheuristic Algorithms Across Cloud, Fog, and Edge Computing Networks: A Comprehensive Survey and State-of-the-Art Schemes. Sustain. Comput. Inf. Syst. 2025, 45, 101080. [Google Scholar]
- Shi, Y.; Yang, K.; Jiang, T.; Zhang, J.; Letaief, K.B. Communication-Efficient Edge AI: Algorithms and Systems. IEEE Commun. Surv. Tutor. 2020, 22, 2167–2191. [Google Scholar] [CrossRef]
- Saeik, F.; Avgeris, M.; Spatharakis, D.; Santi, N.; Dechouniotis, D.; Violos, J. Task Offloading in Edge and Cloud Computing: A Survey on Mathematical, Artificial Intelligence and Control Theory Solutions. Comput. Netw. 2021, 195, 108177. [Google Scholar] [CrossRef]
- Lin, X.; Wang, Y.; Xie, Q.; Pedram, M. Task scheduling with dynamic voltage and frequency scaling for energy minimization in the mobile cloud computing environment. IEEE Trans. Services Comput. 2015, 8, 175–186. [Google Scholar] [CrossRef]
- Mach, P.; Becvar, Z. Mobile edge computing: A survey on architecture and computation offloading. IEEE Commun. Surveys Tuts. 2017, 19, 1628–1656. [Google Scholar] [CrossRef]
- Meng, J.; Tan, H.; Xu, C.; Cao, W.; Liu, L.; Li, B. Dedas: Online task dispatching and scheduling with bandwidth constraint in edge computing. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 2287–2295. Available online: https://ieeexplore.ieee.org/document/8737577 (accessed on 24 June 2024).
- Tran, T.X.; Pompili, D. Joint task offloading and resource allocation for multi-server mobile-edge computing networks. IEEE Trans. Veh. Technol. 2019, 68, 856–868. [Google Scholar] [CrossRef]
- Schrittwieser, J.; Antonoglou, I.; Hubert, T.; Simonyan, K.; Sifre, L.; Schmitt, S. Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model. Nature 2020, 588, 604–609. [Google Scholar] [CrossRef]
- Satheeshbabu, S.; Uppalapati, N.K.; Fu, T.; Krishnan, G. Continuous Control of a Soft Continuum Arm Using Deep Reinforcement Learning. In Proceedings of the 3rd IEEE International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 15 May–15 July 2020; pp. 497–503. Available online: https://ieeexplore.ieee.org/document/9116003 (accessed on 2 June 2025).
- Zhang, T.; Shen, S.; Mao, S.; Chang, G.-K. Delay-Aware Cellular Traffic Scheduling with Deep Reinforcement Learning. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Taipei, Taiwan, 7–11 December 2020; pp. 1–6. Available online: https://ieeexplore.ieee.org/document/9322560 (accessed on 29 July 2024).
- Zhan, Y.; Guo, S.; Li, P.; Zhang, J. A Deep Reinforcement Learning Based Offloading Game in Edge Computing. IEEE Trans. Comput. 2020, 69, 883–893. [Google Scholar] [CrossRef]
- Moghaddasi, K.; Rajabi, S.; Gharehchopogh, F.S. Multi-Objective Secure Task Offloading Strategy for Blockchain-Enabled IoV-MEC Systems: A Double Deep Q-Network Approach. IEEE Access 2024, 12, 3437–3463. [Google Scholar] [CrossRef]
- Tang, M.; Wong, V.W.S. Deep Reinforcement Learning for Task Offloading in Mobile Edge Computing Systems. IEEE Trans. Mob. Comput. 2022, 21, 1985–1997. [Google Scholar] [CrossRef]
- Min, H.; Rahmani, A.M.; Ghaderkourehpaz, P.; Moghaddasi, K.; Hosseinzadeh, M. A Joint Optimization of Resource Allocation Management and Multi-Task Offloading in High-Mobility Vehicular Multi-Access Edge Computing Networks. Ad Hoc Netw. 2025, 166, 103656. [Google Scholar] [CrossRef]
- Moghaddasi, K.; Rajabi, S.; Gharehchopogh, F.S.; Ghaffari, A. An Advanced Deep Reinforcement Learning Algorithm for Three-Layer D2D-Edge-Cloud Computing Architecture for Efficient Task Offloading in the Internet of Things. Sustain. Comput. Inf. Syst. 2024, 43, 100992. [Google Scholar] [CrossRef]
- Huang, L.; Bi, S.; Zhang, Y.-J.A. Deep reinforcement learning for online computation offloading in wireless powered mobile-edge computing networks. IEEE Trans. Mobile Comput. 2020, 19, 2581–2593. [Google Scholar] [CrossRef]
- Mao, N.; Chen, Y.; Guizani, M.; Lee, G.M. Graph mapping offloading model based on deep reinforcement learning with dependent task. In Proceedings of the 2021 International Wireless Communications and Mobile Computing (IWCMC), Harbin, China, 28 June–2 July 2021; pp. 21–28. [Google Scholar]
- Liu, S.; Yu, Y.; Lian, X.; Feng, Y.; She, C.; Yeoh, P.L. Dependent Task Scheduling and Offloading for Minimizing Deadline Violation Ratio in Mobile Edge Computing Networks. IEEE J. Sel. Areas Commun. 2023, 41, 538–554. [Google Scholar] [CrossRef]
- Yan, J.; Bi, S.; Zhang, Y.J.A. Offloading and Resource Allocation with General Task Graph in Mobile Edge Computing: A Deep Reinforcement Learning Approach. IEEE Trans. Wireless Commun. 2020, 19, 5404–5419. [Google Scholar] [CrossRef]
- Zhu, Q.; Guo, J. Research on Dependent Task Offloading Based on Deep Reinforcement Learning. In Proceedings of the 6th International Conference on Natural Language Processing (ICNLP), Xi’an, China, 22–24 March 2024; pp. 705–709. Available online: https://ieeexplore.ieee.org/document/10692374 (accessed on 3 March 2025).
- Wang, J.; Hu, J.; Min, G.; Zomaya, A.Y.; Georgalas, N. Fast adaptive task offloading in edge computing based on meta reinforcement learning. IEEE Trans. Parallel Distrib. Syst. 2021, 32, 242–253. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, P.; Wang, J.; Guo, S. Just-in-time code offloading for wearable computing. IEEE Trans. Emerg. Topics Comput. 2015, 3, 74–83. [Google Scholar] [CrossRef]
- Mahmoodi, S.E.; Uma, R.N.; Subbalakshmi, K.P. Optimal joint scheduling and cloud offloading for mobile applications. IEEE Trans. Cloud Comput. 2019, 7, 301–313. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Q.; Gong, Y.; Zhang, K. Computation offloading and resource allocation for cloud assisted mobile edge computing in vehicular networks. IEEE Trans. Veh. Technol. 2019, 68, 7944–7956. [Google Scholar] [CrossRef]
- Hong, Z.; Chen, W.; Huang, H.; Guo, S.; Zheng, Z. Multi-hop cooperative computation offloading for industrial IoT–edge–cloud computing environments. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 2759–2774. [Google Scholar] [CrossRef]
- Wu, H.; Wolter, K.; Jiao, P.; Deng, Y.; Zhao, Y.; Xu, M. EEDTO: An energy-efficient dynamic task offloading algorithm for blockchain-enabled IoT-edge-cloud orchestrated computing. IEEE Internet Things J. 2021, 8, 2163–2176. [Google Scholar] [CrossRef]
- Yang, G.; Hou, L.; He, X.; He, D.; Chan, S.; Guizani, M. Offloading time optimization via Markov decision process in mobile-edge computing. IEEE Internet Things J. 2021, 8, 2483–2493. [Google Scholar] [CrossRef]
- Deng, M.; Tian, H.; Fan, B. Fine-granularity based application offloading policy in cloud-enhanced small cell networks. In Proceedings of the 2016 IEEE International Conference on Communications Workshops (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 638–643. Available online: https://ieeexplore.ieee.org/document/7503859 (accessed on 4 February 2023).
- Liu, J.; Ren, J.; Zhang, Y.; Peng, X.; Zhang, Y.; Yang, Y. Efficient dependent task offloading for multiple applications in MEC-cloud system. IEEE Trans. Mobile Comput. 2021; early access. [Google Scholar]
- Zou, J.; Hao, T.; Yu, C.; Jin, H. A3C-DO: A Regional Resource Scheduling Framework Based on Deep Reinforcement Learning in Edge Scenario. IEEE Trans. Comput. 2021, 70, 228–239. [Google Scholar] [CrossRef]
- Xiao, L.; Lu, X.; Xu, T.; Wan, X.; Ji, W.; Zhang, Y. Reinforcement learning-based mobile offloading for edge computing against jamming and interference. IEEE Trans. Commun. 2020, 68, 6114–6126. [Google Scholar] [CrossRef]
- Rahmani, A.M.; Haider, A.; Moghaddasi, K.; Gharehchopogh, F.S.; Aurangzeb, K.; Liu, Z. Self-learning adaptive power management scheme for energy-efficient IoT-MEC systems using soft actor-critic algorithm. Internet Things 2025, 31, 101587. [Google Scholar] [CrossRef]
- Ra, M.-R.; Sheth, A.; Mummert, L.; Pillai, P.; Wetherall, D.; Govindan, R. Odessa: Enabling Interactive Perception Applications on Mobile Devices. In Proceedings of the 9th International Conference on Mobile Systems, Applications, and Services (MobiSys), Bethesda, MD, USA, 28 June–1 July 2011; pp. 43–56. [Google Scholar]
- Chai, F.; Zhang, Q.; Yao, H.; Xin, X.; Gao, R.; Guizani, M. Joint multi-task offloading and resource allocation for mobile edge computing systems in satellite IoT. IEEE Trans. Veh. Technol. 2023, 72, 7783–7795. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]




| Notation | Description |
|---|---|
| The total count of tasks defined within the DAG structure [2] | |
| The i-th task in a DAG | |
| Predecessor and successor tasks corresponding to node in the DAG | |
| Dependency between task and task , where is the predecessor of | |
| Delays in uploading, execution, and downloading when task is offloaded | |
| Total delay when task is offloaded | |
| Local execution delay of task | |
| Delay of all tasks executed locally | |
| Total delay for completing the entire DAG | |
| The LPU and VPU clock frequencies | |
| Uplink and downlink transmission rates of the task | |
| Data size of task for upload and postprocessing | |
| CPU cycles required to execute task | |
| Available time of uplink, edge host, downlink, and local unit for task | |
| Energy consumption of all locally computed tasks | |
| Total energy consumption of the entire DAG [38] | |
| Energy consumption of local execution and offloading for task | |
| Delay benefit and energy consumption benefit from scheduling | |
| Uploading power and returning power for offloading tasks | |
| Comprehensive profit related to and | |
| Decision sequence for DAG task offloading | |
| C | Semantic vector in the attention layer |
| Encoder and decoder conversion functions | |
| Hidden states in encoder and decoder | |
| Weight value for hidden state in encoder |
| Parameter | Value |
|---|---|
| , | [25 KB, 150 KB] |
| , | 1 GHz, 9 GHz |
| , | 1.258 W, 1.181 W |
| , | {3, 5, 7, 9, 11, 13, 15, 17} Mbps |
| , | 0.5, 0.5 |
| , | 0.5, 0.5 |
| to cycles/s | |
| Encoder layer type | GRU |
| Encoder layers | 2 |
| Decoder layer type | GRU |
| Decoder layers | 2 |
| Encoder and Decoder Hidden Units | 256 |
| Learning rate | |
| Discount Factor [2] | 0.99 |
| Adv. Discount Factor [25] | 0.95 |
| Activation function | tanh |
| Clipping parameter | 0.2 |
| Nodes | APPGM | Greedy | HEFT | RR | Random | Significance (APPGM vs. Others) |
|---|---|---|---|---|---|---|
| 10 | 0.505 ± 0.006 | 0.287 ± 0.011 | 0.279 ± 0.013 | 0.330 ± 0.008 | 0.309 ± 0.012 | * p < 0.05 |
| 18 | 0.521 ± 0.005 | 0.288 ± 0.016 | 0.303 ± 0.014 | 0.354 ± 0.010 | 0.325 ± 0.015 | ** p < 0.01 |
| 26 | 0.524 ± 0.006 | 0.323 ± 0.011 | 0.308 ± 0.010 | 0.374 ± 0.020 | 0.328 ± 0.020 | ** p < 0.01 |
| 34 | 0.529 ± 0.011 | 0.341 ± 0.012 | 0.341 ± 0.030 | 0.369 ± 0.011 | 0.334 ± 0.008 | * p < 0.05 |
| 42 | 0.620 ± 0.007 | 0.356 ± 0.009 | 0.361 ± 0.022 | 0.378 ± 0.021 | 0.345 ± 0.014 | ** p < 0.01 |
| 50 | 0.644 ± 0.011 | 0.369 ± 0.016 | 0.371 ± 0.016 | 0.389 ± 0.013 | 0.355 ± 0.012 | ** p < 0.01 |
| Algorithm | Average Inference Time (ms) | Perfermance Evaluation |
|---|---|---|
| APPGM | 16.4 | Optimal performance with low latency |
| HEFT | 45.7 | Heuristic approach, slower speed |
| Greedy | 23.1 | Relatively fast, sub-optimal performance |
| RR | 12.2 | Fast, but with large fluctuations |
| Random | 9.5 | The fastest, yet with the poorest results |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, R.; Zhou, L.; Li, L.; Song, Y.; Xie, X. Dependent Task Graph Offloading Model Based on Deep Reinforcement Learning in Mobile Edge Computing. Electronics 2025, 14, 3184. https://doi.org/10.3390/electronics14163184
Guo R, Zhou L, Li L, Song Y, Xie X. Dependent Task Graph Offloading Model Based on Deep Reinforcement Learning in Mobile Edge Computing. Electronics. 2025; 14(16):3184. https://doi.org/10.3390/electronics14163184
Chicago/Turabian StyleGuo, Ruxin, Lunyu Zhou, Linzhi Li, Yuhui Song, and Xiaolan Xie. 2025. "Dependent Task Graph Offloading Model Based on Deep Reinforcement Learning in Mobile Edge Computing" Electronics 14, no. 16: 3184. https://doi.org/10.3390/electronics14163184
APA StyleGuo, R., Zhou, L., Li, L., Song, Y., & Xie, X. (2025). Dependent Task Graph Offloading Model Based on Deep Reinforcement Learning in Mobile Edge Computing. Electronics, 14(16), 3184. https://doi.org/10.3390/electronics14163184





