A Privacy-Enhanced Multi-Stage Dimensionality Reduction Vertical Federated Clustering Framework

Abstract

Federated Clustering (FL clustering) aims to discover latent knowledge in multi-source distributed data through clustering algorithms while preserving data privacy. Federated learning is categorized into horizontal and vertical federated learning based on data partitioning scenarios. Horizontal federated learning is applicable to scenarios with overlapping feature spaces but different sample IDs across parties. Vertical federated learning facilitates cross-institutional feature complementarity, which is particularly suited for scenarios with highly overlapping sample IDs yet significantly divergent features. As a classic clustering algorithm, k-means has seen extensive improvements and applications in horizontal federated learning. However, its application in vertical federated learning remains insufficiently explored, with room for enhancement in privacy protection and communication efficiency. Simultaneously, client feature imbalance may lead to biased clustering results. To improve communication efficiency, this paper introduces Product Quantization (PQ) to compress high-dimensional data into low-dimensional codes by generating local codebooks. Leveraging the inherent k-means algorithm within PQ, local training preserves data structures while overcoming privacy risks associated with traditional PQ methods that require server-side data reconstruction (which may leak data distributions). To enhance privacy without compromising performance, Multidimensional Scaling (MDS) maps codebook cluster centers into distance-preserving indices. Only these indices are uploaded to the server, eliminating the need for data reconstruction. The server executes k-means on the indices to minimize intra-group similarity and maximize inter-group divergence. This scheme retains original codebooks locally for strict privacy protection.The nested application of PQ and MDS significantly reduces communication volume and frequency while effectively alleviating clustering bias caused by client feature dimension imbalance. Validation on the MNIST dataset confirms that the approach maintains k-means clustering performance while meeting federated learning requirements for privacy and efficiency.

1. Introduction

Federated learning (FL) is a distributed machine learning approach whose core concept involves multiple clients (e.g., mobile devices or enterprises) collaboratively training a shared global model without sharing local data [1]. Federated learning clustering integrates federated learning and clustering algorithms to mine latent knowledge from multi-source distributed data while ensuring data privacy protection [2]. Federated learning faces multiple challenges including data heterogeneity [3,4], communication bottlenecks [1,5], and privacy protection [6].

Federated learning is categorized into horizontal federated learning (horizontal federated learning, HFL) [7] and vertical federated learning (vertical federated learning, VFL) [8] based on data distribution patterns. In horizontal federated learning, participating parties share identical features but possess distinct sample IDs [9]. In vertical federated learning scenarios, the data distribution pattern entails different clients owning distinct feature sets while sharing identical sample IDs. Horizontal federated learning finds widespread application in edge computing and IoT collaboration [10,11]. Vertical federated learning’s value lies in cross-institutional feature complementarity, which is particularly suitable for scenarios with highly overlapping sample IDs yet significantly divergent features, such as in healthcare [12], finance [13], and other industries.

Current research on federated clustering algorithms predominantly focuses on the horizontal federated domain, with relatively limited exploration in vertical federated settings. Compared to horizontal federated learning, vertical federated learning relies more heavily on high-frequency encrypted interactions and high-dimensional feature transmission [14], imposing greater demands on communication. Simultaneously, vertical federated learning requires multi-party collaboration to compute loss functions and gradients. Due to features being dispersed across different participants, it necessitates reliance on Secure Multi-Party Computation (MPC), homomorphic encryption (HE), and other technologies to achieve joint training under privacy protection, all incurring substantial computational costs [15].

In 2020, Avishek et al. proposed an iterative federated clustering algorithm, which achieves efficient clustering by alternately estimating user identities and optimizing model parameters [16]. This method holds significant reference value for feature alignment. In 2023, Zitao Li et al. proposed a differentially private k-means clustering algorithm based on the Flajolet–Martin (FM) technique [17]. By aggregating differentially private cluster centers and membership information of local data on an untrusted central server, they constructed a weighted grid as a summary of the global dataset, ultimately generating global centers by executing the k-means algorithm. Subsequently, in the paper [18], they introduced Flajolet–Martin (FM) sketches to encode local data and estimate cross-party marginal distributions under differential privacy constraints, thereby constructing a global Markov Random Field (MRF) model to generate high-quality synthetic data. Federico [19] proposed a vertical federated k-means algorithm based on homomorphic encryption and differential privacy protection, demonstrating its superior clustering performance (e.g., k-means loss and clustering accuracy) over traditional privacy-preserving k-means algorithms while maintaining the same privacy level. Li et al. [20] proposed a vertical federated density peaks clustering algorithm based on a hybrid encryption framework. Building upon the merged distance matrix, they introduced a more effective clustering method under nonlinear mapping, enhancing density peaks clustering (DPC) performance while addressing privacy protection issues in vertical federated learning (VFL). Duan et al. [21] introduced communication models for federated learning and three state-of-the-art algorithms, and proposed a k-median clustering optimization algorithm. Huang et al. [22] conducted an in-depth analysis of vertical federated clustering mechanisms, proposing a privacy attack model targeting vertical federated k-means clustering. Their findings revealed the possibility of reconstructing raw data in vertical federated learning, thereby causing data privacy leakage.

This study addresses the privacy protection issues of k-means clustering in vertical federated learning scenarios by proposing a federated clustering framework based on lightweight multi-stage dimensionality reduction. It primarily resolves three major challenges: privacy constraints, communication bottlenecks, and feature imbalance problems.

Our main contributions are as follows:

(1)

We innovatively propose a multi-stage dimensionality reduction framework applicable to vertical federated learning clustering based on Product Quantization (PQ) and Multidimensional Scaling (MDS) techniques. Locally, feature compression and codebook generation effectively reduce data volume, while PQ-quantized parameters inherently provide noise injection effects to enhance privacy. Innovatively, we introduce one-dimensional MDS embedding to map clustering centers in the codebook into distance-preserving indices. This achieves zero raw codebook upload, abandons data reconstruction on the server side, and fundamentally eliminates the risk of data distribution leakage.

(2)

The multi-stage dimensionality reduction mechanism significantly reduces transmitted data volume and communication frequency while ensuring clustering accuracy, thereby improving communication efficiency.

(3)

The combination of PQ dimensionality reduction and MDS embedding algorithms mitigates clustering bias caused by feature imbalance in vertical federated learning.

(4)

Extensive experiments on the MNIST dataset validate that our algorithm satisfies federated learning privacy requirements while preserving clustering accuracy.

The structure of our paper is arranged as follows: Section 2 discusses existing clustering algorithms, challenges in VFL, and theoretical analyses of various dimensionality reduction techniques; Section 3 details our algorithmic design; Section 4 presents the experimental process and results analysis conducted to validate our algorithm; finally, Section 5 concludes the paper.

2. Related Work

2.1. K-Means Clustering Algorithm

k-means is an unsupervised learning algorithm (Algorithm 1) that aims to partition n data objects into k clusters (k < n), such that similarity within the same cluster is maximized while similarity between different clusters is minimized [23].

The core principle involves iteratively optimizing cluster centroid positions to minimize the sum of squared errors (SSEs) within clusters:

$$\underset{C}{min}\sum _{k=1}^K\sum _{x\in C_k}\parallel x-{\mu }_k\parallel$$

where ${\mu }_k$ is the centroid of cluster $C_k$.

k-means exhibits linear time complexity growth [24], making it suitable for large-scale data while being simple, intuitive, and highly interpretable. However, it has several limitations: sensitivity to initial values [25], requirement of preset k-value, susceptibility to noise, and restrictions on cluster shapes. Its core challenges (k-value selection, sensitivity to initial centroids) can be mitigated through methods like the elbow method, silhouette coefficient, and k-means++.

Algorithm 1 k-means [23] algorithm steps.

Input: Dataset $X=\left\{x_1,x_2,\dots ,x_n\right\}$, number of clusters K, maximum iterations T. Output: Partitioning result of K clusters.     Steps:  1:    Randomly select k samples as initial cluster centroids ${\mu }_1^{\left(0\right)},{\mu }_2^{\left(0\right)},\dots ,{\mu }_3^{\left(0\right)}$,  2:    Iterate until convergence: (1) Assign each sample xi to the nearest cluster centroid: $$C_k^t=\{x_i:\parallel x_i-{\mu }_k^{\left(t\right)}{\parallel }^2\le \parallel x_i-{\mu }_j^{\left(t\right)}{\parallel }^2,\forall j\}$$ (2) Update cluster centroids as the mean of cluster members: $${\mu }_k^{\left(t\right)}={\displaystyle \frac{1}{\mid C_k^{\left(t\right)}\mid }}\sum _{x\in C_k^{\left(t\right)}}x$$ Termination conditions: i.  Centroid changes below threshold, ii.    Maximum iterations reached.

2.2. Vertical Federated Learning

Horizontal federated learning involves clients sharing the same feature space but having different sample spaces. Vertical federated learning, in contrast, deals with datasets sharing the same sample space but possessing different feature spaces. Vertical federated learning demonstrates broad application prospects across multiple fields such as healthcare, finance, government affairs, and agriculture. In the medical domain, different institutions (e.g., hospitals and insurance companies) may possess partial patient data but cannot directly share this information. Vertical federated learning enables data collaboration among these institutions while safeguarding patient privacy. For example, the 2022 paper [26] explored federated learning applications in healthcare, covering optimized algorithms, data distribution, privacy protection, and model architecture. Vertical federated learning finds significant applications in the financial sector. Within finance, data silos may exist among banks and financial institutions—for instance, banks hold customer transaction records while insurers possess customer health data. Through vertical federated learning, these entities can collaboratively train models without sharing raw data, enhancing accuracy in risk assessment and credit scoring. The 2023 paper [27] detailed such financial applications and proposed multiple privacy-preserving and security mechanisms. Dwarampudi et al. explored federated learning in smart agricultural systems in their paper [28], highlighting how it leverages machine learning capabilities while resolving data privacy concerns. The study emphasized that vertical federated learning can provide localized recommendations for specific agricultural conditions by integrating data from different geographical regions. This approach can also extend to edge computing scenarios such as poultry farming [29].

The vertical federated learning process comprises two stages: encrypted entity alignment (Private Set Intersection, PSI) (A Privacy-preserving Data Alignment Framework for Vertical Federated Learning) [30] and model training.

During the encrypted entity alignment stage, participants hash user IDs (e.g., using SHA-256) or encrypt them with RSA. They then perform secure intersection: exchanging encrypted IDs and comparing them through blinding and re-encryption techniques to avoid exposing non-overlapping samples. Ultimately, participants only learn the intersection ID list, with raw feature data remaining undisclosed [30].

In the model training phase, different participants own distinct feature spaces, while labels may be held by one party. To ensure privacy, encryption techniques (e.g., asymmetric encryption or homomorphic encryption) are typically employed during communication to transmit model updates or gradients, preventing data leakage. The central server or coordinator aggregates encrypted model updates from data providers securely [31].

Communication costs in vertical federated learning often become bottlenecks for training efficiency, particularly due to network heterogeneity among parties and the large volume of encrypted data. Coordinating communications incurs additional overhead. It is critical to minimize communication overhead without compromising model performance. As participant data dimensions increase, transmitting high-dimensional feature vectors significantly escalates communication burdens, requiring compression mechanisms to reduce bandwidth usage [32].

Privacy risks in vertical federated learning primarily stem from data distribution characteristics and multi-party data interactions. Sharing identical sample IDs across participants enables attackers to reconstruct user profiles through correlation analysis. During training, transmitting gradients or intermediate results may leak raw data distributions—for example, malicious participants could infer user scale or distribution during PSI. Model training requires collaborative computation of loss functions and gradients across parties. With features dispersed among participants, Secure Multi-Party Computation (MPC) and homomorphic encryption (HE) [31] are essential for privacy-preserving joint training, incurring substantial computational costs for security.

Two common approaches address privacy-security challenges: reducing communication volume (data quantity and transmission frequency) or transforming data. Reducing transmission volume and frequency simultaneously enhances communication efficiency.

Numerous approaches reduce communication volume, such as compression techniques including quantization, sparsification, model pruning, knowledge distillation, and embedding compression [33], which decrease transmitted model parameters. Quantization compresses gradients by reducing numerical precision, while sparsification transmits only critical gradient components while discarding insignificant ones. Communication strategies may also be optimized—for example, clients performing multiple local updates before server communication, or randomly selecting subsets of clients per round. Alternatively, constructing virtual datasets for unified server-side training reduces communication frequency.

Data processing methods involve homomorphic encryption, secure multi-party computation, differential privacy, random masking, etc. Current solutions face limitations: fully homomorphic encryption offers theoretical security but suffers from slow speeds; partially homomorphic variants are more practical yet provide compromised protection [34]. Differential privacy sacrifices model accuracy through noise injection [35].

Vertical federated learning faces an additional challenge: when participants (clients) exhibit significant disparities in feature quantities (e.g., one party’s feature dimension dA ≫ dB), this substantially impacts model performance, training efficiency, and privacy-security. The high-dimensional feature party carries greater information volume, potentially causing the model to over-rely on its features and drowning out the contributions of the low-dimensional party. In secure aggregation, the party with fewer features is vulnerable to statistical correlation attacks by the high-dimensional party. The computational/communication overhead of the high-dimensional party A far exceeds that of B, becoming a system bottleneck. Existing solutions to this problem include mapping features from different clients into a unified space and employing dual regularization (local consistency + complementary consistency) to reduce distribution discrepancies [36]. Other methods prioritize adjusting client weights based on feature importance; for instance, the FedFSA algorithm dynamically weights the loss function according to feature quality [37]. Constraining the feature norms of local model outputs can also prevent high-dimensional clients from dominating updates and enhance generalization capability [37]. Embedding compression serves as another effective strategy, using PCA or sparse coding to reduce dimensions of high-dimensional embedding vectors (e.g., from 100-dimensional to 20-dimensional) [38]. Adopting asynchronous updating mechanisms can alleviate this issue by allowing low-dimensional clients to submit updates more frequently, reducing waiting time [39].

This research focuses on implementing the k-means clustering algorithm within vertical federated learning. The core challenge lies in collaboratively computing the distances between sample points (to centroids) and determining cluster assignments for samples, as well as updating centroids, all while ensuring participant data remains local (privacy protection). We propose using the Product Quantization (PQ) process instead of local model training. This serves a dual purpose: firstly, it leverages PQ’s inherent column-wise k-means clustering to replace the original global dimension k-means clustering; secondly, it utilizes PQ to compress data dimensionality and transmitted parameters. The objective of clustering algorithms is to partition a dataset into groups (clusters) based on inherent similarities, achieving high intra-cluster similarity and low inter-cluster similarity. Given that clustering relies on distance features, as long as the index can accurately represent the distance relationships among the cluster centers within the codebook, the codebook itself can remain local. Only the index needs uploading to the server for subsequent clustering, thereby minimizing transmitted data volume. Consequently, we designed a PQ- and MDS-based multi-stage dimensionality reduction framework specifically for vertical federated scenarios, achieving the dual objectives of privacy preservation and communication efficiency. Adopting a multi-stage dimensionality reduction strategy (as opposed to a single-step direct reduction) is crucial for another key reason: significant disparities in feature dimensions across clients. Direct global dimensionality reduction could disproportionately favor clients with higher feature dimensions, leading to inaccurate results. Our framework effectively balances the impact of features with varying dimensions and avoids such bias through secondary dimensionality reduction in subspace.

2.3. PQ Quantization Technique

The PQ quantization technique (Product Quantization) [40] is a quantization technique used for compressing high-dimensional vector data and approximate nearest neighbor search. Its fundamental principle decomposes the high-dimensional vector space into the Cartesian product of multiple low-dimensional subspaces, then quantizes each subspace separately. In PQ quantization, the original vector is divided into multiple subvectors. Each subvector undergoes clustering via the k-means algorithm to generate a codebook, and the original vector is replaced by its nearest centroid, thereby achieving efficient compression.

Current applications of quantization techniques in federated learning primarily focus on communication efficiency optimization, storage optimization, computational acceleration, personalized training, and enhanced privacy protection. For instance [41] indicates that quantization can reduce communication costs by two orders of magnitude. Quantized compressed models require less device storage, accelerate computation, and suit edge deployment. Product Quantization (PQ) can mitigate data heterogeneity issues in federated learning (Optimized Product Quantization), such as clients generating personalized codebooks based on local data for server usage. PQ-quantized parameters inherently provide noise injection effects. For example, the medical federated learning framework FL-TTE adds Gaussian noise ($\xi$ = 1.0) to quantized hazard ratio parameters, increasing model bias by only 0.5% while meeting privacy requirements (Gradient Obfuscation Gives a False Sense of Security in Federated Learning) [42].

However, traditional PQ techniques primarily emphasize data compression, and a critical step involves uploading the codebook to the server for data reconstruction. Although reconstructed data exhibits reduced accuracy compared to raw data, it still risks exposing the original data distribution. This research focuses on implementing clustering algorithms in vertical federated learning—where clustering is a classification problem rather than regression. Consequently, the server requires no data reconstruction. Capitalizing on clustering’s reliance on distance features, we innovatively re-encode the codebook indices to ensure they represent distance relationships among cluster centers within the codebook. This enables retaining the codebook locally while uploading only indices to the server for clustering, maximally preserving local data and reducing computational overhead on the server side.

The core process of Product Quantization (PQ) is as follows:

(1)

Space Decomposition:Decompose a vector of dimension D into Msubspaces, each with dimension D/M (requiring Dmod M = 0).

Mathematical Expression:The original vector v ∈$R^d$ s partitioned into M subvectors vi ∈ $R^{d/M}$, with each subvector quantized independently

(2)

Subspace Quantization: Perform k-means clustering on each subspace to generate a codebook containing k cluster centers.

(3)

Encoding Representation:The original vector is represented by a combination of indices corresponding to the nearest cluster centers of its subvectors. For example, a 128-dimensional vector can be compressed into eight 8-bit indices (requiring only 64 bits of storage, achieving a compression ratio of up to 97%).

The advantages of PQ quantization are as follows: The codebook in PQ is a collection of multi-stage cluster centers, decomposing high-dimensional problems into low-dimensional subproblems through space partitioning; by utilizing Cartesian product combinations, it covers an enormous search space with minimal storage, achieving high compression ratios and rapid approximate computations through index mapping. This characteristic enables PQ to significantly reduce storage and computational overhead while maintaining acceptable accuracy loss [43].

The loss in PQ quantization stems from the destruction of correlations due to subspace partitioning and information truncation from discrete quantization [44]. Mathematically, it manifests as follows:

(1)

Reconstruction Error:

Each subspace generates K centroids via k-means ($C={\left\{c_{m,k}\right\}}_{k=1}^K$). Subvector $V_m$ is quantized to its nearest centroid $c_m^{*}$, with reconstruction error:

$${\mathcal{L}}_{\mathrm{recon}}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\sum _{m=1}^M{\parallel v_m^{\left(i\right)}-c_m^{*}\parallel }_2^2$$

This error decreases as K increases.

(2)

Subspace Partitioning Error:

A D-dimensional vector is partitioned into M subspaces (each of dimension d = D/M). For an original vector v∈$R^D$, partitioned as $[v_1,v_2,\dots ,v_M]$. Independent quantization across subspaces destroys interdimensional correlations, and the lower bound of the reconstruction error for $v^{\wedge }=[q_1\left(v_1\right),q_2\left(v_2\right),\dots ,q_M\left(v_M\right)]$ is as follows:

$$\parallel v-\widehat{v}\parallel 2^2\ge \sum {m=1}^M{\parallel v_m-q_m\left(v_m\right)\parallel }_2^2$$

When subspace partitioning does not align with the principal components of the data distribution (e.g., without PCA preprocessing), the error increases significantly.

2.4. MDS Mapping Method

To ensure a mapping relationship between indices and cluster centers in the codebook, multiple mathematical methods can map point sets in n-dimensional space to one-dimensional values while preserving original distance relationships as much as possible. Examples include PCA projection [45], one-dimensional MDS embedding [46], random projections, and kernel PCA. PCA is simpler but preserves variance rather than pairwise distances. The one-dimensional MDS embedding method suits small datasets by directly optimizing distance preservation. We adopt the one-dimensional MDS embedding algorithm in Algorithm 2.

Classical one-dimensional MDS embedding maps points in high-dimensional space to a one-dimensional line, ensuring that Euclidean distances (absolute differences) between projected points approximate the original distances as closely as possible. It essentially solves for the optimal linear projection direction through eigenvalue decomposition.

Core ideas:

Given m n-dimensional points $x_1,x_2,...,x_m$, the goal is to find a mapping as follows:

$$f:{\mathbb{R}}^n\to \mathbb{R},f\left(x_i\right)=z_i$$

where the one-dimensional distance satisfies the following:

$$\left|z_i-z_j\right|\approx ∥x_i-x_j∥,\forall i,j$$

Optimization Objective: Minimize the stress function (Stress).

$$Stress=\sqrt{{\displaystyle \frac{{\sum }_{i<j}(\parallel x_i-x_j\parallel -\parallel z_i-z_j{\parallel )}^2}{{\sum }_{i<j}{\parallel x_i-x_j\parallel }^2}}}$$

Loss Analysis:

During one-dimensional embedding, the loss is primarily caused by distance distortion, which can be strictly quantified using the stress function.

According to the Johnson–Lindenstrauss lemma, when embedding any n points from high-dimensional space to one dimension, distance distortion inevitably exists:

$$\exists i,j\mathrm{s}.\mathrm{t}.{\displaystyle \frac{|d_{ij}-\widehat{d_{ij}}|}{d_{ij}}}\ge ϵ>0$$

where $\epsilon$ is determined by the intrinsic dimensionality of the data.

Theoretical Lower Bound of Loss:For any dataset, the minimum achievable stress for one-dimensional embedding satisfies the following:

$$Stres{s}_{min}\ge \sqrt{1-{\displaystyle \frac{{\lambda }_1}{{\sum }_{k=1}^n{\lambda }_k}}}$$

where ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_n$ are the eigenvalues of the double-centered matrix B.

Algorithm 2 MDS [46] one-dimensional embedding algorithm steps.

Input: m×ndata matrixX, distance metric (default: Euclidean distance). Output: One-dimensional coordinate vector $z=(z_1,z_2,\dots ,z_m)\in R_m$    Steps:  1:    Compute distance matrix $$D_{ij}=\parallel x_i-x_j\parallel ,D\in {\mathbb{R}}^{m\times n}$$  2:    Square the distance matrix $$D^{\left(2\right)}=\left[D_{ij}^2\right]$$  3:    Double-centering $$B=-{\displaystyle \frac{1}{2}}J{D}^{\left(2\right)}J$$       Where: J is the centering matrix: $J=I_m-{\displaystyle \frac{1}{m}}{\mathbf{11}}^T$, 1 is an all-ones column vector, B geometrically represents the inner product matrix, $B=Z{Z}^T$ (Z is centered coordinates)  4:    Eigen decomposition $$B=V\wedge V^T,\Lambda =\mathrm{diag}({\lambda }_1,{\lambda }_2,...,{\lambda }_m)$$    Sort eigenvalues: ${\lambda }_1>{\lambda }_2>...>{\lambda }_m$  5:    Select the largest eigenvalue       Take ${\lambda }_{max}={\lambda }_1$, and its corresponding eigenvector $v_1={\left[v_{11},v_{12},...,V_{1m}\right]}^T$  6:    Compute one-dimensional coordinates $$z=\sqrt{{\Lambda }_{max}}·v_1$$

2.5. Baseline

The DP-VFC algorithm (Algorithm 3) originates from Paper [17]. Algorithm idea: DP-VFC extends the classical k-means (which minimizes the within-cluster sum of squared errors, SSEs) to a multi-party vertical federated setting under ($ϵ,\delta$)-differential privacy. Assuming S participants each hold non-overlapping feature blocks of the same batch of users $X^{\left(\mathsf{\ell }\right)}\in {\mathbb{R}}^{n\times d_{\mathsf{\ell }}}$, the global objective remains as minimizing SSE.

$$\mathrm{SSE}=\sum _{k=1}^K\sum _{x_i\in C_k}{\left|x_i-{\mu }_k\right|}_2^2,{\mu }_k={\displaystyle \frac{1}{|C_k|}}\sum _{x_i\in C_k}{x}_i$$

DP VFC comprises four steps: First, locally run differentially private k-means with local budget ${ϵ}_{loc}$ at each participant to obtain noisy centers and record cluster membership indices;

Then, encode these membership sets using differentially private Flajolet–Martin partition sketches (DPFMPSs), and upload them along with local centers to the server in one transmission without disclosing individual user affiliations;

The server performs Cartesian products on all local centers to form candidate global sample grids, and leverages the uploaded sketches to estimate the intersection cardinality of members at each grid point under the same budget ${ϵ}_{mem}$ using the inclusion–exclusion principle or a two-phase iterative method;

Finally, execute noise-free weighted k-means on this set of “weighted pseudo-samples,” iteratively updating centers until convergence, thereby outputting global k cluster centers satisfying ($ϵ,\delta$)-differential privacy within a single communication round.

$$c_j={\displaystyle \frac{{\displaystyle \sum _{g\in {\mathcal{G}}_j}{\widehat{w}}_{g}g}}{{\displaystyle \sum _{g\in {\mathcal{G}}_j}{\widehat{w}}_g}}},{\mathcal{G}}_j=\{g:j=arg\underset{h}{min}{\parallel g-c_h\parallel }_2^2\}$$

Thus concludes the iteration formula.

The DF-VFC algorithm ensures approximately minimizing the global SSE without disclosing either individual samples or cluster membership relationships.

Algorithm 3 DP-VFC [17] algorithm steps.

Input: ${\{X^{\left(\mathsf{\ell }\right)}\in {\mathbb{R}}^{n\times d_{\mathsf{\ell }}}\}}_{\mathsf{\ell }=1}^S$    , per-party local data $k,k^{\prime }$    , global, local number of clusters $({\epsilon }_{\mathrm{loc}},{\epsilon }_{\mathrm{mem}})$    , privacy budget split Output:    Global centers $C=\{c_1,\dots ,c_k\}$ Setps: 1: Phase 1: Local DP clustering 2: for  $\mathsf{\ell }=1,\dots ,S$ do 3:     $[C^{\left(\mathsf{\ell }\right)},{\left\{M_i^{\left(\mathsf{\ell }\right)}\right\}}_{i=1}^{k^{\prime }}]\leftarrow \mathrm{DP}\_\mathrm{kmeans}\left(X^{\left(\mathsf{\ell }\right)},k^{\prime },{\epsilon }_{\mathrm{loc}}\right)$ 4:     ${\mathrm{Sketch}}^{\left(\mathsf{\ell }\right)}\leftarrow \mathrm{DPFMPS}\_\mathrm{Encode}\left(\left\{M_i^{\left(\mathsf{\ell }\right)}\right\},{\epsilon }_{\mathrm{mem}}\right)$ 5:     send $C^{\left(\mathsf{\ell }\right)},{\mathrm{Sketch}}^{\left(\mathsf{\ell }\right)}$ to server 6: end for 7: Phase 2: Server-side weight estimation 8: receive ${\{C^{\left(\mathsf{\ell }\right)},{\mathrm{Sketch}}^{\left(\mathsf{\ell }\right)}\}}_{\mathsf{\ell }=1}^S$ 9: $G\leftarrow C^{\left(1\right)}\times \dots \times C^{\left(S\right)}$ 10: for all $g=(c_{i_1}^{\left(1\right)},\dots ,c_{i_S}^{\left(S\right)})\in G$ do 11:     $w_g\leftarrow \mathrm{EstimateIntersection}\left({\left\{{\mathrm{Sketch}}_{i_{\mathsf{\ell }}}^{\left(\mathsf{\ell }\right)}\right\}}_{\mathsf{\ell }=1}^S\right)$ 12: end for 13: Phase 3: Weighted global k means 14:    initialize $C\leftarrow \{c_1,\dots ,c_k\}$ 15: repeat                 ▹ Assignment step 16:     for all $g\in G$ do 17:         assign g to $arg{min}_{c_j\in C}{\parallel g-c_j\parallel }^2$ 18:     end for                  ▹ Update step 19:     for $j=1,\dots ,k$ do 20:         $c_j\leftarrow {\displaystyle \frac{{\sum }_{g\to j}{w}_{g}g}{{\sum }_{g\to j}{w}_g}}$ 21:     end for 22: until convergence 23: return   C

3. Method

The essence of clustering is grouping data points based on similarity. As long as compressed data preserves the “proximity relationships among data points” (i.e., distant samples remain separated and close samples remain aggregated), clustering on compressed data remains effective. Motivated by this principle, we design a multi-level dimensionality-reduction-based clustering framework for vertical federated learning that jointly accounts for feature imbalance, communication overhead, and privacy protection.

This framework is implemented based on PQ quantization and MDS techniques. After privacy-preserving alignment across multiple clients, the Product Quantization technique replaces traditional local model training. Algorithmically, PQ fundamentally relies on k-means clustering principles, compressing high-dimensional features into low-dimensional codes to significantly reduce communication overhead. Regarding privacy protection design: directly uploading codebooks (cluster center sets) risks exposing original data distributions. We observe clustering effectiveness heavily depends on relative distances between cluster centers. Thus, we employ the MDS one-dimensional embedding algorithm, $f:{\mathbb{R}}^n\to \mathbb{R},f\left(x_I\right)=z_i$ ensuring the following:

$$\left|z_i-z_j\right|\approx ∥x_i-x_j∥,\forall i,j$$

The server executes a one-shot clustering algorithm on distance-preserving indices to obtain the clustering structure, achieving maximized intra-group similarity and maximized inter-group divergence

This approach preserves raw codebook privacy locally while maintaining distance relationships essential for clustering through indices, ensuring algorithmic performance and further enhancing communication efficiency.

The adoption of multi-stage dimensionality reduction instead of direct dimensionality reduction is partially due to significant disparities in feature counts across clients. Direct reduction would bias clustering results toward certain features under such imbalances.

Figure 1 illustrates the data flow diagram of the entire algorithm. Locally on the client side, the total data dimension is D-dimensional. The original data is partitioned into M groups of subvectors, each with a dimension of D/M. After performing PQ quantization on them, a codebook is generated. At this stage, original data values are converted into indices within the codebook. Subsequently, the MDS one-dimensional embedding algorithm is executed on the cluster centers in this codebook to obtain remapped values. These values replace the original indices in the data. Finally, these local indices are uploaded to the server side. After aligning all data by columns on the server side, the k-means clustering algorithm is executed to obtain global cluster centers.

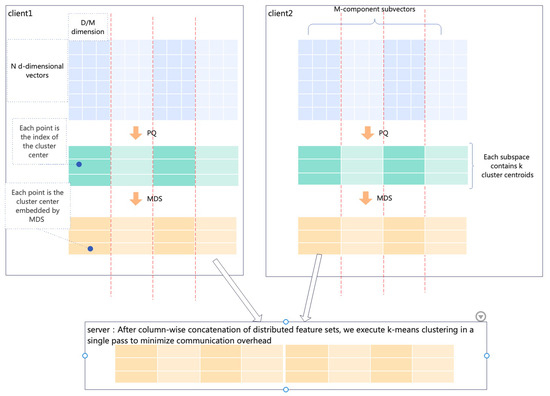
Figure 1. Data flow diagram.

3.1. Algorithm Design

Suppose there is a federated learning framework with m clients. The global dataset is D with global dimension dim, distributed across clients. $D^g$ denotes the dataset of the g-th client, where data points in $D^g$ are $di{m}^g-dimensional$ vectors. There are $\sum di{m}^g=dim$. Define sub_dim as the subspace dimensionality in PQ quantization, and sub_k as the number of cluster centers per subspace in PQ quantization. $Codeboo{k}^g$ represents the codebook of the g-th client, and ${cod{e}^g}_i$ denotes the cluster center set of the i-th subspace for the g-th client, ${cod{e}^g}_i$ is the data index set of the g-th client, and B is the global data index set.

Algorithm mainly consists of the following steps:

1.

Encrypted Entity Alignment

Select common samples: Extract common samples from each party’s dataset.

2.

Local Initialization and Training of PQ Quantizer:

(1)

Pad dimensions: Determine whether the local dimension dim is divisible by sub_dim. If not divisible, pad dimensions.

First, calculate the number of dimensions p to pad:

$$di{m}^{\prime }=sub\_di{m}^{\prime }\times sub\_k$$

$$p=di{m}^{\prime }-dim$$

Then, pad the original vector by appending p zeros to its end.

$$v^{\prime }=[v_1,v_2,\dots ,v_{\dim },\underset{p}{\underbrace{0,0,\dots ,0}}]$$

(2)

Generate subspace codebooks based on training data.

3.

Secondary mapping:

Perform secondary mapping on cluster centers in subspace codebooks using MDS one-dimensional embedding algorithm, then use the normalized mapped values as codebook indices.

4.

Data transmission:

Codebooks are stored locally. Transfer the indices to the server side.

5.

Server-side global cluster center aggregation:

Execute k-means algorithm on the indices uploaded by clients at the server side to obtain abstract global cluster centers.

When using abstract cluster centers, apply the same mapping operation to local data, then compute distances to global abstract cluster centers to determine true cluster assignments.

The algorithm requires only one round of communication.

Table 1 shows the explanation of symbols:

Table 1. Symbolexplanation.

Symbol	Description
D	Description
sub_dim	Subspace data dimensionality
sub_k	k-value for the g-th client
$D^g$	Dataset of the g-th client
$codeboo{k}^g$	Codebook of the g-th client
${cod{e}^g}_i$	Cluster center set of the i-th subspace for the g-th client
Bg	Data index set of the g-th client
B	Global data index set

Algorithm 4 pseudocode:

Algorithm 4 our algorithm

Input: Distributed dataset $D=D_1,D_2,\dots ,D_m$, where $D_g$ is the data of the g-th client. Number of clusters k. Maximum iterations T. Output: Global cluster centers $C=c_1,c_2,\dots ,c_k$.    Steps:  1:    RSA Private Set Intersection (1) Server generates RSA key pair and broadcasts public key (2) Clients blind their own elements (3) Server signs blinded elements (4) Clients unblind received signatures (5) Clients send unblinded signatures to server (6) Server computes intersection signatures and sends to clients (7) Clients map signatures back to original elements  2:    Model Training: (1) Server distributes parameters: sub_dim (subspace dimensionality), ks (number of subspace cluster centers) (2) At local client (g-th client):    if dim% sub_dim !=0:       pad dimensions with zeros.    codebook=pq.train(sub_dim,ks)    for code in codebook:       MDS dimensionality reduction:code = mds (code)       Normalization:code = normalize (code)       Add to code_list:code_list.append (code)    Convert data to code indices: data_codes = pq.encode (data,code_list)    Upload encrypted data indices to server (3) Server aggregation:    Collect data indices from all clients.    Global index set $B=\Phi$    for client in client_list:       Column-wise merge: $B=B\cup B^g$    In abstract index set B:    Initialize cluster centers by randomly selecting k data points as initial global cluster centers.    Perform k-means clustering on sample set using initialized global centers to obtain final cluster centers C$:c_1,c_2,\dots ,c_k$

3.2. Cluster Accuracy Analysis

The performance guarantee of the algorithm stems from the multi-stage dimensionality reduction framework preserving critical information required for clustering tasks—namely, the relative similarity (distance structure) between data points.

3.2.1. PQ Quantization

PQ quantization reduces dimensionality via subspace decomposition. Its core principle is distributing high-dimensional quantization errors across low-dimensional subspaces, thereby controlling overall information loss and preserving fundamental similarity for subsequent clustering.

As shown in the error analysis of PQ quantization in Section 2, when the codebook size k is sufficiently large, the quantization error $\parallel x_i^{\prime }-x_i{\parallel }_2$ in each subspace converges to the inherent noise level (e.g., data variance) of that subspace. Consequently, the total error $\parallel x^{\prime }{-x\parallel }_2$ is bounded. As m increases (subspace dimensionality decreases), errors distribute more uniformly, avoiding error explosion caused by the “curse of dimensionality” in high-dimensional spaces.

Clustering relies on the property that “similar data points are closer in space”. For any two raw data points x, y, if x and y are similar (${\parallel x-y\parallel }_2$ small), their corresponding subvectors $x_i$, $y_i$ should also be similar ($\parallel x_i-y_i{\parallel }_2$ small) across subspaces. With bounded PQ quantization errors, the quantized distance satisfies the following:

$$|\parallel x^{\prime }-y^{\prime }{\parallel }_2{-\parallel x-y\parallel }_2|\le \parallel x^{\prime }{-x\parallel }_2+{\parallel y^{\prime }-y\parallel }_2\le 2\epsilon$$

($\epsilon$ denotes the maximum quantization error of a single vector).

When $\epsilon \ll {\parallel x-y\parallel }_2$, the trend of $\parallel x^{\prime }-y^{\prime }{\parallel }_2$ aligns with $\parallel x_i-y_i{\parallel }_2$—that is, quantized distances between similar data points remain smaller than those between dissimilar points, preserving the fundamental similarity required for clustering.

3.2.2. MDS Mapping

Multidimensional Scaling (MDS) seeks to preserve the original pairwise distance relationships in a low-dimensional embedding. Because clustering (especially k-means) is driven by relative distances, as long as the distance ordering after the MDS mapping is consistent with that of the original space, clustering accuracy can be maintained. As shown in Section 2, in MDS the stress function attains its minimum when the mapping uses the eigenvector associated with the largest eigenvalue; equivalently, the squared error between the one-dimensional mapped distances and the original distances $d_{ij}$ is minimized. In this case, pairs that are close in the original space remain close in one dimension, and pairs that are far remain far, thereby preserving the global distance structure.

Assume that in the original codebook, $c_i,c_j$ belong to the same class (small $d_{ij}$) and $c_i,c_k$ belong to different classes (large $d_{ik}$). Because the MDS stress is minimized, the mapping preserves this relation with high probability, i.e., the mapped distances satisfy $|z_i-z_j|<|z_i-z_k|$, so intra-class distances remain smaller than inter-class distances.

Even under a one-dimensional mapping, as long as this “intra-class near, inter-class far” trend is maintained, clustering will correctly group the points. The advantage of a one-D embedding is that it suppresses high-dimensional noise while compressing global distance relations into a simple numerical ordering, which is well suited for cross-party concatenation and global clustering.

3.2.3. Effectiveness of the Two-Stage Joint Compression

In this framework, although the errors introduced by PQ and by MDS are not independent, their accumulated effect does not destroy the distance structure required for clustering.

(1)

Bound of the error-propagation chain:

i.

PQ: quantizes the original vector x to x′ with a bounded reconstruction error ${\epsilon }_1={\parallel x^{\prime }-x\parallel }_2$

ii.

MDS: maps the codebook centroids $x^{\prime }$ to a one-dimensional embedding z with a bounded distance distortion ${\epsilon }_2=|d_{ij}-|z_i-z_j\left|\right|$, where ${\epsilon }_2$ is small due to stress minimization.

The joint effect on clustering appears as the probability of similarity inversion (i.e., pairs that were similar becoming dissimilar, or vice versa). By theoretical analysis, when ${\epsilon }_1$ and ${\epsilon }_2$ are both smaller than the gap between the maximum intra-class distance and the minimum inter-class distance in the original data, the probability of such inversions trends to zero, and the clustering result on the compressed data coincides with that on the original data.

(2)

Consistency between the multi-stage compression and the clustering objective: The k-means algorithm seeks to minimize the within-cluster sum of squared errors (SSEs), denoted as follows:

$$J=\underset{C}{min}\sum _{k=1}^K\sum _{x\in C_k}\parallel x-{\mu }_k\parallel$$

After PQ quantization, the corresponding SSE $J_{PQ}$ differs from J by the total quantization distortion. Similarly, when applying MDS to the PQ centroids, the resulting SSE $J_{MDS}$ deviates from $J_{PQ}$ by the distance-preservation error of the embedding. Because both the PQ and MDS errors can be made arbitrarily small (by choosing sufficiently large codebook size and by minimizing the MDS stress), the optimal cluster centers obtained on the fully compressed data (minimizer of $J_{MDS}$) will coincide closely with those of the original problem (minimizer of J). In other words, the two-stage compressed representation still admits an approximately optimal k-means solution.

Overall, PQ controls the quantization error by decomposing the feature space into low-dimensional subspaces, thereby preserving local similarity among data points. MDS then preserves the global distance structure by embedding codebook centroids into one dimension. Because both PQ and MDS introduce bounded distortions that are compatible with the clustering criterion—“intra-cluster points remain closer than inter-cluster points”—the two-stage compression can guarantee that, for sufficiently large codebook size and sufficiently small MDS stress, clustering on the compressed data closely approximates the result on the original data.

3.3. Hyperparameter Selection and Trade-Offs

In our framework, PQ quantization granularity is controlled by the subspace dimension ($sub\_dim$) and the number of codebook centroids per subspace ($sub\_dim$).

A smaller $sub\_dim$ (more subspaces) disperses quantization errors more evenly but increases the number of codebooks, raising both computational and communication costs. A larger $sub\_k$ yields higher quantization fidelity (smaller error) and thus better global clustering performance, but reduces compression ratio and increases privacy and communication overhead.

In our experiments, we evaluated combinations with $sub\_dim\in 1,2,4,8$ and $sub\_dim\in 10,64,128,256$ to quantify performance under varying PQ granularities.

3.4. Impact of Dimension Padding

Padding dimensions may introduce additional information or noise. In our solution, since we pad with zeros, these dimensions may not contribute to the original data’s features yet increase computational and storage demands. Although the padded values are zeros, each subspace quantization must process these dimensions as distance calculations during quantization still account for them. This cost remains relatively acceptable compared to PQ quantization’s data compression benefits.

However, dimension padding may disrupt natural correlations between subspaces. High-dimensional features in real data often exhibit local correlations (e.g., adjacent dimensions in image features). When padded dimensions are irrelevant to the original data, they may break intrinsic intra-subspace correlations. Consequently, the quantized indices fail to accurately reflect the original structure, thereby increasing quantization error.

3.5. Comparison with Other Dimensionality-Reduction Methods

Consistency with the clustering objective: PCA excels at preserving global linear variance but does not directly preserve pairwise distances, which can distort the “near-dense, far-sparse” structure that clustering exploits. MDS explicitly preserves both local and global distance relationships, making it more effective for similarity-based clustering.

Information loss vs. communication cost: One-dimensional MDS retains only the principal distance variations, incurring higher information loss. Two-dimensional MDS or PCA can capture more complex relationships but multiply the communication cost and risk leaking additional distributional information. Thus, for vertical federated clustering under strict privacy and communication constraints, our PQ and 1D MDS two-stage approach strikes a balanced trade-off between fidelity, privacy, and efficiency.

3.6. Privacy Enhancement

The privacy protection mechanism of this algorithm derives from two aspects: For one thing, PQ quantization technology reduces dimensionality and processes raw data, preventing its direct upload to the server. For another, locally retained PQ codebooks avoid leakage of original data distributions.

Additionally, to defend against attacks like membership inference analysis, differential privacy noise protection can be incorporated. Differential privacy provides a rigorous framework, ensuring analytical results never reveal individual information. By adding noise to data or intermediate results, attackers cannot determine any individual’s presence in the dataset. According to differential privacy serial/parallel theorems [47] we have the following:

1.

Serial Composition: For a given dataset D, assume there exists random algorithms $M_1,M_2,\dots ,M_n$, with privacy budgets ${ϵ}_1,{ϵ}_2,\dots ,{ϵ}_n$, respectively. The composition algorithm $M(M_1\left(D\right),M_2\left(D\right),\dots ,M_n\left(D\right))$ provides $\left({\sum }_{i=1}^n{ϵ}_i\right)$ - DP protection. That is, for the same dataset, applying a series of differentially private algorithms sequentially provides protection equivalent to the sum of privacy budgets.

2.

Parallel Composition: For disjoint datasets $D_1,D_2,\dots ,D_n$, assume there exists random algorithms $M_1,M_2,\dots ,M_n$, with privacy budgets ${ϵ}_1,{ϵ}_2,\dots ,{ϵ}_n$, respectively. $M(M_1\left(D_1\right),M_2\left(D_2\right),\dots ,M_n\left(D_n\right))$ provides ($max{ϵ}_i$)-DP privacy budgets. That is, for disjoint datasets, applying different differentially private algorithms separately in parallel provides privacy protection equivalent to the maximum privacy budget among the composed algorithms.

Adding differential privacy noise to raw data or codebooks can effectively enhance privacy protection.

4. Experiments and Results

4.1. Experimental Settings

4.1.1. Dataset

The MNIST dataset is adopted, with columns split according to client feature ratios, and different subsets are distributed to different clients.

4.1.2. Parameter Settings

• Total number of clients: 2;
• Total number of client features: 784;
• Client feature ratios: (1:1), (1:6), (1:13);
• PQ quantization subspace dimensions: 1, 2, 4, 8;
• Number of PQ quantization cluster centers per subspace: 10, 64, 128, 256.

4.1.3. Evaluation Metrics

The evaluation employs NMI and ARI metrics.

4.2. Performance Analysis

Centralized data clustering serves as the baseline for validation.

4.2.1. Comparison Between Proposed Method and Centralized Kmeans

This experiment involves two clients, each with 392 data dimensions at a 1:1 ratio. As shown in Table 2, the proposed algorithm achieves slightly higher average NMI and ARI values under various subspace dimensions and cluster center counts than centralized k-means, indicating effective extraction of original data features. When the subspace dimension is 1, equivalent to performing k-means on each data column and replacing values with cluster centers, PQ loss is minimized. Data confirms superior performance in this scenario. Performance improves with fewer cluster centers per subspace, partly because the sparse MNIST dataset can be effectively represented by fewer clusters.

Table 2. Algorithm performance comparison.

Dispersion Coefficient	Hash Dimension	Proposed Method		Without MDS Algorithm Using Codebook Indices at Server		Without MDS Algorithm, Restored Data at Server		Centralized Algorithm		DP-VFC (Under a Privacy Budget of $\mathit{ϵ}$ = 1.0)
		NMI	ARI	NMI	ARI	NMI	ARI	NMI	ARI	NMI	ARI
1	10	0.53403	0.42542	0.50209	0.41110	0.51871	0.40490	0.49581	0.36387	0.2703	0.1456
2	10	0.49353	0.37211	0.47981	0.38815	0.49406	0.38168
4	10	0.51018	0.38628	0.44081	0.33740	0.52128	0.40873
8	10	0.52476	0.43289	0.42186	0.31696	0.52207	0.40520
1	64	0.49707	0.36712	0.48437	0.37222	0.51585	0.40136
2	64	0.53773	0.42763	0.44766	0.33290	0.49617	0.36369
4	64	0.50124	0.37786	0.42137	0.32132	0.49500	0.38318
8	64	0.48329	0.39052	0.41128	0.34143	0.49390	0.36302
1	128	0.48375	0.36266	0.50666	0.41889	0.49081	0.36068
2	128	0.49855	0.38596	0.46257	0.35915	0.49043	0.36039
4	128	0.48026	0.35906	0.42605	0.34344	0.49403	0.38208
8	128	0.47704	0.37444	0.40413	0.31093	0.48159	0.37014
1	256	0.52029	0.40768	0.49181	0.40905	0.49049	0.36069
2	256	0.48873	0.36059	0.49902	0.39875	0.48150	0.35965
4	256	0.49801	0.39486	0.43289	0.35194	0.49628	0.36436
8	256	0.46309	0.36877	0.41015	0.34877	0.48375	0.36400

4.2.2. Impact of MDS on Algorithm Performance

To evaluate MDS’s impact, we compare against two alternative implementations without MDS: One clusters codebook indices at the server, and another reconstructs data using PQ quantization at the server. A privacy comparison is as follows: direct index clustering > proposed method > data reconstruction.

As Table 2 shows, performance comparison is as follows: proposed method ≥ data reconstruction direct index clustering. When subspace dimension = 1, direct index clustering performs comparably to other methods. However, its performance declines sharply as PQ subspace dimension increases, indicating insufficient capture of data distance features. The proposed method better captures data distance features, yielding slightly superior performance over data reconstruction.

4.2.3. Impact of Client Feature Quantity on Performance

As Table 3 shows, by varying the feature-partition ratios among clients (1:1, 1:6, and 1:13), our algorithm consistently achieves NMI scores of approximately 0.5 and ARI scores of approximately 0.4, significantly outperforming the baseline. Moreover, its performance remains stable within a narrow range, indicating that the relative number of features held by each client has minimal effect on clustering quality and that the method effectively overcomes feature-dimension imbalance.

Table 3. Experimental results: impact of client feature quantity on performance.

Number of Clients	Feature Ratio Among Clients	Subspace Dimension	Cluster Centers per Subspace	Proposed Method			DP VFC
				NMI	ARI	Mds Stress	NMI	ARI
2	1:1	1	10	0.53403	0.42542	0.82306	0.2703	0.1456
		2	10	0.49353	0.37211	4.44490
		4	10	0.51018	0.38628	10.73975
		8	10	0.52476	0.43289	18.34833
	1:6	1	10	0.51950	0.40631	0.79459	0.1973	0.0747
		2	10	0.51160	0.39005	4.41391
		4	10	0.51162	0.38794	10.97604
		8	10	0.52514	0.42123	18.58371
	1:13	1	10	0.49672	0.36139	0.77438	0.2351	0.1418
		2	10	0.49207	0.36924	4.34313
		4	10	0.51211	0.38790	10.96123
		8	10	0.53030	0.44559	18.55026

5. Conclusions

Based on the characteristics of clustering algorithms, this study transforms the core contradiction of federated clustering—“data utility vs. privacy preservation vs. communication efficiency”—into a verifiable distance-preserving optimization problem, providing a secure clustering implementation framework for vertical federated learning. The proposed algorithm can address communication challenges in vertical federated learning while preserving privacy.

Addressing three core challenges of k-means clustering in vertical federated learning—inadequate privacy protection, excessive communication overhead, and feature dimension imbalance—this paper innovatively proposes a multi-level dimensionality reduction federated clustering framework integrating Product Quantization (PQ) and Multidimensional Scaling (MDS). By compressing original high-dimensional features into low-dimensional codes via PQ and further reducing dimensionality through one-dimensional MDS embedding on codebooks, communication efficiency is significantly enhanced. Privacy protection is achieved through the following: (1) dimensionality reduction lowering data precision and transmission volume, and (2) mapping sensitive codebooks to secure indices via MDS embedding, transmitting only distance-preserving indices to the server. The original codebooks and feature data remain exclusively on local clients.

Experimental results demonstrate that our algorithm significantly outperforms the baseline algorithm DP-VFC across multiple scenarios and even marginally surpasses centralized algorithms. This indicates that while performing data dimensionality reduction and compression, our algorithm effectively preserves distance characteristics of the data. Through varying the ratio of feature dimensions across clients during experiments, the stability of the algorithm is validated. We conclude that in federated settings, our approach enhances communication efficiency and privacy while reducing sensitivity to data distribution, demonstrating strong performance stability.

Nevertheless, this study has certain limitations. Currently, uniform quantization granularity is adopted during data quantization. To better handle heterogeneous data, personalized granularity warrants further investigation—for example, allowing participants to set parameters based on their local data characteristics. The trade-off between privacy protection and compression loss also requires deeper exploration. Although single-round communication improves efficiency, critical information loss in client-uploaded statistical features (due to noise or compression) cannot be corrected through multiple rounds of interaction. This is especially so in extreme heterogeneity scenarios, as single-pass compression may cause irreversible deviation in global clustering, leading to an accuracy–efficiency trade-off dilemma. Consequently, single-round communication imposes exceptionally high requirements on local data training and compression quality. Subsequent research will address these aspects theoretically and experimentally.

Beyond clustering applications, the multi-stage dimensionality reduction framework for vertical federated learning can be readily extended to other machine learning algorithms, such as replacing global aggregation mechanisms. Future work may explore optimization and integration of multi-layered privacy-preserving techniques, including the fusion of secure multi-party computation (MPC) with homomorphic encryption (HE), as well as multi-tier privacy protection policies.