Energy Management of Hybrid Electric Commercial Vehicles Based on Neural Network-Optimized Model Predictive Control
Abstract
1. Introduction
- The minimum fuel energy management strategy for hybrid electric vehicles under a given driving cycle is investigated, with consideration of the influence of transmission gear information, and mixed-integer programming is introduced into problem solving.
- The energy management strategy is optimized using a model predictive control algorithm, and a PINN is designed to address the issue of long solution time arising from the application of MPC.
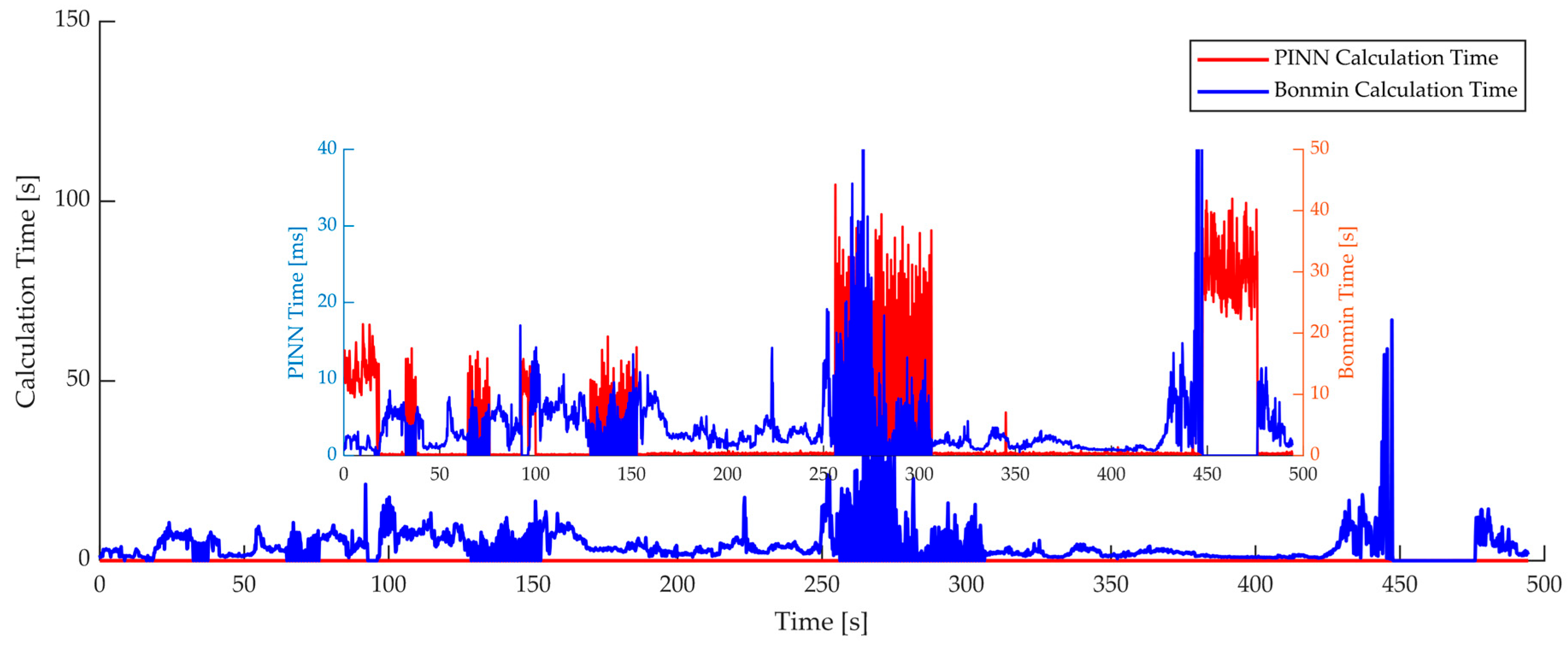
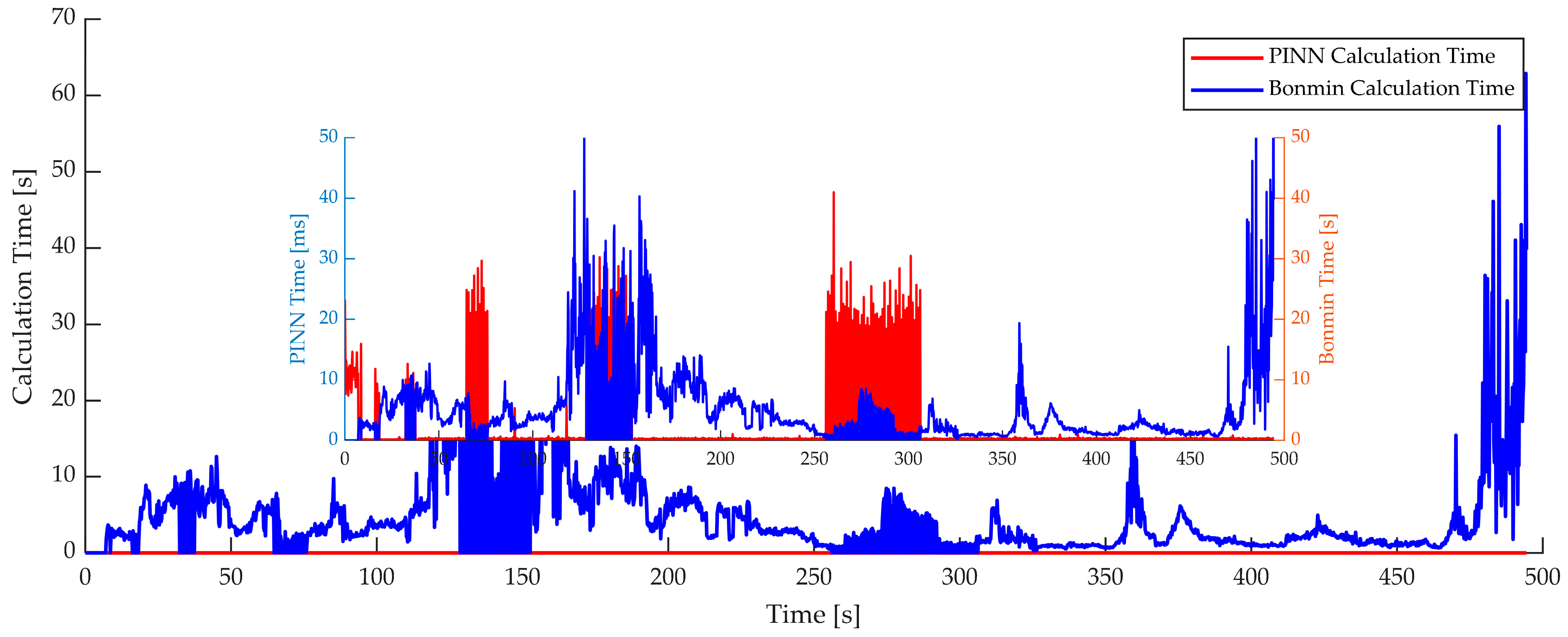
- Hardware-in-the-loop (HIL) simulation tests are conducted. The experimental results demonstrate that under the experimental conditions, the energy consumption optimization effect achieved is nearly consistent with that of the BONMIN mixed-integer solver (with errors of only 0.9% and 0.25%), while the solution time is reduced from an average of 10 s to approximately 5 milliseconds.
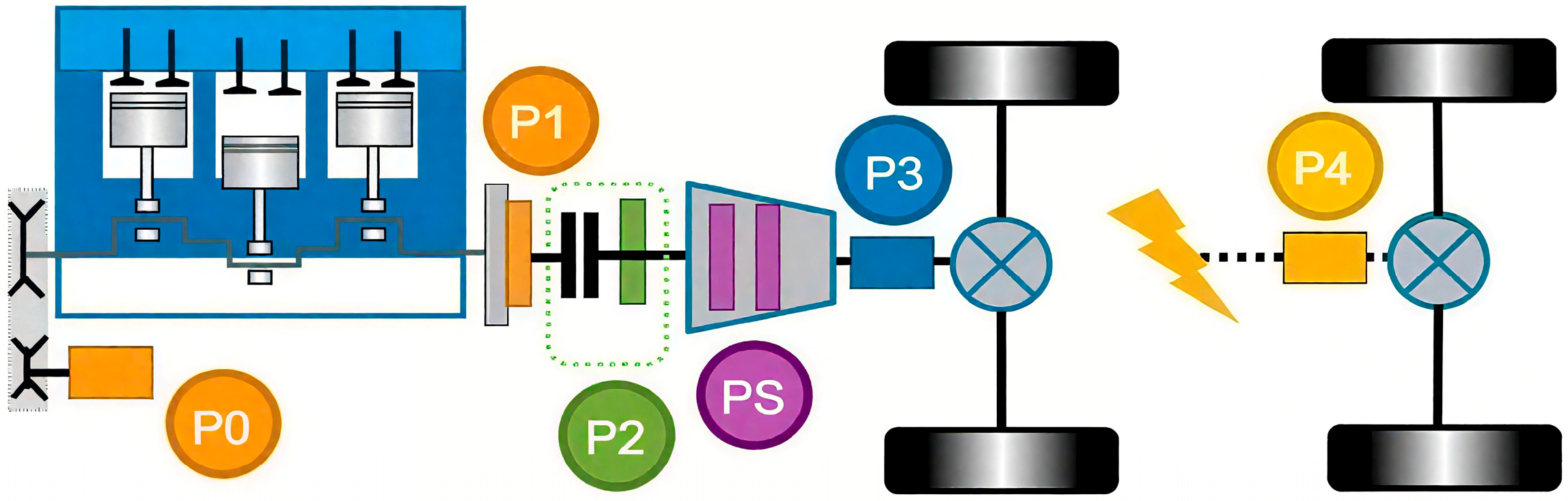
2. Vehicle Modeling
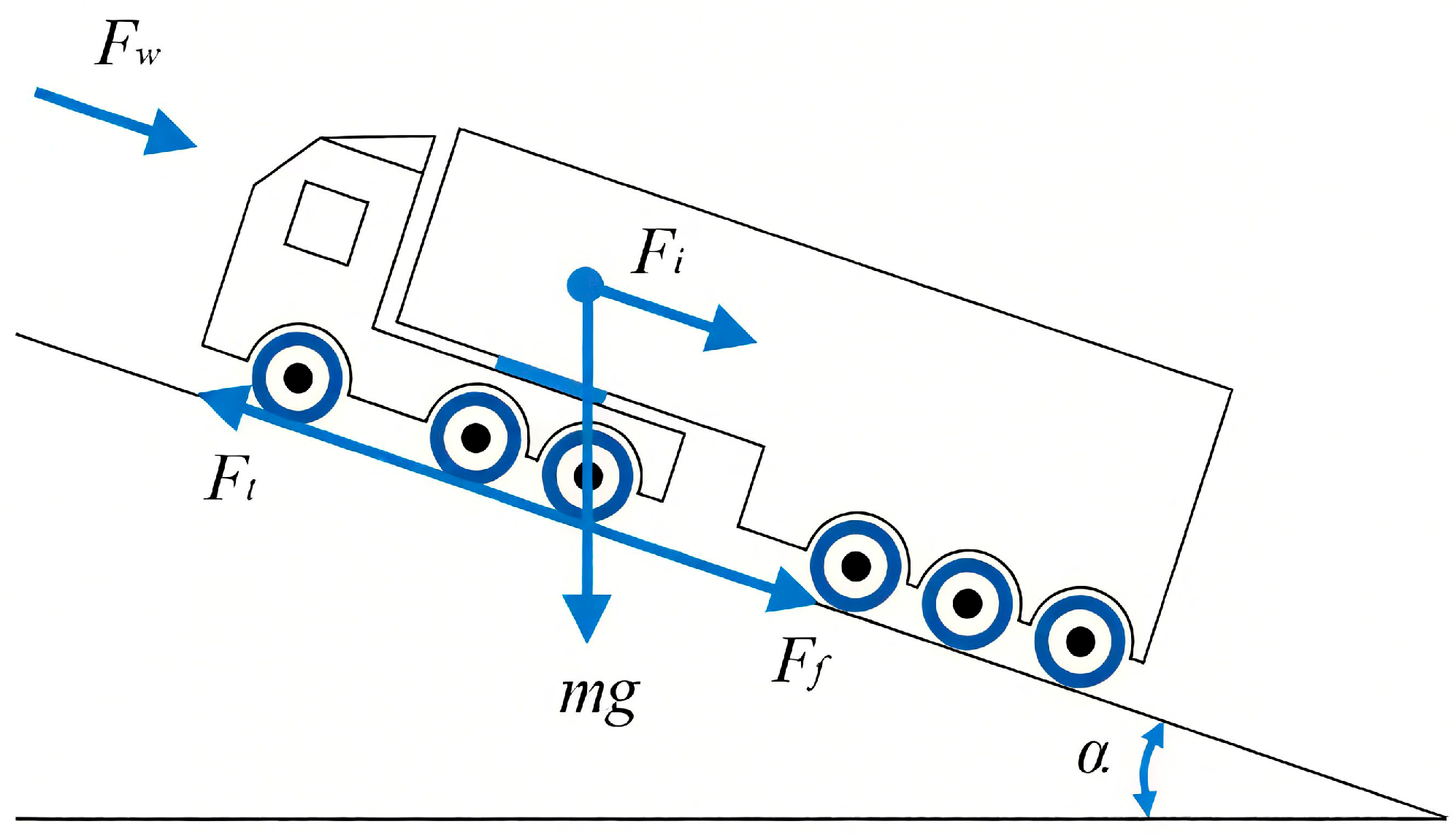
2.1. Vehicle Dynamics
2.2. Engine Model
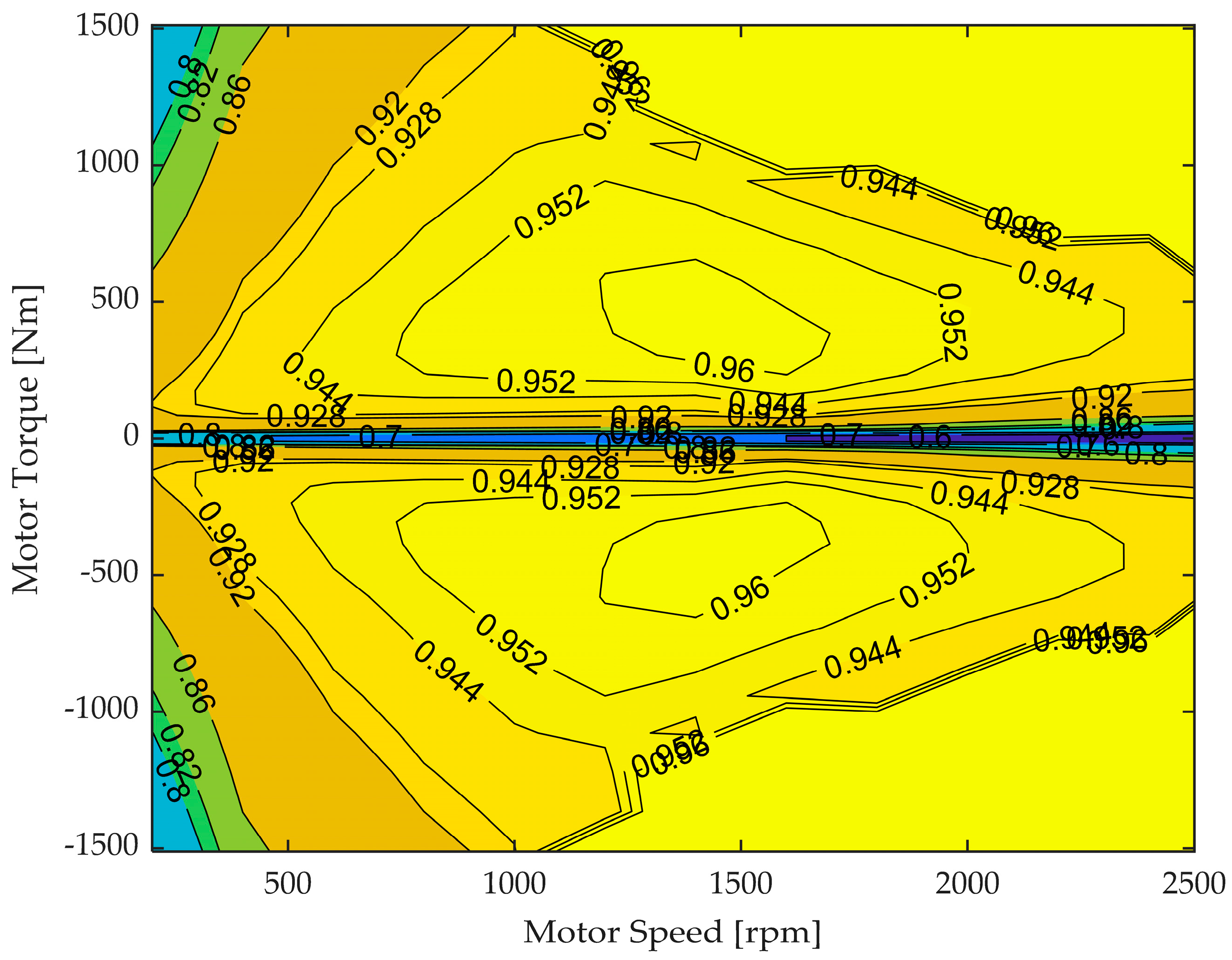
2.3. Motor Model
2.4. Battery Model
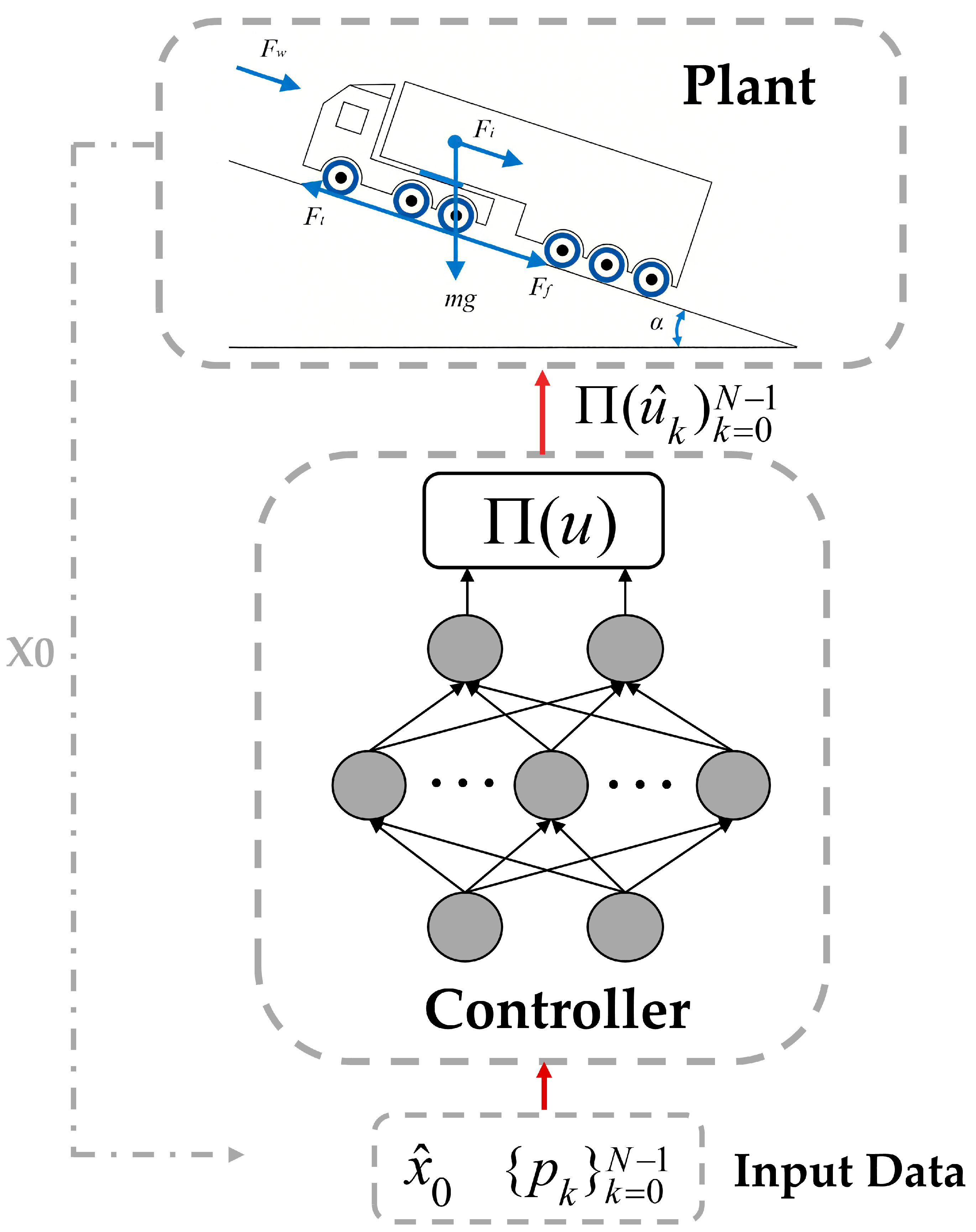
3. Learning-Based Energy Management Strategy
3.1. Problem Description
3.1.1. System State Equations
3.1.2. Objective Function
3.1.3. Variables and Constraints
3.2. MPC-Based Controller
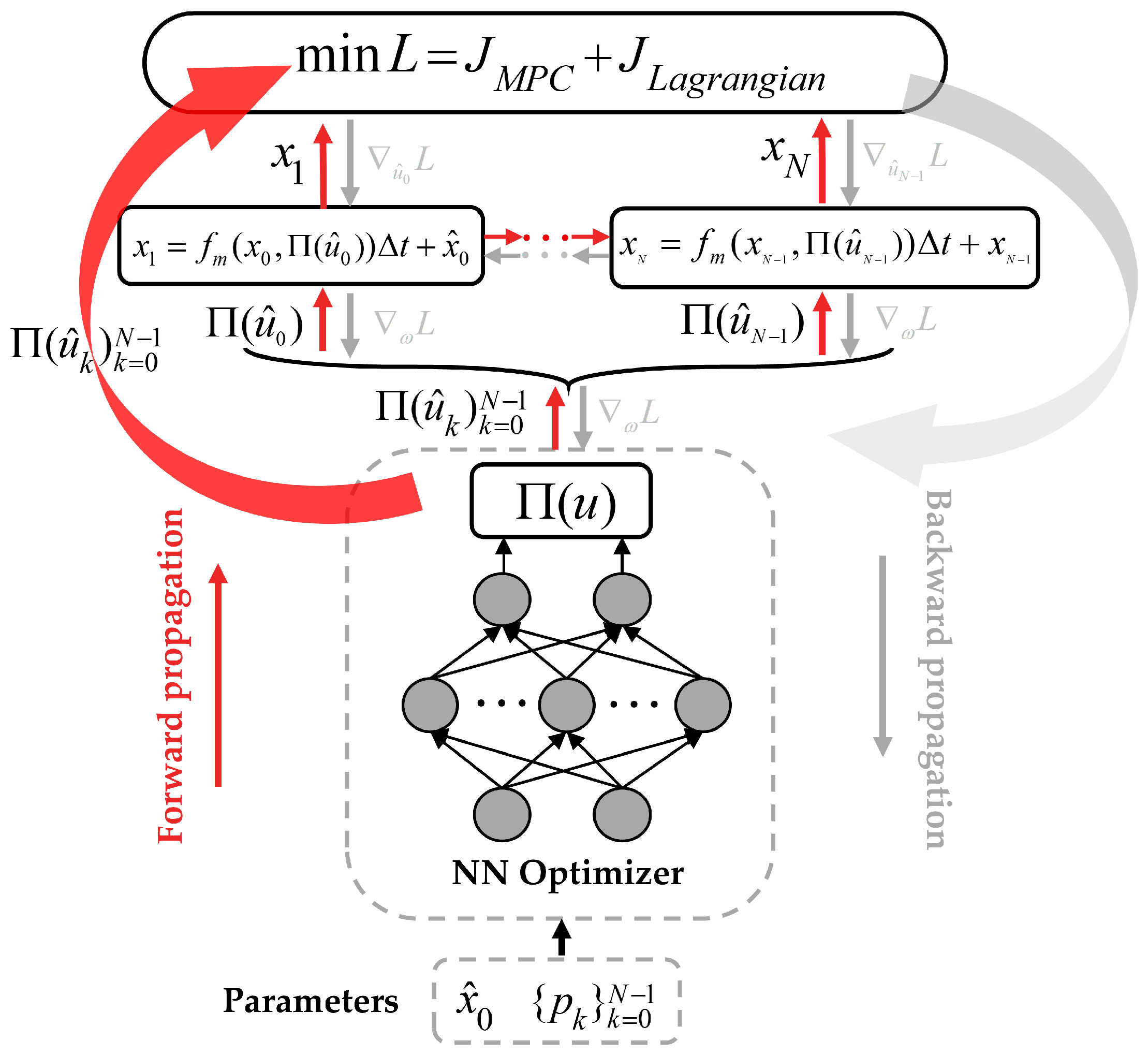
3.3. Neural Network Optimizer
3.3.1. Extraction of Characteristic Parameters for Driving Scenarios
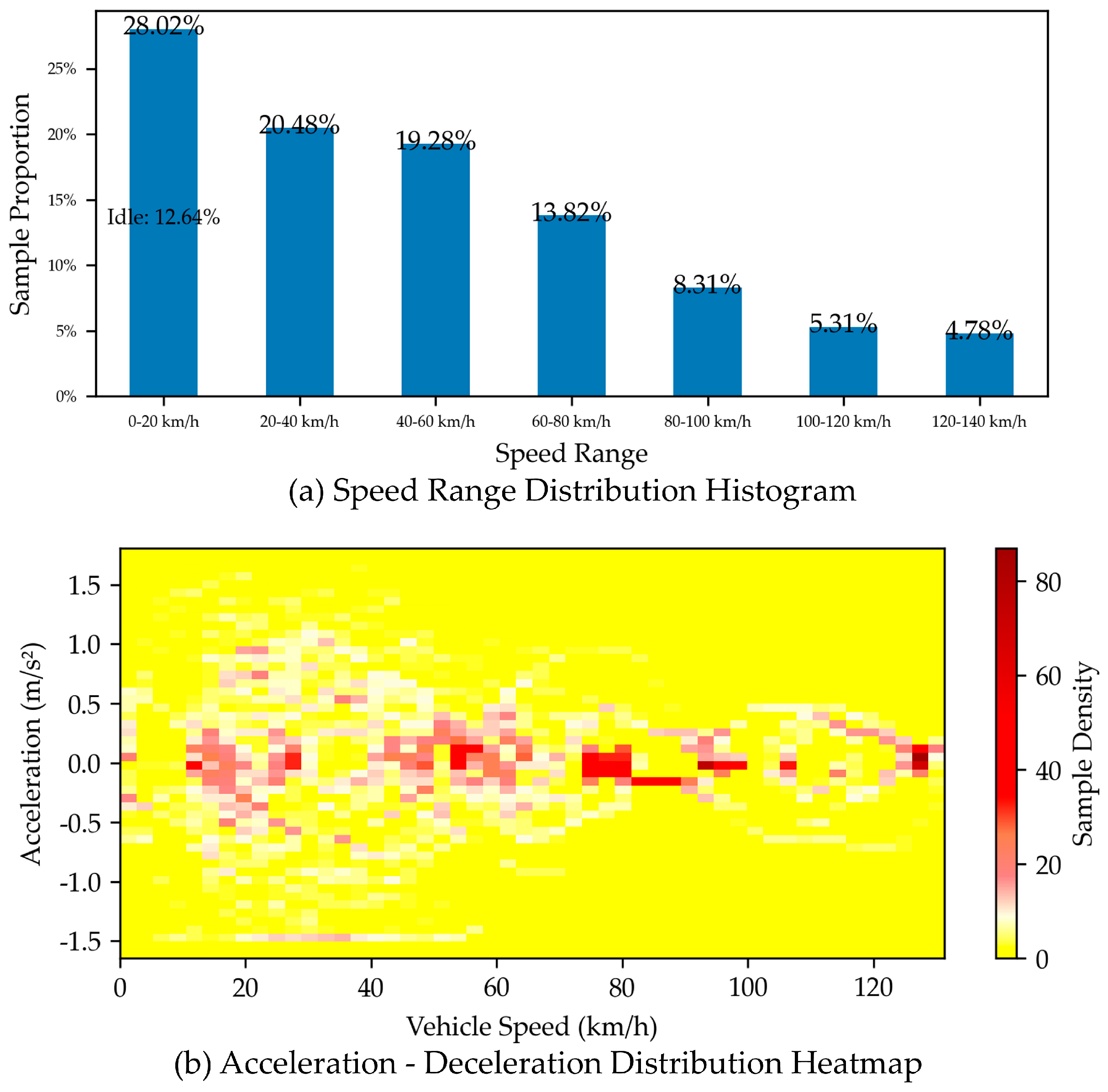
- Sampling frequency setting: Under the WLTC, the initial state speed is sampled every 0.2 s to ensure the time resolution of the data; the reference speed sequence is sampled continuously for 10 steps with a time step of 0.6 s to capture the speed change trend during vehicle driving; meanwhile, the sampling interval for the initial state of battery SOC is set to 0.1 to ensure that changes in energy state are fully recorded.
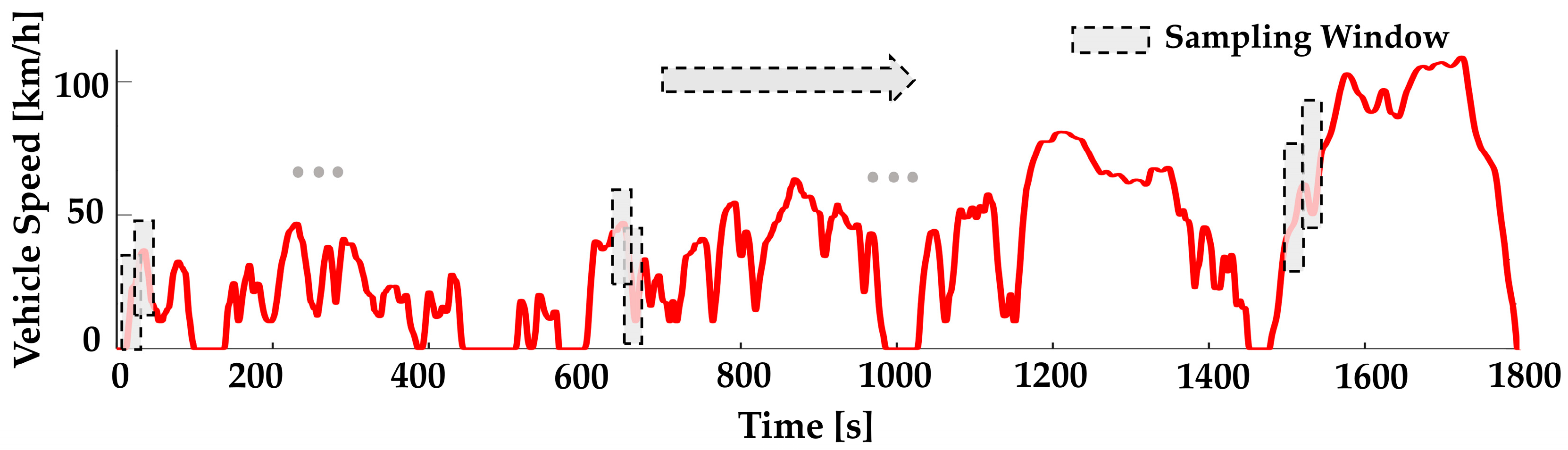
- Data extraction window: As shown by the gray box in the figure, the position of the data extraction window is determined according to vehicle speed information. Each window not only extracts the initial speed but also synchronously extracts the reference speed sequence within the future prediction horizon. This method ensures the temporal consistency of the data and enables the feature dimensions to fully reflect the dynamic characteristics of the vehicle.
- Data integration and matching: After sampling each individual data stream, the speed, reference speed sequence, and initial state of battery SOC are integrated uniformly. During data integration, outliers and noise interference are removed, and interpolation and smoothing processing are adopted to ensure the temporal continuity and accuracy of the data, ultimately constructing a high-quality training dataset.
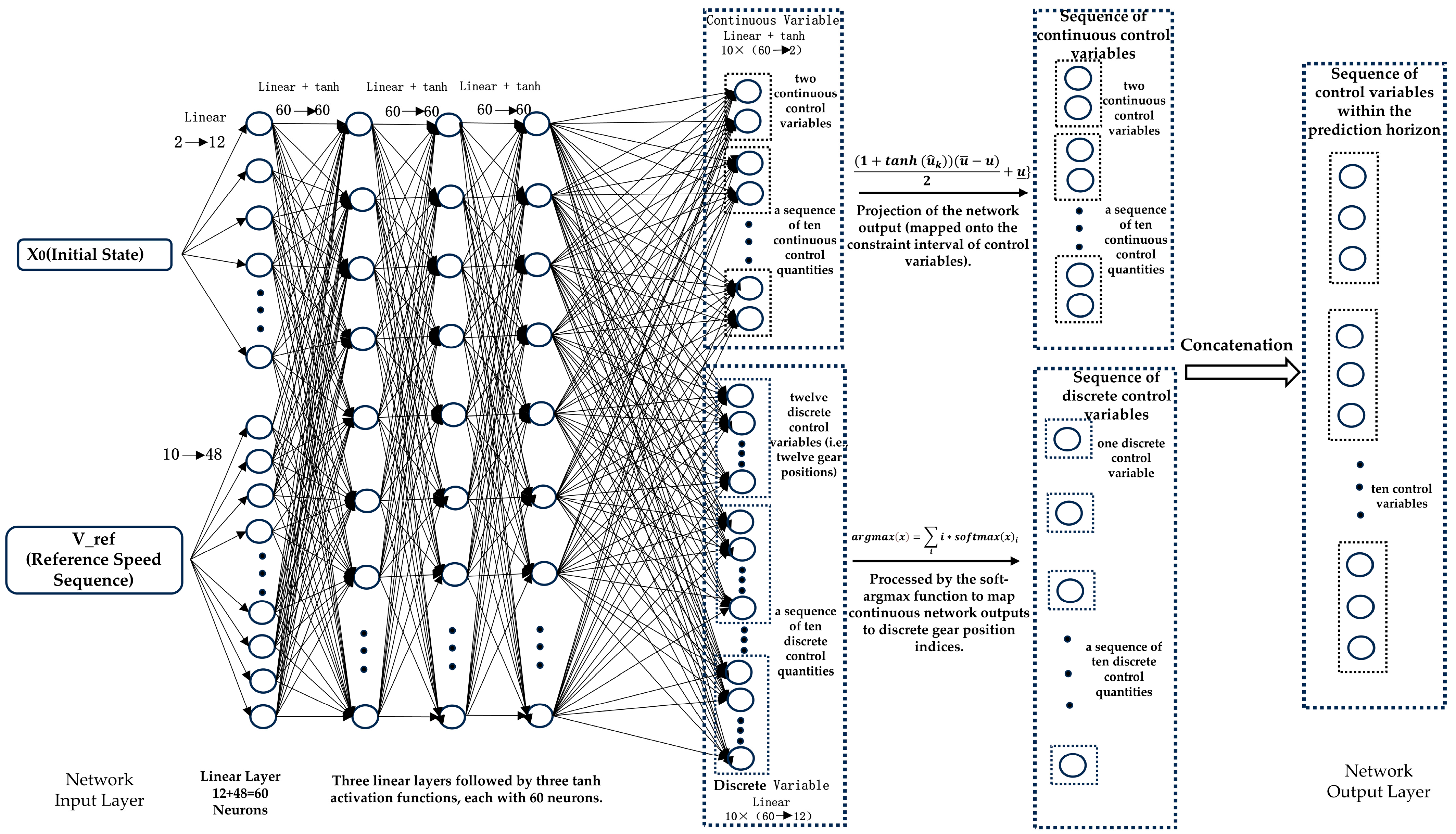
3.3.2. Neural Network Architecture Design
3.3.3. Network Training (Offline Implementation Issues)
4. Simulation Verification and Discussion
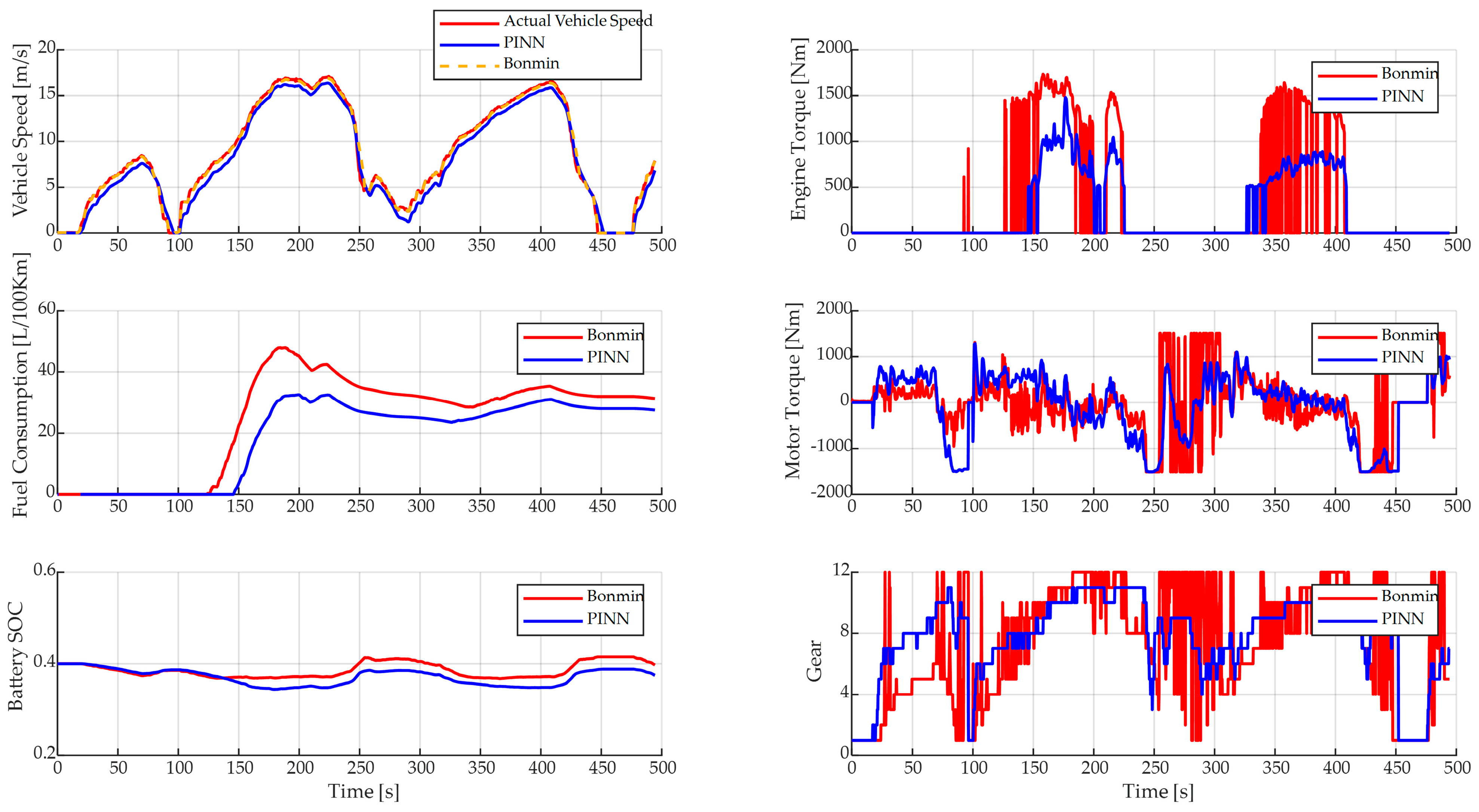
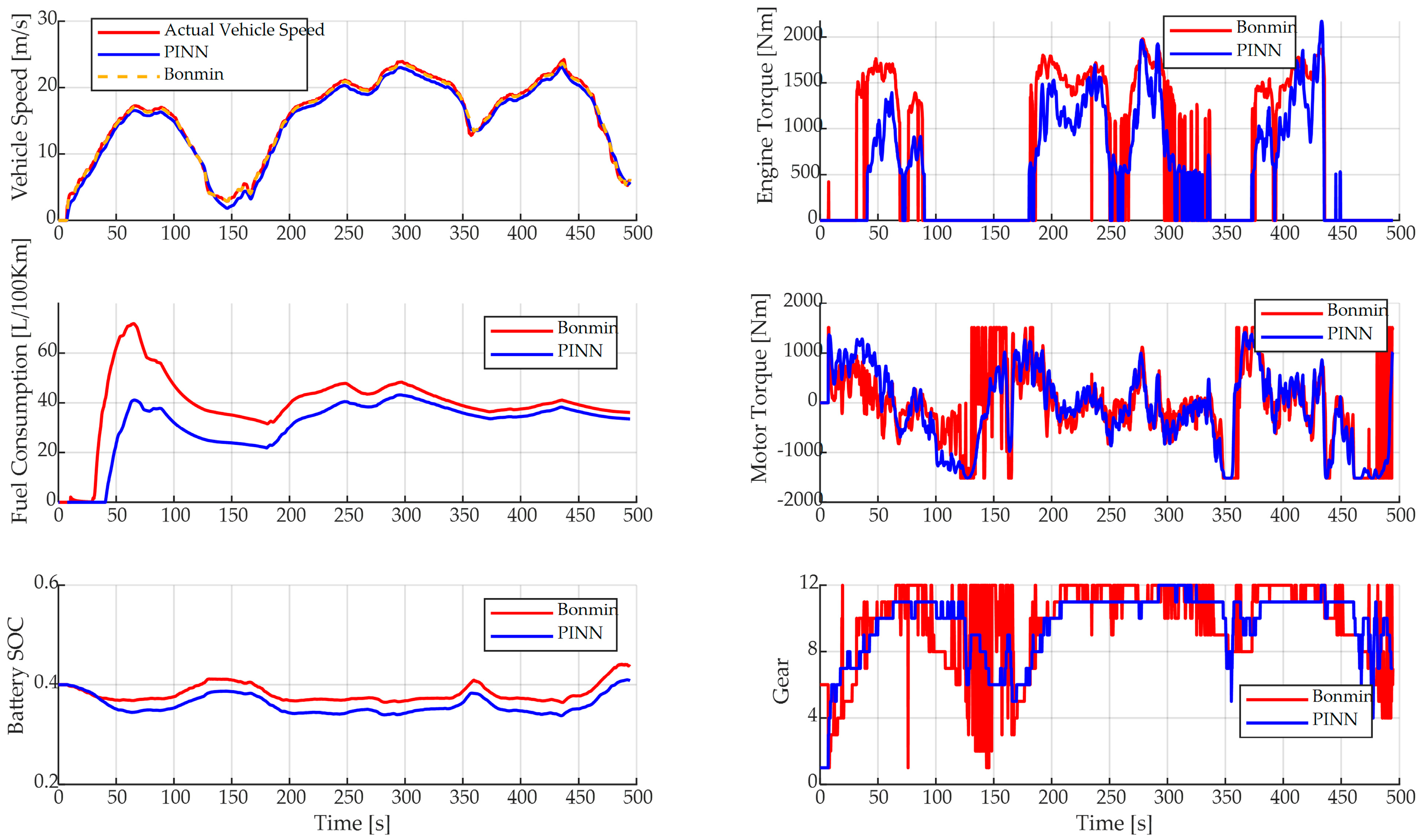
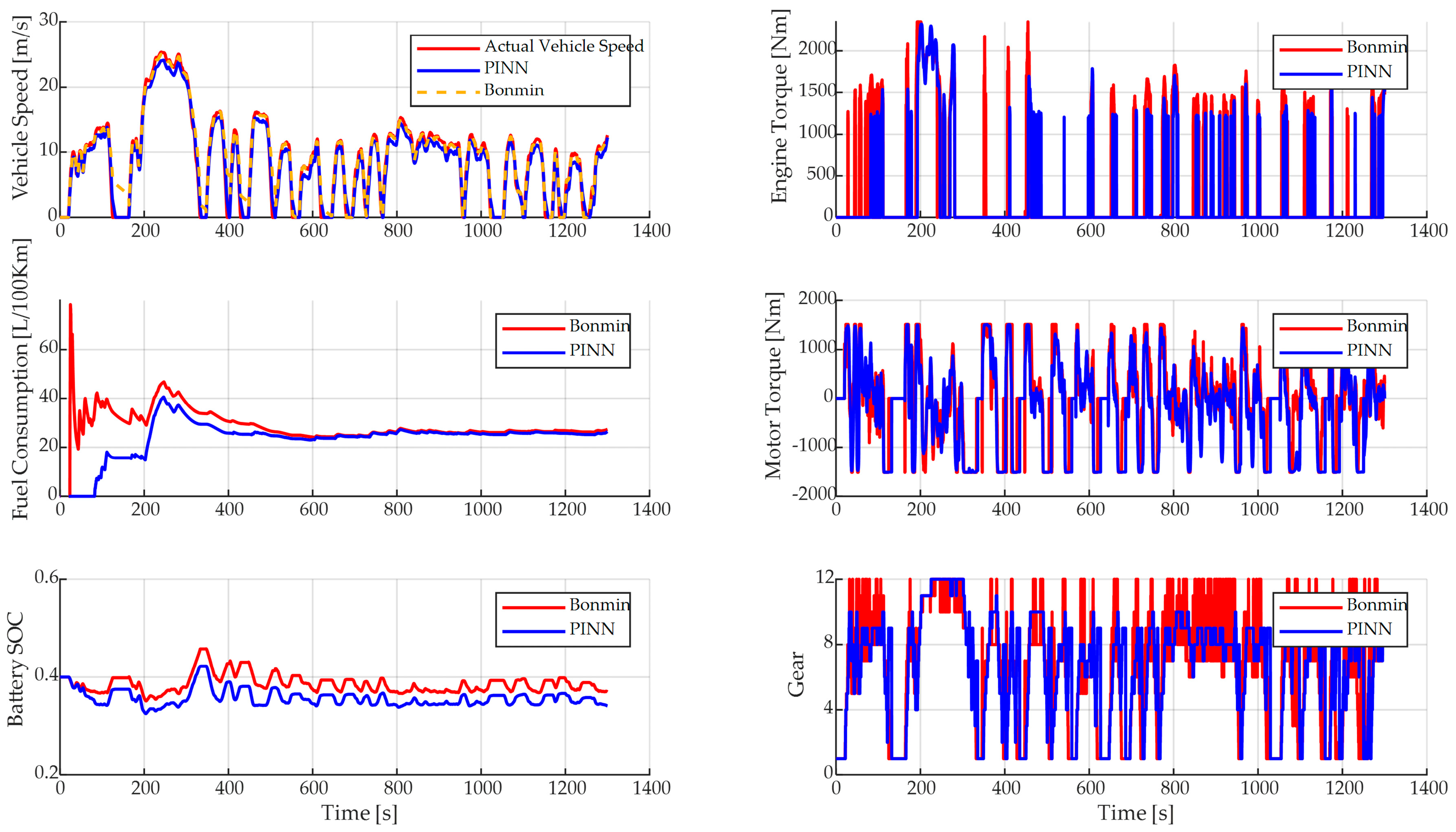
4.1. Online Simulation and Analysis
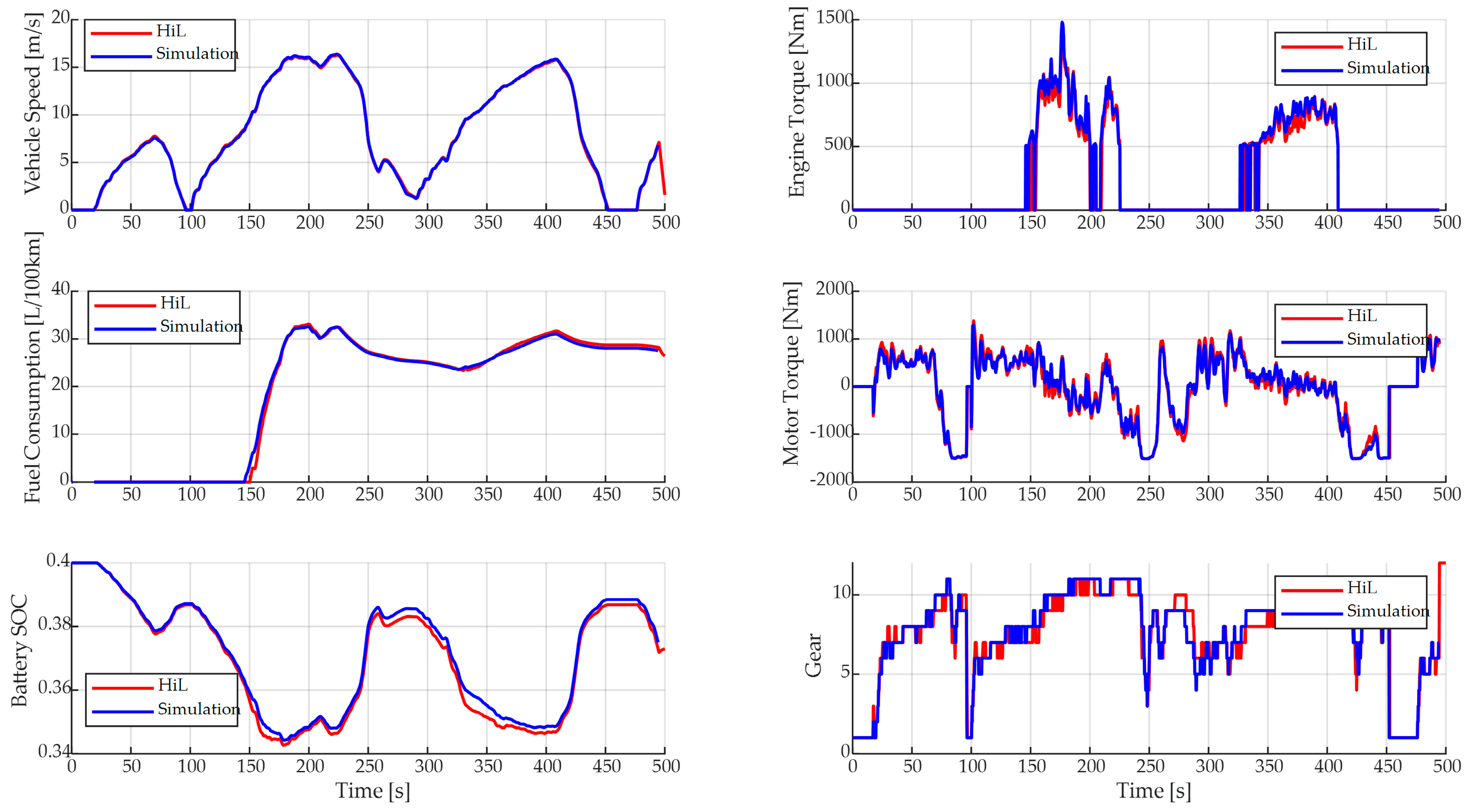
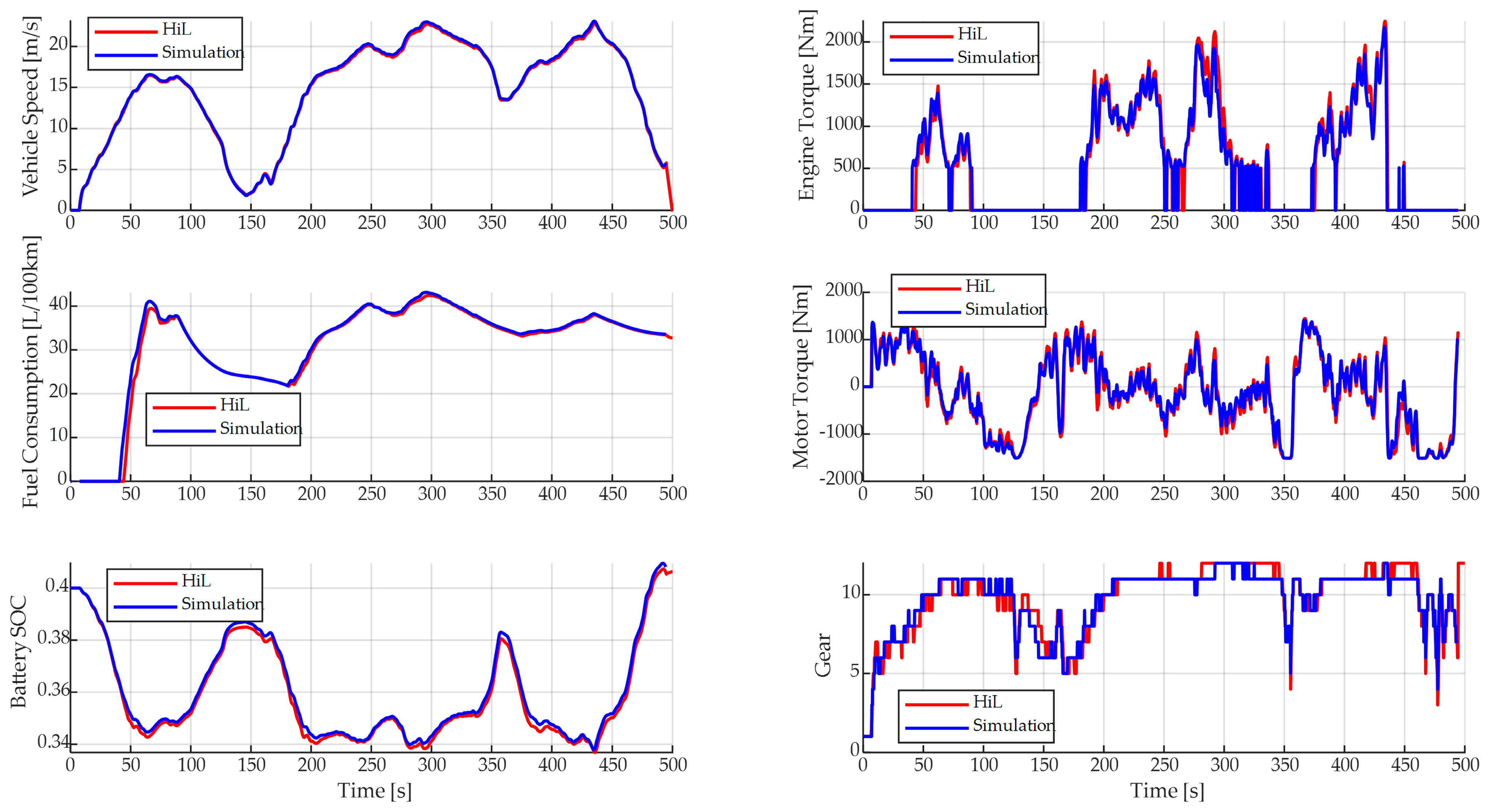
4.2. HIL Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Letnik, T.; Farina, A.; Mencinger, M.; Lupi, M. Božičnik, S. Dynamic management of loading bays for energy efficient urban freight deliveries. Energy 2018, 159, 916–928. [Google Scholar] [CrossRef]
- Kast, J.; Vijayagopal, R.; Gangloff, J.; Marcinkoski, J. Clean commercial transportation: Medium and heavy duty fuel cell electric trucks. Int. J. Hydrogen Energy 2017, 42, 4508–4517. [Google Scholar] [CrossRef]
- Ard, T.; Guo, L.; Han, J.; Jia, Y.; Vahidi, A.; Karbowski, D. Energy-Efficient Driving in Connected Corridors via Minimum Principle Control: Vehiclein-the-Loop Experimental Verification in Mixed Fleets. IEEE Trans. Intell. Veh. 2023, 8, 1279–1291. [Google Scholar] [CrossRef]
- Anselma, P.G.; Kollmeyer, P.J.; Feraco, S.; Bonfitto, A.; Belingardi, G.; Emadi, A.; Amati, N.; Tonoli, A. Economic payback time of battery pack replacement for hybrid and plug-in hybrid electric vehicles. IEEE Trans. Transp. Electrific. 2023, 9, 1021–1033. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Li, G.; Liu, Y.; Huang, Y. A novel model predictive control based co-optimization strategy for velocity planning and energy management of intelligent PHEVs. IEEE Trans. Veh. Technol. 2022, 71, 12667–12681. [Google Scholar] [CrossRef]
- Herrera, V.I.; Milo, A.; Gaztañaga, H.; Ramos, J.; Camblong, H. Adaptive and non-adaptive strategies for optimal energy management and sizing of a dual storage system in a hybrid electric bus. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3435–3447. [Google Scholar] [CrossRef]
- Shi, C.; Wang, T.; Liao, X.; Qie, B.; Yang, P.; Chen, M.; Wang, X.; Srinivasan, A.; Cheng, Q.; Ye, Q.; et al. Accordion-like stretchable Li-ion batteries with high energy density. Energy Storage Mater. 2019, 17, 136–142. [Google Scholar] [CrossRef]
- Hadjigeorgiou, A.; Timotheou, S. Real-Time Optimization of FuelConsumption and Travel-Time of CAVs for Cooperative Intersection Crossing. IEEE Trans. Intell. Veh. 2023, 8, 313–329. [Google Scholar] [CrossRef]
- Fayaz, M.; Khan, J.; Bilal, M. Effectual Energy Consumption and User Comfort Optimization Based on Dynamic User Set Parameters in Electric Vehicles. IEEE Trans. Intell. Veh. 2023, 9, 178–189. [Google Scholar] [CrossRef]
- Ghandriz, T.; Jacobson, B.; Murgovski, N.; Nilsson, P.; Laine, L. Real-time predictive energy management of hybrid electric heavy vehicles by sequential programming. IEEE Trans. Veh. Technol. 2021, 70, 4113–4128. [Google Scholar] [CrossRef]
- Sehla, K.; Nguyen, T.M.T.; Pujolle, G.; Velloso, P.B. Resource allocation modes in C-V2X: FromLTE-V2X to 5G-V2X. IEEE Internet Things J. 2022, 9, 8291–8314. [Google Scholar] [CrossRef]
- Hou, S.; Chen, H.; Yin, H.; Zhao, J.; Xu, F.; Gao, J. Energy Management Based on Mixed-Integer Nonlinear Model Predictive Control for Hybrid Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2024, 25, 17432–17451. [Google Scholar] [CrossRef]
- Zhang, F.; Xi, J.; Langari, R. Real-Time Energy Management Strategy Based on Velocity Forecasts Using V2V and V2I Communications. IEEE Trans. Intell. Transp. Syst. 2017, 18, 416–430. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2017, 185, 1633–1643. [Google Scholar] [CrossRef]
- Phan, D.; Bab-Hadiashar, A.; Fayyazi, M.; Hoseinnezhad, R.; Jazar, R.N.; Khayyam, H. Interval type 2 fuzzy logic control for energy management of hybrid electric autonomous vehicles. IEEE Trans. Intell. Veh. 2020, 6, 210–220. [Google Scholar] [CrossRef]
- Kamal, E.; Adouane, L. Intelligent energy management strategy based on artificial neural fuzzy for hybrid vehicle. IEEE Trans. Intell. Veh. 2018, 3, 112–125. [Google Scholar] [CrossRef]
- He, Y.; Zhou, Q.; Makridis, M.; Mattas, K.; Li, J.; Williams, H.; Xu, H. Multiobjective co-optimization of cooperative adaptive cruise control and energy management strategy for PHEVs. IEEE Trans. Transp. Electrif. 2020, 6, 346–355. [Google Scholar] [CrossRef]
- Hu, Q.; Amini, M.R.; Kolmanovsky, I.; Sun, J.; Wiese, A.; Seeds, J.B. Multihorizon model predictive control: An application to integrated power and thermal management of connected hybrid electric vehicles. IEEE Trans. Control. Syst. Technol. 2022, 30, 1052–1064. [Google Scholar] [CrossRef]
- Dong, S.; Chen, H.; Gao, B.; Guo, L.; Liu, Q. Hierarchical Energy-Efficient Control for CAVs at Multiple Signalized Intersections Considering Queue Effects. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11643–11653. [Google Scholar] [CrossRef]
- Mei, P.; Karimi, H.R.; Xie, H.; Chen, F.; Huang, C.; Yang, S. A deep reinforcement learning approach to energy management control with connected information for hybrid electric vehicles. Eng. Appl. Artif. Intell. 2023, 123, 106239. [Google Scholar] [CrossRef]
- Cui, N.; Cui, W.; Shi, Y. Deep reinforcement learning based PHEV energy management with co-recognition for traffic condition and driving style. IEEE Trans. Intell. Veh. 2023, 8, 3026–3039. [Google Scholar] [CrossRef]
- Hou, S.; Yin, H.; Xu, F.; Benjamín, P.; Gao, J.; Chen, H. Multihorizon predictive energy optimization and lifetime management for connected fuel cell electric vehicles. Energy 2023, 266, 126466. [Google Scholar] [CrossRef]
- Ali, A.M.; Moulik, B.; Söffker, D. Intelligent real-time power management of multi-source HEVs based on driving state recognition and offline optimization. IEEE Trans. Intell. Transp. Syst. 2023, 24, 247–257. [Google Scholar] [CrossRef]
- Maamria, D.; Gillet, K.; Colin, G.; Chamaillard, Y.; Nouillant, C. Computation of ECO-driving cycles for hybrid electric vehicles: Comparative analysis. Control Eng. Pract. 2018, 71, 44–52. [Google Scholar] [CrossRef]
- Chowdhri, N.; Ferranti, L.; Iribarren, F.S.; Shyrokau, B. Integrated nonlinear model predictive control for automated driving. Control Eng. Pract. 2021, 106, 104654. [Google Scholar] [CrossRef]
- Wang, H.; Liu, B.; Ping, X.; An, Q. Path Tracking Control for Autonomous Vehicles Based on an Improved MPC. IEEE Access 2019, 7, 161064–161073. [Google Scholar] [CrossRef]
- Anselma, P.G. Dynamic programming based rapid energy management of hybrid electric vehicles with constraints on smooth driving, battery state-of-charge and battery state-of-health. Energies 2022, 15, 1665. [Google Scholar] [CrossRef]
- Liu, Q.; Wei, J.; Sun, H.; Lin, Y.; Xu, S.; Liu, D. Smulation study on predictive cruise control strategy for an electric heavy duty trucks. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference, Nanjing, China, 23–25 December 2021; pp. 3593–3597. [Google Scholar]
- Shen, M.H.; Dollar, R.A.; Molnar, T.G.; He, C.R.; Vahidi, A.; Orosz, G. EnergyEfficient Reactive and Predictive Connected Cruise Control. IEEE Trans. Intell. Veh. 2023, 9, 944–957. [Google Scholar] [CrossRef]
- Hong, J.; Luo, X.; Wu, H.; Na, X.; Chu, H.; Gao, B.; Chen, H. Energy-Saving Driving Assistance System Integrated With Predictive Cruise Control for Electric Vehicles. IEEE Trans. Intell. Veh. 2024, 9, 4518–4528. [Google Scholar] [CrossRef]
- Dong, S.; Ghezzi, A.; Harzer, J.; Frey, J.; Gao, B.; Chen, H.; Diehl, M. Real-Time NMPC With Convex–Concave Constraints and Application to Eco-Driving. IEEE Trans. Control. Syst. Technol. 2025, 33, 807–814. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Z.; Wu, J.; Huo, W.; He, H.; Chen, Y. Multi-Vehicle InteractionAware Energy Management for Connected Hybrid Electric Vehicles via Deep Reinforcement Learning. In Proceedings of the 2024 IEEE 14th International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Copenhagen, Denmark, 16–19 July 2024; pp. 434–439. [Google Scholar]
- Zhang, H.; Peng, J.; Dong, H.; Ding, F.; Tan, H. Integrated velocity optimization and energy management strategy for hybrid electric vehicle platoon: A multi-agent reinforcement learning approach. IEEE Trans. Transp. Electrif. 2023, 10, 2547–2561. [Google Scholar] [CrossRef]
- Luo, X.; Dong, S.; Hong, J.; Wang, X.; Gao, B.; Chen, H. Online Ecological Gearshift Strategy via Neural Network with Soft-Argmax Operator. IFAC-PapersOnLine 2024, 50, 415–420. [Google Scholar] [CrossRef]
- Shi, W.; Luo, X.; Hong, J.; Zhao, C.; Gao, B.; Chen, H. Accelerating Model Predictive Control with Neural Network Optimizer. In Proceedings of the 2023 7th CAA International Conference on Vehicular Control and Intelligence (CVCI), Changsha, China, 27–29 October 2023; pp. 1–7. [Google Scholar]


| State Update Method | Loss Function | Solution Method | |
|---|---|---|---|
| General MIP-MPC Algorithm | System state equation | Determined by control objectives | Branch and bound |
| PINN-MPC Algorithm | System state equation | Determined not only by control objectives, but also with the addition of restrictions on state variables and control variables to guide training | Using neural network parameters for matrix operations |
| Parameter | Value |
|---|---|
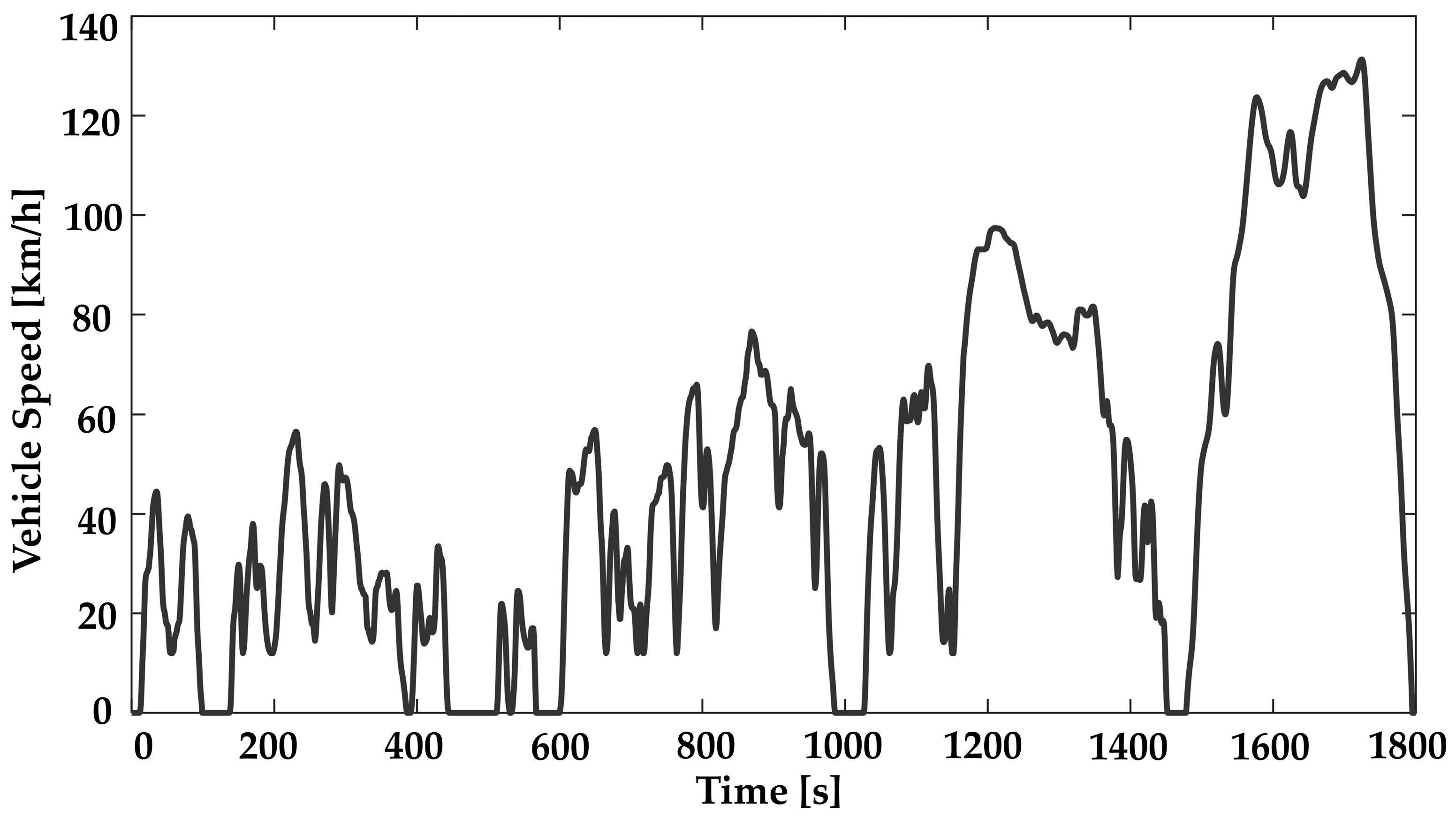
| Total Duration | 1800 s |
| Total Distance | 23.27 km |
| Average Speed | 46.5 km/h |
| Maximum Speed | 131.3 km/h |
| Idling Time Ratio | 13.40% |
| Frequency of Acceleration/Deceleration | Similar to real traffic conditions |
| The First Condition | |||||
| Average speed (actual vehicle speed, 8.489 m/s) | Equivalent fuel consumption (L/100 km) | Average calculation time (s) | Maximum calculation time (s) | Energy consumption error | |
| BONMIN solver | 8.478 | 31.7338 | 4.456 | 142.8 | 0.90% |
| PINN solver | 8.202 | 32.019 | 2.83 × 10−3 | 0.0354 | |
| The Second Condition | |||||
| Average speed (actual vehicle speed, 15.33 m/s) | Equivalent fuel consumption (L/100 km) | Average calculation time (s) | Maximum calculation time (s) | Energy consumption error | |
| BONMIN solver | 15.26 | 32.6981 | 5.037 | 62.92 | 0.25% |
| PINN solver | 14.97 | 32.7794 | 1.27 × 10−3 | 0.041 | |
| Average Speed (m/s) | Equivalent Fuel Consumption (L/100 km) | Average Calculation Time (s) | Maximum Calculation Time (s) | Energy Consumption Error | |
|---|---|---|---|---|---|
| BONMIN solver | 8.98 | 29.069 | 3.135 | 111.2 | 1.91% |
| PINN solver | 8.77 | 29.626 | 3.3 × 10−3 | 0.043 |
| The First Condition | |||||
| Average speed (m/s) | Equivalent fuel consumption (L/100 km) | Average calculation time (s) | Maximum calculation time (s) | Energy consumption error | |
| Online Simulation | 8.202 | 32.019 | 0.0028 | 0.0354 | 0.60% |
| HIL Test | 8.188 | 32.238 | 0.0032 | 0.0038 | |
| The Second Condition | |||||
| Average speed (m/s) | Equivalent fuel consumption (L/100 km) | Average calculation time (s) | Maximum calculation time (s) | Energy consumption error | |
| Online Simulation | 14.97 | 32.7794 | 0.0013 | 0.041 | 0.14% |
| HIL Test | 14.84 | 32.8252 | 0.0035 | 0.004 | |
| Indicator | Value | Description |
|---|---|---|
| CPU Utilization | Around 30% | Maximum load within a single control cycle |
| Memory Usage | 1–2 GB | Includes neural network weights and cache |
| Control Cycle Execution Rate | 100% | Successfully executed per cycle, no overflow or lag |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, J.; Yang, F.; Luo, X.; Na, X.; Chu, H.; Tian, M. Energy Management of Hybrid Electric Commercial Vehicles Based on Neural Network-Optimized Model Predictive Control. Electronics 2025, 14, 3176. https://doi.org/10.3390/electronics14163176
Hong J, Yang F, Luo X, Na X, Chu H, Tian M. Energy Management of Hybrid Electric Commercial Vehicles Based on Neural Network-Optimized Model Predictive Control. Electronics. 2025; 14(16):3176. https://doi.org/10.3390/electronics14163176
Chicago/Turabian StyleHong, Jinlong, Fan Yang, Xi Luo, Xiaoxiang Na, Hongqing Chu, and Mengjian Tian. 2025. "Energy Management of Hybrid Electric Commercial Vehicles Based on Neural Network-Optimized Model Predictive Control" Electronics 14, no. 16: 3176. https://doi.org/10.3390/electronics14163176
APA StyleHong, J., Yang, F., Luo, X., Na, X., Chu, H., & Tian, M. (2025). Energy Management of Hybrid Electric Commercial Vehicles Based on Neural Network-Optimized Model Predictive Control. Electronics, 14(16), 3176. https://doi.org/10.3390/electronics14163176










