Improvement of Tracking-Integrated Photovoltaic Systems Using Secondary Optical Elements
Abstract
1. Introduction
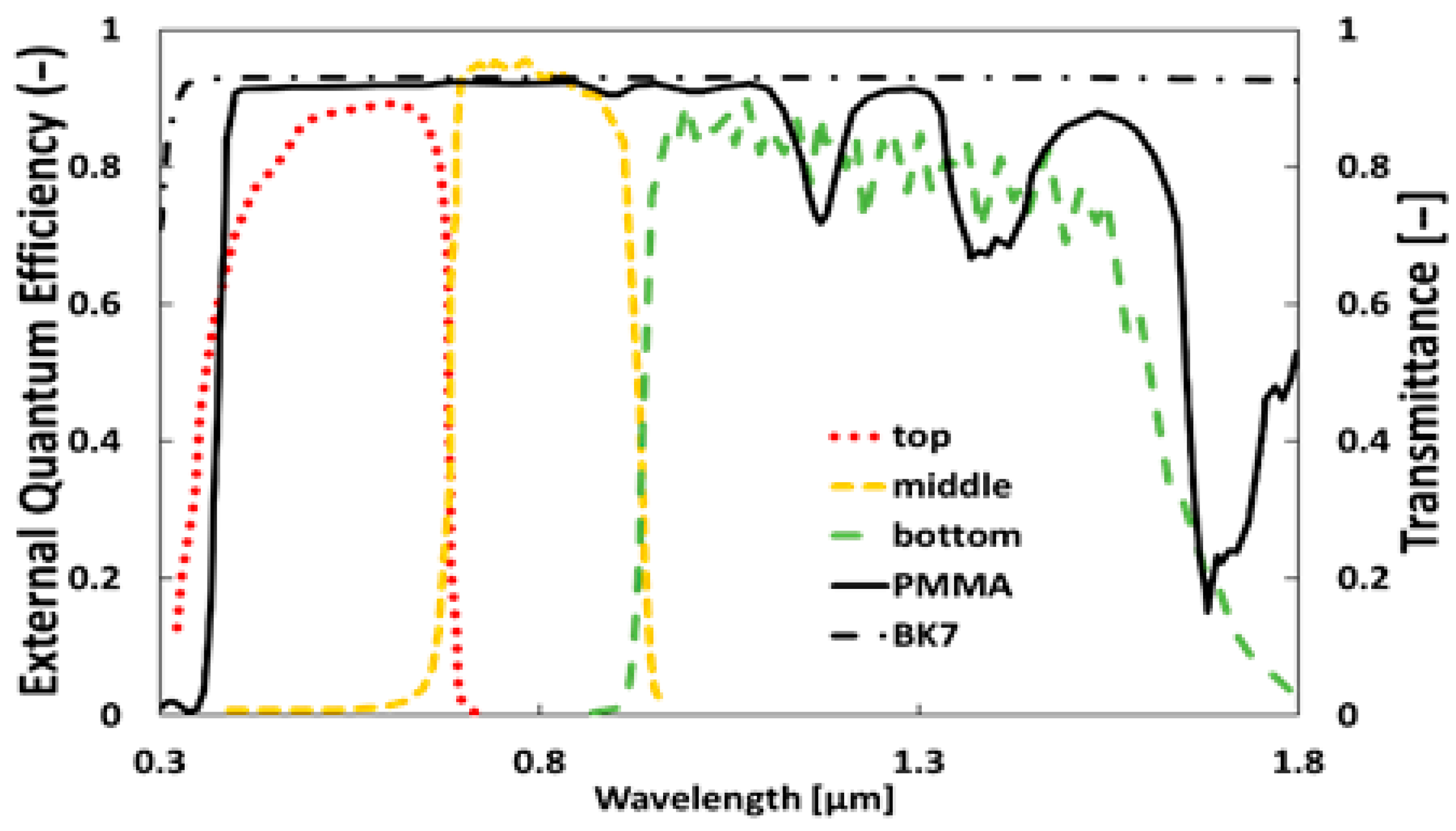
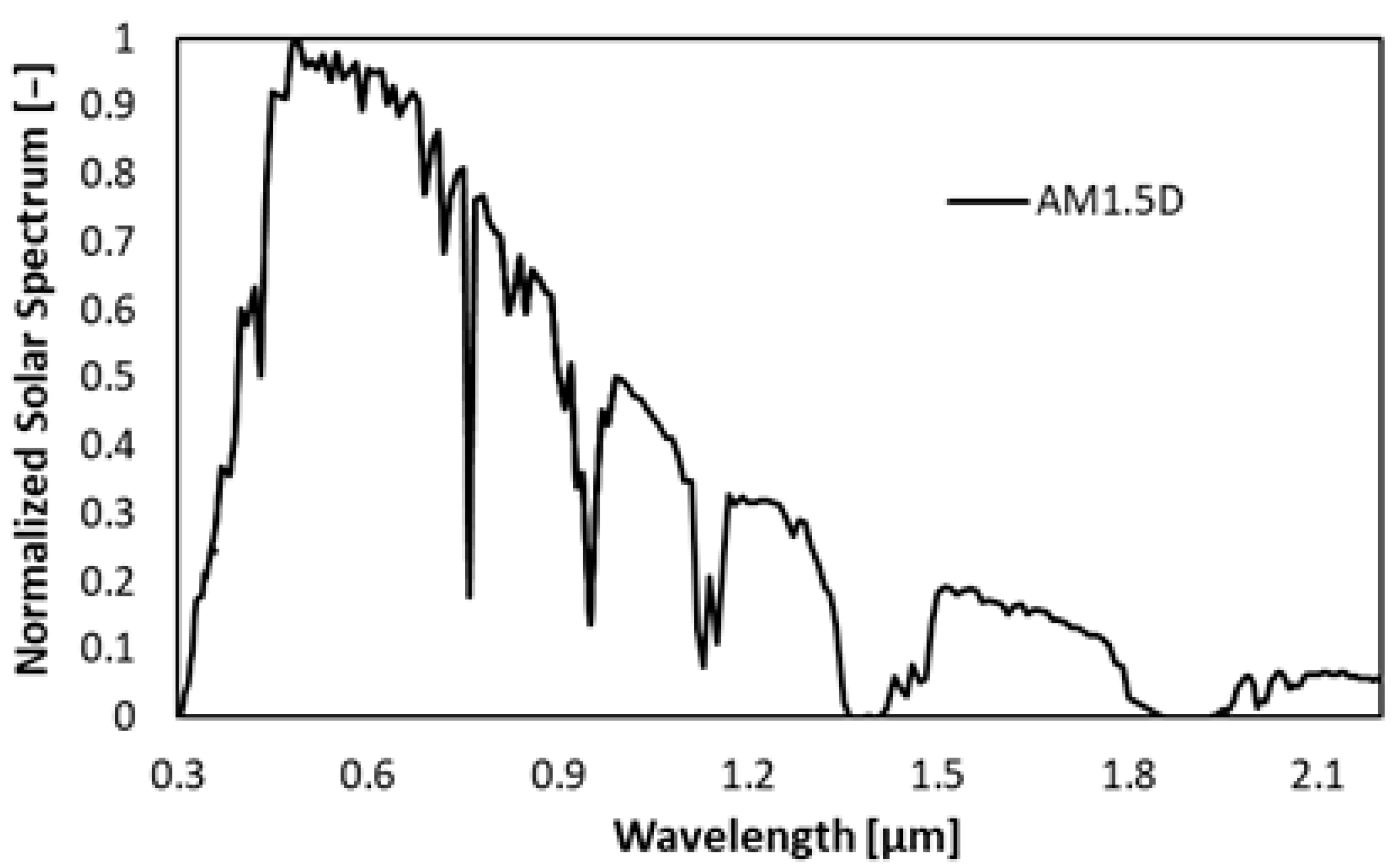
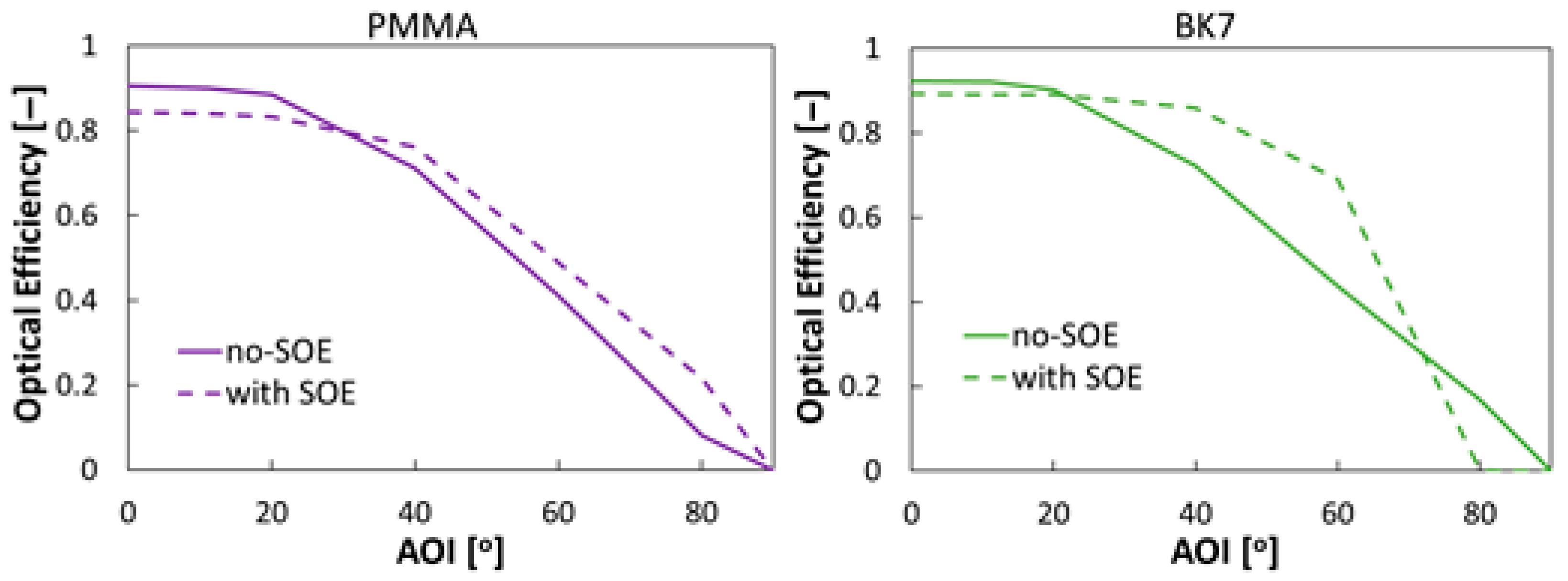
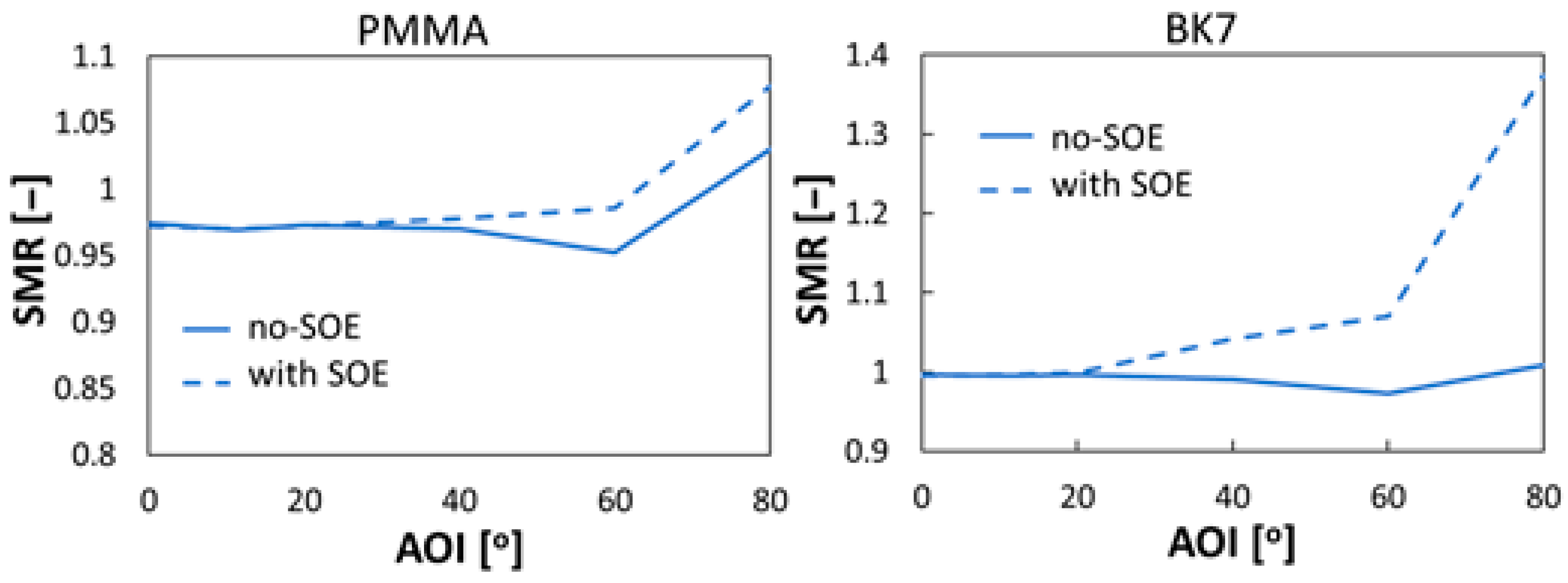
2. Materials and Methods
3. Analysis of the Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| AOI | Angle of incidence (°) |
| CPV | Concentrator photovoltaic |
| CSTCs | Concentrator standard test conditions |
| DII | Direct inclined irradiation |
| DNI | Direct normal irradiance |
| EQE | External quantum efficiency (−) |
| MJ | Multi-junction |
| PMMA | Poly(methylmethacrylate) |
| POE | Primary optical element |
| PV | Photovoltaic |
| SMR | Spectral matching ratio |
| SOE | Secondary optical element |
| TICPV | Tracking-integrated concentrator photovoltaic |
| TMY | Typical meteorological year |
| Parameters | |
| Acell | Area of the cell (mm2) |
| APOE | Area of the POE (mm2) |
| Cg | Geometric concentration (x) |
| JSC | Short-circuit current density (A/m2) |
| ηopt | Optical efficiency (%) |
References
- Khamooshi, M.; Salati, H.; Egelioglu, F.; Hooshyar Faghiri, A.; Tarabishi, J.; Babadi, S. A Review of Solar Photovoltaic Concentrators. Int. J. Photoenergy 2014, 1, 958521. [Google Scholar] [CrossRef]
- Geisz, J.F.; France, R.M.; Schulte, K.L.; Steiner, M.A.; Norman, A.G.; Guthrey, H.L.; Young, M.R.; Song, T.; Moriarty, T. Six-Junction III–V Solar Cells with 47.1% Conversion Efficiency under 143 Suns Concentration. Nat. Energy 2020, 5, 326–335. [Google Scholar] [CrossRef]
- Doeleman, H. Limiting and Realistic Efficiencies of Multi-Junction Solar Cells; Photonic Materials Group: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Shanks, K.; Senthilarasu, S.; Mallick, T.K. Optics for Concentrating Photovoltaics: Trends, Limits and Opportunities for Materials and Design. Renew. Sustain. Energy Rev. 2016, 60, 394–407. [Google Scholar] [CrossRef]
- Iqbal, W.; Ullah, I. Optical Developments in Concentrator Photovoltaic Systems—A Review. Sustainability 2023, 15, 10554. [Google Scholar] [CrossRef]
- Victoria, M.; Domínguez, C.; Antón, I.; Sala, G. Comparative Analysis of Different Secondary Optical Elements for Aspheric Primary Lenses. Opt. Express 2009, 17, 6487–6492. [Google Scholar] [CrossRef] [PubMed]
- Luque, A.; Sala, G.; Luque-Heredia, I. Photovoltaic Concentration at the Onset of Its Commercial Deployment. Prog. Photovoltaics Res. Appl. 2006, 14, 413–428. [Google Scholar] [CrossRef]
- Chemisana, D. Building Integrated Concentrating Photovoltaics: A Review. Renew. Sustain. Energy Rev. 2011, 15, 603–611. [Google Scholar] [CrossRef]
- Paliyal, P.S.; Mondal, S.; Layek, S.; Kuchhal, P.; Pandey, J.K. Automatic Solar Tracking System: A Review Pertaining to Advancements and Challenges in the Current Scenario. Clean Energy 2024, 8, 237–262. [Google Scholar] [CrossRef]
- Trommsdorff, M.; Campana, P.E.; Macknick, J.; Fernández Solas, A.; Gorjian, S.; Tsanakas, I. Dual Land Use for Agriculture and Solar Power Production: Overview and Performance of Agrivoltaic Systems; International Energy Agency: Paris, France, 2025; ISBN 9783907281703. [Google Scholar]
- Algora, C.; Rey-Stolle, I. Handbook on Concentrator Photovoltaic Technology; Wiley: Hoboken, NJ, USA, 2016; ISBN 9781118755631. [Google Scholar]
- Kalogirou, S. McEvoy’s Handbook of Photovoltaics: Fundamentals and Applications, 3rd ed.; Academic Press: New York, NY, USA, 2018; ISBN 978-0-12-809921-6. [Google Scholar]
- Ceballos, M.A.; Pérez-Higueras, P.J.; Fernández, E.F.; Almonacid, F. Tracking-Integrated CPV Technology: State-of-the-Art and Classification. Energies 2023, 16, 5605. [Google Scholar] [CrossRef]
- Price, J.S.; Sheng, X.; Meulblok, B.M.; Rogers, J.A.; Giebink, N.C. Wide-Angle Planar Microtracking for Quasi-Static Microcell Concentrating Photovoltaics. Nat. Commun. 2015, 6, 6223. [Google Scholar] [CrossRef]
- Ito, A.; Sato, D.; Yamada, N. Optical Design and Demonstration of Microtracking CPV Module with Bi-Convex Aspheric Lens Array. Opt. Express 2018, 26, A879. [Google Scholar] [CrossRef]
- Ceballos, M.A.; Valera, Á.; Sanmartín, P.; Almonacid, F.; Fernández, E.F. Development and Indoor Characterization of a Concentrator Photovoltaic Assembly for Tracking-Integrated Systems. Sol. Energy 2023, 255, 292–300. [Google Scholar] [CrossRef]
- Nardin, G.; Domínguez, C.; Aguilar, Á.F.; Anglade, L.; Duchemin, M.; Schuppisser, D.; Gerlich, F.; Ackermann, M.; Coulot, L.; Cuénod, B.; et al. Industrialization of Hybrid Si/III–V and Translucent Planar Micro-tracking Modules. Prog. Photovoltaics Res. Appl. 2021, 29, 819–834. [Google Scholar] [CrossRef]
- Nakatani, M. Calculation of the Interaction between an Overlapping Spherical Lens and a Pin-Type Second Optical Element for Spherical Lens Microtracking Concentrator Photovoltaic with a Wide Angle of Incidence. Jpn. J. Appl. Phys. 2024, 63, 052002. [Google Scholar] [CrossRef]
- O’Gallagher, J.J. Nonimaging Optics in Solar Energy; Morgan & Claypool Publishers: San Rafael, CA, USA, 2008; ISBN 9781598293302. [Google Scholar]
- Cooper, T.; Dähler, F.; Ambrosetti, G.; Pedretti, A.; Steinfeld, A. Performance of Compound Parabolic Concentrators with Polygonal Apertures. Sol. Energy 2013, 95, 308–318. [Google Scholar] [CrossRef]
- Fu, L.; Leutz, R.; Annen, H.P. Secondary Optics for Fresnel Lens Solar Concentrators. Nonimaging Opt. Effic. Des. Illum. Sol. Conc. VII 2010, 7785, 778506–778509. [Google Scholar] [CrossRef]
- Reddy, K.S.; Mallick, T.K.; Srihari Vikram, T.; Sharon, H. Design and Optimisation of Elliptical Hyperboloid Concentrator with Helical Receiver. Sol. Energy 2014, 108, 515–524. [Google Scholar] [CrossRef]
- Ramachandran, A.M.; S, S.M.; Thampi, A.S.; Singh, M.; Asok, A. A Comprehensive Review on Optics and Optical Materials for Planar Waveguide-Based Compact Concentrated Solar Photovoltaics. Results Eng. 2022, 16, 100665. [Google Scholar] [CrossRef]
- El Himer, S.; El Ayane, S.; El Yahyaoui, S.; Salvestrini, J.P.; Ahaitouf, A. Photovoltaic Concentration: Research and Development. Energies 2020, 13, 5721. [Google Scholar] [CrossRef]
- Miller, D.C.; Khonkar, H.I.; Herrero, R.; Antón, I.; Johnson, D.K.; Hornung, T.; Schmid-Schirling, T.; Vinzant, T.B.; Deutch, S.; To, B.; et al. An End of Service Life Assessment of PMMA Lenses from Veteran Concentrator Photovoltaic Systems. Sol. Energy Mater. Sol. Cells 2017, 167, 7–21. [Google Scholar] [CrossRef]
- Miller, D.C.; Kurtz, S.R. Durability of Fresnel Lenses: A Review Specific to the Concentrating Photovoltaic Application. Sol. Energy Mater. Sol. Cells 2011, 95, 2037–2068. [Google Scholar] [CrossRef]
- Miller, D.C.; Kempe, M.D.; Kennedy, C.E.; Kurtz, S.R. Analysis of Transmitted Optical Spectrum Enabling Accelerated Testing of Multijunction Concentrating Photovoltaic Designs. Opt. Eng. 2011, 50, 13003. [Google Scholar] [CrossRef]
- Beadie, G.; Brindza, M.; Flynn, R.A.; Rosenberg, A.; Shirk, J.S. Refractive Index Measurements of Poly(Methyl-Methacrylate) (PMMA) from 0.4–1.6μm. Appl. Opt. 2015, 54, F139–F143. [Google Scholar] [CrossRef] [PubMed]
- SCHOTT Optical Glass Data Sheets; SCHOTT North America, Inc.: Duryea, PA, USA, 2014.
- AzurSpace Concentrator Triple Junction Solar Cell. Cell Type: 3C44. Application: Concentrating Photovoltaic (CPV) Modules. Available online: https://www.azurspace.com/images/products/0004355-00-01_3C44_AzurDesign_10x10.pdf (accessed on 1 May 2025).
- IEC 62670-1:2013; Photovoltaic Concentrators (CPV)—Performance Testing—Part 1: Standard Conditions. IEC: Geneva, Switzerland, 2013.
- Ferrer-Rodríguez, J.P.; Baig, H.; Fernández, E.F.; Almonacid, F.; Mallick, T.; Pérez-Higueras, P. Optical Modeling of Four Fresnel-Based High-CPV Units. Sol. Energy 2017, 155, 805–815. [Google Scholar] [CrossRef]
- Benítez, P.; Miñano, J.C.; Zamora, P.; Mohedano, R.; Cvetkovic, A.; Buljan, M.; Chaves, J.; Hernández, M. High Performance Fresnel-Based Photovoltaic Concentrator. Opt. Express 2010, 18, A25–A40. [Google Scholar] [CrossRef]
- Domínguez, C.; Antón, I.; Sala, G.; Askins, S. Current-Matching Estimation for Multijunction Cells within a CPV Module by Means of Component Cells. Prog. Photovolt Res. Appl. 2013, 21, 1478–1488. [Google Scholar] [CrossRef]
- Núñez, R.; Jin, C.; Antón, I.; Sala, G. Spectral Classification of Worldwide Locations Using SMR Indexes. AIP Conf. Proc. 2016, 1766, 90007-1. [Google Scholar] [CrossRef]
- Domínguez, C.; Askins, S.; Antón, I.; Sala, G. Characterization of Five CPV Module Technologies with the Helios 3198 Solar Simulator. In Proceedings of the 2009 34th IEEE Photovoltaic Specialists Conference (PVSC), Philadelphia, PA, USA, 7–12 June 2009; pp. 1004–1008. [Google Scholar] [CrossRef]
- Perez-Higueras, P.; Ceballos, M.A.; Mouhib, E.; Bessa, J.G.; Montes-Romero, J.; Mata-Campos, R. Comparative Analysis of Direct Inclined Irradiance Data Sources for Micro-Tracking Concentrator Photovoltaics. Electron. 2025, 14, 2297. [Google Scholar] [CrossRef]
- Fernández, E.F.; Talavera, D.L.; Almonacid, F.M.; Smestad, G.P. Investigating the Impact of Weather Variables on the Energy Yield and Cost of Energy of Grid-Connected Solar Concentrator Systems. Energy 2016, 106, 790–801. [Google Scholar] [CrossRef]
- Su, L. Room Temperature Growth of CsPbBr3 Single Crystal for Asymmetric MSM Structure Photodetector. J. Mater. Sci. Technol. 2024, 187, 113–122. [Google Scholar] [CrossRef]
- Xia, Z.; Chen, Y.; Su, L.; Chen, H. Bioinspired Artificial Optoelectronic Synapse for Encrypted Communication Realized via a MoSe 2 Based MIS Structural Photodiode. J. Mater. Sci. Technol. 2026, 243, 129–138. [Google Scholar] [CrossRef]



| PMMA | BK7 | |||
|---|---|---|---|---|
| No-SOE | SOE | No-SOE | SOE | |
| POE Lens diagonal [mm] | 39.24 | 39.24 | 39.24 | 39.24 |
| POE Focal length [mm] | 54 | 36.5 | 41 | 30.5 |
| POE Thickness [mm] | 12.5 | 21.5 | 16.45 | 25.2 |
| Dome-Shaped SOE Radius of Curvature [mm−1] | - | 0.095 | - | 0.095 |
| Electrical Parameters | No SOE | With SOE |
|---|---|---|
| VSC | ±0.72% | ±0.58% |
| ISC | ±0.21% | ±0.17% |
| Pmp | ±0.39% | ±0.42% |
| Vmp | ±1.03% | ±1.56% |
| Imp | ±0.16% | ±0.17% |
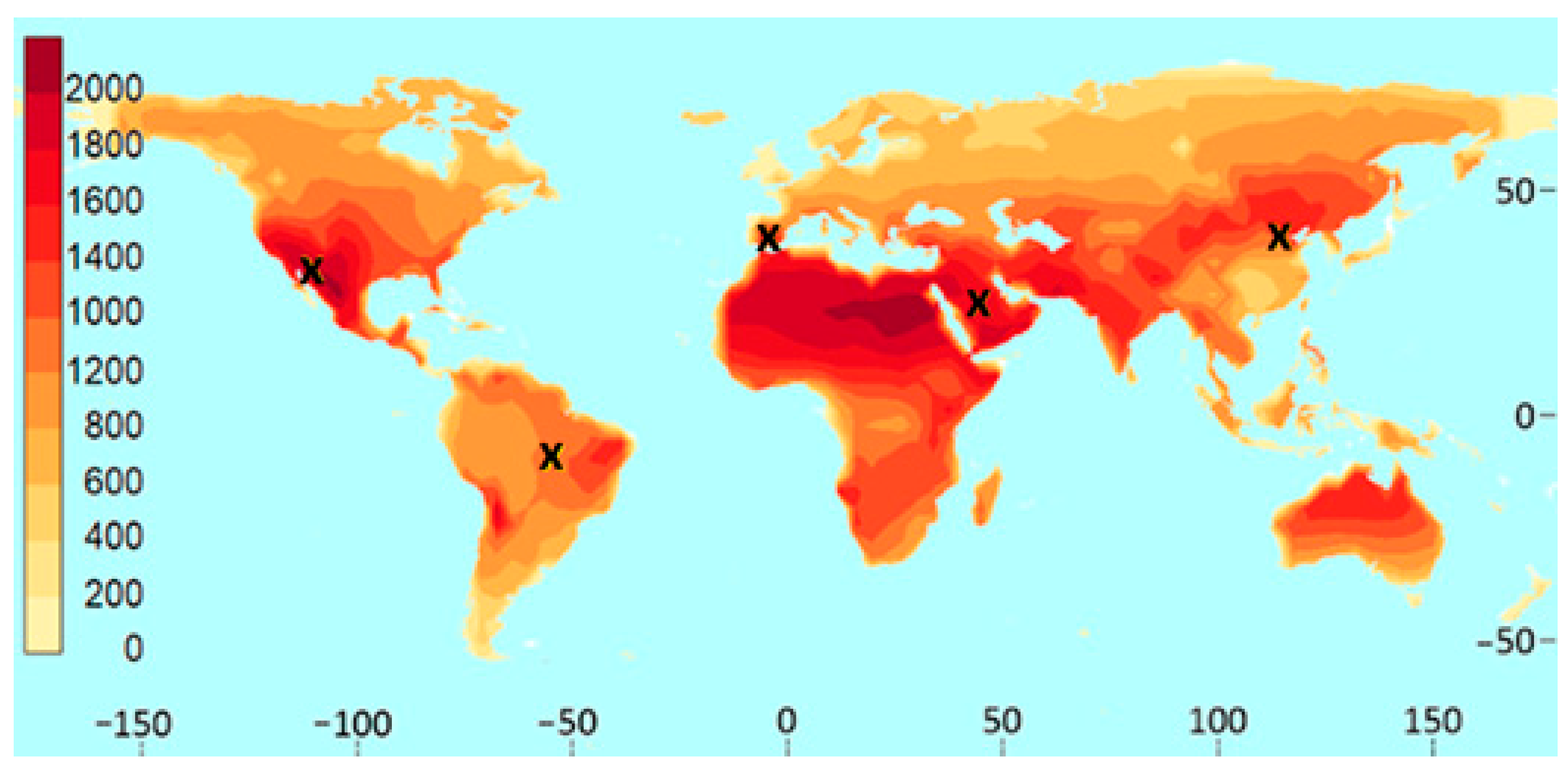
| Jaén | Alta Floresta | Solar Village | Santa Ana | Beijing | |
|---|---|---|---|---|---|
| Latitude | 37.7797° N | 9.8797° S | 24.7743° N | 30.542° N | 40.191° N |
| Longitude | 3.7797° N | 56.0853° W | 46.7386° E | 111.121° S | 116.412° S |
| Annual energy no-SOE (kWh/m2∙year) | 305.12 | 240.38 | 342.61 | 419.51 | 283.55 |
| Annual energy with SOE (kWh/m2∙year) | 348.26 | 273.98 | 389.48 | 480.91 | 323.34 |
| Gain (%) | 14.14 | 13.98 | 13.68 | 14.64 | 14.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ceballos, M.A.; Perez-Higueras, P.; Shanks, K.; Montes-Romero, J.; Valera, A.; Almonacid, F.; Fernández, E.F. Improvement of Tracking-Integrated Photovoltaic Systems Using Secondary Optical Elements. Electronics 2025, 14, 3175. https://doi.org/10.3390/electronics14163175
Ceballos MA, Perez-Higueras P, Shanks K, Montes-Romero J, Valera A, Almonacid F, Fernández EF. Improvement of Tracking-Integrated Photovoltaic Systems Using Secondary Optical Elements. Electronics. 2025; 14(16):3175. https://doi.org/10.3390/electronics14163175
Chicago/Turabian StyleCeballos, Maria A., Pedro Perez-Higueras, Katie Shanks, Jesus Montes-Romero, Alvaro Valera, Florencia Almonacid, and Eduardo F. Fernández. 2025. "Improvement of Tracking-Integrated Photovoltaic Systems Using Secondary Optical Elements" Electronics 14, no. 16: 3175. https://doi.org/10.3390/electronics14163175
APA StyleCeballos, M. A., Perez-Higueras, P., Shanks, K., Montes-Romero, J., Valera, A., Almonacid, F., & Fernández, E. F. (2025). Improvement of Tracking-Integrated Photovoltaic Systems Using Secondary Optical Elements. Electronics, 14(16), 3175. https://doi.org/10.3390/electronics14163175








