A Survey of Analog Computing for Domain-Specific Accelerators

Abstract

Analog computing has re-emerged as a powerful tool for solving complex problems in various domains due to its energy efficiency and inherent parallelism. This paper summarizes recent advancements in analog computing, exploring discrete time and continuous time methods for solving combinatorial optimization problems, solving partial differential equations and systems of linear equations, accelerating machine learning (ML) inference, multi-beam beamforming, signal processing, quantum simulation, and statistical inference. We highlight CMOS implementations that leverage switched-capacitor, switched-current, and radio-frequency circuits, as well as non-CMOS implementations that leverage non-volatile memory, wave physics, and stochastic processes. These advancements demonstrate high-speed, energy-efficient computations for computational electromagnetics, finite-difference time-domain (FDTD) solvers, artificial intelligence (AI) inference engines, wireless systems, and related applications. Theoretical foundations, experimental validations, and potential future applications in high-performance computing and signal processing are also discussed.

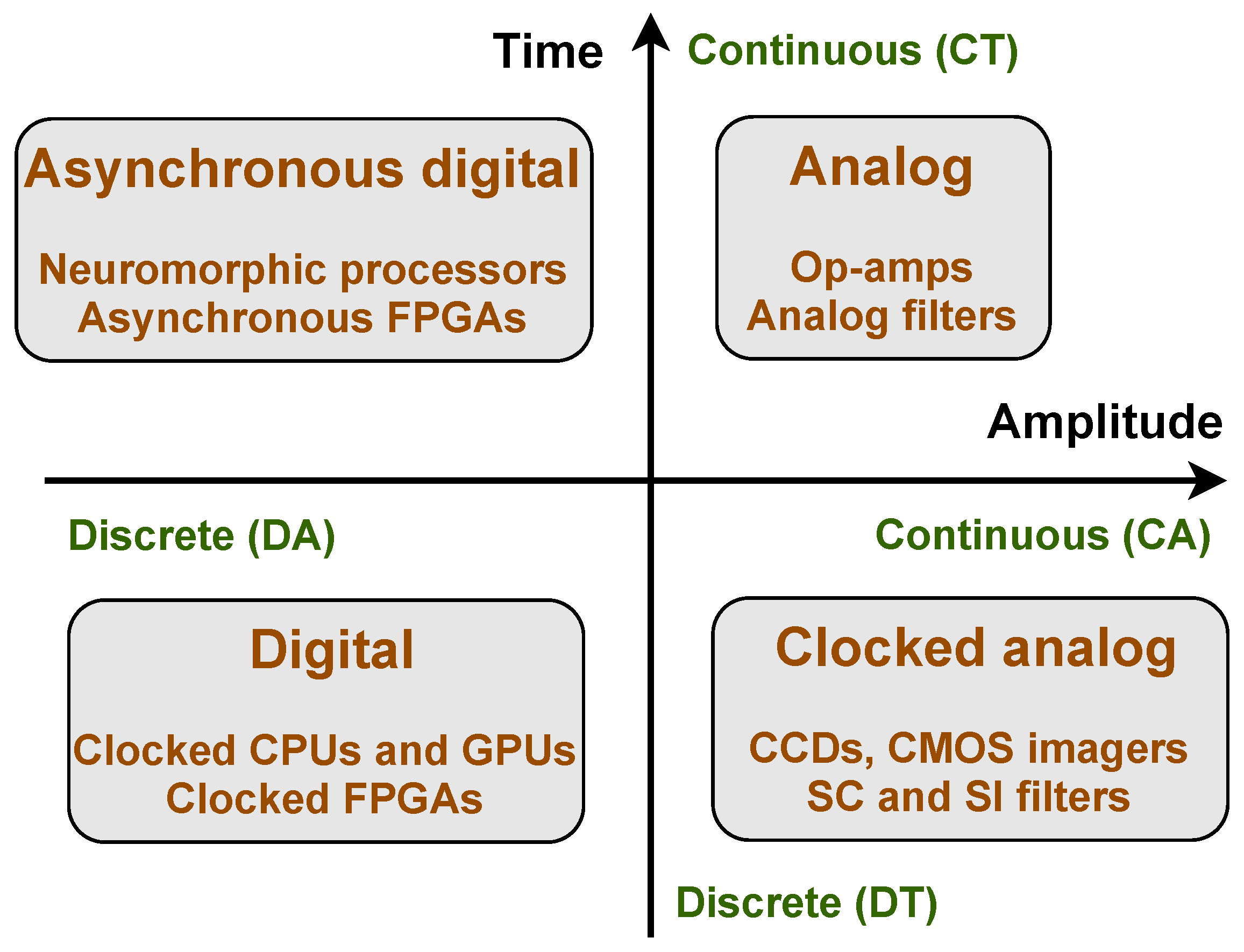
1. Introduction

Analog computing, once the dominant paradigm for numerical simulation but mostly forgotten, is experiencing a resurgence. This revival is driven by the demand for energy-efficient, high-throughput computation and by the limitations facing digital systems as Moore’s Law slows [1]. Unlike the vacuum tube-based machines of the World War II era [2,3], today’s analog computing systems are realized using advanced CMOS and other semiconductor technologies, enabling integrated, high-speed, low-power platforms tailored for domain-specific applications and their computational challenges [4,5,6,7,8]. This review discusses advances in analog computing, with a focus on recent advances in integrated implementations and their growing relevance across diverse application domains.

By definition, analog computers represent and process information using continuous (non-quantized) variables. However, the signals that encode these variables can be quantized along other dimensions [9]. For example, either the amplitude or the time-dependence of a waveform, $s\left(t\right)$, can be quantized, resulting in the four main computational domains shown in Figure 1.

Here we focus on the three quadrants where at least one of the variables is continuous, which we denote as analog (continuous amplitude, continuous time), clocked analog (continuous amplitude, discrete time), and asynchronous digital (discrete amplitude, continuous time). Conventional digital computers reside in the third quadrant where both dimensions are quantized.

While programmable digital computers—grounded in the theory of computational automation and Turing machines—have long benefited from Moore’s Law scaling and have successfully simulated a wide range of natural phenomena, they face limitations [11]. Many workloads, such as scientific computing, optimization, and machine learning, use variables that are inherently analog in nature and demand levels of energy efficiency that are increasingly difficult to achieve with conventional digital architectures. The shift toward data-centric computing has further exposed the inefficiencies of conventional digital architectures, particularly when performing operations like matrix–vector multiplications that dominate machine learning workloads.

Analog real-valued computation offers a promising alternative by relying on the physical properties of physical systems. For example, operations such as integration, differentiation, and multiplication can be performed naturally by analog circuits, often without the need for energy-intensive data conversion or large digital logic blocks [10]. As early as 1990, Mead projected that analog processors could offer up to a 100× area advantage and a 1000× energy savings over digital counterparts [12]. These benefits arise from the fact that analog computers use continuous variables and can be easily mapped to fully parallel architectures at the physical layer.

However, analog systems are not without significant challenges. The accuracy and precision of analog computations is typically limited by harmonic distortion, thermal or $1/f$ noise, device mismatch, and/or design complexity [13,14]. Thus, analog computing is best suited for applications with moderate accuracy and precision requirements (typically, no more than 10–12 bits). Unlike digital design, analog circuit design also requires manual circuit sizing, careful biasing, and meticulous layout practices to obtain acceptable accuracy and precision, with automation efforts still at an early stage [15,16,17,18,19,20,21,22]. Calibration and compensation techniques are also typically necessary to ensure stable and accurate operation across environmental and process variations [23,24].

Despite renewed interest, analog computing faces another critical barrier to broader adoption—namely, the difficulty of programming and calibrating analog systems. Unlike digital platforms with mature software stacks, analog computing lacks standardized toolchains, making it challenging to configure or reconfigure systems for new tasks. This programmability gap is one of the primary hurdles in transitioning analog computing from laboratory demonstrations to commercial applications.

Table 1. Mainstream challenges in analog computing.

Challenge	Description and Implications
Limited Precision	Susceptibility to noise, nonlinearity, and mismatch limits accuracy. Analog systems typically operate at 4–8 bits of effective precision.
Calibration	Device characteristics vary with temperature, aging, and process variations, requiring regular calibration, which is complex and often manual.
Programmability	Lack of high-level software and compiler toolchains makes analog systems hard to reconfigure for general-purpose use.
Scalability	Interconnect complexity and device variability significantly increase the implementation complexity of large-scale analog systems.
Toolchain Maturity	Unlike digital flows (e.g., Verilog/VHDL + synthesis), analog flows lack standardized, modular toolchains for design, simulation, and verification.
Variability	Device mismatch and manufacturing tolerances introduce computational uncertainty, necessitating adaptive or robust design techniques.

summarizes the key challenges currently limiting the scalability and adoption of analog computing, along with their implications. Due to their generality, these issues apply to all the analog computing platforms discussed in this article.

The limitations discussed above have historically confined analog computing to niche domains, but recent advances are opening up new opportunities. For instance, research in low-power analog design has introduced key circuit techniques such as energy-efficient signal sensing [25], discrete time signal processing based on switched capacitors [26,27] and nonlinear signal processing based on the translinear principle [28,29], which provide building blocks for energy-efficient computation. Advancements in energy-efficient analog circuits for signal processing and feature extraction have enabled wearable, low-power, and non-invasive biomedical systems for continuous health monitoring [30,31]. An important application for such systems is real-time seizure detection using electroencephalography (EEG) signals. The ultra-low-power received signal strength indicator (RSSI) amplifier discussed in [32] consumes only 31.6 nW, enabling efficient EEG seizure detection compared to digital front-ends that typically require several $\mu$W to mW. Similarly, joint analog demodulation and decoding (JADD) of digitally modulated signals in wireless transceivers has been shown to reduce power consumption by $12\times$ to $30\times$ compared to digital implementations [33]. Similar power efficiency benefits were also obtained for other critical operations such as phase estimation and channel equalization [34].

Moreover, in-memory computing (IMC) architectures have emerged as a promising solution for accelerating matrix–vector multiplication directly within memory arrays [35], significantly reducing data movement and improving energy efficiency [36,37]. Field-programmable analog arrays (FPAAs) offer another promising analog computational paradigm [38]. A generic FPAA consists of an array of computational analog blocks (CABs) with field-programmable interconnects [39,40,41,42], and is thus analogous to a field-programmable gate array (FPGA). FPAAs with floating gate (FG)-based programmability have been used to demonstrate analog implementations of linear algebra kernels, including vector–matrix multiplication (VMM) [43,44]. Programmable analog standard cell libraries for automated synthesis of complex functions are also available [45,46]. These developments have paved the way for more complex analog systems, such as neuromorphic processors, which mimic the structure and function of biological neural networks to enable highly parallel, energy-efficient computation [47,48].

The convergence of analog and digital computing has also led to the emergence of hybrid architectures that combine the speed and low-power benefits of analog computation with the precision and programmability of digital logic [49]. Hybrid computing is particularly well-suited for real-time sensory processing in neuromorphic systems and robotics, since the analog circuits can efficiently process continuous streams of data while digital logic provides programmability and control. Such architectures are not only computationally efficient but are also robust to noise and device-level variability, which is an increasingly important requirement for implementations in modern nanoscale technologies.

Analog computing is gaining attention in energy-constrained edge devices due to its superior energy efficiency for low- and moderate-precision operations. The Internet of Things (IoT) and embedded AI applications require computation close to the sensor with minimal power budgets. Massively parallel analog or hybrid architectures can offer a viable path toward meeting these requirements due to their low latency and energy per operation. Companies such as Bluemind, Aspinity, and Mythic [50,51,52] are developing energy-efficient analog AI processors for such applications.

Furthermore, the growing variability of transistors in advanced CMOS nodes facilitates the implementation of statistical computing paradigms such as stochastic and probabilistic computing. These techniques embrace uncertainty and noise as computational assets rather than liabilities, aligning naturally with the analog domain and further reinforcing the relevance of analog computation in the post-Moore era.

Previous review papers [6,10,53,54,55] mostly focus on a few specific application domains that do not reflect the diversity of state-of-art applications of analog computing. For example, ref. [6] discusses the solution of ordinary and partial differential equations (ODEs and PDEs) and computational fluid dynamics as examples of large scale scientific computing applications. However, this work does not discuss machine learning applications of analog computing. Similarly, while [10] reviews integrated analog computers and their advantages as domain-specific accelerators, the discussion does not extend to other important applications such as linear algebra, combinatorial optimization via Ising machines, event-driven neuromorphic processors, or high-speed analog inference engines for machine learning. Other recent reviews focuses exclusively on analog signal processing for communications [55] and advancements in ultra-low-power (sub-$\mu$W) analog computing circuits tailored for real-time audio signal processing in edge devices [54].

By contrast, this review explores recent progress in integrated analog computing platforms across several broad categories—including IMC architectures in Section 2, Ising machines in Section 3, mathematical solvers in Section 4, neuromorphic processors in Section 5, and other applications such as quantum-inspired systems, stochastic simulations, and statistical inference in Section 7—and highlights their potential for addressing the energy and performance bottlenecks of contemporary computing.

2. In-Memory Computing

In-memory computing (IMC), also known as compute-in-memory (CIM), is arguably the most actively researched application of analog computing today. It has implications in neuromorphic computing [56] (see Section 5), neural networks [57,58] (see Section 6), machine learning [59] (see Section 6), and signal processing [56], and addresses one of the most significant performance and energy bottlenecks in modern computing systems: data movement [35]. It is estimated that up to 90% of energy consumption in traditional digital architectures is spent moving data between memory and the processor. IMC breaks this traditional von Neumann bottleneck by enabling computation directly within memory arrays, reducing data transfer and improving system-level energy efficiency and throughput.

IMC can be implemented in either the digital or analog domain. In this article, we focus on analog implementations of IMC, which have gained significant interest recently for AI/ML workloads involving large matrix or tensor operations. This interest stems from analog IMC’s ability to employ fundamental physical properties—such as Ohm’s and Kirchhoff’s laws—for efficient analog accumulation directly within memory arrays. Another key advantage of analog IMC is its ability to activate multiple rows simultaneously, enabling massively parallel operations like matrix–vector multiplication to be executed in a single computational step. While digital IMC architectures also exploit parallelism, particularly for bitwise operations, analog approaches naturally support bulk multi-row processing. This makes them especially well-suited for data-intensive edge AI applications, where tight power and area constraints make conventional digital processing pipelines less efficient.

To realize analog IMC, circuit implementations often leverage charge- or current-based accumulation using memory technologies such as floating-gate circuits [38,60,61,62], flash [63], SRAM-based capacitive arrays [35,64], or emerging non-volatile memory (NVM) technologies such as resistive RAM (ReRAM), ferroelectric RAM (FRAM), phase-change memory (PCM), and spin-transfer torque magnetoresistive RAM (STT-MRAM) [65]. These approaches compute within the memory array itself, minimizing external data movement and taking advantage of the memory array’s high internal bandwidth. Applications of such IMC architectures to end-to-end ML workloads are discussed in greater detail in Section 6.

Implementing analog IMC requires several peripheral circuits. Sense amplifiers (SAs) are needed to detect small differences in resistance or charge levels corresponding to stored data. Additional reference generation circuits may also be required to supply suitable currents or voltages for accurate comparisons. For example, in STT-MRAM-based implementations, SAs are designed to distinguish between parallel and antiparallel resistance states in magnetic tunnel junctions (MTJs), enabling in-memory bitwise operations [66,67]. ADC and DAC circuits are also needed for converting data between analog and digital domains [57]. To ensure reliable operation under process, voltage, and temperature (PVT) variations, error detection and correction (EDC) mechanisms are also integrated into analog IMC systems. EDC techniques such as error-correcting codes (ECCs) can be adapted for in-memory processing to detect and correct single-bit errors and identify more severe multi-bit errors, thereby improving robustness. Integrating analog IMC into general-purpose computing platforms also requires architectural support [68]. This includes extending instruction set architectures (ISAs) to accommodate in-memory operations, adapting on-chip buses for additional control signaling, and employing data mapping strategies that place operands in memory locations optimized for parallel in-memory execution.

Despite its promise, analog IMC still faces challenges in scaling to large systems and handling diverse workloads. Issues such as device-level variability and drift [69], limited precision [56], and system integration complexity [70] can hinder its broad adoption. As a result, recent research has turned toward hybrid analog–digital architectures to overcome these limitations [71]. These heterogeneous systems combine massively parallel, low-precision analog IMC arrays with smaller, high-precision digital compute cores [72]. This hybrid design allows workloads to be partitioned, e.g., early layers of neural networks with larger spatial dimensions but fewer channels may be more efficiently handled by flexible digital cores, while deeper layers with high channel counts can exploit the parallelism of analog IMC. Similarly, operations requiring high flexibility—such as depthwise convolutions or fully connected layers—benefit from the programmability of digital accelerators. By tailoring the processing resources to specific workload characteristics, hybrid analog–digital systems enable better utilization, improved performance, and greater adaptability across a wide range of AI and edge computing tasks.

Although a wide range of analog IMC design techniques have been demonstrated, their energy efficiency advantage over digital architectures is narrowing. Several factors contribute to this trend: (1) IMC is a full-stack (device-to-system) technology; (2) it inherently trades energy efficiency for computational accuracy, precision, and signal-to-noise ratio (SNR); and (3) ML workloads are statistical in nature and vary widely in metrics. Moreover, the absence of a rigorous benchmarking methodology—an issue shared with digital systems [73,74]—further obscures the fundamental trade-offs. To address this issue, refs. [73,74] introduced a benchmarking framework that avoids simple table-based comparisons. Instead, the authors employ a hybrid analysis consisting of the following steps:

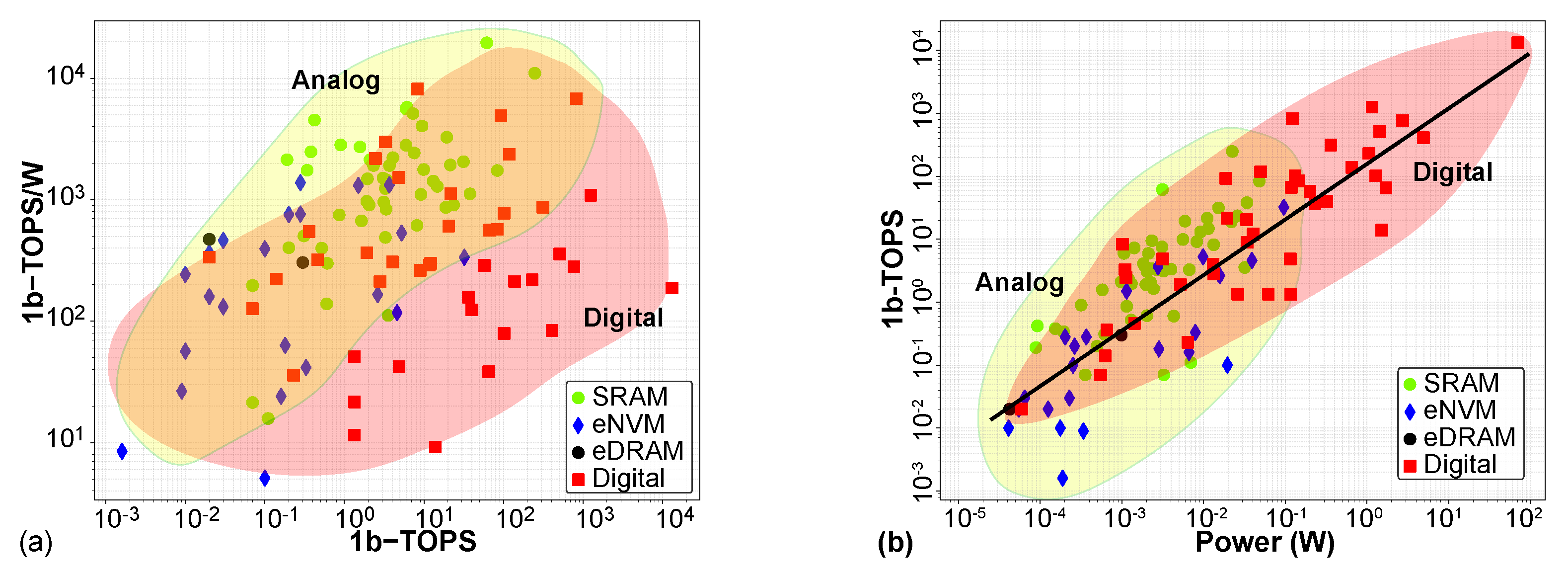
• Normalized efficiency: Reported bank-level energy efficiency is scaled by arithmetic precision to yield normalized efficiency (in units of 1b-TOPS/W).
• ADC analysis: Column ADC parameters are extracted to determine the number of bits processed per read cycle, input information content, and row/column parallelism.
• Throughput: Normalized throughput (in units of 1b-TOPS) is computed from the ADC and energy parameters and normalized by reported power.
• Density: Compute density is verified by dividing the bottom-up throughput by the layout area (estimated from the die photo if needed).
• Raw energy efficiency numbers (in 1b-TOPS/W) are reported without normalization to avoid ambiguity.

Applying this methodology to the recent IMC literature enables a graphical comparison of analog and digital IMC performance, as summarized in Figure 2.

Compared to earlier results from 2022 [73,74], the energy efficiency gap between analog and digital IMC accelerators has narrowed. While analog IMCs previously outperformed digital designs by a factor of 13×, the best analog implementations now show only a 2.4× advantage in energy efficiency, as illustrated in Figure 2a. Additionally, while analog IMCs still lead in energy efficiency, digital accelerators achieve the highest throughput—up to 53× greater than the maximum achieved by analog IMCs. However, analog and digital designs exhibit different throughput versus power scaling behaviors, as shown in Figure 2b:

• Overall trend: 1b-TOPS = 215 $\times {\mathrm{Power}}^{0.84}$
• Analog IMC trend: 1b-TOPS = 500 $\times {\mathrm{Power}}^{0.86}$
• Digital accelerator trend: 1b-TOPS = 170 $\times {\mathrm{Power}}^{0.8}$

These trends indicate that the throughput of analog IMCs scales more favorably with power, exhibiting both a larger scaling coefficient and a higher exponent. This behavior aligns with the energy-efficiency observation in Figure 2a, suggesting that current analog IMCs convert power into computational throughput more efficiently than digital accelerators. As a result, analog IMCs have the potential to narrow—if not close—the throughput gap with digital accelerators for designs with higher power budgets.

3. Ising Machines

Many real-world challenges, such as route planning, graph partitioning, and VLSI placement, can be formulated as combinatorial optimization problems (COPs). However, complex COPs are known to be NP (nondeterministic polynomial time)-hard problems, which implies that they can be verified, but not solved, in polynomial time. Ising machines are specialized computational devices designed to accelerate the solution of complex COPs by finding low-energy configurations of a system described by the Ising model—a mathematical framework from statistical physics originally used to explain ferromagnetism [76]. Such machines are gaining traction because they offer hardware acceleration for a broad class of NP-hard problems, potentially achieving faster or more energy-efficient solutions than general-purpose digital computers.

At the core of the Ising machine lies the concept of energy minimization. The Ising model represents a system of interacting spins, akin to magnetic dipoles in ferromagnetic materials, where spin interactions drive the system toward a minimum-energy state described by the Ising Hamiltonian. This physical principle can be harnessed to solve a variety of real-world COPs, including VLSI placement, which is one of the most computationally challenging tasks in integrated circuit design. Analog Ising machines exploit this behavior by using physical systems to perform the minimization directly, providing an efficient alternative to digital algorithms implemented in software or specialized digital hardware. In particular, their ability to continuously evolve system dynamics toward low-energy configurations offers a compelling approach to solving such NP-hard problems. Recent research has focused on improving the scalability, performance, and robustness of analog Ising machines, which can be realized using either conventional CMOS technologies or hybrid architectures that combine CMOS and beyond-CMOS technologies to accelerate convergence and improve reliability [77].

Activation functions—or their analogs—are essential in Ising machines to introduce nonlinearity and control spin update dynamics, allowing the system to effectively minimize energy and escape local minima. Without such mechanisms, the system may oscillate, converge poorly, or become stuck in suboptimal states. Whether implemented as oscillatory functions [78], thresholding circuits [79], sigmoid-like responses [80], or probabilistic updates [81], these behaviors help ensure robust and efficient convergence. They are especially critical when mapping complex optimization problems to the Ising model. Oscillatory activation functions encode binary states using phase differences between coupled oscillators. These systems often rely on subharmonic injection locking (SHIL) signals to achieve the desired phase binarization [77,82,83,84]. Representative implementations include $LC$ oscillators, ring oscillators, and nanoelectromechanical system (NEMS) oscillators. By contrast, sigmoidal activation functions encode binary states using voltage levels, which can be approximated using standard CMOS design topologies, such as operational amplifiers or transconductance amplifiers.

Implementing weighted connections in Ising machines is crucial for accurately modeling spin interactions. Such connections can either be real-valued (resistive) or imaginary (reactive). CMOS implementations commonly realize binary-weighted resistive connections using analog switches, such as transmission gates. For higher-precision weights, memory elements (including memristors and floating-gate transistors) or capacitor arrays are commonly used. Among these options, floating-gate devices have demonstrated superior bit precision and lower power consumption [85,86], making them the preferred choice for implementing high-accuracy weights in CMOS Ising machines.

The network architecture of Ising machines plays a key role in determining scalability and computational efficiency. Sparse mesh topologies, such as lattice and King’s graph, are effective for encoding sparse problem instances [87,88]. For moderately dense problems, the Manhattan architecture—commonly found in field-programmable gate arrays (FPGAs)—offers a good trade-off between connectivity and routing complexity by enabling local interconnections within computational analog blocks [89]. For the most demanding problems, all-to-all (A2A) connection architectures support maximum density but face practical limitations due to increased routing overhead [90].

3.1. Applications to NP-Hard Problems

Recent work has demonstrated the effectiveness of analog Ising machines in solving various NP-hard problems. Notable examples include max-cut [78], Boolean satisfiability (3SAT) [91], and the traveling salesman problem (TSP) [92]. For instance, the Lechner–Hauke–Zoller (LHZ) architecture transforms A2A connectivity into local interactions, enabling scalable CMOS implementations [93]. Analog LHZ tiles, built using voltage-controlled oscillators (VCOs) and auxiliary circuits, have shown high stability and accuracy in simulation, with competitive power and time-to-solution performance when compared to state-of-the-art methods [94].

3.2. Probabilistic Ising Machines (PIMs)

Probabilistic Ising machines (PIMs) [95] represent a promising direction in analog computing, incorporating both stochastic and deterministic components to update probabilistic bits (p-bits) [81,96]. Various energy minimization algorithms have been evaluated in this context, including simulated annealing (SA), parallel tempering (PT), and simulated quantum annealing (SQA) [97,98]. Among these, SQA has demonstrated superior performance and robustness to device variability, making it an attractive choice for hybrid CMOS-spintronics PIM implementations.

3.3. Discussion

Both analog and digital Ising machines solve COPs by minimizing an Ising Hamiltonian, but they differ significantly in implementation and performance trade-offs. Digital CMOS Ising machines primarily simulate Ising models using Monte Carlo methods and fall into categories such as classical annealing (CA), digital annealing (DA), and parallel annealing (PA), each offering different degrees of parallelism and architectural complexity. DA and PA improve convergence speed by evaluating multiple spin flips per step, while PA allows full parallel updates. Extensions like simulated quantum annealing (SQA) and simulated bifurcation (SB) mimic quantum or oscillator dynamics, but often require extensive random number generation or multiply–accumulate (MAC) units. In contrast, analog oscillator-based Ising machines (OIMs) exploit the physical dynamics of oscillator networks (LC, ring, Schmitt trigger, differential) to solve Ising problems directly. These machines offer advantages in time-to-solution, energy efficiency, and solution quality, leveraging phenomena like SHIL and continuous time evolution. For example, LC-OIMs naturally reach near-ground states through oscillator phase locking, while ring oscillator Ising machines (ROIMs) provide higher integration density and scalability on-chip. Designs like Schmitt trigger OIMs (ST-OIMs) eliminate the need for external SHIL signals, reducing area and enhancing scalability, and differential OIMs (DOIMs) achieve higher precision through tunable oscillators.

While analog Ising machines benefit from low-power, real-time processing, they also face challenges in precision, noise robustness, and interconnection scaling. Digital Ising machines, by contrast, are more programmable and can implement more complex annealing schedules but at the cost of higher power and often longer solution times. Overall, analog and digital approaches are complementary: analog machines offer superior energy-delay product for certain problem classes, while digital machines provide flexibility, precision, and broader programmability [99].

4. Analog Solvers

4.1. PDE Solvers

Analog computing systems have emerged as powerful tools for solving systems of linear and nonlinear partial differential equations (PDEs), offering unique advantages over conventional digital processors due to their inherent parallelism, low latency, and energy efficiency [100,101,102]. By adopting fully parallel architectures with co-located compute and memory elements, these systems bypass the memory bottleneck of the traditional von Neumann architecture [103], which faces scaling challenges as Moore’s Law slows. Additionally, such analog solvers directly emulate the physical dynamics described by PDEs to improve solution speed and energy efficiency, thus making them particularly well suited for scientific computing and edge processing workloads.

Several design strategies have been explored to realize analog PDE solvers. For example, it is possible to directly leverage the physics of wave propagation to encode and process information [104]. For instance, wave propagation in 2D passive $LC$ lattices can be used to implement high-speed Fourier transforms [105] and quantizers [106]. Similarly, wave propagation in 1D active $LC$ transmission lines can be utilized for efficient broadband real-time RF spectrum analysis [107,108,109] and source localization [110]. In another example of this approach, ultrasonic metasurfaces were configured to solve ordinary and partial differential equations by controlling how ultrasonic waves interact with engineered structures [111]. Systems of this type often incorporate elements such as ultrasonic Fourier Transform (UFT) blocks and spatial filtering metasurfaces (SFMs) to perform mathematical operations. Simulations of these architectures show strong agreement with analytical solutions, validating their computational accuracy.

It is also possible to discretize the spatial and/or temporal dimensions of the PDE to facilitate the hardware implementation. For example, continuous time analog computing for solving both linear and nonlinear PDEs can be implemented by discretizing the spatial dimension(s), as demonstrated in [100,102,112]. One approach for implementing such analog continuous time PDE solvers relies on delay-based spatial discretization using analog all-pass filters (APFs) in place of the difference operators found in traditional finite-difference time-domain (FDTD) methods [113]. This spatially discrete, time-continuous (SDTC) strategy enables real-time solutions to both linear and nonlinear PDEs with prescribed boundary and initial conditions. Fabricated ICs using this approach have achieved wide bandwidths and low power consumption for simulating linear 1D wave equations, making them practical for real-time embedded systems [100].

Additionally, a similar SDTC approach has been developed to handle nonlinearities and validated in implementations targeting acoustic shock wave models [102]. These circuits utilize analog arithmetic (multiplication, scaling, summation, and time delays) performed in parallel using fully differential op-amps, analog multipliers, and APFs. Performance evaluation using standard metrics such as mean squared error (MSE) and signal-to-noise ratio (SNR) confirms the viability of such SDTC analog solvers for high-accuracy computations of nonlinear PDEs [114].

The temporal dimension of a PDE can also be discretized by sampling (but not quantizing) all analog waveforms at a high enough rate to avoid temporal aliasing, thus resulting in discrete time analog computation. Switched capacitor (SC) versions of such discrete time architectures allow transfer functions to be defined purely by well-controlled capacitor ratios, thus enabling high precision [26,27]. Discrete time operation also enables the use of various circuit schemes, such as autozeroing and correlated double sampling (CDS) to remove the effects of device mismatch [115]. Finally, discrete time operation also enhances the robustness of analog solvers to propagation delays by synchronizing computation with a reference clock. Several 0.18 $\mu$m CMOS prototypes for solving Maxwell’s equations based on SC and switched current (SI) circuits have demonstrated considerable speedup compared to digital counterparts while also avoiding the need for time-consuming post-fabrication calibration [101,116], thus underscoring the potential of discrete time analog solvers for rapid electromagnetic simulations.

In summary, analog computing provides a rich framework for solving PDEs, especially in contexts where energy efficiency, speed, and parallelism are critical. From wave-based metasurfaces to SC networks and delay-based continuous time solvers, a variety of hardware strategies have been successfully developed. The integration of these principles with modern CMOS technology is providing new avenues for accelerating real-time scientific and engineering computation, potentially expanding the role of analog systems as complementary to digital methods. Nevertheless, fully parallel implementations suffer from two key scaling challenges, namely (1) the 2D geometry of integrated circuits, which makes it difficult to simulate PDEs with more than two spatial dimensions; and (2) the lack of hardware reuse, which makes it difficult to expand the solution grid to improve spatial resolution or enlarge the simulation domain. Thus, there is a need to develop analog solver architectures that are not completely parallel (or “flat”) but rather allow for a certain amount of hardware reuse. Coarse-grained reconfigurable arrays (CGRAs), which are being intensively studied for energy-efficient and reconfigurable digital processors [117], provide a promising paradigm for such scalable analog solvers. In its most basic form, a CGRA consists of an array of general-purpose programmable elements (PEs) with nearest-neighbor connectivity. Analog CGRAs can be implemented by replacing digital PEs with discrete time analog equivalents. Such PEs can be efficiently realized using SI circuits, as demonstrated earlier for focal plane analog vision processors [118].

In summary, several recent studies have demonstrated that analog computing can significantly outperform conventional digital platforms in solving PDEs, particularly in terms of energy efficiency and solution latency. Analog solvers exploit continuous time, massively parallel computation, enabling real-time solutions without the clock cycle bottlenecks of digital systems. For example, Udayanga et al. [100] and Liang et al. [101] reported analog solvers achieving up to 420× speedup and over 1000× improvement in energy efficiency compared to GPU- and CPU-based FDTD solvers. Even when compared to modern FPGA implementations, such as the Xilinx RFSoC, analog systems demonstrated 2.8–15× speed and power advantages, despite being built in an older 0.18 $\mu$m CMOS technology.

These benefits, however, are accompanied by key limitations. Analog solvers typically lack the flexibility and scalability of digital platforms, with constraints stemming from die area, limited programmability, and sensitivity to process variations. For example, Huang et al. [112] showed that analog accelerators could solve nonlinear systems up to 16 × 16 in size, with 100× lower power density than CPUs, but scaling beyond that required architectural decomposition. Despite these constraints, analog systems remain highly attractive for fixed-function, energy-constrained, or real-time applications. Moreover, hybrid approaches that use analog accelerators to seed digital solvers (e.g., GPUs) have shown promising results—reducing solution time and energy by 5.7× and 11.6×, respectively [112]. These developments suggest that future high-performance computing systems may benefit from tightly integrated hybrid analog–digital architectures.

4.2. Linear Algebra Solvers

Analog computing’s use of continuous variables, direct representation of time derivatives, and ability to implement dynamical analogs makes it especially suitable for the real-time solution of ODEs and PDEs, as discussed in the previous sub-section. In addition, analog computing has also been explored for obtaining energy-efficient, continuous time solutions to important linear algebra problems such as

$$\mathbf{Ax}=\mathbf{b},$$

(1)

where $\mathbf{A}$ is the input matrix, $\mathbf{b}$ is the input vector, and $\mathbf{x}$ is the solution vector [119,120,121]. Analog methods for linear algebra can be advantageous in scenarios where digital computation is challenged by the complexity and resource demands of matrix decomposition techniques such as LU decomposition, or where power and chip area overheads arise due to repeated analog-to-digital and digital-to-analog conversions.

A system of linear equations like (1) can be interpreted as describing a network of resistors along with independent and dependent voltage and current sources. However, because passive resistive networks cannot realize arbitrary matrices $\mathbf{A}$, active circuit elements are required. An active analog approach was proposed in [119], where iterative techniques transform the linear system into a differential equation of the form

$$\tau {\displaystyle \frac{d\mathbf{x}}{dt}}+\mathbf{Ax}=\mathbf{b},$$

(2)

where $\tau$ is a network time constant. Operational transconductance amplifiers (OTAs), acting as voltage-controlled current sources, are employed to implement (2), enabling the construction of general constraint matrices in analog hardware. This work used an FPAA [40] to realize matrix $\mathbf{A}$ using OTAs biased in the subthreshold region for low power consumption. The input vectors were applied to the OTA inputs, which functioned as current sources. The resulting analog network adjusted voltages and currents iteratively until the solution converged. This setup enabled a continuous time circuit architecture capable of solving linear systems, with experimental results demonstrating high energy efficiency and convergence times significantly shorter than those of digital methods.

As with analog IMC architectures, most analog linear algebra solvers operate with full parallelism and local parameter storage, thus eliminating the memory bottlenecks that introduce delays in conventional von Neumann architectures. The use of such fully parallel architectures, coupled with the continuous-state nature of analog computation, offers the potential for high energy efficiency and low latency. Nevertheless, fully parallel architectures do not scale with problem size, so some form of hardware reuse (e.g., a CGRA architecture) is required for solving larger problems.

As described in [119], analog implementations of linear equation solvers in 0.35 $\mu$m CMOS are significantly more compact and energy-efficient than their digital counterparts at low and moderate precision levels. For example, a floating-gate transconductance amplifier occupies just 1500 $\mu {\mathrm{m}}^2$, compared to 0.25 ${\mathrm{mm}}^2$ for a 16 × 16 digital MAC unit. When scaled to 40 nm CMOS, both analog and digital designs scale quadratically, preserving a substantial area advantage—approximately 167× in favor of the analog implementation. At 0.35 $\mu$m and assuming a 100-kHz bandwidth, a custom analog stage consumes about 16 $\mu$W, while the digital equivalent consumes 6 mW. At 40 nm, analog power decreases further due to reduced capacitance, while digital improvements are limited by the energy-efficiency wall, even under optimistic assumptions. These trends are expected to continue at advanced technology nodes, maintaining the area and efficiency advantages of analog solvers. However, reductions in transistor gate area are accompanied by an increase in device mismatch and $1/f$ noise [14], which tends to reduce the intrinsic SNR of analog solvers. Thus, scaled analog solvers may need to implement mismatch cancellation methods such as CDS to obtain adequate solution accuracy.

4.3. Low-Complexity Beamforming

Wideband multi-beam beamforming is a key ingredient of modern wireless networks due to its potential to significantly improve channel capacity and thus available data rates [122]. Mathematically, an N-beam beamformer is a linear transform (LT) that implements a bank of N spatial filters (i.e., beams). Thus, it can be represented by a matrix–vector multiplication (MVM) of the form

$$\mathbf{y}=\mathbf{Ax},$$

(3)

where $\mathbf{x}$ is the N-element input signal vector, $\mathbf{A}$ is the $N\times N$ beamforming matrix, and $\mathbf{y}$ is the N-element output vector. The hardware cost of implementing this MVM can be minimized by using multi-layer hybrid beamforming, i.e., by combining analog beamforming (ABF) in the first layer with one or more digital beamforming (DBF) layers [123].

In general, the entries of the beamforming matrix, $\mathbf{A}$, are complex numbers with irrational real and imaginary parts. Thus, a naive implementation of the MVM requires $N^2$ high-resolution multiplications, which dominate the overall computational cost. For relatively narrowband applications, a common choice for $\mathbf{A}$ is the discrete Fourier transform (DFT) matrix. The computational cost of the DFT can be reduced to $\mathcal{O}\left(N{log}_{2}N\right)$ multiplications by using iterative algorithms such as the fast Fourier transform (FFT). Additionally, completely multiplier-free implementations are possible by relaxing the requirement for the bins to be orthogonal, i.e., by replacing $\mathbf{A}$ with a suitable approximate beamforming matrix, $\tilde{\mathbf{A}}$. For instance, approximate discrete Fourier transform (a-DFT) matrices can be designed to approximate the DFT while only using small integer coefficients (e.g., 0, $\pm 1$, and $\pm 2$) that can be digitally implemented as simple bit shifts [124].

The MVM within an analog beamformer can be efficiently implemented using current-mode circuits. In this approach, coefficient multiplications (i.e., scaling) are realized using current mirrors, while additions are realized for “free” using Kirchhoff’s current law (KCL). For example, cascoded current mirrors were used to accurately compute 4-point and 8-point radix-2 FFTs [125]. This design reduced hot carrier injection (HCI) effects by utilizing lower current density values than a simple current mirror realization. Nevertheless, the irrational values of the FFT coefficients makes it difficult to obtain adequate accuracy within the current mirrors by using device scaling alone. By contrast, a-DFT matrices contain only simple rational numbers, thus allowing the corresponding ABFs to be accurately realized using only current mirrors [126,127].

Based on the considerations discussed above, continuous time current mirrors were used to implement a-DFT matrices with $N=8$ and 16 output beams in 65 nm CMOS technology [128]. However, while such continuous time designs were shown to have several GHz of bandwidth, they are also sensitive to device mismatches, which generate current offsets and ultimately errors in the output beam patterns. These errors can be eliminated by operating in discrete time, i.e., by using dynamic current mirrors (DCM) to cancel offsets, but at the cost of lower bandwidth. An $N=8$ beam a-DFT design in 0.18 $\mu$m CMOS technology was measured to have a dynamic range (DR) of 54 dB and support channel capacities up to 4.7 Gbps [129].

Analog MVMs can also be implemented using voltage-mode circuits. For example, an analog/mixed-signal FFT processor for significantly reducing ADC power consumption in broadband orthogonal frequency division multiplexing (OFDM) systems was proposed in [130]. This architecture used analog multipliers to compute the FFT before digitization, which substantially lowered power usage compared to traditional high-speed ADC-based FFT processing. Later in [131], a prototype FFT processor IC was shown to efficiently compute an 8-point FFT at a sampling rate of 1 GSps using discrete time analog multipliers and sample-and-hold circuits.

4.4. Antenna Array Signal Processing

Antenna arrays are crucial for exploiting real-world millimeter-wave (mmW) channels, as they enable the formation of multiple sharp and steerable beams. As conventional transceivers often overlook the relationships between signals, noise, interference, and nonlinear distortion across the array, spatially oversampled arrays can be designed to spectrally shape the noise and nonlinearities of components like amplifiers, mixers, and data converters, ensuring they remain outside the region of support (ROS) of propagating electromagnetic (EM) waves. This innovative technique, called spatio-temporal noise shaping, resembles $\Delta$-$\Sigma$ modulation in principle but functions within a two-dimensional spatio-temporal domain. An analog spatial integration and amplification module (SIAM) suitable for RF-IC implementations of spatio-temporal noise shaping was first introduced in [132]. Later, a 32-element array receiver that is suitable for driving first-order spatio-temporal $\Delta$-$\Sigma$ noise-shaping ADCs was introduced as a proof-of-concept [133].

In order to map the spatial $\Delta$-$\Sigma$ noise shaping into CMOS or BiCMOS analog designs, an N-port noise-shaped Low-Noise Amplifier (LNA) array architecture along with a passive spatial integration network at its input was designed in a 65 nm RF-CMOS process [134], where for the designed center frequency at 4 GHz, a gain of 9.5 dB and a Noise Figure (NF) of 3.5 dB were observed. The latest approach for the $\Delta$-$\Sigma$ noise shaping, discussed in [135], avoids on-chip passive networks while implementing the LNA, adder, and subtractor in each SIAM to reduce chip area, albeit at the cost of noise and linearity. An implementation in a 65 nm CMOS process achieved a gain of 20 dB and a NF of 3.9 dB over a 5 GHz bandwidth for $2\times$ spatial oversampling. A 28 GHz fully integrated demonstration of spatial $\Delta$-$\Sigma$ noise shaping was recently described in [136]. This 4-port receiver demonstrator achieved average improvements over a reference design of 1.6 dB in NF, 2.25 dB in input 1-dB compression point (IP1dB), and 1.4 dB in third-order intercept point (IIP3). It demonstrated NF = 2.6 dB, IP1dB = −18.7 dBm, and IIP3 = −12.5 dBm while consuming 19.8 mW/ch. Initial results of a new multiple chiplet-based multi-beam beamforming chip for RF spectral sensing that uses a joint analog–digital hybrid approximation are summarized in [137].

4.5. Programmable Wave-Based Metastructures

Analog computing with programmable metastructures is a rapidly expanding field that utilizes wave-based physical systems to perform real-time mathematical operations like differentiation, integration, matrix inversion, and PDE solving [138]. These systems offer benefits such as parallel processing, low power consumption, and fast computation by manipulating wave propagation through engineered metasurfaces and metamaterials [139]. A nanophotonic platform utilizing epsilon-near-zero (ENZ) materials was shown to solve PDEs directly in the analog domain in [140]. The system enables strong nonlocal interactions via electric displacement conduction and wavelength stretching in zero-index media, allowing solutions to a wide range of PDEs to be achieved through monitoring. A review of spatial analog computation using meta-optics in [141] details how computational metastructures, designed for transfer characteristics based on spatial Fourier or Green functions, can perform operations such as edge detection, convolution, and spatial differentiation. In [142], a meta-programmable over-the-air wave-based differentiator was demonstrated in which the massive number of degrees of freedom offered by a programmable metasurface inside a complex scattering system was leveraged to tune scattering zeros onto the real frequency axis. The system offers in situ tunability, supports parallel and higher-order differentiation, and achieves reprogrammable analog signal processing with simple, low-power hardware using metasurfaces inside a metallic enclosure.

Further advancements in programmable wave-based analog computing were proposed in [143], showing inference times in the nanosecond range by operating directly at the speed of light, which contrasts with digital processors that are limited by clock rates in the MHz to GHz range. This system can perform both stationary computations (matrix inversion) and non-stationary computations (Newton’s method and inverse design using Lagrange multipliers) using reconfigurable voltage-controlled phase shifters and amplifiers in a waveguide-based matrix. The accuracy of an RF prototype designed for real-time massively parallel linear algebra computations has been experimentally verified. This analog programmable metastructure used a direct complex matrix (DCM)-based waveguide system, showed iteration times on the nanosecond scale, and computed solutions in under 87 iterations. Moreover, each operation consumed energy on the order of nanoseconds multiplied by milliwatt-level power, thus yielding nanojoule-scale energy per operation. However, a recent study in [144] demonstrated a digital metasurface consuming approximately 415 mW total power, with reconfiguration speeds limited to kilohertz due to control electronics latency. In summary, from the comparison between the studies of [143,144], it can be said that, while digitally coded metasurfaces provide superior reconfigurability, analog metasurfaces significantly outperform them in terms of speed and energy consumption.

5. Neuromorphic Processors

Neuromorphic processors are designed to mimic the architecture and electrical functionality of the human brain, enabling energy-efficient and massively parallel computation. Using the principles of neural computation, such as spiking dynamics, event-driven communication, and local learning, these systems offer a fundamentally different computational paradigm from conventional von Neumann architectures [145]. Recent innovations in neuromorphic design have focused on enhancing adaptability, scalability, and real-time learning capabilities [146] while also integrating with emerging technologies like memristors and advanced semiconductor processes [147,148].

A key direction in this evolution is the integration of analog computation with asynchronous digital communication to balance precision, power efficiency, and scalability. For example, the Dynap-SEL processor is a demonstration of this hybrid approach [146]. It features four neural processing cores with analog neurons and programmable synapses, alongside a fifth core with plastic synapses and on-chip learning circuits—all implemented in both 0.18 $\mu$m CMOS and 28 nm FDSOI technologies. This architecture supports run-time reconfigurability and on-line learning, making it highly suitable for dynamic environments where adaptability is critical [149].

Furthermore, analog-dominant systems like the BrainScaleS platform [150,151] directly emulate the equations describing the temporal evolution of neuron and synapse variables. The electronic neuron and synapse circuits act as physical models for these equations. By operating faster than biological time, BrainScaleS enables rapid exploration of neural dynamics and learning processes. Its blend of analog processing for spike computation and digital control for configuration and monitoring makes it particularly well-suited for neuroscience-inspired computing, such as large-scale network simulations and rapid parameter tuning.

In addition, specialized architectures such as 2D integrate-and-fire winner-takes-all (2DIFWTA) chips [146] illustrate how neuromorphic hardware can capture complex network dynamics. A 2DIFWTA chip implements a two-dimensional array of integrate-and-fire neurons with local excitatory synapses that realize recurrent cooperative interactions. Such architectures support both nonlinear decision-making and linear transformations, enabling efficient computation in both rate and time domains.

While still evolving, analog neuromorphic processors are increasingly capable of solving diverse computational problems with remarkable energy efficiency and speed. As architectures continue to evolve—blending analog and digital domains, incorporating novel devices like memristors, and supporting flexible learning mechanisms—neuromorphic computing may one day enable next-generation applications in AI, machine learning, real-time sensory processing, and brain–machine interfacing.

Muir and Sheik [152] compared neuromorphic (NM) processors to other computing architectures in terms of state representation and energy efficiency across a range of tasks. Digital architectures use binary memory cells on advanced nodes, offering standard integration but limited resolution and higher switching energy. Analog NM architectures store continuous values on circuit nodes, achieving higher energy efficiency and storage density, though at the cost of circuit complexity, mismatch sensitivity, and use of older process nodes. In benchmarks, NM processors show major energy efficiency advantages: for spiking neural network (SNN) inference, they outperform NVIDIA RTX 2070 GPUs from NVIDIA Corporation, Santa Clara, CA, USA by 280–21,000×, edge ANN accelerators (Coral Edge TPU from Google LLC., Mountain View, CA, USA and Intel Neural Compute Stick 2 from Intel Corporation, Santa Clara, CA, USA) by 3–50×, and the Raspberry Pi by 75× on tasks such as Sudoku. For physics simulations, analog IMC NM processors yield 150–1300× gains versus GPUs and 1500–3500× versus CPUs. On deep learning tasks (ImageNet, CIFAR-10, LLM inference), IMC processors improve energy efficiency by 10–1000× and compute density by ∼10×. Additionally, SNN processors show 4.2–225× energy savings versus desktop GPUs, 380× versus mobile GPUs, and 12× versus desktop CPUs on an MNIST image reconstruction task. For sensory tasks such as gesture and keyword recognition, NM processors achieve 4–1700× average power savings over low-power digital ASICs. Their strongest benefits emerge in real-time temporal signal analysis, such as keyword spotting, where they outperform CPUs, GPUs, and mobile GPUs by several orders of magnitude.

6. Machine Learning

Building on the discussion of IMC architectures in Section 2, this section focuses on broader applications of analog computing in ML, including analog accelerators for neural networks (NNs), convolutional and recurrent architectures, and alternative analog paradigms such as spiking and wave-based ML. In general, analog multipliers and IMC architectures enable energy-efficient implementation of neural network operations, such as multiply–accumulate (MAC), at the low- and moderate-precision levels (8 bits and below) that typically suffice for ML inference. Thus, although digital designs currently dominate ML hardware, hybrid analog–digital approaches show potential in reducing power consumption and increasing computational parallelism [72].

The use of analog computing in enhancing the efficiency of ML algorithms has been largely focused on the inference phase of artificial neural networks (ANNs). By leveraging the continuous nature of analog signals, these systems can perform MAC, matrix multiplication, and other fundamental operations using IMC methods, which means that they may allow efficiency factors beyond what is possible with the same technology node for their digital counterparts. The power and the number of steps required to compute MAC operations (i.e., dot products) can be further reduced by applying the mathematics of Fourier transforms to analog circuits for matrix multiplication, which in turn enables faster learning rates for modern large language models (LLMs) [153]. This approach is also beneficial for deep learning models, which require extensive computational resources. It is, however, important to compare apples with apples, as comparisons across architectures and algorithms across very different technology nodes is not straightforward.

With reference to analog computing for ML, one promising approach is the use of analog resistive memory devices, such as memristors, to implement synaptic weights in neural networks [154,155] and employ IMC to avoid data transfer between memory and processing units. This can not only accelerate computation but can also reduce energy consumption, making it ideal for edge devices and other energy-constrained environments. However, the same concerns described in Section 2 involving analog IMC apply.

Another area of interest is the development of analog accelerators for specific machine learning tasks, such as convolutional neural networks (CNNs) [156,157] and recurrent neural networks (RNNs) [158,159]. Such analog accelerators can operate in any of the three “analog” domains shown in Figure 1. The use of asynchronous digital systems to implement SNNs is of particular interest due to their biological realism and activity-dependent power consumption [155]. It is also possible to exploit continuous spatial dynamics (generally modeled using PDEs) to obtain greater speed and energy efficiency than digital accelerators. For example, the authors in [104] show that the dynamics of the wave equation in inhomogeneous media can be mapped to an analog RNN. A medium suitable for running the chosen machine learning task (e.g., classification of audio inputs) can then be realized via inverse design methods. Such analog accelerators can also be integrated with digital processors to create hybrid systems that combine the best of both worlds: the precision and flexibility of digital computation with the speed and energy efficiency of analog processing.

7. Other Applications of Analog Computing

7.1. Quantum-Inspired Systems

Previous sections discussed some specific application cases for analog computing. That list, however, is not at all exhaustive; there are potentially many other applications. For example, the emulation of quantum-inspired dynamical systems using classical analog circuits is an promising application [160,161,162,163]. In [160], the authors described analog circuits that can store a superposition of $2^N$ quantum states as the spectrum of two real and imaginary outputs. This was achieved by using analog circuit components to realize Planck capacitance, quantum admittance elements, quantum transadmittance elements, and quantum transadmittance mixer elements. The authors in [161] describe a circuit theoretic formulation for simulating the Schrödinger equation using classical analog circuits. An FDTD solver with absorbing boundary conditions (ABCs) was mapped into a discrete time SC circuit and implemented in 0.18 $\mu$m CMOS technology. By contrast, the authors in [162] used continuous time analog circuits to emulate quantum behavior. In this approach, the state of each qubit is represented by the amplitude of a pair of sinusoidal signals and manipulated using op-amp-based summing amplifiers. A prototype in a 0.18 $\mu$m CMOS technology was experimentally demonstrated to be 400× faster than a Ryzen 5600x six-core processor at performing a simulation of Grover’s search algorithm with six qubits, thus highlighting the benefits of analog computing for performing quantum simulations. In [163], extension of the procedure for emulating finite state vector dynamics using four fundamental analog circuit components was performed to include density matrix dynamics under a noise condition. This approach enabled further exploration into noisy quantum emulation and simulation for systems of arbitrary large and small systems.

7.2. Stochastic Simulations

Another significant application of analog computing is in the modeling and simulation of stochastic chemical reactions, genetic networks, and molecular dynamics. Mandal and Sarpeshkar’s original work [164,165] illustrated how the detailed mathematical analogies between chemical reactions and subthreshold analog circuits can be exploited to model the stochastic behavior of bimolecular reactions, achieving a 30× speedup over Gillespie’s widely used stochastic simulation algorithm (SSA) on a standard desktop computer. Later work [166,167,168,169] extended these analogies to develop fast, scalable, and digitally programmable analog CMOS integrated circuits for modeling genetic networks, including the processes of gene activation, transcription, and translation. These models are particularly useful for (1) rapid parameter space exploration of genetic networks, and (2) studying the intrinsic and extrinsic noise in gene expression, which is crucial for understanding cellular processes and developing synthetic biology applications. The prototype CMOS and BiCMOS chips designed for this purpose include circuits for simulating elementary chemical reactions, transcription delays, transcription dynamics, and translation dynamics. For example, the 0.35 $\mu$m BiCMOS chip in [167] yielded a $311\times$ speedup in the simulation time of Gillespie’s SSA over COPASI, a fast biochemical reaction software simulator that is widely used in computational biology. Some of these chips also utilize adaptive on-chip noise generators [170] to automatically adjust the simulated signal-to-noise ratios to match biological conditions.

7.3. Statistical Inference

Statistical inference is another area where analog computing shows promise. Vigoda’s work on Bayesian logic circuits presents an approach to implementing statistical inference algorithms using analog circuits [171,172]. These circuits, designed to perform probabilistic computations using the formalism of belief propagation (BP) [173], offer significant advantages in terms of power efficiency and computational speed compared to traditional digital processors. By representing signals as probabilistic populations of particles and using analog circuits as soft “gate” functions to transform these ensembles, the resulting Bayesian logic circuits can efficiently solve complex inference problems [174]. This approach is particularly relevant for applications in machine learning, data mining, and error correction, where statistical inference is a critical component.

8. Conclusions

Integrated analog computers potentially offer an energy-efficient alternative for domain-specific tasks such as PDE solving and ML acceleration. Recent CMOS implementations have validated their practical benefits for solving linear and nonlinear PDEs and accelerating ML inference, while more exotic implementations using photonics [175], wave propagation [139], biological cells [176,177], chemical reactions [178], and quantum systems [179,180] are being actively studied by various research groups. While analog computing faces intrinsic challenges in precision and scalability, ongoing research is also addressing these limitations, thus paving the way for broader adoption in scientific and industrial applications. Generally speaking, however, programming analog computers and calibrating them is very difficult. Compared to digital systems, which have well established software flows, analog computer softwarization is in its infancy and perhaps forms the biggest hurdle in the commercial deployment of analog computer approaches. The development of a software stack that takes standard PDE or ML simulation codes and compiles them to run efficiently on an analog processor is crucial for the success of the analog computing paradigm [181,182]. Several efforts in this direction are underway [38,183,184,185], but significant gaps remain. Perhaps this task can be facilitated by using AI/ML approaches; it is too early to tell at the time of writing.

The advancements discussed in this paper nevertheless highlight the versatility and potential of analog computing in various fields. From solving complex optimization problems with Ising machines to accelerating machine learning algorithms, analog computing provides a powerful tool for tackling some of the most challenging problems in modern computing. As technology continues to evolve, the integration of analog and digital systems will play a crucial role in shaping the future of high-performance computing.

Looking ahead, several key research directions merit further attention. These include the development of scalable and automated calibration techniques, improved robustness to device variability, and analog–digital co-design methodologies that leverage the strengths of both paradigms. Additionally, new domains such as probabilistic computing, real-time edge AI, and stochastic simulation offer promising opportunities for analog hardware. Perhaps most critically, progress in programming models and compilation toolchains—enabling the translation of high-level algorithms into analog-executable instructions—will be essential to realizing the full potential of analog computing.