Transformer Fault Diagnosis Using Hybrid Feature Selection and Improved Black-Winged Kite Optimized SVM
Abstract
1. Introduction
- A hybrid feature selection mechanism is proposed, in which LightGBM and Random Forest algorithms are combined to construct a multi-model evaluation matrix. The dual-model scores are then integrated using the entropy weight Technique for Order Preference by Similarity to Ideal Solution (Entropy-TOPSIS), enabling the objective selection of a highly discriminative feature subset.
- Designing a multi-strategy improved black-winged kite algorithm (IBKA): Enhancing population diversity through Tent chaotic mapping, combining Gompertz dynamic step size to balance convergence efficiency between the exploration and exploitation phases, and introducing Morlet wavelet variation strategies to avoid local optima, significantly improving the algorithm’s optimization performance.
- Building a transformer fault diagnosis model based on IBKA-SVM: Using IBKA to optimize the key hyperparameters of SVM (kernel function parameter g and penalty factor C) improves the diagnostic accuracy and efficiency of the model, and the superiority of the method is verified through example simulations.
2. Data Reconstruction and Feature Selection Methods
2.1. Data Reconstruction Method
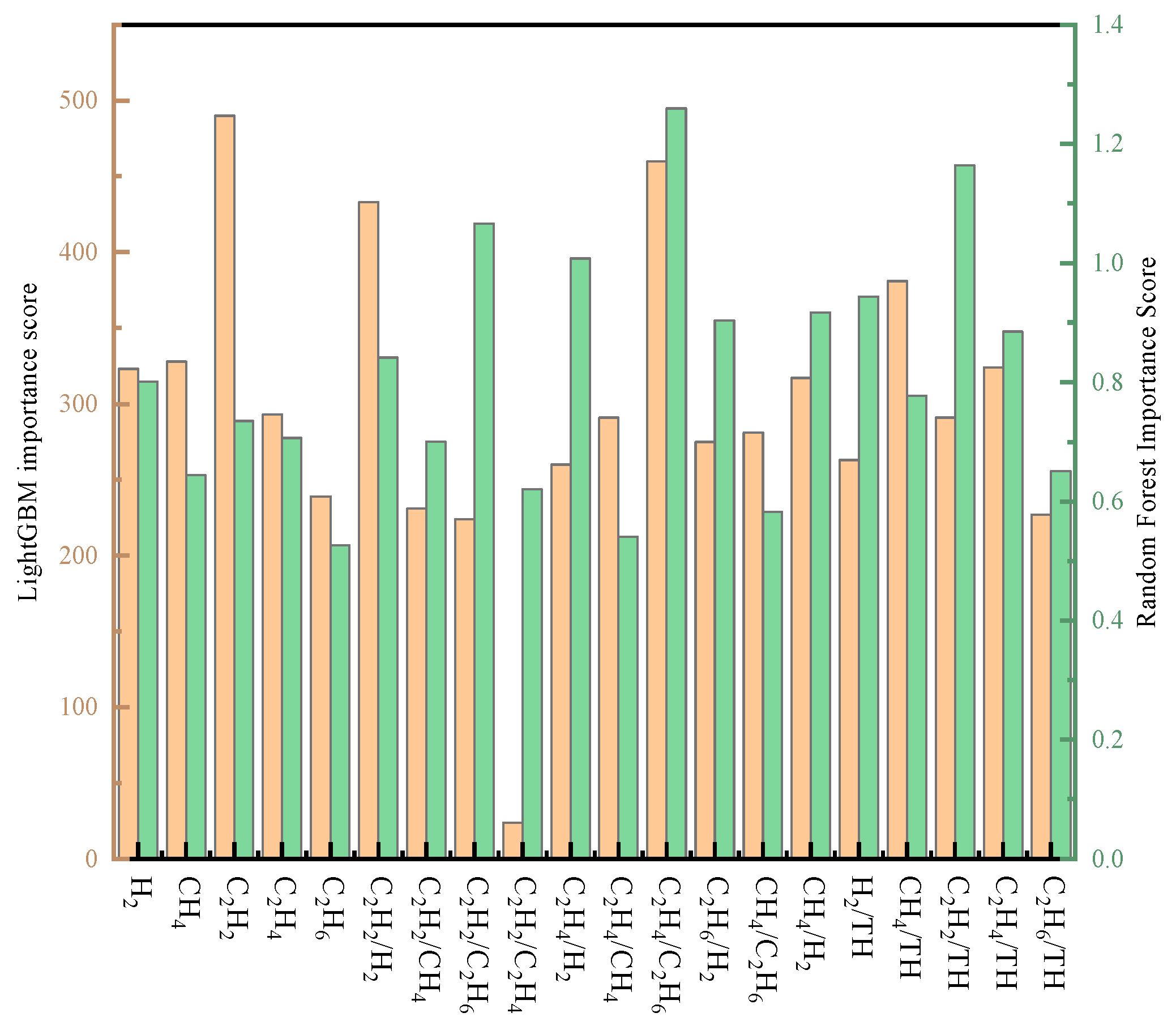
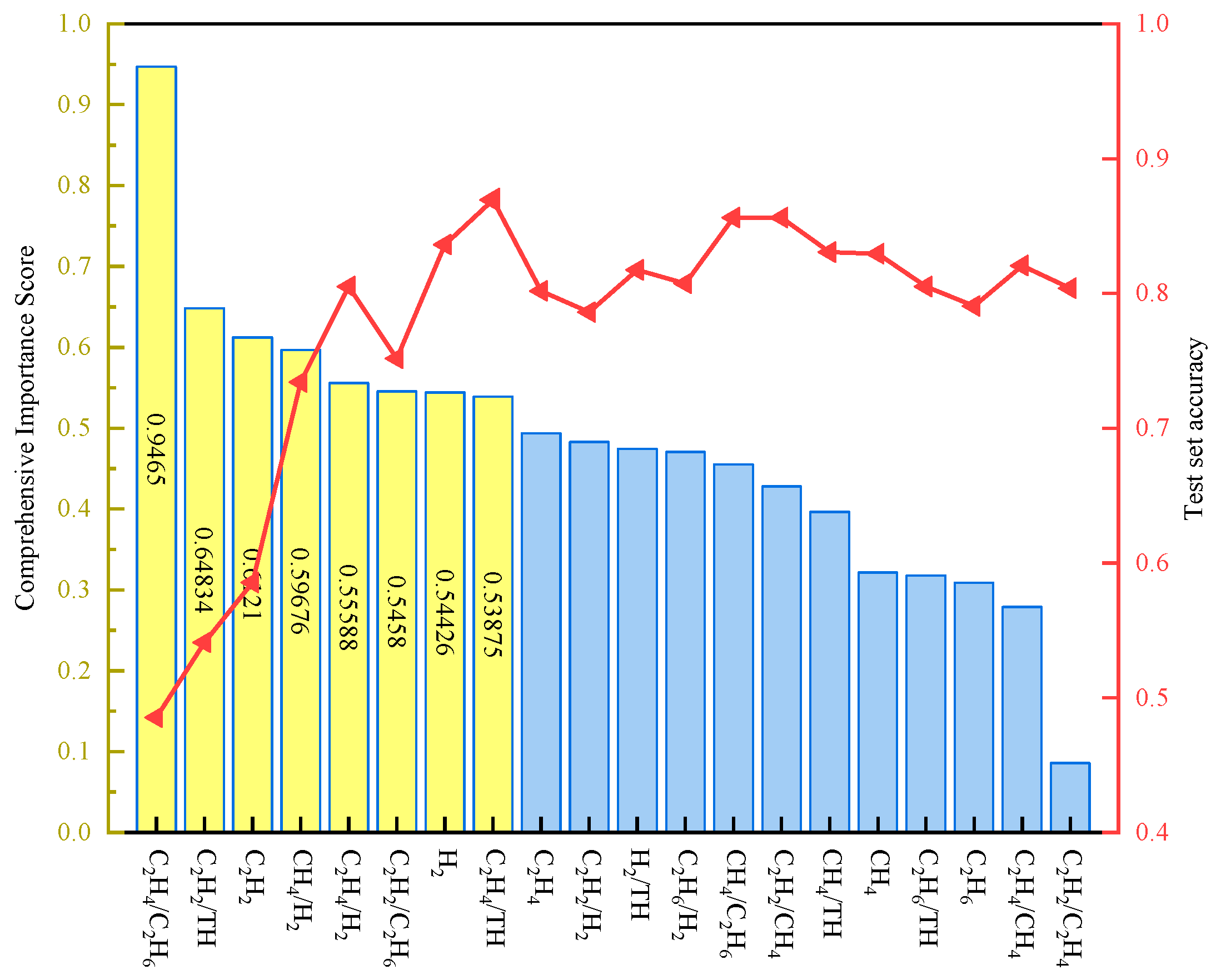
2.2. Feature Dimensionality Reduction Based on Multi-Criteria Decision-Making
| Algorithm 1. Workflow of Entropy-TOPSIS Method |
| Input: Feature importance matrix m: number of features, n: number of models (e.g., LightGBM, RF) Output: in descending order) |
3. Improved Black-Winged Kite Algorithm
3.1. Research on Multi-Strategy Hybrid Improvement
3.1.1. Population Initialization Strategy Based on Tent Chaos Mapping
3.1.2. Step Length Improvement Strategy Based on Gompertz Growth Model
3.1.3. Morlet Wavelet Variation Strategy
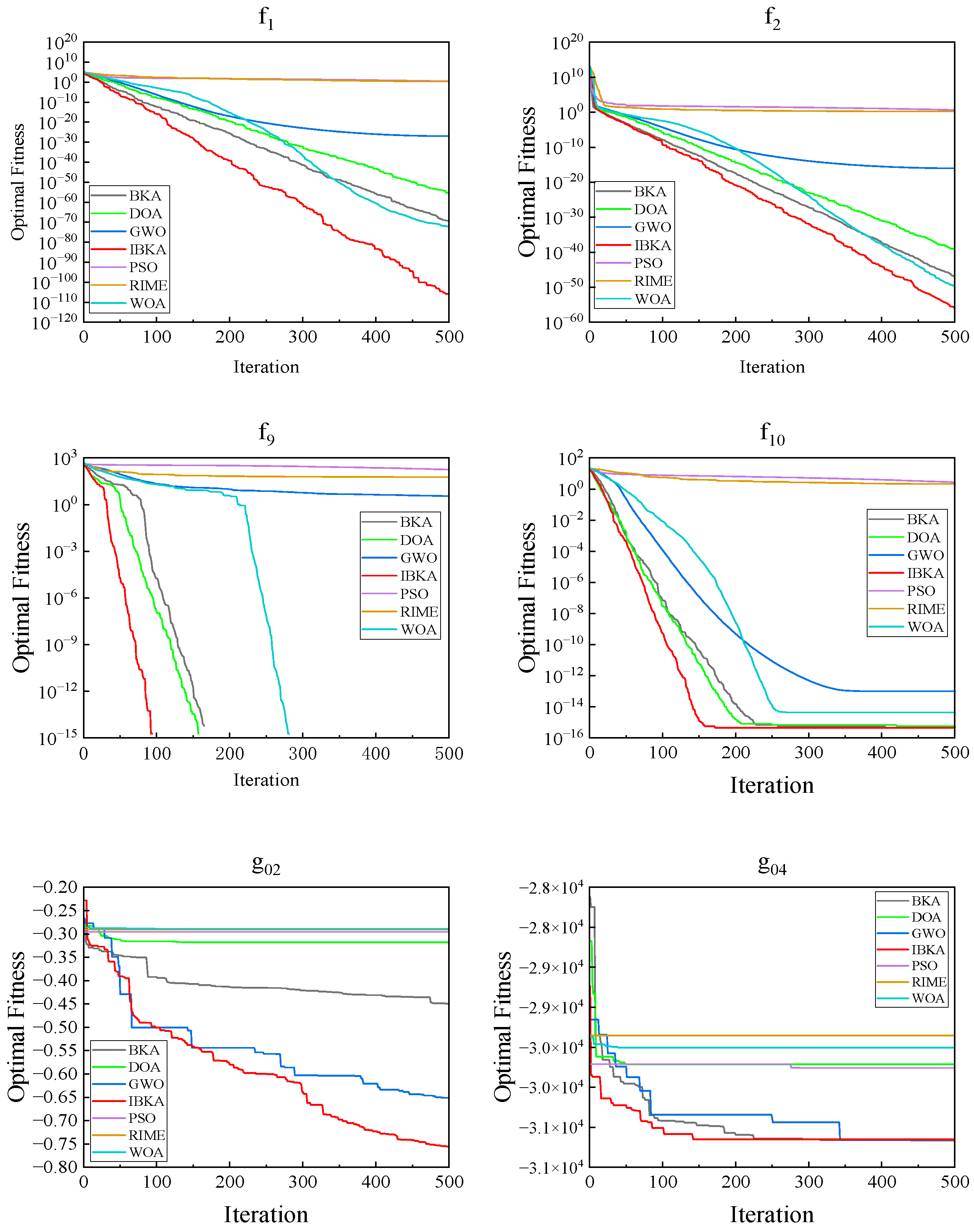
3.2. Performance Analysis of Improved Black-Winged Kite Algorithm
4. Fault Diagnosis Model Based on Feature Selection and IBKA-SVM
4.1. Optimize the SVM Hyperparameters Based on IBKA
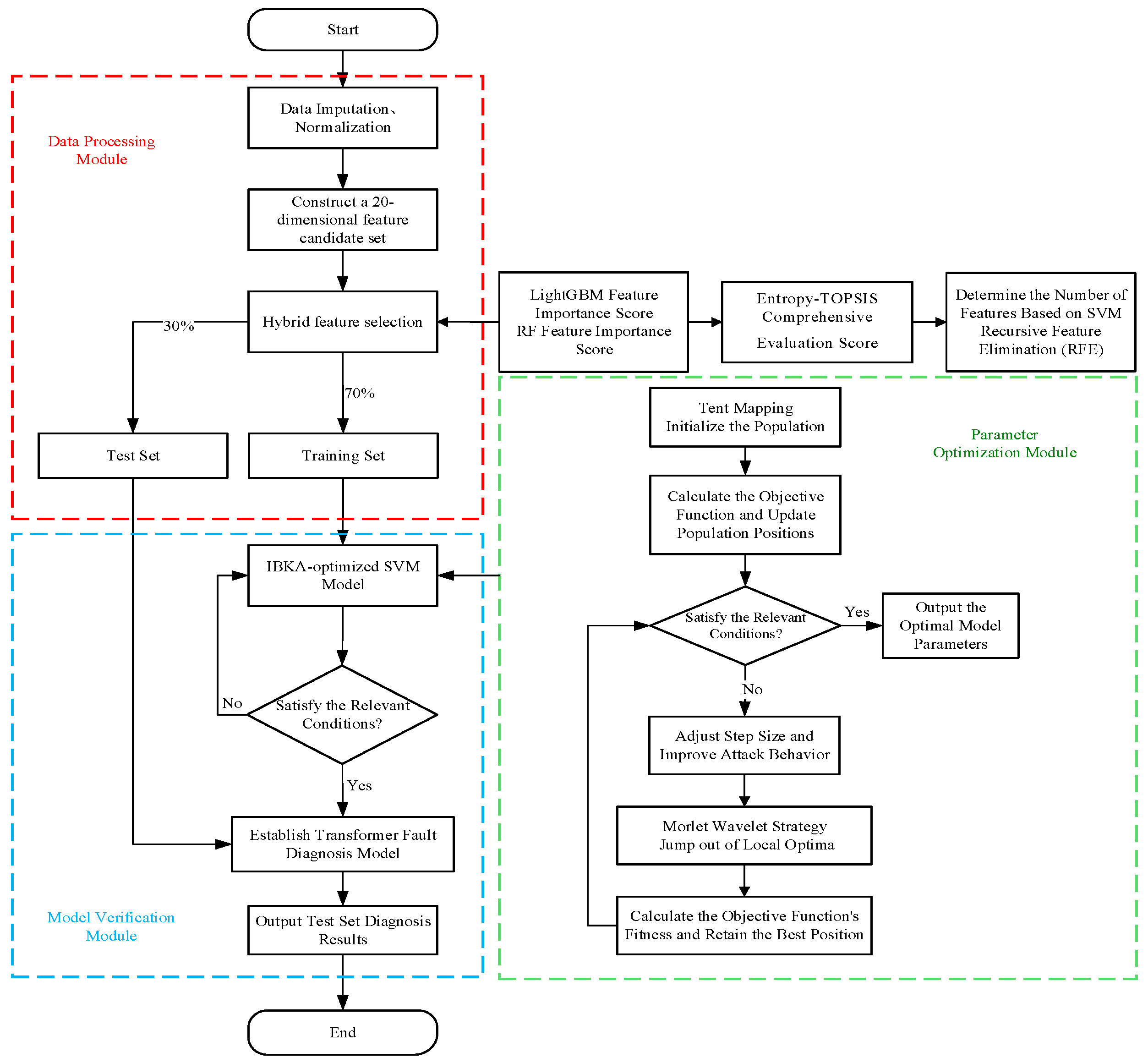
4.2. Construction Process of Fault Diagnosis Model
5. Statistical Analysis
5.1. Selection of Transformer Fault Characteristics
5.2. Ablation Experiments
5.3. Performance Evaluation of Fault Diagnosis Methods
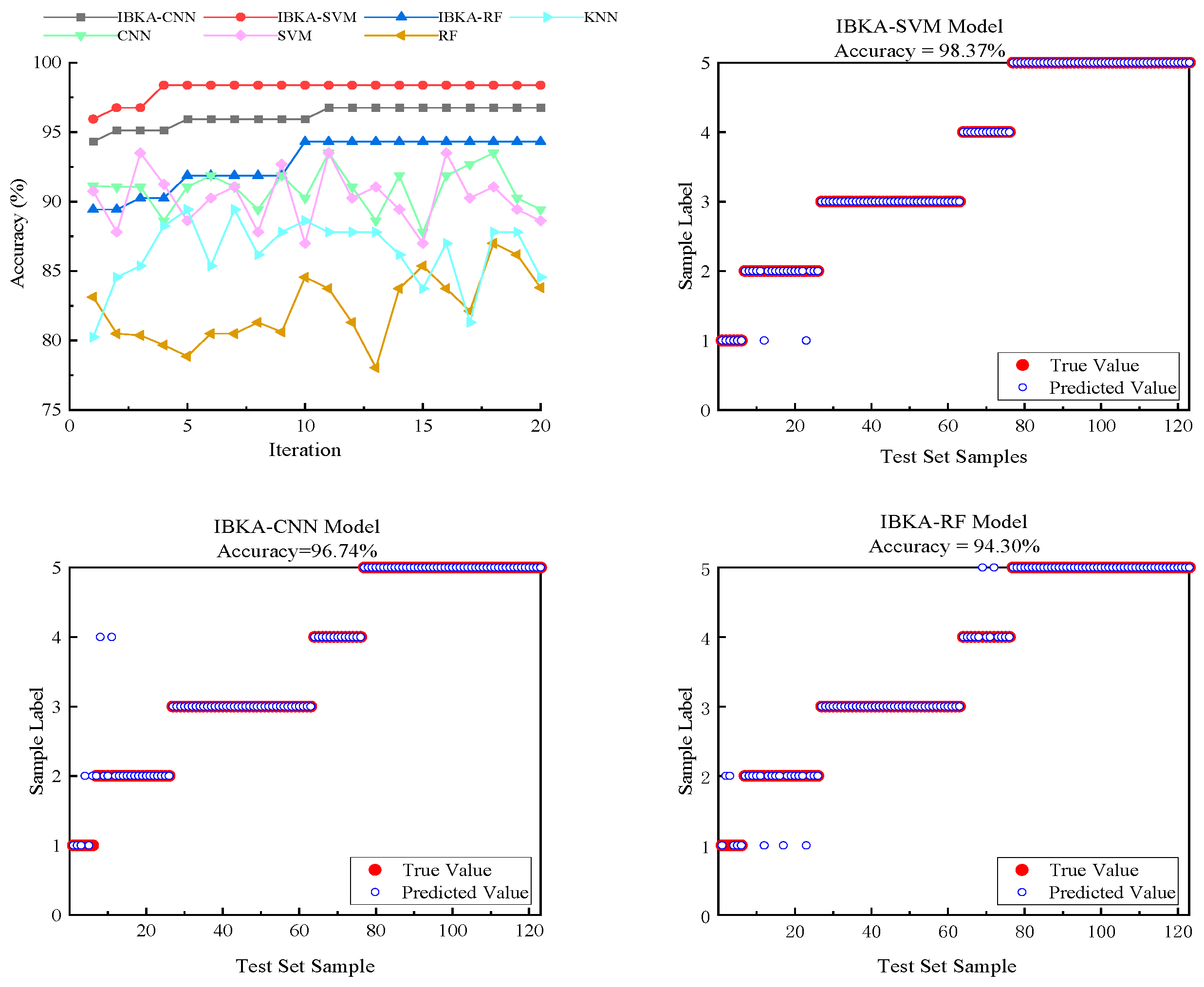
5.4. Comparative Analysis of Different Fault Classification Models
5.5. Comparative Analysis of Characteristic Variable Selection
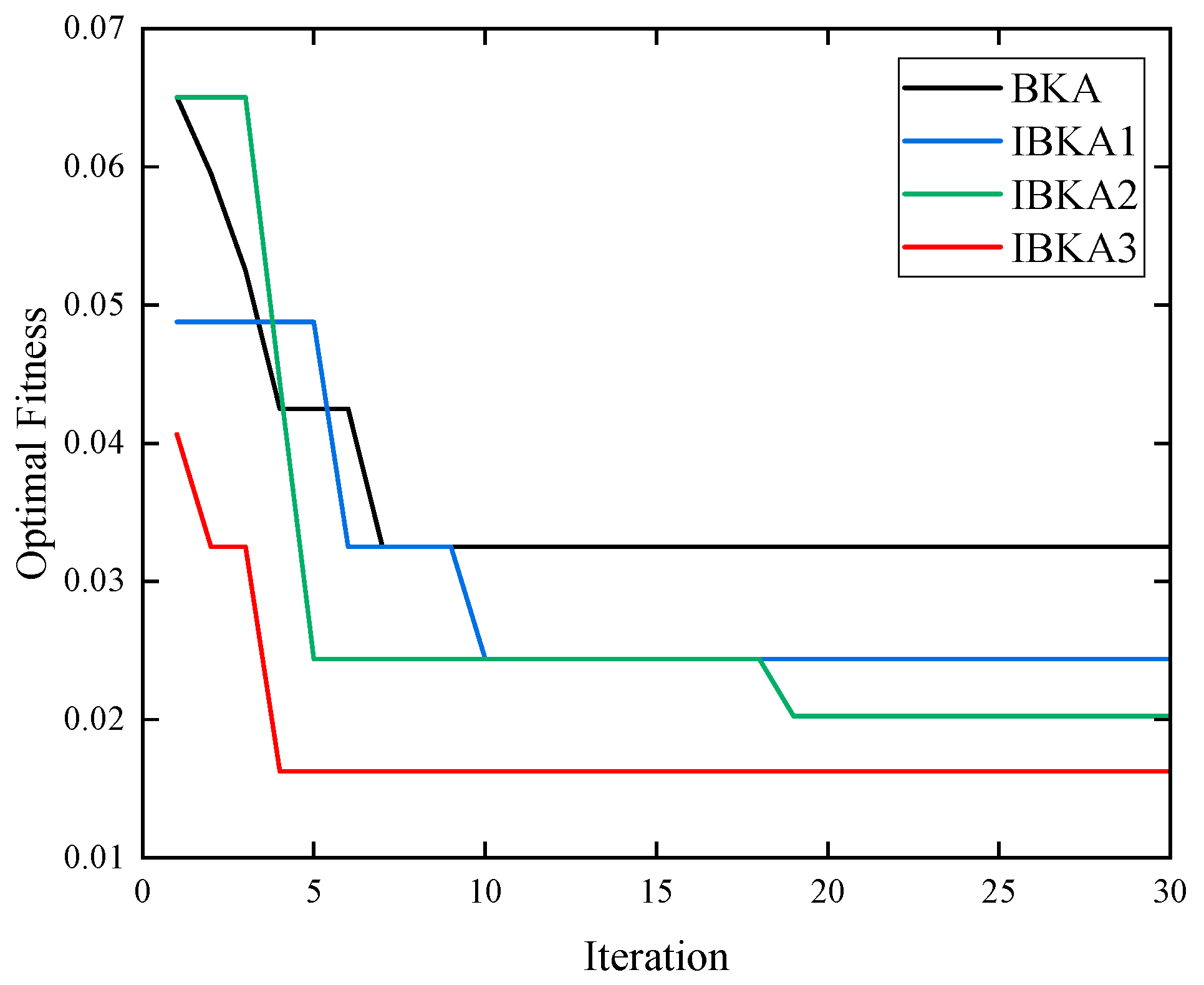
5.6. Comparative Analysis of Different Optimization Algorithms
6. Discussion and Conclusions
- (1)
- In the selection of feature variables for transformer fault diagnosis, by conducting quantitative analysis with LightGBM-RF and employing entropy weight-TOPSIS for comprehensive evaluation, an 8-dimensional subset of highly discriminative features was selected from the original 20-dimensional DGA feature set. This method effectively removes the influence of redundant features while preserving critical fault-sensitive information, resulting in a 60% reduction in model input dimensionality.
- (2)
- Aiming at the common problem that traditional optimization algorithms are prone to fall into local optimum, this paper adopts Tent chaotic mapping, Gompertz growth model, and Morlet wavelet variation strategy to improve the BKA algorithm. Benchmark tests based on the CEC2005 and CEC2017 functions demonstrate that, compared to the DOA, PSO, RIME, GWO, WOA, and BKA algorithms, the IBKA achieves at least a 15% improvement in convergence speed, thereby providing a highly robust foundation for SVM parameter optimization.
- (3)
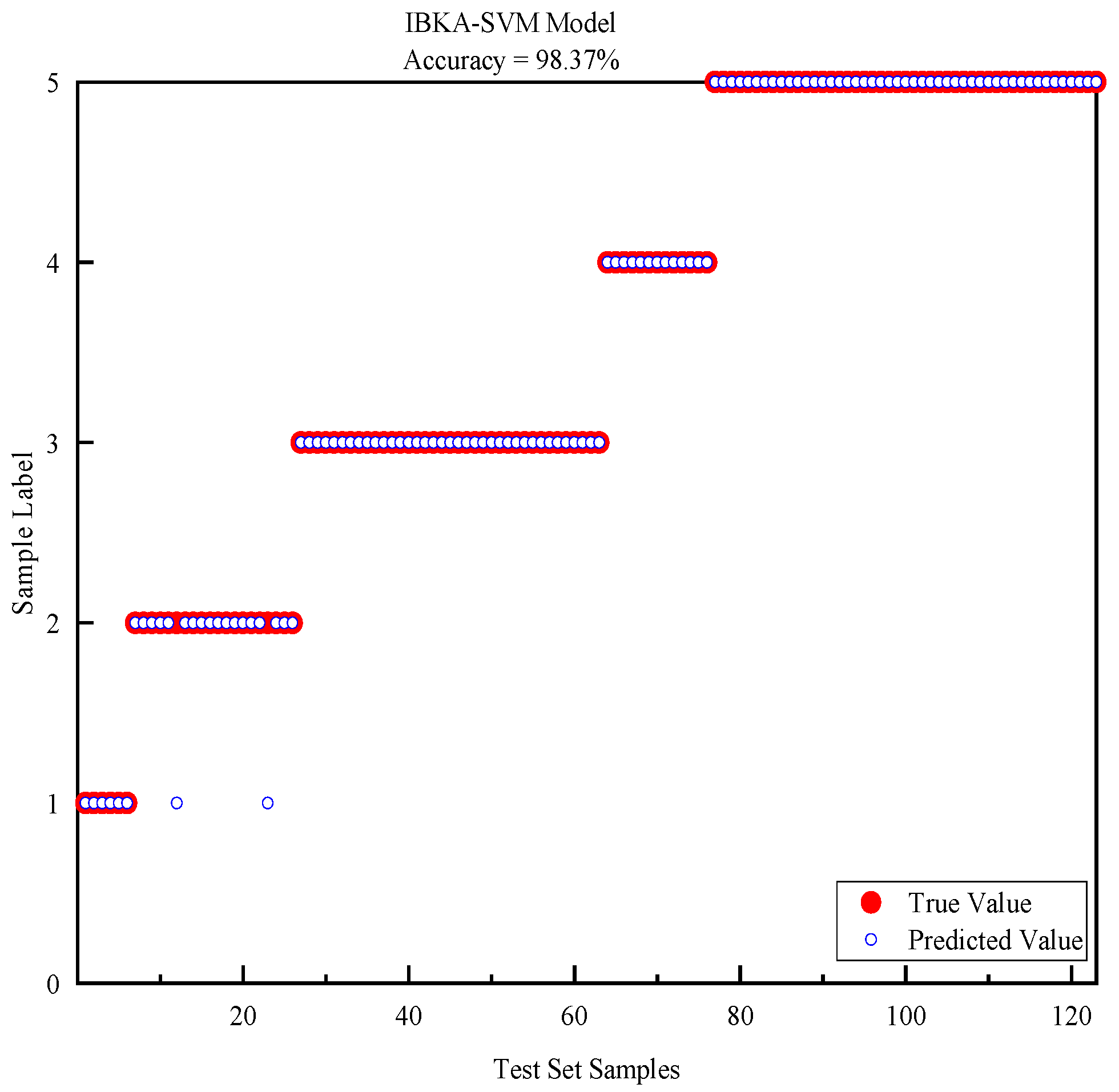
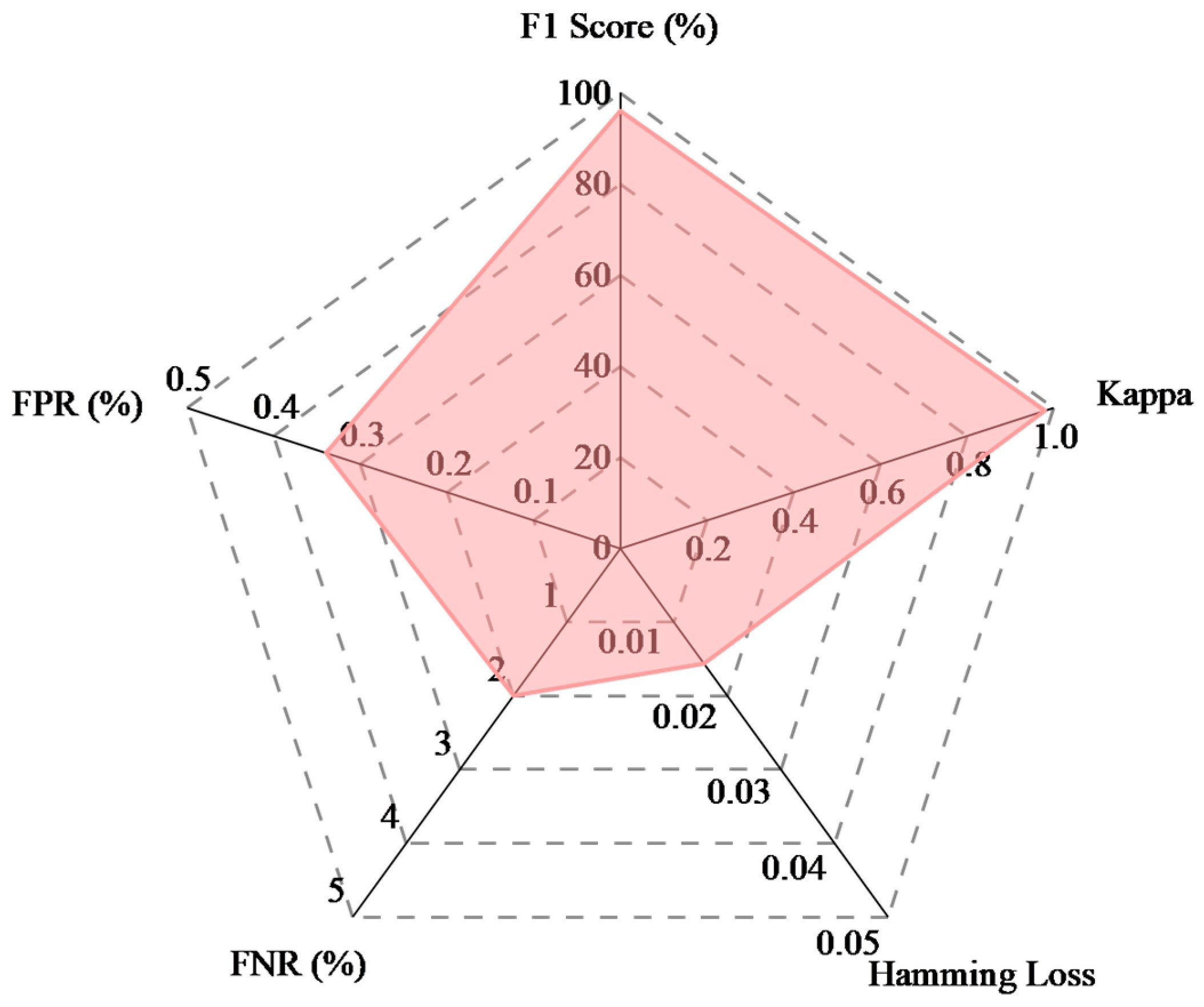
- To address the limitations of manual experience in selecting SVM hyperparameters, the IBKA is used to optimize the penalty factor C and the kernel parameter g. The optimized SVM fault classification accuracy reaches 98.37%, which is 1.63% and 4.07% higher than that of the IBKA-CNN and the IBKA-RF, respectively. Moreover, convergence is achieved in only four iterations—50% fewer than IGWO-SVM—while the total computation time is just 0.3 s, fully meeting the real-time requirements of IEC 61850. On the imbalanced IEC TC10 dataset, the model attains a Kappa coefficient of 0.98 and a miss rate of less than 5%, demonstrating strong generalization capability.
- (4)
- It should be noted that the present study covers only the basic transformer fault types of single discharge (D1/D2) and overheating (T1–T3), and does not yet address more complex scenarios such as moisture-related faults or electrothermal composite faults. Future work will focus on exploring the correlation mechanisms between dissolved gas data and multiphysical field faults (e.g., the coupled effects of insulation moisture and overheating), with the goal of developing a more comprehensive fault diagnosis framework.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, T.; Chen, X.; Du, M.; Guo, W.; Zhang, J.; Li, Y. LightGBM-ICOA-CNN Transformer Fault Diagnosis Method Based on DGA. J. Electr. Eng. 1–10. Available online: https://link.cnki.net/urlid/10.1289.TM.20240820.1122.012 (accessed on 4 August 2025).
- Shao, X.; Cai, B.; Zou, Z.; Shao, H.; Yang, C.; Liu, Y. Artificial intelligence enhanced fault prediction with industrial incomplete information. Mech. Syst. Signal Process. 2025, 224, 112063. [Google Scholar] [CrossRef]
- Taha, I.B.; Hoballah, A.; Ghoneim, S.S. Optimal ratio limits of rogers’ four-ratios and IEC 60599 code methods using particle swarm optimization fuzzy-logic approach. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 222–230. [Google Scholar] [CrossRef]
- Hechifa, A.; Lakehal, A.; Labiod, C.; Nanfak, A.; Mansour, D.-E.A.; Said, D. The effect of source data on graphical pentagons DGA methods for detecting incipient faults in power transformers. In Proceedings of the 2023 International Conference on Decision Aid Sciences and Applications (DASA), Annaba, Algeria, 21–23 November 2023; pp. 152–157. [Google Scholar]
- Hechifa, A.; Lakehal, A.; Nanfak, A.; Saidi, L.; Labiod, C.; Kelaiaia, R.; Ghoneim, S.S. Improved intelligent methods for power transformer fault diagnosis based on tree ensemble learning and multiple feature vector analysis. Electr. Eng. 2024, 106, 2575–2594. [Google Scholar] [CrossRef]
- Houxian, D.; Hao, L.; Longwu, L.; Jie, T.; Jianye, H.; Guoming, M. Power Transformer Fault Detection Based on Multi-Eigenvalues of Vibration Signal. Trans. China Electrotech. Soc. 2023, 38, 83–94. [Google Scholar] [CrossRef]
- Leijiao, G.; Wenlong, L.; Yusen, W.; Like, S. Data Augmentation Method for Transformer Fault Based on Improved Auto-Encoder Under the Condition of Insufficient Data. Trans. China Electrotech. Soc. 2021, 36, 84–94. [Google Scholar] [CrossRef]
- Leixiao, L.; Yigang, H.; Qixin, Y.; Zhikai, X. Zero-Shot Fault Diagnosis Technique of Transformer Based on Weighted Attribute Matrix. Trans. China Electrotech. Soc. 2024, 39, 6577–6590. [Google Scholar] [CrossRef]
- Yuwei, Z. Transformer Fault Diagnosis Based on Fuzzy Rogers 4 Rogers Method. Electr. Eng. 2021, 546, 89–92. [Google Scholar] [CrossRef]
- Zhao, B.; Yang, D.; Karimi, H.R.; Zhou, B.; Feng, S.; Li, G. Filter-wrapper combined feature selection and adaboost-weighted broad learning system for transformer fault diagnosis under imbalanced samples. Neurocomputing 2023, 560, 126803. [Google Scholar] [CrossRef]
- Huidong, W.; Haiyan, Y.; Qiang, G.; Xiaoling, Y.; Xufeng, Z.; Longkun, C. A transformer fault diagnosis method based on multiscale 1DCNN. J. Electr. Power Sci. Technol. 2023, 38, 104–112. [Google Scholar] [CrossRef]
- Ping, L.; Genming, H. Transformer Fault Diagnosis Method Based on the Fusion of Improved Neural Network and Ratio Method. High Volt. Eng. 2023, 49, 3898–3906. [Google Scholar] [CrossRef]
- Yuehan, Q.; Hongshan, Z.; Libo, M.; Shice, Z.; Zengqiang, M. Multi-depth Neural Network Synthesis Method for Power Transformer Fault Identification. Proc. CSEE 2021, 41, 8223–8231. [Google Scholar] [CrossRef]
- Haifeng, Q.; Ning, S.; Songlin, T. Research on the application of improved support vector machine in power transformer fault diagnosis. Electr. Meas. Instrum. 2022, 59, 48–53. [Google Scholar] [CrossRef]
- Hu, S.; Wu, J.; Ciren, O.; Zhu, R. Fault diagnosis of power transformers based on t-SNE and ECOC-TEWSO-SVM. AIP Adv. 2024, 14, 055126. [Google Scholar] [CrossRef]
- Xingzhen, B.; Yuan, Z.; Leijiao, G.; Changyun, L.; Jing, L.; Xiyao, Y. Selection Method of Feature Derived from Dissolved Gas in Oil for Transformers Fault Diagnosis. High Volt. Eng. 2023, 49, 3873–3886. [Google Scholar] [CrossRef]
- Yeshuang, Z.; Shichun, L.; Ling, L. Transformer Fault Diagnosis Based on Multi-strategy ISOA Optimized SVM. Digit. Power Grid Technol. 2023, 51, 38–44. [Google Scholar]
- Yunhao, L.; Richang, X.; Haiqiang, Z.; Feilong, Z.; Jiayang, L.; Wei, W.; Zengyue, L. Fault Diagnosis for Power Transformers Based on Improved Grey Wolf Algorithm Coupled with Least Squares Support Vector Machine. Power Syst. Technol. 2023, 47, 1470–1478. [Google Scholar] [CrossRef]
- Guozhi, Z.; Kang, C.; Rongxing, F.; Kun, W.; Xiaoxing, Z. Transformer fault diagnosis based on DGA and a whale algorithm optimizing a LogitBoost-decision tree. Power Syst. Prot. Control 2023, 51, 63–72. [Google Scholar] [CrossRef]
- Xue, W.; Tao, H. Transformer fault diagnosis based on Bayesian optimized random forest. Electr. Meas. Instrum. 2021, 58, 167–173. [Google Scholar] [CrossRef]
- Liqian, S.; Hongbo, L.; Yadong, H.; Chenhao, H.; Jiantao, Z. Short-Term Power Load Forecasting Based on Feature Selection and Optimized Extreme Learning Machine. J. Xi’an Jiaotong Univ. 2022, 56, 165–175. [Google Scholar]
- Wang, F.; Li, Z. ResearchontransformerfaultdiagnosisbasedonEBWO-SVM. Electron. Meas. Technol. 2024, 47, 101–107. [Google Scholar] [CrossRef]
- Kong, X.; Cai, B.; Yu, Y.; Yang, J.; Wang, B.; Liu, Z.; Shao, X.; Yang, C. Intelligent diagnosis method for early faults of electric-hydraulic control system based on residual analysis. Reliab. Eng. Syst. Saf. 2025, 261, 111142. [Google Scholar] [CrossRef]
- Liu, Z.; He, W.; Liu, H.; Luo, L.; Zhang, D.; Niu, B. Fault identification for power transformer based on dissolved gas in oil data using sparse convolutional neural networks. IET Gener. Transm. Distrib. 2024, 18, 517–529. [Google Scholar] [CrossRef]
- Shang, H.; Liu, Z.; Wei, Y.; Zhang, S. A Novel Fault Diagnosis Method for a Power Transformer Based on Multi-Scale Approximate Entropy and Optimized Convolutional Networks. Entropy 2024, 26, 186. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef]
- Guoqing, A.; Zhewen, S.; Shifeng, M.; Xiaohui, H.; Zhenbin, D.; Chunlin, Z. Fault Diagnosis of WOA-SVM Transformer Based on RF Feature Optimization. High Volt. Appar. 2022, 58, 171–178. [Google Scholar] [CrossRef]
- Xin, O.; Zhibin, L. Transformer fault diagnosis technology based on sample expansion and feature. selection and SVM optimized by IGWO. Power Syst. Prot. Control 2023, 51, 11–20. [Google Scholar] [CrossRef]
- Jinxin, Y.; Caibo, L.; Xiong, H.; Wenqing, Z.; Xu, Z.; Bang, L. Transformer fault diagnosis based on DGA and TPE-LightGBM. J. Electr. Power Sci. Technol. 2024, 39, 70–77. [Google Scholar] [CrossRef]
- Du, C.; Zhang, J.; Fang, J. An innovative complex-valued encoding black-winged kite algorithm for global optimization. Sci. Rep. 2025, 15, 932. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, W.-C.; Hu, X.-X.; Qiu, L.; Zang, H.-F. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Zhao, H.; Li, P.; Duan, S.; Gu, J. Inversion of image-only intrinsic parameters for steel fibre concrete under combined rate-temperature conditions: An adaptively enhanced machine learning approach. J. Build. Eng. 2024, 94, 109836. [Google Scholar] [CrossRef]
- Chaoyueling, L.; Yunxin, Z.; Zhenyu, X.; Yulong, X.; Mingcheng, D.; Li, L. Improved GWO-SVM Transformer Fault Diagnosis Method Based on Borderline-SMOTE-IHT Mixed Sampling. Power Grid Anal. Study 2023, 51, 108–114. [Google Scholar]
- Xiangxi, Y.; Ying, Z.; Guozhi, Z.; Jun, L.; Mingwei, W. SCNGO-SVM-AdaBoost Transformer Fault Diagnosis Technology Based on Data Augmentation and Fault Feature Optimization. South. Power Syst. Technol. 2025, 19, 1–11. [Google Scholar]
- Xiaohua, Z.; Yuchen, F.; Xuchu, H.; Wenguang, L.; Yongge, L. Transformer Fault Diagnosis Based on SVM Optimized by Bald Eagle Search Algorithm. South. Power Syst. Technol. 2023, 17, 99–106+116. [Google Scholar] [CrossRef]
- DL/T 722-2014; Guide to the Analysis and the Diagnosis of Gases Dissolved in Transformer Oil. National Energy Administration: Beijing, China, 2014.
- IEC 60599:2015; Mineral Oil-Impregnated Electrical Equipment in Service—Guide to the Interpretation of Dissolved and Free Gases Analysis. International Electrotechnical Commission: Geneva, Switzerland, 2015.
- Wei, S. Transformer Fault Diagnosis Based on DLH-GWO-SVM. J. Phys. Conf. Ser. 2023, 2527, 012050. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, H. Transformer Fault Diagnosis Based on Multi-Strategy Enhanced Dung Beetle Algorithm and Optimized SVM. Energies 2024, 17, 6296. [Google Scholar] [CrossRef]
- IEC/IEEE 61850-9-3:2016; Communication Networks and Systems for Power Utility Automation—Part 9-3: Precision Time Protocol Profile for Power Utility Automation. IEC/IEEE: Geneva, Switzerland, 2016. [CrossRef]
- Shi, X.; Li, T.; Fang, F.; Zhu, Y.; Yang, W.; Luo, B. Dissolved gas analysis for power transformer fault diagnosis combining domain knowledge and capsule network. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 3386–3395. [Google Scholar] [CrossRef]
- Guan, S.; Yang, H.; Wu, T. Transformer fault diagnosis method based on TLR-ADASYN balanced dataset. Sci. Rep. 2023, 13, 23010. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Hai, C.; Feng, Z.; Li, G. A Transformer Fault Diagnosis Method Based on Parameters Optimization of Hybrid Kernel Extreme Learning Machine. IEEE Access 2021, 9, 126891–126902. [Google Scholar] [CrossRef]
- Yang, X.; Chen, W.; Li, A.; Yang, C.; Xie, Z.; Dong, H. BA-PNN-based methods for power transformer fault diagnosis. Adv. Eng. Inform. 2019, 39, 178–185. [Google Scholar] [CrossRef]

| Number | Feature | Number | Feature |
|---|---|---|---|
| 1 | n(H2) | 11 | n(C2H4)/n(CH4) |
| 2 | n(CH4) | 12 | n(C2H4)/n(C2H6) |
| 3 | n(C2H2) | 13 | n(C2H6)/n(H2) |
| 4 | n(C2H4) | 14 | n(CH4)/n(C2H6) |
| 5 | n(C2H6) | 15 | n(CH4)/n(H2) |
| 6 | n(C2H2)/n(H2) | 16 | n(H2)/n(TH) |
| 7 | n(C2H2)/n(CH4) | 17 | n(CH4)/n(TH) |
| 8 | n(C2H2)/n(C2H6) | 18 | n(C2H2)/n(TH) |
| 9 | n(C2H2)/n(C2H4) | 19 | n(C2H4)/n(TH) |
| 10 | n(C2H4)/n(H2) | 20 | n(C2H6)/n(TH) |
| Test Function | Search Range | Optimal Solution |
|---|---|---|
| [−100, 100] | 0 | |
| [−100, 100] | 0 | |
| [−5.12, 5.12] | 0 | |
| [−32, 32] | 0 | |
| [0, 10] | −0.803619 | |
| [78, 102] [33, 45] [27, 45] | −30,665.539 |
| Operating Condition | Status Code | Number of Samples |
|---|---|---|
| Partial Discharge | 1 | 20 |
| Low-Energy Discharge | 2 | 66 |
| High-Energy Discharge | 3 | 124 |
| Low-to-Medium Temperature Overheating | 4 | 44 |
| High-Temperature Overheating | 5 | 156 |
| Algorithm | Introduced Strategies | Parameter Settings |
|---|---|---|
| BKA | None | None |
| IBKA1 | Tent chaotic map | u = 0.5 |
| IBKA2 | Tent chaotic map | u = 0.5 |
| Gompertz model | A = 1.0, B = 0.5, Y = 0.1 | |
| IBKA3 | Tent chaotic map | u = 0.5 |
| Gompertz model | A = 1.0, B = 0.5, Y = 0.1 | |
| Morlet wavelet variation | a = 5, b = 10 |
| Classification Method | Accuracy (%) |
|---|---|
| CNN | 90.27 |
| SVM | 90.59 |
| RF | 82.40 |
| KNN | 86.95 |
| IBKA-CNN | 96.74 |
| IBKA-RF | 94.30 |
| IBKA-SVM | 98.37 |
| Feature Variable Type | Parameters (C, g) | Accuracy (%) |
|---|---|---|
| Three-Ratio Method | (11.74, 1.68) | 73.81 |
| Rogers Ratio Method | (31.2, 7.23) | 84.13 |
| Basic Features | (23.34, 1.27) | 68.25 |
| Hybrid feature selection | (42.4, 3.32) | 98.37 |
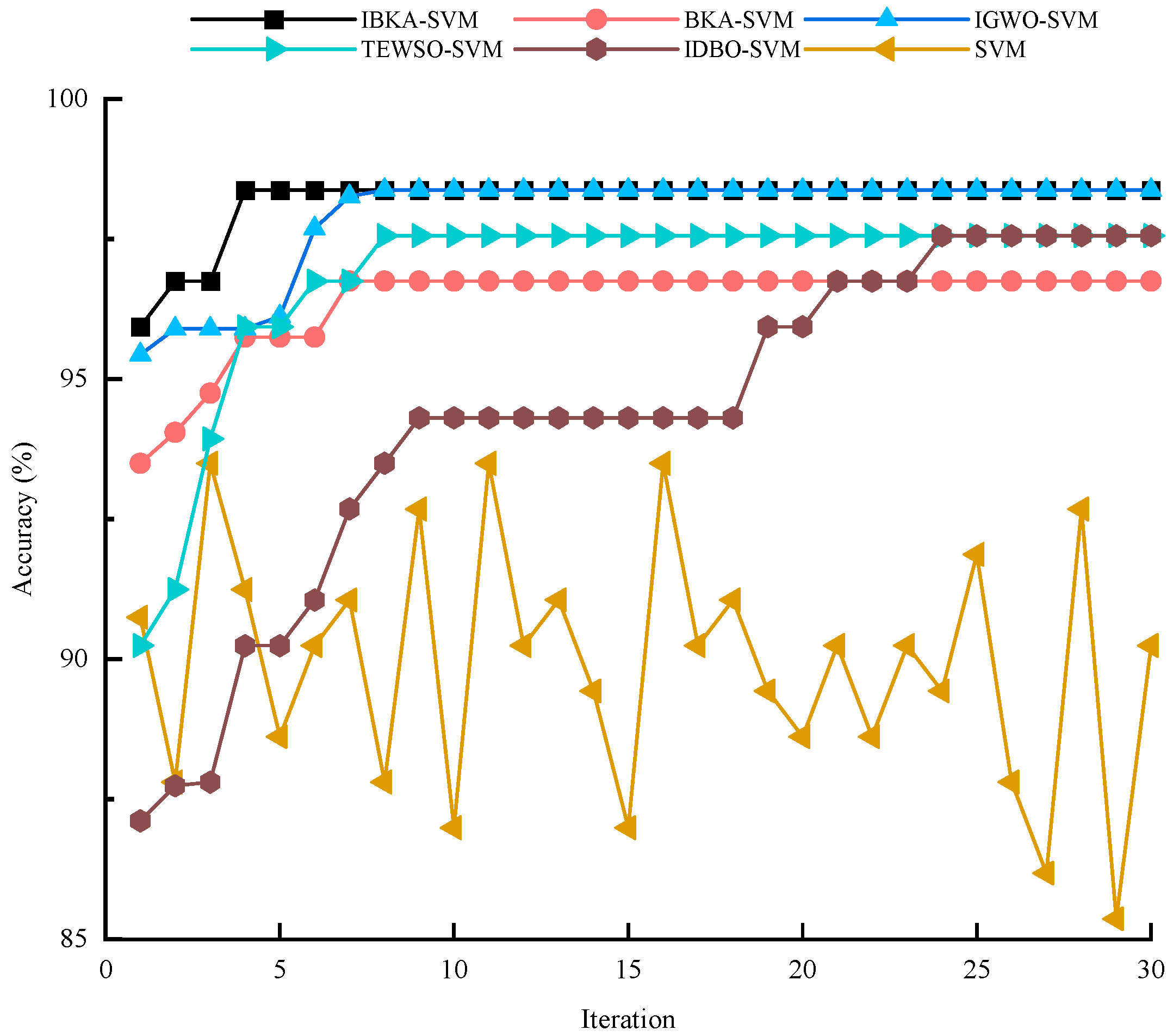
| Models | Accuracy (%) | Convergence Iterations | Time per Iteration (ms) | Total Time (s) |
|---|---|---|---|---|
| IBKA-SVM | 98.37 | 4 | 74.66 | 0.3 |
| BKA-SVM | 96.74 | 7 | 64.18 | 0.45 |
| IGWO-SVM | 98.37 | 8 | 43.95 | 0.35 |
| IDBO-SVM | 97.56 | 24 | 34.52 | 0.83 |
| TEWSO-SVM | 97.56 | 8 | 35.75 | 0.28 |
| Model Name | Accuracy (%) | F1 Score (%) | Kappa | Recall (%) | FPR (%) |
|---|---|---|---|---|---|
| IBKA-SVM | 98.37 | 96.09 | 0.9801 | 98.00 | 0.34 |
| CapsNet | 95.93 | 91.7 | 0.9505 | 91.59 | 1.03 |
| MGWO-KELM | 92.68 | 89.18 | 0.9104 | 90.66 | 1.77 |
| SO-RF | 96.75 | 93.37 | 0.9603 | 95.46 | 0.78 |
| GA-BPNN | 95.93 | 92.59 | 0.9438 | 94.38 | 1.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, F. Transformer Fault Diagnosis Using Hybrid Feature Selection and Improved Black-Winged Kite Optimized SVM. Electronics 2025, 14, 3160. https://doi.org/10.3390/electronics14163160
Li J, Wang F. Transformer Fault Diagnosis Using Hybrid Feature Selection and Improved Black-Winged Kite Optimized SVM. Electronics. 2025; 14(16):3160. https://doi.org/10.3390/electronics14163160
Chicago/Turabian StyleLi, Jifang, and Feiyang Wang. 2025. "Transformer Fault Diagnosis Using Hybrid Feature Selection and Improved Black-Winged Kite Optimized SVM" Electronics 14, no. 16: 3160. https://doi.org/10.3390/electronics14163160
APA StyleLi, J., & Wang, F. (2025). Transformer Fault Diagnosis Using Hybrid Feature Selection and Improved Black-Winged Kite Optimized SVM. Electronics, 14(16), 3160. https://doi.org/10.3390/electronics14163160





