Data Sampling System for Processing Event Camera Data Using a Stochastic Neural Network on an FPGA
Abstract
1. Introduction and Background
1.1. Problem Addressed by This Paper
1.2. Comparison with Existing Camera Data Processing Methods
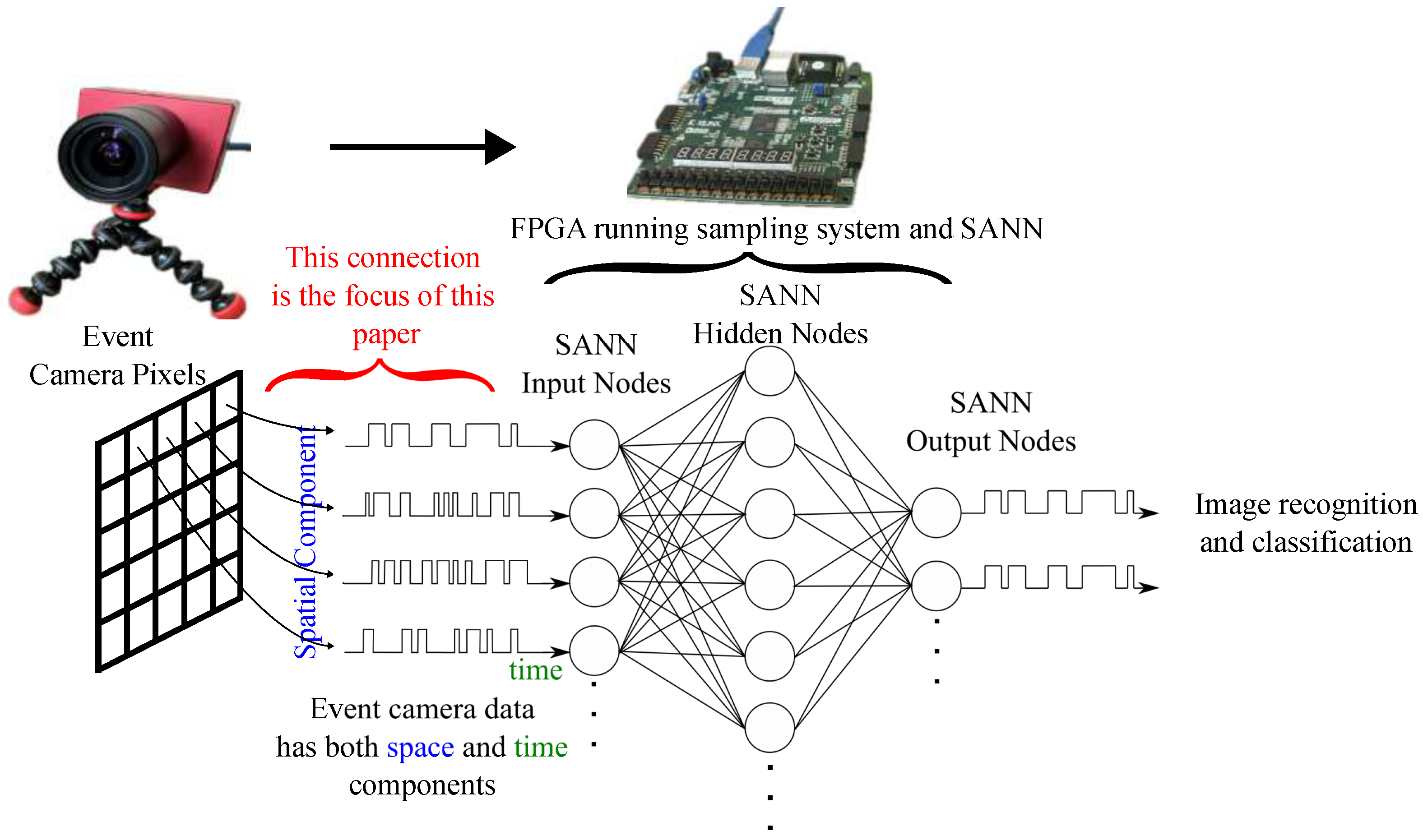
2. System Components
2.1. Image Recognition
2.2. Event Cameras
2.3. Stochastic Computing and Stochastic Artificial Neural Networks
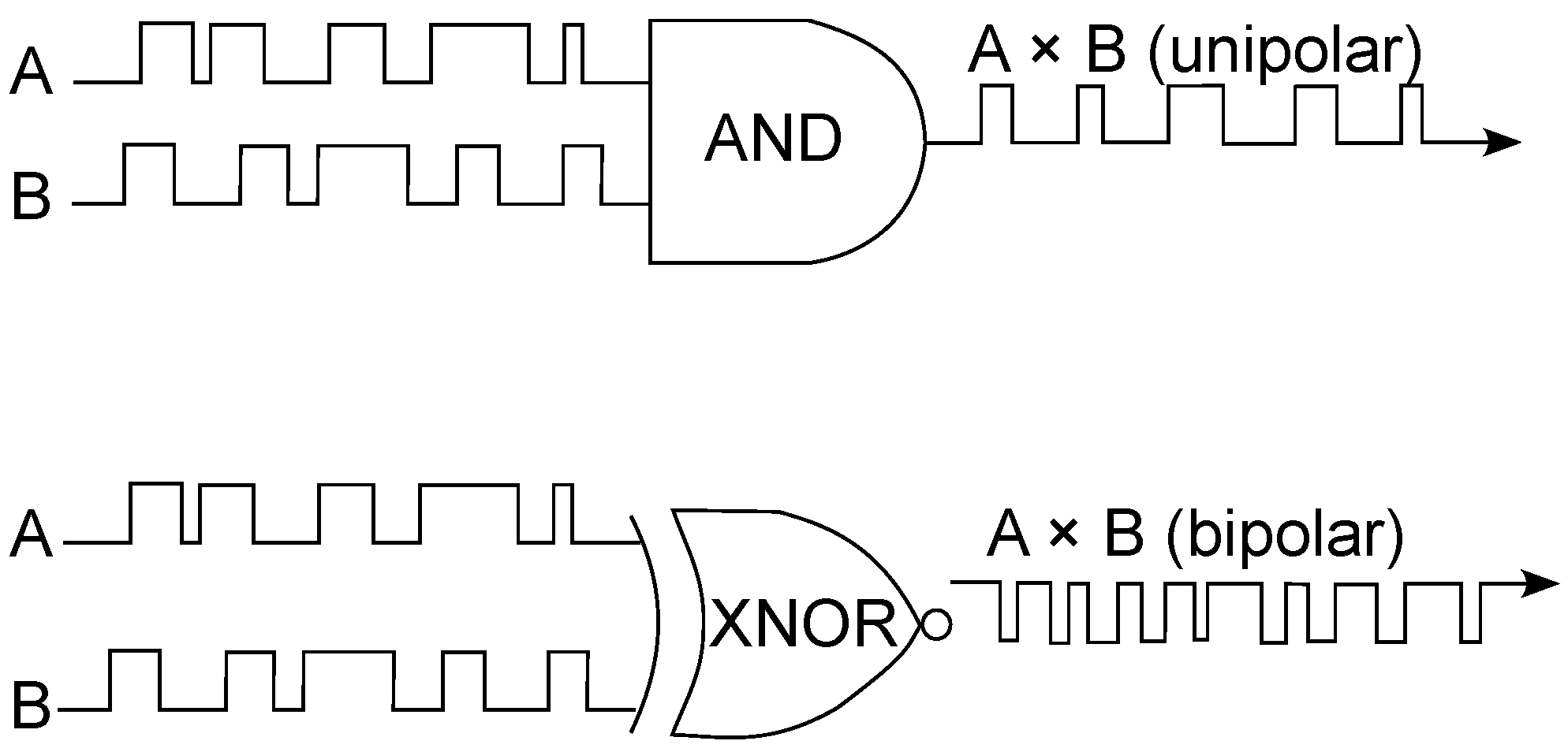
2.3.1. Stochastic Computing
2.3.2. Stochastic Artificial Neural Networks
2.4. Using a SANN with Event Camera Data
2.5. Illustration of Problem Addressed by This Paper
2.6. Proposed SANN Front-End Architecture
3. Materials and Methods
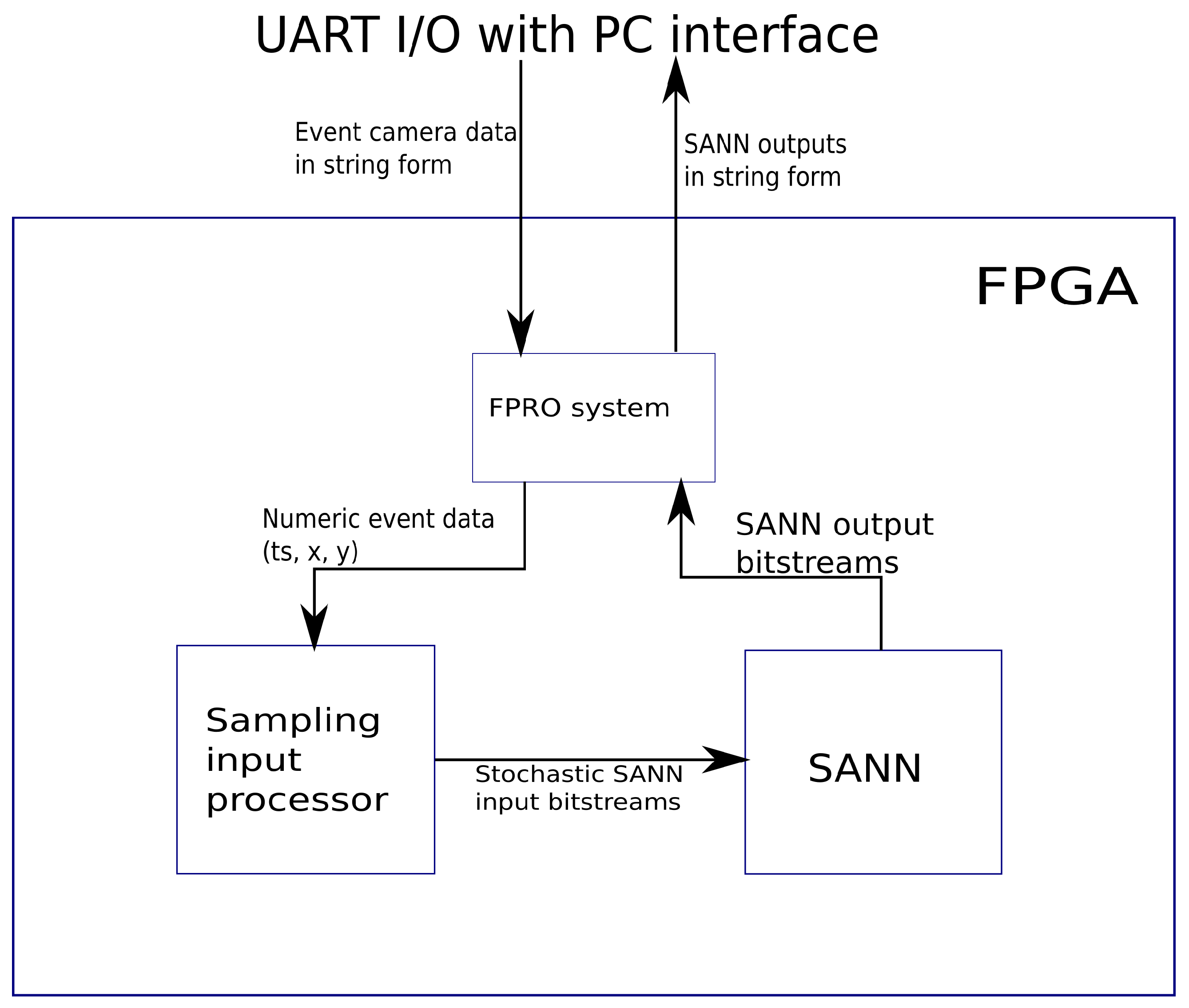
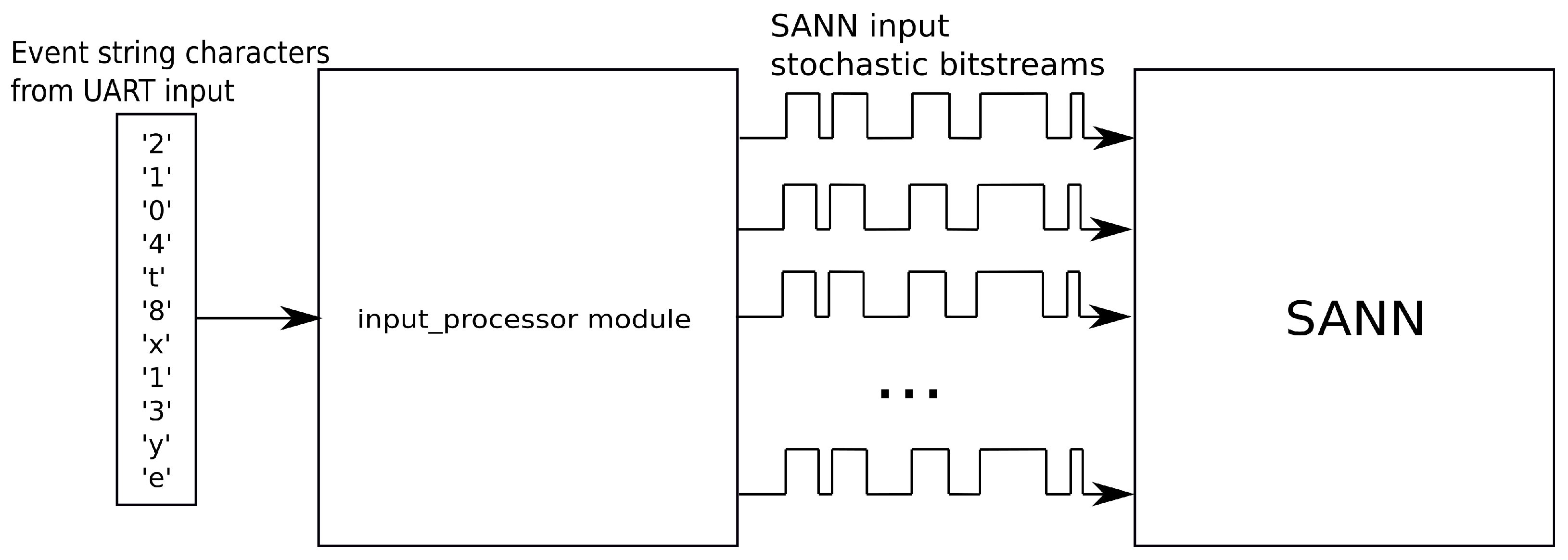
3.1. Background—UART Interface and SANN
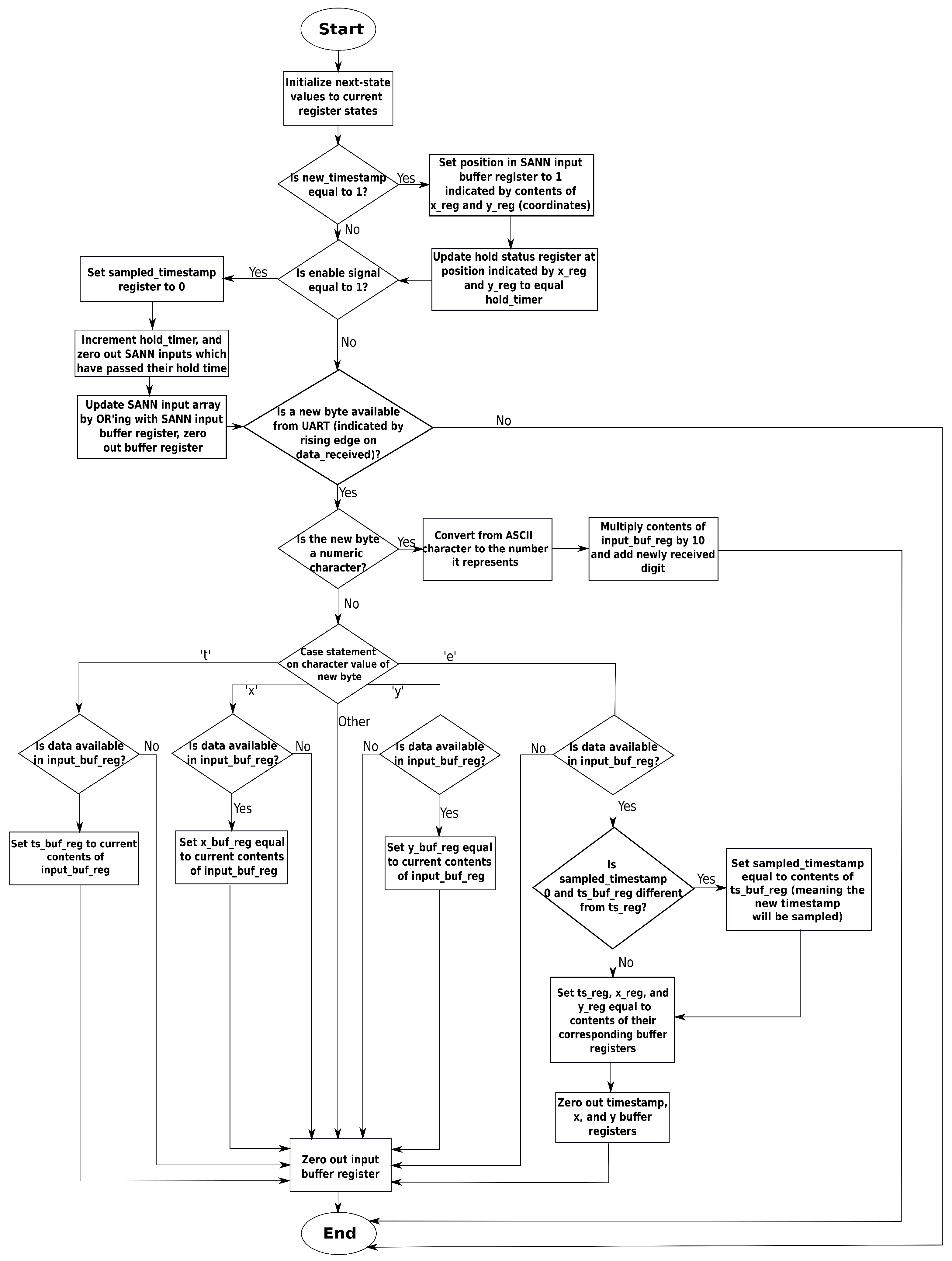
3.2. Overview of the Sampling Input Processor System
- First, it converts the ASCII character data received through the UART serial port back into numeric representations of the timestamp, x- and y-coordinate, Section 3.2.1.
- Secondly, it selects one timestamp per to sample, Section 3.2.2, and translates the x- and y-coordinates of all events received with that timestamp into SANN input positions, Section 3.2.3.
- Finally, at the end of each sampling period, it writes 1’s to the SANN input array for each position accumulated from the sampled events, Section 3.2.4.
3.2.1. Translating Event Strings into Numeric Event Data
3.2.2. Sampling Events at Selected Timestamps
3.2.3. Translating Event Data to SANN Input Positions
3.2.4. Update the SANN Input Array
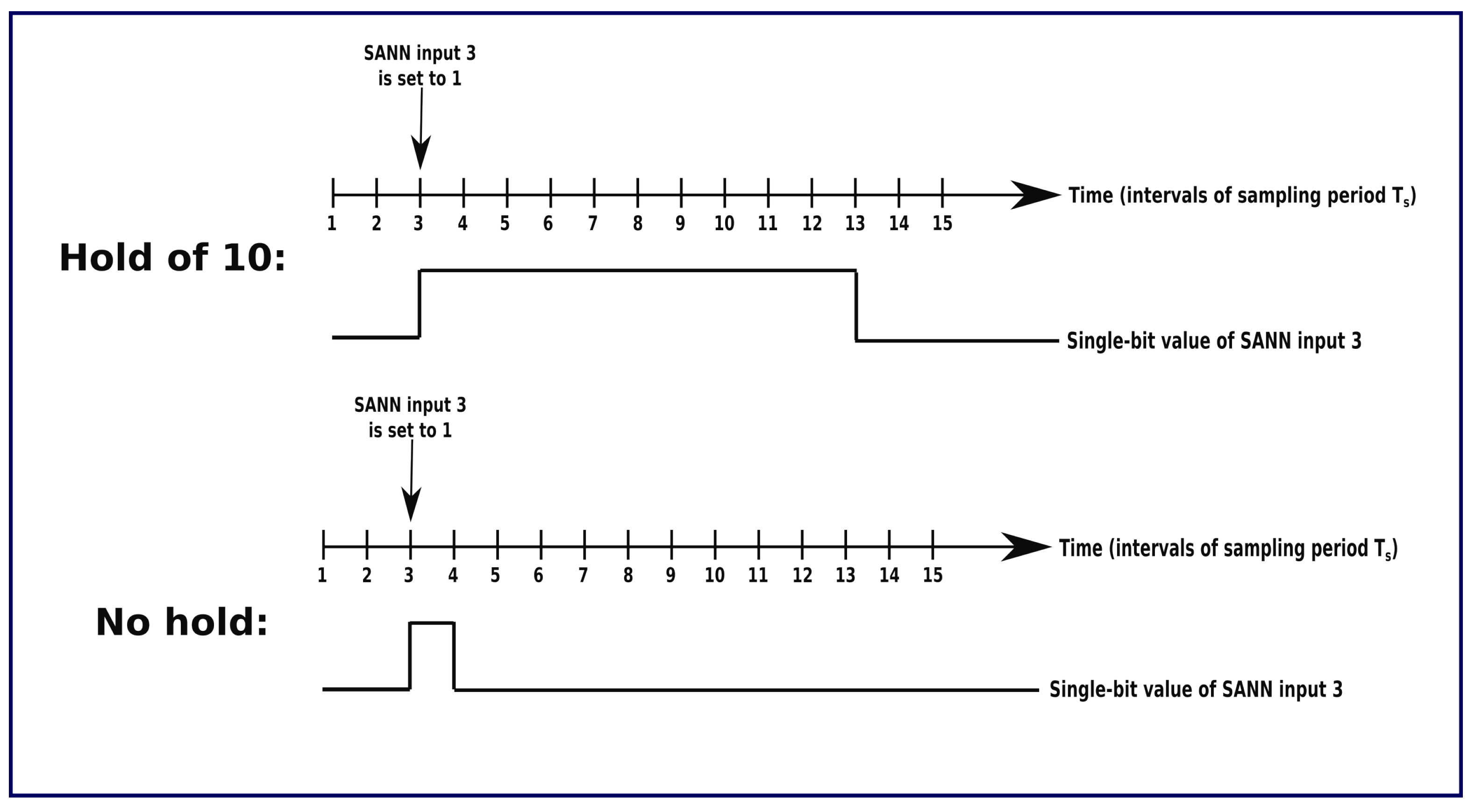
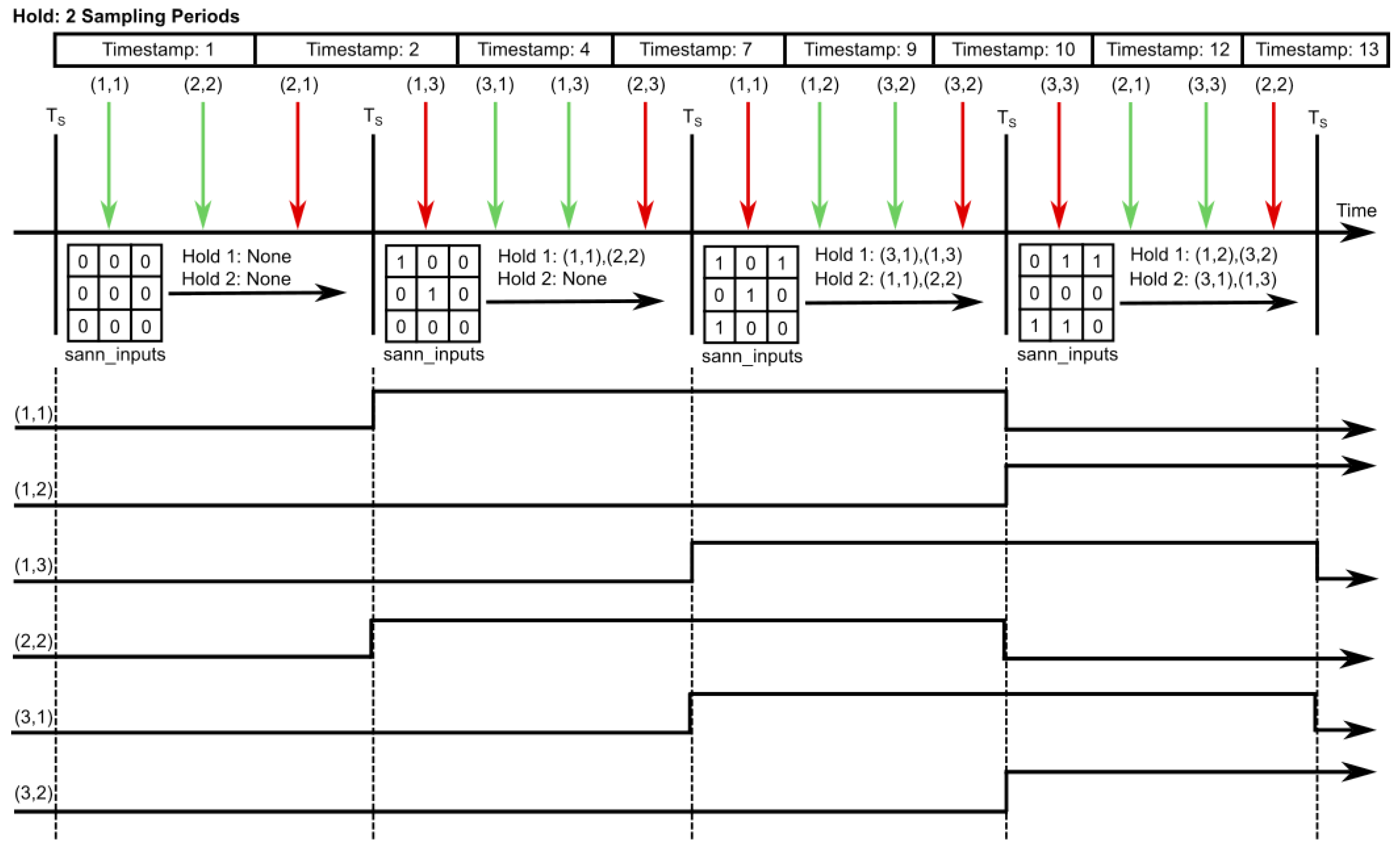
3.3. Hold Functionality
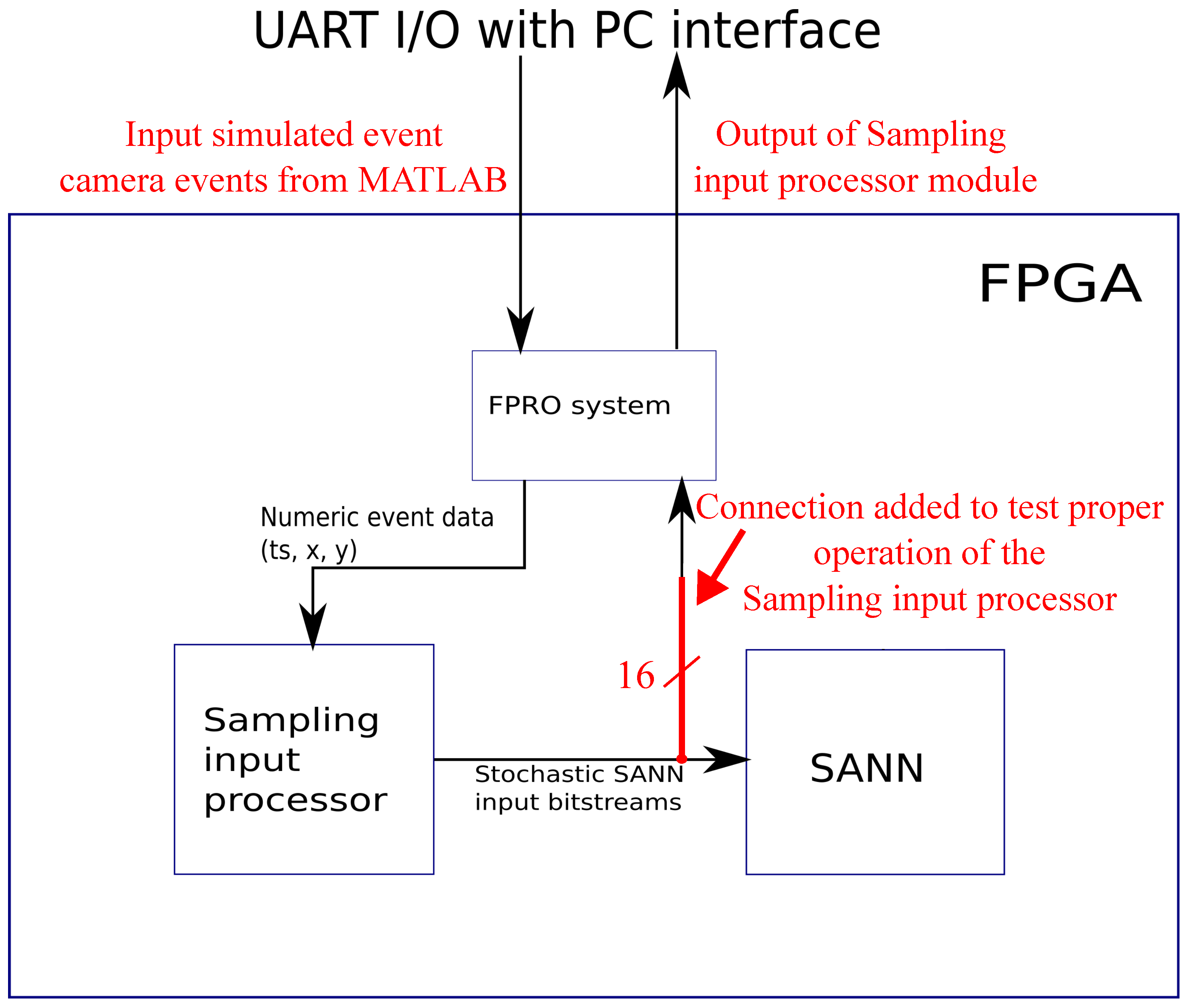
4. Test Setup
5. FPGA Hardware Results
5.1. Unit Test 1 of Sampling Input Processor Module: Non-Sparse Input and No Hold
5.2. Unit Test 2 of Sampling Input Processor Module: Sparse Input and No Hold
5.3. Unit Test 3 of Sampling Input Processor Module: Sparse Input and Hold of 2
6. Analysis, Discussion, and Supplemental FPGA Results
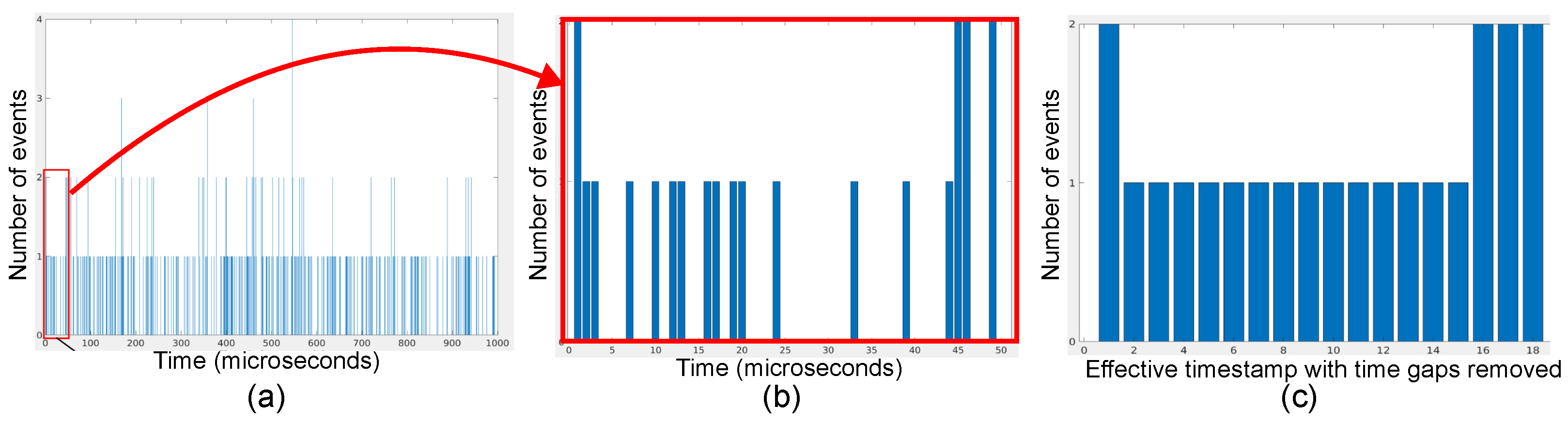
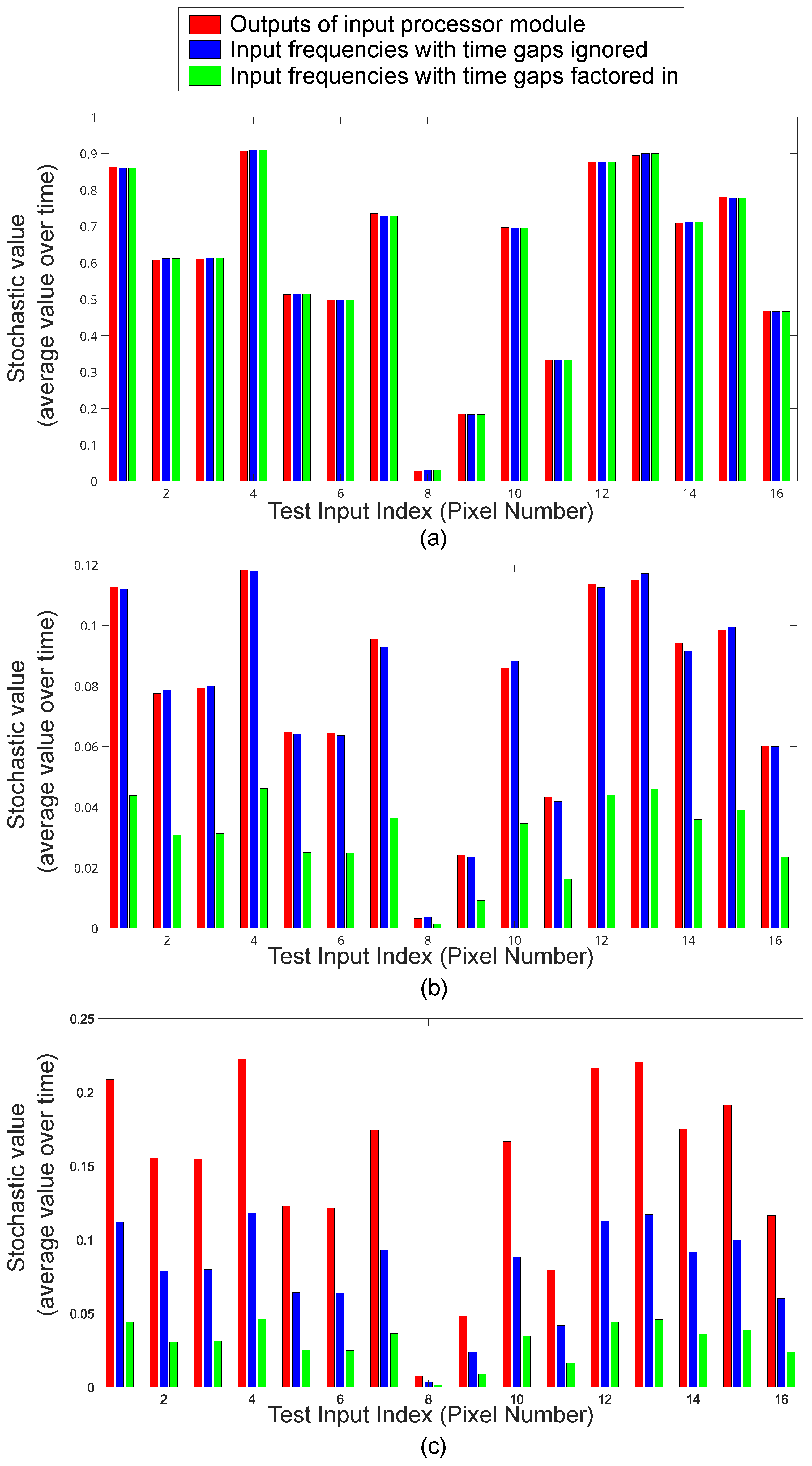
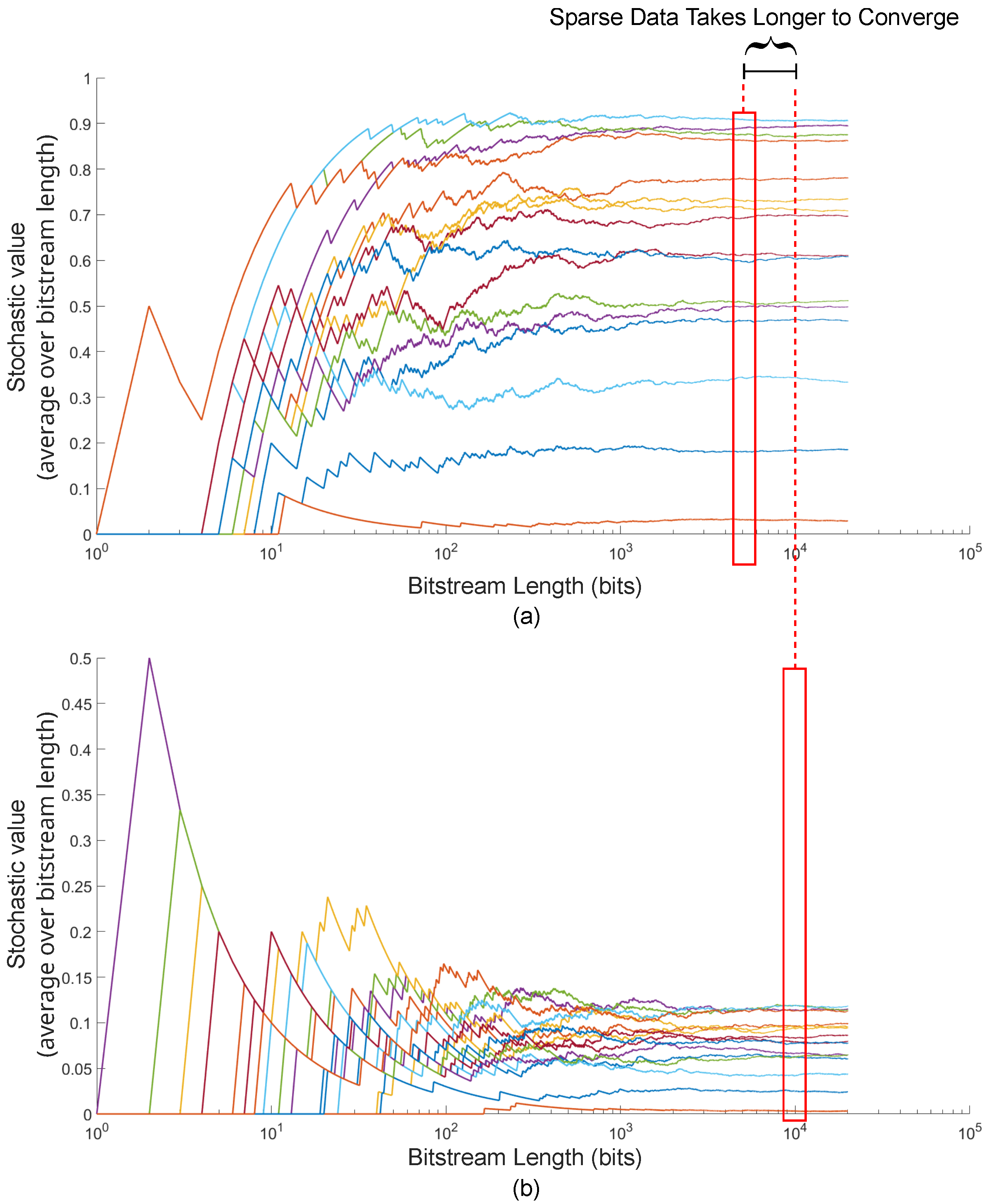
6.1. Sparse Data Analysis
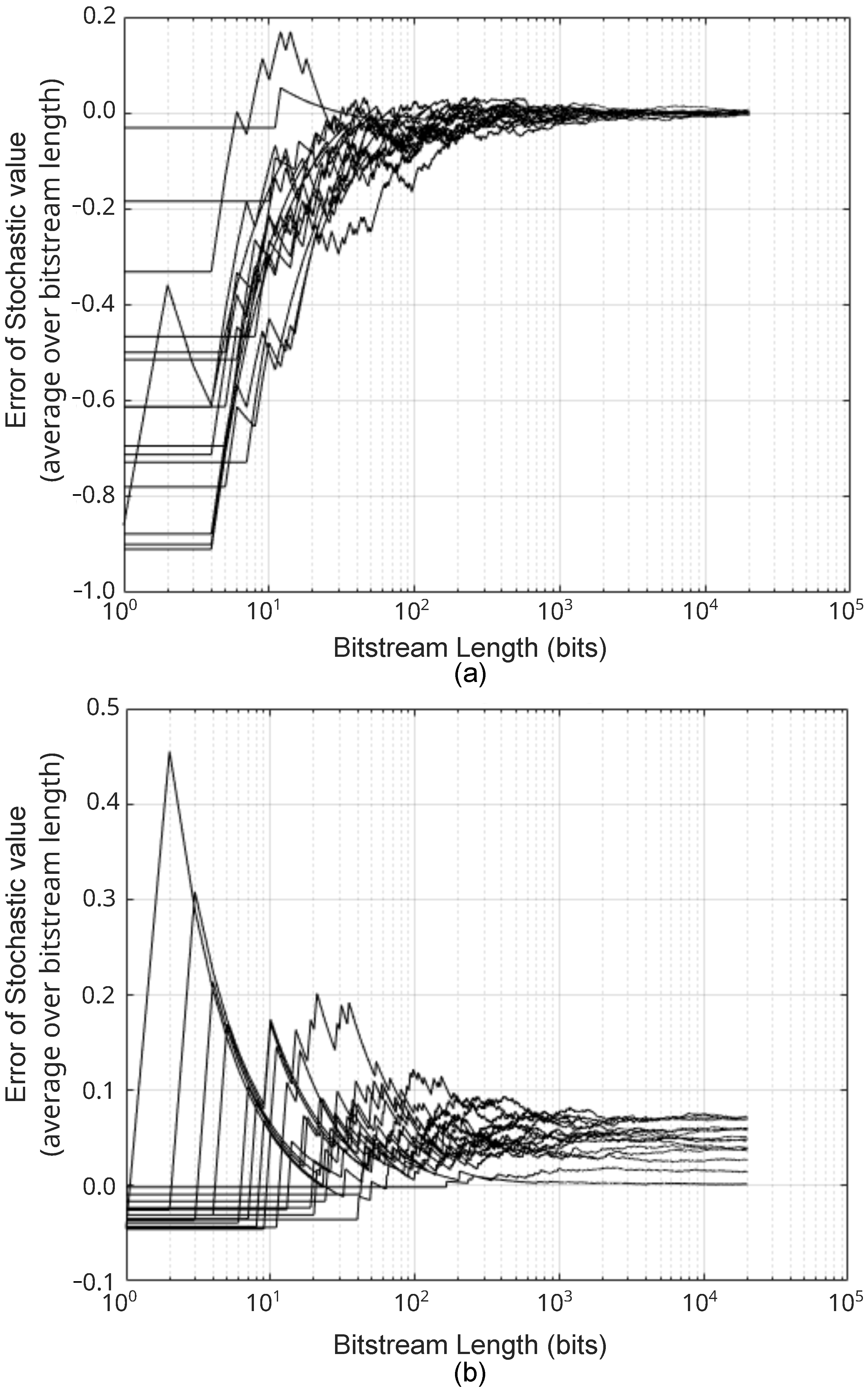
6.2. Convergence Time Analysis
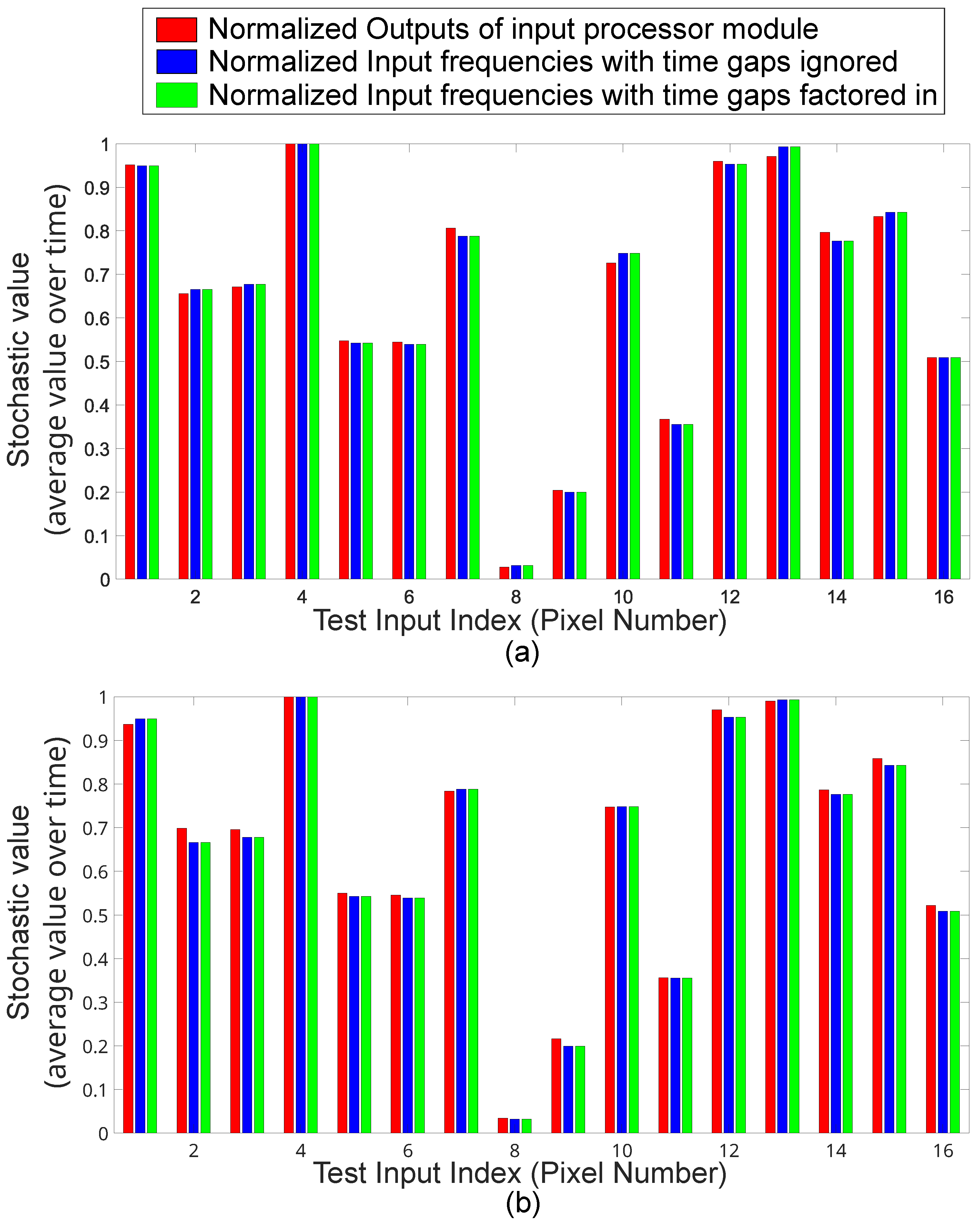
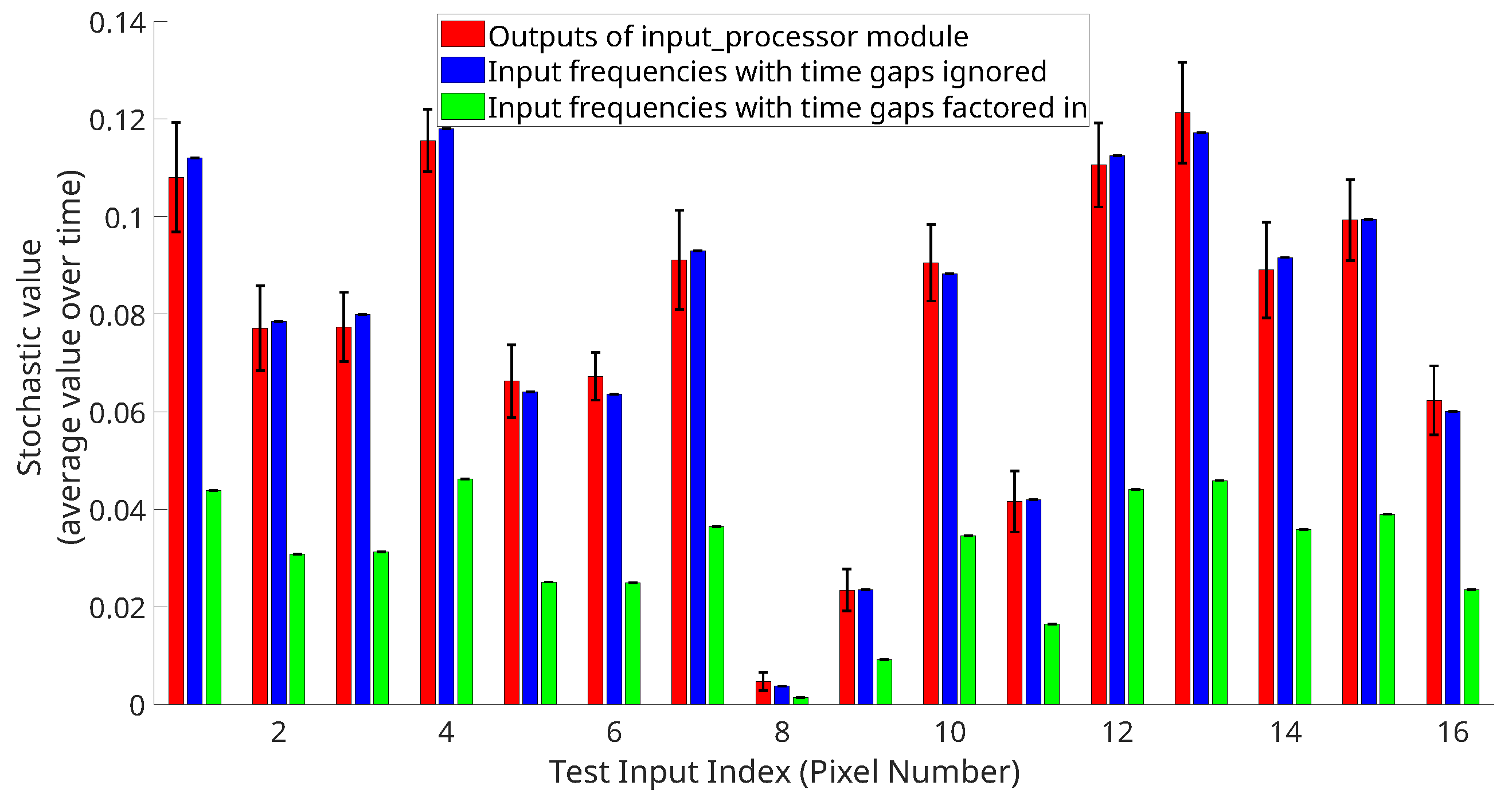
6.3. Normalized Data Analysis
6.4. Repeatability Analysis
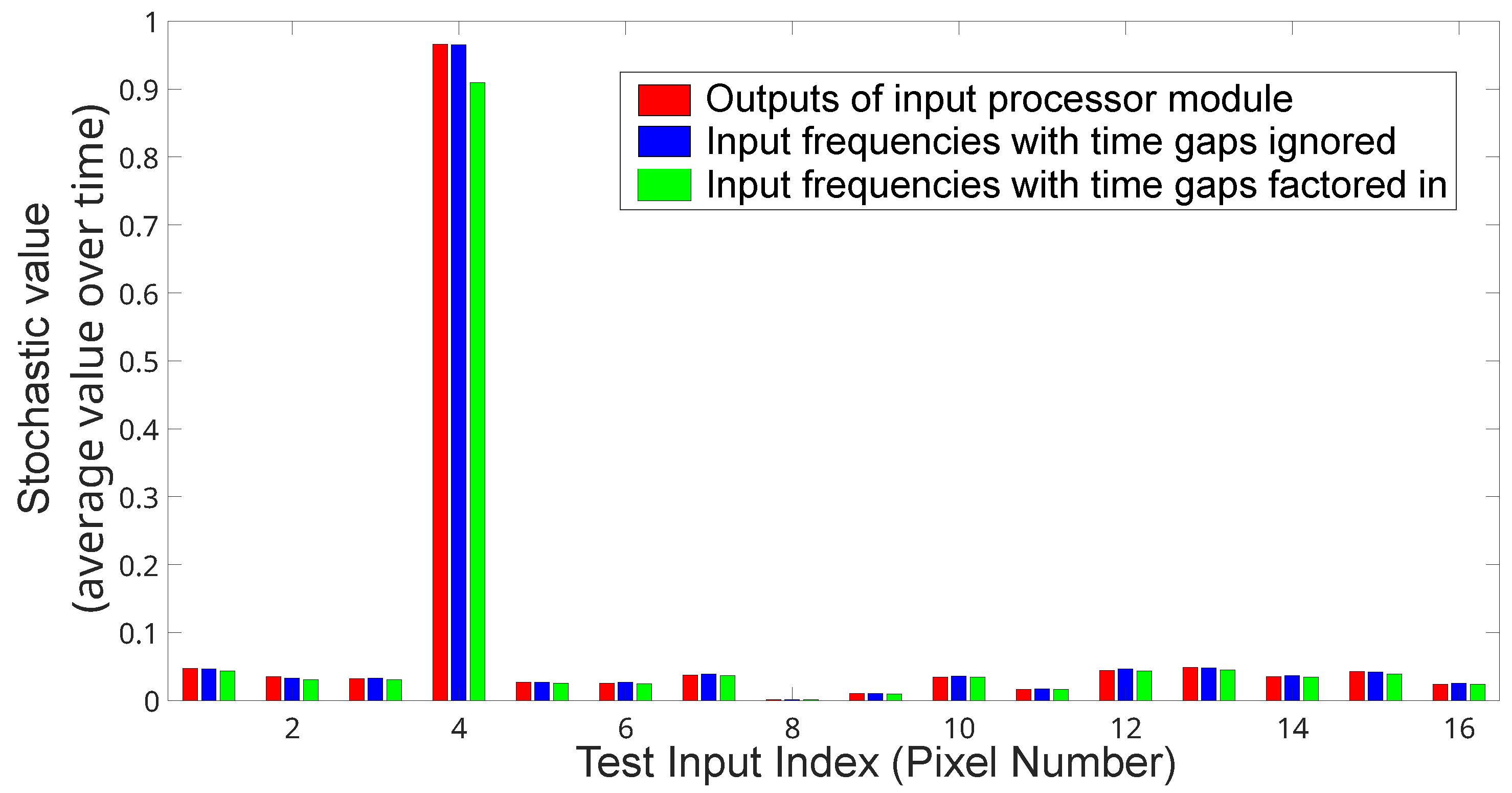
6.5. Range of Input Value Analysis
6.6. Hold System Analysis
7. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AER | Address-event representation |
| BRAM | Block Random Access Memory |
| CNN | convolutional neural network |
| FF | Flip Flop |
| FPGA | Field Programmable Gate Array |
| FPro System | FPGA Prototyping System |
| I/O | Input/Output |
| LUT | Lookup Table |
| NN | neural network |
| RAM | Random Access Memory |
| SANN | Stochastic Neural Network |
| SNG | Stochastic Number Generator |
| UART | Universal Asynchronous Receiver/Transmitter |
| XNOR | exclusive NOR |
References
- Gallego, G.; Delbrück, T.; Orchard, G.; Bartolozzi, C.; Taba, B.; Censi, A.; Leutenegger, S.; Davison, A.J.; Conradt, J.; Daniilidis, K.; et al. Event-Based Vision: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 154–180. [Google Scholar] [CrossRef] [PubMed]
- Afshar, S.; Nicholson, A.P.; van Schaik, A.; Cohen, G. Event-Based Object Detection and Tracking for Space Situational Awareness. IEEE Sens. J. 2020, 20, 15117–15132. [Google Scholar] [CrossRef]
- Monforte, M.; Gava, L.; Iacono, M.; Glover, A.; Bartolozzi, C. Fast Trajectory End-Point Prediction with Event Cameras for Reactive Robot Control. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Vancouver, BC, Canada, 17–24 June 2023; pp. 4036–4044. [Google Scholar] [CrossRef]
- Maqueda, A.I.; Loquercio, A.; Gallego, G.; García, N.; Scaramuzza, D. Event-Based Vision Meets Deep Learning on Steering Prediction for Self-Driving Cars. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5419–5427. [Google Scholar] [CrossRef]
- Mitrokhin, A.; Fermüller, C.; Parameshwara, C.; Aloimonos, Y. Event-Based Moving Object Detection and Tracking. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Lagorce, X.; Meyer, C.; Ieng, S.H.; Filliat, D.; Benosman, R. Asynchronous Event-Based Multikernel Algorithm for High-Speed Visual Features Tracking. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1710–1720. [Google Scholar] [CrossRef] [PubMed]
- Gehrig, D.; Scaramuzza, D. Low-latency automotive vision with event cameras. Nature 2024, 629, 1034–1040. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Su, M.; Zhang, Z.; Sun, L.; Yu, Y.; Qiu, W. A Novel Coded Excitation Imaging Platform for Ultra-High Frequency (>100 MHz) Ultrasound Applications. IEEE Trans. Biomed. Eng. 2025, 72, 1298–1305. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Rodriguez, L.E.; Rodriguez-Resendiz, J.; Martinez-Hernandez, M.A. An open-source FPGA-based control and data acquisition hardware platform. In Proceedings of the 2021 XVII International Engineering Congress (CONIIN), Queretaro, Mexico, 14–18 June 2021; pp. 1–11. [Google Scholar] [CrossRef]
- Vaithianathan, M.; Udkar, S.; Roy, D.; Reddy, M.; Rajasekaran, S. FPGA-Based Motor Control Systems for Industrial Automation. In Proceedings of the 2024 International Conference on Sustainable Communication Networks and Application (ICSCNA), Theni, India, 11–13 December 2024; pp. 249–254. [Google Scholar] [CrossRef]
- Lichtsteiner, P.; Posch, C.; Delbruck, T. A 128× 128 120 dB 15 μs Latency Asynchronous Temporal Contrast Vision Sensor. IEEE J. Solid-State Circuits 2008, 43, 566–576. [Google Scholar] [CrossRef]
- Carrano, M.; Koziol, S.; Chabot, E.; Boline, J.; DiCecco, J. FPGA/MATLAB Hardware in the Loop Testbed for Stochastic Artificial Neural Networks. In Proceedings of the ASEE 2021 Gulf-Southwest Annual Conference, Waco, TX, USA, 24–26 March 2021. [Google Scholar]
- Shively, S. Sampling System for Processing Event Camera Data Using a Stochastic Neural Network and Behavioral Analysis of the Binary Hyperbolic Tangent Algorithm. Master’s Thesis, Baylor University, Waco, TX, USA, 2024. [Google Scholar]
- Alaghi, A.; Hayes, J.P. Survey of Stochastic Computing. ACM Trans. Embed. Comput. Syst. 2013, 12, 1–19. [Google Scholar] [CrossRef]
- Zietz, E.; Shively, S.; Chabot, E.; DiCecco, J.; Koziol, S. Optimizing Event Camera Data Processing with Asynchronous Hold for Stochastic Neural Networks (To Be Published). In Proceedings of the 2025 IEEE 68th International Midwest Symposium on Circuits and Systems (MWSCAS), Lansing, MI, USA, 10–13 August 2025. [Google Scholar]
- Massa, R.; Marchisio, A.; Martina, M.; Shafique, M. An Efficient Spiking Neural Network for Recognizing Gestures with a DVS Camera on the Loihi Neuromorphic Processor. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–9. [Google Scholar] [CrossRef]
- Viale, A.; Marchisio, A.; Martina, M.; Masera, G.; Shafique, M. CarSNN: An Efficient Spiking Neural Network for Event-Based Autonomous Cars on the Loihi Neuromorphic Research Processor. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Bitton, A.; Duwek, H.C.; Tsur, E.E. Adaptive Attention with a Neuromorphic Hybrid Frame and Event-based Camera. In Proceedings of the 2022 IEEE 21st International Conference on Cognitive Informatics and Cognitive Computing (ICCI*CC), Toronto, ON, Canada, 8–10 December 2022; pp. 242–247. [Google Scholar] [CrossRef]
- Lee, H.; Hwang, H. Ev-ReconNet: Visual Place Recognition Using Event Camera with Spiking Neural Networks. IEEE Sens. J. 2023, 23, 20390–20399. [Google Scholar] [CrossRef]
- Cordone, L.; Miramond, B.; Ferrante, S. Learning from Event Cameras with Sparse Spiking Convolutional Neural Networks. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Barchid, S.; Mennesson, J.; Djéraba, C. Bina-Rep Event Frames: A Simple and Effective Representation for Event-Based Cameras. In Proceedings of the 2022 IEEE International Conference on Image Processing (ICIP), Bordeaux, France, 16–19 October 2022; pp. 3998–4002. [Google Scholar] [CrossRef]
- Zietz, E.; Chabot, E.; DiCecco, J.; Koziol, S. Image Recognition Using an Event Camera and a Stochastic Neural Network. In Proceedings of the 2024 IEEE 67th International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, 11–14 August 2024; pp. 113–117. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.L.; Zhou, X.L. Application and analysis of image recognition technology based on Artificial Intelligence—Machine learning algorithm as an example. In Proceedings of the 2020 International Conference on Computer Vision, Image and Deep Learning (CVIDL), Chongqing, China, 10–12 July 2020; pp. 173–176. [Google Scholar] [CrossRef]
- Gonzalez-Guerrero, P.; Guo, X.; Stan, M. SC-SD: Towards Low Power Stochastic Computing Using Sigma Delta Streams. In Proceedings of the 2018 IEEE International Conference on Rebooting Computing (ICRC), McLean, VA, USA, 7–9 November 2018; pp. 1–8. [Google Scholar] [CrossRef]
- de Aguiar, J.M.; Khatri, S.P. Exploring the viability of stochastic computing. In Proceedings of the 2015 33rd IEEE International Conference on Computer Design (ICCD), New York, NY, USA, 18–21 October 2015; pp. 391–394. [Google Scholar] [CrossRef]
- Hajduk, Z. Field-Programmable Gate Array-Based True Random Number Generator Using Capacitive Oscillators. Electronics 2024, 13, 4819. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Wang, Y.; Lombardi, F.; Han, J. A Survey of Stochastic Computing Neural Networks for Machine Learning Applications. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2809–2824. [Google Scholar] [CrossRef] [PubMed]
- Stangebye, T.; Carrano, M.; Koziol, S.; Chabot, E.; DiCecco, J. Stochastic Computing with Simulated Event Camera Data. In Proceedings of the 2021 IEEE International Midwest Symposium on Circuits and Systems (MWSCAS), Lansing, MI, USA, 9–11 August 2021; pp. 437–440. [Google Scholar] [CrossRef]
- AMD. AMD MicroBlaze Processor: A Flexible and Efficeint Soft Processor. 2024. Available online: https://www.xilinx.com/products/design-tools/microblaze.html (accessed on 29 July 2025).
- Chu, P.P. FPGA Prototyping by SystemVerilog Examples; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Digilent. Nexys 4. 2024. Available online: https://digilent.com/shop/nexys-a7-amd-artix-7-fpga-trainer-board-recommended-for-ece-curriculum/ (accessed on 29 July 2025).




| Event Data Processing Method | Neural Network Architecture(s) | Advantages |
|---|---|---|
| Time-based Frame Accumulation | Spiking NN, CNN | Preserves temporal information of event camera data |
| Quantity-based Frame Accumulation | Spiking NN, CNN | Only uses information corresponding to actual event activity |
| Bina-Rep Method | CNN | Takes order at which events are received into account |
| Sampling method described in this paper | SANN | Does not combine events from multiple timestamps into one frame, only uses information corresponding to actual event activity |
| Timestamp | X-Coordinate | Y-Coordinate |
|---|---|---|
| 2100 | 4 | 7 |
| 2100 | 13 | 2 |
| 2101 | 9 | 1 |
| 2101 | 1 | 10 |
| 2101 | 14 | 16 |
| 2104 | 5 | 12 |
| 2106 | 2 | 8 |
| Register as FF | Block RAM | Slice LUTs | Slice Registers | Slice | LUT as Logic |
|---|---|---|---|---|---|
| 853 | 32 | 870 | 853 | 327 | 870 |
| Character Sent | Initial State | 2 | 1 | 0 | 4 | t | 8 | x | 1 | 3 | y | e |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Input buffer | 0 | 2 | 21 | 210 | 2104 | 0 | 8 | 0 | 1 | 3 | 0 | 0 |
| Timestamp buffer | 0 | 0 | 0 | 0 | 0 | 2104 | 2104 | 2104 | 2104 | 2104 | 2104 | 0 |
| x buffer | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 8 | 8 | 8 | 0 |
| y buffer | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 0 |
| Timestamp register | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2104 |
| x register | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 |
| y register | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 |
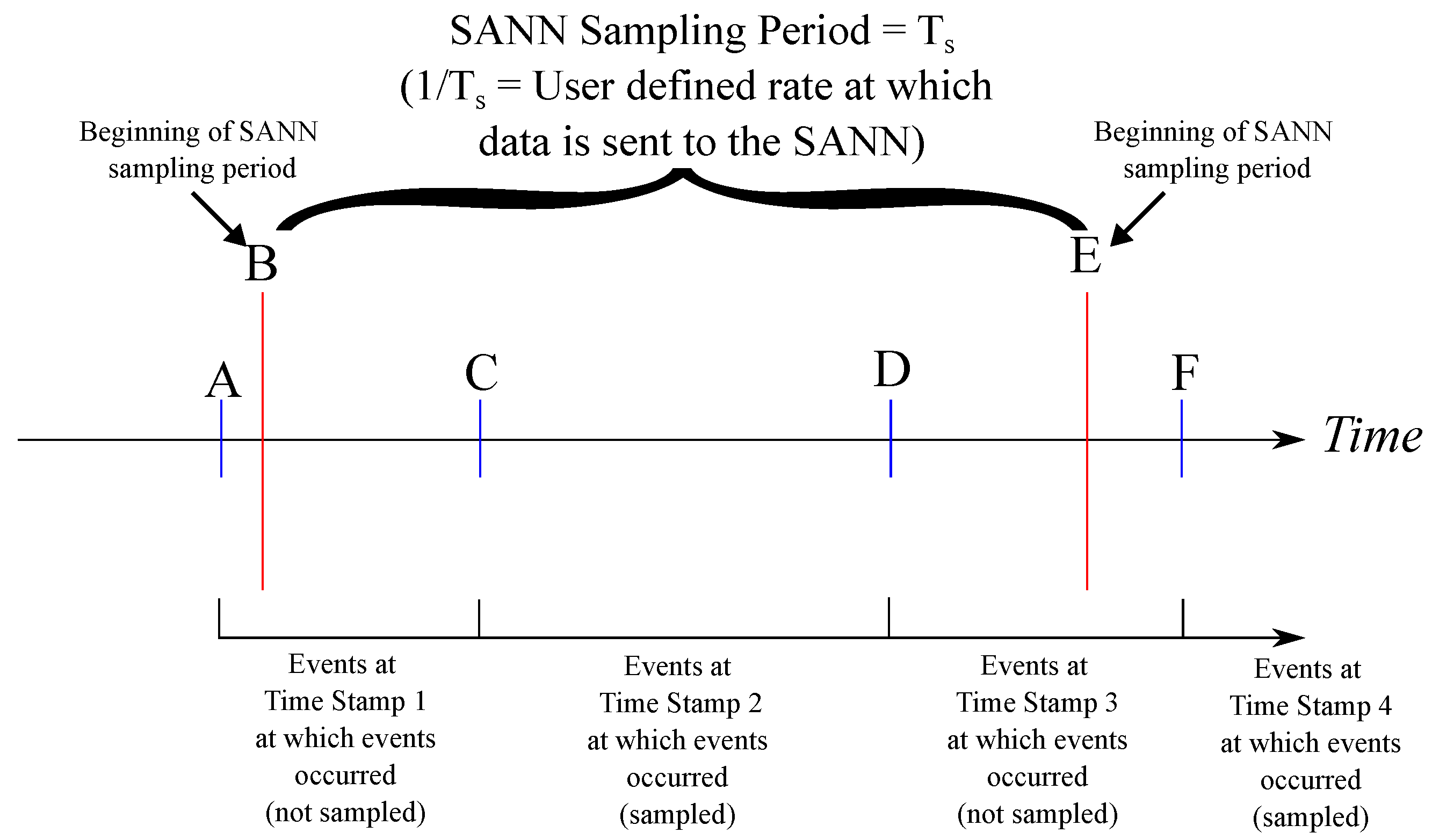
| Point on Figure 7 | Actions |
|---|---|
| A | First event at timestamp 1 received. Events at this timestamp will not be sampled. |
| B | Beginning of sampling period. sampled_timestamp is set to zero at this time, to alert the system that the next new timestamp should be sampled |
| C | First event at timestamp 2 received, events at this timestamp will be sampled. sampled_timestamp now contains the value 2, and the signal new_timestamp will equal 1 |
| D | First event at timestamp 3 received. The signal new_timestamp will become 0 at this point, as the value in ts_reg is now different from the value in sampled_timestamp (2), and events from this timestamp will not be sampled |
| E | Beginning of new sampling period. At this point, all events collected from timestamp 2 (which were converted to SANN input positions and stored to buffer register) will be written to the SANN inputs, and sampled_timestamp will be set to 0 again |
| F | First event at timestamp 3 received. This is the next timestamp to be sampled, and sampled_timestamp will now contain 3. The process will repeat again. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shively, S.; Jackson, N.; Chabot, E.; DiCecco, J.; Koziol, S. Data Sampling System for Processing Event Camera Data Using a Stochastic Neural Network on an FPGA. Electronics 2025, 14, 3094. https://doi.org/10.3390/electronics14153094
Shively S, Jackson N, Chabot E, DiCecco J, Koziol S. Data Sampling System for Processing Event Camera Data Using a Stochastic Neural Network on an FPGA. Electronics. 2025; 14(15):3094. https://doi.org/10.3390/electronics14153094
Chicago/Turabian StyleShively, Seth, Nathaniel Jackson, Eugene Chabot, John DiCecco, and Scott Koziol. 2025. "Data Sampling System for Processing Event Camera Data Using a Stochastic Neural Network on an FPGA" Electronics 14, no. 15: 3094. https://doi.org/10.3390/electronics14153094
APA StyleShively, S., Jackson, N., Chabot, E., DiCecco, J., & Koziol, S. (2025). Data Sampling System for Processing Event Camera Data Using a Stochastic Neural Network on an FPGA. Electronics, 14(15), 3094. https://doi.org/10.3390/electronics14153094






