Abstract
With the rapid technological advancements in wearable devices, motion and health management have significantly improved, enabling the measurement of various biometric data with compact equipment. Our research focuses on motion measurement but, in general, full-body motion estimation requires motion capture systems or multiple inertial sensors, making it necessary to directly measure movement itself. In this study, we propose estimating full-body posture using inverse kinematics based on trunk posture and limb-end information collected through wearable devices. To enhance estimation accuracy in this underdetermined problem, we employ Physics-Informed Neural Networks (PINNs), which efficiently learn using physical laws as a loss function, along with a high-precision inverse kinematics model of a digital human. Through this approach, we enable high-accuracy full-body posture estimation even with wearable devices in underdetermined scenarios.
1. Introduction
Advancements in wearable sensors have made it easier to measure body movements and health conditions, allowing various biometric data to be monitored using compact devices [1,2,3]. Furthermore, advancements in AI technology have made it possible to analyze these data and gain a more accurate understanding of body movements and health conditions. In particular, motion measurement plays a crucial role in various fields, including rehabilitation, sports science, and entertainment.
We have also been developing signal processing techniques and sensor fusion algorithms aimed at high-precision human motion analysis using wearable sensors [4,5]. Our research focuses on the measurement of body movements; however, full-body motion estimation generally requires a motion capture system or multiple inertial sensors, making it necessary to directly measure the movements themselves. Additionally, Inverse Kinematics (IK), a fundamental problem in robotics, can be used to estimate the angles of intermediate joints based on the position information of the end effector. However, this is an underdetermined problem, meaning multiple possible solutions may exist.
This study proposes a method for estimating full-body posture using an inverse kinematics-based estimator, leveraging torso posture and limb-end data collected from wearable devices. To improve estimation accuracy in this underdetermined problem, we incorporate Physics-Informed Neural Networks (PINNs), which efficiently learn physical laws as loss functions, along with a high-precision inverse kinematics model for digital humans. This approach enables high-accuracy full-body posture estimation using wearable devices, even in underdetermined scenarios.
The wearable sensor envisioned in this study is a neckband-type device. It functions as an IMU to detect neck and upper body posture and is also expected to acquire front-facing images of the human body via an embedded camera. A suitable example of such a sensor is the “THINKLET” developed by Fairy Devices Inc. (Bunkyo-ku, Tokyo, Japan) [6], which is compact and lightweight, making it unobtrusive even in demanding environments such as construction sites or caregiving settings. This device is capable of recording Full HD video at 30 Frames Per Second (FPS), and it can measure device orientation at a frequency of 100 Hz using its built-in IMU. Unlike motion capture systems, wearable sensors do not restrict the measurement space and can be deployed at relatively low cost—typically a few hundred dollars—allowing for simultaneous monitoring of multiple individuals.
Several prior studies have explored wearable sensors that leverage first-person visual information, such as Rogez et al.’s “First-person Pose Recognition Using Egocentric Workspaces” [7] and Deshpande et al.’s “Novel First Person View for Human 3D Pose Estimation” [8]. The former is based on depth estimation, while the latter employs YOLOv7-based pose recognition. Both approaches rely on advanced AI-based image processing techniques. From the perspective of embedded signal processing, the authors have previously developed techniques specifically tailored for wearable sensor applications [4,9,10]. Viewed from this standpoint, conventional methods pose challenges for real-time implementation and battery life constraints. To address these issues, the present study seeks to utilize a simple and implementation-friendly architecture—namely, a Multilayer Perceptron (MLP). In order to enhance both training efficiency and estimation accuracy, the approach integrates PINNs.
PINNa are increasingly being applied in various fields where traditional analysis has been conducted using differential equations. For example, the application of PINNs to kinematic wave theory utilizes hydrological and hydraulic physical phenomena to describe flood and traffic flow dynamics [11]. The application of neural network-based IK solutions has been widely explored in the robotics field [12,13,14]. Additionally, there are examples of neural IK methods being used for human motion analysis [15], but the fusion with PINNs remains a relatively unexplored research area.
The scope of this study is illustrated in Figure 1. As illustrated in the figure, this study focuses on inverse kinematics within the broader field of kinematics, aiming to develop an appropriate posture estimation model that enables more human-like posture representation. In this study, the 3D spatial position of the end-effector, which is used as input, is treated as a measurable quantity. This assumes hand recognition is performed using a first-person camera mounted on a wearable device. The approach is based on Google Research’s MediaPipe [16] and is being developed as a separate study within this project.
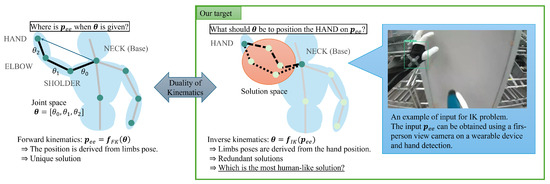
Figure 1.
Overview of the research target. By using a known 3D hand position, incorporating human structural characteristics through PINNs, and representing nonlinear IK with a MLP, this study aims to achieve high-precision full-body posture estimation with minimal input data.
2. Methods
2.1. Concept of High-Precision Posture Estimation from Limited Information
The proposed system consists of three main components: wearable sensors, a digital human model, and a PINN. The wearable sensors are used to collect base posture and limb-end position data from the subject. The wearable sensor in this setup is assumed to incorporate an IMU and a first-person view camera. The IMU measures the orientation of the coordinate system, while the first-person view camera captures the end-effector position using tools such as MediaPipe Hand Detector. The digital human model serves as a high-precision inverse kinematics model to estimate possible full-body postures based on the collected data. The PINN incorporates physical constraints into its training process, allowing it to refine the estimated postures by learning from both the sensor data and the underlying physics. The system overview is illustrated in Figure 2.
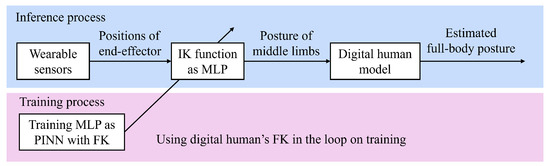
Figure 2.
Overview of the proposed system for full-body posture estimation. The system integrates wearable sensors, a digital human model, and a PINN to achieve accurate posture estimation from torso and limb-end data.
The following subsections describe the details of the IK network designed in this study, the application of the PINN to the IK network, and the utilization of the digital human model, proposing a method to achieve high-accuracy full-body posture estimation even with small data.
2.2. Inverse Kinematics Network (IK-N) Based on MLP
IK is a mathematical process used to determine the joint angles of a robotic arm or a digital human model based on the desired position of the end effector (e.g., hand or foot). In this study, we utilize an MLP network to perform IK calculations. The MLP takes as input the torso posture and limb-end positions and outputs the estimated joint angles for the full-body posture.
Typically, IK is defined in the field of robotics as a problem of determining the end-effector position and joint angles based on the robot’s geometric constraints, as suggested by the term “kinematics.” This can be formulated as follows:
Here, represents the postures of middle-limbs, is the inverse kinematics function, and is the end-effector position. In the case of simple joint structures like those in robots, can be analytically determined. However, for complex joint structures, such as those found in the human body, analytical solutions become challenging. Therefore, we consider approximating this function using machine learning techniques. Additionally, one of the advantages of using machine learning is that it can exclude infeasible solutions among redundant solutions by using an appropriate dataset. In this study, is represented using a 4-layer MLP, where each layer has 32 dimensions, as shown in Figure 3. The network size was experimentally determined to obtain appropriate outputs. As this study focuses on conceptual validation of the proposed approach, the hyperparameters have not yet been fully optimized. In anticipation of future embedded implementation—where techniques such as model distillation and pruning may be applied—the current settings were chosen to provide the MLP with a minimal level of nonlinear expressive power required for the task.
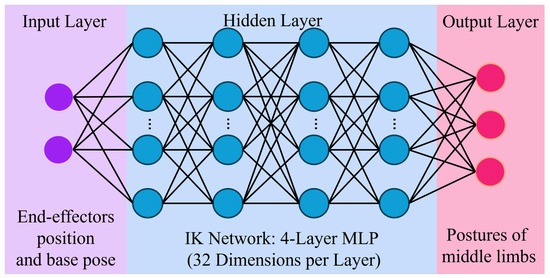
Figure 3.
Overview of the Inverse Kinematics Network (IK-N) based on MLP. The MLP takes torso posture and limb-end positions as input and outputs estimated joint angles for full-body posture estimation.
Potential IK network candidates include more complex Deep Neural Networks (DNNs) [17,18,19], as well as the integration of Recurrent Neural Networks (RNNs) [20,21] and Transformer models [22] for representing motion. However, as mentioned earlier, this study aims to develop technology that can be integrated into wearable devices. Therefore, a simple network architecture using MLP is adopted to balance the expressive power of nonlinear mappings in neural networks with computational cost. By incorporating physical laws using the PINN described later, we confirm that even MLP has sufficient expressive power for IK.
The MLP is trained using a dataset of known joint angles and corresponding end effector positions, allowing it to learn the mapping between these inputs and outputs. The network architecture consists of multiple hidden layers with activation functions such as ReLU or tanh, enabling it to capture complex relationships in the data. The output layer provides the estimated joint angles, which can then be used to reconstruct the full-body posture of the digital human model.
2.3. Physics-Informed Neural Networks for IK Network Refinement
PINNs are a type of neural network that incorporate physical laws into the training process. They are designed to solve Partial Differential Equations (PDEs) and other physics-based problems by embedding the governing equations as constraints in the loss function. This allows the network to learn not only from data but also from the underlying physics, leading to more accurate and robust predictions.
In this study, we use PINNs to refine the estimated full-body postures obtained from the inverse kinematics model. The PINN is trained using both the sensor data and physical constraints, such as joint limits, dynamics, and kinematic consistency. The loss function of the PINN includes terms that penalize deviations from these physical constraints, ensuring that the estimated postures are not only accurate but also physically plausible. By combining the predictions of the IK model with the PINN, we achieve high-accuracy full-body posture estimation even in underdetermined scenarios.
The training scheme of the PINN is illustrated in Figure 4.
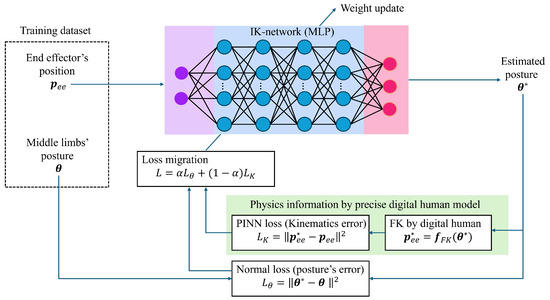
Figure 4.
PINN training scheme. Physics information is obtained by the precise digital human model and the effect of the PINN is controlled by the parameter . This scheme not only minimizes posture error but also efficiently achieves human-like movement.
The MLP is designed to learn to estimate joint angles from torso posture and limb-end positions through standard supervised learning. The loss function at this stage is set to minimize the Mean Squared Error (MSE) between the estimated joint angles and the actual joint angles.
where is the actual joint angles, is the estimated joint angles, and N is the estimatid middle-limbs. However, this alone does not guarantee that the estimated postures will be physically plausible, as the IK problem is underdetermined and may yield multiple solutions. Therefore, it is necessary to learn the physical constraints using PINNs.
In the PINN training process, we incorporate physical constraints into the loss function. The PINN’s loss function is defined as follows:
where is the actual end-effector position, is the estimated end-effector position obtained from the forward kinematics function using the precise digital human model, and M is the number of end-effectors.
The final loss function of the PINN is defined as a weighted combination of the two loss functions:
where is a hyperparameter that controls the balance between the two loss functions. This hyperparameter allows us to adjust the influence of the physical constraints on the training process, enabling the network to learn both the mapping from torso posture and limb-end positions to joint angles and the physical laws governing human-like motion. If is close to 0, the influence of physical constraints becomes strong, and the estimated postures are physically plausible. Conversely, if is close to 1, the influence of physical constraints weakens, and the estimated postures are based more on the sensor data.
2.4. Digital Human Model for In-the-Loop IK-N Training
Digital human models are systems used to analyze human body shapes and movements in conjunction with motion capture systems. It provides a detailed and accurate representation of human anatomy, including joint structures, muscle dynamics, and kinematic constraints. In this study, we employ DhaibaWorks [23], a high-precision digital human model that allows for accurate inverse kinematics calculations. This model serves as the basis for estimating full-body posture from the data collected by wearable devices. Therefore, by passing through a digital human model rather than simply using the estimated body segment data obtained from skin surface markers measured through motion capture, we can acquire more natural and appropriate posture and movement. This approach takes into account the internal variations in joint centers and the range of motion occurring within the human body. Thus, rather than relying solely on estimated body segment data derived from skin-surface marker information captured via motion capture, incorporating a digital human model enables more accurate and human-like posture and movement. This approach accounts for internal joint center variations and the range of motion occurring within the body. Specifically, the joint angles required for PINN are obtained using a digital human model. This means that the solution space of IK-N, implemented via an MLP, is constrained by joint angles that are both feasible and appropriate for human motion.
The accuracy of the digital human model used in this study has been investigated in prior research. The model employed in DhaibaWorks can estimate full-body dimensions based on a limited number of anthropometric inputs. For the upper limb, which is the focus of this study, the estimation error is approximately 3%, demonstrating highly precise calibration capabilities [24]. This level of accuracy is particularly significant in multi-degree-of-freedom and redundant human body measurements. As a result, the impact of error introduced by the digital human model on overall system angle estimation remains minimal. From the perspective of anthropometric analysis, the constraints imposed by the digital human model help yield the most probable solution consistent with human anatomical limitations.
The digital human model is integrated into the PINN training process shown in Figure 5, allowing the network to learn from both the sensor data and the physical constraints imposed by the model. The realization of such a system is made possible by the non-proprietary nature of the DhaibaWorks digital human model developed by the co-authors, which allows for flexible customization.
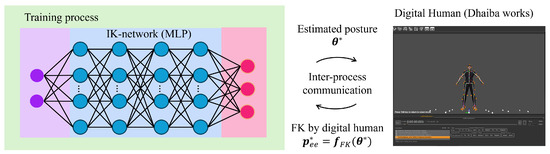
Figure 5.
Digital Human Model (DhaibaWorks) for in-the-loop IK-N training. The digital human model can be integrated into the MLP training system as a set of physical laws representing human-like motion, enabling in-the-loop training. For more details on DhaibaWorks, please refer to [23].
This allows for the visualization of the final estimated results, providing insights into the accuracy and physical plausibility of the estimated full-body postures. In the next section, we conduct experiments to verify the accuracy improvement achieved by PINN and visualize the estimation results using the digital human model.
3. Results
Here, we present experimental results to verify the effectiveness of the proposed method. The experiments aim to evaluate the accuracy improvement of the IK-N using PINNs and visualize the estimation results using a digital human model. Therefore, by adjusting the parameter , we control the effectiveness of PINN and examine the impact of incorporating physical laws.
3.1. Validation Experiment of IK-N Using Simple Motions
As a preliminary step, we verify that the proposed method functions as an inverse kinematics solution through experiments involving simple motions. We conducted repeated trials of a simple motion in which the hand moves back and forth in front of the body. This setup assumes that the fingertips are clearly visible in the first-person perspective camera of the wearable sensor. Furthermore, by focusing on linear hand movements, the relevant joint motion is limited to the elbow, thereby simplifying the evaluation process.
For concept validation, we use fingertip position data obtained from a motion capture system as input. To further validate generalization performance, experiments were conducted using a different subject from the one whose data were used for training the IK-N model.
We focus on evaluating the estimated motion of the right elbow as a representative example. The results estimated by the proposed method are shown in Figure 6.
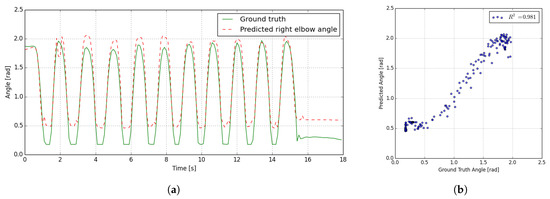
Figure 6.
Example of estimating simple extension motion of the right elbow joint: (a) Time-series data of ground truth and estimated values. (b) Correlation plot of ground truth and estimated values.
The experimental results demonstrate that the flexion and extension of the elbow are accurately estimated without any issues. The correlation plot further confirms the high estimation accuracy, with a coefficient of determination of .
The estimation accuracy is lower when the elbow is fully flexed, i.e., at small joint angles. This is attributed to the absence of such extreme flexion cases in the training data. As this study represents a conceptual proposal, the collection of additional training data for further accuracy improvement remains a topic for future work.
3.2. Generalizability to Diverse Motions and Design Hyperparameters of the PINN Loss Function
In this section, we evaluate the inference capability of the model, not on the simple motions verified during baseline experiments but on more complex movements representative of typical human activities. When introducing new loss components as part of the PINN framework, it is necessary to determine the relative weight of the PINN loss in the overall training process, which constitutes a hyperparameter. We conduct training using multiple configurations of this hyperparameter and analyze its influence empirically.
The motion addressed in this section simulates the act of driving screws into a wall using an impact driver. The motion data were recorded using the wearable sensor THINKLET, which serves as the target device in this study, while ground-truth measurements were obtained using the OptiTrack motion capture system Ptime41. To evaluate generalization performance, we conducted experiments with a different subject than the one used in the previous section’s simple motion tests.
The hyperparameters for training are set as follows: is set to 0.0, 0.5, 0.99, and 1.0; the learning rate is set to 0.001; and the number of epochs is set to 50. The evaluation is conducted by observing how much the Mean Squared Error (MSE) used in each loss function decreases. The results of the experiments are shown in Figure 7.
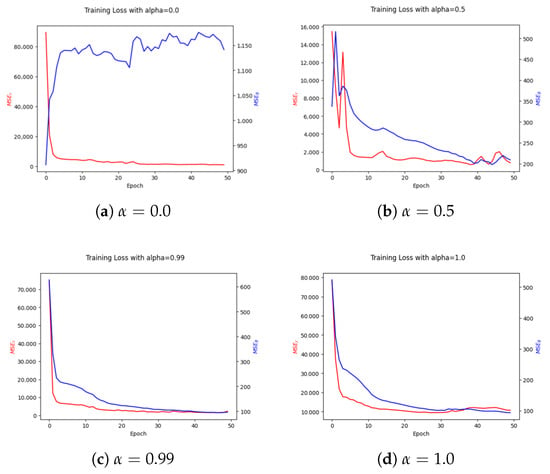
Figure 7.
Trends of loss reduction during training. The red line represents the IK-N loss function , and the blue line represents the PINN loss function . The effect of PINN varies according to the value of . In (a), where kinematics is not considered, does not decrease at all. In (b), with , the kinematic results are improved by PINN. In (c,d), with and , respectively, it is observed that convergence is faster with , which considers position errors, than with , which does not consider position errors at all.
The results show that the loss function of the IK-N decreases significantly, indicating that the MLP is effectively learning to estimate joint angles from torso posture and limb-end positions. The PINN loss function also decreases, especially when is set to 0.5 or 0.99, indicating that the physical constraints are being effectively incorporated into the training process. In the case of , the PINN does not contribute to the loss reduction, as it does not consider physical constraints. In contrast, when , the PINN focuses solely on the kinematics error, leading to a slower convergence compared to . This suggests that a balanced approach, such as or , is more effective in achieving accurate full-body posture estimation.
The estimated full-body postures are visualized using the digital human model, as shown in Figure 8 and Figure 9. The green and red bodies illustrate the true and estimated values, respectively.
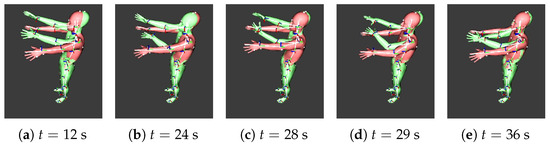
Figure 8.
The experimental results of IK-N without PINN (). The green and red bodies represent the true and estimated poses, respectively. The parameter t indicates the elapsed time in the experiment. Without PINN, the overall hand position error is significantly larger.
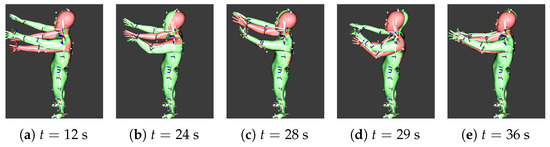
Figure 9.
The experimental results of IK-N using PINN (). The green and red bodies represent the true and estimated poses, respectively. The parameter t corresponds to the same timing as in Figure 8. By utilizing PINN, the estimation accuracy of the elbow joint has improved, leading to a highly precise reconstruction of the hand position.
In Figure 8, where , the estimated posture shows significant misalignment of the hands, indicating that the IK-N alone is not sufficient to achieve accurate full-body posture estimation without considering physical constraints.
In contrast, in Figure 9, where , the estimated posture is much closer to the true posture, demonstrating that the incorporation of physical laws through PINN significantly improves the end-effector position error. This indicates that the proposed method effectively estimates full-body postures from torso and limb-end data, achieving high accuracy and physical consistency.
The overall average estimation error from this experiment is presented in Figure 10. The estimation error was normalized based on the maximum value of the motion and compared accordingly. The resulting error rates were 17.3% without PINN and 9.8% with PINN, demonstrating a 7.5-point improvement through the introduction of PINN.
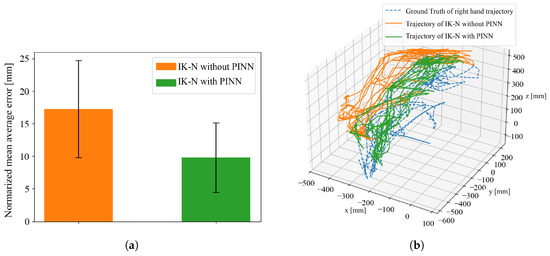
Figure 10.
Comparison of mean average error between IK-N model with and without PINN. (a) The normalized mean errors and their corresponding standard deviations. (b) Each right-hand trajectory used in this analysis.
The results of the experiments confirm that the proposed method, which combines inverse kinematics with PINNs, effectively improves the accuracy of full-body posture estimation.
4. Discussion
4.1. Synergistic Integration of MLP and PINN for Efficient Posture Estimation
We adopted an MLP architecture for our network design based on several key considerations. First, from the perspective of embedded system deployment, MLPs are significantly easier to implement on wearable sensors than other network types, and their inference requires lower computational cost. Second, since the network is trained using human motion data, which involves relatively high data collection costs, it is crucial that the model can learn effectively from limited data. Third, because PINNs incorporate complex physical phenomena into the loss function during training, the network itself does not require sophisticated feature extraction capabilities. It is sufficient that the model has enough expressive power to capture nonlinear dynamics.
These requirements are well addressed by using an MLP. Although the MLP is a classical network architecture, it continues to be utilized in modern developments such as the MLP-Mixer [25]. Despite its simple structure, it can serve as a highly versatile model when applied appropriately. This chapter discusses its particularly favorable compatibility with PINNs.
While recent architectures such as CNNs and Transformers can learn IK even without incorporating PINNs, they typically require deeply trained feature extraction layers to model unknown phenomena, followed by the training of inference modules. Consequently, such models must search over vast solution spaces, demanding complex architectures and large-scale datasets. In contrast, while MLPs do not possess advanced feature extraction capabilities, they offer sufficient nonlinear inference capacity. On their own, this may not be adequate; however, when paired with PINNs the physical constraints encoded in the loss function compensate for the lack of complex feature extraction by narrowing the solution space. Thus, meaningful results can be achieved without a deep network structure. Moreover, MLPs offer advantages in terms of architectural simplicity and the ability to learn from limited data, making them particularly favorable for deployment on wearable devices and for situations where motion data collection is costly and constrained.
To illustrate the advantages of using an MLP in the problem setting proposed in this study, we begin with a simplified example. Ultimately, the IK problem can be reduced to determining joint angles relative to a reference coordinate system, given known link lengths and the positional relationship between the origin and the end-effector. We use the function as an example of the type of nonlinearity involved in this learning task.
Figure 11 presents the experimental results of learning this mapping using three network architectures: MLP, DNN, and Transformer. The corresponding learning curves and training costs are presented in Figure 12. These experiments were conducted using an Core i9-10920X @ 3.50 GHz (Intel Corporation, Santa Clara, CA, U.S.) and an Quadro RTX5000 (NVIDIA Corporation, Santa Clara, CA, U.S.).
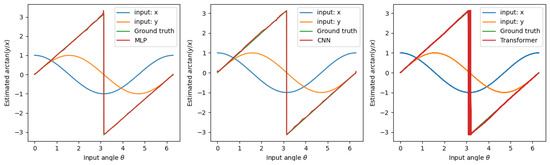
Figure 11.
Comparison of simple angle estimation problem using MLP, CNN, and Transformer architectures. Despite its simplicity, MLP demonstrates comparable expressive power for nonlinear phenomena relative to more complex inference models. Due to its sequence-based learning mechanism, the Transformer requires approximately ten times more data to stably represent discontinuities.
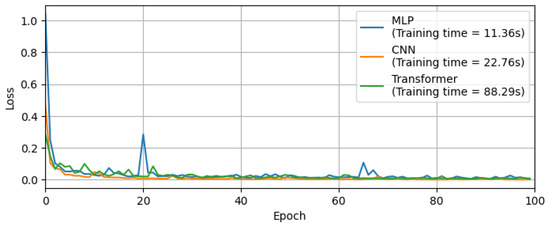
Figure 12.
Learning curves and training time for simple angle estimation using MLP, CNN, and Transformer architectures. The MLP achieves training speeds approximately twice as fast as CNN and eight times faster than Transformer, while maintaining sufficient nonlinear expressive power for effective implementation within the PINN framework.
In this simplified problem setting, all three architectures—MLP, DNN, and Transformer—converge within approximately 20 epochs. However, the training time per epoch differs significantly: the MLP requires only 0.11 s per epoch, while the Transformer takes 0.88 s. Thus, the MLP demonstrates roughly eight times faster training speed.
This outcome is consistent with widely recognized understanding: CNNs and Transformers generally possess strong inference capabilities, while MLPs—with their simpler architecture—can learn efficiently even from limited data and exhibit faster training speed.
In conclusion, since PINNs are employed in this IK learning approach, the goal is not to extract governing physical laws of unknown phenomena from large-scale data. Instead, it is to transfer the physics defined in the loss function directly into the network, ensuring reproducibility. Accordingly, the key requirement is to adequately represent the nonlinearity inherent in inverse kinematics, which can be sufficiently achieved using an MLP (a simple form of DNN) within the PINN framework.
In summary, the following points highlight the advantages of using MLP and PINN:
- Simple Architecture: Since the goal is to deploy the model on wearable systems, a simple structure is desirable for embedded implementation.
- Small-Data Learning: Given that the target domain is human motion, data collection is costly; the combination of PINN and MLP enables effective learning with limited data.
- Sufficient nonlinear representation capacity: The MLP possesses sufficient nonlinear expressive power for effective integration with PINNs.
4.2. Analysis of the Mechanism of Estimation Accuracy Improvement
In this section, we analyze the mechanism of estimation accuracy improvement achieved by the proposed method. The proposed method combines inverse kinematics with PINNs to estimate full-body postures from torso and limb-end data. In typical robotic systems with clearly defined joint structures, IK can be solved analytically. However, in the case of human bodies, the joint structures are highly complex. This not only makes it difficult to solve IK analytically but also introduces degrees of freedom that cannot be fully represented, such as in the shoulder joint. In fact, the shoulder joint is highly variable depending on the movement of the scapula and the position of the arm, making it a very challenging problem that has been extensively studied in the literature [26,27,28]. In recent years, dedicated IK models for shoulder joints have also been proposed, highlighting the complexity of this challenge [29]. Therefore, the IK problem in human bodies is often underdetermined, meaning that there are multiple possible solutions for a given set of end-effector positions.
In such a problem setting, the combination of machine learning methods that allow for nonlinearity and PINNs that can constrain the solution space to the vicinity of “human-like motion” is effective. This is because the joint structures of the human body have redundant degrees of freedom and are very complex from the perspective of anatomical structure. However, from the perspective of human motion, the solution space is constrained to some extent, and PINNs can learn such physical constraints. This allows the model trained with a high-precision digital human model to learn efficiently in about 50 epochs and enables it to perform maximum likelihood estimation of human-like motion.
4.3. Advantages and Limitations of Proposed Method
In this study, we proposed a method for estimating full-body posture using inverse kinematics based on torso posture and limb-end data collected from wearable devices. By incorporating PINNs and a high-precision digital human model, we achieved high-accuracy full-body posture estimation even in underdetermined scenarios. The results demonstrated the effectiveness of the proposed method, showing significant improvements in accuracy and physical consistency compared to baseline methods. The proposed method has several advantages over traditional approaches. First, it can handle underdetermined scenarios where the number of sensors is limited, making it suitable for wearable devices. Second, by using PINNs, the method can incorporate physical laws into the estimation process, leading to more accurate and physically plausible results. Third, the use of a digital human model allows for the visualization of the estimated postures, providing insights into the accuracy and physical plausibility of the results.
However, there are some limitations to the proposed method. First, the method relies on the accuracy of the digital human model, which may not perfectly represent all individuals. Second, the method requires a sufficient amount of training data to learn the mapping between torso posture, limb-end positions, and joint angles. Third, the computational cost of training the PINN may be high, especially for complex digital human models. Future work will focus on addressing these limitations and exploring the practical applications of the proposed method in various fields, such as healthcare, sports, and virtual reality. The proposed method has the potential to revolutionize the way we estimate and analyze human postures, enabling more accurate and efficient applications in various domains.
5. Conclusions
In this study, we proposed a method for estimating full-body posture using inverse kinematics based on torso posture and limb-end data collected from wearable devices. By incorporating PINNs and a high-precision digital human model, we achieved high-accuracy full-body posture estimation even in underdetermined scenarios. The results demonstrated the effectiveness of the proposed method, showing significant improvements in accuracy and physical consistency compared to baseline methods. The proposed method has several advantages over traditional approaches, including the ability to handle underdetermined scenarios, incorporate physical laws into the estimation process, and visualize the estimated postures using a digital human model. However, there are some limitations to the proposed method, including reliance on the accuracy of the digital human model, the need for sufficient training data, and the potential high computational cost of training the PINN. Future work will focus on addressing these limitations and exploring the practical applications of the proposed method in various fields, such as healthcare, sports, and virtual reality. The proposed method has the potential to revolutionize the way we estimate and analyze human postures, enabling more accurate and efficient applications in various domains.
Furthermore, we aim to integrate the system into wearable sensors not only by incorporating kinematic constraints into the PINN loss function, but also by adding dynamic constraints. Techniques such as hyperparameter tuning, model distillation, and pruning are applied to enhance efficiency. Since the chosen network is an MLP, the feasibility of embedded implementation is exceptionally high, and we seek to demonstrate the practical utility of a PINN–MLP-embedded system.
Author Contributions
Conceptualization, Y.H., T.K. and T.T.; data curation, N.S. and N.Y.; formal analysis, Y.H.; investigation, Y.H.; methodology, Y.H., T.K. and T.T.; project administration, Y.D.; software, Y.H.; supervision, T.T., Y.T., Y.D., Y.E., M.T. and N.M.; validation, Y.H., T.K. and T.T.; visualization, Y.H. and T.K.; writing—original draft, T.K.; writing—review & editing, T.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author (privacy and ethical restrictions).
Acknowledgments
We sincerely appreciate the invaluable guidance and support provided by Ixchel G. Ramirez-Alpizar and Enrique Coronado throughout this research. Their insightful feedback and encouragement greatly contributed to the development of this study.
Conflicts of Interest
Author Yoshifumi Tanaka was employed by the company TAISEI Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Ometov, A.; Shubina, V.; Klus, L.; Skibińska, J.; Saafi, S.; Pascacio, P.; Flueratoru, L.; Gaibor, D.Q.; Chukhno, N.; Chukhno, O.; et al. A Survey on Wearable Technology: History, State-of-the-Art and Current Challenges. Comput. Netw. 2021, 193, 108074. [Google Scholar] [CrossRef]
- Gomes, N.; Pato, M.; Lourenço, A.R.; Datia, N. A Survey on Wearable Sensors for Mental Health Monitoring. Sensors 2023, 23, 1330. [Google Scholar] [CrossRef] [PubMed]
- Alattar, A.E.; Mohsen, S. A Survey on Smart Wearable Devices for Healthcare Applications. Wirel. Pers. Commun. 2023, 132, 775–783. [Google Scholar] [CrossRef]
- Kusaka, T.; Tanaka, T. Stateful Rotor for Continuity of Quaternion and Fast Sensor Fusion Algorithm Using 9-Axis Sensors. Sensors 2022, 22, 7989. [Google Scholar] [CrossRef] [PubMed]
- Kitaura, K.; Kusaka, T.; Shimatani, K.; Tanaka, T. Stabilization of Signal Decomposition Based on Frequency Entrainment Phenomena. Electronics 2025, 14, 1163. [Google Scholar] [CrossRef]
- THINKLET®|Fairy Devices. Available online: https://mimi.fairydevices.jp/technology/device/thinklet/en/ (accessed on 20 July 2025).
- Rogez, G.; Supancic, J.S.; Ramanan, D. First-person pose recognition using egocentric workspaces. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar] [CrossRef]
- Deshpande, K.; Heindl, C.; Stübl, G.; Kollingbaum, M.J.; Pichler, A. Novel First Person View for Human 3D Pose Estimation in Robotic Applications Using Fisheye Cameras. In Proceedings of the 2024 10th International Conference on Automation, Robotics and Applications (ICARA), Athens, Greece, 22–24 February 2024; pp. 112–116, ISSN 2767-7745. [Google Scholar] [CrossRef]
- Kusaka, T.; Tanaka, T. Fast and Accurate Approximation Methods for Trigonometric and Arctangent Calculations for Low-Performance Computers. Electronics 2022, 11, 2285. [Google Scholar] [CrossRef]
- Kusaka, T.; Tanaka, T. Pseudo-Normalization via Integer Fast Inverse Square Root and Its Application to Fast Computation without Division. Electronics 2024, 13, 2955. [Google Scholar] [CrossRef]
- Hou, Q.; Li, Y.; Singh, V.P.; Sun, Z.; Wei, J. Physics-informed neural network for solution of forward and inverse kinematic wave problems. J. Hydrol. 2024, 633, 130934. [Google Scholar] [CrossRef]
- Bensadoun, R.; Gur, S.; Blau, N.; Shenkar, T.; Wolf, L. Neural Inverse Kinematics. arXiv 2022, arXiv:2205.10837. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Zou, T.; Jiang, X. A Neural Network Based Approach to Inverse Kinematics Problem for General Six-Axis Robots. Sensors 2022, 22, 8909. [Google Scholar] [CrossRef] [PubMed]
- Hamarsheh, Q.; Baniyounis, M.; Biesenbach, R.; Jernaz, M. An Artificial Neural Network Approach in Solving Inverse Kinematics of a 6 DOF KUKA Industrial Robot. In Proceedings of the 2023 20th International Multi-Conference on Systems, Signals & Devices (SSD), Mahdia, Tunisia, 20–23 February 2023; pp. 157–163, ISSN 2474-0446. [Google Scholar] [CrossRef]
- Korol, A.; Rodzin, T.; Zabava, K.; Gritsenko, V. Neural Networks-Based Approach to Solve Inverse Kinematics Problems for Medical Applications. In Proceedings of the 2024 46th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 15–19 July 2024. [Google Scholar]
- Zhang, F.; Bazarevsky, V.; Vakunov, A.; Tkachenka, A.; Sung, G.; Chang, C.L.; Grundmann, M. MediaPipe Hands: On-device Real-time Hand Tracking. arXiv 2020, arXiv:2006.10214. [Google Scholar] [CrossRef]
- Calzada-Garcia, A.; Victores, J.G.; Naranjo-Campos, F.J.; Balaguer, C. A Review on Inverse Kinematics, Control and Planning for Robotic Manipulators With and Without Obstacles via Deep Neural Networks. Algorithms 2025, 18, 23. [Google Scholar] [CrossRef]
- Accelerating Deep Learning Based Large-Scale Inverse Kinematics with Intel® Distribution of OpenVINO™ Toolkit. Available online: https://www.intel.com/content/www/us/en/developer/articles/technical/accelerating-deep-learning-based-large-scale-inverse-kinematics-with-intel-distribution-of.html (accessed on 30 May 2025).
- Shah, M.F.; Khan, N.A.; Jamwal, P.K.; Chetty, G.; Goecke, R.; Hussain, S. Inverse kinematics solution for a six-degree-of-freedom upper limb rehabilitation robot using deep learning models. Neural Comput. Appl. 2025, 37, 12991–13009. [Google Scholar] [CrossRef]
- Martinez, J.; Black, M.J.; Romero, J. On human motion prediction using recurrent neural networks. arXiv 2017, arXiv:1705.02445. [Google Scholar]
- Fragkiadaki, K.; Levine, S.; Felsen, P.; Malik, J. Recurrent Network Models for Human Dynamics. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4346–4354. [Google Scholar] [CrossRef]
- Alkhodary, A.; Gur, B. Kinematics Transformer: Solving The Inverse Modeling Problem of Soft Robots using Transformers. arXiv 2022, arXiv:2211.06643. [Google Scholar]
- Endo, Y.; Tada, M.; Mochimaru, M. Dhaiba: Development of Virtual Ergonomic Assessment System with Human Models. In Proceedings of the Conference: Digital Human Modeling 2014, Crete, Greece, 22–27 June 2014. [Google Scholar]
- Nohara, R.; Endo, Y.; Murai, A.; Takemura, H.; Kouchi, M.; Tada, M. Multiple regression based imputation for individualizing template human model from a small number of measured dimensions. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 2188–2193, ISSN 1558-4615. [Google Scholar] [CrossRef]
- Tolstikhin, I.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Steiner, A.; Keysers, D.; Uszkoreit, J.; et al. MLP-Mixer: An all-MLP Architecture for Vision. arXiv 2021, arXiv:2105.01601. [Google Scholar] [CrossRef]
- Mukai, T. Modeling ranges of limb motion for real-time inverse kinematics. In Proceedings of the SIGGRAPH Asia 2011 Posters, Hong Kong, China, 14 December 2011; p. 1. [Google Scholar] [CrossRef]
- Barnamehei, H.; Tabatabai Ghomsheh, F.; Safar Cherati, A.; Pouladian, M. Kinematic models evaluation of shoulder complex during the badminton overhead forehand smash task in various speed. Inform. Med. Unlocked 2021, 26, 100697. [Google Scholar] [CrossRef]
- Yang, J.J.; Feng, X.; Kim, J.H.; Xiang, Y.; Rajulu, S. Joint Coupling for Human Shoulder Complex. In Digital Human Modeling; Duffy, V.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 72–81. [Google Scholar] [CrossRef]
- Kim, Y.; Park, B.H.; Jung, K.M.; Han, J. Data-driven Shoulder Inverse Kinematics. arXiv 2016, arXiv:1612.07353. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).