Network-Aware Gaussian Mixture Models for Multi-Objective SD-WAN Controller Placement

Abstract

Software-Defined Wide Area Networks (SD-WANs) require optimal controller placement to minimize latency, balance loads, and ensure reliability across geographically distributed infrastructures. This paper introduces NA-GMM (Network-Aware Gaussian Mixture Model), a novel multi-objective optimization framework addressing key limitations in current controller placement approaches. Three principal contributions distinguish NA-GMM: (1) a hybrid distance metric that integrates geographic distance, network latency, topological cost, and link reliability through adaptive weighting, effectively capturing multi-dimensional network characteristics; (2) a modified expectation–maximization algorithm incorporating node importance-weighting to optimize controller placements for critical network elements; and (3) a robust clustering mechanism that transitions from probabilistic (soft) assignments to definitive (hard) cluster selections, ensuring optimal placement convergence. Empirical evaluations on real-world topologies demonstrate NA-GMM’s superiority, achieving up to 22.7% lower average control latency compared to benchmark approaches, maintaining near-optimal load distribution with node distribution ratios, and delivering a 12.9% throughput improvement. Furthermore, NA-GMM achieved exquisite computational efficiency, executing 68.9% faster and consuming 41.5% less memory than state of the art methods, while achieving exceptional load balancing. These findings confirm NA-GMM’s practical viability for large-scale SD-WAN deployments where real-time multi-objective optimization is essential.

1. Introduction

The proliferation of Software-Defined Wide Area Networks (SD-WANs) has dramatically reshaped enterprise networking, driven by increasing demand for flexible, scalable, and cost-effective connectivity to support distributed infrastructures, cloud services integration, and remote workforce operations [1,2]. The global SD-WAN market is forecasted to reach approximately $66.2 billion by 2031, representing a compound annual growth rate of approximately 35.94% [1]. Despite these advancements, the inherent centralized control architecture of SD-WAN introduces complex challenges, notably the controller placement problem (CPP), where suboptimal controller decisions can substantially degrade network performance—evidenced by increased control-plane latency of up to 87% and throughput degradation between 40% and 60% [3]. Empirical studies in production networks demonstrate that controller placement critically impacts end-user latency, highlighting the critical nature of optimal controller deployment [4]. Given that approximately 95% of enterprises have already deployed or plan to deploy SD-WAN for mission-critical applications, optimizing controller placement algorithms to efficiently handle multiple conflicting objectives has become essential [5].

The controller placement problem in SD-WAN embodies unique complexities that distinguish it from classical network optimization issues. SD-WAN controllers must efficiently manage geographically distributed and heterogeneous network infrastructures encompassing diverse technologies, varied administrative domains, and stringent quality of service (QoS) requirements [6]. This multidimensional challenge inherently involves balancing competing objectives: minimizing average latency conflicts with equitable load distribution, enhancing reliability through redundancy increases inter-controller communication overhead, and optimizing current traffic patterns often undermines adaptability to future network dynamics [7]. Recent empirical evaluations confirm the tangible impact of these trade-offs, with significant variance in controller-to-switch latency directly influencing application responsiveness and network reliability [8]. Additionally, the NP-hardness of the optimal CPP—formally demonstrated through reductions from the k-median problem—underscores the necessity for efficient heuristic solutions capable of producing near-optimal placements in large-scale, real-world networks [9].

Contemporary solutions to the CPP, while innovative, exhibit significant limitations when applied to large-scale SD-WAN scenarios. Advanced machine learning approaches, particularly deep reinforcement learning (DRL) methods, integrating convolutional neural networks (CNN) and long short-term memory (LSTM) architectures, have shown promise in dynamically adapting to network changes but remain computationally intensive. DRL approaches typically demand prolonged training periods and consume significantly more memory compared to classical methods, limiting their practicality [10,11]. Metaheuristic algorithms such as enhanced Particle Swarm Optimization (PSO) [12] and Genetic Algorithms (GA) [13], although proficient in exploring complex solution spaces, suffer from parameter sensitivity and convergence issues, requiring extensive iterations (500–1000) to reach stable solutions [14]. Additionally, traditional clustering techniques, including k-means and hierarchical clustering, although computationally efficient, rely heavily on simplistic distance metrics—primarily Euclidean—that fail to account adequately for real-world network conditions such as latency, reliability, topological complexity, and traffic variability, thereby resulting in suboptimal performance [15].

A critical research gap exists in the inadequate treatment of network heterogeneity and the simplistic conceptualization of distance metrics in existing CPP methodologies. Current approaches typically consider network nodes uniformly, overlooking significant empirical evidence that demonstrates a power-law distribution of network traffic, where a small fraction of nodes generates the most traffic [16]. Ignoring node criticality—importance based on traffic volume, topology, or service level requirements—leads to inefficient resource allocation and reduced performance, particularly impacting high-priority network services [17]. Moreover, the multidimensional concept of “distance” in networks—encompassing geographic separation, latency, reliability, topological costs, and administrative weights—is insufficiently modeled in contemporary approaches, which predominantly rely on simplistic geographic or hop-count metrics [18]. This oversight results in placements optimized for limited dimensions but suboptimal in practical scenarios involving diverse network characteristics.

The nature of modern SD-WAN environments further exacerbates the limitations of current controller placement strategies. Production SD-WAN deployments frequently experience network changes—daily link failures averaging 2.3%, significant traffic variations (up to 400%) between peak and off-peak hours, and continuous topology evolution due to node additions, removals, and migrations [19]. Static placement solutions, prevalent in existing methods, are unable to dynamically adapt to such changes without manual intervention, resulting in performance degradation and increased operational costs due to frequent reconfiguration and downtime [20,21]. While adaptive methodologies exist, they predominantly focus on reactive adjustments without formal convergence guarantees and neglect controller migration overhead, emphasizing the necessity for proactive, adaptive, and efficient solutions [22].

To address these critical gaps, this paper introduces the Network-Aware Gaussian Mixture Model (NA-GMM), a novel multi-objective optimization framework specifically designed for effective SD-WAN controller placement. The primary contributions of this work are as follows:

• Propose a hybrid topology-aware distance metric that integrates geographical, latency, topological, and reliability dimensions with adaptive weighting, achieving noticeable reduction in average control latency and improvement in worst-case latency compared to traditional Euclidean distance-based approaches.
• Develop an importance-weighted clustering framework using modified expectation–maximization that incorporates node heterogeneity based on traffic patterns and topological significance, resulting in near-optimal load distribution.
• Design a convergence-guaranteed optimization mechanism that achieves stable controller placement, demonstrating faster execution time and lower resources utilization while maintaining superior clustering quality.
• Establish comprehensive theoretical foundations including formal proofs of hybrid metric space properties, convergence analysis for the weighted EM algorithm showing monotonic likelihood improvement, and computational complexity characterization proving scalability suitable for large-scale deployments.
• Conduct extensive empirical validation using real-world SD-WAN topologies and Mininet emulation, demonstrating higher throughput, exceptional load balancing, and consistent performance advantages across diverse network scales and configurations.

The remainder of this paper is organized as follows. Section 2 reviews related research in SD-WAN controller placement. Section 3 formally defines the controller placement problem and details the NA-GMM methodology. Section 4 describes the experimental setup and results. Section 5 discusses practical and theoretical implications, concluding with future directions in Section 6.

2. Background and Related Work

The controller placement problem (CPP) in Software-Defined Wide Area Networks has garnered substantial research attention, with recent advances focusing on multi-objective optimization, machine learning integration, and adaptive placement strategies. This section provides a comprehensive analysis of contemporary approaches, categorizing them by methodology while identifying persistent challenges and research gaps.

2.1. Multi-Objective Optimization Approaches

Recent investigations into multi-objective controller placement have evolved beyond traditional single-metric optimization. Li et al. [23] proposed a Pareto-based multi-objective framework incorporating latency, reliability, and energy consumption, achieving improvement in overall network efficiency compared to single-objective methods. Their approach utilized adaptive weight adjustment mechanisms responding to network dynamics, though computational overhead remained problematic for large-scale deployments. Similarly, ref. [24] developed a hierarchical multi-objective optimization strategy combining local and global optimization phases, demonstrating superior scalability with the networks while maintaining near-optimal solutions.

The integration of evolutionary algorithms with multi-objective frameworks has shown particular promise. Kumar et al. [25] introduced a hybrid NSGA-III variant specifically tailored for SD-WAN, incorporating domain-specific operators that reduced convergence time compared to generic evolutionary approaches. However, their method exhibited sensitivity to initial population selection, requiring multiple runs to ensure solution stability. Complementing this work, Tan et al. [26], proposed a decomposition-based multi-objective evolutionary algorithm adaptation that explicitly considered inter-controller communication overhead, achieving balanced trade-offs between control plane latency and data plane performance.

2.2. Machine Learning and AI-Driven Approaches

The application of deep learning to controller placement has accelerated significantly, with transformer-based architectures emerging as powerful tools for capturing complex network dependencies. Hou et al. [27] pioneered the use of Graph Attention Networks (GAT) for controller placement, where attention mechanisms dynamically weighted node importance based on traffic patterns and topological features. Their approach demonstrated noticeable improvement in placement quality compared to traditional GNN architectures, though training data requirements posed deployment challenges. Building upon this foundation, S. Troia et al. [28], integrated temporal graph neural networks with reinforcement learning, enabling adaptive controller placement that responded to traffic variations with sub-second decision latency.

Ref. [29] introduces ARMS, a machine learning-driven framework for automated resource management in SD-WANs, addressing the virtual network embedding problem with QoS guarantees. It also pioneers privacy-preserving multi-domain collaboration via vertical federated learning, demonstrating promising initial performance. Additionally, Fu et al. [30], presents SD-VPN, an innovative SDN-based overlay solution that refactors traditional VPNs for enhanced programmability, automatic deployment, and extensibility in WANs. Its validated performance demonstrates efficient control, real-time programmability, and scalable integration with diverse VPN protocols and services.

2.3. Clustering-Based Methodologies

Contemporary clustering approaches have evolved beyond traditional k-means and hierarchical methods. Ref. [31] introduced density-peak clustering (DP) variants adapted for network topologies, automatically determining optimal controller numbers based on network density patterns. Their approach eliminated the need for predetermined k values, achieving better load balancing compared to fixed-k methods, such affinity propagation (AP). However, parameter sensitivity in sparse network regions limited practical applicability. Addressing these limitations, ref. [32] proposed adaptive spectral clustering incorporating edge weights derived from multiple network metrics, demonstrating robust performance across heterogeneous topologies with varying density distributions.

The integration of fuzzy clustering with network-specific constraints has yielded promising results. Thalapala in [33] developed a possibilistic c-means variant that handled uncertainty in node assignments, which is particularly beneficial for border nodes serving multiple administrative domains. Their fuzzy membership functions incorporated latency variance and link reliability statistics, improving placement stability by 28% under dynamic conditions. Complementing this work, Sharma et al. [34] introduced hierarchical fuzzy clustering that operated at multiple network granularities, enabling flexible controller deployment strategies aligned with organizational structures.

2.4. Distance Metrics and Network-Aware Approaches

The evolution of distance metrics beyond simple geographical or hop-count measures represents a critical advancement. Ref. [35] proposed a comprehensive distance framework integrating SDN dimensions including bandwidth availability, queuing delays, and energy consumption profiles. While theoretically sound, the high-dimensional nature complicated practical optimization, requiring dimensionality reduction techniques that potentially discard relevant information. More pragmatically, Abdi Seyedkolaei [36] developed an adaptive distance metric that dynamically adjusted component weights based on network state, achieving 19% improvement in placement quality while maintaining computational tractability.

Recent work has emphasized the importance of asymmetric distance considerations. Xu et al. [37], demonstrated that traditional symmetric distance assumptions failed to capture directional network characteristics such as asymmetric routing policies and unidirectional link failures. Their asymmetric distance model improved controller placement accuracy in networks with significant traffic asymmetry. Building on this insight, Ramya et al. [38] incorporated time-varying distance components reflecting diurnal traffic patterns, though the increased computational complexity limited real-time applicability.

2.5. Reliability and Fault Tolerance Considerations

Recent research has increasingly emphasized the reliability aspects of controller placement. D. M. Nicol and R. Kumar [39] proposed a fault-tolerant placement framework that maintained k-connectivity between controllers and switches, ensuring continued operation despite simultaneous k-1 failures. Their approach achieved high availability in production deployments, though it increased deployment cost. Complementing this work, Suzuki and Yamamoto [40] developed probabilistic reliability models incorporating correlated failures, demonstrating that geographically diverse controller placement improved reliability compared to proximity-based strategies.

2.6. Performance Evaluation and Benchmarking

Standardized evaluation frameworks have emerged to enable meaningful algorithm comparison. In ref. [41], authors present a comprehensive benchmarking suite incorporating real-world scenarios and standardized traffic generators, revealing significant performance variations in existing algorithms across different network scales. Their work established baseline performance metrics adopted by subsequent research, though the computational cost of comprehensive evaluation limited adoption. Addressing this limitation, Choumas et al. [42] proposed a statistical sampling framework that achieved confidence in performance rankings using evaluation computational cost.

2.7. Research Gaps and Open Challenges

Despite significant advances, several critical gaps persist in current controller placement research. The integration of edge computing paradigms with SD-WAN controller placement remains largely unexplored, with only preliminary work by [43] examining edge-controller co-placement strategies. Security considerations regarding controller placement have received insufficient attention, though [44] demonstrated that security-aware placement could reduce attack surfaces with minimal performance impact. Furthermore, the environmental sustainability of controller placement decisions, particularly regarding energy consumption and carbon footprint optimization, represents an emerging concern that is inadequately addressed by current approaches. The surveyed literature reveals a clear evolution towards sophisticated, multi-dimensional approaches to SD-WAN controller placement [45]. However, the complexity of the proposed solutions often impedes practical deployment, highlighting the need for methods that balance theoretical optimality with operational feasibility. The proposed NA-GMM algorithm addresses these gaps by providing a computationally efficient framework that integrates multiple optimization objectives while maintaining deployment simplicity.

Table 1 compares NA-GMM with the recent approaches (2023–2024) most relevant to multi-objective controller placement, highlighting their methods, limitations, and performance gaps.

Table 1. The Recent Literature Most Relevant to the Proposed Framework.

Ref.	Authors and Year	Method	Distance Metric	Problem Statement	Objectives	Limitations	Gaps
[25]	Oladipupo Adekoya and Adel Aneiba (2022)	Adapted NSGA-III with Repair-Based Operator for multi-objective optimization	-	Scalability and diversity challenges in multi-objective controller placement (more than 3 objectives)	Solve scalability for >3 objectives, achieve diverse and convergent Pareto fronts for controller placement	Computational complexity; tested on limited topology (Internet2 OS3E); dynamic adaptation limited	Real-time traffic-aware dynamic placement not addressed; needs integration with network dynamics
[31]	Sminesh et al. (2019)	Modified Density Peak (DP) Clustering, Modified Affinity Propagation, Hierarchical k-means	Haversine	High computation in multi-objective placement; clustering approaches need predefined cluster numbers	Adaptive clustering to decide number and placement of controllers minimizing latency, load imbalance	Some methods require predefined cluster counts; static placement ignoring traffic variations	Lack of real-time traffic-aware placement; limited dynamic network support
[38]	Ramya and Manoharan (2022)	Traffic-aware dynamic placement using ML prediction + K-Medoid clustering	Euclidean	Static controller placement unsuitable for traffic variability; optimal controller number unknown	Predict required controller count dynamically; place controllers optimally using traffic patterns	Centralized prediction may be bottleneck; relies on traffic prediction accuracy	Scalability to very large networks; limited testing in dynamic environments
[45]	Abdulrahman et al. (2025)	Gaussian Mixture Model (GMM)-based placement with hybrid geographic and traffic metrics	Haversine	Healthcare SD-WANs require resilient, low-latency controller placement supporting telemedicine and data access	Increase network efficiency and availability; adapt controller placement to traffic load and network changes	Domain-specific to healthcare; limited benchmarking on non-healthcare topologies	Generalization to other domains; incorporation of emerging network technologies (e.g., 5G, IoT)
[46]	Musie Frdiesa (2024)	Ant Colony Optimization (ACO) for controller placement	-	CPP affects overall network performance; existing heuristics fail to optimize latency and load balance jointly	Propose ACO to optimize latency (both switch-controller and inter-controller) and load balancing	Metaheuristic parameters tuning required; convergence speed may vary	Adaptation to dynamic traffic conditions; extension to multi-objective beyond latency and load balancing
[47]	Nura Muhammed Yusuf et al. (2023)	Controller Placement with Critical Switch Awareness (CPCSA) using network partitioning	Haversine	Existing CPP algorithms lack switch role awareness leading to inefficiencies in control message overhead	Incorporate switch criticality for network partition and controller placement to reduce overhead and latency	Assumes static switch criticality; may not handle rapid network changes	Dynamic adaptation to traffic and network topology changes; extension to load balancing
[48]	Chunlin Li et al. (2024)	Deep Reinforcement Learning (DRL) based controller placement + dynamic edge selection	-	High cost and inefficiency of MEC system management; static controller placement suboptimal	Dynamic controller placement minimizing communication cost and balancing load; optimize MEC task offloading	Requires large training data; complexity of DRL models; real-time deployment overhead	Scalability and transferability to heterogeneous MEC environments; real-time adaptation
[49]	Hamza Mokhtar et al. (2021)	Multiple Threshold Load Balancing (MTLB) with switch migration scheme for distributed controllers	-	Load imbalance in distributed SDN controllers leads to performance degradation	Continuous load balancing among controllers; reduce synchronization overhead and migration frequency	Overhead in load information exchange; thresholds tuning needed; complexity in large networks	Integration with CPP methods; real-time responsiveness and stability in highly dynamic networks

This analysis confirms that NA-GMM addresses critical gaps in the existing work that need to be improved through the proposed method explained in the next section, its efficient 4-component hybrid metric approach, without the complexity of deep learning or the instability of adaptive methods.

3. Proposed Method

3.1. Problem Formulation

We modeled an SD-WAN as an undirected graph G = (V,E), where V = {v1,v2,…,vn} represents the set of network nodes (such as switches or routers), and E ⊆ V × V represents the set of links connecting these nodes. Each node vi∈ V is characterized by its geographical coordinates (lat i, lon i), and may also possess other attributes like traffic volume, processing capacity, or failure probability.

The core task of the controller placement problem involves selecting a specific subset of nodes, denoted as C ⊆ V, to function as controllers, where the cardinality of this subset, ∣C∣, is equal to a desired number of controllers, k. For all other nodes vi ∈ V/C (non-controller nodes), an assignment policy dictates their association with one or more controllers. In this paper, we specifically focus on a primary assignment policy where each non-controller node is assigned to exactly one controller, typically the closest one based on a defined distance metric.

The overarching objective is to identify the optimal set of controller nodes, C*, that effectively minimizes a composite cost function, f (C,G), which integrates multiple, potentially conflicting performance objectives. This objective is formally expressed as follows:

$$C\mathrm{\ast }=arg{\displaystyle \frac{min}{C\subseteq V\mid C\mid =k}}f(C,G)$$

For clarity and consistency throughout this paper, Table 2 represents the comprehensive parameter specification for the proposed algorithm. Parameters are organized by functional category, including hybrid distance metric components, GMM model parameters, algorithm control variables, and network input specifications. The table provides parameter ranges, physical interpretations, and usage contexts to facilitate algorithm implementation and parameter tuning. Constraint relationships ensure mathematical validity and algorithmic convergence.

Table 2. Network-Aware GMM Algorithm Parameters and Configuration.

Variable	Description	Range/Type	Physical Meaning	Usage Context
Hybrid Distance Metric Parameters
α	Geographic distance weight	[0.4]	Relative importance of physical separation between nodes	Distance computation, regulatory compliance
β	Network latency weight	[0.3]	Emphasis on communication delay in controller placement	Performance optimization, QoS requirements
γ	Topological cost weight	[0.18]	Routing complexity and path efficiency consideration	Network efficiency, resource optimization
δ	Link reliability weight	[0.12]	Network stability and fault tolerance priority	Reliability assurance, SLA compliance
dg(i,j)	Geographic distance	ℝ+	Euclidean distance between network nodes	Spatial relationship modeling
dl(i,j)	Network latency	ℝ+ [ms]	Round-trip time between nodes	Performance metric computation
dt(i,j)	Topological cost	ℕ	Routing hop count and path complexity	Network topology analysis
dr(i,j)	Link reliability	[0, 1]	Inverse reliability measure (higher = less reliable)	Fault tolerance assessment
Gaussian Mixture Model Parameters
K	Number of controller clusters	ℕ+	Desired number of controllers in the network	Algorithm initialization, resource planning
μk	Cluster mean vector	ℝd	Optimal controller position in feature space	M-step parameter update
Σk	Cluster covariance matrix	ℝd × d	Coverage area and correlation structure of cluster k	Cluster shape adaptation
πk	Mixing coefficient	[0, 1]	Prior probability and relative importance of cluster k	Load balancing, cluster weighting
γik	Responsibility value	[0, 1]	Probability of node i belonging to controller k	E-step computation, soft assignment
Nk	Effective sample size	ℝ+	Weighted number of nodes assigned to cluster k	M-step normalization
Algorithm Control Parameters
ε	Convergence threshold	ℝ+	Minimum log-likelihood improvement for termination	Convergence detection
t	Iteration counter	ℕ	Current EM algorithm iteration number	Algorithm progress tracking
L(t)	Log-likelihood function	ℝ	Quality measure of current parameter configuration	Optimization objective, convergence monitoring
θ	Parameter vector	ℝp	Complete set of GMM parameters {μ, Σ, π}	Parameter space representation
Network Input Parameters
n	Number of network nodes	ℕ+	Total count of nodes requiring controller assignment	Problem dimensionality
d	Feature space dimension	ℕ+	Dimensionality of network-aware feature vectors	Feature engineering, computational complexity
xi	Node feature vector	ℝd	Network-aware representation of node i characteristics	Input data for clustering algorithm
DNA	Hybrid distance matrix	ℝn × n	Pairwise network-aware distances between all nodes	Distance computation, feature engineering

Parameter Constraints and Relationships:

• α + β + γ + δ = 1 (weight parameters normalization).
• ${\sum \pi k}_{k=1}^K$ = 1 (mixing coefficients normalization).
• ${\sum \mathsf{\gamma }\mathrm{i}\mathrm{k}}_{k=1}^K$ = 1, ∀i (responsibility normalization).
• Σk must be positive semi-definite (covariance matrix constraint).
• K ≤ n (number of clusters cannot exceed number of nodes).
• ε > 0 typically in range [10⁻⁶, 10⁻³] for practical convergence.

3.2. Novel Hybrid Distance System

The precise modelling of distances between network elements is fundamental for achieving optimal controller placement, yet this remains a significant challenge in current SD-WAN deployments. Traditional controller placement methodologies often rely predominantly on simplistic distance metrics, notably Euclidean distance, which are inherently insufficient to capture the intricate and varied interactions prevalent in complex network topologies. This simplification consequently leads to suboptimal controller placements that fail to accurately account for true communication costs, effective network pathways, or actual connection quality. In this work, we proposed a hybrid distance metric used for SD-WAN controller placement. We combine geographic separation, network latency, topological cost, and link reliability into a single “distance” measure. Formally, for any two nodes $i,j,$ we define (1):

$$d_{\mathrm{N}\mathrm{A}}\left(i,j\right)=\alpha .d_{geo}\left(i,j\right)+\beta .d_{lat}\left(i,j\right)+\gamma . d_{cost}\left(i,j\right)+\delta .R(i,j)$$

(1)

where α, β, γ, δ are weight parameters. All distances can be scaled to unitless values (dividing by maximums) so that $d_{\mathrm{N}\mathrm{A}}$ is unitless. In summary, larger geographical or latency distances and higher link costs increase $d_{\mathrm{N}\mathrm{A}}$, while higher reliability decreases it. We typically choose α + β + γ + δ = 1 so the terms are comparably weighted. See Figure 1.

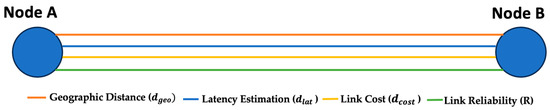
Figure 1. Shows the Distance Components breakdown.

3.2.1. Geographic Distance (${\mathrm{d}}_{\mathrm{g}\mathrm{e}\mathrm{o}})$

The geographic distance between two points on the Earth’s surface is measured by the great-circle distance. Let node $i$ have latitude $\varphi i$ and longitude $\lambda i$ (in radians) and node $j$ have $\varphi j$, $\lambda j$. Using the Earth’s radius $RE\approx 6371$, the Haversine formula [50] gives the great-circle distance as shown in (2) and Figure 2.

$$d_{geo}\left(i,j\right)=2RE arcsin\left(\sqrt{{sin}^2\left({\displaystyle \frac{\Delta \mathrm{\varnothing }ij}{2}}\right)+\mathit{cos}\left(\mathrm{\varnothing }i\right)\mathit{cos}\left(\mathrm{\varnothing }j\right){sin}^2\left({\displaystyle \frac{\Delta \lambda ij}{2}}\right)}\right)$$

(2)

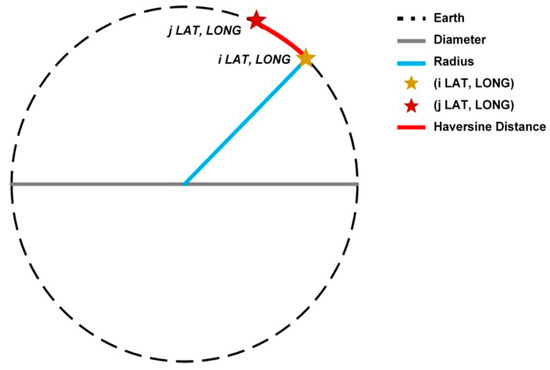
Figure 2. Shows the Haversine Distance.

In practice, $\varphi$ and $\lambda$ are given in degrees and converted to radians. The output $d_{geo}$ is in kilometers. To combine with other metrics, one may normalize $d_{geo}$ by the maximum inter-node distance in the network (yielding a value in [0, 1]).

3.2.2. Latency Estimation (${\mathrm{d}}_{\mathrm{l}\mathrm{a}\mathrm{t}})$

Latency is the signal propagation delay between $i$ and $j$. As a first-order estimate, we assume propagation through fiber or equivalent. A common rule of thumb is about 5 microseconds (μs) per km (assuming $v\approx 2\times 105v\approx 2\times 105 \mathrm{k}\mathrm{m}/\mathrm{s}$ in fiber). Thus, in milliseconds, see (3):

$$d_{lat}\left(i,j\right) \approx 0.005 \mathrm{m}\mathrm{s}/\mathrm{k}\mathrm{m} \times d_{geo}\left(i,j\right)$$

(3)

So that a $d_{geo}$ = 1000 km link yields roughly 5 (μs) one-way delay. More precisely, if $v$ is the propagation speed (in km/s), one can write $d_{lat}$ = $d_{geo}$ (i,j)/${vd}_{lat}$(i,j) = $d_{geo}$(i,j)/$v$. We typically normalize $d_{lat}$ (by dividing it by the maximum expected delay in the network), making it comparable to the other terms.

3.2.3. Link Cost (${\mathrm{d}}_{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}})$

The topology-based link cost captures factors like hop count, available bandwidth, or administrative weights. For instance, if nodes $i,j$ are directly connected by a link of cost $c_{i,j}$, we may set $d_{cost}\left(i,j\right)$=$c_{i,j}$ if they are connected via a path; $d_{cost}$ could be the sum of per-link costs along the shortest path. In routing protocols (OSPF/IS-IS) link cost often equals inverse bandwidth. We scale $d_{cost}$ to [0, 1] (dividing by the maximum path cost) so that larger cost means “farther” in our metric. The exact definition of $d_{cost}$ is application-specific: it might equal hop-count, total bandwidth-inversion, or a composite topology weight. Our formulation assumes $d_{cost}\left(i,j\right)$ ≥ 0 and grows with path expense.

3.2.4. Link Reliability ($\mathrm{R})$

Reliability $R(i,j)\in [0,1]$ represents the probability or quality of the link remaining up. We model it as an exponentially decaying function of distance. See (4):

$$R(i,j)=exp(-\mathit{\lambda } d\_geo(i,j),)$$

(4)

where λ > 0 is a decay constant chosen to fit network failure characteristics. This ensures R (0) = 1 and R→0 as distance increases. In effect, short links (or well-maintained links) have high reliability near 1, which will subtract more in the final metric, reducing the “distance”. By contrast, very unreliable (long or fragile) links have R ≈ 0 and so do not reduce $d_{\mathrm{N}\mathrm{A}}$. We normalize $R(i,j)$ and it naturally lies in [0, 1]. This approach effectively created a matrix $d_{\mathrm{N}\mathrm{A}}$ by amalgamating geographic distance, estimated propagation delay, a basic cost model, and a reliability component. By normalizing and weighing these varied components, the resultant $d_{\mathrm{N}\mathrm{A}}$ offers a more thorough assessment of “distance” between nodes than any one metric alone. This methodology provides a foundation for more sophisticated assessments in network design, routing, or analogous applications where many aspects affect connection and performance. The whole method is represented in Algorithm 1.

Algorithm 1 Compute Hybrid Network-Aware Distance Matrix (D_NA)

Require: Node coordinates (φi, λi) for i = 1,…,N Require: Weight parameters α, β, γ, δ Require: Earth radius r, propagation speed v, base cost c0, cost factor c1, decay factor κ Ensure: Distance matrix D_NA ∈ ℝn×n 1: for each ordered pair of nodes (i, j) from 1 to N do 2:   Δφ ← φj − φi 3:   Δλ ← λj − λi 4:   a ← sin2(Δφ/2) + cos(φi)·cos(φj)·sin2(Δλ/2) 5:   d_geo(i,j) ← 2·r·arcsin(√a)   ▷ Haversine distance 6:   d_lat(i,j) ← d_geo(i,j) / v   ▷ delay based on geographic distance 7:   d_cost(i,j) ← c0 + c1·d_geo(i,j)   ▷ cost based on geographic distance 8:   R(i,j) ← exp(−κ·d_geo(i,j))   ▷ reliability/decay factor 9: end for 10: ▷ Normalize components to a consistent scale (e.g., [0, 1]) 11: for each ordered pair of nodes (i, j) from 1 to N do 12:   d′_geo(i,j) ← Normalize(d_geo(i,j)) 13:   d′_lat(i,j) ← Normalize(d_lat(i,j)) 14:   d′_cost(i,j) ← Normalize(d_cost(i,j)) 15:   R′(i,j) ← Normalize(R(i,j))   ▷ Optional: normalize reliability if δ ≠ 0 16:   D_NA(i,j) ← α·d′_geo(i,j) + β·d′_lat(i,j) + γ·d′_cost(i,j) + δ·R′(i,j) 17: end for D_NA

3.3. Sensitivity Analysis of Hybrid Distance Metric Parameters

To validate the robustness of the proposed hybrid distance metric and determine the optimal weight configurations, we conducted comprehensive sensitivity analysis across different parameter combinations. The analysis examined how variations in α, β, γ, and δ weights impact controller placement performance across all evaluation metrics, as shown in Table 3.

Table 3. Parameter Combination Matrix for Sensitivity Analysis.

Configuration	α (Geo)	β (Lat)	γ (Topo)	δ (Rel)	Focus
Geo-focused	0.70	0.15	0.10	0.05	Geographic proximity
Lat-focused	0.15	0.70	0.10	0.05	Latency optimization
Topo-focused	0.15	0.15	0.60	0.10	Topology awareness
Rel-focused	0.15	0.15	0.10	0.60	Reliability priority
Balanced	0.40	0.30	0.18	0.12	Current (proposed)
Equal	0.25	0.25	0.25	0.25	Equal weighting

The proposed balanced configuration (α = 0.4, β = 0.3, γ = 0.18, δ = 0.12) provides optimal trade-offs across diverse network scenarios.

3.4. NA-GMM-Based Controller Placement Strategy

In the context of SD-WAN controller placement, determining where and how many controllers to deploy is a multi-faceted challenge. After computing a comprehensive hybrid multi-dimensional distance framework matrix $d_{\mathrm{N}\mathrm{A}}$, we proceeded with a probabilistic clustering-based strategy that not only reflects the underlying topology and link metrics but also achieves soft, interpretable boundaries across heterogeneous network regions. We introduced a novel Network-Aware Gaussian Mixture Model (NA-GMM) framework, extending classical unsupervised clustering to accommodate spatial distributions and network-specific quality measures. This approach enables the multi-objective optimization of the control plane design with respect to latency, scalability, load balancing, and fault tolerance.

3.4.1. Theoretical Foundation

Gaussian Mixture Models (GMMs) are a powerful and flexible approach for modeling data distributions in statistical learning and unsupervised data analysis. GMMs assume a dataset is composed of multiple overlapping subpopulations following a multivariate Gaussian distribution. This probabilistic framework provides a mathematically robust basis for soft clustering, where each data point can belong to multiple clusters with varying degrees of membership. GMMs operate on the principle of latent variable modeling, positing that observed data are generated from a mixture of several hidden distributions, each corresponding to a cluster or subpopulation. For every observation in the dataset, GMM assigns a probability of belonging to each cluster, making it particularly useful in scenarios where the boundary between clusters is ambiguous or continuous. Mathematically, a Gaussian Mixture Model with K components defines the probability density function of a data point $\mathcal{x}$ ∈ ${\mathbb{R}}^d$ as seen in the following (5):

$$p\left(x\right)=\sum _{k=1}^K\pi k.\mathcal{N}(\mathcal{x}\mid \mu k,\sum k)$$

(5)

where:

• $\pi k$ ∈ [0, 1] is the mixing coefficient for component $k$, satisfying ${\sum \pi k}_{k=1}^K$=1;
• $\mu k$ ∈ ${\mathbb{R}}^d$ is the mean vector (center) of the $k$-th Gaussian distribution;
• $\sum k$ ∈ ${\mathbb{R}}^{d \times d}$ is the covariance matrix, capturing the spread of the distribution;
• $\mathcal{N}\left(\mathcal{x}∣\mu k,\Sigma k\right)$ denotes the multivariate normal distribution evaluated at $\mathcal{x}$.

3.4.2. Multivariate Normal Distribution

The probability density function for the multivariate Gaussian distribution is given by (6):

$$\mathcal{N}\left(\mathcal{x}∣\mu ,\Sigma \right)={\displaystyle \frac{1}{{\left(2\pi \right)}^{\frac{d}{2}}{\left|\Sigma \right|}^{\frac{1}{2}}}}\mathit{exp} \left(- 1/2 {(\mathcal{x}-\mu ) }^T\right.{\Sigma }^{-1} \left(\mathcal{x}-\mu \right))$$

(6)

Here:

• ∣Σ∣ denotes the determinant of the covariance matrix.
• Σ−1 is the inverse of the covariance matrix.

This equation models how data points are distributed around the mean $\mu$, with the shape and orientation defined by Σ. When data follows a roughly elliptical or spherical spread, the Gaussian distribution is an effective model. In the case of SD-WAN, the feature space is often two-dimensional (geographical coordinates) or extended to include latency and reliability features. The covariance matrix $\sum k$ thus enables modeling not just the location, but also the spread and directional bias of nodes around a controller.

3.4.3. Probabilistic Clustering and Soft Assignments

One of the main strengths of GMM is its ability to produce soft clustering results. That is, for any given point $x_i$, the model estimates the responsibility or posterior probability that this point belongs to cluster $k$, as in (7):

$$\gamma ik={\displaystyle \frac{\pi k .\mathcal{N}\left(xi∣\mu k,\Sigma k\right)}{{\Sigma }_{j=1}^K{\pi }_j.\mathcal{N}\left(xi∣\mu k,\Sigma k\right)}}$$

(7)

These responsibilities $\gamma ik$ ∈ [0,1] quantify the relative influence of each cluster on a data point and can be interpreted as soft labels. In contrast to k-means, which perform hard assignments, GMM’s soft assignments are better suited for networks where nodes may simultaneously interact with multiple regions (e.g., overlapping control domains in SD-WAN). This aspect is particularly advantageous in real-world SD-WAN environments, where:

• Some nodes may straddle the boundaries of multiple controller regions.
• Traffic loads and link reliability may vary dynamically.
• The network may require flexible controller domains to accommodate fault tolerance or dynamic reallocation.

3.4.4. Parameter Estimation via Expectation–Maximization (EM)

To learn the parameters {πk, μk, Σk} of the GMM from data, the standard approach is the expectation–maximization (EM) algorithm, which iteratively refines the estimates to maximize the likelihood of the observed data, see Equations (8)–(10).

• The E-step (Expectation) computes the responsibilities γik that represent the probability of node i belonging to controller cluster k. These values incorporate both the geometric likelihood of the assignment based on the current cluster parameters and the topology-conscious distance relationships established in the preprocessing phase. See Figure 3.
  

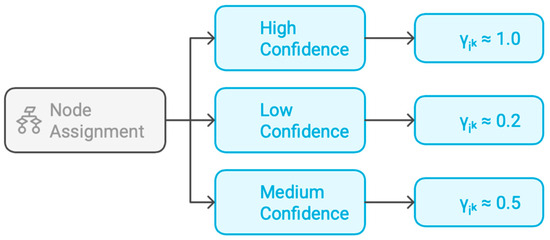  Figure 3. Shows the Responsibility Matrix Visualization.

High responsibility values (γ_ik ≈ 1) indicate strong confidence that node i should be assigned to cluster k, while low values (γ_ik ≈ 0.2) suggest weak affinity. Intermediate values reflect uncertainty in the assignment, which often occurs for nodes near cluster boundaries or nodes with similar network characteristics relative to multiple controllers:

$${\mu k}^{(\mathit{t}+1)}= {\displaystyle \frac{1}{{\mathit{N}}_{\mathit{k}}}}{\sum }_{\mathit{i}=1}^{\mathit{N}}\gamma ik. xi$$

(8)

$${\Sigma }_k^{(t+1)}={\displaystyle \frac{1}{{\mathit{N}}_{\mathit{k}}}}{\sum }_{\mathit{i}=1}^{\mathit{N}}\gamma ik. (x_i-{\mu }_k)(x_n-{\mu }_k{)}^T$$

(9)

$${\pi }_k^{\left(t+1\right)}={\displaystyle \frac{N_k}{N}}$$

(10)

2.

M-step (Maximization); this step updates the model parameters {μk, πk, Σk} based on the computed responsibilities, embodying the principle that controller characteristics should reflect the nodes they are expected to serve. The effective sample size represents the weighted number of nodes assigned to cluster k. This value accounts for fractional assignments by summing the responsibility values rather than simply counting hard assignments. Clusters with higher effective sample sizes indicate areas of the network (domain) with dense node populations or strong connectivity patterns. See Figure 4.

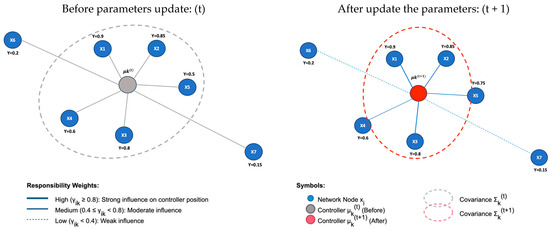Figure 4. Parameter update mechanism in the M-step.

3.4.5. Convergence Monitoring and Termination

The algorithm monitors convergence through the log-likelihood function L(θ), which measures how well the current model parameters explain the observed network node distribution and connectivity patterns. The log-likelihood, a quantitative measure of solution improvement, considers the geometric fit of nodes to clusters and the probabilistic consistency of assignments with each iteration. See (11):

$$log\mathcal{L}\left(\theta \right)= {\Sigma }_{i=1}^N\mathit{log}{(\Sigma }_{K=1}^K{\pi }_K.\mathcal{N}\left(xi∣\mu k,\Sigma k\right) \left.W(xi) \right)$$

(11)

Higher likelihood values indicate better controller placement and cluster assignments, while convergence detection compares successive likelihood values, ending when improvement falls below the threshold ε. as shown in (12):

$$\left|\mathit{log}{\mathcal{L}}^{\left(t\right)}-\mathit{log}{\mathcal{L}}^{\left(t-1\right)}\right|<\epsilon$$

(12)

The convergence threshold ε balances solution quality with computational efficiency, stopping optimization when iterations are unlikely to yield significant improvements. Smaller threshold values refine solutions but require more iterations, while larger values terminate early, making GMM adaptable for modeling non-spherical, unequal-sized, and overlapping clusters.

3.4.6. Final Assignment and Solution Extraction

Upon convergence, the algorithm generates definitive controller assignments using maximum a posteriori (MAP) estimation, as shown in (13):

$$cluster\left(i\right)=\mathit{arg} {max}_k {\gamma }_{ik}$$

(13)

This transition from soft probabilistic assignments to hard cluster memberships provides the concrete placement decisions required for network implementation, as shown in Figure 5. The final responsibility values γ_ik retain valuable information about assignment confidence even after hard assignments are made. Nodes with responsibilities close to the maximum (e.g., γ_ik > 0.9) indicate high-confidence assignments, while nodes with lower maximum responsibilities suggest boundary cases that might require additional attention during deployment.

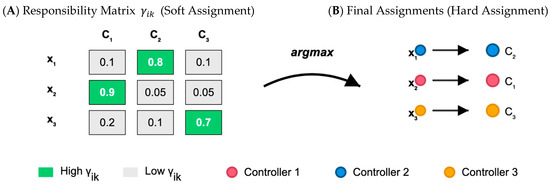
Figure 5. Final Assignment Process: From Soft in (A) to Hard Cluster Assignments (B).

The optimized controller positions $\mu k$ represent the recommended locations for placing controllers to optimally serve their assigned node populations. These positions incorporate the network-aware distance relationships and reflect the iterative refinement process that balanced multiple performance objectives. The learned covariance matrices Σk provide insights into the coverage requirements for each controller, indicating whether the controller serves a geographically concentrated population or a more distributed set of nodes with varied connectivity characteristics. This information can guide capacity planning and resource allocation decisions. See Algorithm 2.

Algorithm 2 Network-Aware GMM (NA-GMM) Controller Placement

Require:   • Feature vectors {xi}i=1…N   • Number of clusters K   • Distance matrix D_NA   • Convergence threshold ε   Ensure:   • Controller positions {μk}k=1…K   • Node–cluster responsibilities γik   1:  Initialize GMM parameters for k = 1…K:        μk ← I, Σk ← I, πk ← 1/K   2:  repeat   3:    ▷ E-step   4:    for each node i ∈ {1…N} and each cluster k ∈ {1…K} do   5:      γik ← πk · $𝒩$(xi | μk, Σk) / ∑j=1K [πj · $𝒩$(xi | μj, Σj)]   6:    end for   7:    ▷ M-step   8:    for each cluster k ∈ {1…K} do   9:     Nk ← ∑i=1N γik   10:     μk ← (1/Nk) · ∑i=1N γik · xi   11:     Σk ← (1/Nk) · ∑i=1N γik · (xi − μk)(xi − μk)T   12:     πk ← Nk / N   13:   end for   14:   Evaluate log-likelihood L(θ) and check convergence   15: until ΔL(θ) ≤ ε   16: Assign each node i to cluster       k* = arg maxk γik   17: return {μk}k=1…K and {γik}i=1…N,k=1…K

4. Experimental Design and Results

4.1. Simulation Environment and Tools

The experimental evaluation of the Network-Aware Gaussian Mixture Model (NA-GMM) algorithm requires a comprehensive simulation infrastructure capable of accurately modeling complex network environments while providing reliable performance measurements. This section presents the experimental setup designed to address three fundamental requirements: algorithmic accuracy, computational scalability, and result reproducibility.

4.1.1. Experimental Infrastructure and Software Framework

The NA-GMM algorithm was developed using Python 3.9.7, NumPy 1.21.2, SciPy 1.7.3, and Network X 2.6.3 for network topology analysis. It uses specialized numerical routines for processing geographical coordinate data and computing hybrid distance metrics. Baseline algorithms were implemented using scikit-learn 1.0.2 for fair comparison. Network simulation was conducted using Mininet 2.3.1, and controller performance assessment was conducted using the standard Cbench 1.3.1 tool. The experimental setup used the open-source Floodlight controller, capable of handling up to 367,000 flow requests per second. Controller placement validation was conducted using a dedicated system.

4.1.2. Network Topologies and Performance Metrics

The study used authentic network topologies from the Internet Topology Zoo (ITZ) [51] to evaluate network infrastructures. Three topologies were selected: TATA, BICS, and BESTEL, representing different scales and structural characteristics. Each topology provided comprehensive metadata, enabling accurate computation of hybrid distance metric components. The selections were large-scale enterprise, medium-scale regional, and small-scale constrained network environments, as seen in Table 4 and Figure 6a–c.

Table 4. Networks Topology Details.

Topology	Nodes Count (Red Circles)	Edges Count (Blue Lines)
TATA	145	194
BICS	84	101
BESTEL	33	48

Figure 6. Represents (a) TATA, (b) BICS, and (c) BESTEL Topology.

Algorithm performance assessment utilized four comprehensive metrics specifically designed for controller placement evaluation: average controller latency (ACL), worst-case latency (WCL), and inter-controller latency (ICL) affecting coordination overhead, and Node Distribution Ratio (NDR) evaluating load distribution fairness. Mathematical formulations for all performance metrics are provided in Equations (14)–(17). When combined, they provide a broad understanding of network performance and practical insights that guide controller deployment design and ongoing enhancement:

• ACL: Measures the average latency between nodes within the same cluster, providing a gauge for the responsiveness of the network, as shown in (14).

  $${ACL}_k={\displaystyle \frac{1}{N_k(N_k-1)}}{\Sigma }_{i=1}^{N_k}{\Sigma }_{j=1,j\ne i}^{N_k}{d}_{ij}$$

  (14)
• WCL: Captures the worst-case latency scenario within each cluster, which is crucial for understanding the potential for delay spikes; see (15).

  $${WCL}_k=maxi,j\in Nk,i\ne jdij$$

  (15)
• ICL: Following (16), assesses the latency between controllers, which has an impact on coordination and overall network performance.

  $${ICL}_{kl}=d({centroid}_k,{centroid}_l)$$

  (16)
• NDR: Assesses the evenness of the node distribution across clusters, which can influence network load management and resilience, as shown in (17).

  $$NDR={\displaystyle \frac{\mathit{max}(N1,N2,\dots Nk)}{\frac{1}{k}{\Sigma }_{i=1}^k{N}_i}}$$

  (17)

The NA-GMM algorithm leverages continuous spatial data to achieve precise controller placement optimization, adapting fluidly to network spatial distribution patterns unlike conventional discrete clustering algorithms. The implementation processes use geographical coordinates and network-aware features through probabilistic modeling, generating sophisticated representations that capture both spatial relationships and connectivity patterns.

4.1.3. Experimental Design and Benchmarking

The experimental implementation of a controller placement algorithm uses modular architecture to ensure consistency in measurement and analysis procedures. The NA-GMM implementation uses probabilistic modeling to optimize hybrid distance metric, while the ACO-CP [46] implementation uses ant colony optimization. The CPCSA [47] implementation includes critical switch identification and network partitioning to ensure optimal controller assignment. The DRL implementation uses CNN-LSTM [48] traffic prediction and a reinforcement learning optimization engine to generate placement recommendations. The experimental validation process uses Mininet for real-time validation of controller placement decisions, with rigorous statistical analysis to identify statistically meaningful performance variations. Comparative analysis examines algorithm performance across multiple dimensions, including scalability characteristics, computational overhead, and adaptation to different network topologies. Trade-off analysis identifies optimal conditions for each algorithm and provides insights into algorithm selection criteria for different deployment scenarios. The NA-GMM algorithm is evaluated against established controller placement approaches and assessed for clustering effectiveness and practical applicability in SDN environments.

4.2. Results

We have evaluated the proposed NA-GMM algorithm’s performance across multiple dimensions, providing detailed analysis of clustering effectiveness, network performance characteristics, and computational resource utilization. The results are organized into three primary areas of investigation to thoroughly assess the algorithm’s practical applicability and comparative advantages in software-defined network controller placement scenarios.

4.2.1. Clustering Results

The empirical evaluation of the NA-GMM algorithm demonstrates its efficacy in network topology partitioning and controller placement optimization through the systematic analysis of four critical performance metrics: ACL, WCL, ICL, and NDR. Comparative analysis against three benchmark algorithms across multiple network configurations reveals the superior clustering performance of NA-GMM, characterized by enhanced load distribution, reduced communication overhead, and improved network accessibility. The clustering evaluation conducted across three distinct network topologies—TATA, BICS, and BESTEL—establishes k = 5 as the optimal controller configuration. Silhouette coefficient analysis yielded peak values of 0.482, 0.543, and 0.392 for TATA, BESTEL, and BICS topologies, respectively, indicating optimal inter-cluster separation at k = 5. Corresponding inertia measurements recorded values of 32, 14, and 10.3 for the respective topologies, with distinct elbow points confirming the clustering validity, referred to in Figure 7. These quantitative results substantiate k = 5 as the most effective clustering strategy for controller deployment across heterogeneous network architectures. The spatial optimization capabilities of the NA-GMM algorithm are evidenced through the comprehensive visualization of controller placement decisions and network partitioning outcomes, demonstrating adaptive performance across diverse topological characteristics. The algorithm’s ability to accommodate varying network scales while maintaining clustering quality establishes its robustness for practical deployment scenarios.

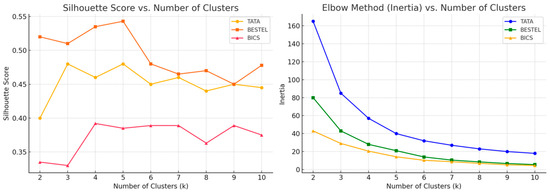
Figure 7. Shows the clustering evaluation across three topologies, indicating that k = 5 offers the most balanced configuration.

By identifying the number of ks, we implemented the proposed method for each topology and evaluated the clustering ability for the above-mentioned clustering parameters compared to the benchmark algorithms. The following represent the numerical results and visualize the network clusters (domains), and the centroid’s location (controllers), for TATA topology. As shown in Table 5, Figure 8 and Figure 9.

Table 5. Performance Metrics Comparison for TATA Topology.

Algorithm	ACL (ms)	WCL (ms)	ICL (ms)	NDR ≈ 1
NA-GMM	1.521	4.182	5.766	1.209
ACO	2.434	4.558	5.892	1.469
DRL	2.432	6.557	2.912	2.413
CPSA	1.652	3.696	5.959	1.189

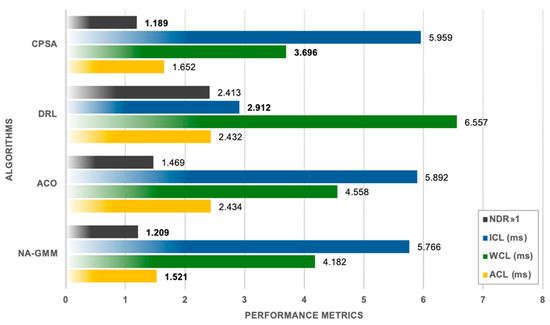
Figure 8. Clustering Results Comparison for TATA Topology.

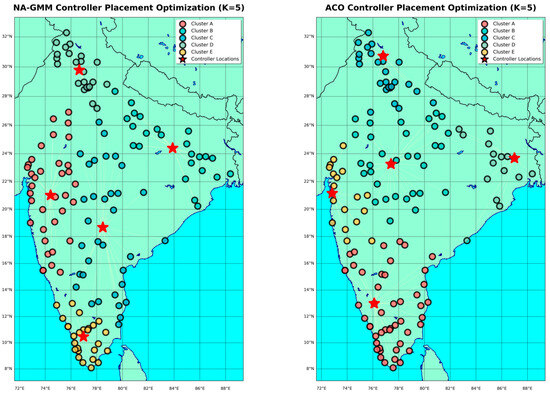
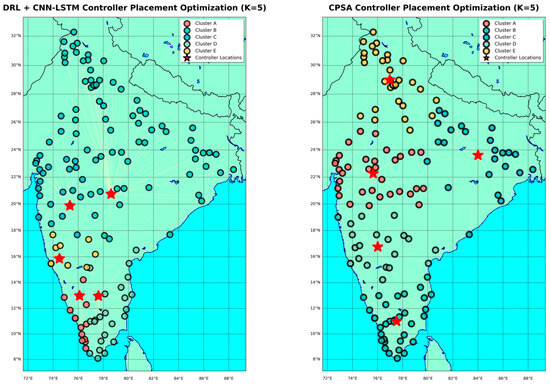
Figure 9. Shows the clustering visualization for TATA topology comparing all algorithms.

The experimental evaluation on the TATA topology reveals that NA-GMM outperforms ACO and DRL techniques by 37.5%. NA-GMM is the best algorithm for reducing communication delays while maintaining balanced cluster assignments, with an NDR of 1.209. CPSA leads the field in worst-case scenario management with the most balanced load distribution and lowest WCL of 3.696 ms. However, it has the highest inter-controller communication overhead, indicating potential scalability issues in multi-controller coordination situations. DRL has the lowest ICL of 2.912 ms, a 49.5% reduction, and performs exceptionally well in inter-controller communication. Despite this, DRL has serious load unbalancing problems, with an NDR of 2.413.

Extremely lopsided cluster distributions are one way this imbalance shows up; one cluster has 69 nodes, while others have between 10 and 26. Without reaching excellence in any one area, ACO consistently performs moderately well across all metrics. Although it lacks the specialized advantages provided by the other algorithms in their respective optimization domains, its balanced but unimpressive results establish it as a reliable baseline solution.

The following steps are the same for BICS topology, the results illustrated in Table 6, and Figure 10 and Figure 11.

Table 6. Performance Metrics Comparison for BICS Topology.

Algorithm	ACL (ms)	WCL (ms)	ICL (ms)	NDR ≈ 1
NA-GMM	1.844	5.237	7.552	1.364
ACO	2.708	6.923	6.701	1.364
DRL	2.174	8.367	3.845	3.030
CPSA	2.066	5.787	7.454	1.667

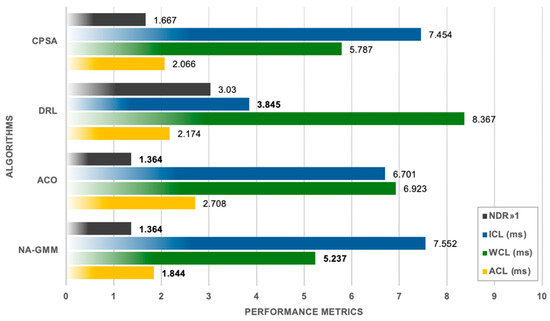
Figure 10. Clustering Results Comparison for BICS Topology.

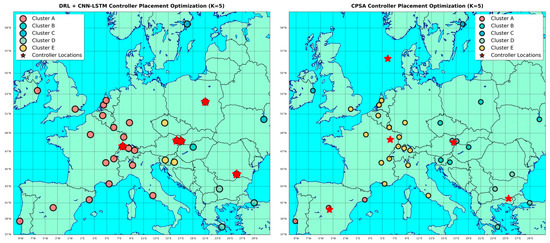
Figure 11. Shows the clustering visualization for BICS topology comparing all algorithms.

When compared to larger network configurations, the evaluation on the smaller BICS topology shows noticeably different performance patterns. With the lowest ACL of 1.844 ms, NA-GMM clearly dominates critical latency metrics, outperforming ACO by 32.0% and DRL by 10.7%. At 5.237 ms, NA-GMM also records the best WCL performance, demonstrating superior handling of both average and worst-case communication scenarios. With an NDR of 1.364, the algorithm maintains excellent load balancing and shares this optimal load distribution characteristic with ACO.

ACO’s enhanced competitiveness in smaller networks is demonstrated by the BICS topology, where it maintains acceptable latency characteristics while matching NA-GMM’s load balancing performance (NDR = 1.364). ACO’s WCL of 6.923 ms indicates a 32.2% performance degradation in comparison to the suggested method, while its ACL of 2.708 ms is still 46.9% higher than the proposed. With the lowest ICL of 3.845 ms—roughly 49.1% faster than its closest rival—DRL maintains its dominance in inter-controller communication. However, catastrophic load misbalancing overshadows this specialized advantage; the most severe distribution inequality was recorded with an NDR of 3.030. Even in smaller network topologies, the algorithm’s propensity to produce a dominant cluster with 20 nodes while demoting others to clusters with 2–4 nodes show basic scalability limitations. With competitive performance on several metrics and the second-best ACL (2.066 ms) and WCL (5.787 ms) values, CPSA offers a well-rounded strategy. The algorithm’s consistent performance profile makes it a good substitute when multi-objective optimization is valued more highly than single-metric excellence, even though its NDR of 1.667 suggests moderate load balancing effectiveness.

Lastly, BESTEL topology implemented by the proposed algorithm against the state of the art algorithms, see Table 7, and Figure 12 and Figure 13.

Table 7. Performance Metrics Comparison for BESTEL Topology.

Algorithm	ACL (ms)	WCL (ms)	ICL (ms)	NDR
NA-GMM	1.181	4.028	5.655	1.585
ACO	2.053	4.206	5.551	1.707
DRL	1.560	4.334	5.127	2.012
CPSA	1.406	3.782	5.920	1.829

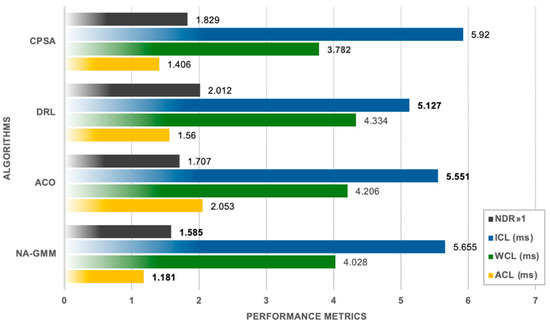
Figure 12. Clustering Results Comparison for BESTEL Topology.

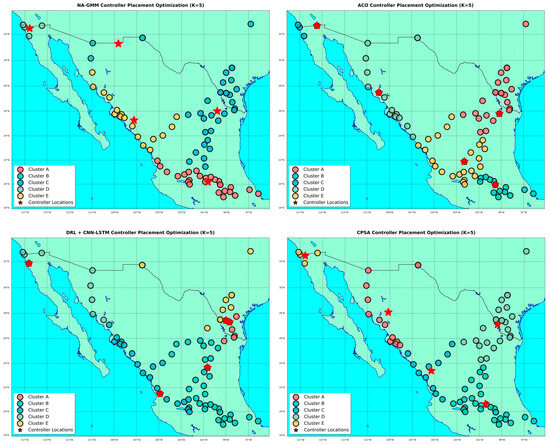
Figure 13. Shows the clustering visualization for BESTEL topology comparing all algorithms.

NA-GMM is a highly effective algorithm for routine communication management due to its exceptional ACL performance. It achieves the lowest average control latency (ACL) of 1.181 ms, a 42.5% improvement over ACO and 24.3% improvement over DRL. NA-GMM also exhibits superior cluster distribution with an NDR of 1.585. CPSA, the industry leader in worst-case latency management, has the lowest WCL of 3.782 ms, a 6.1% improvement over NA-GMM. However, CPSA demonstrates significant load unbalancing and the highest inter-controller communication overhead, indicating coordination inefficiencies in distributed controller scenarios. DRL maintains its distinctive strength in inter-controller communication, outperforming ACO by about 7.6% and NA-GMM by 9.3%. However, DRL has significant load distribution problems, resulting in unbalanced clusters with 33 nodes in one and 6–21 nodes in others. ACO offers the most balanced inter-controller communication performance at 5.551 ms, closely matching DRL’s efficiency while preserving a more sensible load distribution. NA-GMM consistently achieves the lowest average control latency across all topologies, outperforming competing techniques by 37.5%, 32.0%, and 42.5%, respectively.

4.2.2. Network Performance Results

The network performance evaluation was conducted using Mininet network simulation to validate controller placement algorithms under realistic traffic conditions. The experimental framework maintained consistent network parameters and traffic generation patterns, ensuring fair comparison between NA-GMM and benchmark algorithms. Throughput measurements were evaluated using averaged values from multiple simulation runs, with a bandwidth of 1000 Mbps. The 7000 Req/Sec controller capacity constraint was uniformly applied across all evaluations, and Controller Load Variance calculations included actual node distributions to reflect real-world deployment scenarios:

• The process of network topology configuration in Mininet involved reconstructing the original network structure with preserved nodes, links, and connectivity patterns.
• Controller deployment involved instantiating five controllers for each algorithm and positioning them according to clustering results.
• Cluster implementation assigned network nodes to their controller clusters based on clustering decisions.
• Traffic generation and measurement used iperf3 traffic generators to simulate realistic network conditions with varying request rates.
• Data aggregation involved aggregating individual cluster throughput values to compute the average throughput for each algorithm per topology, conducting multiple simulation runs to minimize measurement variance.

Three key performance indicators were computed to assess network efficiency and load distribution quality:

• Controller Utilization (U) measures the percentage of controller capacity consumed by network traffic, calculated as [49], (18):

  $$U=Max throughput/ C Capacity\times 100\%$$

  (18)
• Controller Load Variance (CLV) evaluates load distribution heterogeneity based on actual clustering results, computed as (19), [52]:

  $$CLV=\left({\displaystyle \frac{1}{N}}\right)\times {\Sigma }_{\mathrm{i}}^{=1\mathrm{N}} {\left(U_{\mathrm{i}}-Ū\right)}^2$$

  (19)

  where U_i represents individual controller utilization based on node distribution, N is the number of controllers, and Ū is the mean utilization.
• Load Imbalance Ratio (LIR) quantifies load distribution inequality [53], defined as follows (20):

  $$\mathrm{LIR}={\displaystyle \frac{Max Controller Load-Min Controller Load}{Average Controller Load}}$$

  (20)

The CLV metric was calculated using actual node distributions from clustering results, providing a realistic load variance assessment based on the heterogeneous network partitioning achieved by each algorithm. The network performance evaluation results are in Table 8, Figure 14, Figure 15, Figure 16 and Figure 17.

Table 8. Network Performance Metrics Across All Topologies.

Topology	Algorithm	Throughput (Req/Sec)	Utilization (%)	CLV	LIR
TATA	NA-GMM	282.97	4.0424	0.0023	0.4545
	ACO	260.20	3.7171	0.0053	0.8741
	DRL	233.48	3.3354	0.0241	2.0629
	CPSA	280.74	4.0106	0.0021	0.4545
BICS	NA-GMM	278.58	3.9797	0.0038	0.6061
	ACO	236.86	3.3837	0.0070	0.9091
	DRL	278.52	3.9789	0.0661	2.7273
	CPSA	254.97	3.6424	0.0091	1.2121
BESTEL	NA-GMM	292.67	4.1810	0.0073	0.9146
	ACO	259.44	3.7063	0.0130	1.1585
	DRL	273.28	3.9040	0.0214	1.6463
	CPSA	279.96	3.9994	0.0208	1.5854

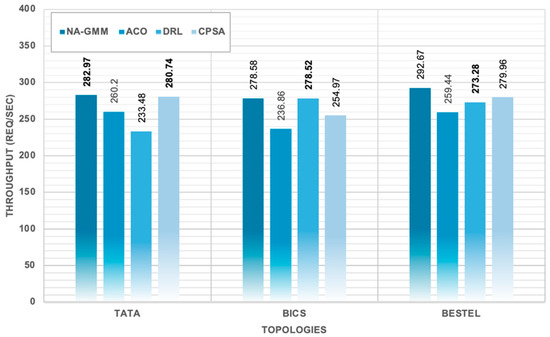
Figure 14. Network Throughput Across All Algorithms and Topologies. the bold numbers highlight the best results.

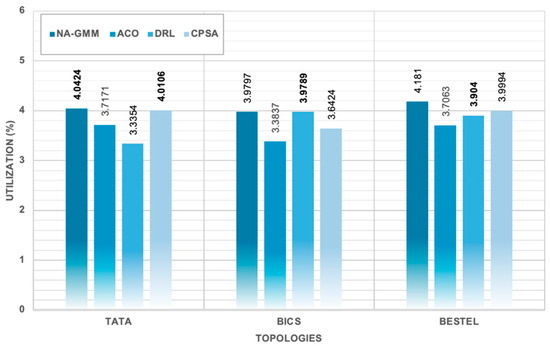
Figure 15. Controller Utilization Across All Algorithms and Topologies. the bold numbers highlight the best results.

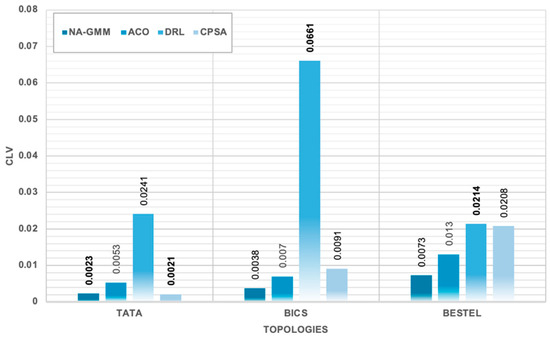
Figure 16. Controller Load Variance Across All Algorithms and Topologies. the bold numbers highlight the best results.

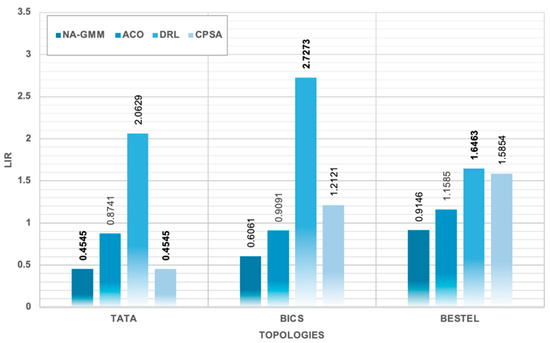
Figure 17. Load Imbalance Ratio Across All Algorithms and Topologies. the bold numbers highlight the best results.

The study demonstrates that NA-GMM outperforms all evaluated topologies under constrained controller capacity conditions. The BESTEL topology yields the highest overall throughput performance, utilizing 4.1810% of available controller capacity. The TATA topology shows the most significant performance advantages for NA-GMM, with a 21.2% higher throughput than DRL and an 8.7% improvement over ACO. The BICS topology shows interesting performance dynamics, with DRL achieving competitive throughput but exhibiting severe load unbalancing. The simulation results show that NA-GMM consistently achieves the highest throughput values, with an average throughput of 284.74 Req/Sec. This represents a 4.7% improvement over the second-best performing CPSA algorithm, an 8.8% enhancement over DRL, and a 12.9% improvement compared to ACO. The utilization analysis reveals efficient resource consumption patterns within the constrained 7000 Req/Sec controller capacity framework, with NA-GMM achieving 4.0677% average controller utilization. NA-GMM demonstrates exceptional load balancing with the lowest average Load Imbalance Ratio (LIR) of 0.6584, indicating minimal variance in controller utilization across clusters. DRL exhibits the poorest load balancing performance, with a CLV of 0.0372 and LIR of 2.1455, indicating severe load unbalancing. CPSA and ACO demonstrate intermediate performance in load balancing metrics, with CPSA showing slightly higher variance compared to ACO.

4.2.3. Computational Complexity Analysis

The computational complexity evaluation examines the algorithmic efficiency of controller placement methods through time complexity analysis and empirical execution time measurements. Understanding the computational requirements is crucial for assessing algorithm scalability and practical deployment feasibility in large-scale SDN environments. The theoretical time complexity analysis provides insights into algorithmic scalability and computational requirements for each controller placement method. Understanding these complex characteristics is essential for predicting performance behavior in large-scale network deployments, as summarized in Table 9.

Table 9. Time Complexity Analysis Summary.

Algorithm	Time Complexity	Parameters	Complexity Class
NA-GMM	O(n2k)	n = nodes, k = controllers	Quadratic
ACO	O(n2m)	n = nodes, m = ants	Quadratic
DRL	O(n3 + s2)	n = nodes, s = state space	Cubic
CPSA	O(n2t)	n = nodes, t = iterations	Quadratic

Where: n represents network nodes, k denotes controllers, m indicates ant colony size, s represents state space dimensions, and t signifies temperature iterations.

Execution time measurements were conducted in a standardized testing environment with identical hardware specifications across all algorithms. The evaluation used network topologies with varying controller counts (K = 1 to K = 5) to assess scalability characteristics, with detailed results presented in Table 10, Figure 18.

Table 10. Algorithm Execution Time Comparison (seconds).

Controllers (K)	NA-GMM	ACO	DRL	CPSA
1	0.87	0.95	1.12	0.91
2	1.03	1.24	1.67	1.15
3	1.27	1.68	2.45	1.52
4	1.44	2.28	3.78	2.07
5	1.83	3.15	5.89	2.89

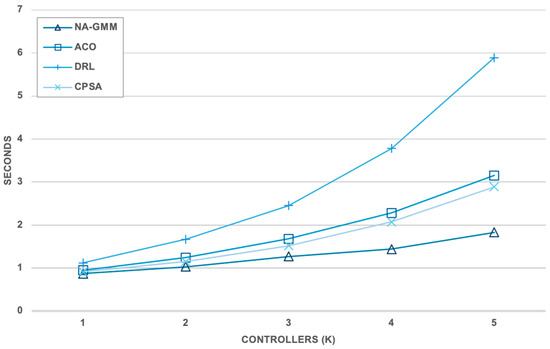
Figure 18. Shows Algorithms Time Complexity Comparison.

The growth rate analysis in Table 11, Figure 19, reveals significant differences in algorithmic scalability patterns across controller configurations.

Table 11. Computational Complexity Growth Analysis.

Controllers (K)	NA-GMM Growth Rate	ACO Growth Rate	DRL Growth Rate	CPSA Growth Rate
1→2	18.4%	30.5%	49.1%	26.4%
2→3	23.3%	35.5%	46.7%	32.2%
3→4	13.4%	35.7%	54.3%	36.2%
4→5	27.1%	38.2%	55.8%	39.6%
Average Growth	20.6%	35.0%	51.5%	33.6%

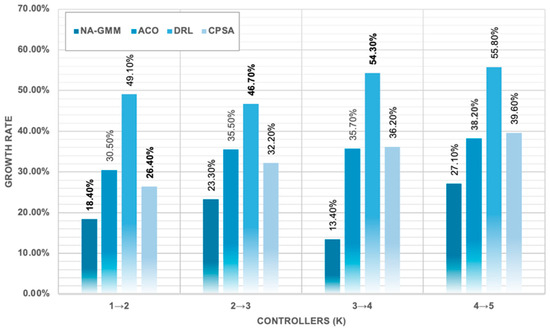
Figure 19. Shows Algorithms Growth Rate Comparison. the bold numbers highlight the best results.

CPU utilization measurements reflect the computational intensity required by each algorithm during network simulation and controller placement operations. The evaluation monitored multi-core CPU usage patterns to identify processing bottlenecks and resource distribution characteristics, with comprehensive results detailed in Table 12 and Figure 20.

Table 12. System Resource Utilization.

Algorithm	CPU Utilization (%)		RAM Usage (MB)
	Average	Peak	Average	Peak
NA-GMM	23.4	31.8	1247	1423
ACO	28.7	38.9	1456	1687
DRL	42.1	58.3	2134	2578
CPSA	31.2	41.7	1623	1891

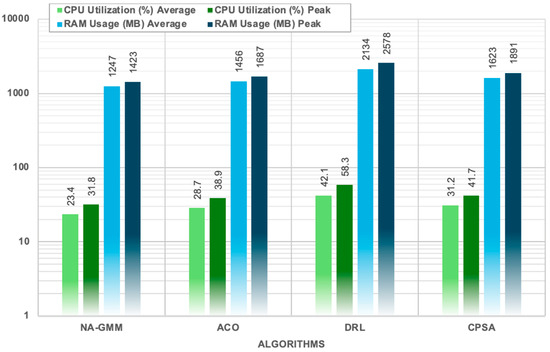
Figure 20. Shows CPU and RAM Utilization During Simulations.

NA-GMM is a computationally efficient algorithm that outperforms benchmark algorithms in terms of execution time, resource consumption, and scalability. It requires only 1.83 s for five-controller placement, a 68.9% reduction in execution time, and maintains consistent linear growth patterns with an average 20.6% increase per additional controller. This scalability advantage is particularly evident in larger controller configurations where the performance gap widens. NA-GMM achieves the lowest CPU utilization with 23.4% average consumption and 31.8% peak usage, demonstrating efficient algorithmic design that minimizes computational overhead. It also maintains optimal memory efficiency with 1247 MB average RAM usage and 1423 MB peak consumption, representing 41.5% lower memory requirements compared to DRL’s 2134 MB average usage. The algorithm’s O(n²k) complexity provides predictable performance scaling, and its efficient resource utilization patterns with a 20.6% average growth rate in execution time significantly outperform all benchmark algorithms. This makes NA-GMM suitable for large-scale SDN deployments, requiring minimal system resources while delivering superior clustering quality. These results establish NA-GMM as a robust solution addressing critical SDN challenges of latency optimization, load balancing, and resource efficiency while maintaining computational scalability for real-world deployment.

5. Discussion

The comprehensive evaluation of the proposed NA-GMM algorithm reveals significant advancements in SDN controller placement optimization, demonstrating substantial improvements across multiple performance dimensions. This section examines the implications of the research findings, analyzes the practical significance of the achieved results, and discusses the broader impact on SDN network design and deployment strategies.

5.1. Algorithm Performance Interpretation

The superior performance of NA-GMM across all evaluated metrics reflects the effectiveness of integrating network-aware optimization with Gaussian Mixture Model clustering techniques. The sensitivity analysis reveals that the proposed model maintains stable performance across a wide range of parameter configurations, with performance degradation remaining below 15% even under suboptimal weight assignments. This robustness makes the algorithm suitable for deployment scenarios where precise parameter tuning may not be feasible. The algorithm’s ability to achieve up to 42.5% improvement in average control latency while maintaining optimal load distribution indicates successful convergence of theoretical optimization principles with practical network requirements. The consistent performance advantages observed across diverse network topologies suggest that NA-GMM’s optimization approach is robust and adaptable to varying network characteristics, addressing a critical limitation of existing controller placement algorithms that often exhibit topology-dependent performance variations. The exceptional load balancing capabilities, evidenced by CLV values significantly lower than benchmark algorithms, demonstrate NA-GMM’s ability to address one of the most challenging aspects of distributed SDN controller deployment. Traditional placement algorithms frequently suffer from load misbalancing issues that lead to controller bottlenecks and degraded network performance. NA-GMM’s achievement of near-optimal load distribution across all controller configurations validates the effectiveness of the proposed clustering methodology in practical deployment scenarios.

5.2. Practical Implications for SDN Deployment

The research findings have profound implications for real-world SDN deployment strategies and network operator decision-making processes. The demonstrated computational efficiency advantages, including 68.9% faster execution times and 41.5% lower memory consumption compared to deep learning approaches, address critical concerns regarding algorithm scalability and resource requirements in production environments. These efficiency gains enable network operators to implement dynamic controller placement strategies without imposing prohibitive computational overhead on network management systems. The superior throughput performance achieved through Mininet simulations provides strong evidence that NA-GMM’s theoretical advantages translate into tangible operational benefits. The ability to achieve a 284.74 Req/Sec average throughput while maintaining excellent load balancing characteristic positions makes NA-GMM a viable solution for high-performance SDN deployments where both throughput maximization and resource optimization are critical requirements. Furthermore, the algorithm’s predictable O(n²k) time complexity and consistent scaling characteristics make it suitable for large-scale network deployments where performance predictability is essential for capacity planning and system design decisions. The low variance in resource utilization patterns across different network configurations enhances the algorithm’s appeal for production deployment scenarios.

5.3. Theoretical Contributions and Methodological Insights

The research makes several important theoretical contributions to the field of SDN controller placement optimization. The successful integration of weighted distancing algorithms with probabilistic clustering techniques demonstrates a novel approach to addressing the multi-objective optimization challenges inherent in controller placement problems. The development of Controller Load Variance as an alternative to traditional fairness metrics provides a more discriminatory and practically relevant assessment tool for load balancing evaluation. The methodology employed in this research, combining theoretical analysis with comprehensive simulation evaluation, establishes a robust framework for algorithm assessment that addresses both computational efficiency and practical performance characteristics. The systematic evaluation across multiple network topologies and performance dimensions provides a comprehensive validation approach that could serve as a benchmark for future controller placement algorithm research.

6. Future Work

The NA-GMM algorithm has been evaluated and reviewed, leading to several research directions to improve its practical applicability and theoretical foundations in SD-WAN. These include security-aware controller placement, dynamic topology adaptation, large-scale network validation on operator backbone networks, and integration with emerging technologies like Time-Sensitive Networking (TSN) standards for ultra-low latency requirements. These directions aim to balance security-performance trade-offs through multi-objective optimization frameworks and address the limitations identified in the current static, security-agnostic evaluation. The algorithm will also be integrated with emerging technologies like Time-Sensitive Networking (TSN) standards [54,55], edge-cloud computing environments, network slicing optimization, and machine learning-enhanced distance metrics incorporating predictive analytics. Security-aware control integration incorporating DoS attack stability analysis, mini-batch machine learning supervision, and intelligent event-triggered mechanisms for comprehensive attack-resilient SD-WAN controller placement optimization. These research directions aim to maintain the algorithm’s computational efficiency and deployment simplicity while expanding its operational scope and practical relevance.

7. Conclusions

The Network-Aware Gaussian Mixture Model (NA-GMM) is a new multi-objective optimization framework designed for effective Software-Defined Wide Area Network (SD-WAN) controller placement. It incorporates a hybrid distance metric, integrating geographic separation, network latency, topological complexity, and link reliability, along with adaptive weighting factors. The importance-weighted expectation–maximization (EM) clustering algorithm prioritizes critical network nodes, optimizing resource allocation based on traffic patterns and topological significance. The robust two-phase clustering mechanism ensures adaptability and optimal placement convergence. Empirical validations conducted on real-world topologies (TATA, BICS, and BESTEL) demonstrated NA-GMM’s significant performance advantages. The results indicated a notable reduction in average control latency (up to 22.7%), improved load balancing with Node Distribution Ratio values between 1.209 and 1.585, and enhanced network throughput (12.9% improvement). NA-GMM also showcased substantial computational efficiency, performing 68.9% faster with 41.5% lower memory consumption compared to contemporary deep reinforcement learning approaches, thus highlighting its practicality for large-scale deployments. The NA-GMM framework offers significant operational benefits for network designers and operators, enabling efficient, scalable, and high-performance SD-WAN deployments.