Abstract
This paper aims to investigate a Nash equilibrium (NE)-seeking approach for the aggregative game problem of second-order multi-agent systems (MAS) with uncontrollable malicious players, which may cause the decisions of global players to become uncontrollable, thereby hindering the ability of normal players to reach the NE. To mitigate the influence of malicious players on the system, a malicious player detection and disconnection (MPDD) algorithm is proposed, based on the fixed-time convergence method. Subsequently, a predefined-time distributed NE-seeking algorithm is presented, utilizing a time-varying, time-based generator (TBG) and state-feedback scheme, ensuring that all normal players complete the game problem within the predefined time. The convergence properties of the algorithms are analyzed using Lyapunov stability theory. Theoretically, the aggregative game problem with malicious players can be solved using the proposed algorithms within any user-defined time. Finally, a numerical simulation of electricity market bidding verifies the effectiveness of the proposed algorithm.
1. Introduction
In the context of aggregative games, each player updates its decision to optimize its local cost function, which depends on both its own decision and the aggregate of all players’ decisions. Any unilateral change made by a player will directly affect the global cost function through this aggregate. The aggregative game problem is prevalent in various fields, such as electric vehicle charging scheduling, energy network management, and drone network configuration (see [1,2,3]).
There has been considerable attention on NE-seeking algorithms for aggregative games, with many meaningful results presented in decentralized or semi-decentralized settings [4,5]. As large-scale systems continue to evolve, distributed strategies have attracted significant interest from researchers, primarily due to their reliance on local information exchange and their scalability. This has led to the further development of network games [6]. In many scenarios, the feasible sets of players’ decisions are interdependent, prompting studies on generalized NE (GNE)-seeking problems for aggregative games, where coupling constraints exist among the decisions of players. For example, the authors of [7] proposed an algorithm based on projected dynamics and nonsmooth tracking dynamics for aggregative games with coupled constraints. A single-layer distributed algorithm was introduced in [8], in which communication between players was only required when their decisions were updated. The variational generalized Nash equilibrium of a class of fuzzy set games was discussed in [9], where each participant’s cost function is fuzzy and nonsmooth, and the strategy configuration is subject to coupling constraints. Recently, reinforcement learning-based multi-agent game algorithms have attracted widespread attention (see, e.g., [10,11]).
To enable players to solve game problems autonomously, several works have combined game theory with physical systems. For example, distributed aggregative games have been studied for second-order nonlinear systems [12], multiple heterogeneous Euler–Lagrange systems [13,14], and players with linear or nonlinear dynamics perturbed by external disturbances [15,16]. In addition, numerous NE- or GNE-seeking problems in noncooperative games have been explored for first-order nonlinear systems [17], second-order systems [18], multi-integrator systems [19], high-order nonlinear systems [20], and population dynamics [21]. Furthermore, many works have focused on distributed resource allocation and optimization problems for second-order systems [22] and high-order nonlinear MASs [23]. These works can be classified into two categories: nominal systems [13,14,18,19,20,21,23,24] and disturbed systems [12,15,16,17,22].
It is clear that the dynamics of players play a crucial role in algorithm design. Specifically, the proposed algorithm must simultaneously ensure system stability and convergence of players’ decisions to the NE. Compared to nominal systems, algorithm design for disturbed systems is more challenging because it must account for the influence of disturbances on the system. However, all the aforementioned works on disturbed systems share a common feature: the perturbations must satisfy certain assumptions, such as being bounded, differentiable, or time-dependent [12,22], which are difficult to meet in practical applications, especially in systems subject to stochastic noise [25]. Moreover, a sufficiently large perturbation can be interpreted as a malicious attack, which may cause the system to become uncontrollable. Examples include military equipment attacked by enemies, battlefield explosions, or servers in cyber-physical systems compromised by hackers. In aggregative games, since the cost function of players depends on global decisions, the existence of even a single maliciously attacked player prevents the decisions of all players from converging to the optimal solution. In such cases, conventional compensation-based methods are no longer applicable.
It is worth noting that, to date, few works have addressed NE seeking in aggregative games with malicious players. However, many approaches have been proposed in the study of resilient consensus in MASs under malicious attacks, such as the trusted-region-based sliding-window weighted approach for single-integrator MASs [26], the delayed impulsive control strategy for second-order integral MASs [27], the attack-isolation-based approach [28], and the appointed-time observer-based approach [29] for higher-order MASs, where the appointed-time observer-based approach significantly relaxes the graph requirement to only needing a directed spanning tree, handles general linear agent dynamics, and operates asynchronously; however, it relies on reliable communication channels for state exchange and is primarily designed for controller attacks rather than communication channel attacks or Byzantine faults. The isolation-based approach achieves resilient consensus in higher-order networks via distributed fixed-time observers and graph isolability. It requires undirected topologies and two-hop neighbor information, limiting scalability in sparse networks compared to neighbor-value exclusion methods like MSR. The impulsive control method eliminates the need to know the number of malicious agents by leveraging trusted nodes and delayed sampled data, but it requires pre-labeled trusted agents and is limited to double-integrator dynamics. All of these approaches require first detecting the attacked players. In contrast to resilient consensus problems, there is less information interaction between players in aggregative games. For example, the output and state of players cannot directly interact with each other, which increases the difficulty of detecting attacked players. Additionally, the objective of each player in an aggregative game is to optimize its local cost function, rather than to reach consensus. Recent surveys, such as [30,31], comprehensively categorize intermittent control methods for multi-agent systems (MASs) under limited communication, highlighting strategies to reduce resource consumption via periodic sampling and event-triggered mechanisms. However, they exhibit limitations in adversarial settings, particularly when malicious players disrupt the optimization process in non-cooperative games, due to their reliance on cooperative dynamics.
Motivated by the above discussion, this paper focuses on aggregative games for second-order MASs under malicious attacks. The primary objective is to develop an approach that detects attacked players within a fixed time and disconnects them from normal players. Ultimately, the decisions of normal players are designed to converge to the NE within the predefined time. The main contributions of this paper are outlined as follows:
- This work considers malicious players who are uncontrollable and can influence the evolution of normal players’ decisions. In contrast to existing works that consider perturbations and eliminate their effects using compensation methods [12,15,16,17,22], this work treats the influence of malicious attacks as less conservative and more representative of real-workd conditions, thereby rendering existing algorithms inapplicable.
- Due to the limited information exchange between neighbors, a virtual system and a distributed observer are introduced to detect and disconnect malicious players. A novel MPDD algorithm, based on the fixed-time convergence method, is proposed to ensure that all malicious players are disconnected from normal players within a fixed time.
- A predefined-time distributed NE-seeking algorithm is proposed, based on the time-varying TBG scheme, to ensure that the decisions of all normal players converge to an arbitrarily small neighborhood of the NE within the predefined time and exponentially converge to the NE after the predefined time. Convergence analysis is performed using Lyapunov stability theory.
The remainder of this paper is organized as follows. In Section II, the necessary preliminaries are introduced and our problem is formulated. In Section III, the main results of this paper are presented, including the MPDD algorithm and the NE-seeking algorithm, along with an analysis of their convergence. In Section IV, a numerical example is presented to verify the effectiveness of the proposed algorithms. In Section V, we present the conclusions.
Notations: In this paper, , , , and denote the set of real numbers, the set of nonnegative real numbers, the set of n-dimensional real vector spaces, and the set of real matrix spaces, respectively. denotes the transpose of matrix A. , and is the ith element of vector x, defined as . denotes the standard Euclidean norm, and ⊗ denotes the Kronecker product. and are the column vectors of n ones and zeros, respectively. denotes an identity matrix. , and is a standard sign function. Given that a set-valued function is convex, if and , . A function is -strongly monotone () if . A function is -Lipschitz () if , .
2. Preliminaries
2.1. Graph Theory
Consider a graph , where is the set of vertices, is the set of edges, and is the adjacency matrix. Each entry of the matrix satisfies if , and otherwise. Additionally, . Denote and . The Laplacian matrix of the graph is . denotes the ith eigenvalue of the matrix L, and for . An undirected graph is connected if there is a path between each pair of nodes. Then, we have and . To facilitate description, we do not discriminate among agents, players, and nodes.
2.2. Problem Formulation
Consider an aggregative game problem with N players, where their communication topology is described by a graph with the node set . There are two types of players in the system: normal players and malicious players. The dynamics of player i are described as
where and represent the position and velocity of player i, respectively; represents the control input; is an unknown time-varying function denoting the influence of malicious attacks; and denote the sets of normal players and malicious players, respectively; and .
Remark 1.
To simplify the description of complicated situations, the dynamics of malicious players are expressed as , . This means that malicious players update their position state without following the preset control algorithm due to malicious attacks, which may occur in the control input or actuator sensor. In this paper, the position state is regarded as the output and decision of players. Therefore, the dynamics of malicious player can also be expressed as
The two types of players are defined below.
Definition 1.
Normal players are those who update their decisions according to the preset control algorithm and send the actual information to all their neighbors. Malicious players, on the other hand, update their decisions but do not follow the preset control algorithm, and the information transmitted to their neighbors is distorted.
Each player has a local cost function that is only available to itself, where represents the decisions of players other than i. Let , and let the aggregate function denote the aggregate of all players’ decisions, indicating that each player’s cost function is affected by the decisions of others. It is defined as
where is a (nonlinear) function representing the local contribution to the aggregate and is globally Lipschitz continuous. The aggregate function specifies the gradients of cost functions as with a function , and , where is the estimate of the aggregate function by player i (because contains global decision information that is not available to players). Moreover, is defined by stacking together the gradients of the cost functions of all players as .
The NE-seeking strategy for MASs considers the influence of the decisions of other players and adjusts the control input to minimize their cost function . Due to the existence of uncontrollable malicious players, the evolution of their decisions does not depend on the designed algorithm and may mislead the game task. Therefore, the objective of this paper is to detect malicious players and filter them out so that all normal players’ decisions reach the NE. That is, each normal player i faces the following optimization problem:
For the game (3), the decision of player is the NE if , which means that no agent can decrease its cost function by unilaterally changing to any other feasible point.
Some standard assumptions are given below, which are widely used in NE-seeking problems (see, e.g., [7,12,32]).
Assumption 1.
The undirected graph considered in this paper is connected.
Assumption 2.
The cost function is convex with respect to for every fixed and is continuously differentiable in , .
Assumption 3.
is ω-strongly monotone and μ-Lipschitz continuous in .
Assumption 4.
There exists at least one normal player among the neighbors of each normal player, and malicious players are not the root node of the communication graph.
Remark 2.
Assumption 1 is the premise that players communicate with neighbors. Assumptions 2 and 3 ensure the existence and uniqueness of the NE solution. By Assumption 4, there is at least one connected edge between all normal players.
Lemma 1
([12]). By Assumptions 2 and 3, is the NE of the game (3) if and only if
where denotes the number of normal players.
Lemma 2
([33]). Suppose that a graph is undirected and connected. For its Laplacian matrix L and any non-unit vector x, we have the following conclusion:
where and denote the second smallest eigenvalue of L and the largest eigenvalue of , respectively.
Lemma 3
([34]). Consider the following system:
where , and is a nonlinear function. There exists a positive, continuously differentiable, and radially unbounded function such that for any solution , , where the parameters satisfy , and . Then, the origin point of system (6) is globally fixed-time stable, and the convergence time satisfies .
3. Algorithm Design for Aggregative Games with Malicious Players
Based on the above analysis, in this section, algorithms are designed to detect and disconnect malicious players, as well as for NE seeking by normal players.
Unlike existing consensus and non-cooperative game problems, in which agents (or neighbors in distributed interactions) can exchange decision-making information, the aggregative game problem presents a different challenge. In this case, players do not directly exchange decision information, and even the function that governs the decision variables cannot be shared. This lack of information exchange makes it impossible to identify malicious individuals by simply comparing interaction data between players. Inspired by the resilient consensus problem in [28], we address the aggregative game problem with malicious players using the following three steps:
- (1)
- Fixed-time stability: A fixed-time stabilization algorithm is developed to ensure that the decisions of all normal players stabilize within a fixed time.
- (2)
- Malicious player detection and disconnection: A malicious player detection and isolation algorithm is designed to detect and disconnect each malicious player from the normal players.
- (3)
- Predefined-time convergence: A predefined-time distributed NE-seeking algorithm is proposed to ensure that all normal players’ decisions converge to the NE at the predefined time.
Remark 3.
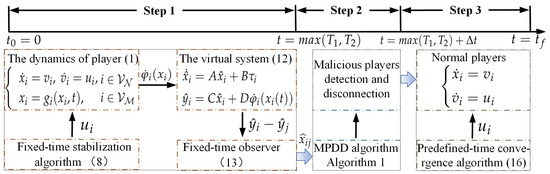
In the flowchart depicted in Figure 1, Steps 1 and 2 serve as additional processes aimed at eliminating the influence of malicious players on normal players. Specifically, the virtual systems and the observer function as hidden layers that do not interfere with the state updates of the players. Unlike noncooperative games or consensus problems, in the aggregative game considered in this paper, state information cannot be exchanged between neighbors. Given this premise, detecting malicious players through state-error calculations is not feasible. Therefore, a novel detection algorithm is proposed.

Figure 1.
Execution process of NE-seeking strategy with malicious players.
3.1. Fixed-Time Stabilization Algorithm
To account for the influence of malicious attacks, a fixed-time convergence algorithm is designed to ensure that the system states of normal players stabilize within a finite time. In contrast, the states of malicious players do not stabilize.
The dynamics of the players (1) imply that convergence of the velocity state to the origin is both a necessary and sufficient condition for the system’s stability. Based on this, a fixed-time stabilization algorithm for player , is designed as follows:
where and are constants. Combining Algorithm (7) and system (1), we get the closed-loop system as
Then, we are in a position to give the following lemma.
Lemma 4.
Proof.
As discussed in Section 3.1, we only need to analyze the stability of the speed state at the origin point. Choose a candidate Lyapunov function as .
Taking the derivative of along (8), we have
With the inequalities that for , and , we can get
Then, (9) can be rewritten as
From Lemma 3, we can deduce that the convergence time satisfies . □
Remark 4.
Lemma 4 illustrates that the states of all normal players are stable for . Meanwhile, the function is stable, which implies that , . For malicious player , however, . Thereafter, can be used as the impact of malicious attacks for the detection of malicious players.
3.2. Detecting and Disconnecting Malicious Players
Due to the fact that a player’s decision , the function , and cannot directly interact with those of neighboring players, it is not possible, for any player , to determine whether the decision information of its neighbors converges to a fixed value based on the fixed-time stability algorithm. Consequently, we cannot identify which neighbors are uncontrollable. First, a virtual system is introduced as
where , and denote the system state, output, and input, respectively, and their dimensions satisfy and . are the constant known system matrices satisfying the corresponding dimensions.
Remark 5.
In the virtual system (12), is appended to the output as an external variable, which affects the update of the system state based on the output feedback algorithm. Then, a consensus problem is defined for the detection of malicious players.
As discussed above, the consensus error for player i with its neighbor j is defined as . The distributed fixed-time observer relying on the relative output is introduced by referring to [35] to estimate the consensus error at the fixed time as
where and are auxiliary variables, with the initial value set to 0 for . is the estimation of . The other matrices are defined as
and , where , , and is the observer gain such that is stable. Additionally, . Invoking Theorem 1 in [35] and Lemma 1 in [28], we obtain the following lemma.
Lemma 5.
Lemma 5 introduces a method for detecting malicious players. Specifically, we can determine whether a player or its neighbors are malicious by evaluating whether the estimation error equals zero. Building on the results from Algorithm (7) and the fixed-time observer, the MPDD algorithm is summarized below.
Theorem 1.
Suppose that Assumptions 1 and 4 hold. All malicious players can be disconnected from normal players under the MPDD algorithm.
Proof.
Remark 6.
Referring to the proof of Theorem 1 in [35], the output of the observer in (13) is independent of the input from the virtual system in (12) and depends solely on the relative output. In contrast to [28] and [35], the consensus error in this paper is defined as the state error between a player and its neighbor, rather than as the sum of state errors across all neighbors. The goal of the MPDD algorithm is to disconnect normal players from malicious players and eliminate the influence of malicious players on the evolution of normal players’ decisions. Notably, it is not necessary to know the identities of the malicious players. Therefore, there is no need to obtain information about two-hop neighbors (i.e., the neighbors of a player’s neighbors). Furthermore, Assumption 4 ensures that the communication graph among normal players remains connected after all malicious players are disconnected.
| Algorithm 1 MPDD algorithm |
|
3.3. Predefined-Time Convergence Algorithm
In this subsection, a distributed NE-seeking algorithm is developed to ensure that all players’ decisions converge to the NE at a predefined time. First, the definition of predefined-time convergence is given.
Definition 2.
The TBG is defined as the following continuous, differentiable function:
Lemma 6
([36,37]). Consider a dynamic system of the following form:
where ε is a positive parameter and with . converges to at a predefined time irrespective of the initial value .
For the game (3) of multi-agent systems described in (1), a predefined-time distributed NE-seeking algorithm is designed as
where is an auxiliary variable, and , and c are positive constants to be determined later. is the time-varying function parameter described in Lemma 6, and the selection of and is aimed at achieving a faster convergence rate and obtaining the predefined-time convergence condition in (33).
Define and . Substituting Algorithm (16) into system (1), we get the closed-loop system in compact form:
Then, we obtain the following lemma regarding (17).
Lemma 7.
Proof.
From (18a) and (18b), we get . Since the communication graph is undirected and connected (i.e., and ), it follows from (18d) that , where . Substituting (18d) into (18c), we obtain
Left-multiplying both sides of the above equation by , we have
Given that , it follows that
Conversely, if is the NE of the game (3), from Lemma 1, we have
It is obvious that (18a), (18b), and (18d) hold. For any , there exists such that . Under Assumption 1, , so . By the fundamental theorem of linear algebra [38], L can be orthogonally decomposed by ker(L) and range(L). Hence, and , and there exists satisfying . In summary, is the equilibrium point of (17). □
Remark 7.
Theorem 2.
Suppose that Assumptions 1-3 hold, and the parameters satisfy , , and for system (1) without malicious players, then the aggregative game (3) can be solved by Algorithm (16) in a predefined time , that is,
where , is the Lyapunov function defined in (25), and Θ and Φ are positive definite matrices defined below.
Proof.
Define , , , , , and . From (17) and (18), one can obtain the following error system:
Take the candidate Lyapunov function as
where , . Obviously, is positive definite, and we have . The time derivative of V with respect to (24) is
According to the value range of and , we get
Note that is -strongly monotone and -Lipschitz continuous, so one can derive that
By Lemma 2, we have the following inequalities:
It follows from Young’s inequality for , and from the fact that is l-Lipschitz continuous, that
Substituting the above inequalities into (26) yields
Since , then , and is negative definite. From (31), one can obtain that
where , , and . From the definitions of , and c, is positive definite, and we have
where denotes the smallest eigenvalue of . From Lemma 6 and the comparison principle, we can deduce that
Moreover, since , we can obtain
For , , we have . We can derive that
Combined with Lemma 7, the above analysis implies that the decision variables x exponentially converge to the NE of the game (3). □
Remark 8.
While resilient consensus methods like [27,28,29] detect malicious agents by leveraging state consensus objectives (i.e., ), our work pioneers a fundamentally different approach tailored to non-consensus aggregative games, in which players optimize individual cost functions. Key innovations include the following:
- (1)
- Problem Transformation: We introduce fixed-time stabilization to generate a detectable signal (specifically, the constancy of for normal agents versus its variability for malicious agents), thereby enabling the adaptation of observer-based detection to game-theoretic settings that lack inherent consensus mechanisms.
- (2)
- Time-Guaranteed Architecture: Unlike the asymptotic and finite-time detection methods in [27,28,29], our MPDD algorithm guarantees* fixed-time isolation within , while the TBG-based NE seeking achieves predefined-time convergence to equilibrium, which is a capability absent in prior game-theoretic works.
- (3)
- Unified Security-Game Framework: We unify malicious player mitigation and game-theoretic optimization into a single protocol with dual time guarantees, addressing security and performance objectives simultaneously. This framework diverges fundamentally from neighbor-value exclusion (e.g., MSR) or robust connectivity methods.
4. Numerical Example
In this section, a numerical example is given to verify the effectiveness of the proposed algorithms. A competition scenario in the electricity market involving six generation systems is considered, where the communication topology is modeled by a connected undirected graph, as depicted in Figure 2.
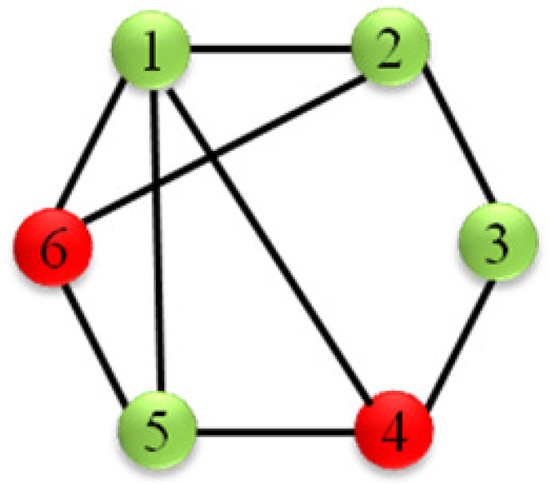
Figure 2.
Communication graph. The green nodes represent normal systems, and the red nodes represent malicious systems.
Each generation system has the following cost function:
where and are the output electrical power and the generation cost of system i, respectively. The generation cost is usually approximated by a quadratic function: , where , and are cost coefficients. The term is the aggregate function, and and are constants. Let , and the other parameters are listed in Table 1.

Table 1.
System parameters.
The system matrix of the virtual system is given by
The observer gain matrices are chosen as
The malicious systems, 4 and 6, are described as
where and represent the effects of malicious attacks, defined as and , with denoting white noise with power 1.
For Equation (7), choose parameters , , and such that . For the distributed fixed-time observer, let the time delay . The simulation results corresponding to Lemmas 4 and 5 are shown in Figure 3 and Figure 4. As seen in Figure 3b, the velocity state of the normal system converges to 0 within the fixed time , whereas the velocity states of the malicious systems do not converge due to the malicious attacks. Figure 4 shows the estimation error , . For , we observe the following: ; ; ; ; ; and . Therefore, it can be deduced that systems 4 and 6, or their neighbors, are malicious. To isolate the malicious influence, we just need to disconnect systems 4, 6, and their immediate neighbors from the normal systems.
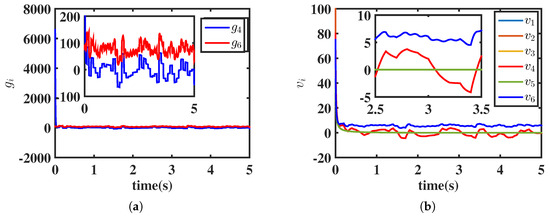
Figure 3.
(a) Influence of malicious attacks. (b) Evolution of velocity states under Equation (7).
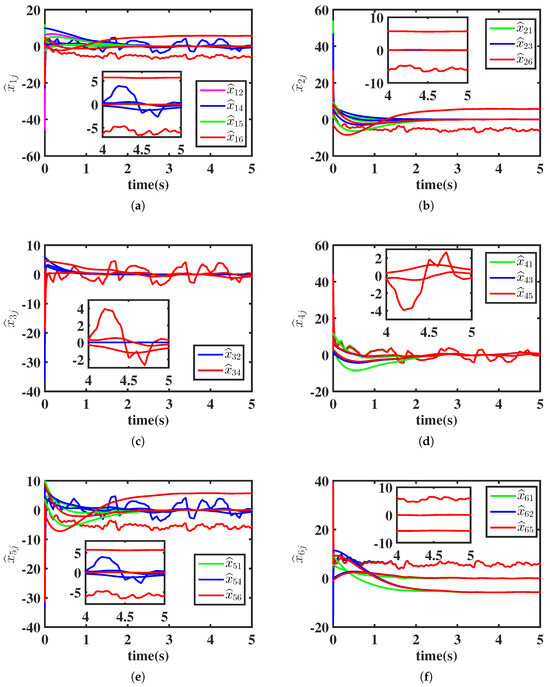
Figure 4.
Estimation error based on the observer (13) and Algorithm 1, where s and s. (a) Estimation error by Agent 1, (b) Estimation error by Agent 2, (c) Estimation error by Agent 3, (d) Estimation error by Agent 4, (e) Estimation error by Agent 5, (f) Estimation error by Agent 6.
Assume that all malicious systems have been disconnected from the normal systems for s. The predefined-time distributed NE-seeking algorithm is then implemented. Let the initialization time be s and the predefined time be s. The TGB is designed as
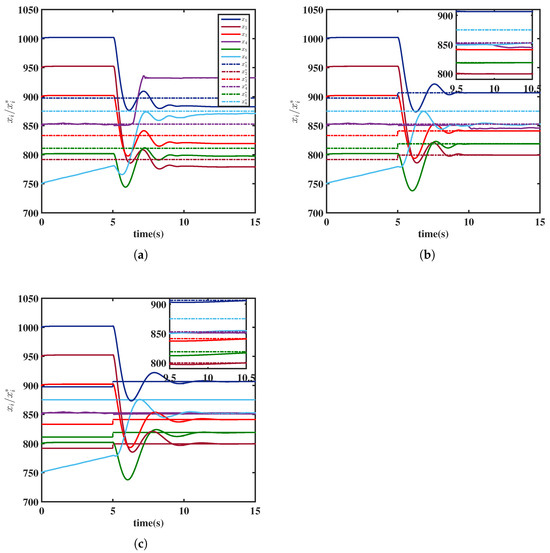
Before the malicious systems are disconnected, the NE solution of the six systems can be manually calculated as . After the malicious systems are disconnected, i.e., for , the new NE solution for the remaining four systems is calculated as . Let , , , and . The evolution of the generation system outputs is shown in Figure 5. As illustrated in Figure 5a, the outputs of all systems cannot converge to the NE due to the existence of malicious systems. Figure 5b shows that the outputs of the normal systems eventually converge to the new NE at the predefined time under the MPDD algorithm and (16). For comparison, Figure 5c displays the outputs under Equation (16) without the TBG, i.e., with , where it can be seen that the convergence time exceeds the predefined time. In summary, the simulation results verify the effectiveness of the proposed algorithms.
5. Conclusions
This paper investigated a predefined-time distributed aggregative game for second-order MASs with malicious players. A novel malicious player detection and disconnection algorithm was proposed, incorporating a fixed-time stabilization technique and a distributed fixed-time observer, which ensures that all malicious players are disconnected from normal players within a predefined time. Subsequently, to ensure that the decisions of normal players converge to the new NE, a predefined-time distributed NE-seeking algorithm was introduced, combining the TBG scheme with a state-feedback approach. The convergence properties of the proposed method were analyzed using Lyapunov stability theory. Numerical simulations demonstrated the effectiveness of the overall framework.
Inspired by [30,31,39], integrating event-triggered schemes (ETSs) into our framework is a critical next step. Potential enhancements include (i) a deception-aware ETS for the MPDD observer to reduce communication overhead during detection; (ii) dynamic triggering rules aligned with the TBG’s time-varying gain to minimize gradient exchanges; and (iii) co-design of security thresholds and triggering conditions to balance resilience with resource efficiency. Current limitations include the following: (1) the proposed method assumes a static communication topology and thus requires further extension to dynamic networks with mobile agents; and (2) it relies on global knowledge of monotonicity and Lipschitz constants for parameter tuning, limiting its plug-and-play applicability in unknown environments. Future work will address these issues by developing more flexible communication schemes and designing fully distributed Nash equilibrium-seeking algorithms that do not rely on global information.
Author Contributions
Conceptualization, X.H. and Z.Z.; methodology, X.H.; software, H.F.; validation, X.H. and Z.C.; investigation, Z.Z.; data curation, H.F.; writing—original draft preparation, X.H.; writing—review and editing, Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant U21A20518 and U23A20341, in part by the Hunan Key Research and Development Program under Grant 2024JK2057.
Data Availability Statement
All data generated or analyzed during this study are included in this article.
Conflicts of Interest
Author Zhengchao Zeng and Haolong Fu were employed by the company Hunan Vanguard Group Corporation Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Liu, Z.; Wu, Q.; Huang, S.; Wang, L.; Shahidehpour, M.; Xue, Y. Optimal Day-Ahead Charging Scheduling of Electric Vehicles Through an Aggregative Game Model. IEEE Trans. Smart Grid 2018, 9, 5173–5184. [Google Scholar] [CrossRef]
- Chen, Y.; Yi, P. Multi-Cluster Aggregative Games: A Linearly Convergent Nash Equilibrium Seeking Algorithm and Its Applications in Energy Management. IEEE Trans. Netw. Sci. Eng. 2024, 11, 2797–2809. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Q.; Jiang, H.; Wang, H.; Xie, Y.; Xu, W.; Zhou, P.; Xu, Z.; Chen, L.; Li, B.; et al. Joint Power and Coverage Control of Massive UAVs in Post-Disaster Emergency Networks: An Aggregative Game-Theoretic Learning Approach. IEEE Trans. Netw. Sci. Eng. 2024, 11, 3782–3799. [Google Scholar] [CrossRef]
- Grammatico, S.; Parise, F.; Colombino, M.; Lygeros, J. Decentralized Convergence to Nash Equilibria in Constrained Deterministic Mean Field Control. IEEE Trans. Autom. Control 2016, 61, 3315–3329. [Google Scholar] [CrossRef]
- Belgioioso, G.; Grammatico, S. Semi-Decentralized Generalized Nash Equilibrium Seeking in Monotone Aggregative Games. IEEE Trans. Autom. Control 2023, 68, 140–155. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, W.; Wen, G.; Chen, G. Distributed Nash Equilibrium Seeking in an Aggregative Game on a Directed Graph. IEEE Trans. Autom. Control 2021, 66, 2746–2753. [Google Scholar] [CrossRef]
- Liang, S.; Yi, P.; Hong, Y. Distributed Nash equilibrium seeking for aggregative games with coupled constraints. Automatica 2017, 85, 179–185. [Google Scholar] [CrossRef]
- Gadjov, D.; Pavel, L. Single-Timescale Distributed GNE Seeking for Aggregative Games Over Networks via Forward-Backward Operator Splitting. IEEE Trans. Autom. Control 2021, 66, 3259–3266. [Google Scholar] [CrossRef]
- Liu, J.; Liao, X.; Dong, J.S.; Mansoori, A. Continuous-Time Distributed Generalized Nash Equilibrium Seeking in Nonsmooth Fuzzy Aggregative Games. IEEE Trans. Control Netw. Syst. 2024, 11, 1262–1274. [Google Scholar] [CrossRef]
- Liang, J.; Miao, H.; Li, K.; Tan, J.; Wang, X.; Luo, R.; Jiang, Y. A Review of Multi-Agent Reinforcement Learning Algorithms. Electronics 2025, 14, 820. [Google Scholar] [CrossRef]
- Zeng, W.; Yan, X.; Mo, F.; Zhang, Z.; Li, S.; Wang, P.; Wang, C. Knowledge-Enhanced Deep Reinforcement Learning for Multi-Agent Game. Electronics 2025, 14, 1347. [Google Scholar] [CrossRef]
- Deng, Z. Distributed Nash equilibrium seeking for aggregative games with second-order nonlinear players. Automatica 2022, 135, 109980. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, G. Distributed Optimization for Aggregative Games Based on Euler-Lagrange Systems With Large Delay Constraints. IEEE Access 2020, 8, 179272–179280. [Google Scholar] [CrossRef]
- Huang, Y.; Meng, Z.; Sun, J. Distributed Nash Equilibrium Seeking for Multicluster Aggregative Game of Euler–Lagrange Systems With Coupled Constraints. IEEE Trans. Cybern. 2024, 54, 5672–5683. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Xiao, F.; Wei, B.; Yu, M.; Fang, F. Nash Equilibrium Seeking for General Linear Systems With Disturbance Rejection. IEEE Trans. Cybern. 2023, 53, 5240–5249. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liang, S.; Wang, X.; Ji, H. Distributed Nash Equilibrium Seeking for Aggregative Games With Nonlinear Dynamics Under External Disturbances. IEEE Trans. Cybern. 2020, 50, 4876–4885. [Google Scholar] [CrossRef]
- Huang, B.; Zou, Y.; Meng, Z. Distributed-Observer-Based Nash Equilibrium Seeking Algorithm for Quadratic Games With Nonlinear Dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7260–7268. [Google Scholar] [CrossRef]
- Ye, M. Distributed Nash Equilibrium Seeking for Games in Systems With Bounded Control Inputs. IEEE Trans. Autom. Control 2021, 66, 3833–3839. [Google Scholar] [CrossRef]
- Shi, X.; Su, Y.; Huang, D.; Sun, C. Distributed Aggregative Game for Multi-Agent Systems With Heterogeneous Integrator Dynamics. IEEE Trans. Circuits Syst. II Express Br. 2024, 71, 2169–2173. [Google Scholar] [CrossRef]
- Ai, X.; Wang, L. Distributed adaptive Nash equilibrium seeking and disturbance rejection for noncooperative games of high-order nonlinear systems with input saturation and input delay. Int. J. Robust Nonlinear Control 2021, 31, 2827–2846. [Google Scholar] [CrossRef]
- Tan, S.; Wang, Y.; Vasilakos, A.V. Distributed Population Dynamics for Searching Generalized Nash Equilibria of Population Games With Graphical Strategy Interactions. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3263–3272. [Google Scholar] [CrossRef]
- Li, S.; Nian, X.; Deng, Z. Distributed resource allocation of second-order multiagent systems with exogenous disturbances. Int. J. Robust Nonlinear Control 2020, 30, 1298–1310. [Google Scholar] [CrossRef]
- Huang, B.; Zou, Y.; Meng, Z.; Ren, W. Distributed Time-Varying Convex Optimization for a Class of Nonlinear Multiagent Systems. IEEE Trans. Autom. Control 2020, 65, 801–808. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, H.; Zhang, Y. Event-Triggered Discrete-Time ZNN Algorithm for Distributed Optimization with Time-Varying Objective Functions. Electronics 2025, 14, 1359. [Google Scholar]
- Du, Y.; Wang, Y.; Zuo, Z.; Zhang, W. Stochastic bipartite consensus with measurement noises and antagonistic information. J. Frankl. Inst. 2021, 358, 7761–7785. [Google Scholar] [CrossRef]
- Zhai, Y.; Liu, Z.W.; Guan, Z.H.; Wen, G. Resilient Consensus of Multi-Agent Systems With Switching Topologies: A Trusted-Region-Based Sliding-Window Weighted Approach. IEEE Trans. Circuits Syst. II Express Br. 2021, 68, 2448–2452. [Google Scholar] [CrossRef]
- Zhai, Y.; Liu, Z.W.; Guan, Z.H.; Gao, Z. Resilient Delayed Impulsive Control for Consensus of Multiagent Networks Subject to Malicious Agents. IEEE Trans. Cybern. 2022, 52, 7196–7205. [Google Scholar] [CrossRef]
- Zhao, D.; Lv, Y.; Yu, X.; Wen, G.; Chen, G. Resilient Consensus of Higher Order Multiagent Networks: An Attack Isolation-Based Approach. IEEE Trans. Autom. Control 2022, 67, 1001–1007. [Google Scholar] [CrossRef]
- Zhou, J.; Lv, Y.; Wen, G.; Yu, X. Resilient Consensus of Multiagent Systems Under Malicious Attacks: Appointed-Time Observer-Based Approach. IEEE Trans. Cybern. 2022, 52, 10187–10199. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.; Zhang, X.; Ding, D.; Ning, B. Distributed coordination control of multi-agent systems under intermittent sampling and communication: A comprehensive survey. Sci. China Inf. Sci. 2025, 68, 151201. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Q.; Ge, X.; Ding, D.; Ning, B.; Zhang, B. An overview of recent advances in event-triggered control. Sci. China Inf. Sci. 2025, 68, 161201. [Google Scholar] [CrossRef]
- Belgioioso, G.; Nedić, A.; Grammatico, S. Distributed Generalized Nash Equilibrium Seeking in Aggregative Games on Time-Varying Networks. IEEE Trans. Autom. Control 2021, 66, 2061–2075. [Google Scholar] [CrossRef]
- Godsil, C.; Royle, G. Algebraic Graph Theory; Springer: New York, NY, USA, 2001. [Google Scholar]
- Polyakov, A. Nonlinear Feedback Design for Fixed-Time Stabilization of Linear Control Systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Lv, Y.; Wen, G.; Huang, T. Adaptive Protocol Design For Distributed Tracking With Relative Output Information: A Distributed Fixed-Time Observer Approach. IEEE Trans. Control Netw. Syst. 2020, 7, 118–128. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, G. Predefined-Time Distributed Optimal Allocation of Resources: A Time-Base Generator Scheme. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 438–447. [Google Scholar] [CrossRef]
- Li, S.; Nian, X.; Deng, Z.; Chen, Z. Predefined-time distributed optimization of general linear multi-agent systems. Inf. Sci. 2022, 584, 111–125. [Google Scholar] [CrossRef]
- Strang, G. The fundamental theorem of linear algebra. Am. Math. Mon. 1993, 100, 848–855. [Google Scholar] [CrossRef]
- Kazemy, A.; Lam, J.; Zhang, X.M. Event-Triggered Output Feedback Synchronization of Master–Slave Neural Networks Under Deception Attacks. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 952–961. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).