Consistency-Oriented SLAM Approach: Theoretical Proof and Numerical Validation
Abstract
1. Introduction
- We propose an interval analysis-based monocular SLAM algorithm that employs an undelayed, bounded-error parametric approach, coupled with a consistency-preserving solution technique. The consistency performance was tested and compared through numerical experiments.
- We present for the first time, a theoretical study and proof of the obtained consistency of the interval analysis-based SLAM method, which could promote applications in safety-critical robotic scenarios.
- In addition, we propose a novel consistency-evaluation method for experimentally validating the consistency of the interval analysis-based location and mapping algorithm.
2. Overview of Interval Analysis and Constraint Propagation
2.1. Interval Analysis and Arithmetic
- Addition:
- Subtraction:
- Multiplication:
- Division:
2.2. Interval Constraint Satisfaction Problem
- A set V consisting of n variables, denoted as .
- A set D consisting of n domains, denoted as . Each variable is associated with a domain containing its possible values.
- A set C consisting of p constraints, denoted as . Each constraint defines a relationship over a subset of variable set V.
2.3. Interval Constraint Propagation (ICP)
3. Interval Analysis-Based Monocular SLAM Algorithm
3.1. Problem Statement
3.2. iMonoSLAM Formulation
3.3. Robot Pose Prediction Stage
3.4. Mapping and Robot Pose Correction Stage
3.4.1. Landmark Parameterization
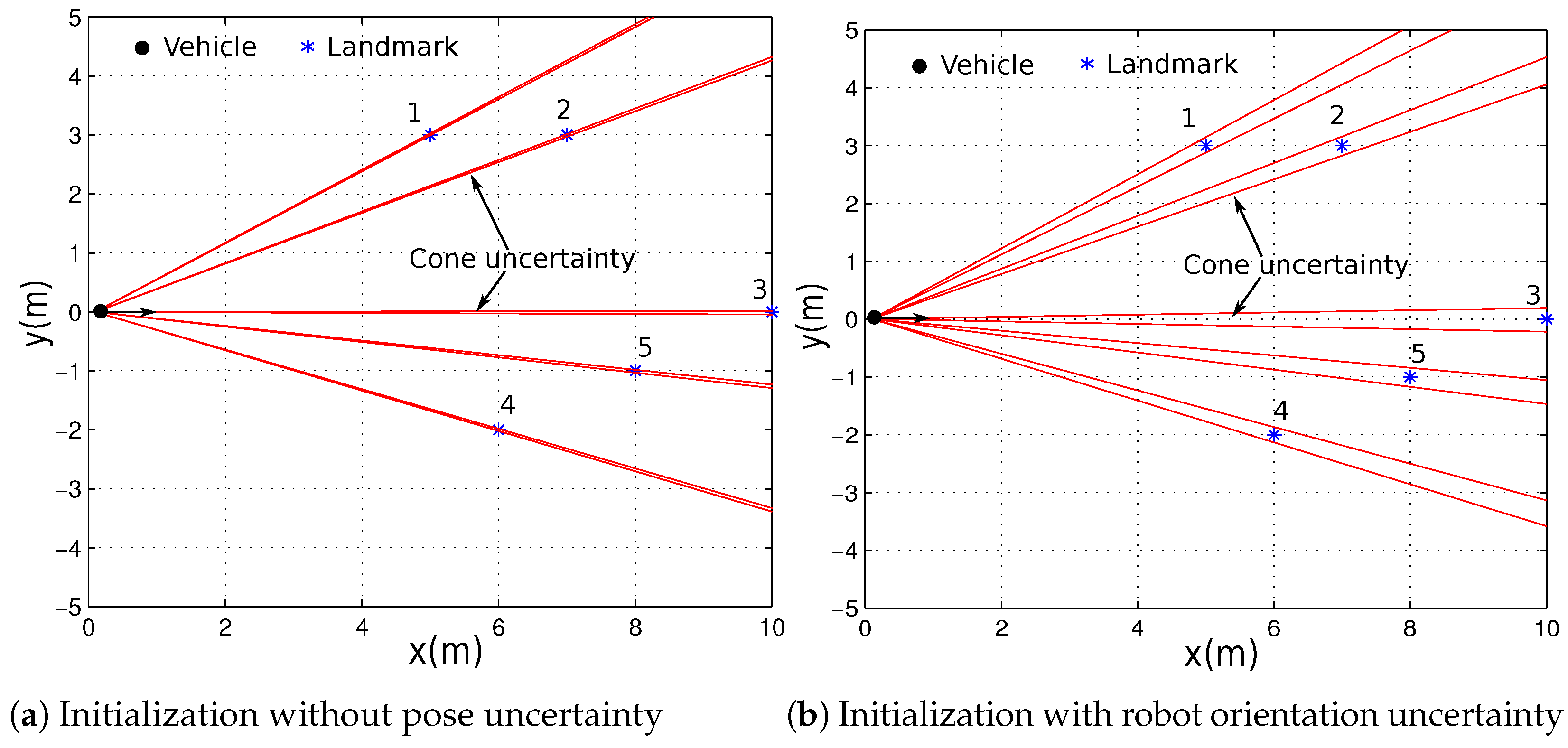
3.4.2. Undelayed Landmark Initialization
- : is the robot position, which is also the camera position for the sake of simplicity. When several landmarks are detected at the same time, they share the same parameter domains.
- , : is the robot heading orientation, and and are the azimuth and elevation angles which are inferred from the pixel coordinate of the feature point related to the landmark . and correspond to an opening and elevation angle, defined by the pinhole model:are the intrinsic parameters of the camera, where f is the focal length, is the principal point, and is the number of pixels per unit length. They can be determined by a camera calibration process.
- : the unknown depth of the landmark; the initialization is guaranteed to contain the real value of for sure.
3.4.3. ICSP-Based Landmark and Robot’s Pose Estimation
- A set of nine variables:
- A set of nine domains:
- A set of two top-level constraints:
4. Theoretical Analysis and Evaluation of Mapping Consistency
4.1. Proposition of Theoretical Basis
4.2. iMonoSLAM Mapping Consistency Statement
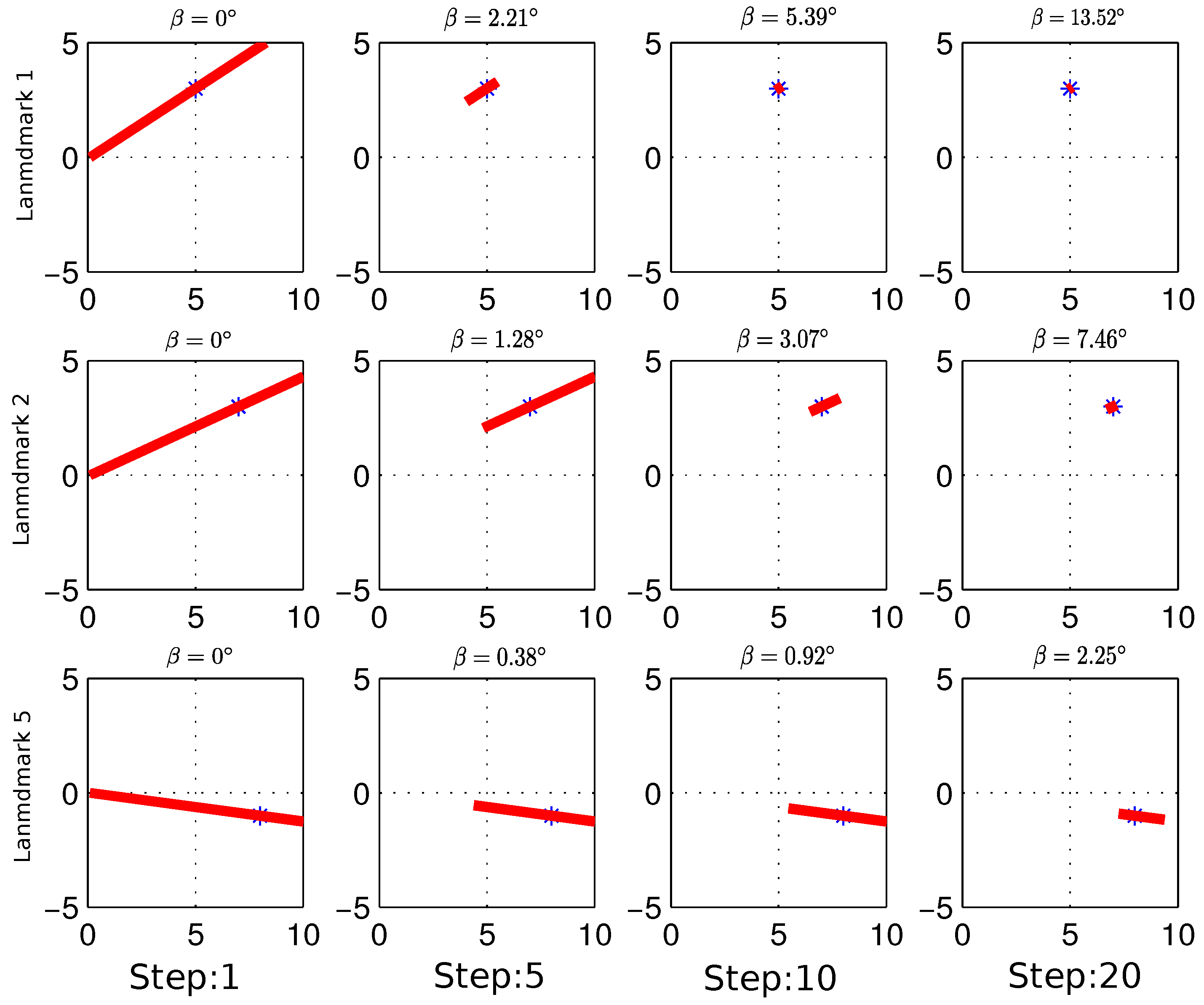
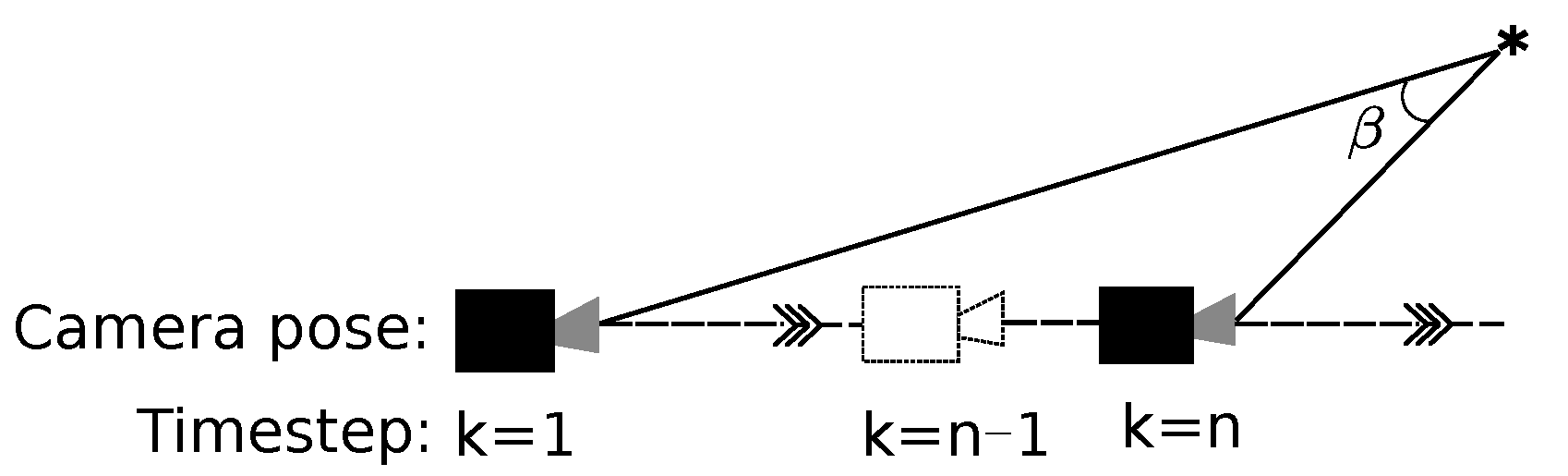
4.3. Proposition of Consistency-Evaluation Method
5. Simulation Result of iMonoSLAM
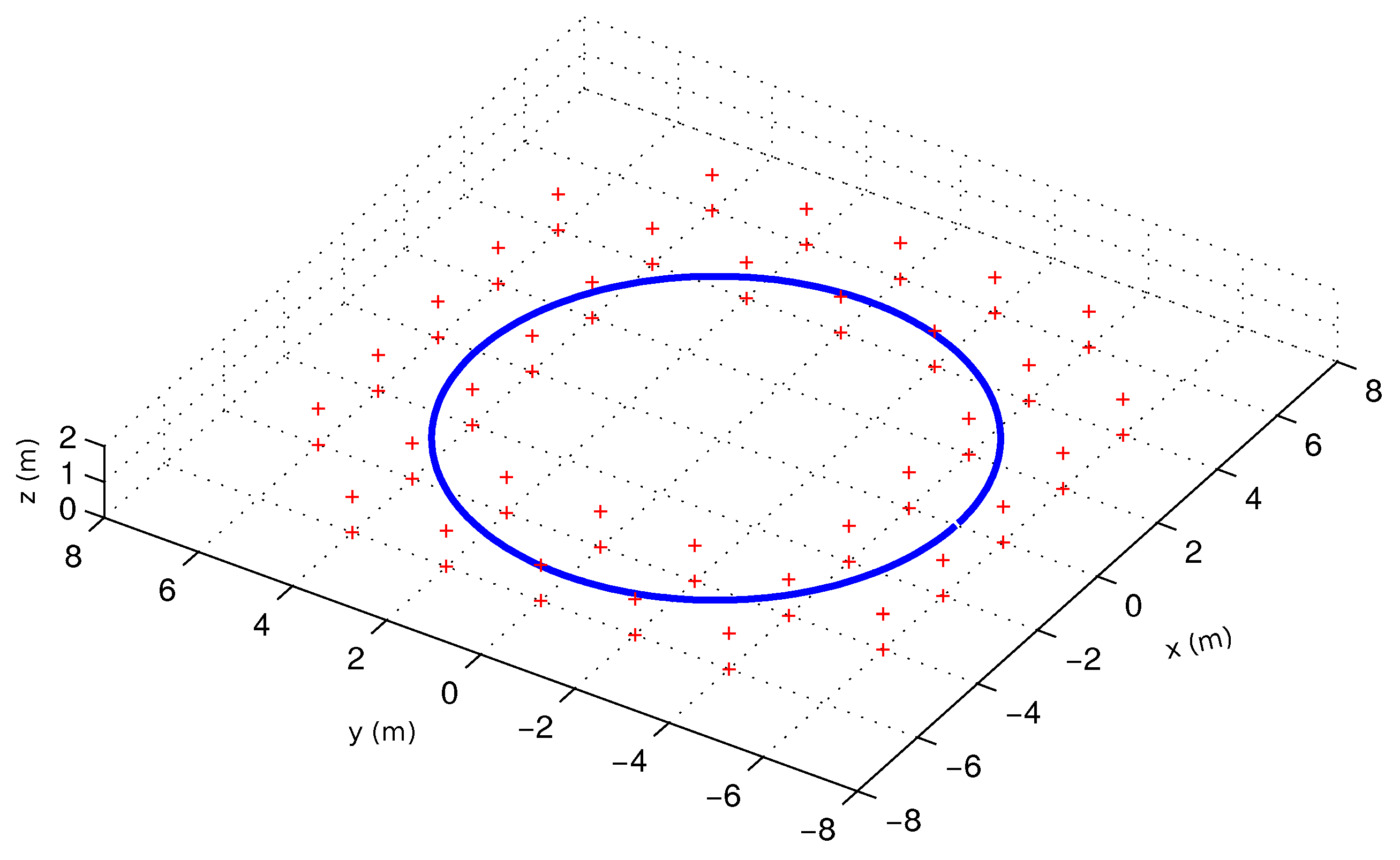
5.1. Experimental Setup
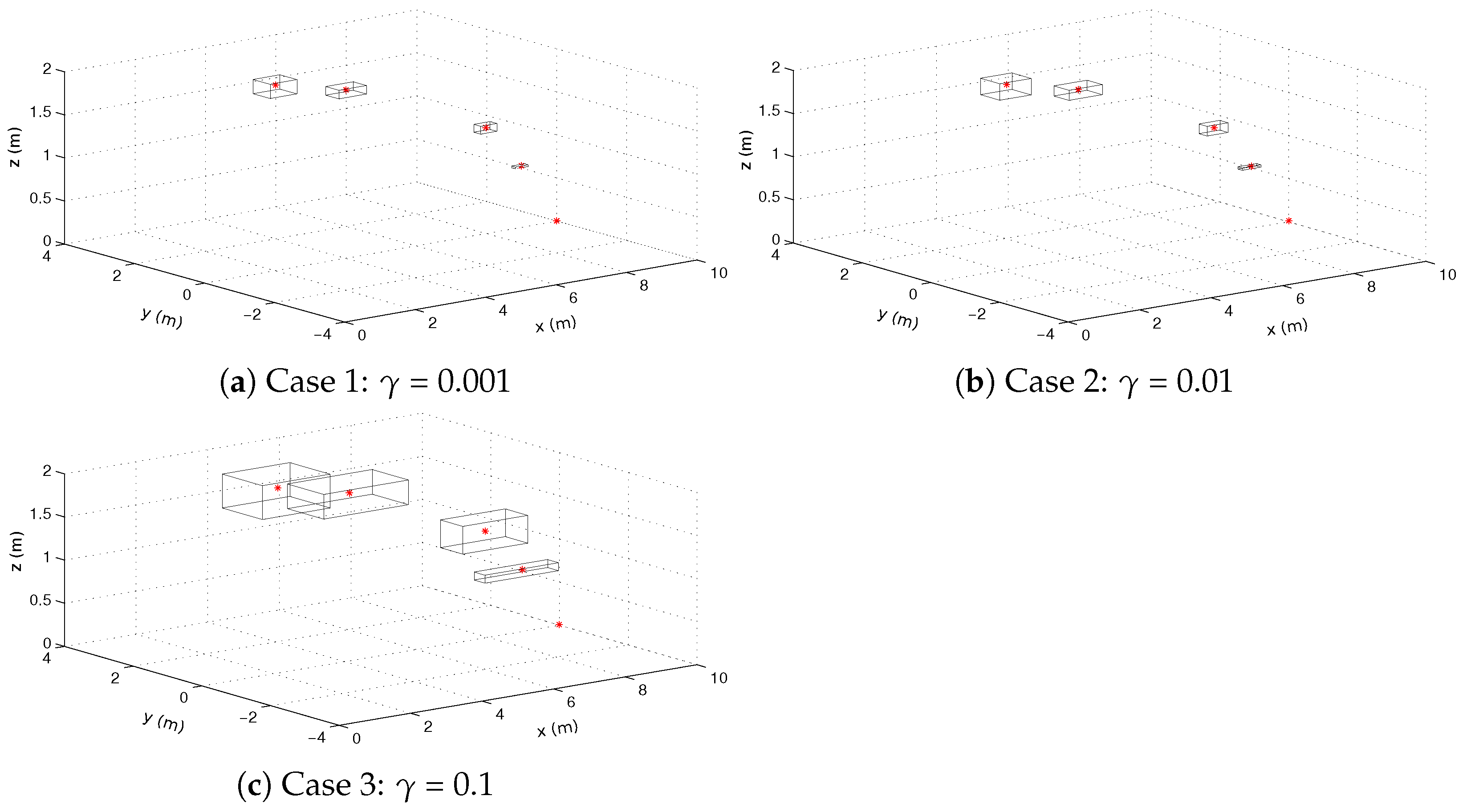
5.2. Landmark Initialization and Estimation
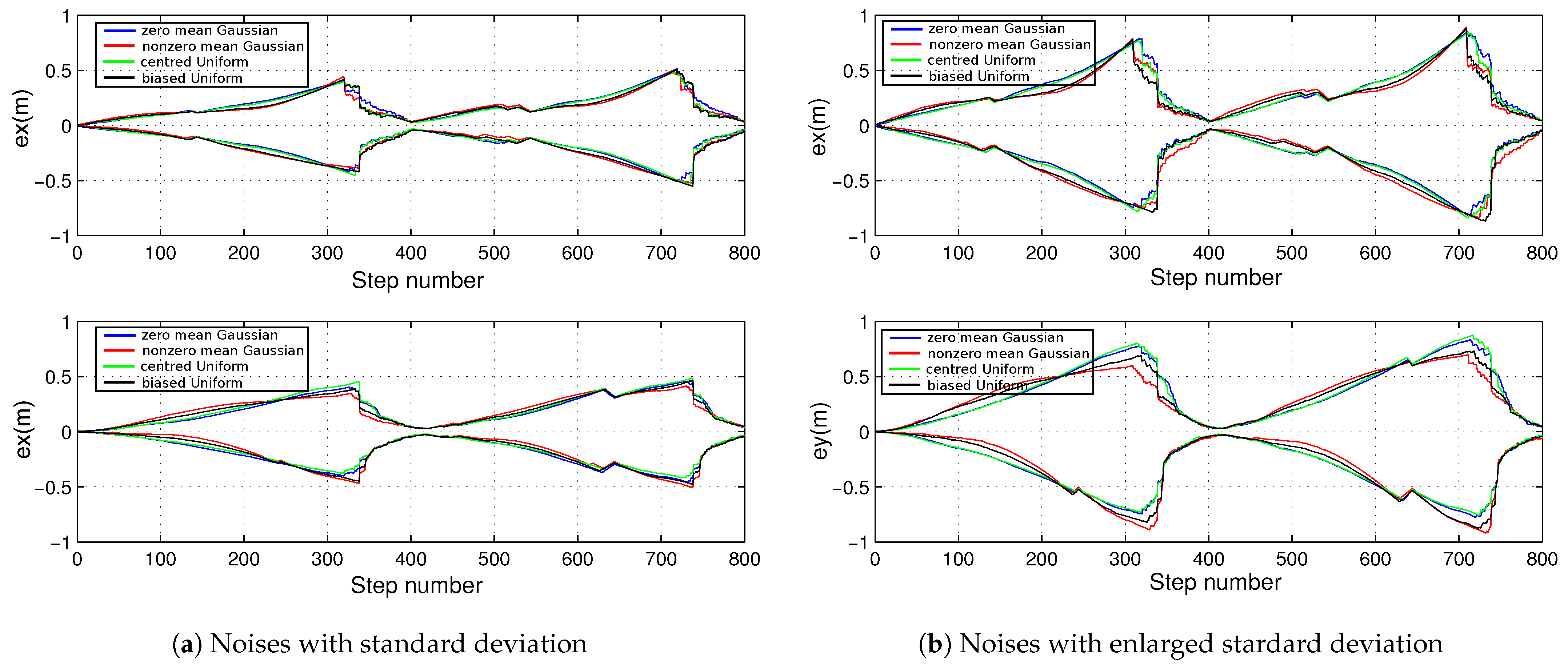
5.3. Analysis of the Effects of Odometric Noise
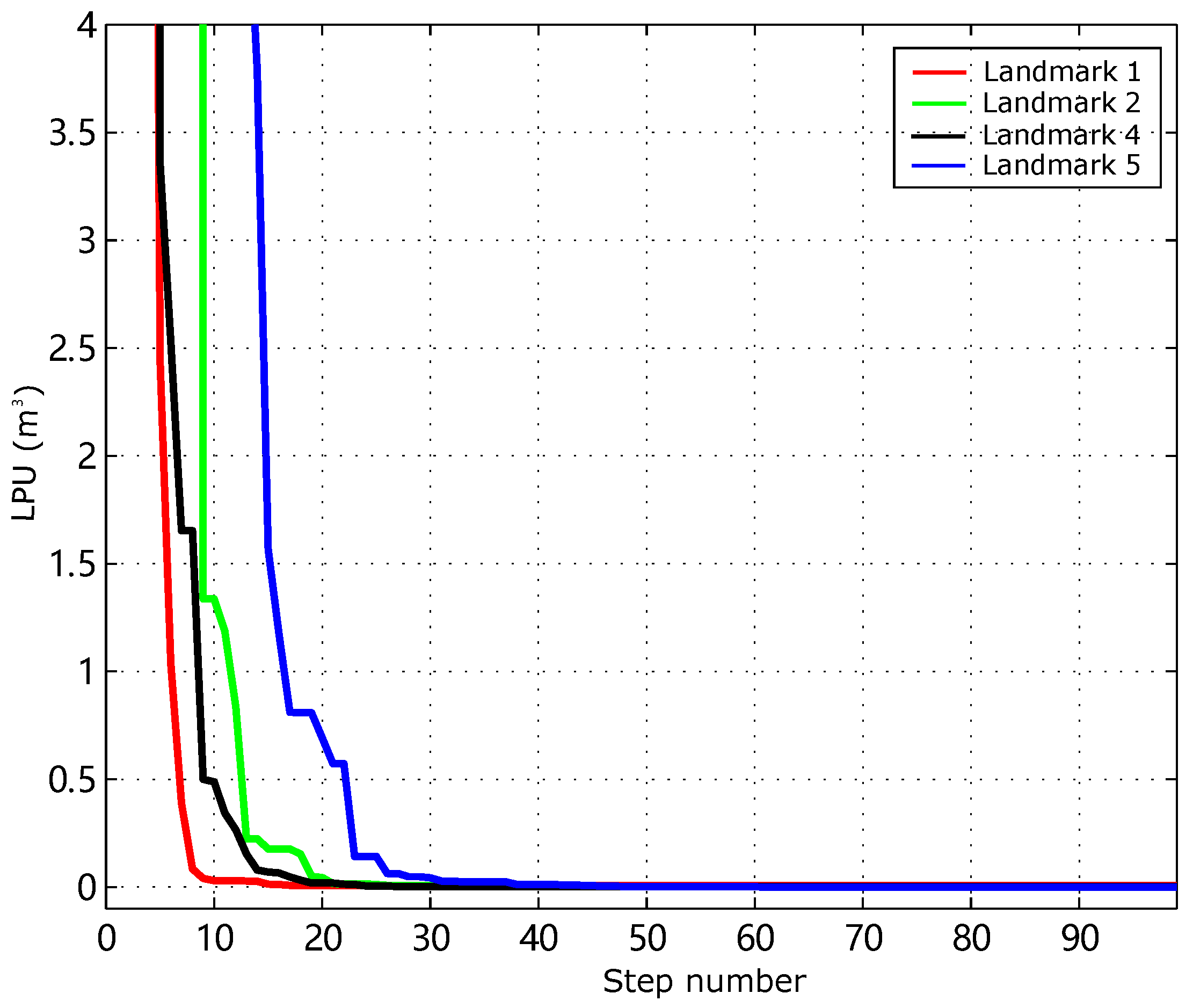
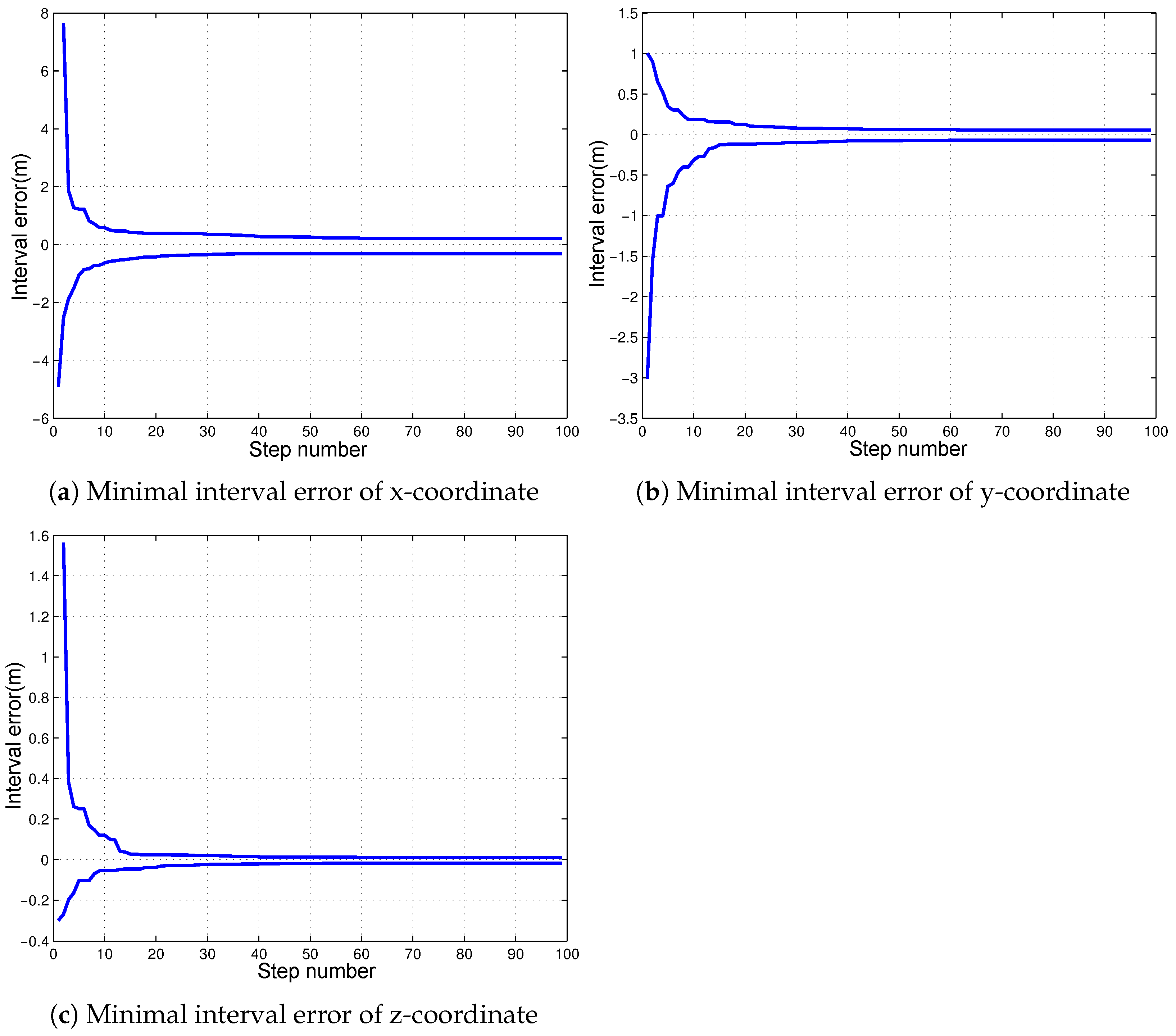
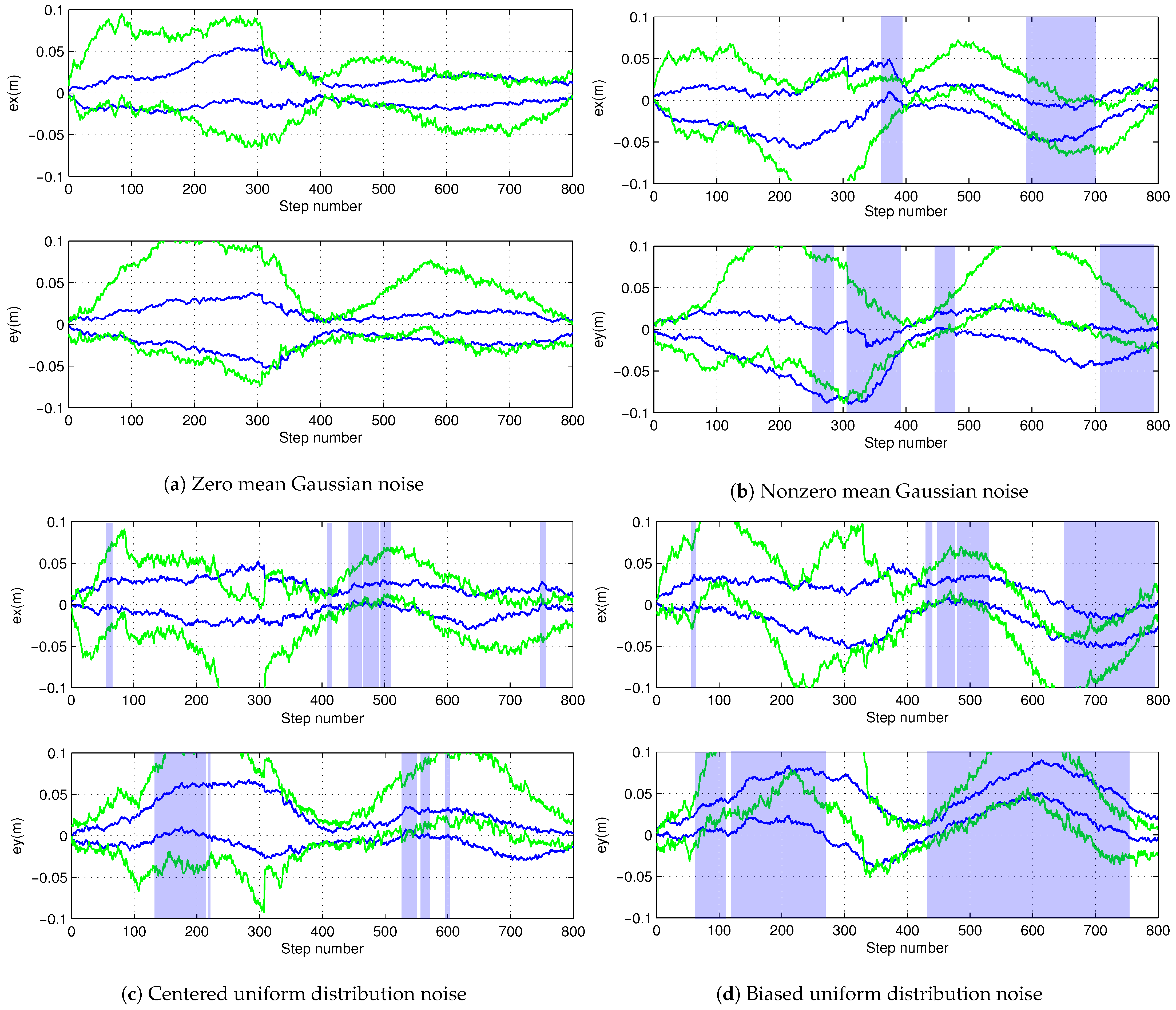
5.4. Consistency Validation of Mapping Result
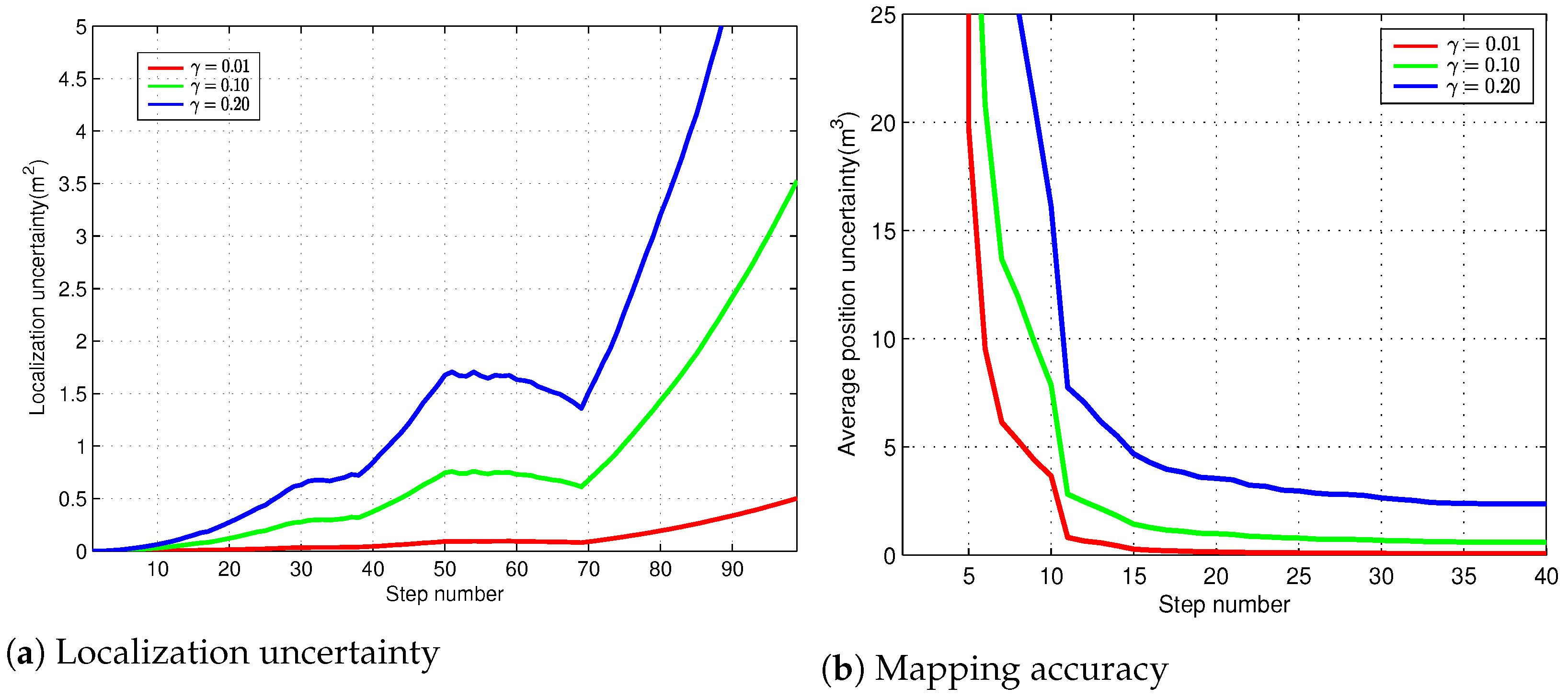
6. Comparison Between iMonoSLAM and EKF-SLAM
6.1. Localization Result Comparison
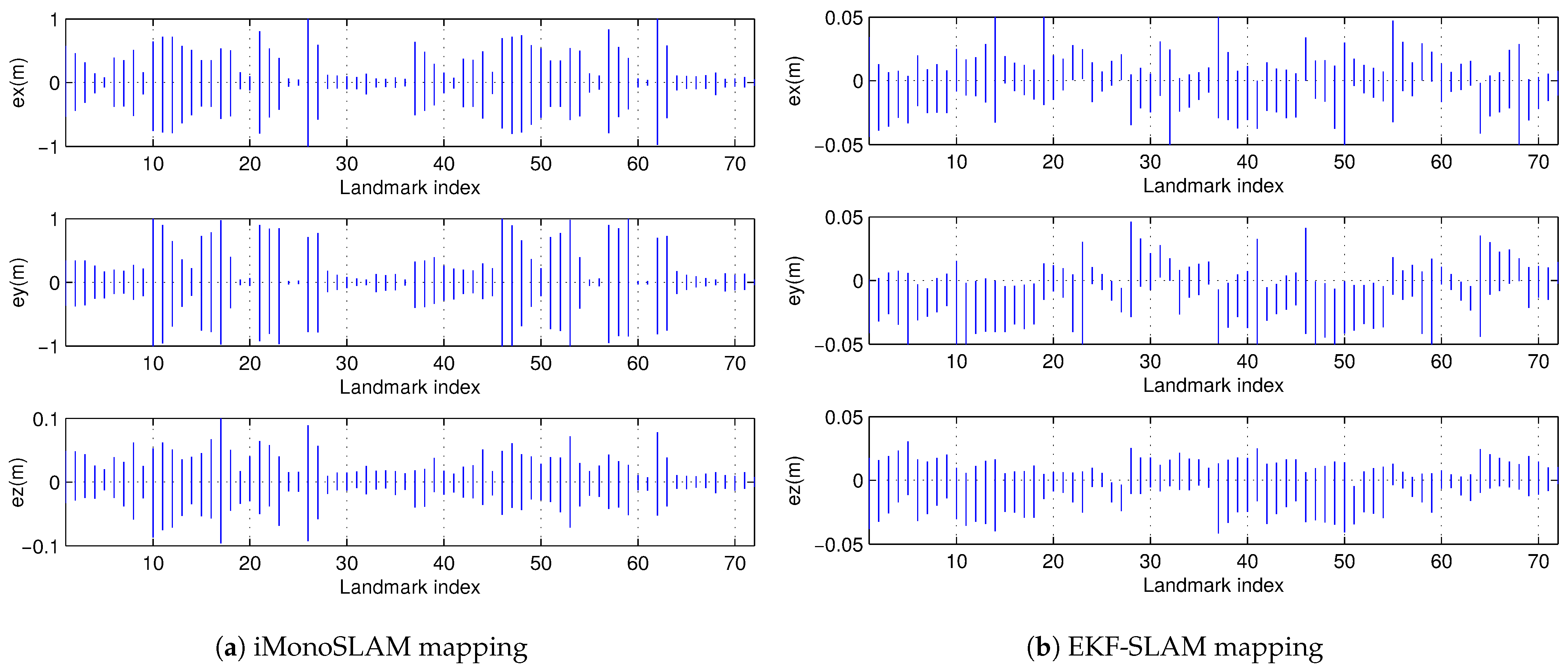
6.2. Mapping Consistency Comparison
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Li, Y.; Cao, Z.; Lv, J.; Huang, Z.; Zhang, W. LiDAR-Inertial SLAM with DEM-driven Global Constraints for Planetary Rover Exploration. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, XLVIII-3-2024, 615–621. [Google Scholar] [CrossRef]
- Teng, S.; Mueller, M.W.; Sreenath, K. Legged Robot State Estimation in Slippery Environments Using Invariant Extended Kalman Filter with Velocity Update. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 3104–3110. [Google Scholar] [CrossRef]
- Steuernagel, S.; Baum, M. Extended Object Tracking by Rao-Blackwellized Particle Filtering for Orientation Estimation. IEEE Trans. Signal Process. 2025, 73, 2590–2602. [Google Scholar] [CrossRef]
- Tian, C.; Hao, N.; He, F. T-ESKF: Transformed Error-State Kalman Filter for Consistent Visual-Inertial Navigation. IEEE Robot. Autom. Lett. 2025, 10, 1808–1815. [Google Scholar] [CrossRef]
- Rozsypálek, Z.; Rouček, T.; Vintr, T.; Krajník, T. Multidimensional Particle Filter for Long-Term Visual Teach and Repeat in Changing Environments. IEEE Robot. Autom. Lett. 2023, 8, 1951–1958. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, K.; Song, J.; Huang, S.; Dissanayake, G. Convergence and consistency analysis for a 3-D invariant-EKF SLAM. IEEE Robot. Autom. Lett. 2017, 2, 733–740. [Google Scholar] [CrossRef]
- Jamaludin, A.; Mohamad Yatim, N.; Mohd Noh, Z.; Buniyamin, N. Rao-blackwellized particle filter algorithm integrated with neural network sensor model using laser distance sensor. Micromachines 2023, 14, 560. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.; Guo, N.; Cen, Z. Obstacle Avoidance With Dynamic Avoidance Risk Region for Mobile Robots in Dynamic Environments. IEEE Robot. Autom. Lett. 2022, 7, 5850–5857. [Google Scholar] [CrossRef]
- Han, W.; Jasour, A.; Williams, B. Non-Gaussian Uncertainty Minimization Based Control of Stochastic Nonlinear Robotic Systems. arXiv 2023, arXiv:2303.01628. [Google Scholar] [CrossRef]
- Mohanty, S.; Naskar, A.K. Analysis of the Performance of Extended Kalman Filtering in SLAM Problem. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 1031–1036. [Google Scholar] [CrossRef]
- Ehambram, A.; Voges, R.; Brenner, C.; Wagner, B. Interval-based Visual-Inertial LiDAR SLAM with Anchoring Poses. In Proceedings of the 2022 IEEE International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 7589–7596. [Google Scholar] [CrossRef]
- Mustafa, M.; Stancu, A.; Delanoue, N.; Codres, E. Guaranteed SLAM–An interval approach. Robot. Auton. Syst. 2018, 100, 160–170. [Google Scholar] [CrossRef]
- Wang, Z.; Lambert, A.; Zhang, X. Dynamic ICSP Graph Optimization Approach for Car-Like Robot Localization in Outdoor Environments. Computers 2019, 8, 63. [Google Scholar] [CrossRef]
- Wang, Z.; Lambert, A. A Low-Cost Consistent Vehicle Localization Based on Interval Constraint Propagation. J. Adv. Transp. 2018, 2018, 2713729. [Google Scholar] [CrossRef]
- Wang, Z.; Lambert, A. A reliable and low cost vehicle localization approach using interval analysis. In Proceedings of the IEEE International Conference on Dependable, Autonomic and Secure Computing, Athens, Greece, 12 August 2018; pp. 480–487. [Google Scholar]
- Di Marco, M.; Garulli, A.; Lacroix, S.; Vicino, A. Set membership localization and mapping for autonomous navigation. Int. J. Robust Nonlinear Control 2001, 11, 709–734. [Google Scholar] [CrossRef]
- Drocourt, C.; Delahoche, L.; Brassart, E.; Marhic, B.; Clérentin, A. Incremental construction of the robot environmental map using interval analysis. In Proceedings of the International Workshop on Global Optimization and Constraint Satisfaction, Lausanne, Switzerland, 18–21 November 2003; Springer: Lausanne, Switzerland, 2003; pp. 127–141. [Google Scholar]
- Jaulin, L.; Kieffer, M.; Didrit, O.; Walter, E. Applied Interval Analysis: With Examples in Parameter and State Estimation, Robust Control and Robotics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Porta, J.M. CuikSlam: A kinematics-based approach to SLAM. In Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18 April 2005; pp. 2425–2431. [Google Scholar]
- Jaulin, L. A nonlinear set membership approach for the localization and map building of underwater robots. IEEE Trans. Robot. 2009, 25, 88–98. [Google Scholar] [CrossRef]
- Jaulin, L. Range-only slam with occupancy maps: A set-membership approach. IEEE Trans. Robot. 2011, 27, 1004–1010. [Google Scholar] [CrossRef]
- Ou, Y.; Fan, J.; Zhou, C.; Cheng, L.; Tan, M. Water-MBSL: Underwater Movable Binocular Structured Light-Based High-Precision Dense Reconstruction Framework. IEEE Trans. Ind. Inform. 2024, 20, 6142–6154. [Google Scholar] [CrossRef]
- Codreş, A.; Codreş, B.; Stancu, A. Guaranteed SLAM-A pure interval approach. In Proceedings of the International Conference on System Theory, Control and Computing, Sinaia, Romania, 19 October 2022; pp. 176–181. [Google Scholar]
- Mohamed, M. Guaranteed SLAM–An Interval Approach. Ph.D. Thesis, University of Manchester, Manchester, UK, 2017. [Google Scholar]
- Moore, R.E.; Kearfott, R.B.; Cloud, M.J. Introduction to Interval Analysis; Society for Industrial Mathematics: Philadelphia, PA, USA, 2009. [Google Scholar]
- Khun, J.; Schmidt, J. Interval Constraint Satisfaction: Towards Edge Acceleration. In Proceedings of the 2022 11th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 7–11 June 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Cleary, J.G. Logical arithmetic. Future Comput. Syst. 1987, 2, 125–149. [Google Scholar]
- Xu, W.; Pan, Y.; Chen, X.; Ding, W.; Qian, Y. A Novel Dynamic Fusion Approach Using Information Entropy for Interval-Valued Ordered Datasets. IEEE Trans. Big Data 2023, 9, 845–859. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kueviakoe, K.; Wang, Z.; Lambert, A.; Frenoux, E.; Tarroux, P. Localization of a Vehicle: A Dynamic Interval Constraint Satisfaction Problem-Based Approach. J. Sens. 2018, 2018, 3769058. [Google Scholar] [CrossRef]
| Noise Level | 0 ∈ | |||
|---|---|---|---|---|
| = 0.001 | [−0.423, 0.338] | [−0.275, 0.218] | [−0.096, 0.071] | yes |
| [−0.406, 0.373] | [−0.210, 0.169] | [−0.052, 0.048] | yes | |
| [−0.245, 0.212] | [−0.103, 0.095] | [0.048, 0.043] | yes | |
| [−0.223, 0.136] | [−0.061, 0.044] | [−0.013, 0.008] | yes | |
| = 0.01 | [−0.495, 0.385] | [−0.247, 0.199] | [−0.111, 0.080] | yes |
| [−0.492, 0.440] | [−0.210, 0.169] | [−0.062, 0.056] | yes | |
| [−0.312, 0.275] | [−0.125, 0.116] | [−0.058, 0.055] | yes | |
| [−0.319, 0.204] | [−0.069, 0.055] | [−0.017, 0.011] | yes | |
| = 0.1 | [−1.045, 0.848] | [−0.646, 0.529] | [−0.219, 0.174] | yes |
| [−1.258, 1.112] | [−0.571, 0.490] | [−0.148, 0.139] | yes | |
| [−0.938, 0.878] | [−0.330, 0.323] | [−0.161, 0.161] | yes | |
| [−1.194, 0.864] | [−0.156, 0.163] | [−0.055, 0.037] | yes |
| Algorithm | Zero Mean Gaussian | Nonzero Mean Gaussian | Centred Uniform | Biased Uniform |
|---|---|---|---|---|
| EKF-SLAM | 0 | 18 | 6 | 17 |
| 0 | 16 | 26 | 33 | |
| 0 | 6 | 3 | 7 | |
| iMonoSLAM | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Lambert, A.; Meng, Y.; Yu, R.; Wang, J.; Wang, W. Consistency-Oriented SLAM Approach: Theoretical Proof and Numerical Validation. Electronics 2025, 14, 2966. https://doi.org/10.3390/electronics14152966
Wang Z, Lambert A, Meng Y, Yu R, Wang J, Wang W. Consistency-Oriented SLAM Approach: Theoretical Proof and Numerical Validation. Electronics. 2025; 14(15):2966. https://doi.org/10.3390/electronics14152966
Chicago/Turabian StyleWang, Zhan, Alain Lambert, Yuwei Meng, Rongdong Yu, Jin Wang, and Wei Wang. 2025. "Consistency-Oriented SLAM Approach: Theoretical Proof and Numerical Validation" Electronics 14, no. 15: 2966. https://doi.org/10.3390/electronics14152966
APA StyleWang, Z., Lambert, A., Meng, Y., Yu, R., Wang, J., & Wang, W. (2025). Consistency-Oriented SLAM Approach: Theoretical Proof and Numerical Validation. Electronics, 14(15), 2966. https://doi.org/10.3390/electronics14152966







