Iterative Fractional Doppler Shift and Channel Joint Estimation Algorithm for OTFS Systems in LEO Satellite Communication

Abstract

An iterative fractional Doppler shift and channel joint estimation algorithm is proposed for orthogonal time frequency space (OTFS) satellite communication systems. In the algorithm, we search the strongest path and estimate its fractional Doppler offset, and compensate the Doppler shift to the nearest integer to estimate the coefficient of the path. Then signal of the path and its inter-Doppler interference are reconstructed and canceled from the received data with these two estimated parameters. The estimation and cancel process are iteratively conducted until the strongest path in the remained paths is less than the predetermined threshold. The channel information can be reconstructed by the estimated parameters of the paths. The normalized mean squared error (NMSE) of the proposed channel estimation algorithm is less than 1/5 of the available algorithms at a high signal-to-noise ratio (SNR) region, and its BER has about 4dB SNR gain compared with those of the available algorithms when the bit error rate (BER) is ${10}^{-3}$.

1. Introduction

With the rapid development of satellite technology, low-Earth orbit (LEO) satellites have emerged as a disruptive innovative technology, playing a key role in multiple fields such as telecommunications, Earth observation, scientific research, and national security [1]. LEO satellites are typically located at an altitude between 160 km and 2000 km. Satellites in this orbit travel around the Earth at extremely high speeds, with the time to complete one orbit ranging from approximately 90 min to 120 min [2]. A critical issue that must be addressed in such high-speed movement for wireless communications is the significant Doppler shift. High Doppler shift and multipath effects lead to two-dimensional fading in the time–frequency domain. To address this issue, the orthogonal time frequency space (OTFS) modulation technique has emerged as a promising solution in recent years.

The emerging OTFS modulation [3,4] has a greater advantage than OFDM over time–frequency dual-selective channels in high-mobility scenarios, which transforms the rapidly varying time-domain channel into a nearly static channel in the delay-Doppler (DD) domain [5,6]. Channel estimation and data detection in OTFS systems are often conducted in the DD domain. Channel estimation is a critical technique to improve the performance of OTFS systems. However, in LEO satellite communications, the extreme Doppler spread may cause Doppler shifts that exceed the intrinsic resolution limit of OTFS systems. Therefore, paths of the channel often have non-integer Doppler shifts in practical scenarios. The fractional Doppler shifts make the impact of Doppler paths disperse into all Doppler bins [7], which introduces the inter-Doppler interference (IDI) among data in the DD domain. Additionally, the rapidly varying channel coherence time demands ultra-low-latency estimation algorithms. Therefore, LEO satellite communications require low-complexity algorithms that can achieve accurate channel estimation under fractional Doppler conditions.

Current available channel estimation methods [8,9,10,11,12,13,14,15,16,17,18,19] for OTFS systems can be classified into four categories. The first category is channel estimation methods with the embedded pilot in [8,9,10,11]. This algorithm inserts one or more pilot symbols into the data sequence, serving as a commonly used channel estimation scheme for LEO satellite communications [10,11]. In these methods, the dispersed paths on other Doppler bins due to fractional Doppler shifts are treated as small integer Doppler paths. Due to the limited number of guard symbols, these methods can only estimate a few major bins and cannot account for all of the dispersed Doppler bins. The second category is the correlation-based channel estimation methods, in which the channel response of the pilot signal is correlated with the basis function in the DD domain, as described in [12]. However, in scenarios where a single delay path has multiple non-integer Dopplers paths, the overlapping of dispersed Doppler bins may greatly degrade the performance of correlation processing, which highly increases the errors in channel estimation. To reduce the channel estimation errors, a quasi-Newton method is introduced to iteratively re-estimate the fractional Doppler channel in [13], but the complexity of the channel estimation is significantly increased. The third category is based on the orthogonal matching pursuit (OMP) algorithm. This algorithm was initially applied in the OFDM system [14] and can achieve joint estimation of the frequency offset and channel. However, it is not directly suitable for the Doppler estimation problem in the OTFS system. On this basis, an improved structured sparse adaptive matching pursuit (MSSAMP) algorithm is proposed in [15], which can estimate the Doppler and channel information in the case of unknown channel sparsity. However, the algorithm can only estimate the integer Doppler values and is unable to distinguish fractional Doppler values. A two-step modified orthogonal matching pursuit with fractional refinement (OMPFR) algorithm is proposed in [16], which can distinguish fractional delays and Dopplers. The OMPFR algorithm estimates target parameters iteratively. When the number of paths is large or the signals are weak, more iterations required. As a result, in dense multipath scenarios, the complexity of the algorithm becomes significantly high. The fourth category [17,18] is a channel estimation method based on tensor decomposition. This algorithm has been proven to be applicable in LEO systems [19]. It was initially proposed for the OFDM system, but it also demonstrates an excellent performance in estimating multipath Doppler and channel coefficients. However, this algorithm requires a large number of training subframes to construct the third-order tensor model. At high mobility speeds, excessive training frames can exacerbate the phase accumulation effect caused by the Doppler shift, ultimately degrading the channel estimation performance.

To further improve the accuracy of the channel estimation and reduce the complexity, we propose a joint estimation algorithm for the fractional Doppler and channel coefficients. By searching for the path with the maximum power in the DD domain and compensating for the fractional Doppler of this path, the energy is concentrated on the path of an integer Doppler point, which can enhance the estimation accuracy of the path coefficient. Finally, with these estimated parameters, the interference from the strongest path is reconstructed and iteratively canceled from the received signal until the given condition is satisfied.

The main contributions of this paper are summarized as follows:

• We proposed an estimation and compensation algorithm for the fractional Doppler shift of the delayed propagation path. By optimizing the compensation value for the path, the fractional Doppler shift can be accurately estimated and the estimated fractional Doppler shift is compensated to the nearest integer value. This maximizes the detectable signal energy, thereby enabling precise estimation of the path coefficient.
• We developed an iterative channel estimation scheme with interference cancellation based on the estimation and compensation algorithm of the fractional Doppler of the delay path. The multipath parameters of the channel can be reconstructed by the estimated fractional Doppler shifts and coefficients of paths.
• In the estimation of the fractional Doppler, the Doppler estimation metric function is derived for the proposed algorithm and it is proven that it maintains sharp peaks even under low SNR and multipath conditions, enabling accurate estimation of fractional Doppler shifts.

2. System Model

The model of the embedded pilot signal is shown in Figure 1. The pilot symbol is placed on $(m_p,n_p)$. Let T and $\Delta f$ denote the sampling interval and frequency interval, respectively. The discrete DD domain grid is represented as $\left\{(k/NT,l/M\Delta f),k=0,1,\dots ,N,l=0,1,\dots ,M\right\}$, where $1/NT$ and $1/M\Delta f$ represent the Doppler resolution and delay resolution of the DD domain, respectively. Accordingly, k and l represent the indices of these two dimensions, respectively. The transmitted signal is given as follows:

$$X_{dd}(l,k)=X_{dd}^{pilot}(l_p,k_p)+X_{dd}^{data}(l_d,k_d)$$

(1)

where the pilot symbols can be expressed as follows:

$$X_{dd}^{pilot}(l_p,k_p)=\left\{\begin{array}{cc}0,\hfill & else\hfill \\ a,\hfill & l_p=m_p,k_p=n_p\hfill \end{array}\right.$$

(2)

and the data symbols can be expressed as follows:

$$X_{dd}^{data}(l_d,k_d)=\left\{\begin{array}{cc}0,\hfill & k_d\in [n_p-{\tau }_{max},n_p+{\tau }_{max}]\hfill \\ \hfill & l_d\in [m_p-2k_{max}-k_g,m_p+2k_{max}+k_g]\hfill \\ data,\hfill & else\hfill \end{array}\right.$$

(3)

where ${\tau }_{max}$ and $k_{max}$ represent the maximum delay and Doppler indices in the channel, respectively, while $k_g$ represents the additional guard interval.

Through the inverse symplectic finite fourier transform (ISFFT), the DD domain signal $X_{dd}(l,k)$ is transformed into the time–frequency (TF) domain signal $X_{tf}(n,m)$, which can be expressed as follows:

$$X_{tf}(n,m)={\displaystyle \frac{1}{N}}\sum _{k=0}^{N-1}\sum _{l=0}^{M-1}{X}_{dd}(l,k)e^{j2\pi ({\displaystyle \frac{nk}{N}}-{\displaystyle \frac{ml}{M}})}$$

(4)

where, $n\in [0,N-1]$ and $m\in [0,M-1]$ are the time–frequency grid indices. Then, the TF-domain signal is transformed into the time-domain transmission signal $s(t)$ through the Heisenberg transform, which is expressed as follows:

$$s(t)=\sum _{k=0}^{N-1}\sum _{l=0}^{M-1}{X}_{tf}(n,m)g_{tx}(t-nT)e^{j2\pi m\Delta f(t-nT)}$$

(5)

where $g_{tx}(t)$ denotes the transmit pulse shaping filter at the transmitter.

The sparsity channel impulse response with P paths in the DD domain can be expressed as follows:

$$h(\tau ,v)=\sum _{i=1}^P{h}_i\delta (\tau -{\tau }_i)\delta (v-v_i)$$

(6)

where $h_i$, ${\tau }_i=l_i/M\Delta f$, and $v_i=(k_i+{\kappa }_i)/NT$ are the channel gain, delay, and Doppler shift of the $i^{th}$ path, respectively. $k_i$ and ${\kappa }_i$ donate the integer and fractional Doppler of the path, respectively.

At the receiver, the time–domain signal $r(t)$ can be expressed as follows:

$$r(t)=\int \int h(\tau ,v)e^{j2\pi v(t-\tau )}s(t-\tau )d\tau dv+\omega (t)$$

(7)

where $\omega (t)\sim CN(0,{\sigma }^2)$ is the Gaussian white noise. The received signal is transformed into the TF-domain signal through the Wigner transform, and then the DD domain signal $Y_{dd}(l,k)$ is obtained through the short-time Fourier transform (STFT), which can be expressed as follows:

$$Y_{dd}(l,k)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }r(t)g_{rx}^{\ast }(t-nT)e^{-j2\pi m\Delta f(t-nT)}{e}^{-j2\pi ({\displaystyle \frac{nk}{N}}-{\displaystyle \frac{ml}{M}})}dndm$$

(8)

where $g_{rx}(t)$ is the receiver pulse shaping filter.

Similar to the transmitted DD-domain signal $X_{dd}(l,k)$, the received DD domain signal can be represented as: $Y_{dd}(l,k)=Y_{dd}^{pilot}(l_p,k_p)+Y_{dd}^{data}(l_d,k_d)+\omega (l,k)$, where the received pilot symbols $Y_{dd}^{pilot}(l_p,k_p)$ are given by:

$$\begin{array}{cc}\hfill Y_{dd}^{pilot}(l_p,k_p)=& \sum _{i=1}^P{h}_i{\alpha }_j{e}^{j2\pi {\displaystyle \frac{(k_i+{\kappa }_i)m_p}{MN}}}{X}_{dd}^{pilot}(m_p,n_p)\hfill \\ \hfill & l_p=m_p+l_i,k_p=n_p+k_i-j\hfill \end{array}$$

(9)

and the received data symbols $Y_{dd}^{data}(l_d,k_d)$ are given by:

$$Y_{dd}^{data}(l_d,k_d)=\sum _{i=1}^P\sum _{j=1}^{N-1}[h_i{\alpha }_j{e}^{j2\pi {\displaystyle \frac{(k_i+{\kappa }_i)(l_d-l_i)}{MN}}}{X}_{dd}^{data}({(l_d-l_i)}_M,{(k_d-k_i+j)}_N)]$$

(10)

where, ${\alpha }_j$ represents the IDI caused by the fractional Doppler, which can be specifically expressed as follows:

$${\alpha }_j={\displaystyle \frac{e^{-j2\pi (-j-{\kappa }_i)}-1}{N(e^{-j2\pi (-j-{\kappa }_i)}-1)}}$$

(11)

3. Proposed Iterative Fractional Doppler Shift and Channel Estimation Algorithm

Many existing joint estimation algorithms [20,21] for frequency offset and channel information can exhibit an excellent performance in the OFDM system. However, in the OTFS system with fractional Dopplers, their performance can hardly meet the requirements. To obtain the full channel information with a high accuracy for the channel with fractional Doppler shift paths, we propose an iterative fraction Doppler offset and channel coefficient joint estimation scheme, which includes the search for the strongest path, the fraction Doppler shift and channel coefficient joint estimation, reconstructed interference cancellation, and channel information reconstructed.

In the proposed method, the strongest path is searched in the guard interval in the DD domain. If the searched position of the strong path is $(\widehat{l_i},\widehat{k_i})$, and the actual Doppler offset of the path is $k_i+{\kappa }_i$. $\widehat{k_i}$ is the closest integer to it.

The fractional Doppler of this path is estimated through search-based compensation. The received pilot signal $Y_{dd}^{pilot}(l,k)$ is represented as a vector ${\mathit{Y}}_{\mathit{D}}^{\mathit{pilot}}(\widehat{l_i})$ at the delay $\widehat{l_i}$, as follows:

$${\mathit{Y}}_{\mathit{D}}^{\mathit{pilot}}(\widehat{l_i})=[Y_{dd}^{pilot}(\widehat{l_i},0),\dots ,Y_{dd}^{pilot}(\widehat{l_i},N-1)]$$

(12)

and its corresponding vector in the time domain is ${\mathit{r}}_{\mathit{t}}(\widehat{l_i})=F^{-1}{\mathit{Y}}_{\mathit{D}}^{\mathit{pilot}}(\widehat{l_i})$, where $F^{-1}$ is the inverse matrix of the Fourier transform. By compensating a fractional frequency offset $v_f\in [-1,1]$ to ${\mathit{r}}_{\mathit{t}}(\widehat{l_i})$, the compensated DD domain signal at $(\widehat{l_i},\widehat{k_i})$ can be obtained as follows:

$${\widehat{Y}}_{dd}^{pilot}(\widehat{l_i},\widehat{k_i})=\sum _{j=0}^{N-1}{\mathit{r}}_{\mathit{t}}(\widehat{l_i})e^{j2\pi {\displaystyle \frac{j(\widehat{k_i}-v_f)}{N}}},v_f\in [-1,1]$$

(13)

When the fractional Doppler of this path is compensated to an integer, it satisfies: $(k_i+{\kappa }_i)-\widehat{{\kappa }_i}=\widehat{k_i}$. The signal energy at point $(\widehat{l_i},\widehat{k_i})$ reaches its maximum. Therefore, we can estimate the fractional Doppler of this path as follows:

$$\begin{array}{cc}\hfill & \widehat{{\kappa }_i}=\underset{v_f}{argmax}E(v_f)\hfill \\ \hfill & s.t.v_f\in [-1,1]\hfill \end{array}$$

(14)

where $E(v_f)=|{\widehat{Y}}_{dd}^{pilot}(\widehat{l_i},\widehat{k_i})|$ represents the signal amplitude at $(\widehat{l_i},\widehat{k_i})$. Based on the compensated signal ${\widehat{Y}}_{dd}^{pilot}(\widehat{l_i},\widehat{k_i})$ by $\widehat{{\kappa }_i}$, the coefficient of the path $\widehat{h_i}$ can be estimated as follows:

$$\widehat{h_i}={\displaystyle \frac{{\widehat{Y}}_{dd}^{pilot}(\widehat{l_i},\widehat{k_i})}{X_{dd}^{pilot}(m_p,n_p)e^{j2\pi \frac{m_p\widehat{k_i}}{MN}}}}$$

(15)

Based on (14) and (15), the signal on $(\widehat{l_i},\widehat{k_i})$ and IDI of the path on other Doppler bins can be reconstructed, and subtracted from ${\mathit{Y}}_{\mathit{D}}(\widehat{l_i})$:

$${\mathit{Y}}_{\mathit{D}}^{\mathit{pilot}(\mathit{1})}(\widehat{l_i})={\mathit{Y}}_{\mathit{D}}^{\mathit{pilot}}(\widehat{l_i})-\mathit{A}\left(\widehat{h_i}{e}^{j2\pi {\displaystyle \frac{m_p(\widehat{k_i}+\widehat{{\kappa }_i})}{MN}}}{X}_{dd}^{pilot}(m_p,n_p)\right)$$

(16)

where $\mathit{A}=[{\alpha }_1,{\alpha }_1,...,{\alpha }_N]$ represents the IDI caused by $\widehat{{\kappa }_i}$, and ${\mathit{Y}}_{\mathit{D}}^{\mathit{pilot}(\mathit{1})}(\widehat{l_i})$ is the renewed signal.

The renewed signal in the guard interval is employed to search for the strongest path once more. The searched strong path has the same operation as the above. After a iterations, the operation will stop when the following condition is satisfied:

$$\underset{(\widehat{l_i},\widehat{k_i})}{argmax}\left|{\mathit{Y}}_{\mathit{D}}^{\mathit{pilot}(\mathit{a})}(l,k)\right|<\beta \left({\displaystyle \frac{1}{MN}}\sum _{l=0}^{M-1}\sum _{k=0}^{N-1}\left|Y_{dd}(l,k)\right|\right)$$

(17)

where $\beta$ is a preset threshold that is often employed in the channel estimation of OTFS systems with the embedded pilot.

Based on all the estimated coefficients and fractional Doppler shifts of $\widehat{P}$ paths, the estimated channel coefficient $\widehat{h}(\tau ,v)$ can be reconstructed as follows:

$$\begin{array}{c}\hfill \widehat{h}(\tau ,v)=\sum _{i=1}^{\widehat{P}}{\widehat{h}}_i\delta (\tau -{\displaystyle \frac{{\widehat{l}}_i}{M\Delta f}})\delta (v-{\displaystyle \frac{{\widehat{k}}_i+{\widehat{\kappa }}_i}{NT}})\end{array}$$

(18)

where $\delta (·)$ represents the impulse function.

The estimation process is described in Algorithm 1.

Algorithm 1 Proposed Channel Estimation

1: input: $(\widehat{l_i},\widehat{k_i})$, threshold $\beta$, frequency compensation range $v_f\in [-1,1]$, received time-domain signal ${\mathit{r}}_{\mathit{t}}(\widehat{l_i})$ 2: output: $\widehat{{\kappa }_i}$$\widehat{h_i}$ 3: initialize: $E=\varnothing$ 4: for each $(\widehat{l_i},\widehat{k_i})$ do: 5:        if $\underset{(\widehat{l_i},\widehat{k_i})}{argmax}\left|{\mathit{Y}}_{\mathit{D}}^{\mathit{pilot}(\mathit{a})}(l,k)\right|<\beta \left({\displaystyle \frac{1}{MN}}{\sum }_{l=0}^{M-1}{\sum }_{k=0}^{N-1}\left|Y_{dd}(l,k)\right|\right)$ then 6:              for each $v_f$, step = 0.01, do 7:                   ${\widehat{Y}}_{dd}^{pilot}(\widehat{l_i},\widehat{k_i})={\sum }_{j=0}^{N-1}{\mathit{r}}_{\mathit{t}}(\widehat{l_i})e^{j2\pi {\displaystyle \frac{j(\widehat{k_i}-v_f)}{N}}}$ 8:                   $E=\left[E,\left|{\widehat{Y}}_{dd}^{pilot}(\widehat{l_i},\widehat{k_i})\right|\right]$ 9:              end for 10:           $\widehat{{\kappa }_i}=\underset{v_f}{argmax}E$ 11:           $\widehat{h_i}={\displaystyle \frac{{\widehat{Y}}_{dd}^{pilot}(\widehat{l_i},\widehat{k_i})}{X_{dd}^{pilot}(m_p,n_p)e^{j2\pi \frac{m_p\widehat{k_i}}{MN}}}}$ 12:           Recalculate the interference-canceled signal through (16) 13:       else 14:           break 15:       end if 16: end for

The complexity of the proposed algorithm is mainly derived from the searching and modulus operations, assuming the estimated paths are $\widehat{P}$, and the number of search iterations is Q. The complexity of converting time-domain signals into DD domain signals is $O(MNlo{g}_2(MN))$. The total number of complex addition and multiplication operations of the proposed algorithm is $O(\widehat{P}(QN+Q))$. Therefore, the overall complexity of the proposed algorithm is $O(MNlo{g}_2(MN)+\widehat{P}(QN+Q))$.

4. Simulation Results and Discussions

The performance of the proposed channel estimation method is investigated with that of traditional embedded pilot algorithm [8] and two-stage basis function correlation algorithm [13], two-step modified OMPFR algorithm [16], and tensor decomposition-based channel estimation [18]. Our work focuses on the LEO satellite communication network scenarios specified in 3GPP standards, utilizing the OTFS simulation parameters listed in

Table 1. Simulation Parameter.

Parameter	Value
Number of sub-carriers	$M=64$
Number of time-domain symbols	$N=32$
subcarrier spacing	$\Delta f=62.5$ kHz
Carrier frequency	$f_c=10$ GHz
Max Doppler shift	$k_{max}=50$ kHz
Coding scheme	LDPC
Coding rate	0.667
Pilot information	$X_{dd}(6,8)=100$
Doppler compensation range and step	$v_f=[-1,1],step=0.01$
channel model	$NTN-TDL-D$
stopping threshold coefficient	$\beta =3$
guard symbols overhead	$0.031$

. The message passing (MP) detector in [22] is used in the data detection. The normalized mean square error (NMSE) is employed to evaluate the performance of the channel estimation.

The NTN-TDL-D channel model is an extension of the non-terrestrial network (NTN) model based on the 3GPP TR 38.901 standard [23], which is specifically designed for LEO satellite high-mobility scenarios. Based on this, we adjusted the multipath delay to better suit our simulation system, and others all refer to the 3GPP protocol. The power-delay profile (PDP) of this channel is characterized in

Table 2. Power-delay profile of the channel.

Delay (ns)	0	430	470	890	1110	1190
Power (dB)	0	−1.5	−4.5	−7.4	−10.4	−15.3

.

Figure 2 compares the Doppler estimation metric functions $E(v_f)$ of the proposed algorithm and the basis function correlation algorithm [13] when there are two paths on the same delay tap at −6 dB. The normalized Doppler shifts of the two paths are [6.6, 9.5]. Both algorithms estimate the Doppler shifts of multiple paths by iterative cancellation processing. Figure 2a,b present the metric functions when estimating two paths, respectively. In Figure 2a, the initial metric functions obtained by the two algorithms are shown. The proposed algorithm exhibits two distinct and sharp peaks, whereas the basis function correlation algorithm suffers from significant sidelobes and blurred peaks due to IDI and noise. In Figure 2b, the metric functions after one iteration are given, where the strongest path has been canceled and the remaining paths have a Doppler shift of 6.6. The proposed algorithm still maintains a higher and sharper peak value compared to the basis function correlation algorithm in this scenario.

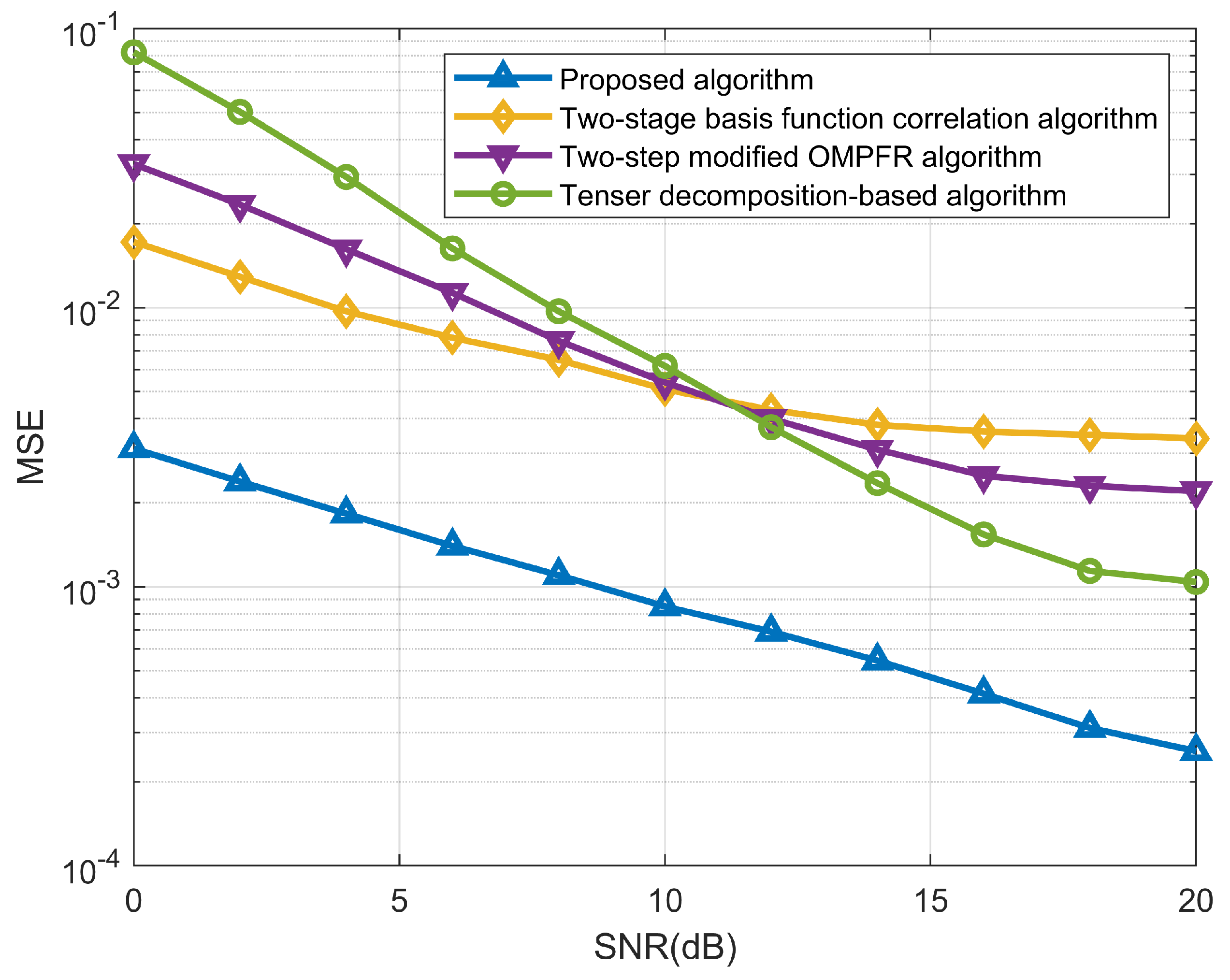
Figure 3 shows the MSE performances of the proposed algorithm, the two-stage basis function correlation algorithm [13], two-step modified OMPFR algorithm [16], and tensor decomposition-based channel estimation [18]. It can be seen that as the SNR increases, the MSE of the proposed algorithm approaches ${10}^{-4}$, which outperforms the other three algorithms. Among the available algorithms, when SNR = 20 dB, the MSE of the tensor decomposition-based algorithm approaches ${10}^{-3}$, but at low SNR levels, its MSE is higher than those of the two-stage basis function correlation algorithm and the two-step modified OMPFR algorithm.

Figure 4 shows the NMSE performances of the proposed algorithm, the embedded pilot algorithm [8], the two-stage basis function correlation algorithm [13], two-step modified OMPFR algorithm [16], and tensor decomposition-based channel estimation [18]. It can be seen that the proposed algorithm outperforms the other four algorithms significantly, and its NMSE is below ${10}^{-2}$ when SNR is 0 dB and approaches ${10}^{-3}$ when SNR is 20 dB. Among the comparative algorithms, the tensor decomposition-based algorithm approaches the performance of the proposed algorithm at $SNR>15$ dB, albeit with a higher computational complexity. Meanwhile, the embedded pilot algorithm and two-step modified OMPFR algorithm exhibit performance saturation in the medium-to-high SNR range, indicating their limited capability to suppress IDI caused by fractional Doppler in multipath scenarios. These results validate the superior balance between estimation accuracy and robustness achieved by the proposed algorithm under dynamic LEO channel conditions.

Figure 5 shows the BER performances of the proposed algorithm, the embedded pilot algorithm [8], the two-stage basis function correlation algorithm [13], two-step modified OMPFR algorithm [16], and tensor decomposition-based channel estimation [18]. When BER is ${10}^{-3}$, the obtained SNR gain of the proposed algorithm is about 7 dB compared with the two-stage basis function correlation algorithm, and only 1 dB SNR loss compared with the perfect channel estimation. It is also seen that the tensor decomposition-based algorithm can achieve a bit error rate below ${10}^{-3}$ under high SNR conditions. The two-step modified OMPFR algorithm demonstrates a marginally better performance than the two-stage basis function correlation algorithm. In contrast, the embedded pilot algorithm exhibits the worst performance due to its limitations in resource efficiency and susceptibility to interference.

The computational complexity of the proposed algorithm is $O(MNlo{g}_2(MN)+\widehat{P}(QN+Q))$. The computational load of the proposed algorithm for converting time-domain signals to the DD domain requires only 20 μs on modern spaceborne DSPs (e.g., TMS320C6678), and each iteration involves approximately 6400 complex multiplications, which takes about 0.2 ms on a 1 GHz processor. Therefore, if $\widehat{P}=10$, the entire synchronization process completes about 2 ms on LEO satellite processors. This is practically acceptable for real-world LEO satellite processors.

5. Conclusions

We proposed a joint fractional Doppler offset and channel estimation iterative algorithm for OTFS systems with non-integer Doppler offsets in LEO satellite communications. The full channel information can be reconstructed by the estimated fractional Doppler offsets and coefficients of paths. The estimation algorithm can greatly improve the BER performance of OTFS systems with slight complexity and be suitable for paths with arbitrary Doppler shifts in the channel for OTFS systems in other high-mobility scenarios.