Research of 110 kV High-Voltage Measurement Method Based on Rydberg Atoms
Abstract
1. Introduction
2. Measurement Principle of Power Frequency Electric Field Based on Rydberg Atoms
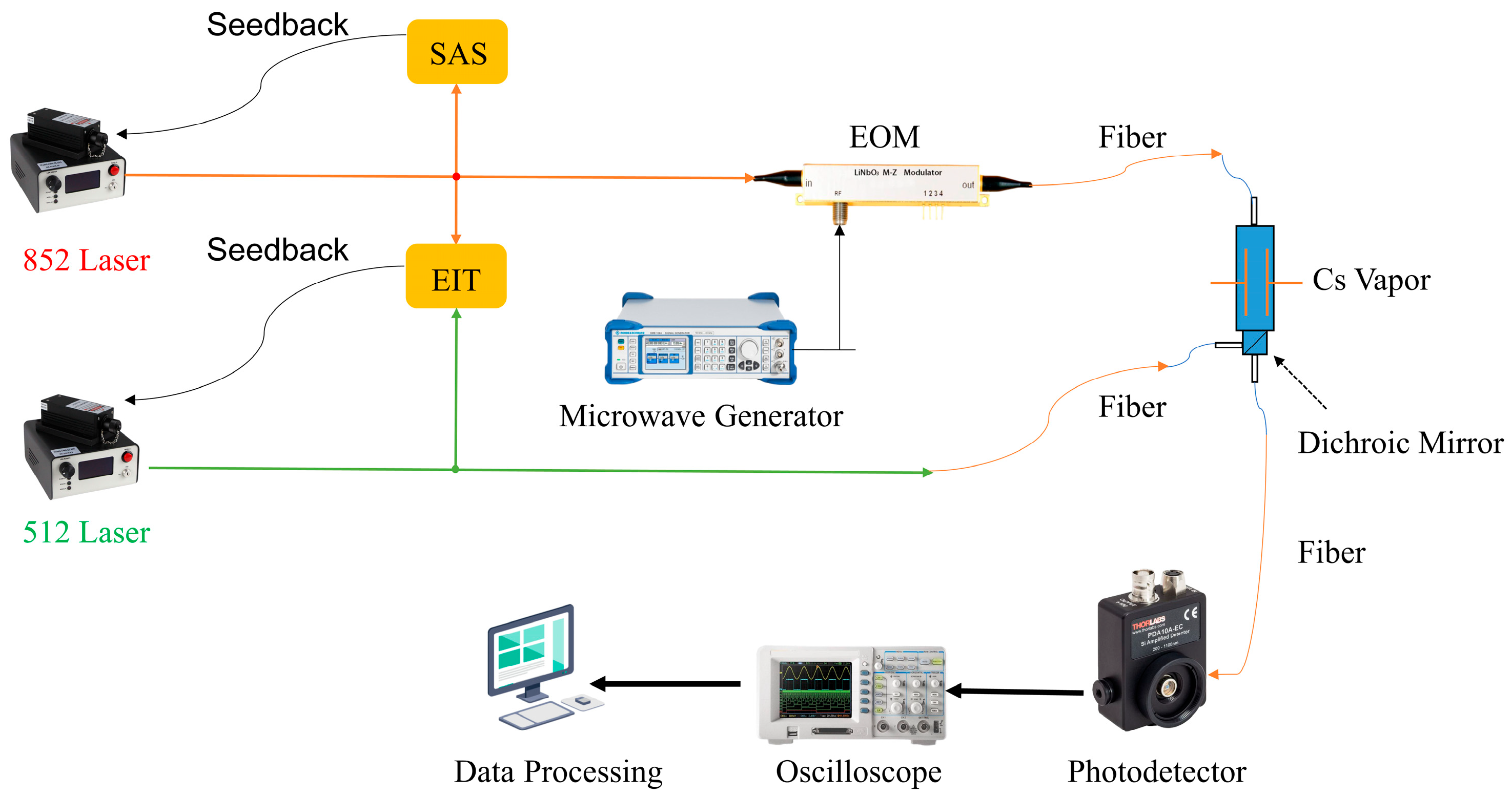
3. Experimental Device
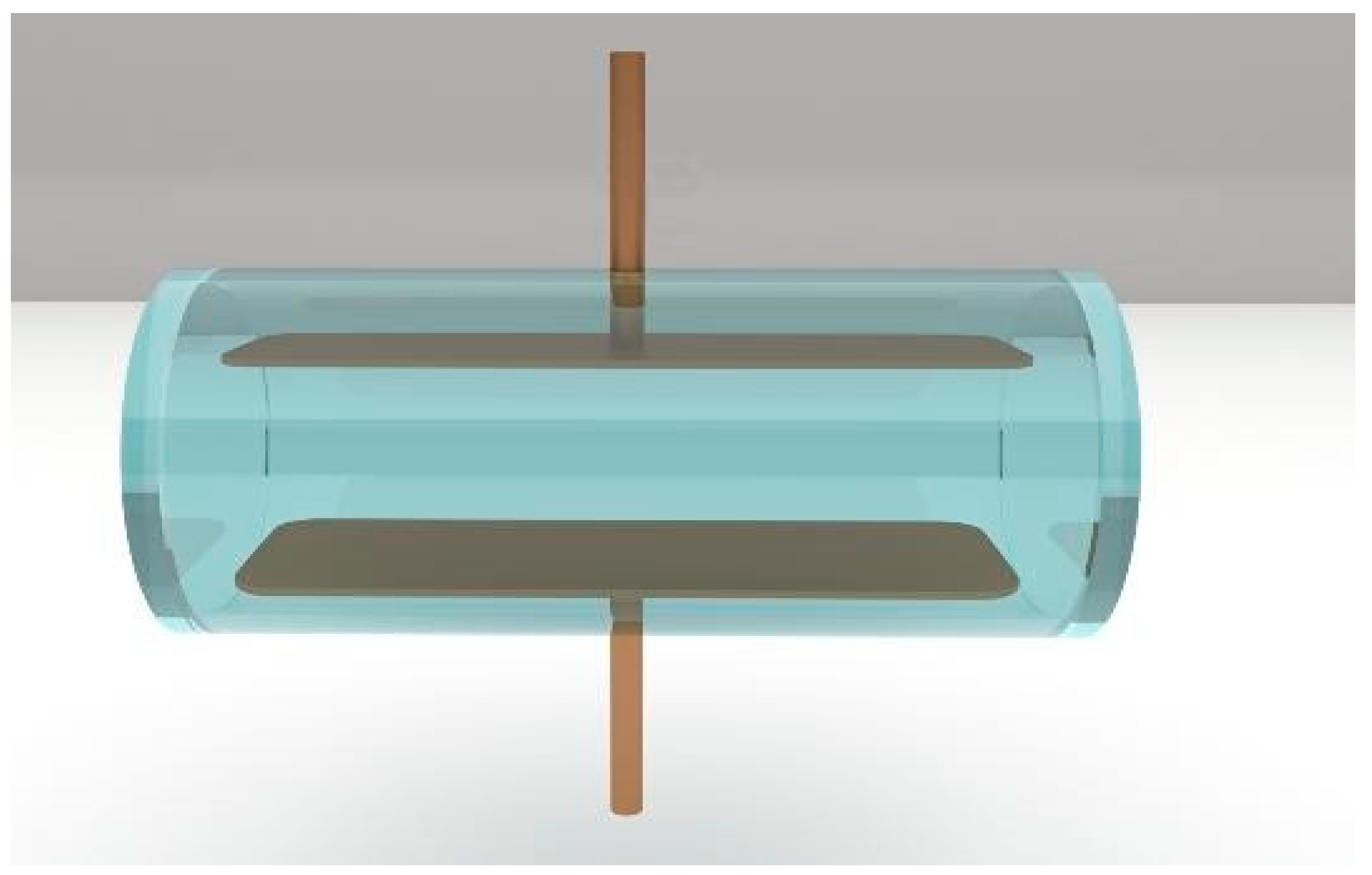
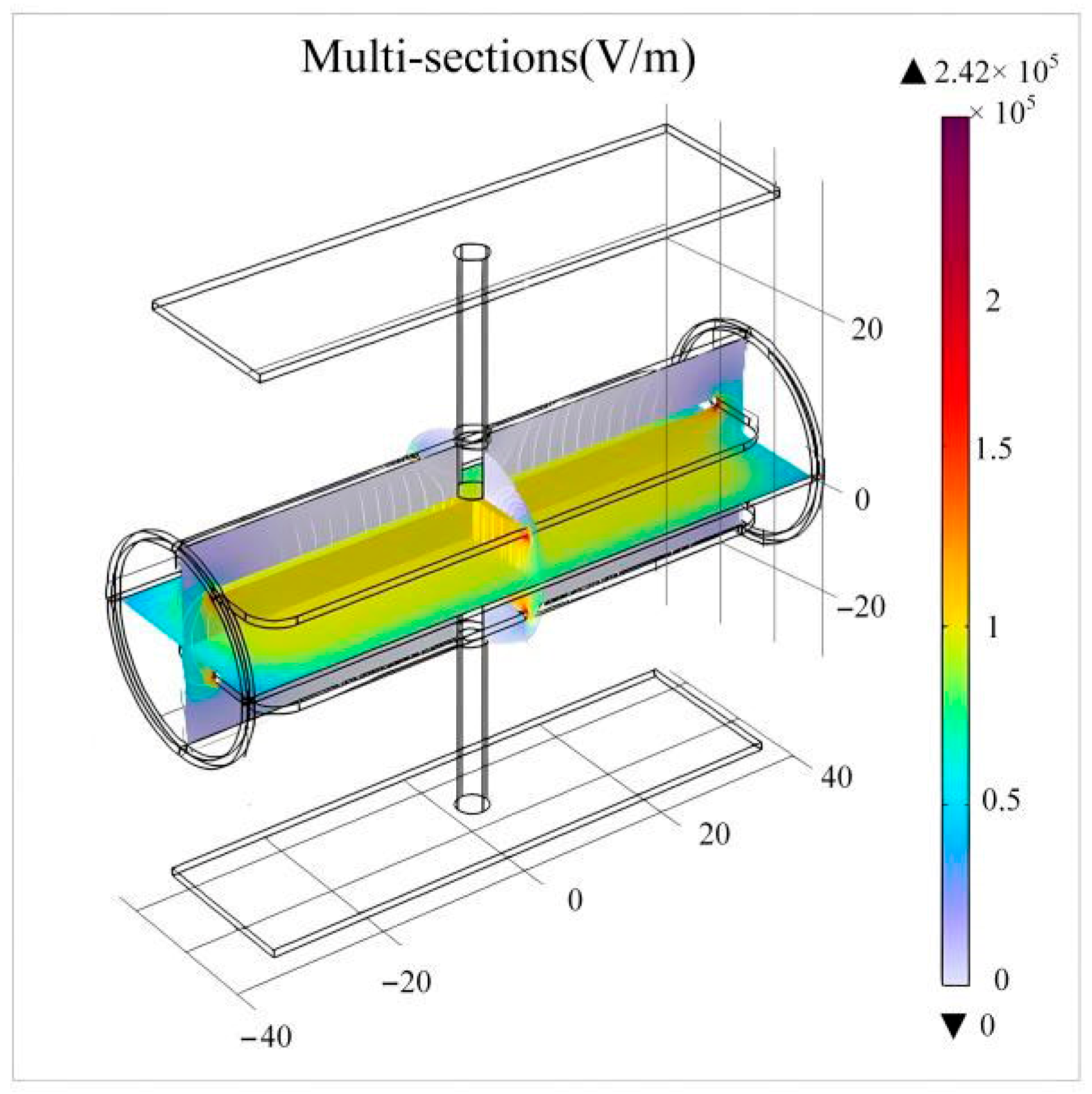
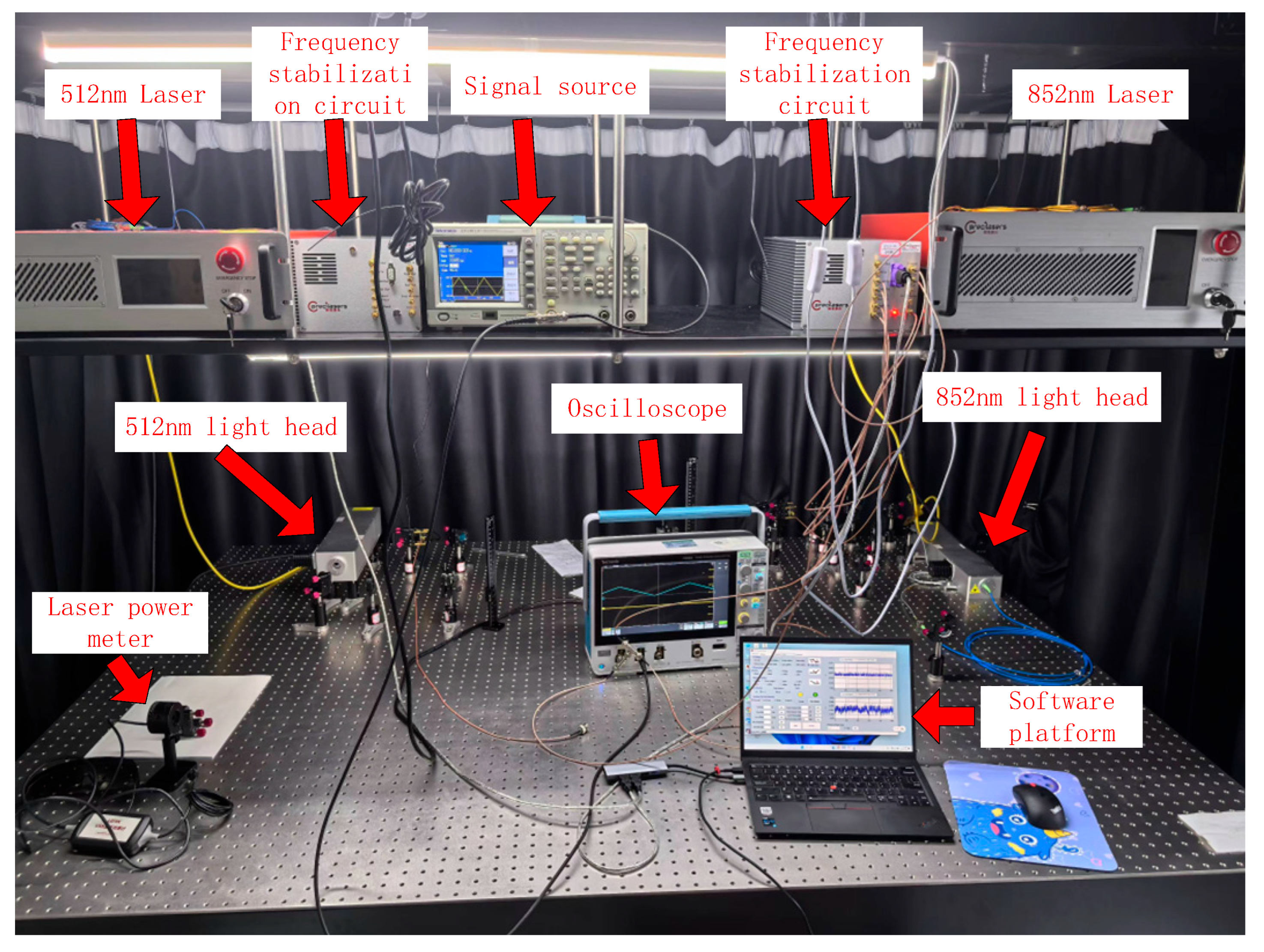
3.1. Rydberg Atom-Based Voltage Measurement Device
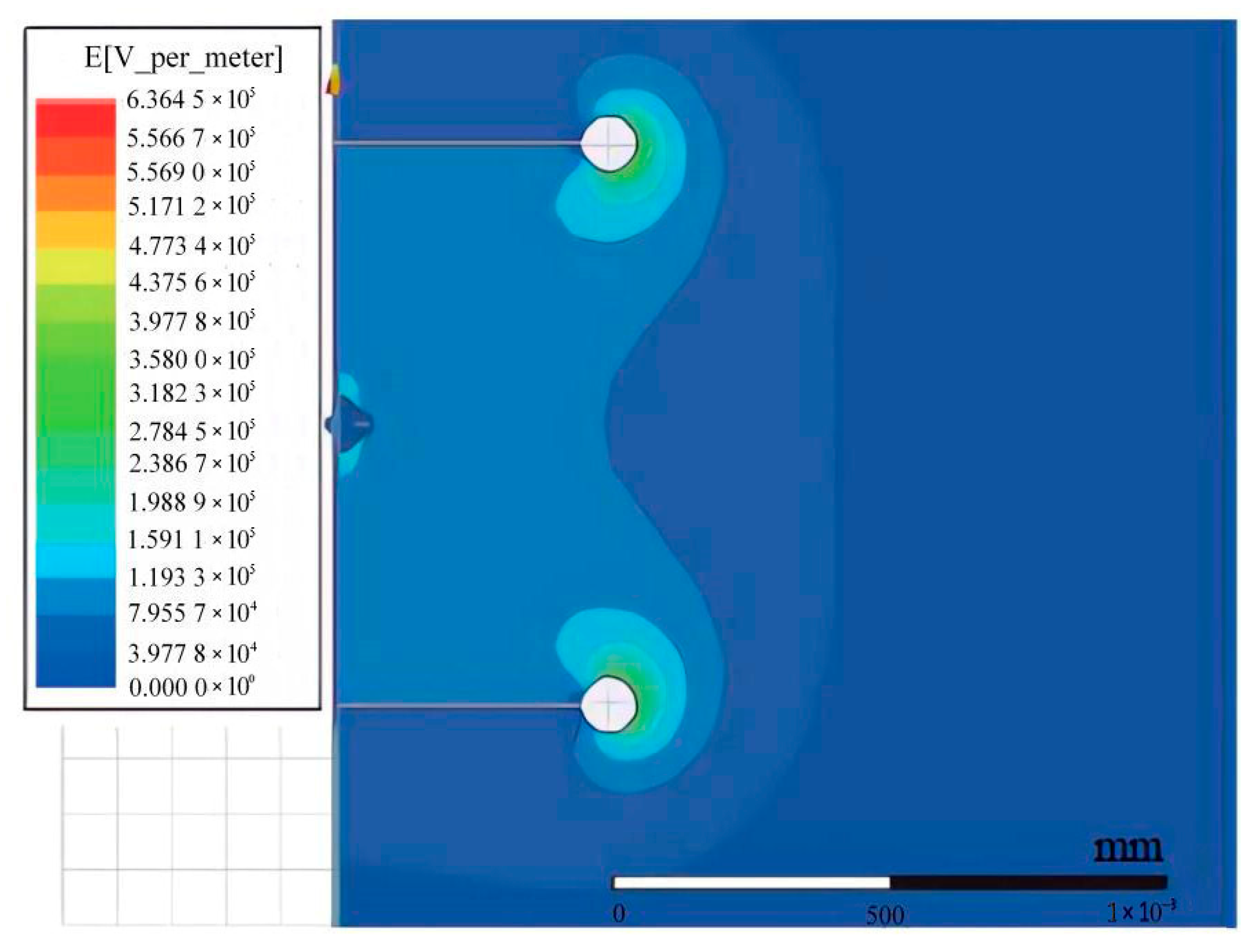
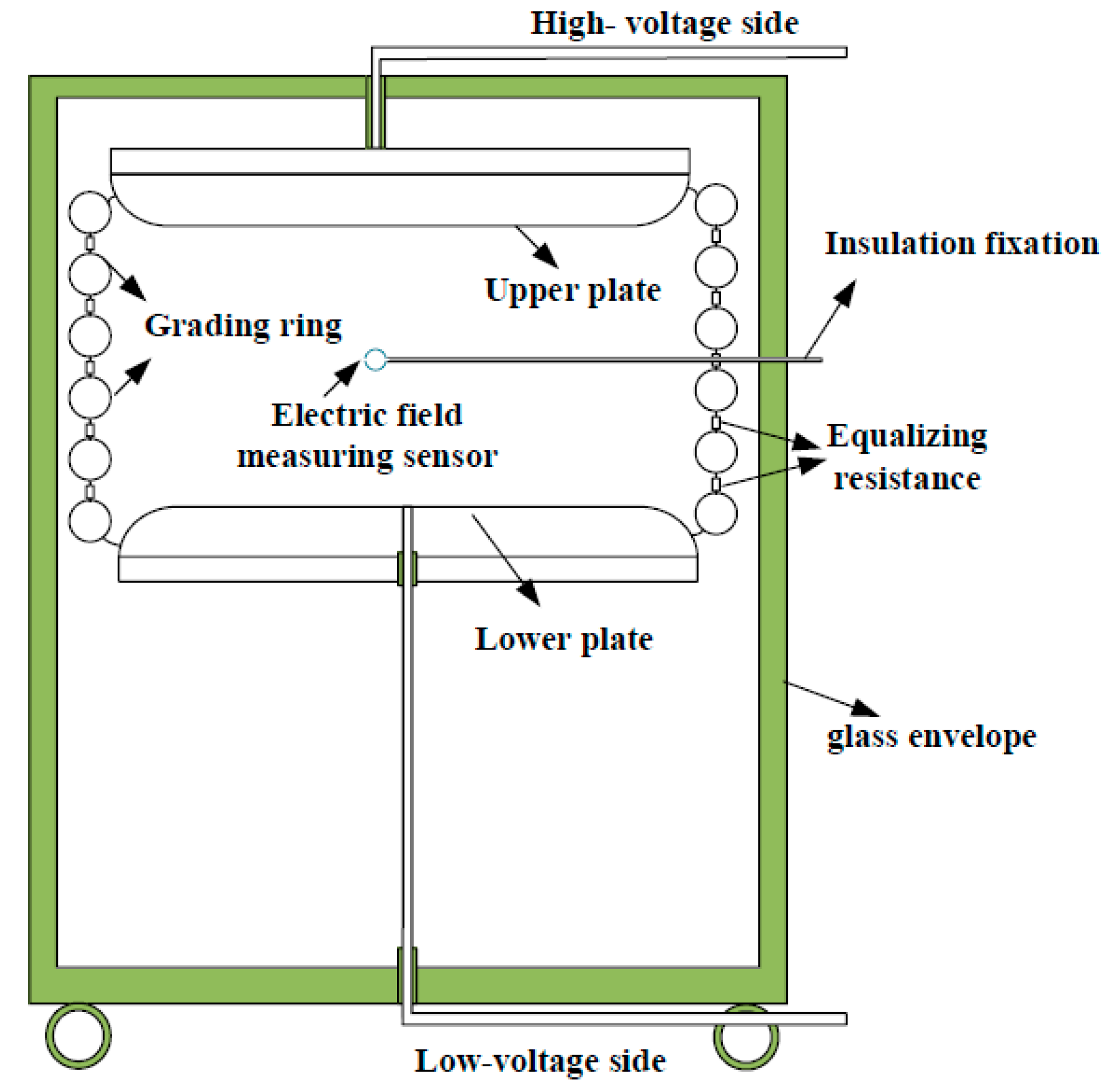
3.2. Voltage Measurement Calibrator
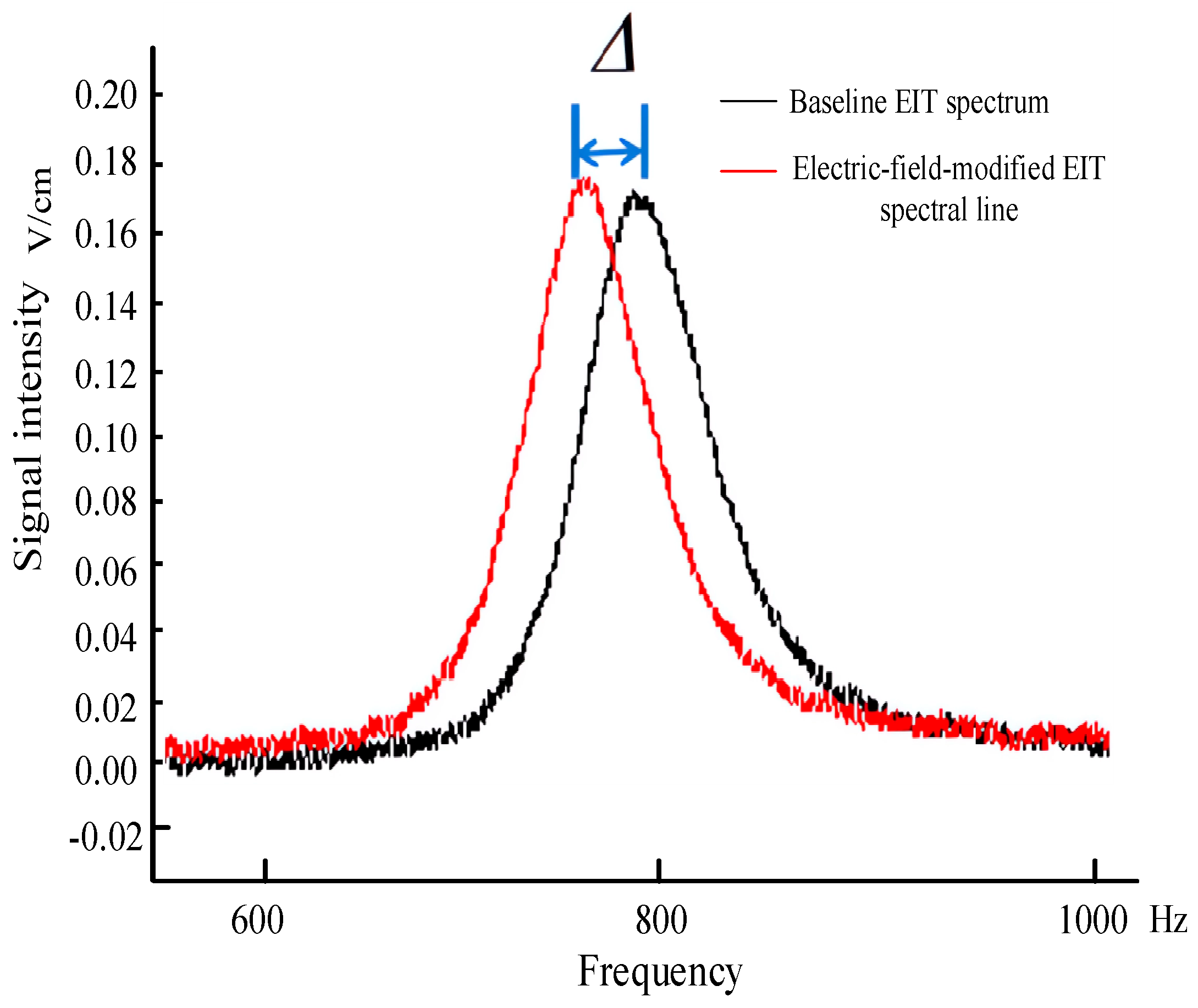
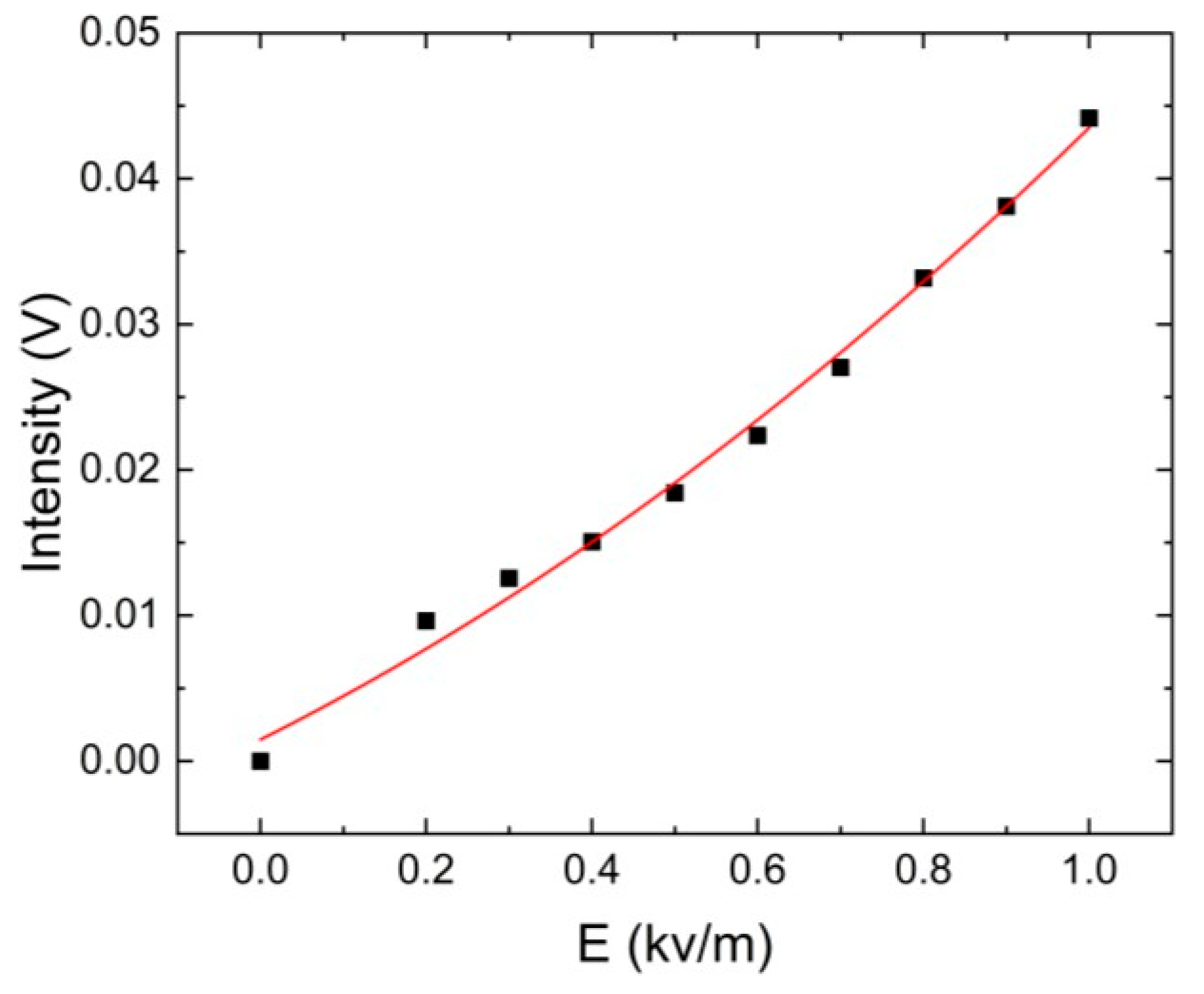
4. Results and Discussion
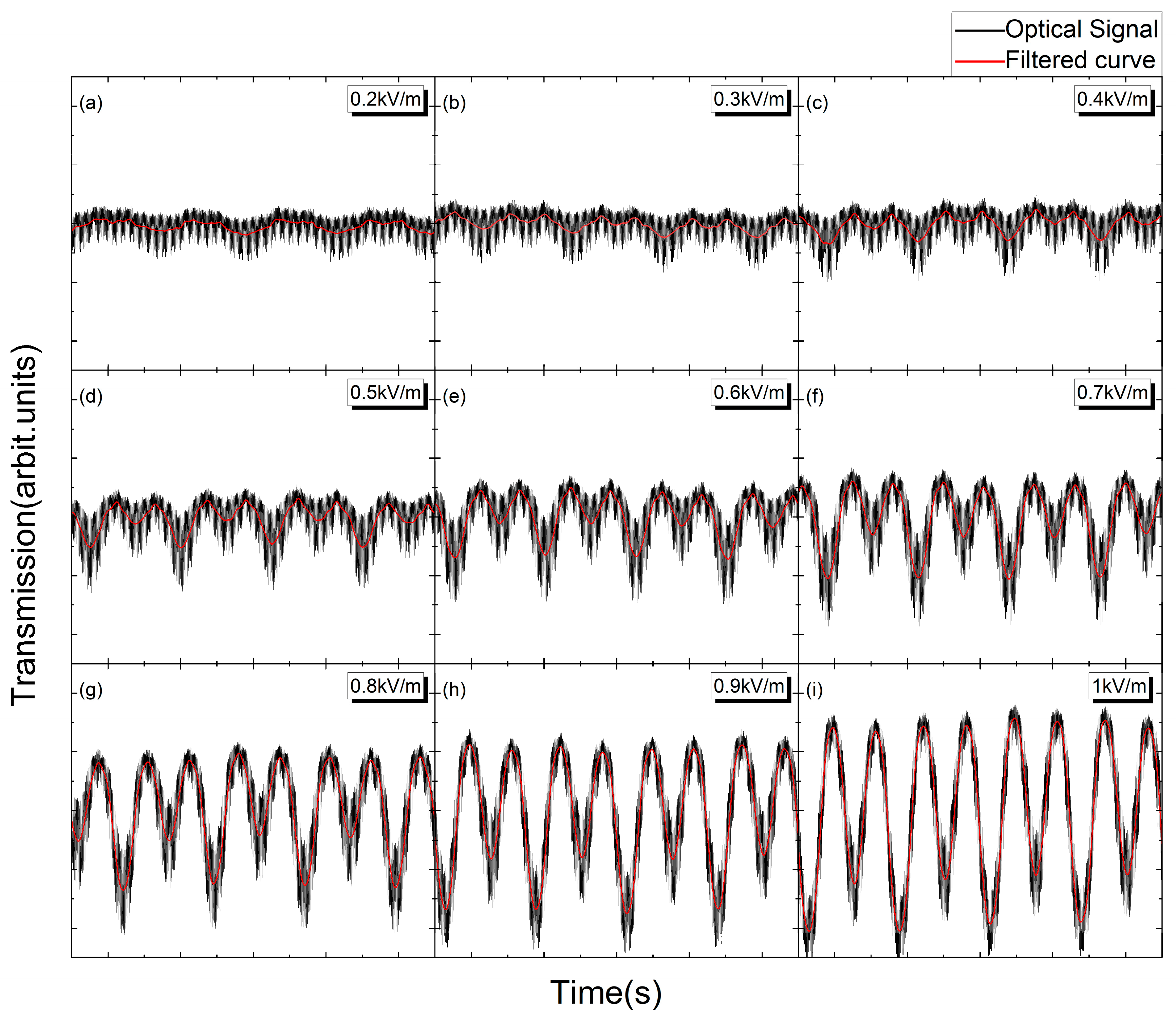
4.1. Power Frequency Voltage Measurement Results
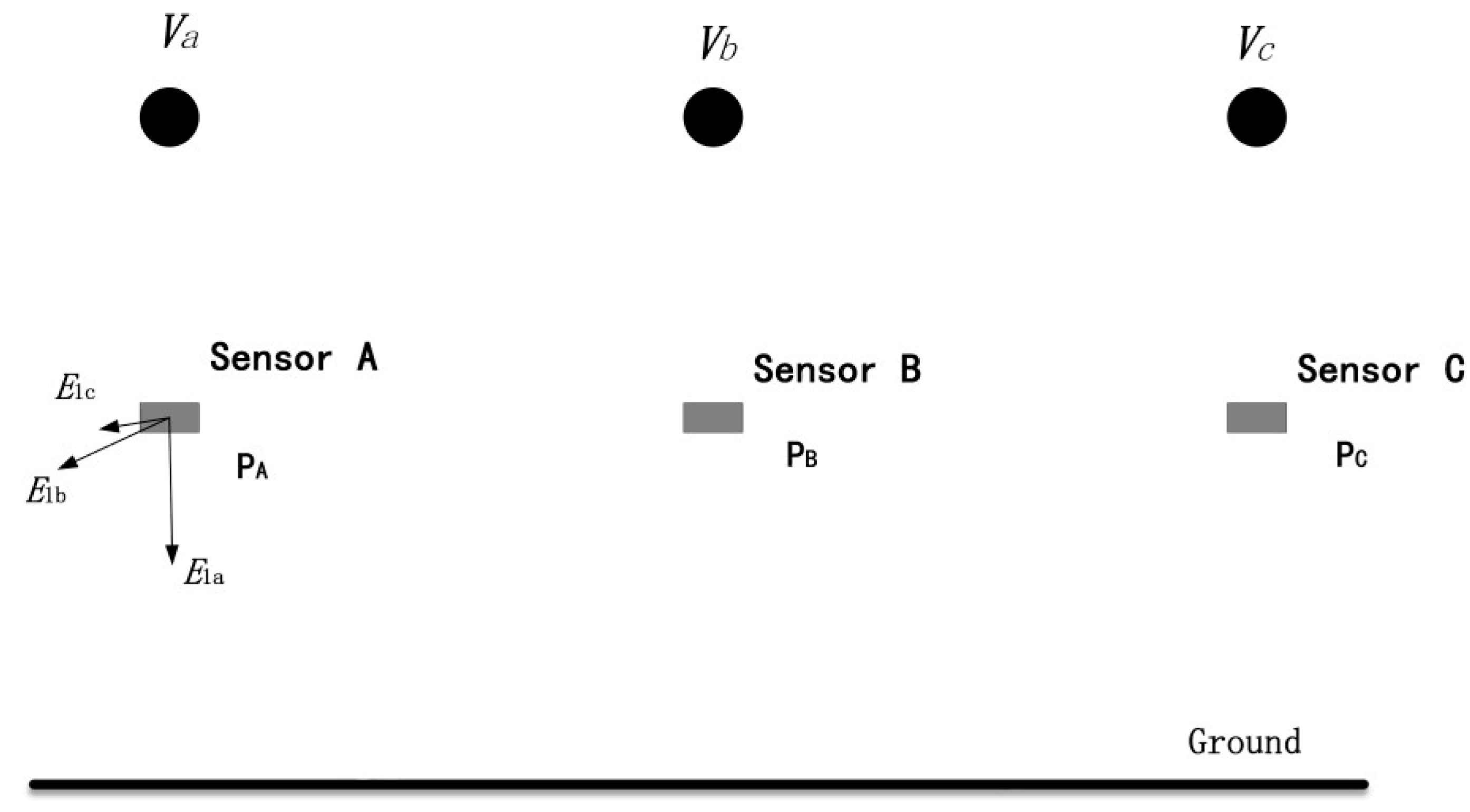
4.2. On-Site Measurement Decoupling of Multi-Phase Overhead Lines
4.2.1. Field Test Method
4.2.2. Asynchronous Transient Voltage Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Q.Q.; Liu, J.; Li, Y.M. Spherical sensor for the measuring transient electric fields based on optical fibre. J. Transducer Technol. 2002, 21, 14–16. [Google Scholar]
- Xiao, D.; Ma, Q.; Xie, Y.; Zheng, Q.; Zhang, Z. A power-frequency electric field sensor for portable measurement. Sensors 2018, 18, 1053. [Google Scholar] [CrossRef] [PubMed]
- Hidaka, K.; Fujita, H. A new method of electric field measurements in corona discharge using Pockels device. J. Appl. Phys. 1982, 53, 5999–6003. [Google Scholar] [CrossRef]
- Niu, B.; Zeng, R.; Li, H.; Wang, B. Design of non-electrode power frequency electric field sensor. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2008, 28, 101–107. [Google Scholar]
- Zhou, F.; Chai, Z.; Diao, Y.; Long, Z. Research on Measurement Techniques for Integrated Optical Waveguide-Based Electric Field Sensors. IEEE Access 2025, 13, 90983–90990. [Google Scholar] [CrossRef]
- Jing, M.Y. Microwave Precision Measurement Based on Rydberg-Atom Superhet; Shanxi University: Taiyuan, China, 2020. [Google Scholar]
- Prajapati, N.; Robinson, A.K.; Berweger, S.; Simons, M.T.; Artusio-Glimpse, A.B.; Holloway, C.L. Enhancement of electromagnetically induced transparency based Rydberg-atom electrometry through population repumping. Appl. Phys. Lett. 2021, 119, 214001. [Google Scholar] [CrossRef]
- Zhang, L.J.; Jing, M.Y.; Zhang, H. Quantum Sensing of Microwave Electric Fields Based on Rydberg Atoms. J. Shanxi Univ. (Nat. Sci. Ed.) 2022, 45, 712–722. [Google Scholar]
- Holloway, C.L.; Prajapati, N.; Artusio-Glimpse, A.B.; Berweger, S.; Simons, M.T.; Kasahara, Y.; Alu, A.; Ziolkowski, R.W. Rydberg atom-based field sensing enhancement using a split-ring resonator. Appl. Phys. Lett. 2022, 120, 204001. [Google Scholar] [CrossRef]
- Cui, S.W. Power Frequency Electric Field Measurement Based on the Spectral Properties of the Rydberg Atom; Shanxi University: Taiyuan, China, 2023. [Google Scholar]
- Zhang, C.G.; Li, W.; Zhang, H.; Jing, M.; Zhang, L. Power Frequency Electric Field Measurement Based on Electromagnetic Induced Transparent Spectrum under Radio Frequency Field. Acta Photonica Sin.-CA 2021, 50, 162–168. [Google Scholar]
- Jau, Y.Y.; Carter, T. Vapor-cell-based atomic electrometry for detection frequencies below 1 kHz. Phys. Rev. Appl. 2020, 13, 054034. [Google Scholar] [CrossRef]
- Anderson, D.A.; Miller, S.A.; Raithel, G.; Gordon, J.A.; Butler, M.L.; Holloway, C.L. Optical Measurements of Strong Microwave Fields with Rydberg Atoms in a Vapor Cell. Phys. Rev. Appl. 2016, 5, 034003. [Google Scholar] [CrossRef]
- Paradis, E.; Raithel, G.; Anderson, D.A. Atomic measurements of high-intensity VHF-band radio-frequency fields with a Rydberg vapor-cell detector. Phys. Rev. A 2019, 100, 013420. [Google Scholar] [CrossRef]
- Holloway, C.L.; Prajapati, N.; Sherman, J.A.; Rüfenacht, A.; Artusio-Glimpse, A.B.; Simons, M.T.; Robinson, A.K.; La Mantia, D.S.; Norrgard, E.B. Electromagnetically induced transparency based Rydberg-atom sensor for traceable voltage measurements. AVS Quantum Sci. 2022, 4, 034401. [Google Scholar] [CrossRef]
- Duspayev, A.; Cardman, R.; Anderson, D.A.; Raithel, G. High-angular-momentum Rydberg states in a room-temperature vapor cell for dc electric-field sensing. Phys. Rev. Res. 2024, 6, 023138. [Google Scholar] [CrossRef]
- Ma, L.; Viray, M.A.; Anderson, D.A.; Raithel, G. Measurement of dc and ac electric fields inside an atomic vapor cell with wall-integrated electrodes. Phys. Rev. Appl. 2022, 18, 024001. [Google Scholar] [CrossRef]
- Ma, K.; Xiao, D.; Zhang, H.; Wang, X.; Wei, X. Study on electric field shielding in SiO2 and CaF2 vapor cell for Rydberg atom electric field sensors. J. Phys. D Appl. Phys. 2025, 58, 135113. [Google Scholar] [CrossRef]
- Cui, S.W.; Peng, W.X.; Li, S.N. Power Frequency Electric Field Measurement Based on Rydberg Atoms. High Volt. Eng. 2023, 49, 644–650. [Google Scholar]
- Li, W. Power-Frequency Electric Field Measurement Based on AC-Stark Effect of Rydberg Atoms. Shanxi University, Taiyuan, China. 2021. Available online: https://m.researching.cn/articles/OJ7f6d339f901f011f/referenceandcitations (accessed on 20 June 2025).
- Adams, C.S.; Pritchard, J.D.; Shaffer, J.P. Rydberg atom quantum technologies. J. Phys. B At. Mol. Opt. Phys. 2019, 53, 012002. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Y.; Yang, X.; Luo, C. Three-dimensional electric field sensor with low inter-axis coupling. J. Meas. Sci. Instrum. 2024, 15, 95–104. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diao, Y.; Qu, Z.; Qu, N.; Cao, J.; Li, X.; Xu, X.; You, S. Research of 110 kV High-Voltage Measurement Method Based on Rydberg Atoms. Electronics 2025, 14, 2932. https://doi.org/10.3390/electronics14152932
Diao Y, Qu Z, Qu N, Cao J, Li X, Xu X, You S. Research of 110 kV High-Voltage Measurement Method Based on Rydberg Atoms. Electronics. 2025; 14(15):2932. https://doi.org/10.3390/electronics14152932
Chicago/Turabian StyleDiao, Yinglong, Zhaoyang Qu, Nan Qu, Jie Cao, Xinkun Li, Xiaoyu Xu, and Shuhang You. 2025. "Research of 110 kV High-Voltage Measurement Method Based on Rydberg Atoms" Electronics 14, no. 15: 2932. https://doi.org/10.3390/electronics14152932
APA StyleDiao, Y., Qu, Z., Qu, N., Cao, J., Li, X., Xu, X., & You, S. (2025). Research of 110 kV High-Voltage Measurement Method Based on Rydberg Atoms. Electronics, 14(15), 2932. https://doi.org/10.3390/electronics14152932





