A Three-Layer Sequential Model Predictive Current Control for NNPC Four-Level Inverters with Low Common-Mode Voltage
Abstract
1. Introduction
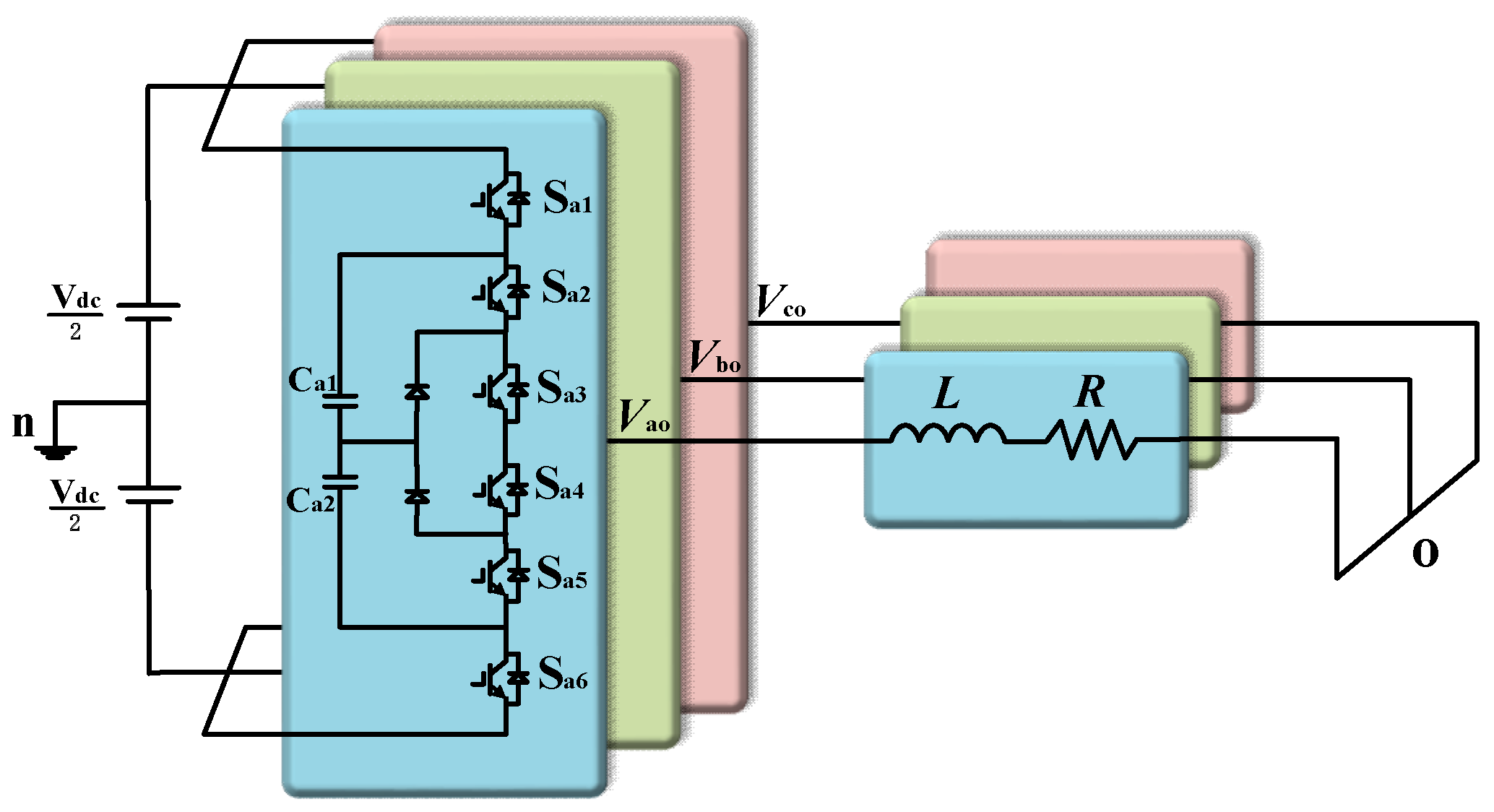
2. Operating Principle of Three Phase 4L-NNPC Inverter
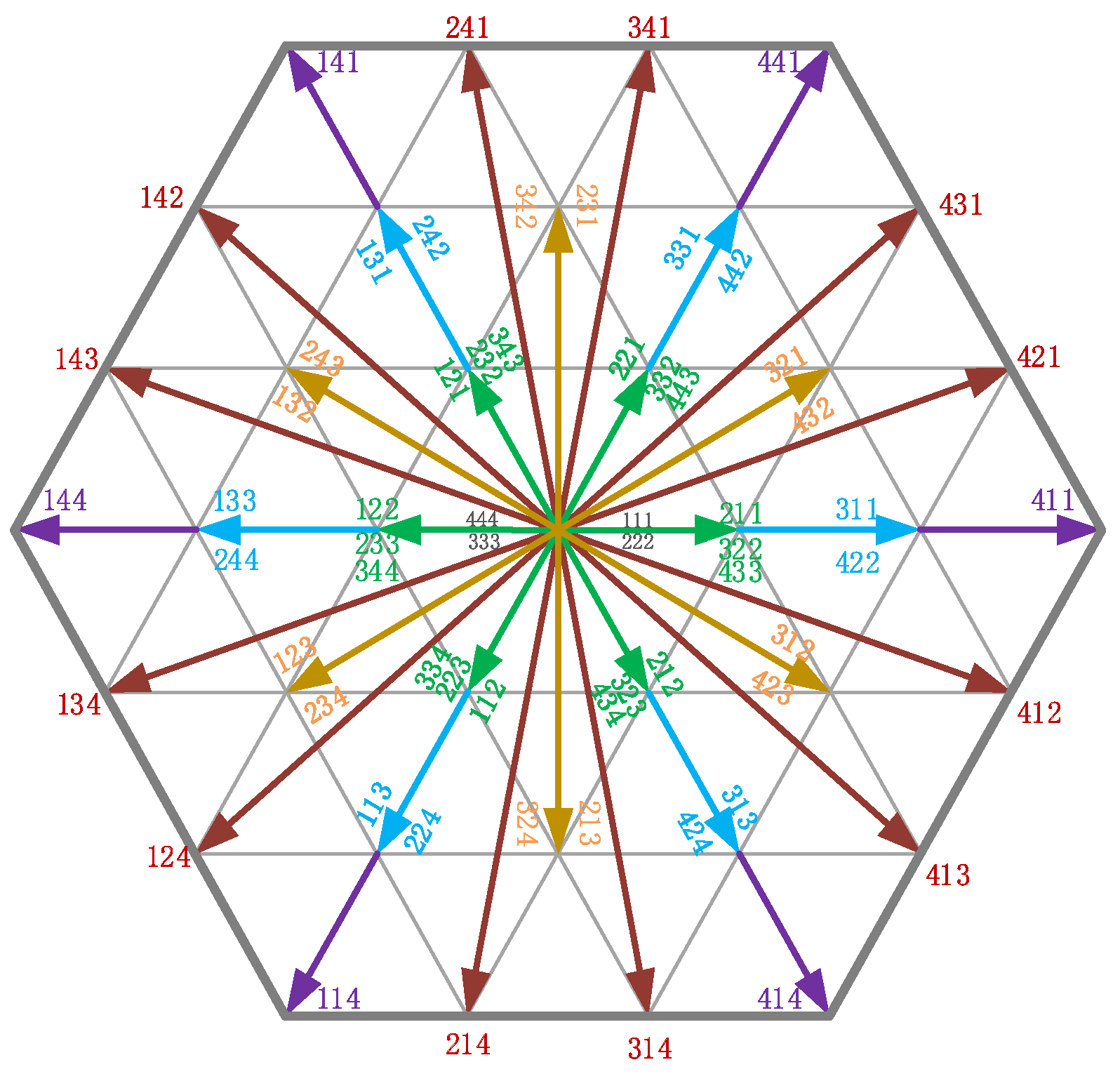
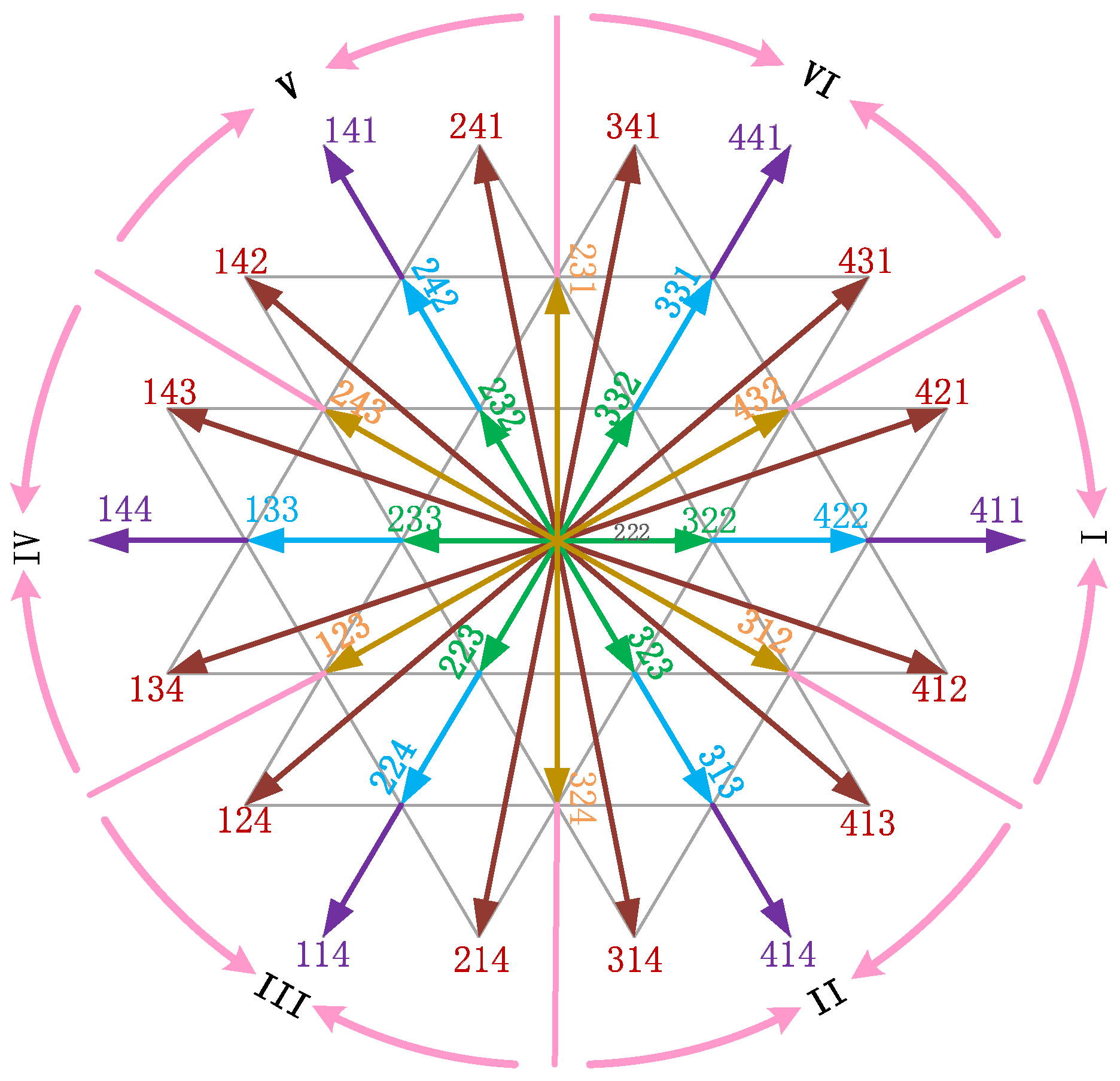
2.1. Space Vectors of 4L-NNPC
2.2. Dynamic Model of Output Current
2.3. Dynamic Model of FCs Voltages
3. Proposed 3LS-MPC for 4L-NNPC Strategy
3.1. CMV Reduction Strategy
3.2. Switch State Disabled Strategy
3.3. Optimal Vector Selection
- (1)
- Sample the three-phase output current iabc(k) at instant k and the DC-side midpoint voltage Uo(k).
- (2)
- Perform the Clarke transformation of the output current iabc(k) from the three-phase stationary coordinate system to the two-phase stationary coordinate system to obtain the currents iα(k) and iβ(k) in the α-β frame.
- (3)
- Using the method of logical function, the disabled RSSs are selected through (19).
- (4)
- Estimate i*α(k + 1), i*β(k + 1) by Lagrange extrapolation (21), and estimate iα(k + 1), iβ(k + 1), Vcx1(k + 1), and Vcx2(k + 1) by prediction Equations (9) and (12).
- (5)
- Substitute i*α(k + 1), i*β(k + 1), iα(k + 1), and iβ(k + 1) into the control set containing 6 L3 voltage vectors, and perform cyclic iteration using the cost function (22) to find the voltage vector that minimizes the cost function value, obtaining the sector where the reference vector is located accordingly.
- (6)
- After determining the sector, select the basic voltage vector with the minimum cost function value among the 6 candidate vectors using (22) in the same way as step (5) to obtain the optimal vector.
4. Simulation Results and Analysis
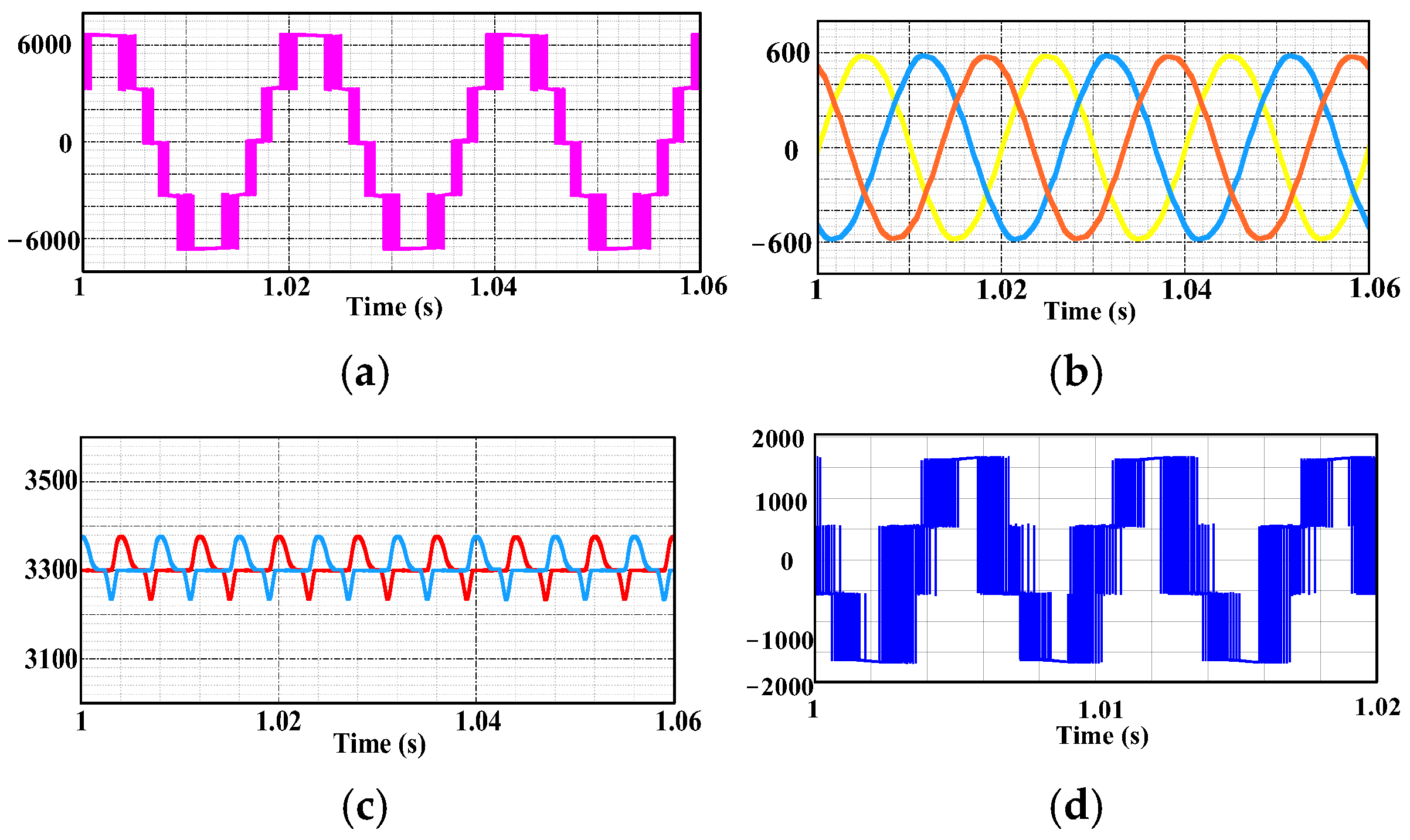
4.1. Steady-State Analysis of Simulation
4.2. Dynamic-State Analysis of Simulation
5. Experimental Results
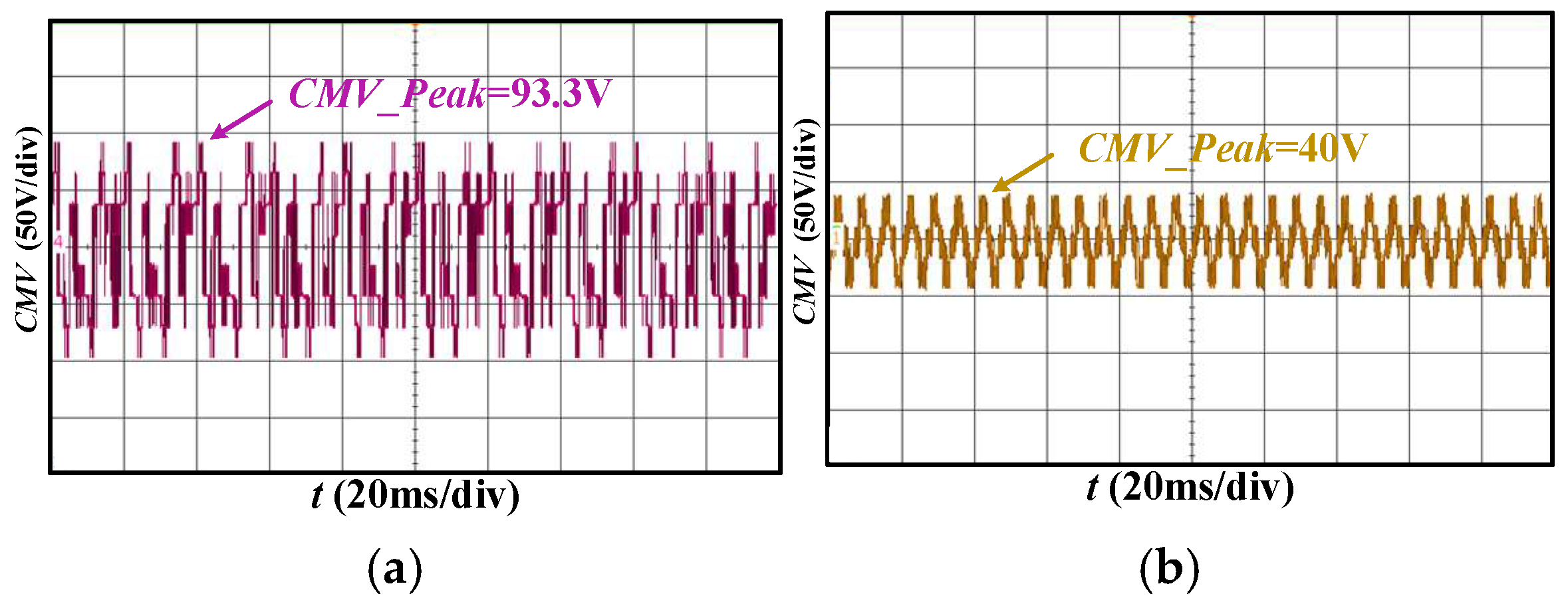
5.1. Comparative Steady-State Analysis of Proposed 3LS-MPC and FCS-MPC Methods
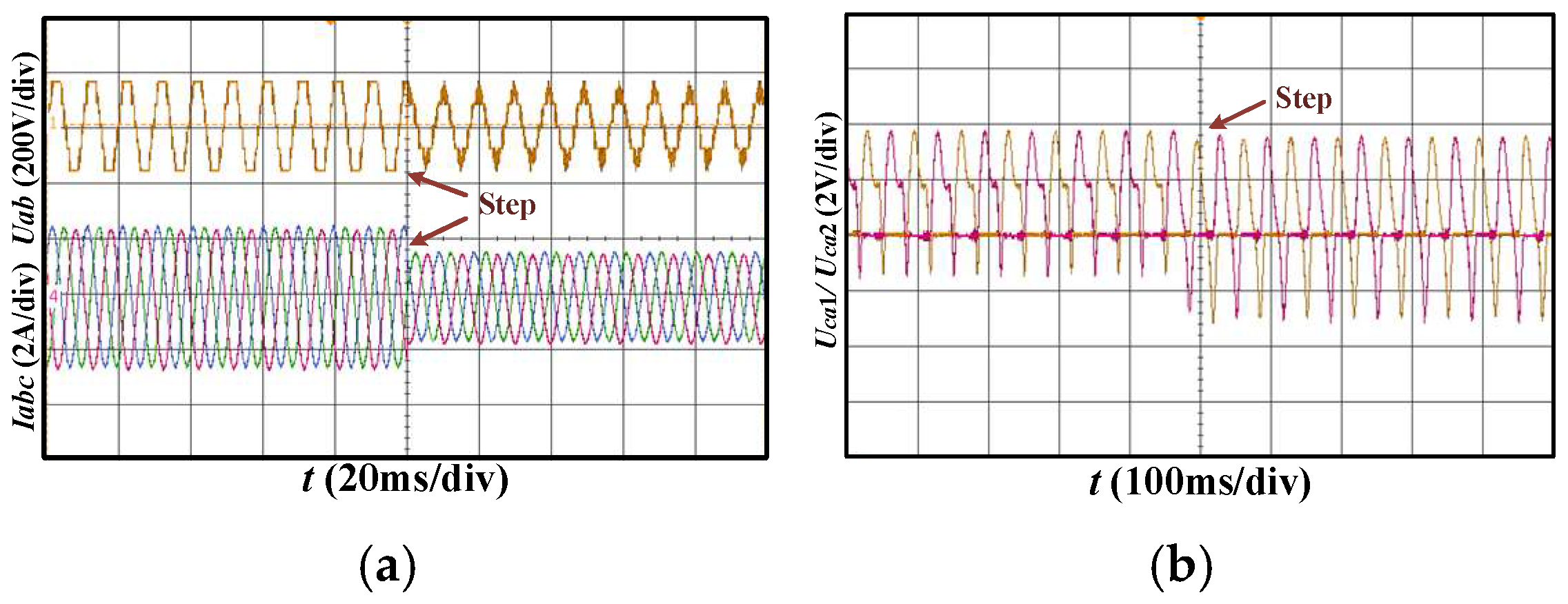
5.2. Dynamic-State Analysis of Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Li, H.; Jin, T. A Novel High-Boost Interleaved DC-DC Converter for Renewable Energy Systems. Prot. Control Mod. Power Syst. 2025, 10, 132–147. [Google Scholar] [CrossRef]
- Li, H.; Chen, Y.; Jin, T. A soft-switched SEPIC-based high voltage gain DC-DC converter for renewable energy applications. IEEE Trans. Ind. Electron. 2025, 72, 3746–3757. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Yuan, Y.; Cao, H.; Liu, P.; Jin, T. Reconfiguration on Novel Unbalance Levels Strategy Adopted in a Three-Level Bidirectional LLC Resonant Converter in HESS to EV Endurance Scheme. IEEE Trans. Transp. Electrif. 2025, 11, 4906–4919. [Google Scholar] [CrossRef]
- Lin, M.; Feng, C.; Chen, Y.; Li, H.; Jin, T. Hybrid Current Stress Optimization Strategy for Three-Level Dual Active Bridge Adapted to Wide Voltage Ranges. IEEE Trans. Power Electron, 2025; 1–13. [Google Scholar] [CrossRef]
- Peng, Y.; Li, Y.; Lee, K.Y.; Tan, Y.; Cao, Y.; Wen, M. Coordinated Control Strategy of PMSG and Cascaded H-Bridge STATCOM in Dispersed Wind Farm for Suppressing Unbalanced Grid Voltage. IEEE Trans. Sustain. Energy 2021, 12, 349–359. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Z.; Xu, Z. DRU Based Low Frequency AC Transmission Scheme for Offshore Wind Farm Integration. IEEE Trans. Sustain. Energy 2021, 12, 1512–1524. [Google Scholar] [CrossRef]
- Manoj, P.; Annamalai, K.; Dhara, S.; Somasekhar, V.T. A Quasi-Z-Source-Based Space-Vector-Modulated Cascaded Four-Level Inverter for Photovoltaic Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 4749–4762. [Google Scholar]
- Vinod, B.R.; Shiny, G. Direct Torque Control Scheme for a Four-Level-Inverter Fed Open-End-Winding Induction Motor. IEEE Trans. Energy Convers. 2019, 34, 2209–2217. [Google Scholar]
- Liu, X.; Qiu, L.; Wu, W.; Ma, J.; Wang, D.; Peng, Z.; Fang, Y. Finite-time ESO-based cascade-free FCS-MPC for NNPC converter. Int. J. Electron. Power Energy Syst. 2023, 148, 108939. [Google Scholar] [CrossRef]
- Wu, W.; Wang, D. An Optimal Voltage-Level Based Model Predictive Control Approach for Four-Level T-Type Nested Neutral Point Clamped Converter With Reduced Calculation Burden. IEEE Access 2019, 7, 87458–87468. [Google Scholar] [CrossRef]
- Narimani, M.; Wu, B.; Cheng, Z.; Zargari, N.R. A New nested Neutral Point Clamped (NNPC) Converter for Medium-Voltage (MV) Power Conversion. IEEE Trans. Power Electron. 2014, 29, 6375–6382. [Google Scholar] [CrossRef]
- Tian, K.; Wu, B.; Narimani, M.; Xu, D.; Cheng, Z.; Zargari, N.R. A Capacitor Voltage-Balancing Method for Nested Neutral Point Clamped (NNPC) Inverter. IEEE Trans. Power Electron. 2016, 31, 2575–2583. [Google Scholar] [CrossRef]
- Bahrami, A.; Narimani, M. A Sinusoidal Pulsewidth Modulation (SPWM) Technique for Capacitor Voltage Balancing of a Nested T-Type Four-Level Inverter. IEEE Trans. Power Electron. 2019, 34, 1008–1012. [Google Scholar] [CrossRef]
- Wu, M.; Li, Y.W.; Tian, H.; Li, Y.; Wang, K. Modified Carrier-Overlapped PWM with Balanced Capacitors and Eliminated Dead-Time Spikes for Four-Level NNPC Converters Under Low Frequency. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6832–6844. [Google Scholar] [CrossRef]
- Tan, L.; Wu, B.; Sood, V.; Xu, D.; Narimani, M.; Cheng, Z.; Zargari, N.R. A Simplified Space Vector Modulation for Four-Level Nested Neutral-Point Clamped Inverters with Complete Control of Flying-Capacitor Voltages. IEEE Trans. Power Electron. 2018, 33, 1997–2006. [Google Scholar] [CrossRef]
- Xu, Y.; Zou, Z.; Liu, Y.; Zeng, Z.; Zhou, S.; Jin, T. Deep Learning-Based Multi-feature Fusion Model for Accurate Open-Circuit Fault Diagnosis in Electric Vehicle DC Charging Piles. IEEE Trans. Transp. Electrif. 2025, 11, 2243–2254. [Google Scholar] [CrossRef]
- Li, X.; Xie, M.; Ji, M.; Yang, J.; Wu, X.; Shen, G. Restraint of Common-Mode Voltage for PMSM-Inverter Systems with Current Ripple Constraint Based on Voltage-Vector MPC. IEEE J. Emerg. Sel. Top. Ind. Electron. 2023, 4, 688–697. [Google Scholar] [CrossRef]
- Monfared, K.K.; Iman-Eini, H.; Neyshabouri, Y.; Liserre, M. Model Predictive Control with Reduced Common-Mode Voltage Based on Optimal Switching Sequences for Nested Neutral Point Clamped Inverter. IEEE Trans. Ind. Electron. 2024, 71, 27–38. [Google Scholar] [CrossRef]
- Le, Q.A.; Lee, D.-C. Reduction of Common-Mode Voltages for Five-Level Active NPC Inverters by the Space-Vector Modulation Technique. IEEE Trans. Ind. Appl. 2017, 53, 1289–1299. [Google Scholar] [CrossRef]
- Guo, F.; Diab, A.M.; Yeoh, S.S.; Yang, T.; Bozhko, S.; Wheeler, P. An Advanced Dual-Carrier-Based Multi-Optimized PWM Strategy of Three-Level Neutral-Point-Clamped Converters for More-Electric-Aircraft Applications. IEEE Trans. Energy Convers. 2024, 39, 356–367. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.; Wu, B.; Rodriguez, J.; Perez, M.; Leon, J. Recent advances and industrial applications of multilevel converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Sudha, V.; Vijayarekha, K.; Sidharthan, R.K.; Prabaharan, N. Combined Optimizer for Automatic Design of Machine Learning-Based Fault Classifier for Multilevel Inverters. IEEE Access 2022, 10, 121096–121108. [Google Scholar] [CrossRef]
- Orfi Yeganeh, M.S.; Sarvi, M.; Blaabjerg, F.; Davari, P. Improved harmonic injection pulse-width modulation variable frequency triangular carrier scheme for multilevel inverters. IET Power Electron. 2020, 13, 3146–3154. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, H.; Li, C.; Lang, X.; Yeoh, S.S. Improved Model Predictive Current Control for Three-Phase Three-Level Converters with Neutral-Point Voltage Ripple and Common Mode Voltage Reduction. IEEE Trans. Energy Convers. 2021, 36, 3053–3062. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, H.; Li, C.; Lang, X.; Yeoh, S.S.; Yang, T.; Rivera, M.; Bozhko, S.; Wheeler, P. A Low-Complexity Optimal Switching Time-Modulated Model-Predictive Control for PMSM With Three-Level NPC Converter. IEEE Trans. Transport. Electrific. 2020, 6, 1188–1198. [Google Scholar] [CrossRef]
- Narimani, M.; Wu, B.; Yaramasu, V.; Cheng, Z.; Zargari, N.R. Finite Control-Set Model Predictive Control (FCS-MPC) of Nested Neutral Point-Clamped (NNPC) Converter. IEEE Trans. Power Electron. 2015, 30, 7262–7269. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B. Model Predictive Decoupled Active and Reactive Power Control for High-Power Grid-Connected Four-Level Diode-Clamped Inverters. IEEE Trans. Ind. Electron. 2014, 61, 3407–3416. [Google Scholar] [CrossRef]
- Monfared, K.K.; Neyshabouri, Y.; Iman-Eini, H.; Liserre, M. An Improved Finite Control-Set Model Predictive Control for Nested Neutral Point Clamped Converter. IEEE Trans. Ind. Electron. 2023, 70, 5386–5398. [Google Scholar] [CrossRef]
- Prajapati, D.; Dekka, A.; Ronanki, D.; Rodriguez, J. High-Performance Sequential Model Predictive Control of a Four-Level Inverter for Electric Transportation Applications. IEEE J. Emerg. Sel. Top. Ind. Electron. 2024, 5, 253–262. [Google Scholar] [CrossRef]
- Ni, Z.; Narimani, M.; Rodriguez, J. Model Predictive Control of a Four-Level T-NNPC Inverter without Weighting Factors. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Phoenix, AZ, USA, 14–17 June 2021; pp. 2133–2138. [Google Scholar]
- Tan, L.; Wu, B.; Narimani, M.; Xu, D.; Liu, J.; Cheng, Z. A space virtual-vector modulation with voltage balance control for nested neutral-point clamped converter under low output frequency conditions. IEEE Trans. Power Electron. 2017, 32, 3458–3466. [Google Scholar] [CrossRef]
- Tan, L.; Wu, B.; Narimani, M.; Xu, D.; Joos, G. Multicarrier-based PWM strategies with complete voltage balance control for NNPC inverters. IEEE Trans. Ind. Electron. 2018, 65, 2863–2872. [Google Scholar] [CrossRef]
- Tian, H.; Li, Y.W. Carrier-based stair edge PWM (SEPWM) for capacitor balancing in multilevel converters with floating capacitors. IEEE Trans. Ind. Appl. 2018, 54, 3440–3452. [Google Scholar] [CrossRef]







| Reference | Method | Characteristics |
|---|---|---|
| [26,27] | FCS-MPC | Simple and intuitive implementation. Including weighting factors. |
| [28] | Improved FCS-MPC | Reduced FCs voltage error. Reduced power loss. Including weighting factors. |
| [29] | Sequential MPC | Reduced switching frequency. Reduced FCs voltage error and ripple. Excluding weighting factors. |
| [30] | Improved FCS-MPC | Reduced CMV. Excluding weighting factors. Increased computational burden. |
| Proposed | 3LS-MPC | Reduced CMV. Excluding weighting factors. Reduced computational burden. |
| Phase Voltage | Level | Switching Vector | Switching State | |||||
|---|---|---|---|---|---|---|---|---|
| Sx1 | Sx2 | Sx3 | Sx4 | Sx5 | Sx6 | |||
| Vdc/2 | 4 | 4 | 1 | 1 | 1 | 0 | 0 | 0 |
| Vdc/6 | 3 | 3a 3b | 1 0 | 0 1 | 1 1 | 1 0 | 0 0 | 0 1 |
| −Vdc/6 | 2 | 2a 2b | 1 0 | 0 0 | 0 1 | 1 1 | 1 0 | 0 1 |
| −Vdc/2 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| Phase Voltage | Switching State | FCs Voltages | |
|---|---|---|---|
| Cx1 | Cx2 | ||
| Vdc/2 | 4 | No Effect | No Effect |
| Vdc/6 | 3a | Discharging (ix > 0) Charging (ix < 0) | Discharging (ix > 0) Charging (ix < 0) |
| 3b | Charging (ix > 0) Discharging (ix < 0) | No Effect | |
| −Vdc/6 | 2a | Charging (ix > 0) Discharging (ix < 0) | Charging (ix > 0) Discharging (ix < 0) |
| 2b | No Effect | Discharging (ix > 0) Charging (ix < 0) | |
| −Vdc/2 | 1 | No Effect | No Effect |
| Common-Mode Voltage | Switch State |
|---|---|
| −Vdc/2 | 111 |
| −7 Vdc/18 | 112 121 211 |
| −5 Vdc/18 | 113 122 131 212 221 311 |
| −Vdc/6 | 114 132 123 141 213 222 231 312 321 411 |
| −Vdc/18 | 124 133 142 214 223 232 241 313 322 331 412 421 |
| Vdc/18 | 134 143 224 233 242 314 323 332 341 413 422 431 |
| Vdc/6 | 144 234 243 324 333 342 414 423 432 441 |
| 5 Vdc/18 | 244 334 343 424 433 442 |
| 7 Vdc/18 | 443 344 434 |
| Vdc/2 | 444 |
| Parameter | Symbol | Simulation | Experimental |
|---|---|---|---|
| Total DC voltage (V) | Vdc | 9900 | 240 |
| Flying capacitance (μF) | Cx1/Cx2 | 4700 | 1150 |
| Load inductance (mH) | L | 10 | 8 |
| Load resistance (Ω) | R | 6 | 3 |
| Sample period (ms) | Ts | 0.1 | 0.1 |
| Nominal voltage (V) | Vn | 6100 | 150 |
| Nominal power (kW) | Pn | 3330 | 2.8 |
| Nominal frequency (Hz) | fn | 50 | 50 |
| Switching frequency (kHz) | fs | 10 | 10 |
| Methods | Amplitude of iref | THD | ΔVpa |
|---|---|---|---|
| Classical Method | 1.5 A | 2.90% | 6 V |
| 2.4 A | 3.22% | 6 V | |
| Proposed Method | 1.5 A | 2.74% | 4 V |
| 2.4 A | 2.97% | 4 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, L.; Chao, W.; Deng, C.; Huang, J.; Wang, Y.; Lin, M.; Jin, T. A Three-Layer Sequential Model Predictive Current Control for NNPC Four-Level Inverters with Low Common-Mode Voltage. Electronics 2025, 14, 2910. https://doi.org/10.3390/electronics14142910
Dai L, Chao W, Deng C, Huang J, Wang Y, Lin M, Jin T. A Three-Layer Sequential Model Predictive Current Control for NNPC Four-Level Inverters with Low Common-Mode Voltage. Electronics. 2025; 14(14):2910. https://doi.org/10.3390/electronics14142910
Chicago/Turabian StyleDai, Liyu, Wujie Chao, Chaoping Deng, Junwei Huang, Yihan Wang, Minxin Lin, and Tao Jin. 2025. "A Three-Layer Sequential Model Predictive Current Control for NNPC Four-Level Inverters with Low Common-Mode Voltage" Electronics 14, no. 14: 2910. https://doi.org/10.3390/electronics14142910
APA StyleDai, L., Chao, W., Deng, C., Huang, J., Wang, Y., Lin, M., & Jin, T. (2025). A Three-Layer Sequential Model Predictive Current Control for NNPC Four-Level Inverters with Low Common-Mode Voltage. Electronics, 14(14), 2910. https://doi.org/10.3390/electronics14142910











