ANHNE: Adaptive Multi-Hop Neighborhood Information Fusion for Heterogeneous Network Embedding

Abstract

Heterogeneous information network (HIN) embedding transforms multi-type nodes into low-dimensional vectors to preserve structural and semantic information for downstream tasks. However, it struggles with multiplex networks where nodes connect via diverse semantic paths (metapaths). Information fusion mainly improves the quality of node embedding by fully exploiting the structure and hidden information within the network. Current metapath-based methods ignore information from intermediate nodes along paths, depend on manually defined metapaths, and overlook implicit relationships between nodes sharing similar attributes. Our objective is to develop an adaptive framework that overcomes limitations in existing metapath-based embedding (incomplete information aggregation, manual path dependency, and ignorance of latent semantics) to learn more discriminative embeddings. We propose an adaptive multi-hop neighbor information fusion model for heterogeneous network embedding (ANHNE), which: (1) autonomously extracts composite metapaths (weighted combinations of relations) via a multipath aggregation matrix to mine hierarchical semantics of varying lengths for task-specific scenarios; (2) projects heterogeneous nodes into a unified space and employs hierarchical attention to selectively fuse neighborhood features across metapath hierarchies; and (3) enhances semantics by identifying potential node correlations via cosine similarity to construct implicit connections, enriching network structure with latent information. Extensive experimental results on multiple datasets show that ANHNE achieves more precise embeddings than comparable baseline models.

1. Introduction

Network representation learning (NRL) [1] effectively embeds information networks into a compact and continuous low-dimensional space. It enables the extraction of valuable insights from networked systems while preserving their structural features, intrinsic properties, and semantic information. NRL supports a range of downstream semantic computing applications, including link prediction [2] and node classification [3], leading to applications in fields like recommender systems [4], social influence analysis [5], and beyond. Notably, DeepWalk [6], LINE [7], and node2vec [8] have been pioneering in integrating deep learning with NRL.

In recent years, the emergence of graph neural networks (GNNs) [9,10,11,12,13,14] has revolutionized the processing of non-Euclidean spatial data, facilitating its direct incorporation into neural networks. This development has facilitated the learning of embedded representations of complex networks enriched with feature information. GNNs employ either spectral methods [10,11] or methods based in the spatial domain [9,12] to compile data from the immediate neighbors of a specific node, enhancing the capabilities for structural analysis and local data integration within graph contexts. The introduction of the attention mechanism, as seen in the graph attention network (GAT) [15], enables selective learning of the importance of single-layer neighbors based on specific tasks, significantly enhancing performance across various downstream tasks. However, this single-layer approach is limited to aggregating information from only the one-hop neighbors.

In practice, numerous connections exist between different objects. Neglecting this heterogeneous information can obscure the distinct characteristics of various node types and the intricate semantic relationships among them, adversely affecting the efficacy of subsequent tasks. To tackle this challenge, multiplexed network representations [16,17,18,19,20,21] leverage metapaths to depict various composite links between nodes. Ref. [16] has extended the GAT model to amalgamate representations from different metapaths, allowing the model to assimilate more comprehensive semantic information. GATNE [22], a trailblazer, introduced AMHEN to NRL. Furthermore, GTN [23] exploits the Transformer architecture to autonomously learn and control the length of useful multi-hop metapaths based on edge-type relations. MHGCN [24] presents a single-layer attributed multi-order graph convolutional network that autonomously explores various metapaths for multi-hop information aggregation learning through homogeneous supervised guidance.

Although metapath-based HIN embedding methods have achieved state-of-the-art results in various tasks, they still suffer from several limitations:

(1)

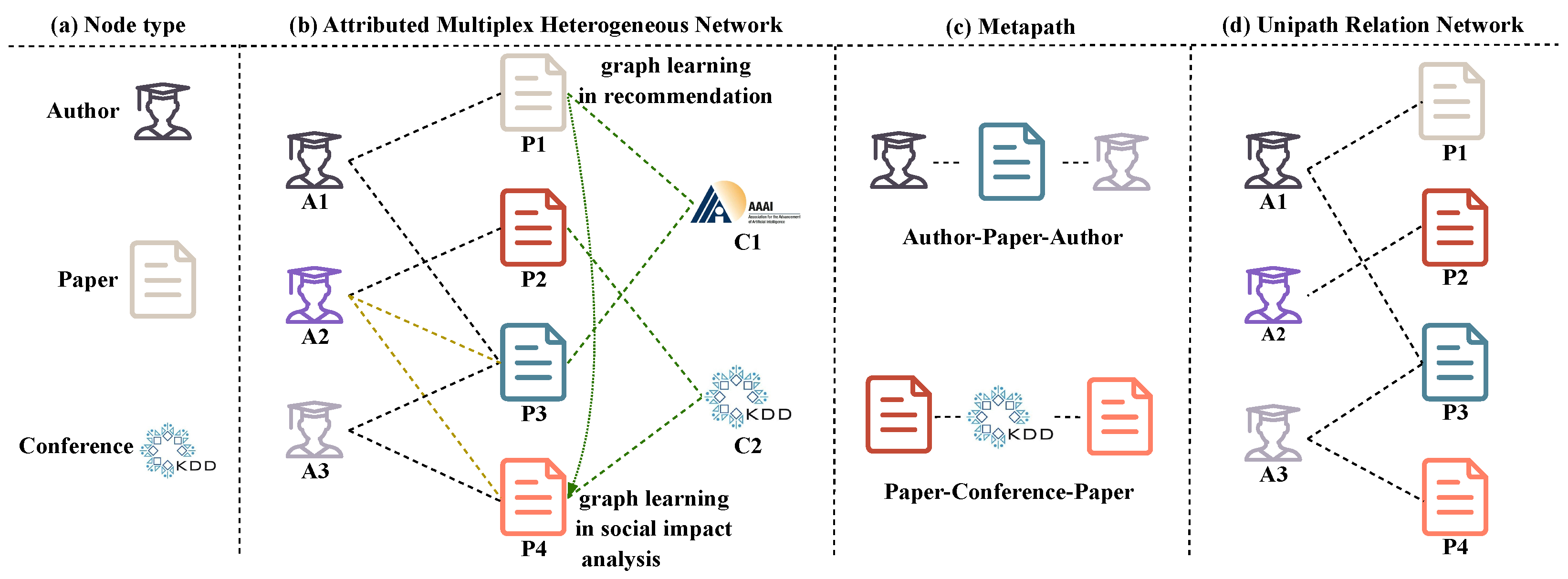
Inadequate information mining along metapaths: Most metapath-based heterogeneous network representations [16,25,26] focus only on the information of the nodes at the two ends of the metapath and ignore the information of the intermediary nodes, which are also crucial for representation learning. As shown in Figure 1b, two authors in the ‘APA’ metapath can collaborate on different papers (A2 and A3), and neglecting the information related to these papers hampers the accurate mining of the relation between the authors. Some state-of-the-art approaches [18,27,28] address this by emphasizing message passing to capture various relations between nodes. However, these methods rely on stacking multiple layers of GNNs to aggregate neighbor information, which can lead to performance degradation and excessive smoothing.

(2)

The common method of determining walking paths through predefined metapaths introduces bias in network structure construction. On the one hand, the learning of network structure heavily depends on the quality of manually designed metapaths, which must be specified in advance based on experience or domain knowledge (e.g., the ‘APA’ and ‘PCP’ metapaths in Figure 1c, which indicate that two authors collaborated on a paper and two papers were presented at the same conference, respectively). Yet, they cannot autonomously extract valuable metapaths tailored to specific task scenarios. Especially for unknown HINs, valid metapaths cannot always be pre-identified [29]. Differently defined metapaths in the same dataset affect GCN performance due to varying semantics and values across different scenarios. On the other hand, the lack of effective integration of different metapaths is not conducive to extracting the network structure for learning. To illustrate, ‘APA’ signifies a scenario where two authors have co-authored a paper, whereas ‘APCPA’ indicates that articles by two authors are featured in the same conference or journal. Different metapaths represent diverse meanings and have varying importance, making their effective integration crucial for improvement.

(3)

Most metapath-based embedding models ignore potential semantic associations between node attributes. Current studies [17,18,30] only learn network embedding representations from primitive network structures. While the primitive structure reflects explicit node relations, it does not encompass all possible relations, missing many implicit relations between nodes. For instance, as depicted in Figure 1b, interdisciplinary papers P1 and P4 may not directly cite each other and lack connecting metapaths owing to their authors and topics originating from different fields. However, they share the same heterogeneous network embedding technique, indicating a latent semantic relation. Capturing these potential correlations between nodes allows for the exploration of deeper semantic relations, resulting in a more comprehensive network structure and improved node representation.

To systematically address limitations (1)–(3), we formulate three research problems (RPs) as the key objectives of this work:

(RP1). How do we adaptively construct multi-length metapaths based on heterogeneous relations? (Section 3.3 and Section 3.4)

(RP2). How do we selectively fuse multi-hop neighborhood information? (Section 3.5)

(RP3). How do we uncover latent semantics ignored by metapaths? (Section 3.6)

To address the aforementioned problems, we propose the adaptive multi-hop neighbor information fusion for heterogeneous network embedding (ANHNE) model. Specifically, we first introduce a composite metapath autonomous extraction (CMAE) model to autonomously learn combinations of sub-metapaths of various lengths without manual design. Based on the composite metapath, we propose a hierarchical semantic attention aggregation (HSAA) model, which selectively aggregates multi-hop structural semantic features to yield precise node representations on a hierarchical scale. Finally, a semantic information enhancement (SIE) model is designed to explore implicit correlations between nodes to unearth deep implicit associations based on the original network structure. An illustration of ANHNE is shown in Figure 2. The most noteworthy contributions of this paper are summarized as follows:

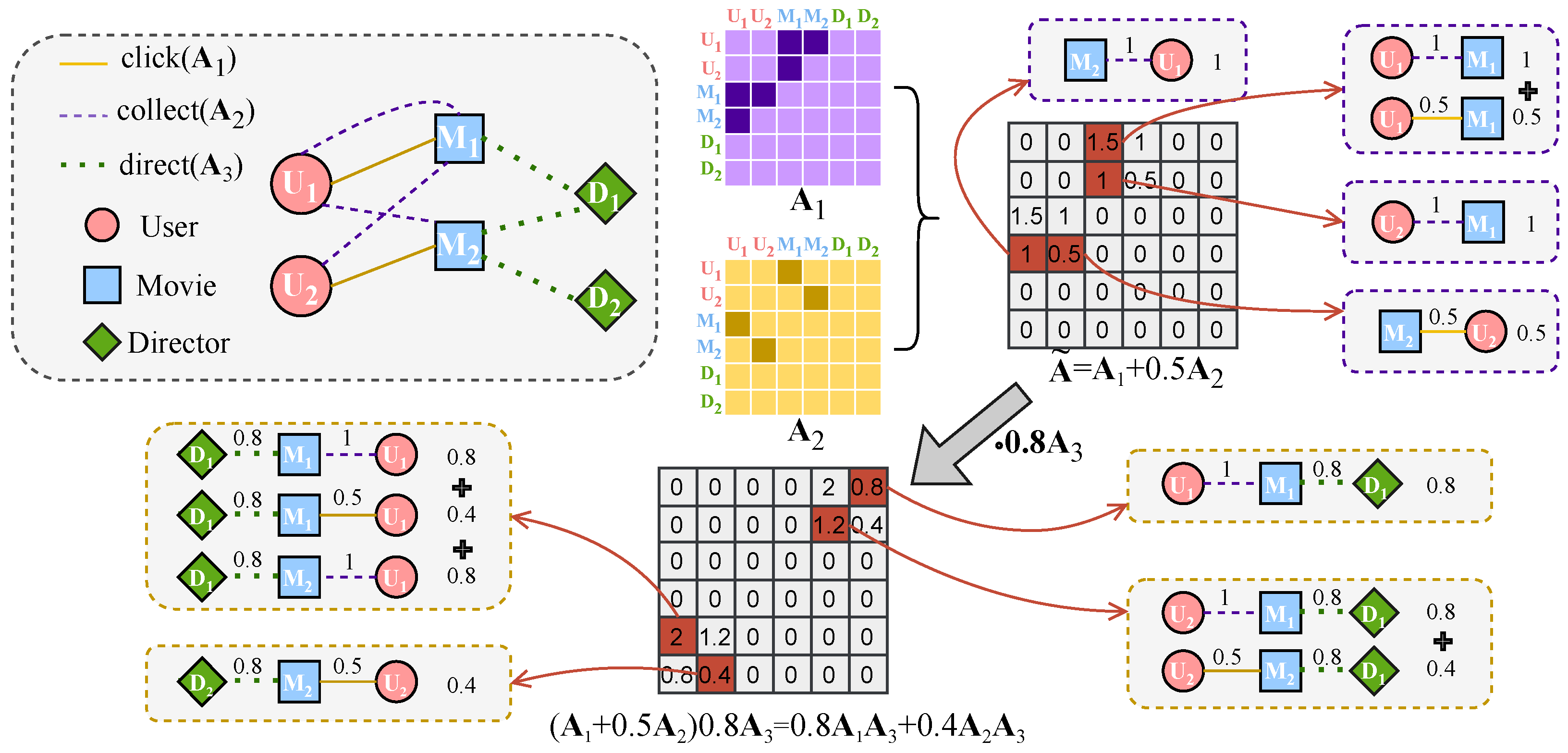
• To the best of our knowledge, this paper presents the concept of composite metapaths for the first time. Unlike the commonly accepted notion of metapaths, composite metapaths are soft combinations of different relations for specific task scenarios, where the topological information of all nodes on the path can be aggregated through the matrix product of unipath relations with different weights.
• We develop a hierarchical semantic attention aggregation model that autonomously determines the relative importance of valuable composite metapaths of specific lengths and selectively aggregates information across different hierarchical levels of neighboring nodes.
• We propose a semantic information enhancement module that mines potential relations between nodes and extensively extracts implicit semantic relations without direct connectivity, enhancing feature representation learning to obtain high-quality representations.
• We conduct extensive experiments on three real-world datasets to indicate the advantage of each module and demonstrate the superiority of our proposal to the state of the art for multiplex heterogeneous networks.

Figure 2. The overview framework of the proposed ANHNE.

Figure 2. The overview framework of the proposed ANHNE.

The remainder of this paper is organized as follows: We discuss related works in Section 2 and briefly describe relevant preliminaries in Section 3. Section 3 also introduces our proposed method in detail. Then in Section 4, we present a series of experiments comparing our method with benchmark approaches and discuss the results. Finally, we conclude our work in Section 5.

2. Related Work

2.1. Graph Convolutional Networks (GCNs)

GCNs aim to derive low-dimensional node embeddings through the feature decomposition of graph Laplacian matrices [31]. Given a homogeneous graph $G=\{V,E\}$ and the feature matrix $\mathbf{X}\in {\mathbb{R}}^{\left|V\right|\times d_f}$ of all nodes projected to the $d_f$-dimension space, the feature transfer between layers can be formulated as

$${\mathbf{H}}^{(l+1)}=\sigma ({\mathbf{D}}^{-1/2}(\mathbf{A}+\mathbf{I}){\mathbf{D}}^{-1/2}{\mathbf{H}}^{\left(l\right)}·{\mathbf{W}}^{\left(l\right)})$$

(1)

where $\mathbf{A}\in {\mathbb{R}}^{N\times N}$ is the adjacency matrix, where ${\mathbf{A}}_{ij}=1$ if nodes i and j are connected. $\mathbf{I}$ denotes the identity matrix, and $\mathbf{D}$ is the degree matrix of $\mathbf{A}+\mathbf{I}$. ${\mathbf{W}}^{\left(l\right)}$ is a trainable weight matrix. ${\mathbf{H}}^{\left(l\right)}$ is the l-layer feature matrix, and ${\mathbf{H}}^{\left(0\right)}=\mathbf{X}$. The depth of the GCN determines the extent to which the model can capture and transmit node features [32].

GraphSAGE [9], a large-scale GCN framework, employs an embedding function to sample and aggregate local neighborhood features of nodes. To selectively prioritize different neighborhood information, GAT introduced an attention-based message passing mechanism. AM-GCN [33] adaptively learns the depth correlation between topology and feature spaces using a multi-channel GCN approach. Scattering-GCN [34] integrates a geometric scattering transform with residual convolution to enhance traditional GCN models. Dual-light GCN [35] eliminates nonlinear embedding projections and aggregates information across multiple scales. Cross-GCN [36] introduces cross-feature map convolution to explicitly model cross-features of arbitrary orders. To streamline GCN models, SGC [37] removes the activation function, pre-computes the higher-order adjacency matrix, and uses it in a single GCN layer to approximate multi-layer information propagation. Zhang et al. [38] utilized the SGC paradigm to capture global cluster structures and adaptively select the appropriate convolution order for different graphs.

However, these initial GCN implementations were designed for homogeneous networks and failed to effectively preserve the heterogeneity and multiplicity of real-world network embeddings.

2.2. Heterogeneous Network Representation Learning

Efforts to enhance heterogeneous network representations using GNNs have been extensive. HGT [26] employs relation-dependent self-attention to model dynamic heterogeneous interactions, but ignores higher-order semantic connections beyond direct neighbors. HeCo [39] improves node embeddings by comparing metapath and network schema views, but requires predefined metapaths and misses implicit relations. DMGI [40] employs a consensus regularization scheme to address relations among specific node embedding types, incorporating perceptual nodes. PF-HIN [41] adopts a pre-training and fine-tuning framework for heterogeneous information network feature learning. MISE [42] uses mechanisms to maximize mutual information between local and global metapath representations, constructing graph structures through implicit node correlations.

The metapath approach is a classical method designed for heterogeneous graph models. HERec [43] employ randomized wandering sampling to construct walking paths on heterogeneous graphs for node embedding. PSHGNAN [44] integrates metapaths and meta-structures through an attention mechanism to learn node embeddings. However, the quality of empirically designed metapaths significantly impacts embedding performance. AMOGCN [45] fuses outputs from different depths of the graph convolutional layer to adaptively learn multi-length metapaths. Many metapath models only aggregate information from the endpoints, overlooking the relations between nodes during the message passing process. To effectively utilize information from intermediate nodes, Ref. [18] combines jointly supervised signals containing extrinsic and intrinsic mutual information, and [27] constructs a multi-behavioral graph convolutional network to represent multi-behavioral data. However, aggregating multi-hop neighbor information by stacking multiple GNN layers can lead to performance degradation and excessive smoothing. To counteract this, Xue et al. [46] aggregate neighbor information across different hops using an attentive mechanism, enabling selective extraction of important multi-hop features. MHNF [47] makes further improvements, allowing for the aggregation of information from multi-hop neighbor nodes in heterogeneous graphs. However, they only considered explicit relations in the network and lacked consideration of the natural homogeneity between node attributes.

To address the above problems, the ANHNE method introduced in this paper not only designs an adaptive learning strategy for multi-length metapaths based on the diverse relations among nodes during the information transfer process, but also considers the natural homogeneity among node attributes to effectively mine and aggregate multi-hop neighbor information in heterogeneous graphs. This capability represents a significant advantage of ANHNE over previous research efforts.

3. Methodology

3.1. Preliminaries

In this section, we summarize a concise overview of the essential definitions utilized throughout this paper in

Table 1. A summary of primary notations in this paper.

Notations	Explanations
$\mathbf{I}\in {\mathbb{R}}^{N\times N}$	The identity matrix.
$\sigma$	The activation function.
$T_i$	The type of node i.
$R_r$	The r-th node relation.
${\mathbf{X}}_{T_i}$	The initial feature matrix of the node of type $T_i$.
${\mathbf{H}}_i$	The projected node feature of type $T_i$.
${\mathbf{A}}_r$	The adjacency matrix under the relation $R_r$.
${\mathbf{A}}^{\left(l\right)}$	The adjacency matrix of the l-layer composite metapath.
${\mathbf{W}}_{T_i}$	The feature mapping matrix for the type $T_i$.
${\mathbf{W}}^{\left(l\right)}$	The trainable weight matrix of l-layer GCN.
${\beta }_i$	The weight of relation i in the composite metapath.
${\alpha }_l$	The composite metapath-based hierarchical attention weight for l-layer neighbors.
$l_f$	The learning parameter to modulate the contribution of auxiliary information.
${\mathbf{S}}^K$	The latent graph structure adjacency matrix.
${\mathbf{Z}}^{\left(l\right)}$	The ndoe embedding of composite metapath based l-layer neighbors.
$\mathbf{Z}$	The node embedding of multi-layer neighbors.
${\mathbf{Z}}_s$	The latent graph structure node embedding.
${\mathbf{Z}}_f$	The final node embedding.
$\mathbf{Y}$	Ground truth.

for quick reference.

Definition 1.

Attributed multiplex heterogeneous network: It can be represented as $G=\left\{G_1,G_2,\dots ,G_r,\dots ,G_{\left|R\right|}\right\}$, where $G_r=\{V,{\mathbf{A}}_r,\mathbf{X}\}$ is a unipath relation network with a particular relation $r\in R$, $\mathbf{X}\in {\mathbb{R}}^{N\times m}$ denotes the attribute feature matrix, and ${\mathbf{A}}_r\in {\{0,1\}}^{N\times N}$ is the adjacency matrix of the network $G_r$. We denote the set of adjacency matrices as $\mathbf{A}=\left\{{\mathbf{A}}_1,{\mathbf{A}}_2,\dots ,{\mathbf{A}}_r,\dots ,{\mathbf{A}}_{\left|R\right|}\right\}$. With a node type mapping function $f_v:V\to T$ and an edge type mapping function $f_e:E\to R$, the node types and edge types in a heterogeneous network should satisfy $\left|T\right|+\left|R\right|>2$.

Definition 2.

Metapath: A metapath is usually formulated in the form of $T_1\stackrel{R_1}{\to }{T}_2\stackrel{R_2}{\to }\dots \stackrel{R_l}{\to }{T}_{l+1}$ and abbreviated as $T_1{T}_2\dots T_{l+1}$. The path indicates that node 1 and $l+1$ have a relation $R=R_1\circ R_2\circ \dots R_l$, where $T_i$ denotes the type of the node i, $R_j$ denotes the type of the edge j, and ∘ denotes the join operator in the relation.

Definition 3.

Composite metapath: Composite metapath is no longer an artificially specified path in Definition 2, but a soft combination of relations determined based on specific task scenarios. In this case, the combination relation R becomes $R^{\prime }={R_1}^{\prime }\circ {R_2}^{\prime }\circ \dots \circ {R_l}^{\prime }=\left({\displaystyle \sum _{m_1\in T}}{w}_{m_1}{R}^{m_1}\right)\circ$

$\left({\displaystyle \sum _{m_2\in T}}{w}_{m_2}{R}^{m_2}\right)\circ \dots \circ \left({\displaystyle \sum _{m_l\in T}}{w}_{m_l}{R}^{m_l}\right)$. Since the combination relation $T_1\stackrel{R_1^{\prime }}{\to }{T}_2\stackrel{{R_2}^{\prime }}{\to }\dots \stackrel{{R_l}^{\prime }}{\to }{T}_{l+1}$ is able to learn different combinations of relations for a specific task, it can be used for mining richer and more valuable relations.

3.2. Overall Framework

In this section, we present the proposed ANHNE model for managing the attributed heterogeneous network, with a detailed depiction in Figure 2. Initially, we introduce the autonomous extraction module for composite metapaths, which autonomously identifies valuable combinations of sub-metapaths containing various relations and effectively integrates the information from each sub-metapath based on their assigned weights. Next, we propose a hierarchical semantic attention aggregation model to selectively aggregate semantic information from different hierarchical neighbors through composite metapaths. Finally, we construct a semantic information enhancement module to further explore implicit correlations between nodes and enrich the embedded network with more comprehensive semantic information. The proposed model is introduced and analyzed through RP1 (Section 3.3 and Section 3.4), RP2 (Section 3.5), and RP3 (Section 3.6):

3.3. Multipath Relation Aggregation

Denoted by $\left\{G_r\right|r=1,2,\dots ,\left|R\right|\}$, each unipath relation network contributes differently in a given task scenario, and accurately determining their relative importance is crucial to reflecting the underlying relations accurately.

Considering scenarios such as multiple user–movie interactions on video streaming platforms, the decomposed unipath relation networks correspond to distinct types of relational links between users and movies. As illustrated in the U–M relation network in Figure 3, click and collect represent different edge types in the network, each exhibiting unique behavioral semantics. The varying importance of ${\mathbf{A}}_1$ and ${\mathbf{A}}_2$ reflects users’ differing behavioral preferences for movies at that time. Thus, multiple user–movie interactions with distinct relation semantics impact the network’s learning process, respectively. To capture these varied node dependencies based on unipath relation types, we propose a multipath relation aggregation approach. The multipath relation matrices of aggregating specific edge types with learned weights $w_{m_r}$ are as follows:

$$\tilde{\mathbf{A}}={\sum }_{r=1}^{\left|R\right|}{w}_{m_r}{\mathbf{A}}_r$$

(2)

where ${\mathbf{A}}_r$ denotes the unipath relation adjacency matrix of relation $R_r$, and the set of weights $\left\{w_{m_r}\right|r=1,2\dots ,\left|R\right|\}$ is a set of trainable parameters that dynamically adjusts according to different tasks.

3.4. Composite Metapath Autonomous Extraction Model (CMAE)

Extracting neighborhood information through metapaths can significantly enhance the performance of embedding models. However, each manually specified metapath represents only a single type of relation, transferring interactions in a way that cannot capture the complex interactions among diverse node types. In practical scenarios, the relations between two nodes are often intricate and varied, with each relation playing distinct roles and possessing varying levels of importance across different tasks. Consequently, it is crucial to construct composite metapaths of specified lengths that learn automatically from the semantic paths of various relations.

Based on Section 3.3, we extend the multipath relation aggregation process to construct composite metapaths with two layers, as depicted in Figure 3. This method accounts for all possible interactions to construct the sub-metapaths and adjusts its weights according to the relative importance of the relations. Thus, when aggregating multiple neighboring nodes, this approach integrates the relations of nodes by considering the specific task scenarios through the learned weights.

More generally, the topological information of the l-layer metapath can be formulated as a combination of different unipath relation adjacency matrices, and the semantic information of the $l^{th}$-hop neighbor can be expressed as:

$${\mathbf{A}}^{\left(l\right)}={\mathbf{A}}_1{\mathbf{A}}_2\dots {\mathbf{A}}_l$$

(3)

To flexibly and harmoniously adjust the relative importance of various relations in composite metapaths, it is necessary to calculate the adjacency matrices of the unipath networks representing these relations and then aggregate them based on their respective weights:

$$\left\{\begin{array}{c}{\mathbf{A}}^{\left(1\right)}={\displaystyle \sum _{i=1}^{\left|R\right|}}{w}_{m_i}{\mathbf{A}}_i\\ {\mathbf{A}}^{\left(2\right)}={\displaystyle \sum _{i=1}^{\left|R\right|}}{\displaystyle \sum _{j=1}^{\left|R\right|}}{w}_{m_i,m_j}{\mathbf{A}}_i{\mathbf{A}}_j\\ ⋮\\ {\mathbf{A}}^{\left(l\right)}=\underset{l}{\underbrace{{\displaystyle \sum _{i=1}^{\left|R\right|}}\dots {\displaystyle \sum _{j=1}^{\left|R\right|}}}}{w}_{\underset{l}{\underbrace{m_i,\dots ,m_j}}}\underset{l}{\underbrace{{\mathbf{A}}_i\dots {\mathbf{A}}_j}}\end{array}\right.$$

(4)

where ${\mathbf{A}}^{\left(l\right)}$ is the adjacency matrix of the l-layer composite metapaths. $w_{m_i,\dots ,m_j}$ represents the learned weights of different relations in the composite metapaths, and a total of ${\displaystyle \sum _{i=1}^l}|R{|}^i$ learning parameters can be used to aggregate the diverse relations. The Conv operation fuses heterogeneous relations using trainable weights $w_{m_i}$, which are autonomously optimized through backpropagation to maximize task performance.

We assert that integrating the CMAE is essential, as it offers the following benefits to ANHNE:

• A distinctive aspect of our approach is that relation weights do not require manual specification; rather, they are autonomously learned while considering the specific task scenarios. This allows for dynamic adjustment of weights based on the actual effects of embedding. For instance, in the academic network shown in Figure 1b, if the collaboration between authors holds more significance, the relations in the ‘APA’ path will carry higher weights. Conversely, if differences in research areas among authors are more important, the relations in the ‘APCPA’ path should have higher weights. This enables us to more precisely capture complex semantic information.
• Our method enables automatic semantic mining. The composite metapaths learnd by CMAE are essentially soft combinations of various relations and can consider numerous sub-metapaths with specific semantics. Consequently, by multiplying and superimposing unipath relation adjacency matrices with varying weights, CMAE can autonomously extract l-layer metapaths, thereby overcoming the limitations of existing methods that require predefined metapaths. Unlike GTN [23], which generates metapaths via multiplication of adjacency matrices, our composite metapaths are weighted combinations of multipath relations.
• We gather multi-layer relation topology information by multiplying matrices with weights, and then proceed to feature aggregation via GCN instead of stacking multi-layer GNNs. This not only reduces computational demands, but also avoids performance degradation due to over-smoothing.

3.5. Hierarchical Semantic Attention Aggregation Model (HSAA)

In many heterogeneous network representation methods, concentrating solely on the start and endpoint information of a metapath leads to incomplete features extraction. While merely linking the data from all nodes along the path offers a potential solution, it fails to effectively differentiate the varying roles of neighboring nodes at different hops in practical task scenarios, often resulting in redundancy.

To address this issue, this paper proposes a strategy for multi-layer neighbor information aggregation. First, based on the composite metapaths of different layers obtained in Section 3.4, the neighbor information of a specific layer is aggregated through one layer of GCN, as shown in Figure 4a. Then, the heterogeneous information of neighboring nodes of different layers is selectively aggregated according to the importance, as shown in Figure 4b. The HSAA model enables correct identification of neighbor semantics and accurate learning of network structure.

First, heterogeneous network data consists of nodes of various types with features residing in distinct semantic spaces. It is necessary to project attributes of nodes from different spaces to the same space. We define a projection matrix ${\mathbf{W}}_{T_i}$, which maps ${\mathbf{X}}_{T_i}$ from the semantic space ${\mathbb{R}}^{d_{T_i}}$ to the common semantic space ${\mathbb{R}}^{d_C}$, and the projection formula is as follows:

$${\mathbf{H}}_i={\mathbf{W}}_{T_i}·{\mathbf{X}}_{T_i}$$

(5)

where ${\mathbf{X}}_{T_i}\in {\mathbb{R}}^{\left|V_{T_i}\right|\times d_{T_i}}$ is the initial feature matrix of type $T_i$, and ${\mathbf{W}}_{T_i}\in {\mathbb{R}}^{d_{T_i}\times d_c}$ is a type-specific projection matrix. For example, ${\mathbf{W}}_P\in {\mathbb{R}}^{d_P\times d_c}$ maps the feature matrix ${\mathbf{X}}_P\in {\mathbb{R}}^{\left|V_P\right|\times d_P}$ of the “Paper” type from the “Paper” space ${\mathbb{R}}^{d_P}$ to a new common space ${\mathbb{R}}^{d_c}$.

Splice mapping feature matrices of diverse types to obtain the new feature mapping matrix of all nodes:

$$\mathbf{H}=[{\mathbf{H}}_1;{\mathbf{H}}_2\dots ;{\mathbf{H}}_{\left|T\right|}]$$

(6)

To reduce computational complexity, we input the l-hop neighbor relation matrix ${\mathbf{A}}^{\left(l\right)}$, which contains multi-layer topology information, into a single-layer GCN to propagate node attributes:

$${\mathbf{Z}}^{\left(l\right)}=\sigma ({\mathbf{D}}_{\left(l\right)}^{-1/2}({\mathbf{A}}^{\left(l\right)}+\mathbf{I}){\mathbf{D}}_{\left(l\right)}^{-1/2}\mathbf{H}·{\mathbf{W}}^{\left(l\right)})$$

(7)

where ${\mathbf{Z}}^{\left(l\right)}\in {\mathbb{R}}^{N\times d}$ is the aggregated information of the l-hop attributed neighbors propagating along the composite metapath, the i-th row ${\mathbf{Z}}_i^{\left(l\right)}$ of ${\mathbf{Z}}^{\left(l\right)}$ denotes the semantic aggregated information of the node i, ${\mathbf{D}}_{\left(l\right)}$ is the degree matrix of ${\mathbf{A}}^{\left(l\right)}+\mathbf{I}$, ${\mathbf{W}}^{\left(l\right)}\in {\mathbb{R}}^{d_c\times d}$ is the learnable matrix parameter, and $\sigma$ is the activation function of ReLu, chosen for its sparsity induction to filter insignificant neighbor activations.

Neighbor nodes at different hops correspond to distinct semantics and properties. To effectively distinguish the importance of embedding expressions of these hop neighbors, we design an attention aggregation model. This model allows us to learn different hop-attention weights, evaluate the roles they actually play, and selectively aggregate the information of them. Specifically, the following equation is employed to determine the significance of various hops:

$${\alpha }_l=\sigma \left[{\delta }^{\left(l\right)}tanh\left(W^{\left(l\right)}{\mathbf{Z}}^{\left(l\right)}\right)\right]$$

(8)

where ${\alpha }_l$ represents the importance of l-hop neighbors’ information under the composite metapath, and ${\delta }^{\left(l\right)}$ denotes the learnable matrix. Furthermore, the importance coefficients for the information at each hop are normalized using the softmax function:

$${\mu }_l={\displaystyle \frac{exp\left({\alpha }_l\right)}{{\displaystyle \sum _{j=1}^L}exp\left({\alpha }_j\right)}}$$

(9)

Finally, the aggregated information representations for various hops under the composite metapath are achieved:

$$\mathbf{Z}=\sum _{l=1}^L{\mu }_l{\mathbf{Z}}^{\left(l\right)}$$

(10)

where $\mathbf{Z}$ is the synthesized information representation containing a combination of soft relations and can be used to perform various tasks.

In this paper, the cross-entropy function is employed as a mechanism to facilitate the effective feedback guidance role of labels on network embedding. The model’s loss can be computed as follows:

$${\mathcal{L}}_{re}(\mathbf{Z},\mathbf{Y})=-\sum _{i\in \Omega }\sum _{j=1}^C{\mathbf{Y}}_{ij}log\left(F\left({\mathbf{Z}}_{ij}\right)\right)$$

(11)

where C denotes the total count of node labels, $\mathbf{Y}$ represents the lable matrix containing 1 or 0 from the training set $\Omega$, and $F\left({\mathbf{Z}}_{ij}\right)$ indicates the prediction result of the node i. Based on this loss function, the model is optimized using the gradient descent mechanism.

In conclusion, Equations (2)–(4) detail the construction of multi-length composite metapaths (RP1), upon which we efficiently aggregate the information across different hops using GCN, as demonstrated in Equations (7) and (10) (RP2).

3.6. Semantic Information Enhancement Model (SIE)

Although various combinations of explicit relations can be adaptively learned through l-layer composite metapaths, many nodes with similar homogeneous semantic information are still inevitably overlooked. These nodes are not connected through any kind of metapath, leading to a lack of implicit information. Consequently, in this section, to further explore implicit relations among nodes, we utilize the matured representation $\mathbf{Z}$ obtained in Section 3.5 to generate the potential network structure. This guides the acquisition of auxiliary node representation ${\mathbf{Z}}_s$ as complementary information to learn a more robust embedded network and achieve node embeddings with superior performance (RP3).

First, to learn the potential graph topology, we measure the semantic relevance of two nodes using the pairwise cosine similarity of the two node representation vectors ${\mathbf{Z}}_i$ and ${\mathbf{Z}}_j$, i.e., $sim({\mathbf{Z}}_i,{\mathbf{Z}}_j)={\displaystyle \frac{<{\mathbf{Z}}_i,{\mathbf{Z}}_j>}{∥{\mathbf{Z}}_i∥∥{\mathbf{Z}}_j∥}}$. The choice of K is motivated by a trade-off between preserving high-confidence semantic edges and suppressing noise: larger K increases computational cost and risks including irrelevant edges, while smaller K may overlook critical latent relations. This aligns with graph sparsification principles in prior work [48]. We choose the top-K semantically similar neighbors for each node to form the implicit adjacency matrix, as described below:

$$s_{ij}^K=\left\{\begin{array}{c}1,s_{ij}\in \mathrm{Top-K}\left({\mathbf{s}}_i\right)\hfill \\ 0,s_{ij}\notin \mathrm{Top-K}\left({\mathbf{s}}_i\right)\hfill \end{array}\right.$$

(12)

where $s_{ij}$ represents the $i^{th}$ row and $j^{th}$ column of the implicit neighbor information matrix $\mathbf{S}\in {\mathbb{R}}^{N\times N}$.

Subsequently, the features of its potential neighbors are captured using the implicit adjacency matrix:

$${\mathbf{Z}}_s=\sigma \left({\mathbf{D}}_s^{-1/2}{\mathbf{S}}^K{\mathbf{D}}_s^{-1/2}\mathbf{H}{\mathbf{W}}_s\right)$$

(13)

where ${\mathbf{D}}_s$ is the degree matrix of the potential neighbor matrix ${\mathbf{S}}^K$ and ${\mathbf{W}}_s$ is the learnable matrix parameter.

Finally, the final node representation is generated by aggregation of the information representation $\mathbf{Z}$ and the auxiliary information representation ${\mathbf{Z}}_s$:

$${\mathbf{Z}}_f=\mathbf{Z}+l_f\cdot {\mathbf{Z}}_s$$

(14)

where $l_f$ is a learning parameter that modulates the contribution of auxiliary information ${\mathbf{Z}}_s$ to the final node representation.

Similarly, the loss in this module is calculated as:

$${\mathcal{L}}_{se}({\mathbf{Z}}_f,\mathbf{Y})=-\sum _{i\in \Omega }\sum _{j=1}^C{\mathbf{Y}}_{ij}log\left(F\left({\mathbf{Z}}_{f,ij}\right)\right)$$

(15)

where ${\mathbf{Z}}_f\in {\mathbb{R}}^{N\times d}$ represents the final low-dimensional embedded feature representation.

The overall procedure is shown in Algorithm 1.

3.7. Model Efficiency Analysis

ANHNE mainly consists of three modules: (1) composite metapath autonomous extraction (CMAE) involves matrix operations to construct multi-length metapaths. For a maximum path length L and relation types $\left|R\right|$, the complexity is $O(L·{\left|R\right|}^L·N^2)$ due to weighted matrix multiplications; (2) hierarchical semantic attention aggregation (HSAA) projects heterogeneous features ($O(N·d_{T_i}·d_c)$) and applies single-layer GCNs for each composite metapath ($O(\left|\epsilon \right|·d+N·d^2)$), with attention-based fusion across L hierarchical levels ($O(L·N·d)$); (3) semantic information enhancement (SIE) computes pairwise node similarities for implicit relations ($O(N^2·d)$ but reduces this via top-K sparsification to $O(NlogN+K·N·d)$, followed by a sparsity-aware GCN.

Overall, ANHNE avoids the high complexity of stacking multi-layer GNNs by leveraging CMAE for multi-hop relation capture and SIE’s sparsification. This design achieves efficiency comparable with state-of-the-art methods (e.g., GTN [23]) with only 1/10–1/100 computational overhead.

4. Experiments and Results Analysis

In this section, to demonstrate the superiority of the model presented in this paper, we undertake a series of experiments using publicly available datasets. Initially, we compare ANHNE against a range of state-of-the-art baseline methods in node classification and clustering tasks. Subsequently, we examine the practical utility of each component in enhancing network structure learning. Furthermore, we perform visualization experiments to assess the spatial distribution quality of the final node representations. Lastly, we conduct a hyperparameter study to investigate the influence of network parameter configurations on model performance.

4.1. Dataset

In our experiments, we utilize three widely recognized open-source heterogeneous network datasets commonly employed in the domain of network representation learning. Each dataset contains both attributes and relation information. The datasets are detailed as follows:

• ACM (http://dl.acm.org (accessed on 3 July 2025)): This widely recognized open-source citation network dataset comprises nodes that represent papers, authors, and topics. The initial features of the papers are obtained through a bag-of-words model applied to the paper keywords, where each node is characterized by 1870 attributes.
• DBLP (https://dblp.uni-trier.de (accessed on 3 July 2025)): This dataset features a citation network with nodes categorized into four types: papers, authors, conferences, and topics. For our experiments, we extracted a subset of the DBLP dataset, selecting 4057 nodes for analysis, which includes three types of paper nodes: information extraction, data mining, and artificial intelligence.
• IMDB (https://www.imdb.com (accessed on 3 July 2025)): This dataset includes a citation network comprising nodes classified into four categories: papers, authors, conferences, and topics. For our experimental analysis, we selected a subset of the DBLP dataset, comprising 4057 nodes, which encompasses three types of paper nodes: information extraction, data mining, and artificial intelligence.

Further details are provided in

Table 2. Datasets of heterogeneous networks.

Datasets	Num.Nodes	Attributes	Node Types	Classes	Train/Val/Test
ACM	Paper(3025)	1870	Paper(P)/Author(A)/Subject(S)	3	600/300/2125
DBLP	Paper(4057)	334	Paper(P)/Author(A)/Conference(C)/Term(T)	4	800/400/2857
IMDB	Movie(3550)	1232	Movie(M)/Actor(A)/Director(D)/Year(Y)	3	600/300/2660

.

4.2. Baselines

In these experiments, the model introduced in this paper was evaluated against a range of cutting-edge methods in the domain of heterogeneous network embedding.

Table 3. Characteristics of different models (Attri.: attributed; Hetero.: for heterogeneous networks; Learnable.: learnable metapaths; Multi-order.: multi-order metapaths).

Methods	Attri.	Hetero.	Learnable.	Multi-Order.
GCN	✓	×	×	×
GAT	✓	×	×	×
HAN	✓	✓	×	×
MAGNN	✓	✓	×	×
GTN	✓	✓	×	×
MHGCN	✓	✓	✓	✓
AMOGCN	✓	✓	✓	✓
ANHNE	✓	✓	✓	✓

offers a summary of these models.

• GCN [10]: Extends traditional CNNs to non-Euclidean network structures, synthesizing neighbor node information at each layer through specific aggregation strategies (e.g., averaging or summing), and enabling in-depth exploration of the graph’s intrinsic properties and structural relations via feature analysis.
• GAT [15]: Aggregates information from single-layer neighbors through an attention mechanism, allowing each node to assess the importance of its one-hop neighbors based on their features. However it can only aggregate information within one-hop neighbors.
• HAN [16]: Learns the importance of nodes and their metapath-based neighbors, introducing semantic-level attention to fuse representations under different metapaths based on GAT, thus facilitating hierarchical feature aggregation through metapath neighbors.
• MAGNN [49]: It projects attributes of heterogeneous nodes into a shared semantic space, then performs intra-metapath and inter-metapath information aggregation to capture the structural and semantic nuances of the network.
• GTN [23]: Learns to softly select combined relations to generate useful metapaths and control lengths automatically. Its metapath generation module shares functionalities with the CMAE model in this study.
• MHGCN [24]: Utilizes an attributed multi-order graph convolutional network to capture multi-relational structural information, explores different metapaths automatically, and employs both unsupervised and semi-supervised learning techniques to learn and derive the final node embeddings.
• AMOGCN [45]: Constructs different order adjacency matrices containing various metapath relations, selectively fuses information from these matrices via SGC, and extracts final node embeddings through supervised learning that incorporates node semantic and labeling information.
• ANHNE. Our proposed method.

4.3. Implementation Details

In the experiments, the ANHNE model is optimized using the Adam optimizer with a learning rate of 0.01, dropout rate of 0.5, and weight decay of 0.001. Other parameters are initialized using the Xavier distribution. The dimensionality of the common latent space after feature mapping is set to 128, while the final node embedding dimension is set to 64. The initial value of $l_f$ is set to 0.01. The length of composite metapaths L is searched within the range $\{1,2,3,4,5\}$, with the optimal value differing by dataset. Specifically, the optimal maximum path length L for the ACM dataset is chosen to be 2, whereas for the DBLP and IMDB datasets, it is selected as 3. An early stopping strategy is employed, with patience set to 15, to feed robust feature representations output from the HSAA module into the SIE module for implicit enhancement. We set K = 20 because at this point, the experimental performance of the three datasets has basically reached its optimum. For hyperparameter selection in all baseline methods, we adhere to the default settings from the original paper, which lead to optimal performance. For methods like GCN and HAN, we utilize a mean-value strategy to aggregate information from neighboring nodes of the target node. In methods such as MAGNN and HAN that require manually specified metapaths, we synthesize the settings from the original paper and use a uniform metapath. The node embedding dimension is consistently set to 64. To ensure result stability, all reported results are averaged over 10 experiments.

All experiments were conducted with the following hardware settings: NVIDIA GeForce RTX4060 GPU (Santa Clara, CA, USA), 16 GB × 2 RAM, Intel CPU i9-13900HX @2.20GHz 24-core, 2T KIOXIA SSD, running Win11 × 64. Our experiments were conducted using PyTorch 2.2.2, an open-source deep learning framework built on Python 3.11. The baseline models were implemented using the OpenHGNN library.

4.4. Performance on Embedding

Network training is initially guided by training set node labels to develop the final network embedding model. Subsequently, test set node feature vectors are fed into each model to perform downstream tasks, evaluating the overall performance of our proposed ANHNE and baseline models. Node classification, a supervised downstream task, and its results are presented in

Table 4. Quantitative results on the node classification task (%). Bold indicates “the best”, and underline indicates “the second best”.

Datasets	Metrics	Training	GCN	GAT	HAN	MAGNN	GTN	MHGCN	AMOGCN	ANHNE
ACM	Macro-F1	20%	86.92	87.87	87.94	90.79	92.57	92.64	92.18	93.78
		40%	87.73	88.44	88.68	90.96	92.53	92.56	92.37	94.01
		60%	87.86	89.25	89.15	91.03	92.84	93.28	92.28	94.11
		80%	88.08	89.55	89.80	91.08	92.65	92.69	92.30	94.02
	Micro-F1	20%	86.72	87.69	87.67	90.63	92.44	92.56	92.07	93.71
		40%	87.55	88.28	88.42	90.78	92.55	92.61	92.40	94.04
		60%	87.69	89.12	88.92	90.86	92.56	93.38	92.38	94.05
		80%	87.94	89.43	89.60	90.89	92.91	92.72	92.38	94.04
DBLP	Macro-F1	20%	90.96	90.05	91.66	92.02	90.46	91.99	92.31	93.33
		40%	91.37	91.20	91.88	92.17	90.69	92.23	92.91	93.80
		60%	91.61	91.35	92.09	92.20	90.99	92.65	92.90	93.86
		80%	91.86	91.44	92.10	92.17	90.93	93.11	93.42	93.97
	Micro-F1	20%	91.84	91.70	92.61	92.92	91.08	92.48	93.10	93.60
		40%	92.18	92.15	92.78	93.06	91.28	92.73	93.34	94.09
		60%	92.43	92.31	93.00	93.10	91.56	93.10	93.11	94.33
		80%	92.66	92.37	93.07	93.06	91.49	93.33	93.58	94.07
IMDB	Macro-F1	20%	45.73	49.44	50.00	51.98	51.13	52.17	51.07	53.43
		40%	48.01	50.64	52.71	52.55	52.07	53.64	52.65	57.67
		60%	49.15	51.90	54.24	54.11	54.29	54.84	53.62	57.32
		80%	51.81	52.99	54.38	54.59	54.68	53.86	52.99	57.49
	Micro-F1	20%	49.78	55.28	59.16	60.77	60.10	62.81	63.07	63.18
		40%	51.71	55.91	60.83	61.37	60.32	65.06	64.64	65.48
		60%	52.29	56.44	62.35	61.77	60.33	66.12	66.65	66.74
		80%	54.16	56.97	63.44	62.76	60.33	66.95	66.11	67.36

, while node clustering, an unsupervised task, is detailed in

Table 5. Quantitative results on the node clustering task (%). Bold indicates “the best”, and underline indicates “the second best”.

Datasets	Metrics	GCN	GAT	HAN	MAGNN	GTN	MHGCN	AMOGCN	ANHNE
ACM	NMI	58.78	63.19	66.49	72.03	74.92	75.83	72.54	78.09
	ARI	62.65	67.75	70.56	76.56	79.80	81.59	78.88	83.05
DBLP	NMI	71.55	74.22	75.49	77.01	77.27	79.30	79.88	81.25
	ARI	76.31	79.43	81.32	81.39	82.10	83.42	83.91	85.01
IMDB	NMI	9.59	10.02	13.08	15.59	17.69	16.83	17.09	17.92
	ARI	6.59	8.69	10.94	13.36	18.68	23.67	22.69	25.29

.

For node classification, we employ Micro-F1 and Macro-F1 scores to gauge the accuracy of each low-dimensional embedding results, offering a balanced and comprehensive assessment of node embedding quality. According to Table 4, ANHNE consistently outperforms in both metrics across various training set proportions. The lower performance of GCN and GAT, typically suited for homogeneous networks, is attributed to their inadequacy in discriminating among the heterogeneous dataset’s diverse node types and complex relations. GAT’s superior performance over GCN suggests that its attention mechanism effectively aids in learning better network embeddings. In contrast, other heterogeneous network methods surpass isomorphic ones, integrating a wider array of node features and network structures. Both MHGCN and AMOGCN lead the baseline models, indicating that multi-stage graph convolution effectively prevents overfitting and achieves high-performance network embeddings. Compared with the best results of the baseline model, ANHEN’s Macro-F1 improves by 1.28%, 0.92%, and 4.90% across three datasets, and Micro-F1 improves by 1.18%, 0.79%, and 0.66%. This demonstrates that ANHEN can achieve effective embedding for node classification tasks. Further assessing model performance, we conduct unsupervised downstream node clustering experiments using a k-means model, setting the number of clusters to match the node category count in each dataset. Employing NMI and ARI as clustering metrics, Table 5 reveals ANHNE’s superiority over all baseline models in node clustering tasks, with average improvements of 2.00% in NMI and 3.31% in ARI scores compared with the best baseline results. Similar to node classification outcomes, heterogeneous network models generally outperform homogeneous ones, and multi-order graph convolution models excel over other baselines.

In summary, the results affirm ANHNE’s effectiveness in node classification and clustering tasks, highlighting its superior node representation learning and general applicability across various downstream tasks.

4.5. Ablation Experiment

ANHNE integrates HIN embedding through the CMAE, HSAA, and SIE modules. To better assess the functionality of each component, we conduct ablation studies to evaluate the impact of various model variants on embedding performance, specifically:

• Only manual metapath aggregation (OMMA), which replaces composite metapaths with manual and fixed ones. This variant aggregates information of multi-hop nodes across common manually defined metapaths instead of composite metapaths with diverse sub-metapaths.
• No layer-level attention aggregation (NOAA), which omits the HSAA module. This variant does not differentiate the semantics of different neighbor layers but aggregates all layers of neighborhood information equally.
• No semantic information enhancement (NOSIE), which overlooks potential inter-node information. This variant discards the consideration of node homogeneity and relies solely on the embedding learned through HSAA outlined in Section 3.5 as the final network representation.

We performed ablation studies using the DBLP dataset, maintaining the same structural framework as ANHNE across three model variants, except for the particular alterations specified. The embedding performance of these variants and ANHNE is depicted in Figure 5.

Analysis of the results shows that all three variants exhibit reduced performance compared with ANHNE. NOSIE demonstrates the most significant performance drop, which is attributable to its disregard for latent node information, focusing solely on explicit relations for feature aggregation. The significant performance gap between ANHNE and NOSIE arises because NOSIE discards latent node correlations derived from attribute homophily. Whereas explicit metapaths encode direct relations, implicit links (e.g., technique-sharing papers P1/P4 in Figure 1b) rely on attribute-based affinities. Ignoring such semantics weakens representation inclusivity, evidenced by NOSIE’s classification clustering degradation. OMMA underperforms compared with ANHNE, indicating that the metapath autonomous extraction module’s ability to derive useful sub-metapath combinations and effectively aggregate features is crucial. This module allows for adjusting the proportions of different sub-metapaths according to the task scenario, enhancing the interaction of effective features and achieving a high-performing network embedding representation. Among the variants, NOAA often shows the best performance, suggesting that the hierarchical attention mechanism proficiently discriminates between the attribute semantics and feature representations of different hierarchical neighbors, selectively aggregating this information to improve generalization capabilities and positively influence embedding outcomes. In summary, our ablation studies confirm the positive contributions of each component to node embedding.

4.6. Analysis Experiment

In this section, we further conduct several experiments necessary to seek a deeper understanding of our ANHNE approach. First, we conduct experiments to demonstrate the effectiveness of the automatic learning of combinatorial metapaths by identifying the learned metapaths. Second, it is verified that the ANHNE method has discriminative aggregation for different layers of neighborhood information. Finally, the nodes represent an intuitive visualization of the discrimination.

(1)

Do the composite metapaths learned by the CMAE module enable automatic semantic mining? We recorded the fusion weights of different relations in the CMAE module. We multiply the weights of different unipath relations with the hierarchical attention, set them to the weights of different sub-metapath relations, and select the paths with the top three weights. As can be seen from

Table 6. The common metapath and the top three metapaths identified across various datasets.

Datasets	Common Metapath	Learned Metapath
ACM	PSP, PAP	PAP, APA, PSP
DBLP	APA, APAPA	APA, APAPA, APCPA
IMDB	MDM, MAM	MAM, AMA, MDM

, our approach not only learns the commonly used metapaths in various domains, which are often used as a priori information for metapath-based models (e.g., HAN), but also further mines metapaths containing rich information to enhance the representation of nodes. For instance, the ‘APAPA’ metapath in DBLP, which represents two authors who have collaborated with the same author on different papers, can be mined for higher-order collaborations. Authors involved in such higher-order collaborations are more likely to be part of the same research field, significantly enhancing the performance of node classification and clustering.

Overall, the CMAE module is able to extract sub-metapaths containing different semantic information, and can autonomously regulate their weights to enhance semantic information aggregation. Meanwhile, the experimental results in Section 4.5 show that the automatic discovery of composite metapaths is more conducive to embedding performance than defining metapaths manually.

(2)

Does our proposed HSAA module effectively distinguish the semantic features of different hopping neighbors? To confirm the efficacy of integrating the information from nodes within the composite metapath, we conducted experiments on the relation between the attention weights of the neighbor information of different layers and the clustering performance of the corresponding layers. Figure 6 illustrates the attention weights for single-layer information alongside the clustering performance of the respective layer. Due to space limitations, we display results only for the ACM and IMDB datasets; however, the DBLP dataset exhibits an identical trend. There is a conspicuous positive correlation between the attention weights and clustering performance. This demonstrates that the model effectively prioritizes the neighborhood information of critical layers, substantially enhancing the overall performance and confirming the efficacy of the HSAA module introduced in Section 3.5. On the other hand, the intermediate layer node information also has higher attention and contribution to the model performance, proving the importance of the metapath internal node information. It is in line with the initial hypothesis that the metapath internal node information can help to accurately mine the complex relationship between the start and destination nodes and improve the model performance.

(3)

Does our proposed ANHNE model effectively enhance the distinction among network representations? We carried out visualization experiments to evaluate the quality of these representations, a standard method for assessing network representation tasks. Employing T-SNE, we compressed the node feature embeddings into a two-dimensional space to benchmark our model against leading techniques in the field. Figure 7 illustrates the distribution of nodes for various models on the DBLP dataset, where different colors denote different node types. In conjunction with the findings presented in Section 4.4, we contend that the low-dimensional feature space distributions generated by all approaches accurately demonstrate the relationships with node classes. Obviously, the homogeneous model GCN has the worst performance, where different types of nodes are mixed together and clusters of nodes do not form clear boundaries. HAN improves on it to a certain extent, but the improvement is not obvious; although the red clusters are clearly separated, the yellow clusters of nodes are collocated with the green and purple clusters of nodes and do not form clear boundaries. In comparison, the performance of AMOGCN is significantly improved, with the node clusters of all four colors forming their own compact regions; however, unfortunately, it has various types of nodes intertwined in the middle region. Compared with the baseline model, our model more effectively compacts the spatial distribution of nodes with identical labels and minimizes the cross-over between nodes of different categories, resulting in a more distinct boundary. This indicates that our model excels in differentiating between various node types, possesses enhanced generalization capabilities, and offers robust support for downstream tasks.

4.7. Hyperparameter Study

In our ANHNE model, we examine the sensitivity by adjusting hyperparameters and observing the resultant variations in node classification and clustering performance. Sensitivity tests conducted on the DBLP dataset demonstrate consistent trends across the ACM and IMDB datasets.

Sensitivity of K, the number of semantically similar nodes: Within our semantic information enhancement module, the parameter K dictates the depth of complementary hidden layer semantics. To assess the impact of various semantic depths on downstream task performance, we explore a range of K values: $\{0,10,30,60,100,150\}$. Figure 8 depicts the embedding performance trend as K increases. Initially, both classification and clustering performances improve with increasing depth of supplementary information, suggesting that a higher K value can unearth richer hidden information and consequently enhance the network structure. However, beyond a K value of 20, performance diminishes significantly, indicative of excessive hidden information leading to long path redundancies and noise introduction, which in turn degrades embedding performance.

Sensitivity of d, the embedding dimension: Different embedding dimensions capture varying degrees of feature and structural information. To investigate the effect of embedding dimensionality on model performance, we set dimensions ranging $\{16,32,64,128,256,512\}$. Figure 8 shows the classification and clustering performance trends, respectively. Initially, performance enhances as all four measures increase with dimensionality, implying that higher dimensional representations capture feature and semantic information more comprehensively. However, at a dimensionality of 512, both classification and clustering performances decline slightly, suggesting that excessively high-dimensional node embeddings introduce noise that can skew the network structure.

4.8. Convergence Analysis

To demonstrate the good convergence of ANHNE, this experiment presents the trends of evaluation metrics and loss values across three test datasets. As shown in Figure 9, accuracy rapidly increases with training iterations and exhibits slight fluctuations after reaching its optimal state, while loss values decrease sharply across all datasets and stably converge within a narrow range above and below a specific value after sufficient iterations. These observations confirm the strong convergence capability of ANHNE.

5. Conclusions

This paper introduces a network embedding model, ANHNE, designed for heterogeneous networks, with three main contributions: First, we expand the multipath relation aggregation approach and design composite metapaths that can autonomously extract diverse lengths containing complex relations. This allows for the automatic mining of deep semantics according to specific task scenarios, thereby addressing the limitations of existing methods that require predefined metapaths. Second, we map the features of different node types to a public semantic space and, using attention coefficients, quantify the importance of various levels of semantic information on composite metapaths to fully leverage neighborhood information. Third, we introduce a semantic information enhancement module to explore implicit node relations, compensating for semantic deficits caused by overlooking node homogeneity and aggregating more implicit features.

Experimental results affirm that ANHNE achieves top-tier or competitive node embedding performance and can autonomously learn valuable composite metapaths based on task scenarios. Currently implemented on a static network, ANHNE’s adaptive metapath learning and multi-hop fusion architecture offer a potential pathway for handling dynamic heterogeneous networks. The semantic attention mechanism, which selectively aggregates neighborhood hierarchies, could be extended to model-evolving node–edge interactions. Future work will deploy ANHNE on large-scale dynamic graphs to refine its scalability, computational efficiency, and real-time adaptability.