QMProt: A Comprehensive Dataset of Quantum Properties for Proteins

Abstract

We introduce Quantum Mechanics for Proteins (QMProt), a dataset developed to support quantum computing applications in protein research. QMProt contains precise quantum-mechanical and physicochemical data, enabling the accurate characterization of biomolecules and supporting advanced computational methods like molecular fragmentation and reassembly. The dataset includes 45 molecules covering all 20 essential human amino acids and their core structural elements: amino terminal groups, carboxyl terminal groups, alpha carbons, and unique side chains. QMProt primarily features organic molecules with up to 15 non-hydrogen atoms (C, N, O, S), offering comprehensive molecular Hamiltonians, ground state energies, and detailed physicochemical properties to enhance reproducibility and advance quantum simulations in molecular biology, biochemistry, and drug discovery.

1. Introduction

Quantum mechanics (QM) plays a crucial role in the accurate modeling of biomolecules. It provides deep insights into molecular structure, interactions, and reactivity, and is a key tool in areas such as drug discovery, protein–ligand binding prediction, and enzyme design [1,2,3]. Furthermore, in recent years, the field has benefited from the development of robust open source simulation frameworks such as PySCF, OpenFermion, and PennyLane that enable reproducibility, experimentation, and interdisciplinary collaboration across quantum computing, chemistry, and machine learning (ML) domains.

However, one of the most significant challenges in applying quantum simulations to biological systems lies in their size and complexity. Proteins, among the most functionally diverse biomolecules, require a large number of qubits for accurate simulation, making direct quantum mechanical calculations computationally prohibitive [4,5]. Fragmentation-based modeling has emerged as a strategy to circumvent the prohibitive computational cost of full biomolecular simulations. These approaches decompose large systems into chemically meaningful subunits, whose properties can be computed independently and later combined with appropriate corrections [6,7,8,9]. In prior work, we extended this paradigm by introducing a fragmentation-and-reassembly strategy tailored to biomolecules, demonstrating that it is possible to reconstruct useful quantum properties for peptides using fragments derived from individual amino acids [10].

Parallel to this, significant progress has been made in the use of artificial intelligence (AI), ML, and quantum machine learning (QML) to predict quantum properties from molecular structures [11,12]. Datasets such as QM7-X [13], QM8, and QM9 [14,15], have been instrumental in training such models, offering the extensive coverage of small organic molecules. QMugs further specializes in drug-like compounds for ML-driven studies [16]. These resources, along with others summarized in recent reviews [17], have enabled major advances in QML applications for small molecules.

Despite these developments, existing datasets remain limited in scope. They primarily focus on molecules with fewer than ten non-hydrogen atoms, making them poorly suited for modeling larger and biologically meaningful systems such as amino acids, peptides, or protein fragments [18]. Moreover, current resources often lack functional groups and side chains found in proteins, and their molecular representations vary in format and completeness, reducing interoperability across tools and pipelines, and there is still no publicly available dataset that provides detailed quantum-mechanical descriptors for biologically relevant fragments. The absence of such a resource hinders the researchers interested in extending quantum simulations to systems of biochemical significance, including proteins and their subunits [19,20]. Furthermore, the lack of standardization across existing datasets, combined with high computational cost and limited interoperability, hinders the development of generalizable models for biomolecular simulation. As a result, efforts remain fragmented and the reuse of quantum simulation data across research groups is limited.

To support the quantum modeling efforts that extend beyond small molecules, more targeted datasets reflecting the modular architecture of biological macromolecules and support chemically informed reassembly are needed. In the next section, we introduce our motivation for creating QMProt, a curated and open access dataset of 45 biologically relevant molecules including all the 20 canonical amino acids, their chemical subgroups, and common bonding partners, and provides for each: molecular geometries, ground-state energies, fermionic Hamiltonians, orbital counts, and other physicochemical descriptors. In this paper, we provide a detailed description of how it was built, its structure, and a case study as an example of its usage. We also provide an extensive discussion of the implications and potential applications of the system, as well as its limitations and future directions for improvement.

2. Motivation

While the field of quantum chemistry has advanced significantly, particularly in terms of tools and small-molecule datasets, it lacks dedicated resources for exploring biologically relevant systems at scale. This limitation impairs the application of quantum methods to important domains such as structural biology and biotechnology.

Current datasets like QM9 and QM7-X have been instrumental in developing and validating QML models, thanks to their size, quality, and accessibility. In parallel, community-wide access to well-documented frameworks like PySCF, OpenFermion and Pennylane, has encouraged reproducibility and lowered the entry barrier for quantum simulation.

However, these advances are primarily confined to small organic molecules, and do not extend naturally to biomolecules like proteins, which involve many more atoms, greater structural variability, and more complex interactions—including protonation, hydrogen bonding, and side chain effects. Furthermore, datasets for these larger systems are practically nonexistent, despite the clear need for simulation-ready Hamiltonians and benchmarkable properties for fragments such as amino acids, which serve as the building blocks of proteins.

This gap represents a lost opportunity. With the growing interest in hybrid quantum-classical models, there is increasing demand for datasets that bridge quantum chemistry and molecular biology. QMProt addresses this need by offering a foundational dataset for amino acid–level modeling. It allows researchers to

• Access precomputed Hamiltonians and energies for biologically meaningful molecules without requiring expensive simulations.
• Reconstruct peptides from molecular fragments using quantum-informed strategies, and explore the accuracy and limitations of such reconstructions.
• Benchmark quantum simulation algorithms under realistic chemical conditions and molecular sizes.

By reducing computational barriers, encouraging reuse, and focusing on molecules of biological significance, QMProt transforms the current state of the field from small-molecule centricity to peptide-scale feasibility. It does not attempt to solve all the complexities of protein simulation, but rather lays the groundwork for others to explore open questions including peptide bond formation, chemical reassembly accuracy, and larger-scale dynamics using a consistent and reproducible dataset.

In doing so, QMProt enables a new wave of quantum-enabled research in life sciences and offers a stepping stone toward simulating full protein behavior on quantum devices or QML pipelines.

3. Methodology

3.1. Dataset Construction

In this section, we describe the methodology followed to construct the dataset, from the selection and fragmentation of molecular structures to the computation of their quantum properties, with the goal of building a consistent, reproducible, and biologically relevant molecular dataset. Figure 1 provides an overview of the general pipeline used for molecular inclusion and quantum feature extraction.

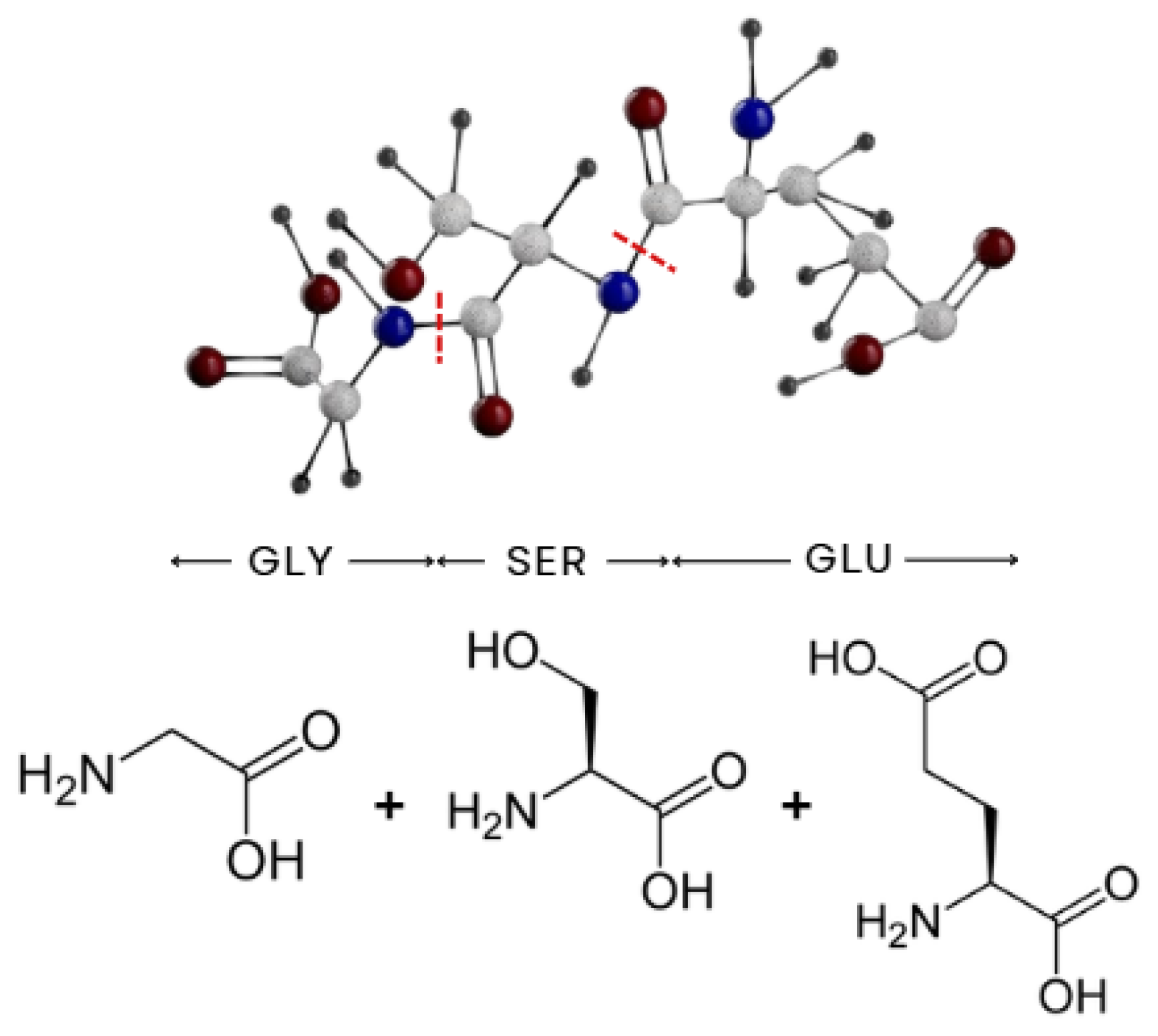
The pipeline begins with the selection of molecules to be included in the dataset, aiming to enable the quantum simulation of any protein. The first step involves fragmenting proteins into their constituent amino acids. For example, a small peptide composed of glycine, serine and glutamic acid would be fragmented into individual amino acids, using the peptide bond as a breaking points, as Figure 2 exemplifies.

However, even single amino acids may be too large for near-term quantum simulations due to the complexity of their side chains. To address this, each amino acid was further decomposed into smaller components. This fragmentation followed a consistent pattern across all amino acids: the amino terminal group (NH₂), the carboxyl terminal group (COOH), the central carbon with the remaining hydrogen (CH), and the specific side chain (R) unique to each of the 20 standard amino acids. Figure 3 illustrates this rationale.

The selection strategy focused on covering a wide range of molecular fragments that can result from protein degradation, with the aim of facilitating quantum simulation and the analysis of biologically meaningful substructures. Therefore, the dataset includes the 20 standard amino acids and their corresponding fragments, in addition to the following small molecules: H₂O, H₂, and CH₃, which are commonly involved in chemical processes such as group addition and bond formation. In total, 45 molecules were included in the dataset.

Table 1. Properties of different molecules and functional groups in QMProt.

Name	Formula	Electrons	Orbitals	Qubits	Coefficients
Histidine	C${⁠}_6$H${⁠}_9$N${⁠}_3$O${⁠}_2$	82	64	128	23,831,261
Leucine	C${⁠}_6$H${⁠}_{13}$NO${⁠}_2$	72	58	116	16,200,242
Isoleucine	C${⁠}_6$H${⁠}_{13}$NO${⁠}_2$	72	58	116	16,379,995
Lysine	C${⁠}_6$H${⁠}_{14}$N${⁠}_2$O${⁠}_2$	80	64	128	23,906,497
Methionine	C${⁠}_5$H${⁠}_{11}$NO${⁠}_2$S	80	60	120	17,802,421
Phenylalanine	C${⁠}_9$H${⁠}_{11}$NO${⁠}_2$	88	71	142	36,125,918
Threonine	C${⁠}_4$H${⁠}_9$NO${⁠}_3$	64	49	94	8,355,908
Tryptophan	C${⁠}_{11}$H${⁠}_{12}$N${⁠}_2$O${⁠}_2$	108	87	159	92,412,988
Valine	C${⁠}_5$H${⁠}_{11}$NO${⁠}_2$	64	51	102	9,819,598
Arginine	C${⁠}_6$H${⁠}_{14}$N${⁠}_4$O${⁠}_2$	94	74	146	43,576,110
Cysteine	C${⁠}_3$H${⁠}_7$NO${⁠}_2$S	66	46	92	6,193,299
Glutamine	C${⁠}_5$H${⁠}_{10}$N${⁠}_2$O${⁠}_3$	78	60	120	18,268,397
Asparagine	C${⁠}_4$H${⁠}_8$N${⁠}_2$O${⁠}_3$	70	57	106	11,309,980
Tyrosine	C${⁠}_9$H${⁠}_{11}$NO${⁠}_3$	96	76	149	48,516,460
Serine	C${⁠}_3$H${⁠}_7$NO${⁠}_3$	56	42	84	4,532,699
Glycine	C${⁠}_2$H${⁠}_5$NO${⁠}_2$	40	30	60	1,164,627
Aspartic acid	C${⁠}_4$H${⁠}_7$NO${⁠}_4$	70	52	104	10,543,213
Glutamic acid	C${⁠}_5$H${⁠}_9$NO${⁠}_4$	78	59	118	17,208,382
Proline	C${⁠}_5$H${⁠}_9$NO${⁠}_2$	62	49	98	8,368,092
Alanine	C${⁠}_3$H${⁠}_7$NO${⁠}_2$	48	37	74	2,725,840
Hydrogen	H${⁠}_2$	2	2	4	15
Water	H${⁠}_2$O	10	7	14	1086
Carboxy group	COOH	23	16	32	54,229
Amino group	NH${⁠}_2$	9	7	14	1086
Methylidyne	CH	7	6	12	631
R_His	C${⁠}_4$H${⁠}_5$N${⁠}_2$	43	34	70	1,978,718
R_Leu	C${⁠}_4$H${⁠}_9$	33	29	58	520,540
R_Ile	C${⁠}_4$H${⁠}_9$	33	29	58	520,540
R_Lys	C${⁠}_4$H${⁠}_{10}$N	41	35	70	2,197,466
R_Met	C${⁠}_3$H${⁠}_6$S	40	30	60	506,627
R_Phe	C${⁠}_7$H${⁠}_7$	49	42	84	3,722,223
R_Thr	C${⁠}_2$H${⁠}_4$O	24	19	38	49,606
R_Trp	C${⁠}_9$H${⁠}_8$N	69	58	116	14,864,603
R_Val	C${⁠}_3$H${⁠}_7$	25	22	44	341,819
R_Arg	C${⁠}_4$H${⁠}_9$N${⁠}_3$	54	44	88	5,411,505
R_Cys	CH${⁠}_3$S	25	17	34	100,148
R_Gln	C${⁠}_3$H${⁠}_6$NO	39	31	62	816,630
R_Asn	C${⁠}_2$H${⁠}_4$NO	31	24	48	288,581
R_Tyr	C${⁠}_7$H${⁠}_7$O	57	47	94	4,268,254
R_Ser	CH${⁠}_3$O	17	13	26	41,068
R_Gly	H	1	1	2	4
R_Asp	C${⁠}_2$H${⁠}_3$O${⁠}_2$	31	23	46	375,266
R_Glu	C${⁠}_3$H${⁠}_5$O${⁠}_2$	39	30	60	1,161,463
R_Pro	C${⁠}_3$H${⁠}_6$	24	22	42	73,108
R_Ala	CH${⁠}_3$	9	8	16	1977

summarizes the complete list of molecules along with their computed quantum resource requirements.

To compute the molecular properties, the SMILES representation of each molecule was used to retrieve atomic coordinates, chemical identifiers (CIDs), and atomic symbols from PubChem [21]. Basic molecular characteristics, including total charge, number of atoms, electrons, orbitals, and spin multiplicity, were then computed. A predefined basis set was applied to derive the quantum Hamiltonian of each molecule. From this, we extracted the number of qubits required for simulation, the number of coefficients in the Hamiltonian, and the ground state energy.

3.2. Properties Included in the Dataset

For each molecule included in the dataset, QMProt provides a comprehensive set of descriptive, physicochemical, and quantum properties to enable accurate characterization. Below is a brief description of each variable:

• Abbreviation: Present only for entire amino acids, this is the formal short name commonly used to refer to them. For instance, Histidine is abbreviated as His.
• Name: The full common name of the molecule.
• Molecular formula (mf): The compact SMILES representation of the molecule, which encodes its atomic composition and connectivity.
• CID: The unique compound identifier from the PubChem database [21], retrieved by inputting the SMILES string and selecting the correct molecular conformation.
• Number of atoms: Calculated by counting the atomic elements present in the SMILES string.
• Charge: Determined based on the contributing amino acids. It reflects the formal net charge of the molecule.
• Number of electrons: Computed based on the atoms present in the molecule using standard valence electron counts: 6 for carbon, 1 for hydrogen, 8 for oxygen, 7 for nitrogen, and 16 for sulfur. This estimation provides an initial idea of the quantum complexity of the system.
• Number of orbitals: Related to the energy levels and electron distribution within the molecule.
• Bond length: Defined as the minimum interatomic distance, computed from the distance matrix derived from the 3D atomic coordinates using the Euclidean norm, as shown in Equation (1).

  $$\mathrm{Bond}\mathrm{length}=min\left(\{d_{ij}\mid i\ne j\}\right)$$

  (1)

  where $d_{ij}$ is the Euclidean distance between atoms i and j.
• Coordinates: The 3D atomic coordinates were obtained from PubChem SDF files and reformatted into HDF5 (.h5) files for computational efficiency.
• Spin: Estimated by determining the number of unpaired electrons based on the atomic composition from the SMILES string. In general, spin was set to 0 for full amino acids (assuming paired electrons), and to 1 for radical fragments.
• Basis: The STO-3G minimal basis set was used for most molecules to reduce computational cost while maintaining acceptable accuracy.
• Number of qubits: Indicates the number of qubits required to simulate the molecule on a quantum computer, which depends on the encoding strategy and molecular complexity.
• Number of coefficients: The total number of terms in the expansion of the molecular wavefunction. A higher number implies increased accuracy but also greater computational cost.
• Hamiltonian: The electronic Hamiltonian was computed using the molecule’s coordinates, charge, spin, and basis set. This operator is fundamental to describe the energy and evolution of the system. Due to its computational cost, it is precomputed and included in the dataset.
• Energy: The ground state energy of the molecule in Hartrees, representing its most stable configuration. This property is also precomputed, facilitating further applications in biomolecular analysis.

3.3. Validation

Most properties in the dataset were computed either from established databases such as PubChem and CCBDB [21,22], or directly derived from the SMILES representation of each molecule. However, certain quantum properties—such as the Hamiltonian and ground state energy—required more advanced quantum chemistry calculations.

Hamiltonian computations were carried out using the OpenFermion library [23], with input parameters including the STO-3G basis set (used in most cases), molecular charge, spin multiplicity (calculated as $M=2S+1$), and 3D atomic coordinates. The molecules were processed using PySCF and self-consistent field (SCF) theory [24], and the resulting Hamiltonians were converted into fermionic operator format following PennyLane conventions [25].

Ground state energies were calculated using the Hartree–Fock (HF) method, which remains a robust and reliable approach given the capabilities of modern classical computing [26]. Coordinates and molecular configurations were extracted from PubChem SDF files and processed using PySCF. Specifically, the restricted Hartree–Fock (RHF) approach with the STO-3G basis set was employed to obtain the total ground state energy for each molecule.

All calculations were initially performed on a personal workstation equipped with an Intel^® Core^TM i7-13700H processor (Intel Corporation, Santa Clara, CA, USA), 32 GB of RAM, and a 64-bit operating system running under the Windows Subsystem for Linux (WSL, version 2; Microsoft Corporation, Redmond, WA, USA). This environment was sufficient for preprocessing and preliminary simulations.

For more computationally intensive tasks, including Hamiltonian construction and large-scale quantum simulations, a dedicated high-performance computing (HPC) server was used. The system featured a 24-core AMD Threadripper Pro 5965WX processor (3.80 GHz), three NVIDIA RTX 6000 Ada GPUs (each with 48 GB of VRAM), and 256 GB of RAM (two 128 GB 3200 MHz DDR4 ECC/REG modules) (BIZOM, Hollywood, FL, USA). This infrastructure enabled efficient manipulation of high-dimensional Hamiltonian matrices and precise ground state energy calculations, ensuring the quality and reliability of the quantum data provided in the dataset.

4. Data Records

This section aims to explain how the database is organized within the H5 files to facilitate efficient extraction and use of the data.

The QMProt dataset is distributed as 45 individual H5 files, each containing various molecular properties stored as attributes. A README file accompanies the dataset, providing technical instructions for accessing and utilizing the data. Within each H5 file, every attribute corresponds to a specific molecular property, as previously described. To enhance organization, related properties are grouped hierarchically; for example, the molecule group includes attributes such as symbols, coordinates, charge, basis, and spin, all formatted for compatibility with PennyLane.

Due to the potentially large size of some molecular Hamiltonians, the corresponding data are partitioned across multiple attributes named hamiltonian_1, hamiltonian_2, and so on. To reconstruct the complete Hamiltonian operator for a given molecule, these partitions must be concatenated in the correct sequence. To support this process, we provide code in our GitHub repository (available at: https://github.com/pifparfait/qmprot_strategy, accessed on 8 July 2025), which was developed and tested using Git version 2.43.0. This code enables both the reconstruction of full Hamiltonians and their subsequent conversion into PennyLane-compatible operators [27].

This data format supports efficient querying and manipulation, enabling straightforward application of computational models and the statistical analyses of molecular properties. Figure 4 illustrates the hierarchical structure of the dataset, showing the organization of groups and attributes within each molecular file.

Finally, Table 1 summarizes the molecules included in the dataset, along with their sizes expressed in terms of number of electrons, orbitals, qubits, and coefficients.

5. Case Study: Glycine

This case study demonstrates how QMProt streamlines the quantum modeling of glycine (C₂H₅NO₂) by utilizing precomputed fragment Hamiltonians and ground state energies. Glycine, as the smallest amino acid, provides an ideal benchmark to explore how fragmentation can significantly reduce computational effort while preserving accuracy.

Traditionally, the electronic structure of glycine is solved at the Hartree–Fock (SCF) level using tools like OpenFermion and PySCF, which generate a fermionic Hamiltonian. This Hamiltonian is then transformed into a qubit representation via the Jordan–Wigner transformation, and the resulting Pauli operator strings are saved for use in quantum simulation frameworks such as PennyLane. However, computing the full Hamiltonian of amino acids or small peptides from scratch in this way typically requires multiple hours of computation and occupies multiple gigabytes of memory.

QMProt bypasses this entire process by providing precomputed Hamiltonians for both the entire molecule and its fragments, enabling an almost instantaneous reconstruction of the full glycine Hamiltonian. This dramatically reduces the computational time and memory requirements while also supplying the resources necessary to study molecular interactions and reassembly approaches. Consequently, QMProt not only saves computational resources but also simplifies the workflow for quantum simulations, greatly facilitating the extraction and application of molecular data in quantum computing studies.

The selected fragments follow the methodology illustrated in Figure 3. In the case of glycine, with only a hydrogen atom as its side chain, the molecule is divided into four groups: the amino group (NH₂), the carboxyl group (COOH), the central CH group, and the hydrogen side chain (H). This fragmentation scheme is shown in Figure 5.

Table 2. Data extracted from QMProt.

Fragment	Qubits	Coefficients	Ground State Energy [Ha]
NH2	14	1086	−54.8393
COOH	32	54,229	−185.5979
CH	12	631	−37.7703
H	2	4	−0.4666
C2H5NO2 (Glycine)	60	1,164,627	−279.1115

summarizes key data extracted from QMProt for glycine and its fragments, including the number of qubits required for simulation, the number of Hamiltonian coefficients, and the ground state energies.

One of the main advantages of using fragmentation is the significant reduction in the number of Pauli terms and Toffoli gates required for the quantum circuit. As shown in

Table 3. Complexity comparison between full and fragmented glycine.

Approach	Coefficients	Toffoli Gates
Full glycine	$1.16\times {10}^6$	14,300
Fragmented	$5.60\times {10}^4$	3380

, this reduction directly impacts the circuit depth, improving the feasibility of implementing these simulations on current noisy intermediate-scale quantum (NISQ) hardware.

This represents a reduction by a factor of approximately 20.7 in the number of coefficients and 4.23 in the number of Toffoli gates. Such simplification not only makes circuit construction more manageable but also enables the use of localized optimization techniques. These can be combined with systematic correction methods to accurately recover the total molecular energy.

To evaluate the accuracy of the fragment-based approach, we compare the ground state energy obtained from the full Hamiltonian with that reconstructed from the fragments. As summarized in

Table 4. Energy estimation for glycine using different approaches.

Method	Energy [Ha]
$E_{\mathrm{literature}}$	−279.1192
$E_{\mathrm{qmprot}}$	−279.1115
$E_{\mathrm{fragmentation}}$	−278.6741

, the energy estimated using the fragmented Hamiltonians ($E_{\mathrm{fragmentation}}$) deviates only slightly from the full Hamiltonian energy ($E_{\mathrm{qmprot}}$) provided by QMProt.

The relative error amounts to just 0.1567%, thereby confirming the reliability of the fragmentation strategy for approximate quantum simulations without significant loss of accuracy.

Finally, by providing direct access to precomputed Hamiltonians, QMProt empowers researchers to bypass traditionally time-consuming steps such as geometry optimization, basis set selection, SCF calculations, Hamiltonian construction, and qubit mapping. With the qubit Hamiltonians readily available, users can immediately:

• Run the variational quantum eigensolver (VQE) to estimate total energies.
• Execute quantum phase estimation (QPE) to resolve eigenvalues or ground state energies.
• Experiment with ansätze and optimize circuit depths using modular fragments, particularly valuable in the NISQ era and beyond.

This capability is especially critical as quantum hardware advances, enabling researchers to move from spending days computing a single Hamiltonian to instantly simulating molecules and scaling their studies to larger systems, including entire proteins.

6. Discussion

The development of QMProt addresses a clear and well-documented need within the quantum chemistry community: the absence of publicly available datasets containing quantum-mechanical properties of biologically relevant molecules. Existing datasets, including QM7-X, QM8, QM9, and QMugs [13,14,15,16], have proven instrumental in training quantum machine learning (QML) models. However, these datasets are limited to relatively small molecules and do not represent amino acids, peptides, or protein fragments, which are central to structural biology, enzymology, and drug design [19,20].

One key strength of the scientific ecosystem is the widespread availability of open quantum tools such as PySCF, OpenFermion, and PennyLane [1,12], which enable accessible and reproducible quantum chemistry workflows. Nevertheless, the quantum simulations of biomolecules are computationally intensive and often infeasible for individual groups without access to high-performance computing infrastructure. Consequently, the exploration of biomolecular simulations at the quantum level has remained largely theoretical, with most efforts constrained to proof-of-concept studies on small molecules.

QMProt provides a curated, open access dataset of 45 biologically relevant molecules, including all 20 standard amino acids and several chemically meaningful substructures. For each molecule, it includes ground state energies, qubit Hamiltonians, molecular orbital information, and additional descriptors. QMProt is designed to reduce computational and technical barriers to support multiple applications, such as benchmarking quantum algorithms, modeling protein fragments, and studying peptide reassembly strategies. Precomputed Hamiltonians are typically expensive to obtain, requiring hours even at the Hartree–Fock level, and these are usually necessary inputs for quantum circuit design, variational algorithms, or quantum pipelines [11]. By providing these Hamiltonians in a standardized, PennyLane-compatible format, QMProt facilitates reproducible and scalable quantum research in biochemistry.

Furthermore, QMProt enables efficient quantum simulations through fragmentation. Our case study on glycine demonstrates that reusing fragment Hamiltonians drastically reduces computational requirements without a significant loss of accuracy. Fragmentation simplifies the Hamiltonian by reducing the number of Pauli terms and Toffoli gates, enabling modular circuit construction and targeted variational optimization. This approach achieves an energy estimation error below 0.2% compared to full molecular simulations, highlighting its practical utility. Moreover, these results align with our previous findings, where we reported a relative error (%RE) of approximately $0.005\%$ for full amino acid fragmentation and $0.268\%$ for further fragmentation into smaller components [10]. This confirms that fragment-based quantum simulations can reliably approximate molecular electronic structure with minimal compromise in accuracy, while significantly reducing computational overhead.

As a result, QMProt not only streamlines the quantum simulation workflow by providing ready-to-use Hamiltonians but also paves the way for scalable and accurate quantum modeling of larger biomolecules, establishing itself as a valuable tool in advancing quantum computational chemistry. This has been further demonstrated in our latest publication [28], which builds directly upon the data and foundational framework provided by QMProt. In this work, we present a scalable and resource-aware strategy for simulating large proteins based on systematic molecular fragmentation and analytical Toffoli gate modeling. We validate the predictive accuracy of the fragmentation approach across biomolecular systems of increasing complexity, while providing empirical resource estimates that enable early-stage feasibility assessments for achieving quantum advantage. These developments, grounded in QMProt’s original fragmentation data and methodology, collectively open new avenues for applying quantum computational methods to increasingly complex biochemical systems. This reinforces QMProt’s role as a foundational platform for future research in quantum-enabled biomolecular modeling.

Additionally, direct access to PennyLane-compatible qubit operators enables the near-instantaneous simulation of biologically relevant molecules, bypassing traditional steps such as geometry optimization, SCF calculations, and qubit mapping. As quantum hardware advances, the ability to rapidly construct and simulate peptide-sized systems using precomputed modular components positions QMProt as a foundational tool to accelerate quantum biochemical research.

However, some limitations must be acknowledged. Peptide reassembly from individual fragments relies on chemical correction strategies that may not fully capture complex electronic interactions or non-covalent effects like hydrogen bonding or van der Waals forces. Such challenges are common in fragmentation-based approaches [6,7,8], and further development is necessary to improve accuracy in these respects. Moreover, the quantum simulations in QMProt were performed at the Hartree–Fock level using the STO-3G basis set. While this is a standard benchmark level balancing accuracy and feasibility, it does not achieve chemical accuracy, particularly for polarizable or highly conjugated systems. More accurate methods like MP2 or coupled-cluster (CCSD) will be required to expand the dataset’s reliability and scope, especially for applications involving energy differences or excitation spectra. Lastly, current quantum hardware remains limited in scale, complicating the use of large biomolecular Hamiltonians. The complexity of peptide bonds and side-chain interactions may require more sophisticated chemical correction schemes beyond those provided. Moreover, users unfamiliar with quantum chemistry might find Hamiltonian-based datasets challenging to interpret, potentially restricting use to expert communities.

Although challenges remain, QMProt lays a solid foundation for the development of more comprehensive datasets, including those accounting for solvent effects, protonation states, and secondary structural motifs. Moreover, it paves the way for tackling more complex applications such as protein absorption spectra. This framework can also facilitate the creation of modular workflows where biomolecules are represented by quantum-computed fragments, enabling efficient hybrid classical-quantum simulations. Therefore, QMProt represents a crucial step forward in making quantum biochemical simulations more accessible and scalable, ultimately accelerating the integration of quantum computing into real-world molecular and pharmaceutical research.

7. Conclusions

The QMProt dataset represents a substantial advancement at the interface of quantum chemistry and structural biology. By providing precomputed quantum properties for a carefully curated set of 45 biologically relevant molecules, QMProt addresses a critical gap left by existing datasets. This collection includes all 20 canonical amino acids and key molecular fragments, furnishing researchers with fundamental building blocks for quantum simulations at the peptide and protein scale, as well as for hybrid quantum-classical workflows in drug discovery. Moreover, the dataset’s modular design naturally supports fragmentation-based simulation approaches, which we have demonstrated to be effective for reconstructing peptide quantum properties through chemically corrected fragments, significantly reducing computational complexity without sacrificing accuracy. By offering ready-to-use Hamiltonians and molecular descriptors, QMProt substantially lowers the entry barrier for quantum research applied to biological systems, circumventing the need for challenging and resource-intensive quantum calculations.