High-Resolution Time-Frequency Feature Selection and EEG Augmented Deep Learning for Motor Imagery Recognition
Abstract
1. Introduction
- (1)
- Enhanced time-frequency representation: GDC-Net utilizes GMWT to generate high-resolution time-frequency scalograms, capturing MI-related EEG features more effectively than traditional wavelet-based techniques.
- (2)
- Data augmentation: To mitigate the problem of data scarcity, the framework incorporates DCGAN, which produces synthetic scalogram images, increasing the diversity and volume of the training data.
- (3)
- Optimized CNN-LSTM architecture: For classification, GDC-Net employs a hybrid model that combines a 2D CNN for spatial feature extraction and LSTM units for learning temporal dynamics within the EEG signals.
2. Materials and Methods
2.1. Dataset Description
2.2. Design of GDC-Net Processing Pipeline
2.3. TimeFrequency Representation Using Generalized Morse Wavelet Transform
2.4. Synthetic Scalogram Generation Using DCGAN
2.5. CNN-LSTM Spatiotemporal Modeling for Motor Imagery Classification
3. Performance Assessment and Results
| Subject | Without DCGAN | With DCGAN | ||
|---|---|---|---|---|
| Kappa | Accuracy | Kappa | Accuracy | |
| S1 | 0.7456 | 85.98 | 0.7962 | 89.81 |
| S2 | 0.4668 | 73.11 | 0.5666 | 78.33 |
| S3 | 0.3940 | 69.36 | 0.4938 | 74.69 |
| S4 | 0.9214 | 93.45 | 0.9712 | 98.56 |
| S5 | 0.8323 | 91.30 | 0.9324 | 96.62 |
| S6 | 0.7652 | 85.69 | 0.8100 | 90.50 |
| S7 | 0.6825 | 81.56 | 0.7380 | 86.90 |
| S8 | 0.8467 | 90.34 | 0.8906 | 94.53 |
| S9 | 0.8142 | 88.12 | 0.8638 | 93.19 |
| Mean | 0.7187 | 84.32 | 0.7847 | 89.24 |
| Std. | 0.1675 | 7.78 | 0.1303 | 8.09 |
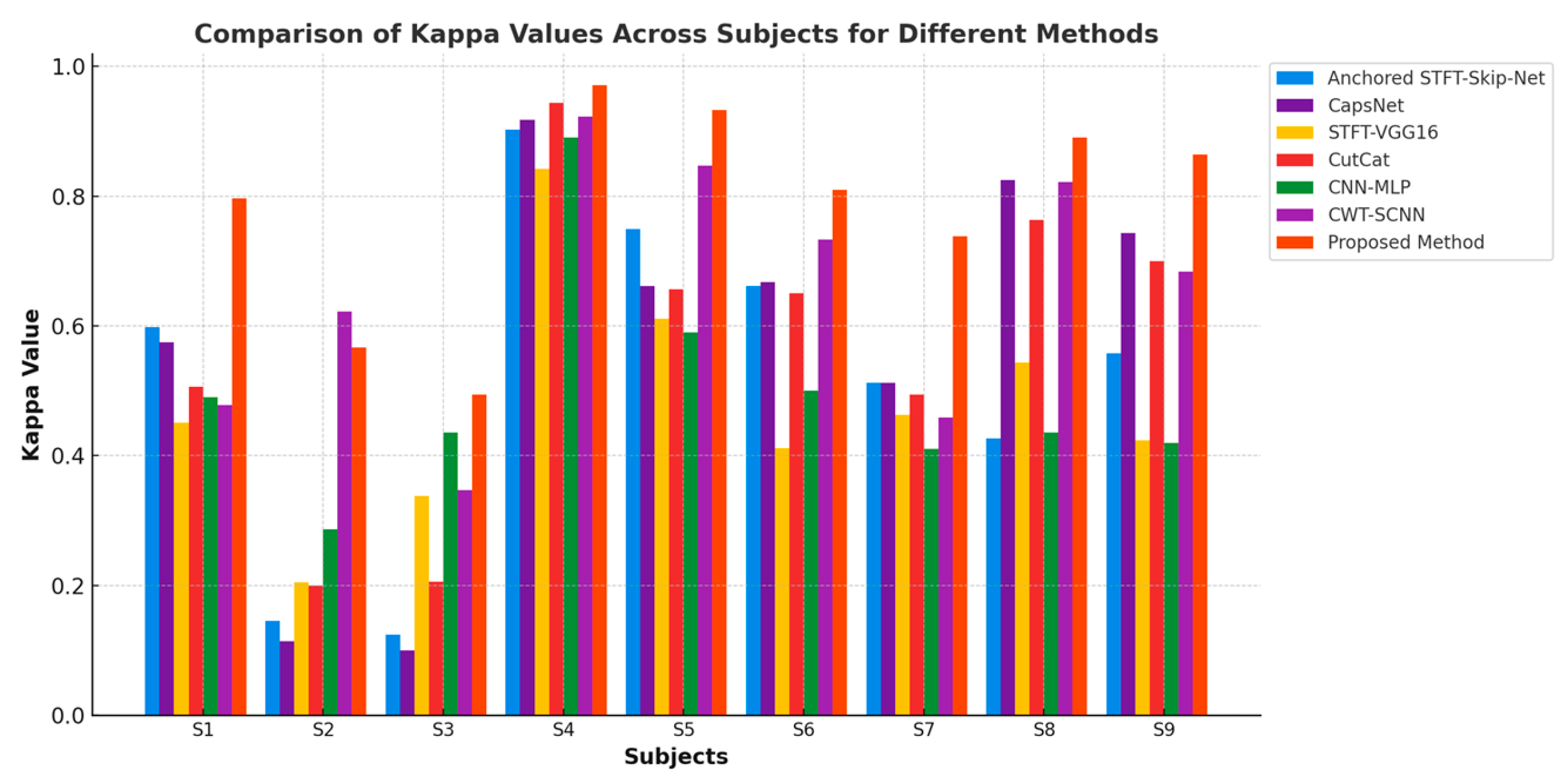
| Subjects | STFT-SkipNet-GNAA [21] | CapsNet [22] | STFT-VGG16 [23] | CutCat [24] | CNN-MLP [25] | CWT-SCNN [26] | ADFCNN [27] | EEG-Conformer [28] | CLT-Net [29] | Proposed GDC-Net |
|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 79.90 | 78.75 | 72.60 | 75.31 | 74.50 | 74.70 | 79.37 | 73.13 | 75.94 | 89.81 |
| S2 | 57.30 | 55.71 | 60.30 | 60.00 | 64.30 | 81.30 | 72.50 | 67.50 | 69.29 | 78.33 |
| S3 | 56.20 | 55.00 | 66.90 | 60.31 | 71.80 | 68.10 | 82.81 | 79.06 | 84.68 | 74.69 |
| S4 | 95.10 | 95.93 | 91.20 | 97.19 | 94.50 | 96.30 | 96.25 | 97.19 | 97.81 | 98.56 |
| S5 | 87.50 | 83.12 | 80.60 | 82.81 | 79.50 | 92.50 | 99.37 | 96.88 | 97.50 | 96.62 |
| S6 | 83.10 | 83.43 | 70.60 | 82.50 | 75.00 | 86.90 | 84.68 | 83.13 | 85.31 | 90.50 |
| S7 | 75.60 | 75.62 | 73.20 | 74.69 | 70.50 | 73.40 | 93.43 | 93.13 | 93.13 | 86.90 |
| S8 | 71.40 | 91.25 | 77.70 | 88.13 | 71.80 | 91.60 | 95.31 | 92.81 | 91.88 | 94.53 |
| S9 | 77.90 | 87.18 | 71.20 | 85.00 | 71.00 | 84.40 | 86.56 | 90.00 | 88.44 | 93.19 |
| Mean | 76.0 | 78.44 | 73.81 | 78.44 | 74.80 | 83.2 | 87.81 | 84.63 | 87.11 | 89.24 |
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, H.; He, B. Brain–Computer Interfaces Using Sensorimotor Rhythms: Current State and Future Perspectives. IEEE Trans. Biomed. Eng. 2014, 61, 1425–1435. [Google Scholar] [CrossRef] [PubMed]
- Phothisonothai, M.; Nakagawa, M. EEG-Based Classification of Motor Imagery Tasks Using Fractal Dimension and Neural Network for Brain-Computer Interface. IEICE Trans. Inf. Syst. 2008, 91, 44–53. [Google Scholar] [CrossRef]
- Zhu, X.; Li, P.; Li, C.; Yao, D.; Zhang, R.; Xu, P. Separated Channel Convolutional Neural Network to Realize the Training Free Motor Imagery BCI Systems. Biomed. Signal Process. Control 2019, 49, 396–403. [Google Scholar] [CrossRef]
- Sakhavi, S.; Member, S.; Guan, C. Learning Temporal Information for Brain-Computer Interface Using Convolutional Neural Networks. In Proceedings of the 2018 6th International Conference on Brain-Computer Interface, Jeju, Republic of Korea, 15–17 January 2018; pp. 5619–5629. [Google Scholar]
- Tabar, Y.R.; Halici, U. A Novel Deep Learning Approach for Classification of EEG Motor Imagery Signals. J. Neural Eng. 2017, 14, 16003. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Tang, F.; Si, B.; Feng, X. Learning Joint Space–Time–Frequency Features for EEG Decoding on Small Labeled Data. Neural Netw. 2019, 114, 67–77. [Google Scholar] [CrossRef]
- Salamon, J.; Bello, J.P. Deep Convolutional Neural Networks and Data Augmentation for Environmental Sound Classification. IEEE Signal Process. Lett. 2017, 24, 279–283. [Google Scholar] [CrossRef]
- Pérez-Benítez, J.L.; Pérez-Benítez, J.A.; Espina-Hernández, J.H. Development of a Brain Computer Interface Interface Using Multi-Frequency Visual Stimulation and Deep Neural Networks. In Proceedings of the 2018 International Conference on Electronics, Communications and Computers (CONIELECOMP), Cholula, Mexico, 21–23 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 18–24. [Google Scholar]
- Li, H.; Zhang, D.; Xie, J. MI-DABAN: A Dual-Attention-Based Adversarial Network for Motor Imagery Classification. Comput. Biol. Med. 2023, 152, 106420. [Google Scholar] [CrossRef]
- Roy, S.; Dora, S.; McCreadie, K.; Prasad, G. MIEEG-GAN: Generating Artificial Motor Imagery Electroencephalography Signals. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Yang, L.; Song, Y.; Ma, K.; Xie, L. Motor Imagery EEG Decoding Method Based on a Discriminative Feature Learning Strategy. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 368–379. [Google Scholar] [CrossRef]
- Habashi, A.G.; Azab, A.M.; Eldawlatly, S.; Gamal, M.A. Generative Adversarial Networks in EEG Analysis: An Overview. J. Neuroeng. Rehabil. 2023, 20, 40. [Google Scholar] [CrossRef]
- Song, Y.; Yang, L.; Jia, X.; Xie, L. Common Spatial Generative Adversarial Networks Based EEG Data Augmentation for Cross-Subject Brain-Computer Interface. arXiv 2021, arXiv:2102.04456. [Google Scholar]
- Leeb, R.; Brunner, C. BCI Competition 2008–Graz Data Set B.; Graz University of Technology: Graz, Austria, 2008; Volume 16, pp. 1–6. [Google Scholar]
- Chung, J.W.; Ofori, E.; Misra, G.; Hess, C.W.; Vaillancourt, D.E. Beta-Band Activity and Connectivity in Sensorimotor and Parietal Cortex Are Important for Accurate Motor Performance. Neuroimage 2017, 144, 164–173. [Google Scholar] [CrossRef] [PubMed]
- Olhede, S.C.; Walden, A.T. Generalized Morse Wavelets. IEEE Trans. Signal Process. 2002, 50, 2661–2670. [Google Scholar] [CrossRef]
- Lilly, J.M. Element Analysis: A Wavelet-Based Method for Analysing Time-Localized Events in Noisy Time Series. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160776. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Ríos, E.A.; Bustamante-Bello, R.; Navarro-Tuch, S.; Perez-Meana, H. Applications of the Generalized Morse Wavelets: A Review. IEEE Access 2022, 11, 667–688. [Google Scholar] [CrossRef]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Mane, D.; Vasudevan, V.; Le, Q.V. Autoaugment: Learning Augmentation Policies from Data. arXiv 2018, arXiv:1805.09501. [Google Scholar]
- Ali, O.; Saif--ur--Rehman, M.; Dyck, S.; Glasmachers, T.; Iossifidis, I.; Klaes, C. Enhancing the Decoding Accuracy of EEG Signals by the Introduction of Anchored -- STFT and Adversarial Data Augmentation Method. Sci. Rep. 2022, 12, 4245. [Google Scholar] [CrossRef]
- Ha, K.W.; Jeong, J.W. Motor Imagery EEG Classification Using Capsule Networks. Sensors 2019, 19, 2854. [Google Scholar] [CrossRef]
- Xu, G.; Shen, X.; Chen, S.; Zong, Y.; Zhang, C.; Yue, H.; Liu, M.; Chen, F.; Che, W. A Deep Transfer Convolutional Neural Network Framework for EEG Signal Classification. IEEE Access 2019, 7, 112767–112776. [Google Scholar] [CrossRef]
- Al-Saegh, A.; Dawwd, S.A.; Abdul-Jabbar, J.M. CutCat: An Augmentation Method for EEG Classification. Neural Netw. 2021, 141, 433–443. [Google Scholar] [CrossRef]
- Yang, B.; Fan, C.; Guan, C.; Gu, X.; Zheng, M. A Framework on Optimization Strategy for EEG Motor Imagery Recognition. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 774–777. [Google Scholar]
- Li, F.; He, F.; Wang, F.; Zhang, D.; Xia, Y.; Li, X. A Novel Simplified Convolutional Neural Network Classification Algorithm of Motor Imagery EEG Signals Based on Deep Learning. Appl. Sci. 2020, 10, 1605. [Google Scholar] [CrossRef]
- Tao, W.; Wang, Z.; Wong, C.M.; Jia, Z.; Li, C.; Chen, X.; Chen, C.L.P.; Wan, F. ADFCNN: Attention-Based Dual-Scale Fusion Convolutional Neural Network for Motor Imagery Brain-Computer Interface. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 154–165. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Zheng, Q.; Liu, B.; Gao, X. EEG Conformer: Convolutional Transformer for EEG Decoding and Visualization. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 710–719. [Google Scholar] [CrossRef]
- Gu, H.; Chen, T.; Ma, X.; Zhang, M.; Sun, Y.; Zhao, J. CLTNet: A Hybrid Deep Learning Model for Motor Imagery Classification. Brain Sci. 2025, 15, 124. [Google Scholar] [CrossRef] [PubMed]
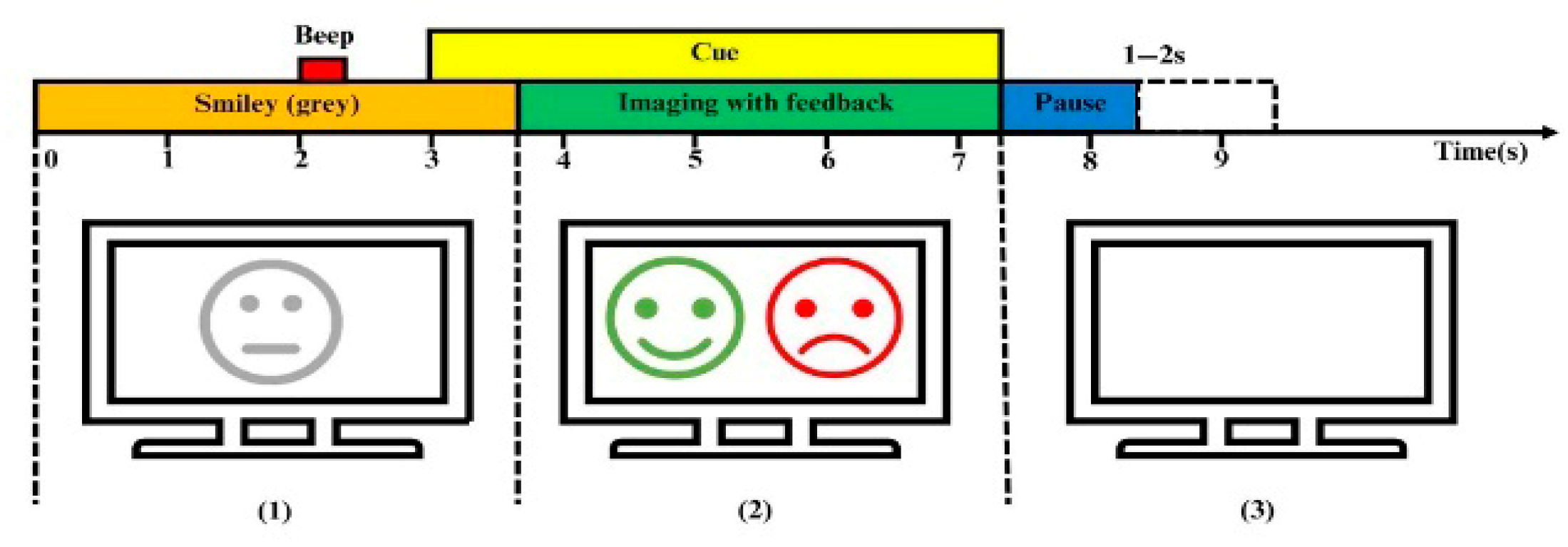

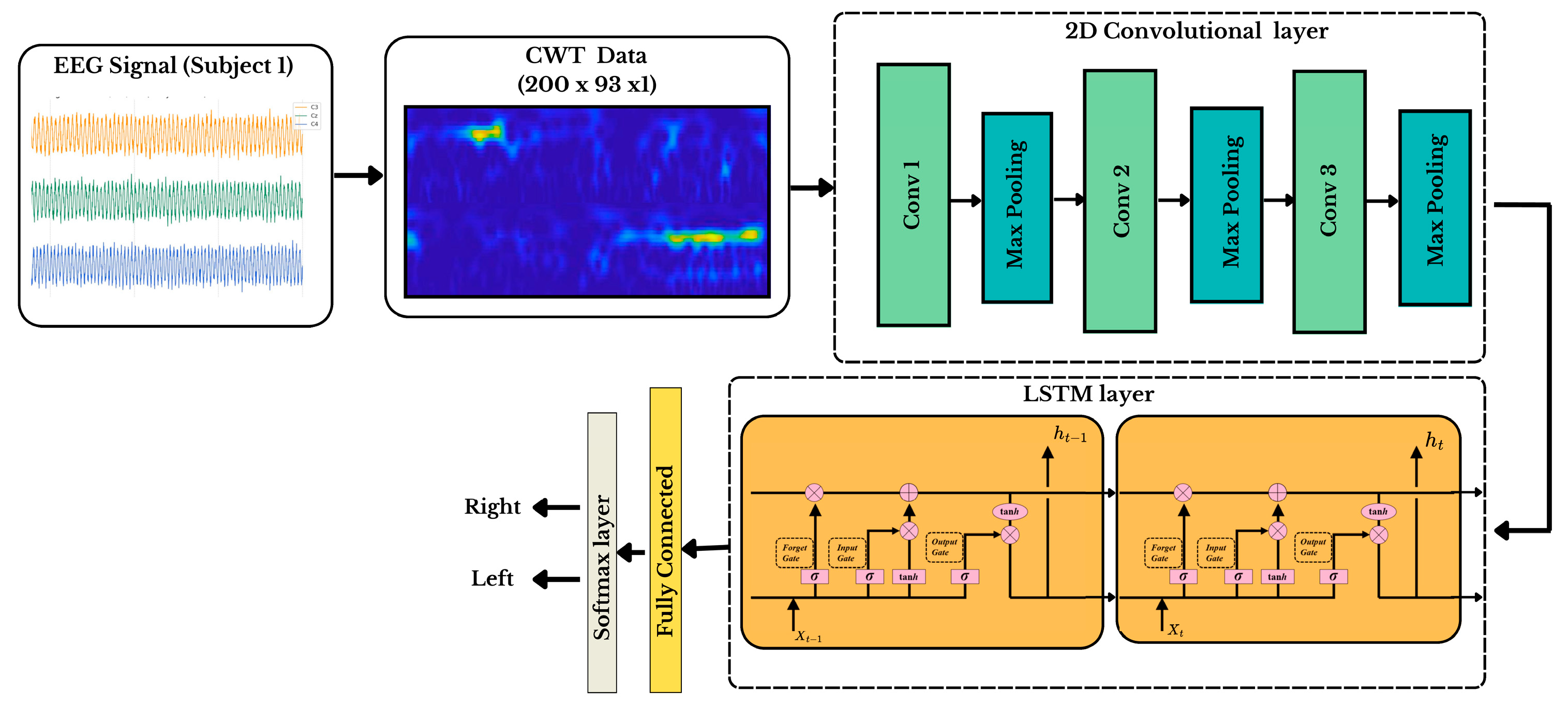

| Hyperparameter | Description | |
|---|---|---|
| CNN architecture | No. of convolutional layers | 3 Conv2D layers |
| Kernel Size | 3 × 3 | |
| Activation function | RELU | |
| Pooling | Max-Pooling (2 × 2) | |
| LSTM Temporal modeling | No. of LSTM Layers | 2 LSTM Layers |
| Hidden layers | 128 units for the 1st LSTM 64 units for the 2nd LSTM | |
| Activation function | tanh | |
| Dropout rate | 0.5 | |
| Fully connected layer | No of dense layers | 1 |
| Final Classification Layer | Softmax (2 Classes: Left/Right) | |
| Optimization & Training | Optimizer | Adam |
| L2 regularization, Weight Decay | 0.0001 | |
| Mini-Batch algorithm | Gradient decent | |
| Cross-validation strategy | 10-Fold cross-validation |
| Method | Data Selection | Classifier | Data Augmentation | Accuracy |
|---|---|---|---|---|
| CNN-SAE * | STFT * | CNN-SAE | No | 77.60% |
| CapsNet * | STFT | CNN | No | 78.44% |
| CWT-SCNN * | CWT * | SCNN | No | 83.20% |
| CNN-MLP * | RNN-LSTM | CNN+MLP | GAN * | 74.80% |
| Skip-NET-GNAA | Anchored STFT | Skip-Net-CNN | GNAA * | 76.00% |
| STFT-VGG16 | STFT | VGG-16 | Cropping | 73.81% |
| CutCat | STFT | Shallow CNN | CutCat | 78.44% |
| ADFCNN * | FFT | ADFCNN | No | 87.81% |
| EEG-Conformer * | No | CNN-Conformer | S&R * | 84.63% |
| CLT-Net | CNN | LSTM | S&R * | 87.11% |
| Proposed GDC-Net | GMWT | CNN-LSTM | DCGAN | 89.24% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouchane, M.; Guo, W.; Yang, S. High-Resolution Time-Frequency Feature Selection and EEG Augmented Deep Learning for Motor Imagery Recognition. Electronics 2025, 14, 2827. https://doi.org/10.3390/electronics14142827
Bouchane M, Guo W, Yang S. High-Resolution Time-Frequency Feature Selection and EEG Augmented Deep Learning for Motor Imagery Recognition. Electronics. 2025; 14(14):2827. https://doi.org/10.3390/electronics14142827
Chicago/Turabian StyleBouchane, Mouna, Wei Guo, and Shuojin Yang. 2025. "High-Resolution Time-Frequency Feature Selection and EEG Augmented Deep Learning for Motor Imagery Recognition" Electronics 14, no. 14: 2827. https://doi.org/10.3390/electronics14142827
APA StyleBouchane, M., Guo, W., & Yang, S. (2025). High-Resolution Time-Frequency Feature Selection and EEG Augmented Deep Learning for Motor Imagery Recognition. Electronics, 14(14), 2827. https://doi.org/10.3390/electronics14142827





