Abstract
We present a scalable and resource-aware framework for the quantum simulation of large proteins, grounded in systematic molecular fragmentation, analytical Toffoli gate modeling, and empirical validation. The ground-state energy of a target biomolecule is reconstructed from capped amino acid fragments, with fixed corrections to account for artificial boundaries. Analytical cost estimates—derived from reduced Hamiltonians—are benchmarked against empirical Toffoli counts using PennyLane’s resource estimation module. Our model maintains predictive accuracy across biologically relevant systems of up to 1852 electrons, capturing consistent patterns across diverse fragments. This framework enables early-stage feasibility assessments for achieving quantum advantage in biochemical simulation pipelines.
1. Introduction
The quantum simulation of biomolecular systems remains a major computational challenge due to the exponential scaling associated with solving the electronic Schrödinger equation. Proteins, in particular, present a formidable case, as they involve a large number of electrons and complex many-body interactions [1,2]. Fragmentation techniques, which decompose macromolecules into smaller subsystems such as amino acids or peptides, have emerged as a viable approach to reducing computational overhead while preserving physical accuracy [3,4,5,6].
Quantum computing offers theoretical advantages in simulating electronic structure problems, where classical methods rapidly become intractable with system size [7,8]. By encoding quantum states directly in qubit-based representations, quantum computers avoid the combinatorial explosion characteristic of classical full-configuration interaction methods. Despite the availability of approximations such as DFT [9] and CAS-CI [10], these approaches face well-known limitations in accuracy or scalability, particularly for systems with strong electronic correlation [11,12].
Exact quantum chemical simulations remain out of reach for full protein systems, even with quantum hardware. As such, methodologically principled reductions in problem size are essential. Our objective is to evaluate a fragmentation-based framework for scalable quantum simulation of proteins, balancing error control with computational feasibility. The methodology builds on our prior work [3], which introduced a reassembly scheme for independently simulated fragments with chemical corrections. That work demonstrated high accuracy on small peptides, achieving relative errors of approximately for amino acid-level fragmentation and for finer subdivisions.
In this study, we extend the methodology to larger and biologically relevant peptides, including Glucagon, Oxytocin, Vasopressin, and Angiotensin II, which vary in electron counts and structural complexity. Among them, Glucagon stands out as a critical benchmark due to its physiological role and its size, comprising 29 amino acids and over 1800 electrons. Its simulation requires addressing more than 1048 coefficients, posing a stringent test for the scalability of our approach.
By systematically evaluating prediction errors and quantum resource estimates across these molecules, we aim to assess the practical applicability of fragmentation-based strategies for quantum chemistry. This work contributes to the broader effort of making accurate electronic structure simulations tractable for systems of biological and chemical relevance. Beyond molecular simulation, the methodology has potential implications in areas such as drug discovery and materials design, where electronic structure accuracy is essential, and classical methods face intrinsic limitations.
The structure of the paper is as follows: Section 2 reviews related work in quantum simulation and fragmentation-based methods. Section 3 introduces our methodology, including regression models, Toffoli gate estimation, and the proposed multi-level fragmentation and reassembly strategy. Section 4 presents experimental validation on a range of peptides and proteins, from small dipeptides to large systems such as Glucagon, along with detailed error and scalability analyses. Section 5 discusses limitations, compares with alternative techniques, and outlines practical implications and future research. Section 6 summarizes our main findings and perspectives. Additional technical derivations and regression diagnostics are provided in the appendices.
2. Related Works
Quantum simulations of biomolecules [5,6,13] have progressed along two converging lines: (i) classical fragment-based electronic-structure methods that exploit locality to curb cost, and (ii) quantum algorithms that aggressively compress qubit and gate resources [14,15]. Our work positions itself at this intersection, extending classical fragmentation ideas into the quantum era and knitting together the most effective resource-optimization tools reported to date.
Fragmentation approaches such as the Fragment Molecular Orbital (FMO) method [16], Our N-Layered Integrated Molecular Orbital and Molecular Mechanics (ONIOM) [17], and adaptive Quantum Mechanics/Molecular Mechanics (QM/MM) [18] mitigate the exponential scaling bottleneck by decomposing proteins into chemically intuitive fragments. However, the high-level electronic treatment of each block is still limited to density-functional or semi-empirical accuracy.
In Equation (1), denotes the total ground-state energy of the reassembled molecule, computed from a set of n fragments. Each is the energy of fragment i, typically obtained from an independent quantum simulation. The term represents an additional correction associated with inter-fragment effects or artificial modifications introduced via fragmentation.
Equation (2) defines two types of corrections that may include the following:
- : the energy of a group assembled or removed during fragmentation (e.g., a capping hydrogen atom to preserve chemical valency);
- : a higher-order many-body interaction correction involving n fragments simultaneously, as in the fragment molecular orbital (FMO) method [16].
The index k denotes the total number of such coupling corrections considered. The ± sign in Equation (1) reflects the fact that these contributions can either increase or decrease the total energy, depending on whether the correction represents an additive or subtractive effect (e.g., insertion/removal of atoms or stabilizing/destabilizing couplings). By introducing the general symbol , we unify the treatment of both structural and energetic corrections into a single formalism. This allows Equations (1) and (2) to remain valid across a wide range of fragmentation strategies, including those that incorporate post-reassembly many-body expansions (MBE).
Bowling et al. [19] exemplify this approach by combining single-residue fragmentation, minimal hydrogen capping, and screened two-body terms within a convergent many-body expansion (MBE) scheme:
Each correction term accounts for interactions omitted at lower orders of the expansion. In particular, truncating the series at the n-body level defines the degree of approximation. For instance, the three-body correction is given by the following:
Although many-body expansions offer chemically accurate results, their combinatorial scaling limits practical applicability. To address this, our method introduces resource-aware fragmentation, statistical estimation, and circuit-level compression to ensure scalability. Prior works, such as MFCC-MBE(2) [20], have improved classical accuracy by incorporating fragment and cap interactions. Extending these ideas, our framework replaces classical subroutines with quantum solvers while preserving compatibility with post-fragmentation corrections, thus enabling seamless integration into hybrid quantum–classical approaches.
Three breakthroughs underpin our scalable workflow:
- Local qubit tapering. Extending the symmetry-based tapering of Bravyi et al. [21], we identify symmetries within each fragment, removing ∼4–6 logical qubits on average.
- SelectSwap oracle synthesis. The SelectSwap network of Zhu et al. [22] prepares fragment phase oracles at a cost of T gates, where is the number of logical qubits required to represent the diagonal coefficients of the fragment.
- Optimal state preparation [23]. Diagonal-unitary synthesis plus exact amplitude amplification [24,25] reduces the non-Clifford depth by 20–50% in published benchmarks (22% for QAOA, 50% for random diagonals) [24,25].
Together, these optimizations shrink the space–time volume of a 400-orbital active site by nearly two orders of magnitude versus the double-factorized algorithm of von Burg et al. [26].
Most prior quantum–chemistry demonstrations target small peptides () or model chromophores. To probe genuine scalability, we select four bio-relevant hormones spanning two decades in electron count and 30 orders in the Hamiltonian-coefficient space:
- Glucagon (29aa, ) — coefficients; 2679 logical qubits after tapering.
- Oxytocin (9aa, ) — coefficients; 778 qubits.
- Vasopressin (9aa, ) — coefficients; 1641 qubits.
- Angiotensin II (8aa, ) — coefficients; 809 qubits.
These systems fill the gap between toy peptides and full enzymes—precisely the scale at which the existing methods begin to break down and where our integrated pipeline is explicitly designed to operate.
Tensor-network simulation methods (e.g., DMRG [27], MPS [28], and TTN [29]) are highly efficient for systems with low or structured entanglement. However, when applied to quantum circuits that generate strong global entanglement—such as GHZ preparation, quantum Fourier transform, or Hamiltonian evolution—the bond dimension grows exponentially, making contraction intractable [29,30]. This limits their applicability to deep circuits or realistic biomolecules.
Most current approaches to quantum simulation remain limited to small peptides with fewer than 150 electrons, where accurate reassembly has been demonstrated with sub-1% errors. However, no previous method integrates fragmentation-aware oracle synthesis and tapering into a scalable pipeline for biomolecules with 500–2000 electrons. Our work addresses this gap by combining these techniques into a unified, resource-efficient framework capable of operating at the hormone scale. While challenges remain—such as chemically informed fragmentation, correlation beyond MP2 [31], and cross-fragment error mitigation—recent advances in entanglement-guided heuristics [32] suggest promising directions to extend the approach.
3. Methodology
Our methodology addresses the challenges of simulating large protein systems on quantum computers by combining fragmentation strategies with advanced quantum algorithms. Below, we outline the key components of our approach, from data modeling and resource estimation to fragmentation and reassembly techniques.
3.1. Fragmentation and Recombination Strategy
Our methodology builds upon the fragmentation protocol introduced in the QMProt framework [33], extending it to enable scalable quantum simulations of large biomolecules. The core idea is to approximate the ground-state energy of a full protein or peptide by summing the energies of chemically meaningful fragments, primarily based on individual amino acid residues. Each fragment is saturated with hydrogen atoms or small chemical groups to preserve valency and molecular stability.
In our framework, the reassembled ground–state energy is given by
where the following applies:
- n denotes the total number of fragments generated;
- is the ground-state energy (GSE) of fragment i;
- k is the number of small molecules added or removed;
- is the GSE of each such molecule;
- is the final GSE of the reassembled molecule.
Here, the index i runs from 1 to n, enumerating each fragment, and j runs from 1 to k, enumerating each added or removed molecule.
To correct the artificial effects introduced at the cutting points, we apply fixed energy corrections based on the capping strategy:
- If a methyl group (CH3) is added to complete valency, we add the energy of a methane molecule as a corrective term.
- If a water molecule is implicitly removed during fragmentation (e.g., in peptide bonds), its reference energy is subtracted.
- If no group is added or removed, no correction is applied.
These correction values are precomputed and consistently reused. This avoids the need for iterative many-body corrections or self-consistent inter-fragment coupling, drastically reducing computational complexity compared to traditional fragmentation schemes.
We apply this fragmentation strategy at two levels:
- Amino acid level: Each amino acid is split into radical and backbone groups. We benchmark the ground-state energy (GSE) and resource estimates (e.g., qubits, Toffoli gates) of the full amino acid against the sum of its fragments, quantifying the reduction factor.
- Peptide/protein level: For representative peptides such as Oxytocin, Angiotensin II, and Glucagon, we compute total energy as the sum of fragment energies plus corrective terms, as expressed in Equation (1). We compare this estimate to the full molecular simulation to evaluate accuracy and resource savings.
This approach maintains high computational efficiency while ensuring that GSE estimates remain within acceptable error bounds. The residual recombination error grows with the number of fragments and is influenced by the precision of the energy evaluation for each fragment. In our current implementation, calculations are performed at the Hartree–Fock (HF) level, which introduces some limitations for large systems. However, the modular nature of the method makes it compatible with more accurate solvers (e.g., DFT, MP2, or quantum algorithms), which are expected to further reduce the error as these techniques mature. Thus, our strategy provides a robust foundation for efficient and scalable quantum simulations of biomolecular systems.
3.2. Modeling Based on Experimental Data
To support our modeling and prediction efforts, we use a dataset—QMProt [33]. This dataset encompasses 45 carefully selected organic molecules, with a particular focus on the 20 canonical amino acids essential to human biology. Each molecule is decomposed into chemically meaningful subunits, including amino and carboxyl termini, central -carbon atoms, and characteristic side chains.
The molecules in QMProt are composed primarily of non-hydrogen atoms such as carbon, nitrogen, oxygen, and sulfur, and they contain up to 15 heavy atoms. For each molecular entry, the dataset provides the following:
- The total number of electrons and molecular orbitals.
- The corresponding number of logical qubits required for simulation.
- The full Hamiltonian encoded as a set of quantum coefficients.
- Ground-state energy estimates derived from quantum mechanical methods
- Additional physicochemical attributes relevant for simulation benchmarking.
This dataset bridges quantum chemical characterization with quantum resource modeling, offering a representative basis for scaling predictions to larger biomolecules. Using this foundation, we develop regression models to forecast quantum resource needs—including qubits and gate counts—based on fundamental descriptors such as the electron number, enabling extrapolation to peptides and protein fragments well beyond the initial dataset.
3.2.1. Linear Model for Qubits
We assume a linear relationship between the number of qubits and the number of electrons:
where is the intercept, is the slope, and is the residual error. The model is fitted using ordinary least squares (OLS), minimizing the squared residuals:
The analytical solution involves solving the normal equations:
3.2.2. Log-Linear Robust Model for Qubits
While the linear model offers a simple baseline, an empirical evaluation revealed that the relationship between electron count and qubit requirements is more accurately captured using a log-transformed regression. Accordingly, we consider the following:
where the parameters and are estimated using robust methods, such as the Huber Regressor [34] and the Theil–Sen Estimator [35], to mitigate the influence of outliers.
To account for structural diversity, we partition the dataset into three molecular complexity segments: Small (electron count ≤ 150), medium (151–500), and large (>500), enabling localized regressions adapted to each scale. Predictions are returned to the original scale via the following:
3.2.3. Exponential Model for Hamiltonian Coefficients
We hypothesize an exponential growth in the number of coefficients concerning the electron count:
with a and b as model parameters. Taking the natural logarithm yields a linearized version:
which is fitted using OLS. The predicted values in the original scale are obtained via exponentiation:
3.2.4. Confidence Intervals
For the linear model, the 95% confidence interval for a prediction is as follows:
where x is the number of electrons for which the confidence interval is being computed, and denotes the sample mean of the observed electron counts.
denotes the estimated standard deviation of the residuals, calculated as , assuming the model is fitted using ordinary least squares, and where denotes the critical value from the Student’s t-distribution with degrees of freedom, corresponding to a two-tailed confidence level of 95%.
For the log-linear robust model, the 95% confidence interval is computed using the delta method. Let denote the log-qubit prediction. The Jacobian vector with respect to the parameters is as follows:
and the variance of the prediction is as follows:
where is the estimated covariance matrix of the fitted parameters. The resulting interval is given by the following:
and transformed back to the original scale as follows:
where . A complete derivation of these expressions and additional justifications for the segment-wise log-qubit modeling can be found in Appendix D.
3.2.5. Error Metrics
We evaluate model performance using standard regression error metrics commonly employed in predictive modeling. The root mean squared error (RMSE) and the mean absolute error (MAE) are used to quantify the average magnitude of residuals, with RMSE giving greater weight to larger errors and MAE providing a more robust central tendency measure less affected by outliers [36].
To contextualize the errors concerning the scale of the observed values, we also report the mean relative error (MRE), expressed as a percentage. Additionally, we compute the relative standard deviation (), which captures the dispersion of predicted values normalized by their mean. These metrics provide a consistent basis for comparing model outputs across different experimental conditions.
3.3. Estimation of Toffoli Gate Count
To estimate the quantum cost, we employ a function inspired by the SelectSwap algorithm [15]. This algorithm achieves a quadratic improvement in gate counts by reducing the number of Toffoli gates to a scale of , where M is the number of coefficients, and f is a multiplicative factor. Without SelectSwap, the cost grows proportionally to M and requires ancillary qubits.
The Toffoli gate count is estimated using the following function:
where
We define the target precision as a function of fragment size, setting for a fragment comprising n logical qubits. Here, b denotes the resolution parameter of the quantum hardware, capturing the logarithmic relationship between numerical accuracy and the size of the Hamiltonian coefficient vector. In our experiments, we fix , corresponding to a 20-bit precision level that reflects realistic thresholds for fault-tolerant quantum architectures. This formulation is consistent with practical accuracy requirements and aligns with resource scaling trends reported in prior studies [22].
Equation (20) expresses the asymptotic scaling of the SelectSwap algorithm and serves as a practical estimator for Toffoli gate counts in fault-tolerant quantum simulations. For all experiments, we assume constant factors unless otherwise stated. Additional implementation details and derivations are provided in Appendix B.
3.4. Experimental Validation
To validate our analytical Toffoli-gate estimates, we employ PennyLane’s resource estimation module, available through the pennylane.labs.resource_estimation interface (Commit 5fc5d02308d25831594ecb41e4acc6f74ce2da30 on GitHub; not yet part of the stable release or fully documented at the time of our study). Using this framework, we instantiate both QROM-based state preparation circuits [37] and qubitization routines [38] for each fragment and benchmark peptide, adapting the templates to match the structure of our reduced Hamiltonians.
For each system, we extract empirical Toffoli counts and compare them against the theoretical predictions obtained from Equations (6)–(20). This experimental procedure serves to verify the internal consistency of our cost model and ensure compatibility with circuit-level resource estimators in current quantum toolchains.
4. Results
We begin by evaluating the accuracy of our fragmentation strategy via regression analysis. Figure 1 shows an exponential fit of the total number of Hamiltonian coefficients versus the electron count, including a 95% confidence interval. In addition, Figure 2 provides a complementary linear interpolation for the smallest molecules in our dataset.
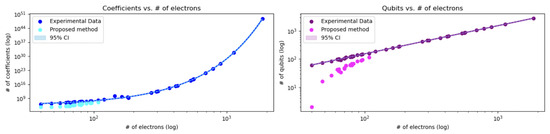
Figure 1.
Scaling of quantum resource requirements with electron count, shown on log–log axes with 95% confidence intervals. (Left) Exponential regression of Hamiltonian coefficient counts versus number of electrons. Experimental data (filled circles), fitted model (solid line), and fragmentation-based predictions (open circles) are plotted. (Right) Linear regression of qubit requirements versus electron count, including measured values (filled circles), regression line (solid), and fragmentation estimates (open). Shaded bands in both panels represent the 95% confidence intervals of the fits.
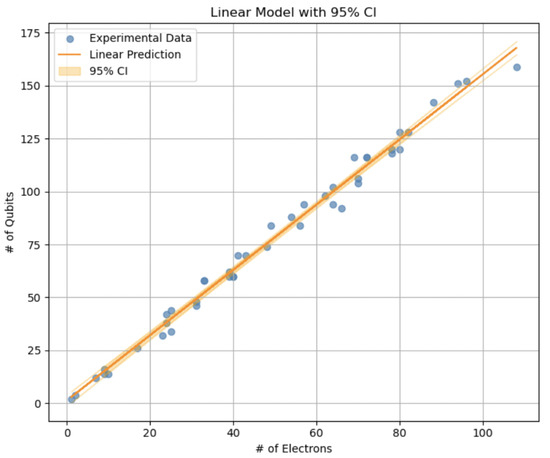
Figure 2.
Linear fit of the required qubits () as a function of the number of electrons (), using data from QMProt [33]. Blue markers denote empirical values, the orange line represents the fitted model , and the shaded band indicates the 95% confidence interval. The nearly linear relationship provides a useful estimate of qubit requirements as system size increases.
Next, we quantify recombination and estimation errors. Table 1 reports fragment recombination errors across all peptides, confirming minimal error accumulation for small fragments and identifying increased errors for larger systems.

Table 1.
Summary of electrons, orbitals, theoretical energy (GT), calculated energy (Em), and relative error (%RE) for different peptides.
We then examine resource-scaling trends. In Figure 3, we plot both Toffoli gate counts and qubit requirements against molecular size, comparing the original full-Hamiltonian approach to our base-structure method. Table 2 summarizes these benchmarks— numbers of the coefficients, Toffoli estimates, reduction factors, and electron counts—for every fragment.
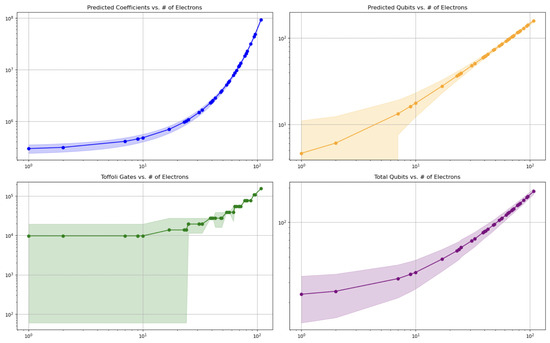
Figure 3.
Predicted quantum resource requirements as a function of the number of electrons. (Top-left) exponential model of coefficient growth. (Top-right) linear model for qubit requirements. (Bottom-left) estimated Toffoli gate counts based on predicted coefficients. (Bottom-right) total qubit requirements. Shaded regions indicate 95% confidence intervals. These trends support the scalability of the resource model across molecular sizes.

Table 2.
Resource comparison for peptide simulations: theoretical Toffoli gate estimates using the full Hamiltonian () versus the proposed fragmentation–reassembly (base-structure) approach. For each molecule and version (Ver.: Orig. = Original; Prop. = Proposed), the table lists the number of Hamiltonian coefficients (# Coeffs.), the estimated Toffoli gate count, the Toffoli reduction factor (Red. (Toffoli)), the electron count (when available), and the coefficient reduction factor (Red. (Coeff.)).
To validate regression robustness, Table 3 presents performance metrics for robust regression models (Huber with varying and Theil–Sen) in predicting log-transformed qubit counts across small, medium, and large molecular complexity segments.

Table 3.
Comparison of regression models (Huber and Theil–Sen) for predicting log-transformed qubit counts across molecular complexity segments. Metrics include , the cross-validated (when applicable), the MAE, the RMSE, the standard deviation, and the coefficient of variation. Segment-specific modeling reveals performance variation by molecular size. Cross-validation scores are omitted (–) where data scarcity limits statistical significance.
Finally, to ground our theoretical Toffoli formula (Equation (20)) in real circuit data, we measured gate counts using PennyLane’s resource_estimation module [39]. Table 4 reports these empirical gate counts alongside the derived coefficients and and their relative errors.

Table 4.
Comparison of analytical Toffoli estimates [Equation (20), ] with empirical counts (Toffoli *) from PennyLane’s resource estimation module [39], applied to each fragment’s qubitization circuit. A global OLS fit gives , (, ), with a mean relative error of 11.9%. See Appendix C for , derivations at different . Ver.: Orig. = Original; Prop. = Proposed; # Coefs. = number of Hamiltonian coefficients.
Using our regression models—linear for qubits and exponential for coefficients—we predicted the resources required to simulate a variety of proteins and peptides, including both well-known and novel examples. Our models provide the following key insights:
- Number of coefficients (): The number of Hamiltonian coefficients exhibits exponential growth with the number of electrons, as captured by the exponential model in Equation (11).
- Number of Qubits (): the number of qubits grows moderately linearly with the number of electrons, as described by the linear model in Equation (6).
- Number of Toffoli Gates: While fragmentation occasionally introduces overhead for small amino acids—due to duplicated setup costs and additional reassembly steps—it proves advantageous at the peptide scale, where monolithic encodings become intractable. This trade-off is acceptable, given the preservation of accuracy and the exponential savings in larger systems. However, for small systems, fragmentation maintains extremely low errors, supporting the method’s accuracy and feasibility. This suggests that, while fragmentation introduces a slight overhead in gate count for small systems, it remains a viable strategy for reducing resource requirements in larger systems.
These predictions were validated on a diverse set of intermediate systems and then extrapolated to full hormone peptides—such as Glucagon—demonstrating that the model retains predictive power across four orders of magnitude in electron count and 30 orders of Hamiltonian complexity.
To further analyze the scalability of our approach, we generated log-log plots that relate the following quantities:
- versus ,
- Toffoli gates versus ,
- Reduction factor versus ,
- Total qubits versus .
These plots reveal that, although the quantum cost increases with system size, the application of fragmentation and the SelectSwap algorithm significantly mitigates this increase. Specifically, the reduction factor achieved through fragmentation keeps the gate count and qubit requirements within acceptable ranges, even for large systems. This demonstrates the effectiveness of our approach in managing the exponential scaling of quantum resources. Further details of these affirmations can be corroborated in Table 2, where the reduction in terms of coefficients and Toffoli gates of our approach is presented, both in the case of protein and amino acid fragmentation levels. These results confirm that, while quantum resource scaling remains exponential, targeted fragmentation combined with modern quantum oracles offers a tractable and chemically accurate pathway to simulate biologically meaningful molecules on future quantum hardware.
To bring the strategy of our previous work to the next level [3], we compute the accuracy of our fragmentation strategy by comparing reference energies () with calculated energies () for a set of larger peptides. Table 1 summarizes the number of electrons, orbitals, theoretical energy, computed energy, and relative error (), starting with some small peptides included in our previous work and continuing with much larger ones to compare the change in accuracy as the system scales up. Key observations include the following:
- Small peptides: Relative errors of 0.0005–0.0065% in dipeptides (e.g., Gly-Gly, Pro-Gly, Gly-Ala). This confirms the high accuracy of our fragmentation strategy for small systems.
- Intermediate peptides: Some (e.g., Aspartame and Phe-Ile) exhibit slightly higher errors (up to 0.065%), confirming again the accuracy of the strategy.
- Large systems: In molecules with hundreds of electrons (e.g., Angiotensin II and IV, Oxytocin, Glucagon), the relative error increases (between 2 and 3%), highlighting the need for further optimization strategies, even though the errors remain within acceptable limits for practical applications.
Our combined methodology—statistical modeling, hierarchical fragmentation, and quantum resource optimization—enables the accurate simulation of complex biomolecules at an unprecedented scale. These results lay the groundwork for near-term beyond applications in quantum biochemistry and offer a scalable framework compatible with fault-tolerant quantum computing architectures.
Experimental Validation
Table 4 presents a detailed comparison between theoretical Toffoli gate counts—computed via Equation (20) with fixed parameters —and empirical counts (Toffoli*) obtained using the pennylane.labs.resource_estimation [40] module for each fragment’s qubitization circuit. Additionally, we perform an ordinary least squares (OLS) fit across all samples to extract empirical scaling coefficients and , along with their deviations. Per-fragment parameter variations under different precision settings are detailed in Appendix C.
5. Discussion
The results presented demonstrate that our fragmentation–reassembly protocol effectively decomposes large protein Hamiltonians into tractable subunits while preserving overall accuracy. By applying Equation (20) with fixed parameters () and validating against PennyLane’s resource_estimation [39] (Table 4), we achieve sub-3% relative energy errors alongside reductions of up to 20 orders of magnitude in Toffoli gate counts (Table 2). This dual attainment of precision and scalability is essential for hybrid quantum–classical workflows on near-term devices.
A key strength of our methodology lies in its modular error propagation: The overall simulation error results from the additive contributions of each independently simulated fragment. Consequently, any improvement in fragment accuracy, whether through higher-order quantum algorithms (e.g., quantum phase estimation [41] or improved state preparation circuits [23], directly results in a lower global error. As logical qubit fidelity advances, we therefore anticipate convergence toward chemical precision without altering the core fragmentation scheme.
Our resource-prediction framework is underpinned by robust regression, with Huber estimators () delivering superior outlier resistance and fit quality across small, medium, and large fragment regimes (Table 3). Compared to Theil–Sen, Huber regression maintains higher values and lower MAE in log space, justifying its selection as the primary model for qubit- and gate-count estimation. The trends illustrated in Figure 3 further corroborate the consistency of these predictions across molecular sizes.
Empirical calibration refines our theoretical scaling: fitting Equation (20) to measured data yields global corrections , , reducing the mean Toffoli-count error to 11.9%. These adjustments preserve the validity of the analytical model while aligning it with practical hardware characteristics, thereby bridging theory and experiment with minimal overhead.
When benchmarked against classical fragmentation approaches (e.g. ONIOM, many-body expansions), our pipeline offers comparable or improved accuracy for small peptides and more favorable scaling for larger biomolecules. Unlike global symmetry tapering [21], which is limited due to the scarcity of protein-wide symmetries, our fragment-wise active-space identification applies universally, enhancing adaptability across diverse protein architectures.
Nonetheless, several limitations remain. Current noise and decoherence on real quantum hardware constrain immediate fault-tolerant implementation. Fragments containing atypical bonds or motifs may introduce systematic deviations; targeted corrections—guided by the QMProt dataset [33]—and refined state-preparation protocols are required to address these edge cases. Moreover, the integration of advanced subroutines will improve fragment precision at the expense of greater circuit complexity, necessitating a careful trade-off between accuracy and resource availability.
In summary, our fragmentation framework provides a scientifically rigorous, modular, and scalable blueprint for quantum simulation of biomolecules. By combining analytical modeling, empirical validation, and error modularity, we propose a scientifically grounded and practically oriented pathway toward achieving quantum advantage in real-world biochemical simulations.
6. Conclusions and Perspectives
We have presented a scalable, resource-efficient protocol for the quantum simulation of large protein systems, based on molecular fragmentation, regression-driven resource estimation, and circuit optimization via the SelectSwap algorithm.
Starting from small peptides and extending to Glucagon, our method maintains relative energy errors below 3% while reducing Toffoli gate counts by up to 20 orders of magnitude. Regression models accurately predict resource requirements and support pre-optimization of quantum workloads for both current and near-term devices.
Future work includes expanding the molecular dataset to improve model robustness, integrating advanced subroutines (e.g. QPE and optimized state preparation) to approach chemical accuracy, and benchmarking on actual hardware to evaluate noise resilience. Comparative analysis with techniques such as Hamiltonian tapering and active-space reduction will further refine the reassembly pipeline, and the modular nature of our framework ensures that hardware improvements map directly to simulation accuracy without altering the core methodology.
Our head-to-head comparison with PennyLane’s resource_estimation module [39] confirms that, once validated, it can serve as a reliable standalone estimator of circuit cost. Simulating each fragment’s qubitization circuit under the chosen precision settings can replace the explicit extraction of empirical coefficients and , simplifying future resource estimates without sacrificing rigor.
Moreover, implementing quantum phase estimation at the fragment level is expected to reduce individual fragment errors to near–chemical precision. Because the total energy error accumulates fragment-wise, improving each fragment’s precision directly lowers the global error. This property is well suited to near-term quantum processors with limited numbers of high-fidelity logical qubits.
Overall, the proposed strategy offers a practical and verifiable route to simulate increasingly large biomolecules, aligning with the current trajectory of quantum hardware development and providing a clear framework for ongoing methodological enhancement.
Author Contributions
Conceptualization, P.A.-A. and L.C.S.; Methodology, P.A.-A. and L.C.S.; Software, P.A.-A.; Validation, P.A.-A. and L.C.S.; Formal Analysis, P.A.-A. and L.C.S.; Investigation, P.A.-A. and L.C.S.; Resources, P.A.-A.; Data Curation, P.A.-A. and L.C.S.; Writing—Original Draft Preparation, P.A.-A.; Writing—Review and Editing, P.A.-A. and L.C.S.; Visualization, P.A.-A. and L.C.S.; Supervision, P.A.-A.; Project Administration, P.A.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The QMProt dataset is publicly available on the Pennylane platform for direct integration with quantum computing pipelines. It can be accessed at: https://pennylane.ai/datasets/collection/qmprot (accessed on 19 May 2025).
Acknowledgments
The authors gratefully acknowledge Guillermo Alonso-Linaje and Diego Guala for their valuable comments and discussions during the development of this project. We also extend our special thanks to the Pennylane team for their ongoing work on the resource_estimation module and for providing helpful guidance that supported the validation and implementation phases of this study.
Conflicts of Interest
Authors Parfait Atchade-Adelomou and Laia Coronas Sala were employed by Lighthouse Disruptive Innovation Group (LDIG). The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A. Source Code
The Python scripts used for model fitting, Toffoli gate estimation, and comparisons between full and fragmented simulations are publicly available at https://github.com/pifparfait/qmprot_strategy (accessed on 19 May 2025).
Appendix B. T-Gate Count from the Big-O Bound
We translate the Big-O bound from the reference [22] on the T-gate count into an explicit formula with constant factors. Specifically, the T-gate count required to implement the quantum lookup table is given by
where is the number of address qubits for a lookup table with N entries, and denotes the allowable error tolerance in the state preparation. The constants and depend on the gate decomposition and error-correction protocols [22].
This formula underpins the analysis in Section 3 and is directly used to estimate the quantum resource cost for each molecule (see Table 2).
The asymptotic bound is given by
which implies that, for a sufficiently large n and small , there exist constants , such that
Our goal is to determine these constant factors explicitly. Following the work developed in [22], the partition the memory into blocks of size is given by
so that the number of blocks is
Each block is processed via a quantum routing tree using non-Clifford operations (e.g., CSWAP or Toffoli gates). Let denote the T-gate cost per block, which includes the decomposition cost (e.g., a Toffoli gate typically decomposes into about 7 T-gates [22,42]) and an extra factor of due to error suppression. Hence, the T-gate cost per block is
After multiplying by the number of blocks in Equation (A3), the primary query cost is
We set
Ancillary operations (uncomputing and error correction, e.g., via entanglement distillation [22]) contribute a cost proportional to . Let be the unit cost for these operations; then,
We define
Adding Equations (A5) and (A6) yields equation Equation (A1)
Two key insights justify this formula:
- 1.
- An optimal block partitioning () results in iterations, each costing T–gates [22].
- 2.
- Ancillary operations add an overhead scaling linearly with [22].
The value of is influenced by the cost of decomposing complex non-Clifford operations. While a raw Toffoli gate might require approximately 7 T-gates [22,42], the unified architecture integrates several optimizations (e.g., reducing SWAP overhead, parallel processing, and gate cancellations) that lower the effective cost per block. Empirical and theoretical analyses in [22] and related literature (including [15,42,43]) support an effective value for in the range of 3 to 10. Similarly, reflects the cost of auxiliary operations for amplitude amplification and uncomputing. The procedure in [22] applies two such operations per query, each with a low, nearly constant T–gate cost (typically around 1 T–gate), leading to .
The expression in Equation (A1) is essential for precise resource estimation in fault-tolerant quantum implementations of lookup tables and is supported by the detailed analyses in [22].
Appendix C. Per-Fragment Coefficient Determination
This appendix rigorously derives the empirical coefficients and employed in Equation (20) and reported in Table 4 of the main text. It supplements the study by formalizing the relation between the measured Toffoli counts and the theoretical scaling parameters.
Let i index each Hamiltonian fragment, with the following:
- , the number of Hamiltonian terms (input).
- , the required qubit-index width.
Two precision settings are chosen a priori to probe sensitivity:
For each , compute the auxiliary variables:
Denote with the Toffoli count measured via PennyLane’s resource_estimation under precision (input). The linear model for each fragment is as follows:
Solving the system yields closed-form expressions:
In practice, the global constants reported in Table 4 are obtained via a least-squares fit across all fragments:
Appendix D. Regression Model Analysis for Qubits
This appendix presents a regression-based analysis to estimate the number of quantum qubits required to simulate molecular systems, based on their electron count. In contrast to classical approaches relying on ordinary least squares (OLSs), we adopt robust regression techniques—namely the Huber regressor and Theil–Sen estimator—combined with molecular segmentation to improve stability and resistance to outliers.
Appendix D.1. Model Formulation
We consider a log-linear model relating the number of logical qubits to the number of electrons :
where and are regression coefficients and is a residual error term. This formulation enables exponential growth in qubit requirements while allowing for linear estimation in the log-domain.
Robust estimators were employed to mitigate the influence of outliers in the training data. Additionally, the dataset was segmented into three groups based on the electron count:
- Small:
- Medium:
- Large:
The predicted qubit counts are then obtained by exponentiating the log prediction:
Appendix D.2. Evaluation Metrics
To assess model performance, we compute the coefficient of determination , defined as follows:
where and represent the observed and predicted values, respectively.
We further report the following:
Appendix D.3. Confidence Interval (95%) via Delta Method
For the log-linear model, 95% confidence intervals are computed using the delta method. Let be the predicted for a given electron count x. The Jacobian vector is as follows:
and the variance of the prediction is as follows:
where is the parameter covariance matrix. The 95% confidence interval in log-space is as follows:
which is back-transformed to yield the following:
where , and is the t-quantile with degrees of freedom for a two-tailed 95% confidence level.
The use of log-linear robust regression models across molecular segments improves the consistency of predictions and their interpretability.
References
- Bryce, R.A. What Next for Quantum Mechanics in Structure-Based Drug Discovery? Methods Mol. Biol. 2020, 2114, 339–353. [Google Scholar] [CrossRef] [PubMed]
- Baiardi, A.; Christandl, M.; Reiher, M. Quantum Computing for Molecular Biology. Chembiochem 2023, 24, e202300120. [Google Scholar] [CrossRef]
- Sala, L.C.; Atchade-Adelemou, P. Efficient Protein Ground State Energy Computation via Fragmentation and Reassembly. arXiv 2025, arXiv:2501.03766. [Google Scholar]
- Li, S.; Li, W.; Jiang, Y. Generalized energy-based fragmentation approach for computing the ground-state energies and properties of large molecules. J. Phys. Chem. A 2007, 111, 2193–2199. [Google Scholar] [CrossRef] [PubMed]
- Deev, V.; Collins, M.A. Approximate ab initio energies by systematic molecular fragmentation. J. Chem. Phys. 2005, 122, 154102. [Google Scholar] [CrossRef]
- Bettens, R.P.A.; Lee, A.M. Accurately reproducing ab initio electrostatic potentials with multipoles and fragmentation. J. Phys. Chem. A 2006, 110, 8777. [Google Scholar] [CrossRef]
- Atchade-Adelomou, P. Quantum algorithms for solving hard constrained optimisation problems. arXiv 2022, arXiv:2202.13125. [Google Scholar]
- Reiher, M.; Wiebe, N.; Svore, K.M.; Wecker, D.; Troyer, M. Elucidating reaction mechanisms on quantum computers. Proc. Natl. Acad. Sci. USA 2017, 114, 7555–7560. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Density functional theory (DFT). Phys. Rev 1964, 136, B864. [Google Scholar] [CrossRef]
- Evangelisti, S.; Bendazzoli, G.L.; Gagliardi, L. Complete active-space configuration interaction with optimized orbitals: Application to Li2. Int. J. Quantum Chem. 1995, 55, 277–280. [Google Scholar] [CrossRef]
- McArdle, S.; Endo, S.; Aspuru-Guzik, A.; Benjamin, S.C.; Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 2020, 92, 015003. [Google Scholar] [CrossRef]
- Yang, P.J.; Sugiyama, M.; Tsuda, K.; Yanai, T. Artificial neural networks applied as molecular wave function solvers. J. Chem. Theory Comput. 2020, 16, 3513–3529. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sawaya, N.P.; et al. Quantum chemistry in the age of quantum computing. Chem. Rev. 2019, 119, 10856–10915. [Google Scholar] [CrossRef]
- Wecker, D.; Bauer, B.; Clark, B.K.; Hastings, M.B.; Troyer, M. Gate-count estimates for performing quantum chemistry on small quantum computers. Phys. Rev. A 2014, 90, 022305. [Google Scholar] [CrossRef]
- Low, G.H.; Kliuchnikov, V.; Schaeffer, L. Trading T gates for dirty qubits in state preparation and unitary synthesis. Quantum 2024, 8, 1375. [Google Scholar] [CrossRef]
- Kitaura, K.; Ikeo, E.; Asada, T.; Nakano, T.; Uebayasi, M. Fragment Molecular Orbital Method: An Approximate Computational Method for Large Molecules. Chem. Phys. Lett. 1999, 313, 701–706. [Google Scholar] [CrossRef]
- Morokuma, M.; collaborators. ONIOM: A Multilayered Integrated MO + MM Method. J. Mol. Struct. 1999, 461–462, 1–21. [Google Scholar]
- ApSimon, J.; J. Bearpark, R. Adaptive QM/MM Methods for Chemical Reaction Dynamics. WIREs Comput. Mol. Sci. 2023, 13, e1618. [Google Scholar]
- Bowling, P.E.; Broderick, D.R.; Herbert, J.M. Convergent Protocols for Computing Protein–Ligand Interaction Energies Using Fragment-Based Quantum Chemistry. J. Chem. Theory Comput. 2023, 19, 3656–3670. [Google Scholar] [CrossRef]
- Vornweg, J.R.; Wolter, M.; Jacob, C.R. A simple and consistent quantum-chemical fragmentation scheme for proteins that includes two-body contributions. J. Chem. Theory Comput. 2022, 18, 4516–4527. [Google Scholar] [CrossRef]
- Bravyi, S.; Gambetta, J.M.; Mezzacapo, A.; Temme, K. Tapering off qubits to simulate fermionic Hamiltonians. arXiv 2017. [Google Scholar] [CrossRef]
- Zhu, S.; Sundaram, A.; Low, G.H. Unified architecture for a quantum lookup table. arXiv 2024, arXiv:2406.18030. [Google Scholar]
- Fomichev, S.; Hejazi, K.; Zini, M.S.; Kiser, M.; Fraxanet, J.; Casares, P.A.M.; Delgado, A.; Huh, J.; Voigt, A.C.; Mueller, J.E.; et al. Initial state preparation for quantum chemistry on quantum computers. PRX Quantum 2024, 5, 040339. [Google Scholar] [CrossRef]
- Gosset, D.; Kothari, R.; Wu, K. Quantum state preparation with optimal T-count. arXiv 2024, arXiv:2411.04790. [Google Scholar]
- Carrera Vazquez, A.; Woerner, S. Efficient state preparation for quantum amplitude estimation. Phys. Rev. Appl. 2021, 15, 034027. [Google Scholar] [CrossRef]
- von Burg, V.; Low, G.H.; Häner, T.; Steiger, D.S.; Reiher, M.; Roetteler, M.; Troyer, M. Quantum computing enhanced computational catalysis. Phys. Rev. Res. 2021, 3. [Google Scholar] [CrossRef]
- Schollwöck, U. The density-matrix renormalization group. Rev. Mod. Phys. 2005, 77, 259–315. [Google Scholar] [CrossRef]
- Perez-Garcia, D.; Verstraete, F.; Wolf, M.M.; Cirac, J.I. Matrix product state representations. arXiv 2006. [Google Scholar] [CrossRef]
- Orús, R.; Mugel, S.; Lizaso, E. Tensor Networks for Complex Quantum Systems. Nat. Rev. Phys. 2019, 1, 538–550. [Google Scholar] [CrossRef]
- Chan, G.K.L.; Zgid, D. The Density Matrix Renormalization Group in Quantum Chemistry. Annu. Rep. Comput. Chem. 2009, 5, 149–162. [Google Scholar]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Zou, H.; Magnusson, E.; Brunander, H.; Dobrautz, W.; Rahm, M. Multireference error mitigation for quantum computation of chemistry. arXiv 2025. [Google Scholar] [CrossRef]
- Sala, L.C.; Atchade-Adelomou, P. QMProt: A Comprehensive Dataset of Quantum Properties for Proteins. arXiv 2025, arXiv:2505.08956. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. In Breakthroughs in Statistics: Methodology and Distribution; Springer: Berlin/Heidelberg, Germany, 1992; pp. 492–518. [Google Scholar]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. Indag. Math. 1950, 12, 173. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- PennyLaneAI Development Team. test_qrom_state_prep.py: QROM State Preparation Test. Available online: https://github.com/PennyLaneAI/pennylane/blob/qrom_state_prep/tests/templates/test_state_preparations/test_qrom_state_prep.py (accessed on 17 June 2025).
- PennyLaneAI Development Team. test_resource_qubitization.py: Resource Qubitization Test. 2025. Available online: https://github.com/PennyLaneAI/pennylane/blob/5fc5d02308d25831594ecb41e4acc6f74ce2da30/pennylane/labs/tests/resource_estimation/templates/test_resource_qubitization.py (accessed on 17 June 2025).
- Xanadu Quantum Technologies Inc. qml.labs.resource_estimation—PennyLane 0.41.1 Documentation. 2024. Available online: https://docs.pennylane.ai/en/stable/code/api/pennylane.labs.resource_estimation.html (accessed on 16 June 2025).
- contributors, P. pennylane.labs.resource_estimation: Resource Estimation Module. 2025. Available online: https://github.com/PennyLaneAI/pennylane/tree/5fc5d02308d25831594ecb41e4acc6f74ce2da30/pennylane/labs (accessed on 16 June 2025).
- Kitaev, A.Y. Quantum measurements and the Abelian stabilizer problem. arXiv 1995. [Google Scholar] [CrossRef]
- Amy, M.; Maslov, D.; Mosca, M.; Roetteler, M. A Meet-in-the-Middle Algorithm for Fast Synthesis of Depth-Optimal Quantum Circuits. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2013, 32, 818–830. [Google Scholar] [CrossRef]
- Ross, N.J.; Selinger, P. Optimal ancilla-free Clifford+ T approximation of z-rotations. arXiv 2014, arXiv:1403.2975. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).