Low-Complexity Sum-Rate Maximization for Multi-IRS-Assisted V2I Systems
Abstract
1. Introduction
1.1. Related Work
1.2. Motivations
1.3. Contributions
- We analyze the Doppler shift of the LoS component and the Doppler expansion of the non-line-of-sight (NLoS) component of the association link of a vehicle in a moving state, and the time-varying communication model for multi-IRS-assisted V2I is established. The V2I capacity is maximized by the joint optimization of base station (BS) active precoding and IRS passive phase shifting.
- The original problem is decomposed into two subproblems: precoding and IRS phase-shift optimization. To address the nonconvexity of the IRS phase-shift subproblem, the problem is simplified based on the sum path gain maximization (SPGM) criterion proposed in [14] to indirectly optimize the sum path gain, and a new algorithm named dimension-wise sine maximization (DSM) is proposed to directly tackle the problem with lower complexity. Then, the precoding of the BS is derived from the obtained IRS phase shift matrix using the water-filling (WF) algorithm.
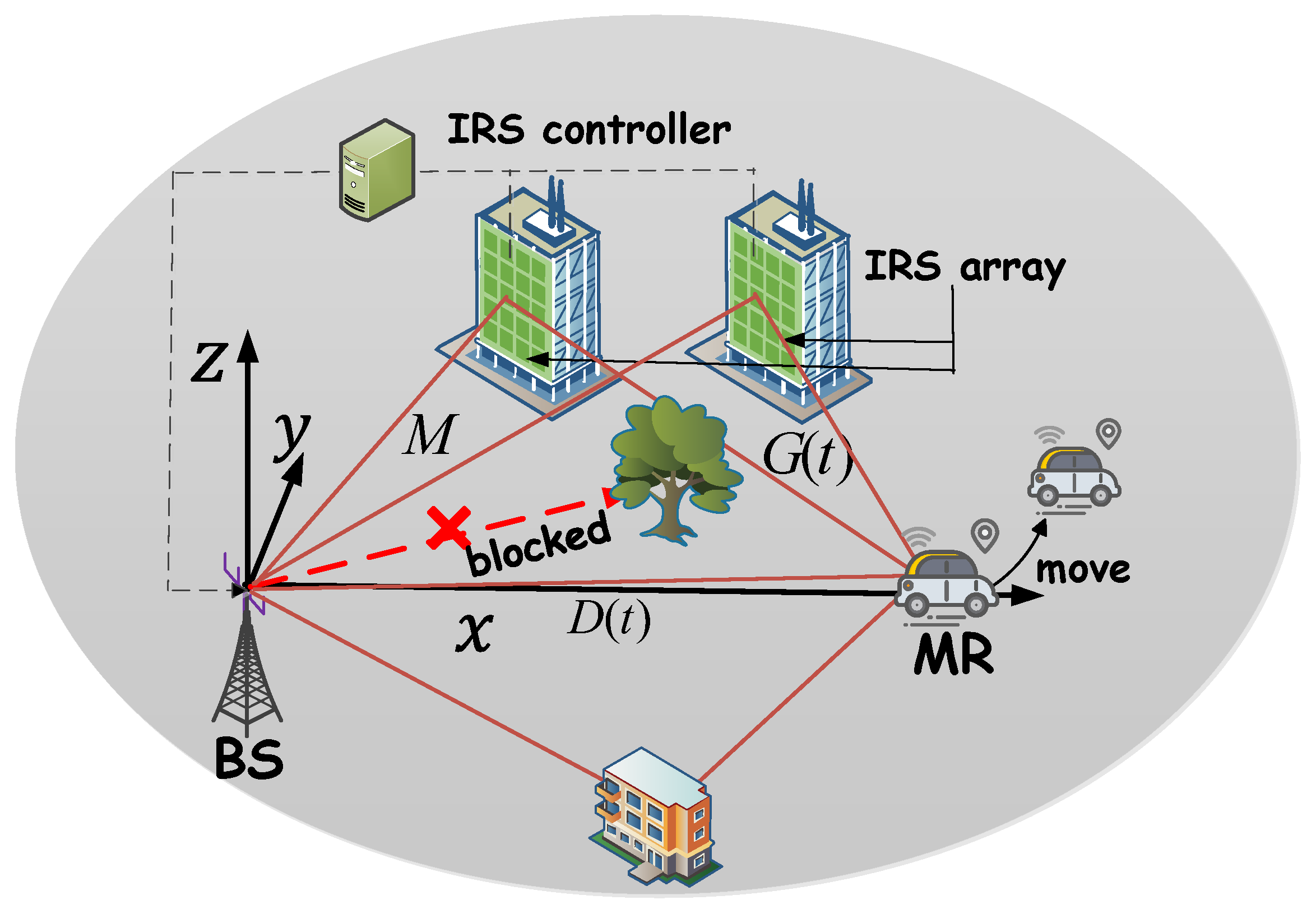
2. System Model
3. Problem Solution
3.1. Phase Shift Matrix Design Under the SPGM Criterion
3.2. Precoding Design with the Obtained Power Allocation Matrix
| Algorithm 1: Proposed DSM Algorithm to Solve (9) |
 |
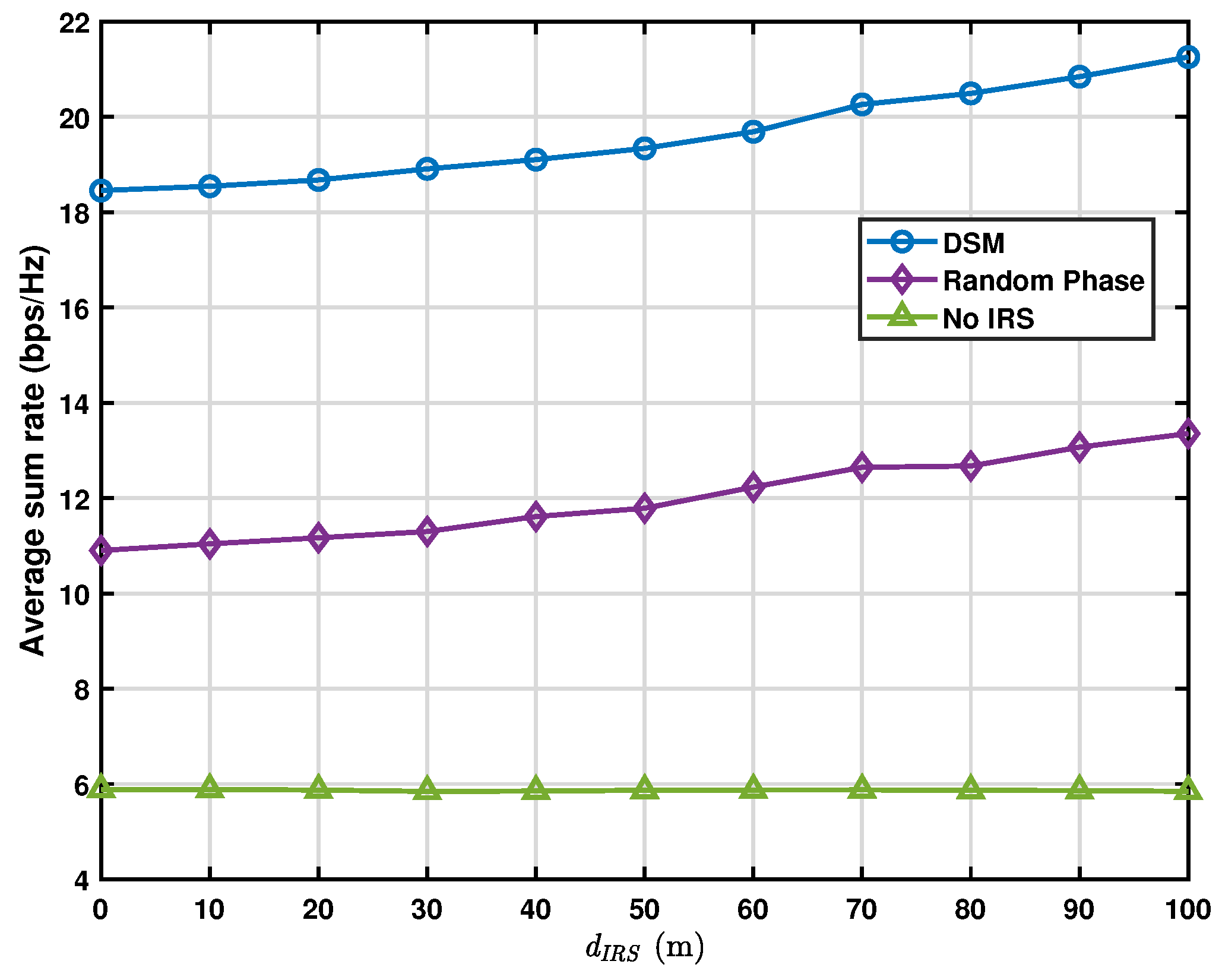
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Xiao, Y.; Ma, Z.; Xiao, M.; Ding, Z.; Lei, X.; Karagiannidis, G.K.; Fan, P. 6G wireless networks: Vision, requirements, architecture, and key technologies. IEEE Veh. Technol. Mag. 2019, 14, 28–41. [Google Scholar] [CrossRef]
- Giordani, M.; Polese, M.; Mezzavilla, M.; Rangan, S.; Zorzi, M. Toward 6G networks: Use cases and technologies. IEEE Commun. Mag. 2020, 58, 55–61. [Google Scholar] [CrossRef]
- Zheng, B.; You, C.; Mei, W.; Zhang, R. A survey on channel estimation and practical passive beamforming design for intelligent reflecting surface aided wireless communications. IEEE Commun. Surv. Tutor. 2022, 24, 1035–1071. [Google Scholar] [CrossRef]
- Choi, J.; Kwon, G.; Park, H. Multiple intelligent reflecting surfaces for capacity maximization in LOS MIMO systems. IEEE Wirel. Commun. Lett. 2021, 10, 1727–1731. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Commun. Mag. 2019, 58, 106–112. [Google Scholar] [CrossRef]
- Pan, C.; Ren, H.; Wang, K.; Kolb, J.F.; Elkashlan, M.; Chen, M.; Di Renzo, M.; Hao, Y.; Wang, J.; Swindlehurst, A.L.; et al. Reconfigurable intelligent surfaces for 6G systems: Principles, applications, and research directions. IEEE Commun. Mag. 2021, 59, 14–20. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Kumar, V.; Zhang, R.; Di Renzo, M.; Tran, L.N. A novel SCA-based method for beamforming optimization in IRS/RIS-assisted MU-MISO downlink. IEEE Wirel. Commun. Lett. 2022, 12, 297–301. [Google Scholar] [CrossRef]
- Hua, B.; Han, L.; Zhu, Q.; Wang, C.X.; Mao, K.; Bao, J.; Chang, H.; Tang, Z. Ultra-Wideband Nonstationary Channel Modeling for UAV-to-Ground Communications. IEEE Trans. Wirel. Commun. 2025, 24, 4190–4204. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, R. Capacity characterization for intelligent reflecting surface aided MIMO communication. IEEE J. Sel. Areas Commun. 2020, 38, 1823–1838. [Google Scholar] [CrossRef]
- Chang, D.; Jiang, H.; Zhou, J.; Zhang, H.; Mukherjee, M. Capacity optimization using augmented lagrange method in intelligent reflecting surface-based MIMO communication systems. China Commun. 2021, 17, 123–138. [Google Scholar] [CrossRef]
- Perović, N.S.; Tran, L.N.; Di Renzo, M.; Flanagan, M.F. Achievable rate optimization for MIMO systems with reconfigurable intelligent surfaces. IEEE Trans. Wirel. Commun. 2021, 20, 3865–3882. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, J.; Zou, Y.; Xie, W.; Liu, Y. Wideband beamforming for RIS assisted near-field communications. IEEE Trans. Wirel. Commun. 2024, 23, 16836–16851. [Google Scholar] [CrossRef]
- Ning, B.; Chen, Z.; Chen, W.; Fang, J. Beamforming optimization for intelligent reflecting surface assisted MIMO: A sum-path-gain maximization approach. IEEE Wirel. Commun. Lett. 2020, 9, 1105–1109. [Google Scholar] [CrossRef]
- Sirojuddin, A.; Putra, D.D.; Huang, W.J. Low-complexity sum-capacity maximization for intelligent reflecting surface-aided MIMO systems. IEEE Wirel. Commun. Lett. 2022, 11, 1354–1358. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, Y.; He, C.; Pan, C.; Wang, K. Energy optimization for IRS-aided SWIPT under imperfect cascaded channels. IEEE Trans. Veh. Technol. 2023, 72, 11631–11643. [Google Scholar] [CrossRef]
- Zhang, H.; Jia, Q.; Han, X.; Yu, H.; Zhao, J. Beamforming Design of IRS-Assisted SWIPT System Based on Deep Reinforcement Learning. IEEE Trans. Ind. Inform. 2024, 21, 733–742. [Google Scholar] [CrossRef]
- He, J.; Yu, K.; Shi, Y. Coordinated passive beamforming for distributed intelligent reflecting surfaces network. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Yin, T.; Li, L.; Lin, W.; Hu, H.; Ma, D.; Liang, J.; Bai, T.; Pan, C.; Han, Z. Joint active and passive beamforming optimization for multi-IRS-assisted wireless communication systems: A covariance matrix adaptation evolution strategy. IEEE Trans. Veh. Technol. 2023, 72, 9281–9292. [Google Scholar] [CrossRef]
- Li, Z.; Hua, M.; Wang, Q.; Song, Q. Weighted sum-rate maximization for multi-IRS aided cooperative transmission. IEEE Wirel. Commun. Lett. 2020, 9, 1620–1624. [Google Scholar] [CrossRef]
- Do, T.N.; Kaddoum, G.; Nguyen, T.L.; Da Costa, D.B.; Haas, Z.J. Multi-RIS-aided wireless systems: Statistical characterization and performance analysis. IEEE Trans. Commun. 2021, 69, 8641–8658. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Z.; Xiong, B.; Dang, J.; Wu, L.; Zhou, J. A 3D stochastic channel model for 6G wireless double-IRS cooperatively assisted MIMO communications. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–5. [Google Scholar]
- Jiang, H.; Xiong, B.; Zhang, H.; Basar, E. Physics-based 3D end-to-end modeling for double-RIS assisted non-stationary UAV-to-ground communication channels. IEEE Trans. Commun. 2023, 71, 4247–4261. [Google Scholar] [CrossRef]
- Lian, Z.; Zhang, W.; Wang, Y.; Su, Y.; Zhang, B.; Jin, B.; Wang, B. Physics-based channel modeling for IRS-assisted mmWave communication systems. IEEE Trans. Commun. 2024, 72, 2687–2700. [Google Scholar] [CrossRef]
- Basar, E. Reconfigurable intelligent surfaces for Doppler effect and multipath fading mitigation. Front. Commun. Netw. 2021, 2, 672857. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, J.H.; Ko, Y.C. Beamforming optimization for IRS-assisted mmWave V2I communication systems via reinforcement learning. IEEE Access 2022, 10, 60521–60533. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, G.; Wu, D.; He, P.; Wang, R.; Liu, Y. RIS-Assisted Unsupervised Beamforming in Internet of Vehicles. IEEE Trans. Veh. Technol. 2024, 74, 1385–1398. [Google Scholar] [CrossRef]
- Ma, Z.; Ai, B.; He, R.; Mi, H.; Yang, M.; Wang, N.; Zhong, Z.; Fan, W. Modeling and analysis of MIMO multipath channels with aerial intelligent reflecting surface. IEEE J. Sel. Areas Commun. 2022, 40, 3027–3040. [Google Scholar] [CrossRef]
- Shabir, M.W.; Nguyen, T.N.; Mirza, J.; Ali, B.; Javed, M.A. Transmit and reflect beamforming for max-min SINR in IRS-aided MIMO vehicular networks. IEEE Trans. Intell. Transp. Syst. 2022, 24, 1099–1105. [Google Scholar] [CrossRef]
- Lian, Z.; Wang, Y.; Su, Y.; Ji, P. A novel beam channel model and capacity analysis for UAV-enabled millimeter-wave communication systems. IEEE Trans. Wirel. Commun. 2023, 23, 3617–3632. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, Q.; Lin, Z.; Chen, J.; Ding, G.; Wu, Q.; Gu, G.; Gao, Q. Sparse bayesian learning-based hierarchical construction for 3D radio environment maps incorporating channel shadowing. IEEE Trans. Wirel. Commun. 2024, 23, 14560–14574. [Google Scholar] [CrossRef]
- Gao, M.; Ai, B.; Niu, Y.; Han, Z.; Zhong, Z. IRS-assisted high-speed train communications: Outage probability minimization with statistical CSI. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Chen, Z.; Guo, Y.; Zhang, P.; Jiang, H.; Xiao, Y.; Huang, L. Physical layer security improvement for hybrid RIS-assisted MIMO communications. IEEE Commun. Lett. 2024, 28, 2493–2497. [Google Scholar] [CrossRef]
- Jiang, H.; Shi, W.; Zhang, Z.; Pan, C.; Wu, Q.; Shu, F.; Liu, R.; Chen, Z.; Wang, J. Large-scale RIS enabled air-ground channels: Near-field modeling and analysis. IEEE Trans. Wirel. Commun. 2024, 24, 1074–1088. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, L.; So, H.C.; Jiang, H.; Zhang, X.Y.; Wang, J. Deep Reinforcement Learning Over RIS-Assisted Integrated Sensing and Communication: Challenges and Opportunities. IEEE Veh. Technol. Mag. 2024, early access. [Google Scholar]
- Ruan, C.; Zhang, Z.; Jiang, H.; Zhang, H.; Dang, J.; Wu, L. Simplified learned approximate message passing network for beamspace channel estimation in mmWave massive MIMO systems. IEEE Trans. Wirel. Commun. 2023, 23, 5142–5156. [Google Scholar] [CrossRef]
- Xing, C.; Jing, Y.; Wang, S.; Ma, S.; Poor, H.V. New viewpoint and algorithms for water-filling solutions in wireless communications. IEEE Trans. Signal Process. 2020, 68, 1618–1634. [Google Scholar] [CrossRef]
- Jiang, H.; Shi, W.; Chen, X.; Zhu, Q.; Chen, Z. High-efficient near-field channel characteristics analysis for large-scale MIMO communication systems. IEEE Internet Things J. 2024, 12, 7446–7458. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Wang, C.X.; Ye, X.; Gomez-Ponce, J.; Cai, X.; Miao, Y.; Cui, Z.; Wu, Q.; Fan, W. A survey on channel sounding technologies and measurements for UAV-assisted communications. IEEE Trans. Instrum. Meas. 2024, 73, 8004624. [Google Scholar] [CrossRef]
- Perović, N.S.; Tran, L.N.; Di Renzo, M.; Flanagan, M.F. On the maximum achievable sum-rate of the RIS-aided MIMO broadcast channel. IEEE Trans. Signal Process. 2023, 70, 6316–6331. [Google Scholar] [CrossRef]
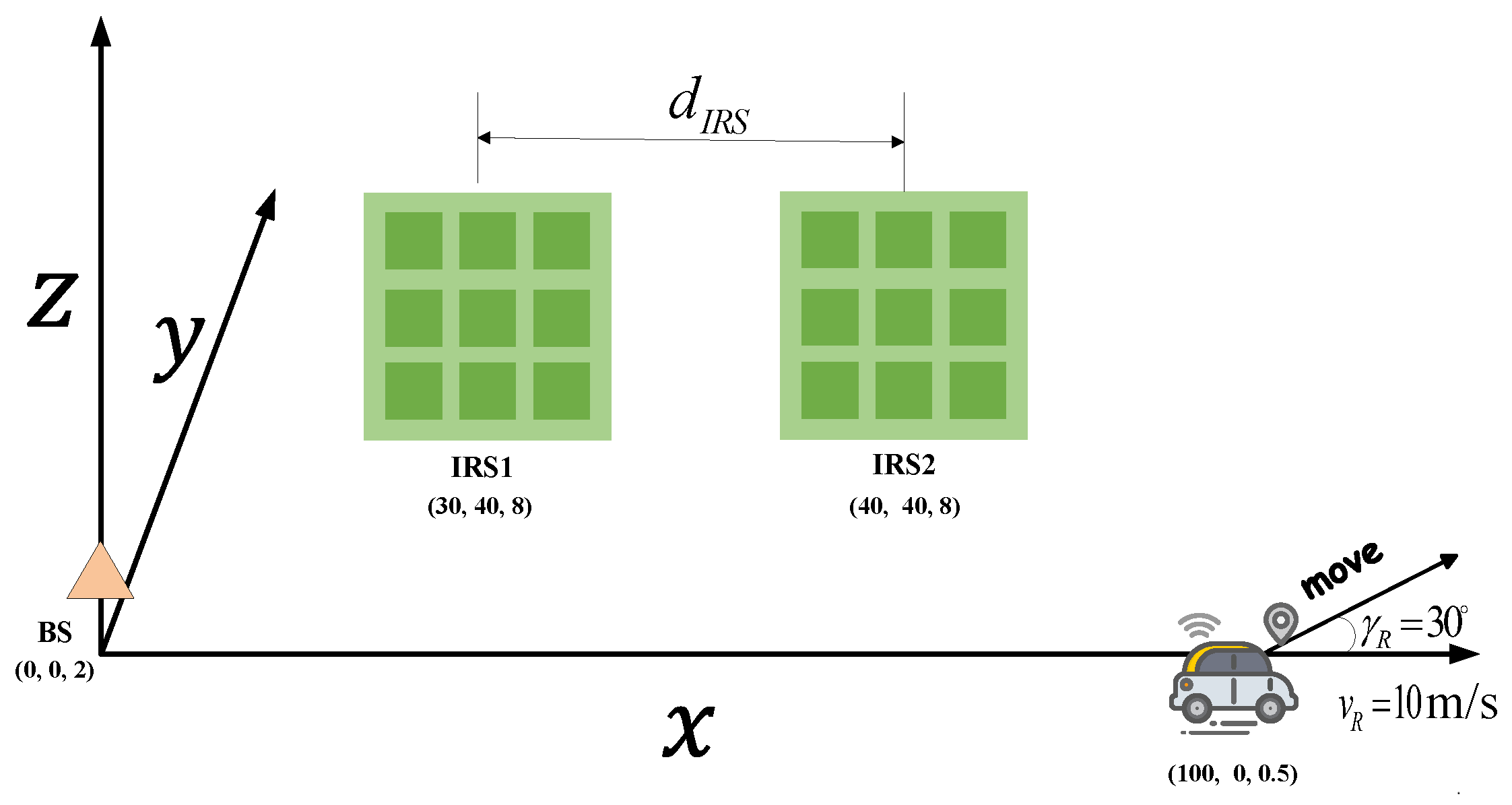







| Literature | System Mode | Method | Consider the Doppler Effects? | Complexity |
|---|---|---|---|---|
| [4] | Single-input–single-output (SISO) | Successive convex approximation (SCA) | No | Modest |
| [8] | MU-MISO | Alternating optimization (AO) | No | High |
| [10,12] | MIMO | AO, Projected gradient | No | High |
| [26] | MIMO | DRL | Yes | High |
| [27] | MU-MISO | Unsupervised learning | Yes | Modest |
| Literature | Method | Complexity |
|---|---|---|
| [7] | Semidefinite relaxation (SDR) | |
| [14] | Alternating direction method of multipliers (ADMM) | |
| This paper | DSM |
| Parameter | Value |
|---|---|
| Carrier frequency: | 2.4 GHz |
| Number of transmit antennas: | 16 |
| Number of receive antennas: | 12 |
| Number of IRSs: | 2 |
| Number of IRS reflection elements: | 64 |
| Antenna and IRS element spacing: | |
| Transmit power at the BS: P | 20 dBm |
| Noise power at the MR: | 0 dBm |
| BS location | (0 m, 0 m, 2 m) |
| IRS1 location | (30 m, 40 m, 8 m) |
| IRS2 location | (40 m, 40 m, 8 m) |
| Reference loss at 1 m: | 30 dB |
| Path-loss exponents: , , and | 3, 2.8, and 2.2 |
| Rician factor: | 4 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Zhou, B.; Zhou, J.; Zhao, Y. Low-Complexity Sum-Rate Maximization for Multi-IRS-Assisted V2I Systems. Electronics 2025, 14, 2750. https://doi.org/10.3390/electronics14142750
Liu Q, Zhou B, Zhou J, Zhao Y. Low-Complexity Sum-Rate Maximization for Multi-IRS-Assisted V2I Systems. Electronics. 2025; 14(14):2750. https://doi.org/10.3390/electronics14142750
Chicago/Turabian StyleLiu, Qi, Beiping Zhou, Jie Zhou, and Yongfeng Zhao. 2025. "Low-Complexity Sum-Rate Maximization for Multi-IRS-Assisted V2I Systems" Electronics 14, no. 14: 2750. https://doi.org/10.3390/electronics14142750
APA StyleLiu, Q., Zhou, B., Zhou, J., & Zhao, Y. (2025). Low-Complexity Sum-Rate Maximization for Multi-IRS-Assisted V2I Systems. Electronics, 14(14), 2750. https://doi.org/10.3390/electronics14142750





