Unsupervised Specific Emitter Identification via Group Label-Driven Contrastive Learning
Abstract
1. Introduction
- A novel unsupervised SEI method based on GLD-CL is proposed. GLD-CL eliminates the need to pre-specify the number of classes and achieves end-to-end SEI without requiring auxiliary datasets or additional hyperparameters.
- The concept of “group label” is introduced by using the continuity of signal timing. Multiple samples obtained from the same signal segment are regarded as having the same implicit label. Using this naturally formed weak supervised information to guide the contrastive learning process, the effective expansion of positive-instance information in the feature space is realized, and the identification performance of unsupervised SEI is improved.
- Extensive experiments conducted on real-world datasets demonstrate the effectiveness of the proposed algorithm. GLD-CL achieves an improvement in identification accuracy ranging from 5.7% to 37.3% compared to baseline algorithms. Furthermore, GLD-CL exhibits robust performance, achieving good identification results across various SNR scenarios.
2. Related Work
3. System Model
3.1. Unsupervised SEI
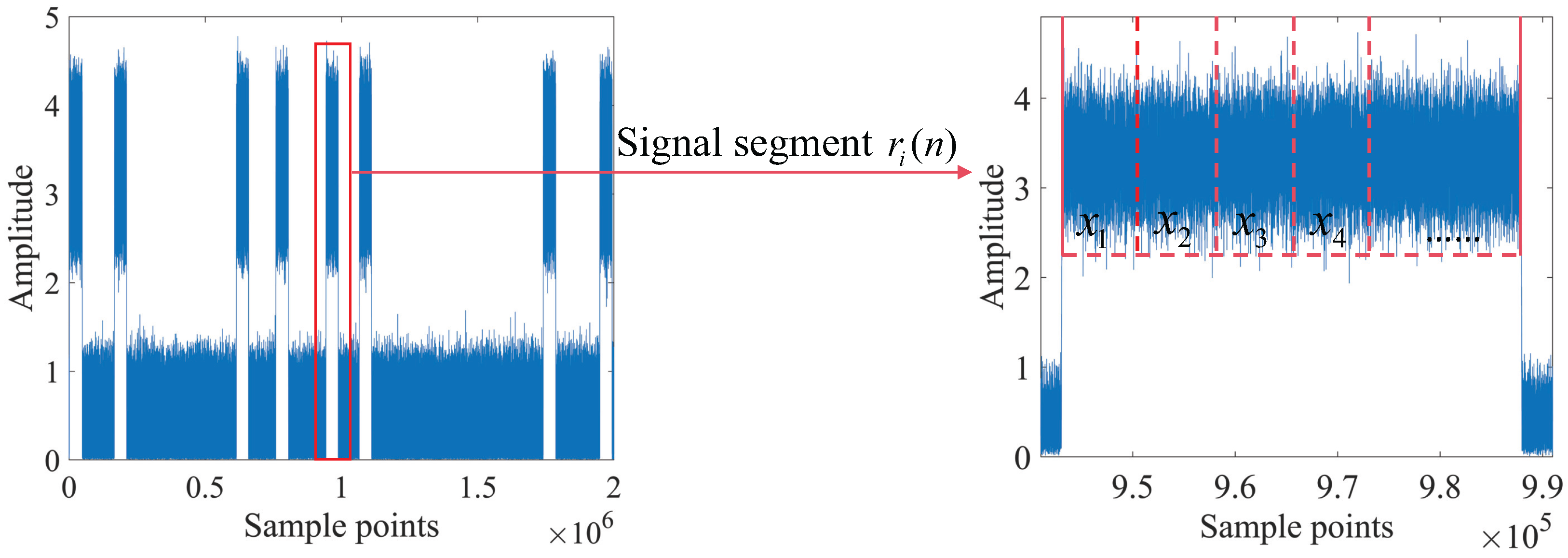
3.2. Group Label
4. Method
4.1. Group Label-Driven Contrastive Learning Framework for Unsupervised SEI
| Algorithm 1 GLD-CL Framework for Unsupervised SEI. |
| Require: Dataset , group labels , feature extractor , projection network , maximum number of training epochs O. Ensure: individual labels for each signal sample // Data augmentation
// Train the feature extractor and the projection network
// Cluster
|
4.1.1. Data Augmentation
4.1.2. Feature Extractor
4.1.3. Projection Network
4.1.4. Cluster
4.2. Data Augmentation
4.2.1. Phase Rotation
4.2.2. Circular Shifting
4.2.3. Random Noise Addition
4.3. Loss Function
4.3.1. SSCL Loss Function
4.3.2. GLD-CL Loss Function
- It can be generalized to multiple positive sample pairs: In contrast to Equation (7), both the augmented samples and all samples sharing the same group label contribute to the numerator. The GLD-CL loss provides tightly aligned representations for all samples with the same group label, reducing the uncertainty between different samples, thereby generating a more robust clustering feature space than the SSCL loss.
- The more negative instances, the stronger the contrastive performance: The denominator of Equation (8) includes the summation of similarities between the anchor and all negative instances, which is consistent with SSCL loss. The more negative instances there are, the more hard negatives are available during contrast, which is more conducive to increasing the distance between the feature vectors of positive and negative instances [27].
- It possesses the ability to mine hard positive/negative instances: Hard positive instances refer to those that share the same label as the anchor but are deemed dissimilar by the model. Hard negative instances, on the other hand, are those that have a different label from the anchor but are incorrectly considered similar by the model. Conversely, samples where the model’s identification aligns with the label are termed easy positive/negative instances. In contrastive learning, mining hard positive/negative instances is crucial for enhancing the model’s discriminative power and generalization ability. Equation (8) inherently possesses the ability to mine hard positive/negative instances without additional strategies. During training, the loss function automatically assigns greater weights to those pairs of samples that are difficult to distinguish (i.e., hard instances), as they contribute more significantly to the loss value.
5. Experiments and Discussion
5.1. Dataset and Data Preprocessing
5.1.1. Dataset
- (1)
- CC2530
- (2)
- ADS-B [29]
5.1.2. Data Preprocessing
5.2. Implementation Details and Evaluation Metrics
5.2.1. Implementation Details
5.2.2. Evaluation Metrics
5.3. Performance Comparison with Existing Methods
- SAE is composed of multiple autoencoder layers stacked together. It learns higher-level features by minimizing the reconstruction error between the input and output of the entire stacked autoencoder.
- DAC recasts the clustering problem into a binary pairwise classification framework to judge whether pairs of images belong to the same clusters.
- DTC first pretrains the model based on an auxiliary dataset, then enhances the model’s feature extraction capabilities using transfer learning and, finally, employs it to cluster samples in the target dataset.
- RFFE-infoGAN uses a GAN to extract distinguishable structured multimodal latent vectors, thereby achieving unsupervised SEI.
- SCSC uses a 1D fingerprint pyramid feature extractor to obtain hierarchical subtle features of emitter signals and generates cluster preference representations in an SSCL manner.
5.4. Component-Wise Ablation Experiment
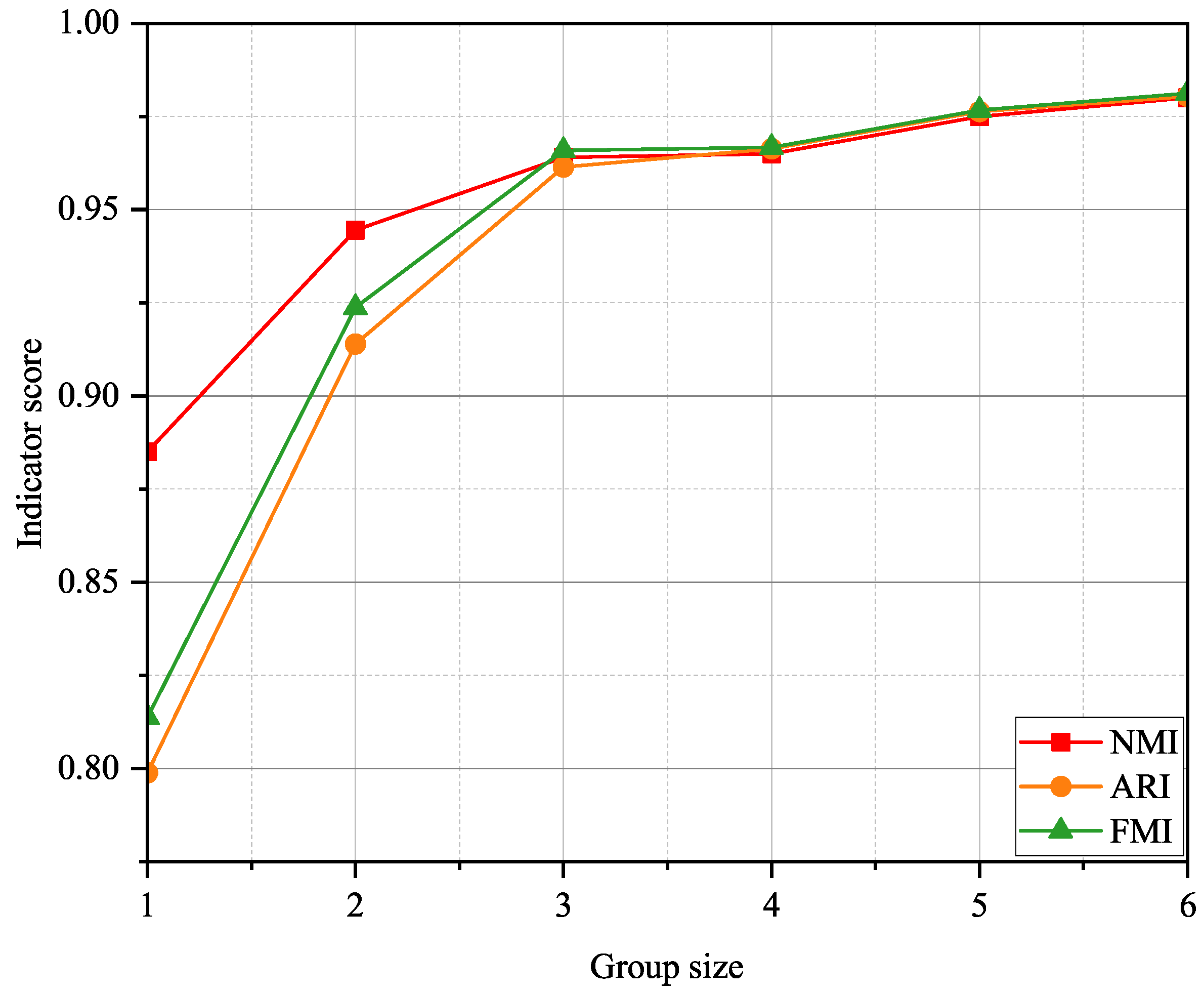
5.5. Performance Comparison of Different Group Sizes
5.6. Performance Comparison Under Different SNRs
5.7. Performance Comparison of Different Sample Lengths
5.8. Performance Comparison of Different Data Augmentation Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Li, D.; Qi, J.; Hong, S.; Deng, P.; Sun, H. A Class-Incremental Approach with Self-Training and Prototype Augmentation for Specific Emitter Identification. IEEE Trans. Inf. Forensics Secur. 2024, 19, 1714–1727. [Google Scholar] [CrossRef]
- Li, D.; Shao, M.; Deng, P.; Hong, S.; Qi, J.; Sun, H. A Self-Supervised-Based Approach of Specific Emitter Identification for the Automatic Identification System. IEEE Trans. Cogn. Commun. Netw. 2024, 1317–1322. [Google Scholar] [CrossRef]
- Sauter, T.; Treytl, A. IoT-Enabled Sensors in Automation Systems and Their Security Challenges. IEEE Sensors Lett. 2023, 7, 1–4. [Google Scholar] [CrossRef]
- Jiang, H.; Shi, W.; Chen, X.; Zhu, Q.; Chen, Z. High-Efficient Near-Field Channel Characteristics Analysis for Large-Scale MIMO Communication Systems. IEEE Internet Things J. 2025, 12, 7446–7458. [Google Scholar] [CrossRef]
- Jiang, H.; Shi, W.; Zhang, Z.; Pan, C.; Wu, Q.; Shu, F.; Liu, R.; Chen, Z.; Wang, J. Large-Scale RIS Enabled Air-Ground Channels: Near-Field Modeling and Analysis. IEEE Trans. Wirel. Commun. 2025, 24, 1074–1088. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Y.; Zhang, P.; Jiang, H.; Xiao, Y.; Huang, L. Physical Layer Security Improvement for Hybrid RIS-Assisted MIMO Communications. IEEE Commun. Lett. 2024, 28, 2493–2497. [Google Scholar] [CrossRef]
- Robyns, P.; Marin, E.; Lamotte, W.; Quax, P.; Singelée, D.; Preneel, B. Physical-Layer Fingerprinting of LoRa Devices Using Supervised and Zero-Shot Learning. In Proceedings of the 10th ACM Conference on Security and Privacy in Wireless and Mobile Networks, Boston, MA, USA, 18–20 July 2017; pp. 58–63. [Google Scholar]
- Shen, G.; Zhang, J.; Marshall, A.; Woods, R.; Cavallaro, J.; Chen, L. Towards Receiver-Agnostic and Collaborative Radio Frequency Fingerprint Identification. IEEE Trans. Mob. Comput. 2022, 23, 7618–7634. [Google Scholar] [CrossRef]
- Shen, G.; Zhang, J.; Marshall, A.; Cavallaro, J.R. Towards Scalable and Channel-Robust Radio Frequency Fingerprint Identification for LoRa. IEEE Trans. Inf. Forensics Secur. 2022, 17, 774–787. [Google Scholar] [CrossRef]
- Shen, G.; Zhang, J.; Marshall, A.; Valkama, M.; Cavallaro, J.R. Toward Length-Versatile and Noise-Robust Radio Frequency Fingerprint Identification. IEEE Trans. Inf. Forensics Secur. 2023, 18, 2355–2367. [Google Scholar] [CrossRef]
- Roy, D.; Mukherjee, T.; Chatterjee, M.; Pasiliao, E. RF Transmitter Fingerprinting Exploiting Spatio-Temporal Properties in Raw Signal Data. In Proceedings of the 18th IEEE International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; pp. 89–96. [Google Scholar]
- Shen, G.; Zhang, J.; Marshall, A.; Peng, L.; Wang, X. Radio Frequency Fingerprint Identification for LoRa Using Deep Learning. IEEE J. Sel. Areas Commun. 2021, 39, 2604–2616. [Google Scholar] [CrossRef]
- Wang, Y.; Gui, G.; Gacanin, H.; Ohtsuki, T.; Dobre, O.A.; Poor, H.V. An Efficient Specific Emitter Identification Method Based on Complex-Valued Neural Networks and Network Compression. IEEE J. Sel. Areas Commun. 2021, 39, 2305–2317. [Google Scholar] [CrossRef]
- Zha, X.; Li, T.; Gong, P. Unsupervised Radio Frequency Fingerprint Identification Based on Curriculum Learning. IEEE Commun. Lett. 2023, 27, 1170–1174. [Google Scholar] [CrossRef]
- Shen, G.; Zhang, J.; Wang, X.; Mao, S. Federated Radio Frequency Fingerprint Identification Powered by Unsupervised Contrastive Learning. IEEE Trans. Inf. Forensics Secur. 2024, 19, 9204–9215. [Google Scholar] [CrossRef]
- Hao, X.; Feng, Z.; Liu, R.; Yang, S.; Jiao, L.; Luo, R. Contrastive Self-Supervised Clustering for Specific Emitter Identification. IEEE Internet Things J. 2023, 10, 20803–20818. [Google Scholar] [CrossRef]
- Roy, D.; Mukherjee, T.; Chatterjee, M.; Pasiliao, E. Detection of Rogue RF Transmitters Using Generative Adversarial Nets. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–7. [Google Scholar]
- Sui, P.; Guo, Y.; Li, H.; Wang, S.; Yang, X. Frequency-Hopping Signal Radio Sorting Based on Stacked Auto-encoder Subtle Feature Extraction. In Proceedings of the 2019 IEEE 2nd International Conference on Electronic Information and Communication Technology (ICEICT), Harbin, China, 20–22 January 2019; pp. 24–28. [Google Scholar]
- Zha, X.; Li, T.; Qiu, Z.; Li, F. Cross-Receiver Radio Frequency Fingerprint Identification Based on Contrastive Learning and Subdomain Adaptation. IEEE Signal Process. Lett. 2023, 30, 70–74. [Google Scholar] [CrossRef]
- Wang, G.; Hu, S.; Yu, T.; Hu, J. A Novel Semi-Supervised Learning-Based RF Fingerprinting Method Using Masked-Contrastive Training. In Proceedings of the 2023 International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 2–4 November 2023; pp. 749–754. [Google Scholar]
- Wu, Z.; Wang, F.; He, B. Specific Emitter Identification via Contrastive Learning. IEEE Commun. Lett. 2023, 27, 1160–1164. [Google Scholar] [CrossRef]
- Zahid, M.U.; Nisar, M.D.; Shah, M.H.; Hussain, S.A. Specific Emitter Identification Based on Multi-Scale Multi-Dimensional Approximate Entropy. IEEE Signal Process. Lett. 2024, 31, 850–854. [Google Scholar] [CrossRef]
- Ye, K.; Huang, Z.; Xiong, Y.; Gao, Y.; Xie, J.; Shen, L. Progressive Pseudo Labeling for Multi-Dataset Detection over Unified Label Space. IEEE Trans. Multimed. 2025, 27, 531–543. [Google Scholar] [CrossRef]
- Han, L.; Zheng, K.; Zhao, L.; Wang, X.; Shen, X. Short-Term Traffic Prediction Based on DeepCluster in Large-Scale Road Networks. IEEE Trans. Veh. Technol. 2019, 68, 12301–12313. [Google Scholar] [CrossRef]
- Xiao, Y.; Liang, F.; Liu, B. A Transfer Learning-Based Multi-Instance Learning Method with Weak Labels. IEEE Trans. Cybern. 2022, 52, 287–300. [Google Scholar] [CrossRef]
- Wang, X.; Qi, G.J. Contrastive Learning with Stronger Augmentations. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 5549–5560. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Xu, D.; Alfarraj, O.; Yu, K.; Guizani, M.; Rodrigues, J.J.P.C. Design of Tiny Contrastive Learning Network with Noise Tolerance for Unauthorized Device Identification in Internet of UAVs. IEEE Internet Things J. 2024, 11, 20912–20929. [Google Scholar] [CrossRef]
- IEEE 802.15.4; IEEE Standard for Local and Metropolitan Area Networks—Part 15.4: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless Personal Area Networks (LR-WPANs). IEEE: New York, NY, USA, 2020.
- Fu, X.; Peng, Y.; Liu, Y.; Lin, Y.; Gui, G.; Gacanin, H.; Adachi, F. Semi-Supervised Specific Emitter Identification Method Using Metric-Adversarial Training. IEEE Internet Things J. 2023, 10, 10778–10789. [Google Scholar] [CrossRef]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 1 January 1967; pp. 281–297. [Google Scholar]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN Revisited, Revisited: Why and How You Should Still Use DBSCAN. ACM Trans. Database Syst. 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Chang, J.; Wang, L.; Meng, G.; Xiang, S.; Pan, C. Deep Adaptive Image Clustering. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5880–5888. [Google Scholar]
- Xuan, Q.; Li, X.; Chen, Z.; Xu, D.; Zheng, S.; Yang, X. Deep Transfer Clustering of Radio Signals. arXiv 2021, arXiv:2107.12237. [Google Scholar]
- Gong, J.; Xu, X.; Lei, Y. Unsupervised Specific Emitter Identification Method Using Radio-Frequency Fingerprint Embedded InfoGAN. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2898–2913. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Repretations. In Proceedings of the 37th International Conference on Machine Learning (ICML), Virtual, 13–18 July 2020; Volume 119, pp. 1597–1607. [Google Scholar]



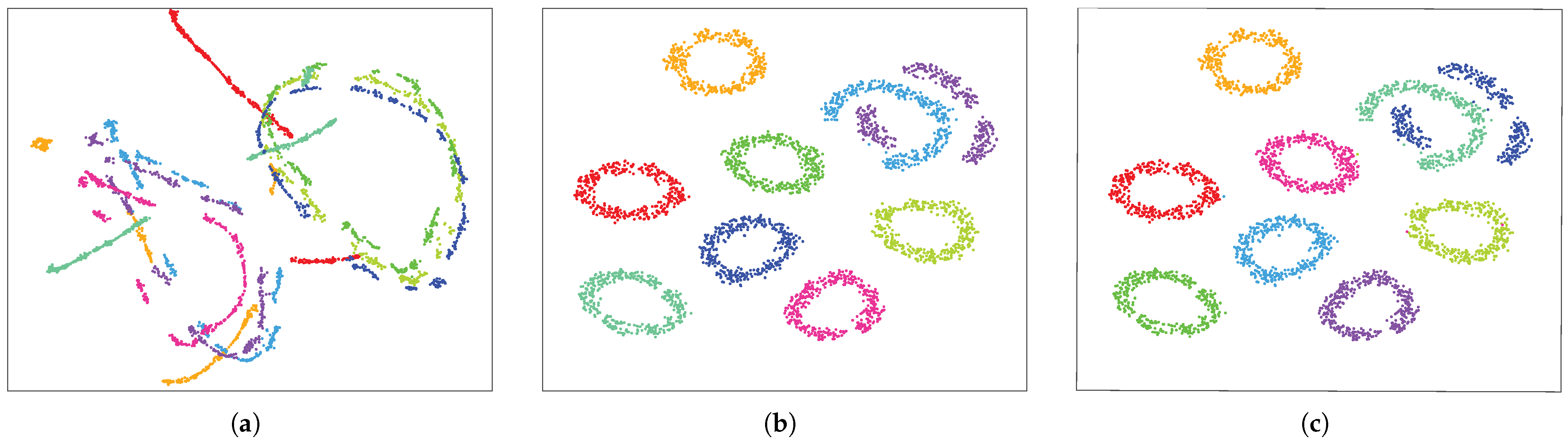

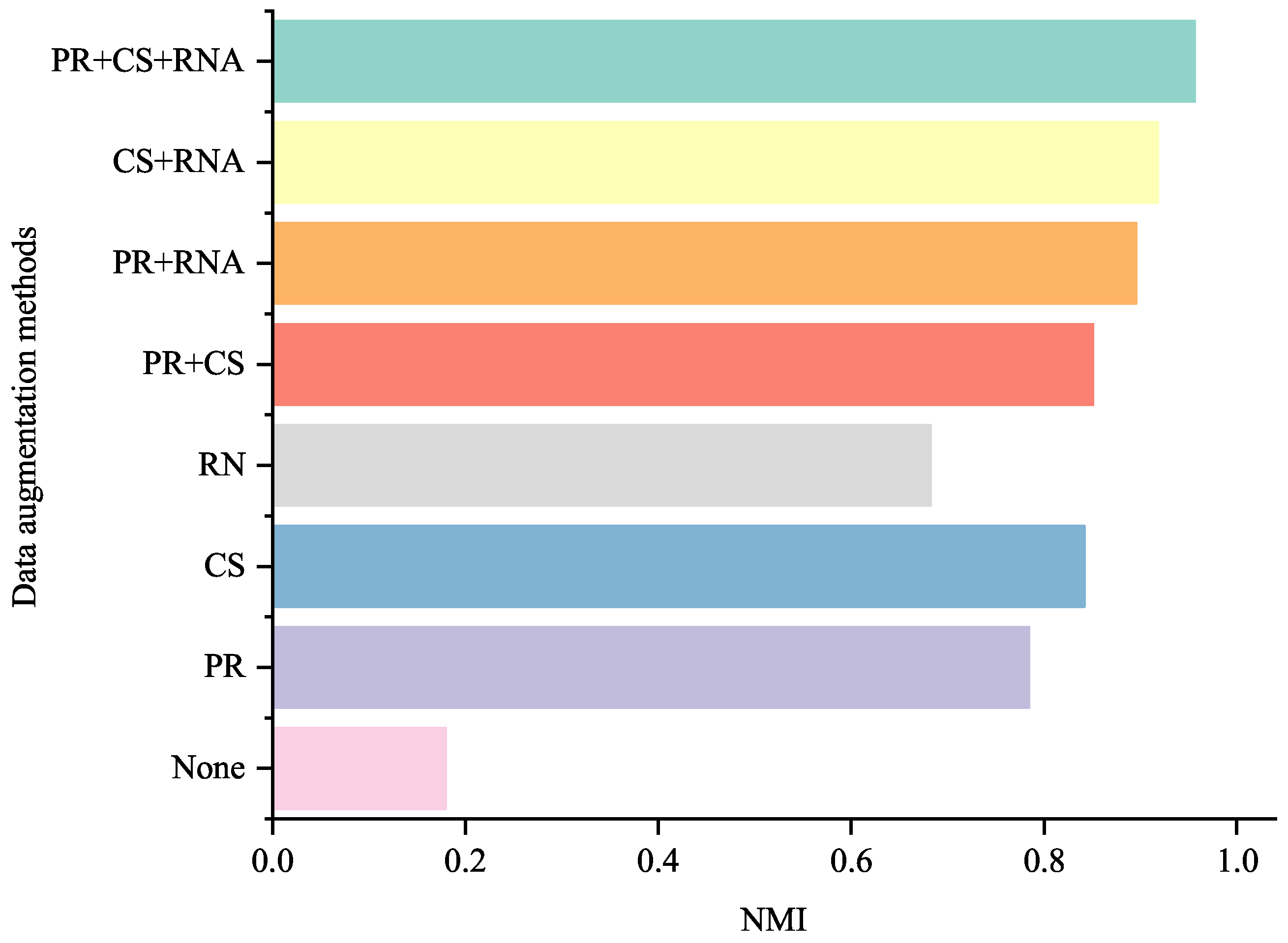
| Hyperparameter | Value |
|---|---|
| Batch size | 1024 |
| Learning rate | 0.0003 |
| Learning rate schedule | StepLR |
| Optimizer | Adam |
| Group size (default) | 3 |
| Input sample length (default) | 2 × 1024 |
| Dataset | Method | NMI | ARI | FMI |
|---|---|---|---|---|
| CC2530 | K-means | 0.1817 | 0.2525 | 0.3609 |
| DBSCAN | 0.3859 | 0.3331 | 0.4706 | |
| SAE | 0.5909 | 0.3939 | 0.5913 | |
| DAC | 0.7421 | 0.5755 | 0.6587 | |
| DTC | 0.8122 | 0.7043 | 0.7048 | |
| RFFE-infoGAN | 0.8846 | 0.7379 | 0.7916 | |
| SCSC | 0.9072 | 0.9053 | 0.9155 | |
| SSCL+k-means | 0.8487 | 0.7315 | 0.7658 | |
| SSCL+DBSCAN | 0.8851 | 0.7989 | 0.8138 | |
| GLD-CL+k-means (ours) | 0.8592 | 0.7269 | 0.7694 | |
| GLD-CL+DBSCAN (ours) | 0.9641 1 | 0.9614 | 0.9659 | |
| ADS-B | K-means | 0.1468 | 0.1837 | 0.2713 |
| DBSCAN | 0.3068 | 0.2643 | 0.3875 | |
| SAE | 0.4952 | 0.3141 | 0.4721 | |
| DAC | 0.6475 | 0.4578 | 0.5382 | |
| DTC | 0.7393 | 0.6015 | 0.6224 | |
| RFFE-infoGAN | 0.8032 | 0.6462 | 0.6947 | |
| SCSC | 0.8724 | 0.8509 | 0.8691 | |
| SSCL+k-means | 0.7789 | 0.6381 | 0.6818 | |
| SSCL+DBSCAN | 0.8143 | 0.7037 | 0.7354 | |
| GLD-CL+k-means (ours) | 0.8353 | 0.7148 | 0.7278 | |
| GLD-CL+DBSCAN (ours) | 0.9286 | 0.9255 | 0.9229 |
| Model Configuration | NMI | |
|---|---|---|
| GLD-CL Loss Function | Data Augmentation | |
| √ | 0.8851 | |
| √ | 0.1912 | |
| √ | √ | 0.9641 |
| Sample Length | NMI | ARI | FMI |
|---|---|---|---|
| 128 | 0.594 | 0.3674 | 0.4167 |
| 256 | 0.7043 | 0.5726 | 0.6714 |
| 512 | 0.7844 | 0.6397 | 0.7115 |
| 1024 | 0.964 1 | 0.9614 | 0.9659 |
| 2048 | 0.9504 | 0.9594 | 0.9526 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, N.; Zhang, B.; Guo, D. Unsupervised Specific Emitter Identification via Group Label-Driven Contrastive Learning. Electronics 2025, 14, 2136. https://doi.org/10.3390/electronics14112136
Yang N, Zhang B, Guo D. Unsupervised Specific Emitter Identification via Group Label-Driven Contrastive Learning. Electronics. 2025; 14(11):2136. https://doi.org/10.3390/electronics14112136
Chicago/Turabian StyleYang, Ning, Bangning Zhang, and Daoxing Guo. 2025. "Unsupervised Specific Emitter Identification via Group Label-Driven Contrastive Learning" Electronics 14, no. 11: 2136. https://doi.org/10.3390/electronics14112136
APA StyleYang, N., Zhang, B., & Guo, D. (2025). Unsupervised Specific Emitter Identification via Group Label-Driven Contrastive Learning. Electronics, 14(11), 2136. https://doi.org/10.3390/electronics14112136





