Research on Circulating-Current Suppression Strategy of MMC Based on Passivity-Based Integral Sliding Mode Control for Multiphase Wind Power Grid-Connected Systems
Abstract
1. Introduction
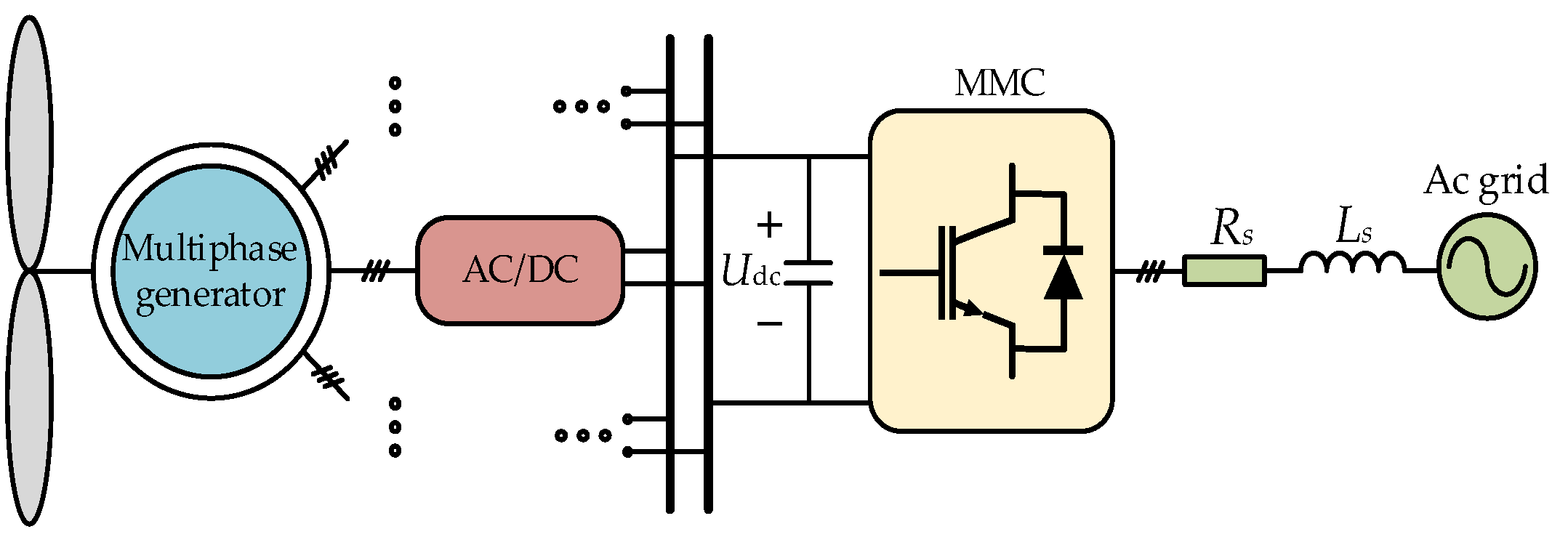
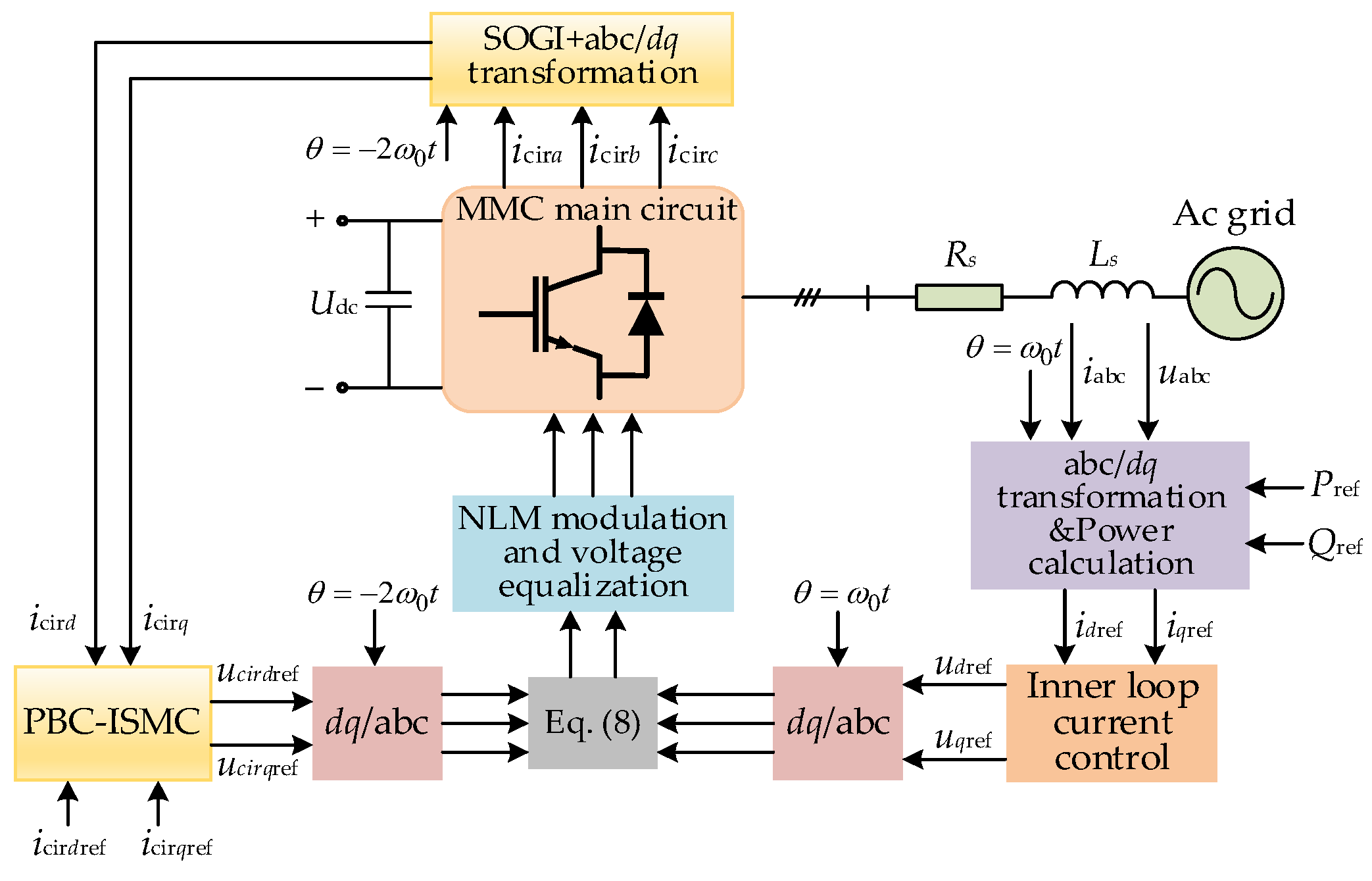
2. Structure and Mathematical Model of MMC-Based Multiphase Wind Power Generation System
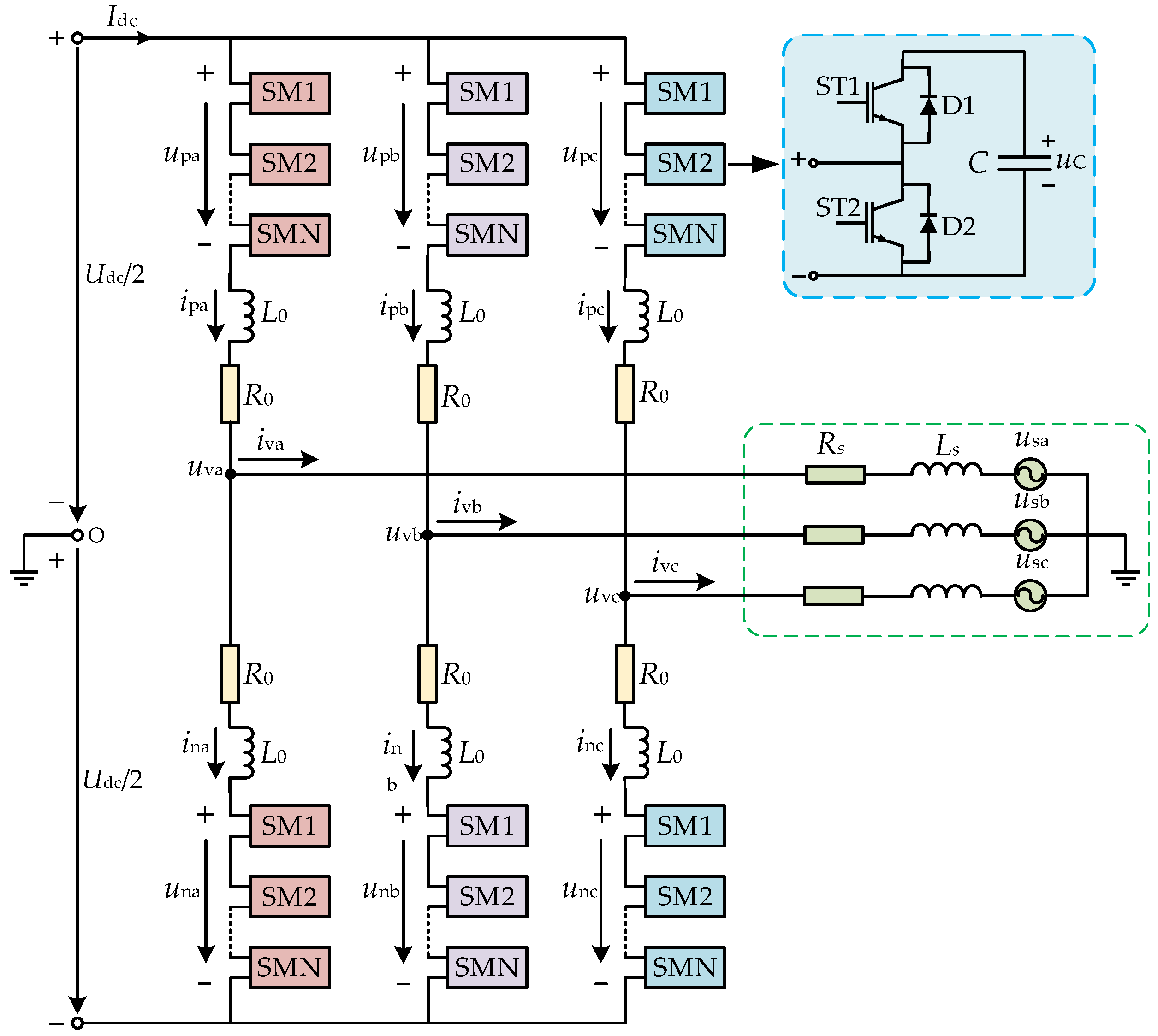
2.1. System Topology
2.2. Mathematical Modeling of Grid-Connected MMC and Analysis of Internal Circulation Generation Mechanism
3. Study of Circulation Suppression Strategies
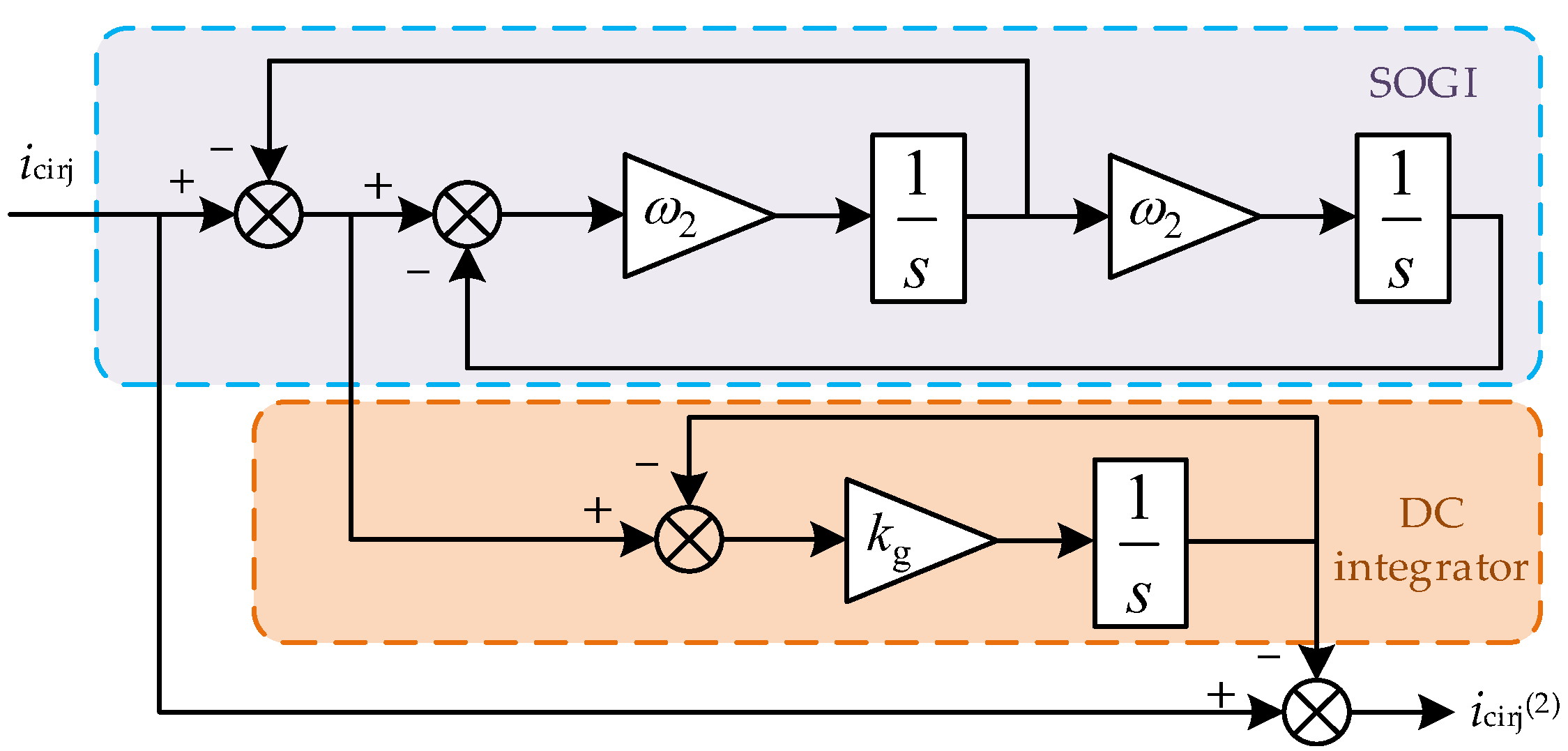
3.1. SOGI-Based Extraction of Twofold Frequency Circulating-Current Components
3.2. Passivity Analysis of MMC Circulation Models
3.3. Passive-Integral Sliding Mode Circulation Suppressor Design
3.4. MMC Output Current and Outer-Loop Power Control
4. Simulation Analysis
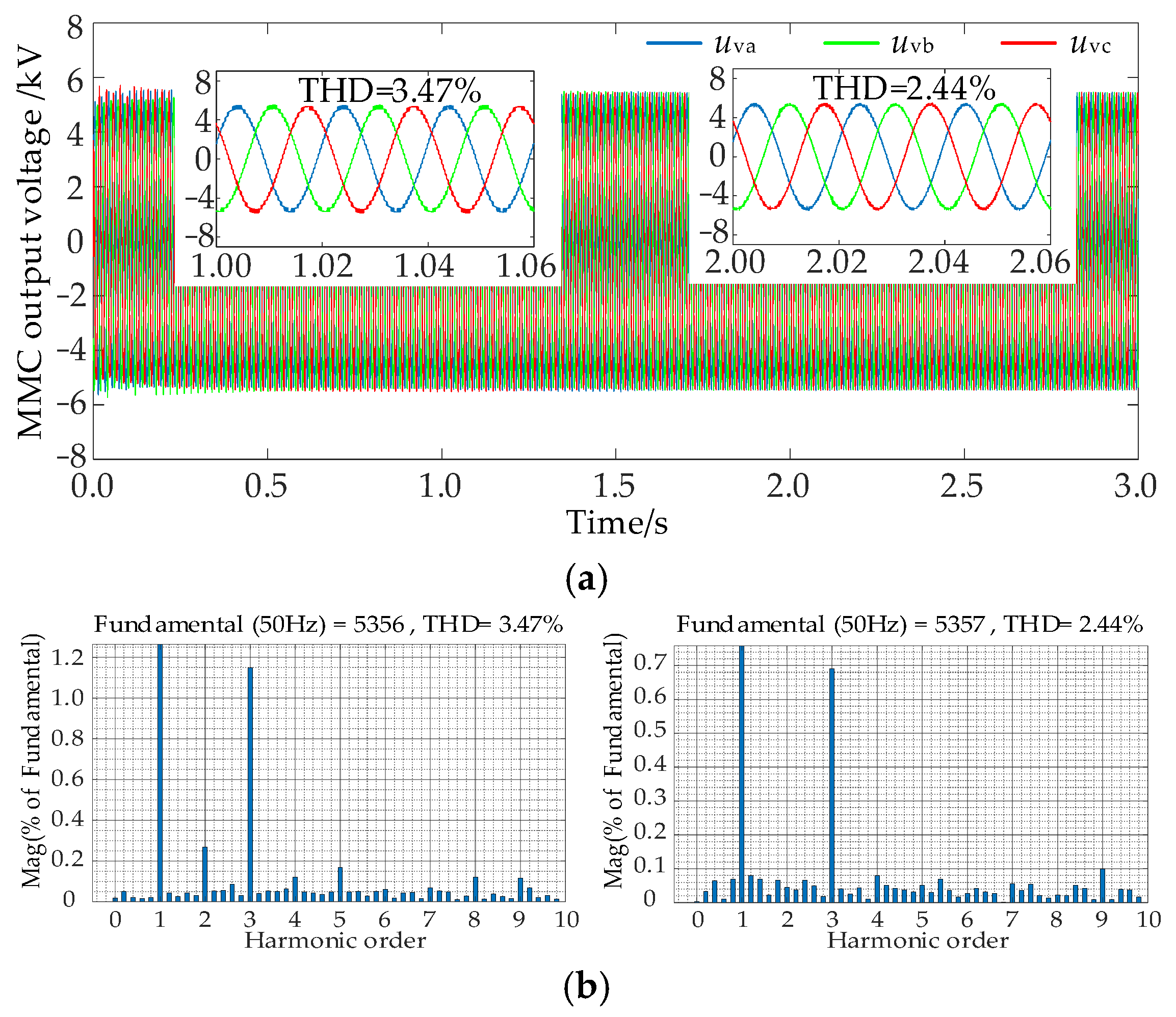
4.1. Output Comparison Before and After Activation of Circulation Suppression
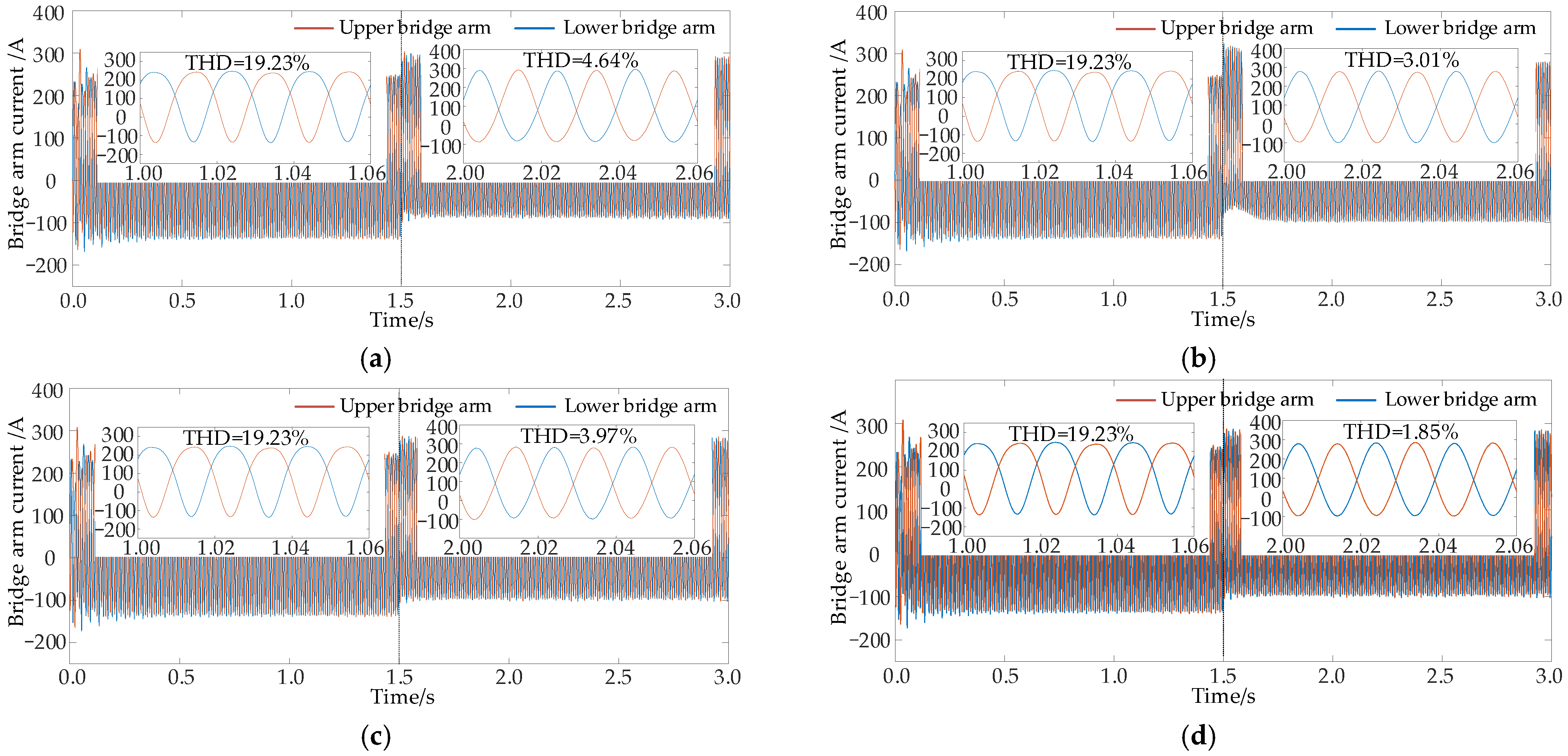
4.2. Performance Comparison with the Traditional Suppression Strategy
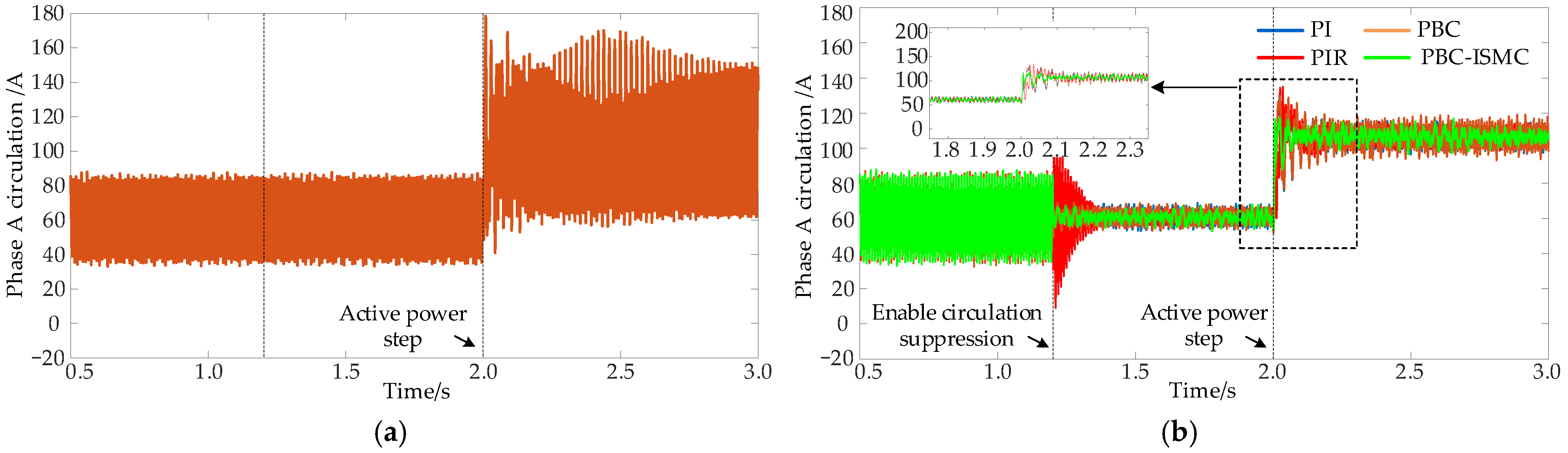
4.3. Comparison of Circulation Suppression Effect When Active Power Changes Abruptly
5. Discussion
6. Conclusions
- (1)
- The proposed circulating-current suppression scheme effectively suppresses the circulating current inside the MMC. It optimizes the terminal voltage and current of the MMC, and the total harmonic distortion (THD) of the output voltage and current is reduced from 3.47% and 1.38% to 2.44% and 0.86%, respectively, after activating the circulating-current suppressor. Reducing its harmonic distortion rate also suppresses the power output pulsations and oscillations.
- (2)
- Compared with the traditional PI, PIR, and single passive control, the strategy proposed in this paper is more effective in suppressing the circulating current, and reduces the circulating-current THD to 3.43%, of which the twofold frequency component is reduced to 1.23%. Compared to the case without suppression, the proposed control strategy reduces the circulating-current THD by 44.62% and the twofold frequency component by 37.51%. Meanwhile, the bridge arm current waveform quality is also significantly improved, with its THD reduced from 19.23% to 1.85% after enabling circulating-current suppression, verifying its superiority in suppressing circulating current and enhancing power quality.
- (3)
- Under dynamic disturbances such as sudden changes in active power, the PBC-ISMC control strategy shows stronger robustness and dynamic adaptability, and the system output is more stable and reliable.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, Q.; Wang, X.; Yuan, J.; Liu, X.; Hu, H.; Lin, P. A review of the development of key technologies for offshore wind power in China. J. Mar. Sci. Eng. 2022, 10, 929. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Lu, J.; Zhang, X.; Wang, K.; Gan, Z.; Liu, X.; Jing, Z.; Cui, X.; Wang, H. Advances in urban wind resource development and wind energy harvesters. Renew. Sustain. Energy Rev. 2025, 207, 114943. [Google Scholar] [CrossRef]
- Chen, H.; Zuo, Y.; Chau, K.T.; Zhao, W.; Lee, C.H.T. Modern electric machines and drives for wind power generation: A review of opportunities and challenges. IET Renew. Power Gener. 2021, 15, 1864–1887. [Google Scholar] [CrossRef]
- Tiismus, H.; Maask, V.; Astapov, V.; Korõtko, T.; Rosin, A. State-of-the-Art Review of Emerging Trends in Renewable Energy Generation Technologies. IEEE Access 2025, 13, 10820–10843. [Google Scholar] [CrossRef]
- Qian, T.; Yao, L. Research on Power Quality Assessment of Wind Power Grid-Connected Systems Based on Game Theory Combination Weighting. Electronics 2025, 14, 1500. [Google Scholar] [CrossRef]
- Cavus, M. Advancing Power Systems with Renewable Energy and Intelligent Technologies: A Comprehensive Review on Grid Transformation and Integration. Electronics 2025, 14, 1159. [Google Scholar] [CrossRef]
- Catalán, P.; Wang, Y.; Arza, J.; Chen, Z. A comprehensive overview of power converter applied in high-power wind turbine: Key challenges and potential solutions. IEEE Trans. Power Electron. 2023, 38, 6169–6195. [Google Scholar] [CrossRef]
- Xue, T.; Lyu, J.; Wang, H.; Cai, X. A complete impedance model of a PMSG-based wind energy conversion system and its effect on the stability analysis of MMC-HVDC connected offshore wind farms. IEEE Trans. Energy Convers. 2021, 36, 3449–3461. [Google Scholar] [CrossRef]
- Mussetta, M.; Le, X.C.; Trinh, T.H.; Doan, A.T.; Duong, M.Q.; Tanasiev, G.N. An Overview of the Multilevel Control Scheme Utilized by Microgrids. Energies 2024, 17, 3947. [Google Scholar] [CrossRef]
- Peng, X.; Liu, Z.; Jiang, D. A review of multiphase energy conversion in wind power generation. Renew. Sustain. Energy Rev. 2021, 147, 111172. [Google Scholar] [CrossRef]
- Zhao, T.; Wu, S.; Cui, S. Multiphase PMSM with asymmetric windings for more electric aircraft. IEEE Trans. Transp. Electrif. 2020, 6, 1592–1602. [Google Scholar] [CrossRef]
- Rao, Z.; Zhang, Z.; Huang, S.; Long, Z.; Wu, G. Characteristics and current harmonic control of N* three-phase PMSG for HVDC transmission Based on MMC. Energies 2020, 13, 178. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Ebraheem, T.; Aljendy, R.; Sultan, H.M.; Ali, Z.M. Optimal design and control of MMC STATCOM for improving power quality indicators. Appl. Sci. 2020, 10, 2490. [Google Scholar] [CrossRef]
- Kok, C.L.; Tang, H.; Teo, T.H.; Koh, Y.Y. A DC-DC Converter with Switched-Capacitor Delay Deadtime Controller and Enhanced Unbalanced-Input Pair Zero-Current Detector to Boost Power Efficiency. Electronics 2024, 13, 1237. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, C.; Cao, K.; Yang, X.; Mao, W.; Jiang, J. Research on high-voltage large-capacity modular multilevel converter (MMC) system. In Proceedings of the 2012 Second International Conference on Intelligent System Design and Engineering Application, Sanya, China, 6–7 January 2012; IEEE: New York, NY, USA, 2012; pp. 1470–1474. [Google Scholar]
- Gomis-Bellmunt, O.; Sau-Bassols, J.; Prieto-Araujo, E.; Cheah-Mane, M. Flexible converters for meshed HVDC grids: From flexible AC transmission systems (FACTS) to flexible DC grids. IEEE Trans. Power Deliv. 2019, 35, 2–15. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Zhang, X.; Liu, C.; Liu, Z.; Luo, B. A Hybrid Low Capacitance Modular Multilevel Converter for Medium Voltage PMSM Drive and Its Control Method. IEEE Access 2023, 11, 92796–92806. [Google Scholar] [CrossRef]
- Zhang, Q.N.; Zhang, Z.R.; Jin, Y.Q.; Xu, Z. DC transmission system suitable for ultra-large-scale offshore wind power grid-connected system. Electr. Power Autom. Equip. 2025, 45, 106–114. (In Chinese) [Google Scholar]
- Zuo, T.; Zhang, Y.; Xie, X.; Meng, K.; Tong, Z.; Dong, Z.Y.; Jia, Y. A review of optimization technologies for large-scale wind farm planning with practical and prospective concerns. IEEE Trans. Ind. Inform. 2022, 19, 7862–7875. [Google Scholar] [CrossRef]
- Mastoi, M.S.; Zhuang, S.; Haris, M.; Hassan, M.; Ali, A. Large-scale wind power grid integration challenges and their solution: A detailed review. Environ. Sci. Pollut. Res. 2023, 30, 103424–103462. [Google Scholar] [CrossRef]
- Wickramasinghe, H.R.; Konstantinou, G.; Pou, J.; Agelidis, V.G. Interactions between indirect DC-voltage estimation and circulating current controllers of MMC-based HVDC transmission systems. IEEE Trans. Power Syst. 2017, 33, 829–838. [Google Scholar] [CrossRef]
- Hui, L.; Peng, Z.; Sijia, L. Transient analysis of MMC circulating current suppression strategy. Power Syst. Prot. Control. 2021, 49, 30–38. (In Chinese) [Google Scholar]
- Reddy, G.A.; Shukla, A. Circulating current optimization control of MMC. IEEE Trans. Ind. Electron. 2020, 68, 2798–2811. [Google Scholar] [CrossRef]
- Tu, Q.; Xu, Z.; Guan, M.; Zheng, X.; Zhang, J. Design of circulating current suppressing controllers for modular multi-level converter. Autom. Electr. Power Syst. 2010, 34, 57–61. (In Chinese) [Google Scholar]
- Tu, Q.; Xu, Z.; Xu, L. Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters. IEEE Trans. Power Deliv. 2011, 26, 2009–2017. [Google Scholar]
- Yang, X.F.; Zheng, Q.L. A novel universal circulating current suppressing strategy based on the MMC circulating current model. Proc. CSEE 2012, 32, 59–65. (In Chinese) [Google Scholar]
- Ban, M.F.; Shen, K.; Wang, J.Z. A Novel Circulating Current Suppressor for Modular Multilevel Converters Based on Quasi-proportional-resonant Control. Autom. Electr. Power Syst. 2014, 38, 85–89. (In Chinese) [Google Scholar]
- Yuan, B.; Xu, J.; Zhao, C.; He, Z.P.; Pang, H.; Ma, W. Optimal design of pr circulating current suppressing controllers for modular multilevel converters. Proc. CSEE 2015, 35, 2567–2575. (In Chinese) [Google Scholar]
- Yan, F.Y.; Tang, G.F.; He, Z.Y. A novel circulating current controller for modular multilevel converter. Proc. CSEE 2014, 38, 104–109. (In Chinese) [Google Scholar]
- He, L.; Zhang, K.; Xiong, J.; Fan, S. A repetitive control scheme for harmonic suppression of circulating current in modular multilevel converters. IEEE Trans. Power Electron. 2014, 30, 471–481. [Google Scholar] [CrossRef]
- Konstantinou, G.; Pou, J.; Ceballos, S.; Picas, R.; Zaragoza, J.; Agelidis, V.G. Control of circulating currents in modular multilevel converters through redundant voltage levels. IEEE Trans. Power Electron. 2015, 31, 7761–7769. [Google Scholar] [CrossRef]
- Chen, X.; Liu, J.; Song, S.; Ouyang, S. Circulating harmonic currents suppression of level-increased NLM based modular multilevel converter with deadbeat control. IEEE Trans. Power Electron. 2020, 35, 11418–11429. [Google Scholar] [CrossRef]
- Ma, K.; Li, E.; He, B.; Cai, X. Mechanism and cancellation of DC current fluctuation in MMC excited by circulating current mitigation under nearest level control. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6822–6831. [Google Scholar] [CrossRef]
- Reddy, G.A.; Shukla, A. Arm-current-sensorless circulating current control of MMC. IEEE Trans. Ind. Appl. 2021, 58, 444–456. [Google Scholar] [CrossRef]
- Yang, X.; Li, Z.; Zheng, T.Q.; You, X.; Kobrle, P. Virtual impedance sliding mode control-based MMC circulating current suppressing strategy. IEEE Access 2019, 7, 26229–26240. [Google Scholar] [CrossRef]
- Priya, M.; Ponnambalam, P. Circulating current control of phase-shifted carrier-based modular multilevel converter fed by fuel cell employing fuzzy logic control technique. Energies 2022, 15, 6008. [Google Scholar] [CrossRef]
- Bergna-Diaz, G.; Zonetti, D.; Sanchez, S.; Ortega, R.; Tedeschi, E. PI passivity-based control and performance analysis of MMC multiterminal HVDC systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 2453–2466. [Google Scholar] [CrossRef]
- Wang, X.G.; Wang, H.L.; Xue, X.; Li, X.Y. Grid-connected current control for MMC-MG adopting nonlinear passive theory. J. Control. Theory Appl. 2022, 39, 1541–1550. (In Chinese) [Google Scholar]
- Aghahadi, M.; Piegari, L.; Lekić, A.; Shetgaonkar, A. Sliding mode control of the mmc-based power system. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; IEEE: New York, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Komurcugil, H.; Biricik, S.; Bayhan, S.; Zhang, Z. Sliding mode control: Overview of its applications in power converters. IEEE Ind. Electron. Mag. 2020, 15, 40–49. [Google Scholar] [CrossRef]



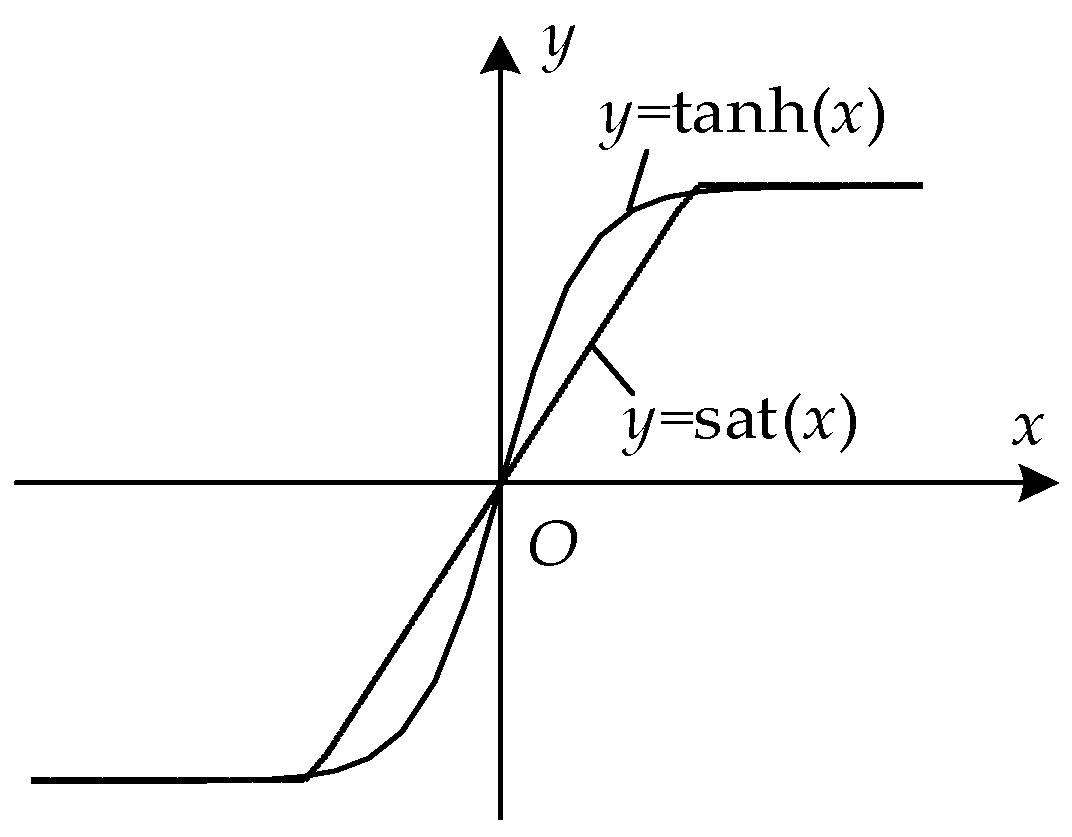




| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Grid-connected active power | 3 MW | Submodule capacitance | 4.7 mF |
| DC voltage | 11 kV | Bridge arm resistance | 0.002 mΩ |
| Effective value of AC side line voltage | 6.6 kV | Bridge arm inductance | 15 mH |
| The number of bridge arm submodules | 22 | Rated grid frequency | 50 Hz |
| Control Method | Parameter |
|---|---|
| PI | Kp = 58.5, Ki = 8.5 |
| PIR | Kp = 12.4, Ki = 0.18, Kr = 32 |
| PBC | Ra1 = Ra2 = 35 |
| PBC-ISMC | Ra1 = Ra2 = 200, kp1 = kp2 = 2.8, ki1 = ki2 = 0.078, λ1 = λ2 = 9000, k1 = k2 = 480 |
| Suppression Method | Proportion of Total Harmonics in Circulation | Proportion of Double Frequency Components | Dc Component in Circulation |
|---|---|---|---|
| Circulation-free suppression | 48.05% | 38.74% | 91.63 A |
| PI | 8.17% | 7.14% | 91.29 A |
| PIR | 5.40% | 4.75% | 90.95 A |
| PBC | 8.16% | 6.79% | 91.18 A |
| PBC-ISMC | 3.43% | 1.23% | 90.91 A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Li, J.; Zhang, M.; Yang, X.; Zhong, D. Research on Circulating-Current Suppression Strategy of MMC Based on Passivity-Based Integral Sliding Mode Control for Multiphase Wind Power Grid-Connected Systems. Electronics 2025, 14, 2722. https://doi.org/10.3390/electronics14132722
Zhang W, Li J, Zhang M, Yang X, Zhong D. Research on Circulating-Current Suppression Strategy of MMC Based on Passivity-Based Integral Sliding Mode Control for Multiphase Wind Power Grid-Connected Systems. Electronics. 2025; 14(13):2722. https://doi.org/10.3390/electronics14132722
Chicago/Turabian StyleZhang, Wei, Jianying Li, Mai Zhang, Xiuhai Yang, and Dingai Zhong. 2025. "Research on Circulating-Current Suppression Strategy of MMC Based on Passivity-Based Integral Sliding Mode Control for Multiphase Wind Power Grid-Connected Systems" Electronics 14, no. 13: 2722. https://doi.org/10.3390/electronics14132722
APA StyleZhang, W., Li, J., Zhang, M., Yang, X., & Zhong, D. (2025). Research on Circulating-Current Suppression Strategy of MMC Based on Passivity-Based Integral Sliding Mode Control for Multiphase Wind Power Grid-Connected Systems. Electronics, 14(13), 2722. https://doi.org/10.3390/electronics14132722







