Comparative Study on Energy Consumption of Neural Networks by Scaling of Weight-Memory Energy Versus Computing Energy for Implementing Low-Power Edge Intelligence
Abstract
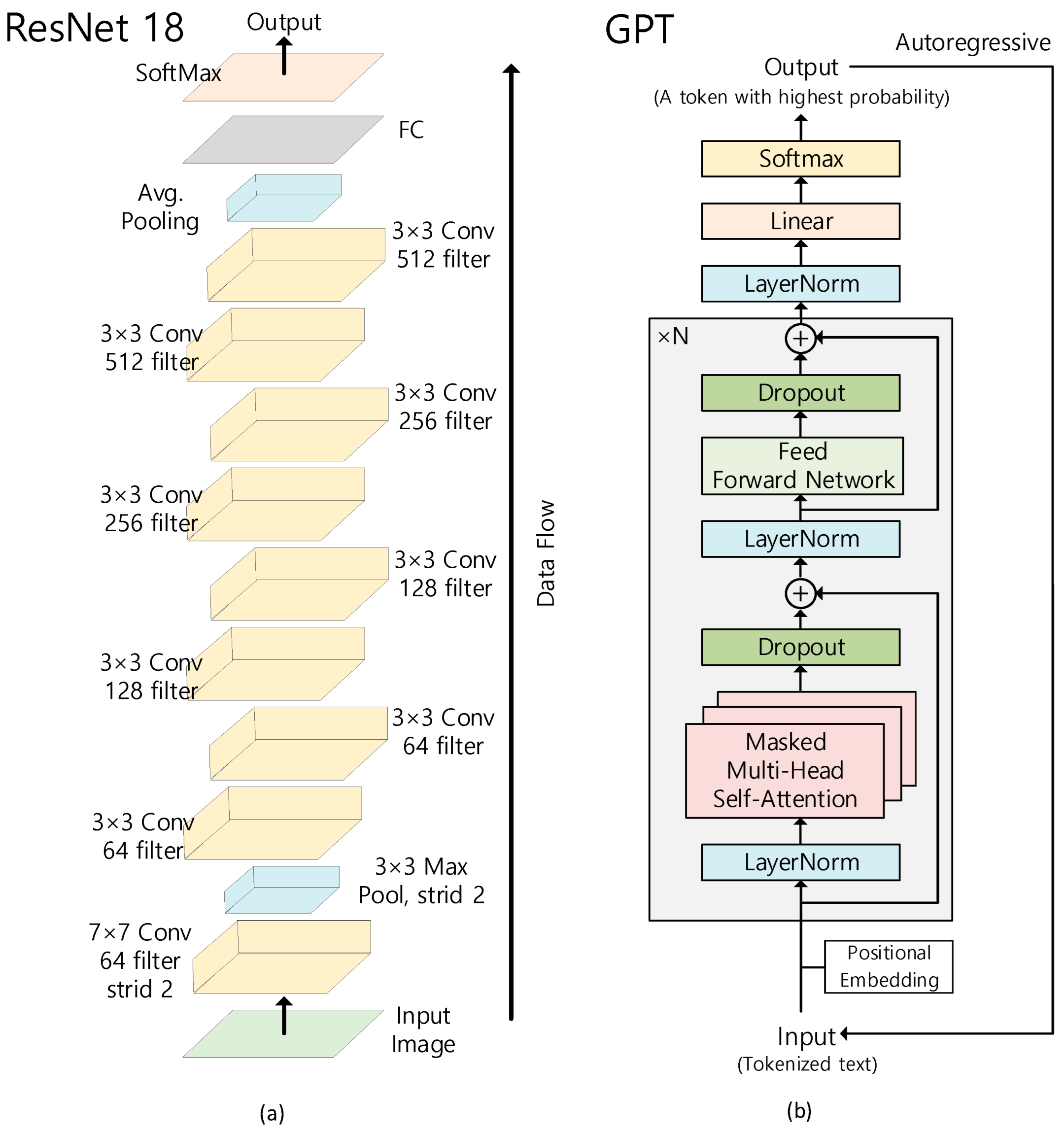
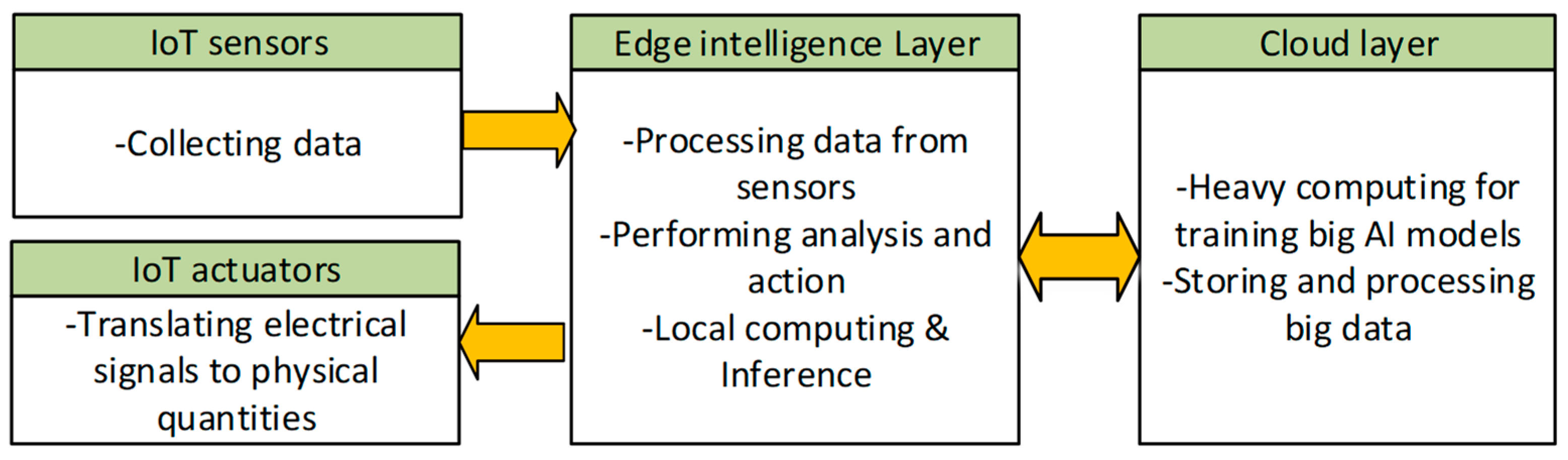
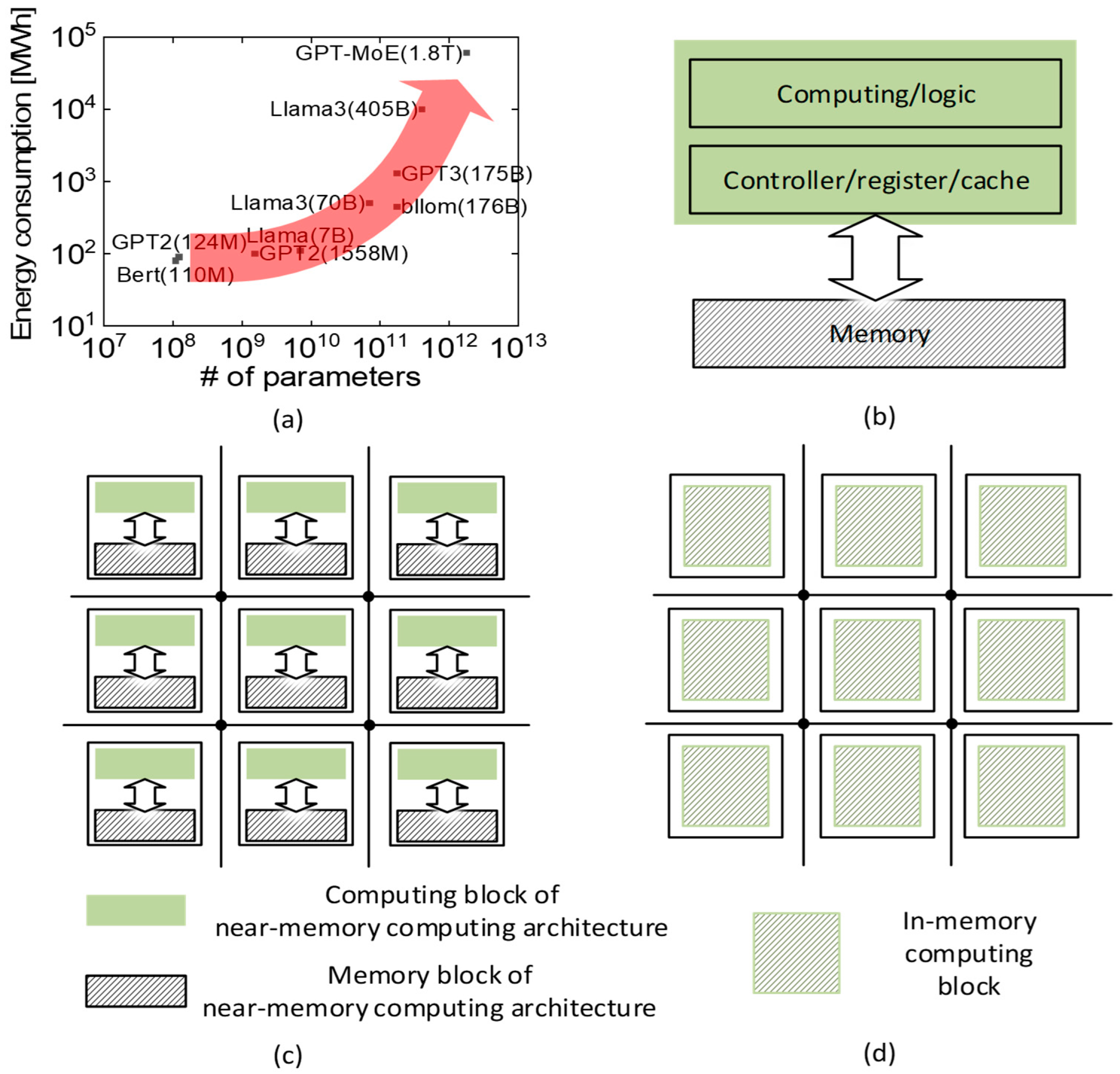
1. Introduction
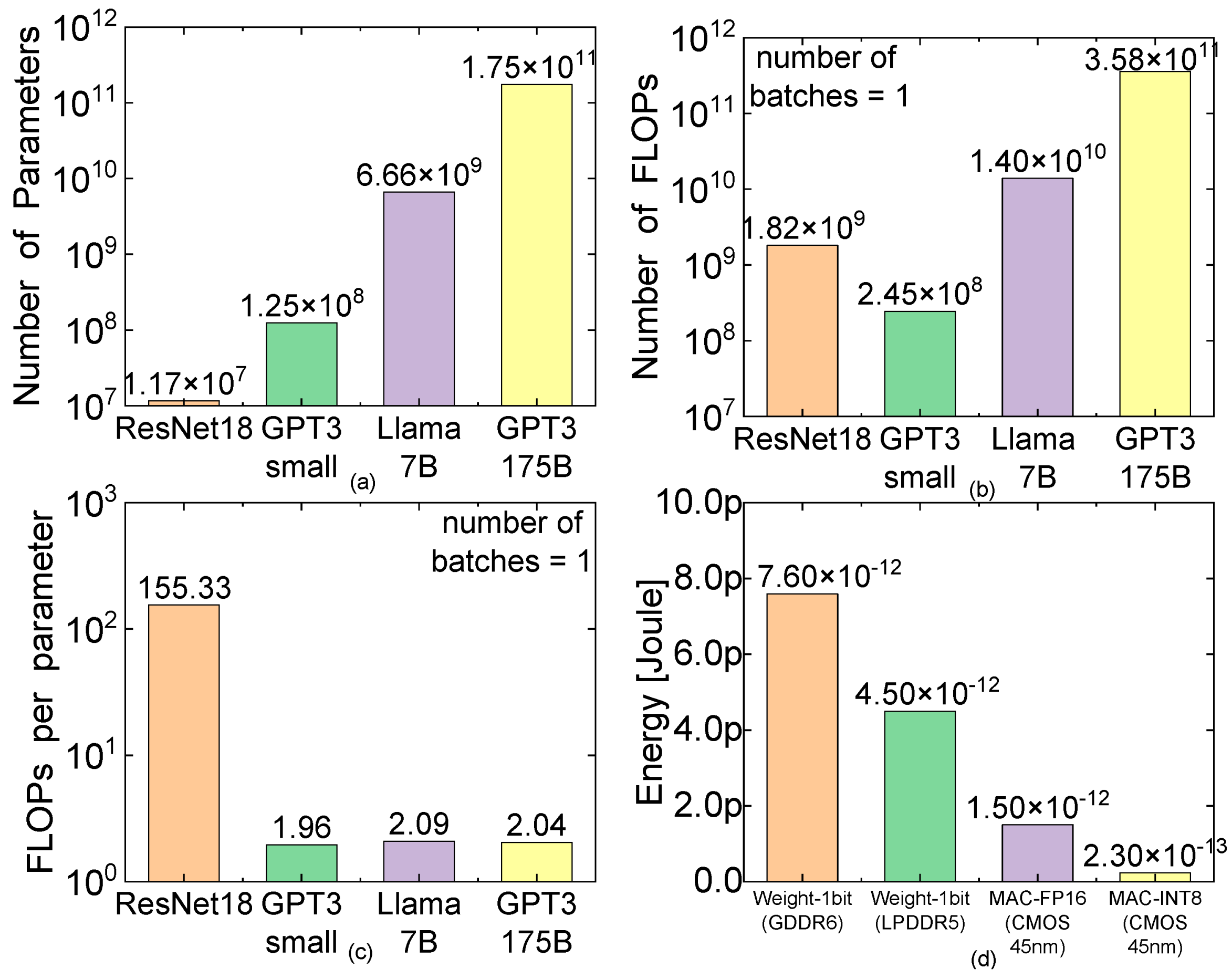
2. Methods
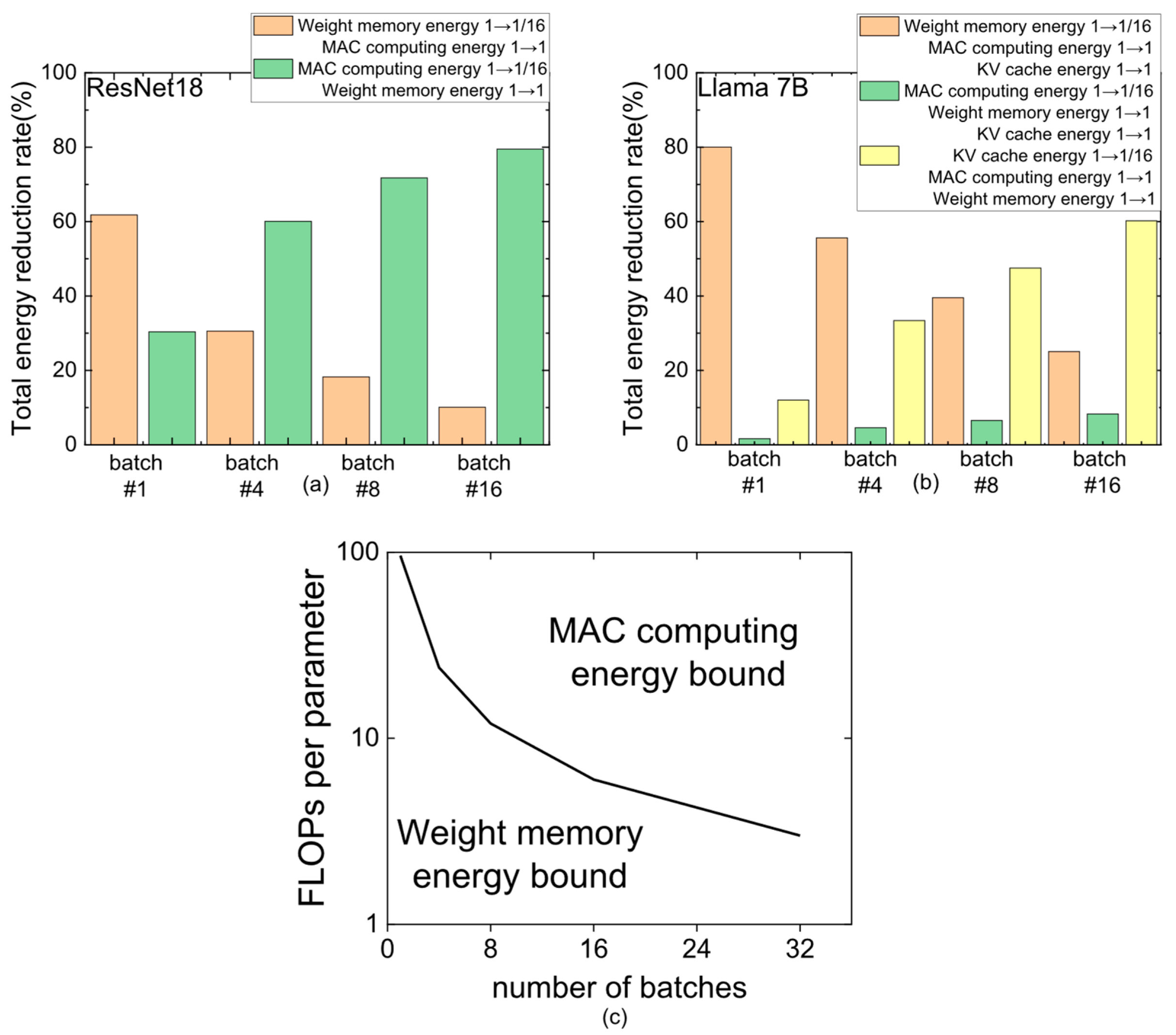
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.H.; Si, Z.Z.; Ju, Z.T.; Feng, H.Y.; Zhang, J.H.; Yan, X.; Dai, C.Q. Convolutional-recurrent neural network for the prediction of formation and switching dynamics for multicolor solitons. Sci. China Physics, Mech. Astron. 2025, 68, 284211. [Google Scholar] [CrossRef]
- Wan, Y.; Wei, Q.; Sun, H.; Wu, H.; Zhou, Y.; Bi, C.; Li, J.; Li, L.; Liu, B.; Wang, D.; et al. Machine learning assisted biomimetic flexible SERS sensor from seashells for pesticide classification and concentration prediction. Chem. Eng. J. 2025, 507, 160813. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; Volume 1, pp. 4171–4186. [Google Scholar]
- Xia, Q.; Ye, W.; Tao, Z.; Wu, J.; Li, Q. A survey of federated learning for edge computing: Research problems and solutions. High-Confidence Comput. 2021, 1, 100008. [Google Scholar] [CrossRef]
- Amin, S.U.; Hossain, M.S. Edge Intelligence and Internet of Things in Healthcare: A Survey. IEEE Access 2021, 9, 45–59. [Google Scholar] [CrossRef]
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge Computing: Vision and Challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Aminifar, A.; Shokri, M.; Aminifar, A. Privacy-preserving edge federated learning for intelligent mobile-health systems. Futur. Gener. Comput. Syst. 2024, 161, 625–637. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, Y.; Qian, B.; Shi, X.; Shu, Y.; Chen, J. A Review on Edge Large Language Models: Design, Execution, and Applications. ACM Comput. Surv. 2025, 57, 1–35. [Google Scholar] [CrossRef]
- Schwartz, R.; Dodge, J.; Smith, N.A.; Etzioni, O. Green AI. Commun. ACM 2020, 63, 54–63. [Google Scholar] [CrossRef]
- Maliakel, P.J.; Ilager, S.; Brandic, I. Investigating Energy Efficiency and Performance Trade-offs in LLM Inference Across Tasks and DVFS Settings. arXiv 2025, arXiv:2501.08219. [Google Scholar]
- Li, Y.; Mughees, M.; Chen, Y.; Li, Y.R. The Unseen AI Disruptions for Power Grids: LLM-Induced Transients. arXiv 2024, arXiv:2409.11416. [Google Scholar]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Strubell, E.; Ganesh, A.; McCallum, A. Energy and policy considerations for deep learning in NLP. arXiv 2019, arXiv:1906.02243. [Google Scholar]
- Dreslinski, R.G.; Wieckowski, M.; Blaauw, D.; Sylvester, D.; Mudge, T. Near-threshold computing: Reclaiming moore’s law through energy efficient integrated circuits. Proc. IEEE 2010, 98, 253–266. [Google Scholar] [CrossRef]
- Horowitz, M. Computing’s energy problem (and what we can do about it). Dig. Tech. Pap. 2014, 57, 10–14. [Google Scholar] [CrossRef]
- Ahn, J.; Hong, S.; Yoo, S.; Mutlu, O.; Choi, K. A scalable processing-in-memory accelerator for parallel graph processing. Procedings of the ACM/IEEE 42nd Annual International Symposium on Computer Architecture, Portland, OR, USA, 13–17 June 2015; pp. 105–117. [Google Scholar] [CrossRef]
- Singh, G.; Chelini, L.; Corda, S.; Awan, A.J.; Stuijk, S.; Jordans, R.; Corporaal, H.; Boonstra, A.J. Near-memory computing: Past, present, and future. Microprocess. Microsyst. 2019, 71, 102868. [Google Scholar] [CrossRef]
- Sheng, X.; Graves, C.E.; Kumar, S.; Li, X.; Buchanan, B.; Zheng, L.; Lam, S.; Li, C.; Strachan, J.P. Low-Conductance and Multilevel CMOS-Integrated Nanoscale Oxide Memristors. Adv. Electron. Mater. 2019, 5, 1800876. [Google Scholar] [CrossRef]
- Chi, P.; Li, S.; Xu, C.; Zhang, T.; Zhao, J.; Liu, Y.; Wang, Y.; Xie, Y. PRIME: A Novel Processing-in-Memory Architecture for Neural Network Computation in ReRAM-Based Main Memory. Proceedings of ACM/IEEE 43rd Annual International Symposium on Computer Architecture, Seoul, Republic of Korea, 18–22 June 2016; pp. 27–39. [Google Scholar] [CrossRef]
- Shafiee, A.; Nag, A.; Muralimanohar, N.; Balasubramonian, R.; Strachan, J.P.; Hu, M.; Williams, R.S.; Srikumar, V. Isaac. ACM SIGARCH Comput. Archit. News 2016, 44, 14–26. [Google Scholar] [CrossRef]
- He, W.; Member, G.S.; Yin, S.; Member, G.S.; Kim, Y.; Member, G.S.; Sun, X.; Member, S.; Kim, J.; Yu, S.; et al. 2-Bit-Per-Cell RRAM-Based In-Memory Computing for Area-/Energy-Efficient Deep Learning. IEEE Solid-State Circuits Lett. 2020, 3, 194–197. [Google Scholar] [CrossRef]
- Lahmer, S.; Khoshsirat, A.; Rossi, M.; Zanella, A. Energy Consumption of Neural Networks on NVIDIA Edge Boards: An Empirical Model. In Proceedings of the 2022 20th International Symposium on Modeling and Optimization in Mobile, Ad hoc, and Wireless Networks, Torino, Italy, 19–23 September 2022; pp. 365–371. [Google Scholar] [CrossRef]
- Latif, I.; Newkirk, A.C.; Carbone, M.R.; Munir, A.; Lin, Y.; Koomey, J.; Yu, X.; Dong, Z. Empirical Measurements of AI Training Power Demand on a GPU-Accelerated Node. IEEE Access 2025, 13, 61740–61747. [Google Scholar] [CrossRef]
- Aquino-Brítez, S.; García-Sánchez, P.; Ortiz, A.; Aquino-Brítez, D. Towards an Energy Consumption Index for Deep Learning Models: A Comparative Analysis of Architectures, GPUs, and Measurement Tools. Sensors 2025, 25, 846. [Google Scholar] [CrossRef]
- Wolters, C. Memory Is All You Need: An Overview of Compute-in-Memory Architectures for Accelerating Large Language Model Inference. arXiv 2024, arXiv:2406.08413. [Google Scholar]
- Wu, Y.; Wang, Z.; Lu, W.D. PIM-GPT: A Hybrid Process-in-Memory Accelerator for Autoregressive Transformers. NPJ Unconv. Comput. 2024, 1, 1. [Google Scholar] [CrossRef]
- Kaplan, J.; McCandlish, S.; Henighan, T.; Brown, T.B.; Chess, B.; Child, R.; Gray, S.; Radford, A.; Wu, J.; Amodei, D. Scaling Laws for Neural Language Models. arXiv 2020, arXiv:2001.08361. [Google Scholar]
- Touvron, H.; Lavril, T.; Izacard, G.; Martinet, X.; Lachaux, M.-A.; Lacroix, T.; Rozière, B.; Goyal, N.; Hambro, E.; Azhar, F.; et al. LLaMA: Open and Efficient Foundation Language Models. arXiv 2023, arXiv:2302.13971. [Google Scholar]
- Johnson, J. Rethinking floating point for deep learning. arXiv 2018, arXiv:1811.01721v1. [Google Scholar]
- Samsung Electronics Co., Ltd. 8 Gb GDDR6 SGRAM (C-Die) Data Sheet, Rev. 1.0.; Samsung Electronics Co., Ltd.: Suwon-si, Gyeonggi-do, Republic of Korea, 2020; Available online: https://datasheet.lcsc.com/lcsc/2204251615_Samsung-K4Z80325BC-HC14_C2920181.pdf (accessed on 1 July 2025).
- Micron Technology, Inc. LPDDR5/LPDDR5X SDRAM Data Sheet, Rev. D.; Micron Technology, Inc.: Boise, ID, USA, 2022; pp. 1–30. Available online: https://www.mouser.com/datasheet/2/671/Micron_05092023_315b_441b_y4bm_ddp_qdp_8dp_non_aut-3175604.pdf (accessed on 1 July 2025).
- Jouppi, N.P.; Yoon, D.H.; Ashcraft, M.; Gottscho, M.; Jablin, T.B.; Kurian, G.; Laudon, J.; Li, S.; Ma, P.; Ma, X.; et al. Ten lessons from three generations shaped Google’s TPU v4i: Industrial product. In Proceedings of the 2021 ACM/IEEE 48th Annual International Symposium on Computer Architecture, Valencia, Spain, 14–18 June 2021; pp. 1–14. [Google Scholar] [CrossRef]
- Ivanov, A.; Dryden, N.; Ben-Nun, T.; Li, S.; Hoefler, T. Data Movement Is All You Need: A Case Study on Optimizing Transformers. arXiv 2020, arXiv:2007.00072. [Google Scholar]
- Yang, T.J.; Chen, Y.H.; Emer, J.; Sze, V. A method to estimate the energy consumption of deep neural networks. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 1916–1920. [Google Scholar] [CrossRef]
- Jain, S.R.; Gural, A.; Wu, M.; Dick, C.H. Trained Quantization Thresholds for Accurate and Efficient Fixed-Point Inference of Deep Neural Networks. In Proceedings of the 3rd Conference on Machine Learning and Systems (MLSys 2020), Austin, TX, USA, 6–8 March 2020; pp. 1–17. [Google Scholar]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2704–2713. [Google Scholar] [CrossRef]
- Luohe, S.; Hongyi, Z.; Yao, Y.; Zuchao, L.; Hai, Z. Keep the Cost Down: A Review on Methods to Optimize LLM’s KV-Cache Consumption. arXiv 2024, arXiv:2407.18003. [Google Scholar]
- Adnan, M.; Arunkumar, A.; Jain, G.; Nair, P.J.; Soloveychik, I.; Kamath, P. Keyformer: KV Cache Reduction through Key Tokens Selection for Efficient Generative Inference. arXiv 2024, arXiv:2403.09054. [Google Scholar] [CrossRef]

| n_word | n_context | d_model | n_layer | n_head | d_head | |
|---|---|---|---|---|---|---|
| GPT3-small | 50,257 | 2048 | 768 | 12 | 12 | 64 |
| Llama-7B | 50,257 | 2048 | 4096 | 32 | 32 | 128 |
| GPT3-175B | 50,257 | 2048 | 12,288 | 96 | 96 | 128 |
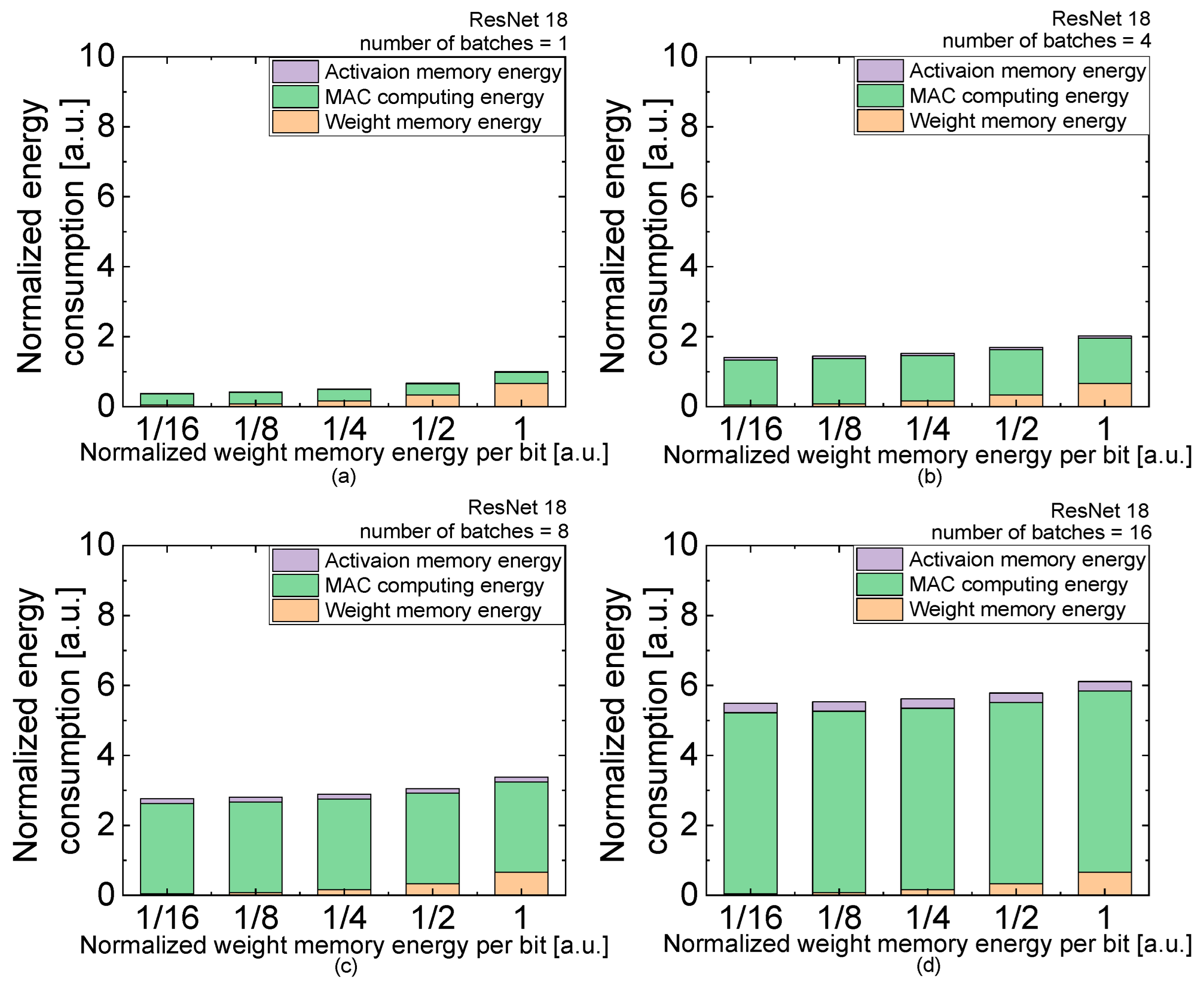
| (a) | Normalized Weight Energy per Bit | 1/16 | 1/8 | 1/4 | 1/2 | 1 |
| number of batches = 1 | activation | 0.01693 | 0.01693 | 0.01693 | 0.01693 | 0.01693 |
| MAC | 0.32393 | 0.32393 | 0.32393 | 0.32393 | 0.32393 | |
| weight | 0.0412 | 0.08239 | 0.16478 | 0.32957 | 0.65914 | |
| total | 0.38206 | 0.42325 | 0.50564 | 0.67043 | 1 | |
| number of batches = 4 | activation | 0.06772 | 0.06772 | 0.06772 | 0.06772 | 0.06772 |
| MAC | 1.29574 | 1.29574 | 1.29574 | 1.29574 | 1.29574 | |
| weight | 0.0412 | 0.08239 | 0.16478 | 0.32957 | 0.65914 | |
| total | 1.40466 | 1.44585 | 1.52824 | 1.69303 | 2.02259 | |
| number of batches = 8 | activation | 0.13545 | 0.13545 | 0.13545 | 0.13545 | 0.13545 |
| MAC | 2.59147 | 2.59147 | 2.59147 | 2.59147 | 2.59147 | |
| weight | 0.0412 | 0.08239 | 0.16478 | 0.32957 | 0.65914 | |
| total | 2.76812 | 2.80931 | 2.8917 | 3.05649 | 3.38606 | |
| number of batches = 16 | activation | 0.2709 | 0.2709 | 0.2709 | 0.2709 | 0.2709 |
| MAC | 5.18294 | 5.18294 | 5.18294 | 5.18294 | 5.18294 | |
| weight | 0.0412 | 0.08239 | 0.16478 | 0.32957 | 0.65914 | |
| total | 5.49504 | 5.53623 | 5.61862 | 5.78341 | 6.11298 | |
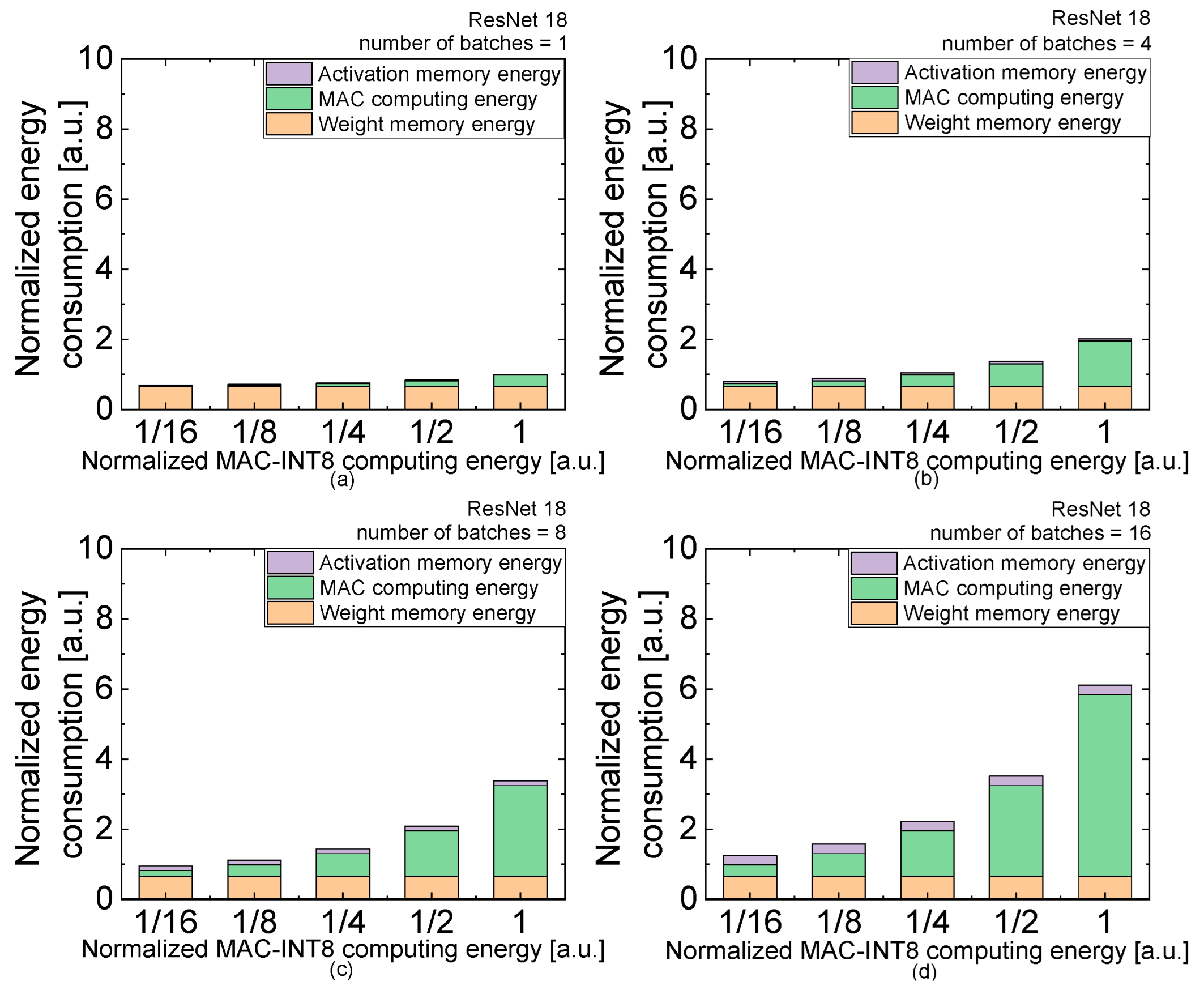
| (b) | Normalized MAC Energy per Bit | 1/16 | 1/8 | 1/4 | 1/2 | 1 |
| number of batches = 1 | activation | 0.01693 | 0.01693 | 0.01693 | 0.01693 | 0.01693 |
| MAC | 0.02025 | 0.04049 | 0.08098 | 0.16197 | 0.32393 | |
| weight | 0.65914 | 0.65914 | 0.65914 | 0.65914 | 0.65914 | |
| total | 0.69631 | 0.71656 | 0.75705 | 0.83803 | 1 | |
| number of batches = 4 | activation | 0.06772 | 0.06772 | 0.06772 | 0.06772 | 0.06772 |
| MAC | 0.08098 | 0.16197 | 0.32393 | 0.64787 | 1.29574 | |
| weight | 0.65914 | 0.65914 | 0.65914 | 0.65914 | 0.65914 | |
| total | 0.80784 | 0.88883 | 1.05079 | 1.37473 | 2.02259 | |
| number of batches = 8 | activation | 0.13545 | 0.13545 | 0.13545 | 0.13545 | 0.13545 |
| MAC | 0.16197 | 0.32393. | 0.64787 | 1.29574 | 2.59147 | |
| weight | 0.65914 | 0.65914 | 0.65914 | 0.65914 | 0.65914 | |
| total | 0.95656 | 1.11852 | 1.44246 | 2.09033 | 3.38606 | |
| number of batches = 16 | activation | 0.2709 | 0.2709 | 0.2709 | 0.2709 | 0.2709 |
| MAC | 0.32393 | 0.64787 | 1.29574 | 2.59147 | 5.18294 | |
| weight | 0.65914 | 0.65914 | 0.65914 | 0.65914 | 0.65914 | |
| total | 1.25397 | 1.57791 | 2.22578 | 3.52151 | 6.11298 | |
| (c) | Normalized Weight Energy per Bit | 1/16 | 1/8 | 1/4 | 1/2 | 1 |
| number of batches = 1 | activation | 4.47059 × 10−4 | 4.47059 × 10−4 | 4.47059 × 10−4 | 4.47059 × 10−4 | 4.47059 × 10−4 |
| MAC | 0.01763 | 0.01763 | 0.01763 | 0.01763 | 0.01763 | |
| weight | 0.05336 | 0.10672 | 0.21343/ | 0.42687 | 0.85374 | |
| KV cache | 0.12819 | 0.12819 | 0.12819 | 0.12819 | 0.12819 | |
| total | 0.19962 | 0.25298 | 0.3597 | 0.57313 | 1 | |
| number of batches = 4 | activation | 0.00179 | 0.00179 | 0.00179 | 0.00179 | 0.00179 |
| MAC | 0.0705 | 0.0705 | 0.0705 | 0.0705 | 0.0705 | |
| weight | 0.05336 | 0.10672 | 0.21343 | 0.42687 | 0.85374 | |
| KV cache | 0.51276 | 0.51276 | 0.51276 | 0.51276 | 0.51276 | |
| total | 0.63841 | 0.69176 | 0.79848 | 1.01192 | 1.43879 | |
| number of batches = 8 | activation | 0.00358 | 0.00358 | 0.00358 | 0.00358 | 0.00358 |
| MAC | 0.14101 | 0.14101 | 0.14101 | 0.14101 | 0.14101 | |
| weight | 0.05336 | 0.10672 | 0.21343 | 0.42687 | 0.85374 | |
| KV cache | 1.02551 | 1.02551 | 1.02551 | 1.02551 | 1.02551 | |
| total | 1.22345 | 1.27681 | 1.38353 | 1.59696 | 2.02383 | |
| number of batches = 16 | activation | 0.00715 | 0.00715 | 0.00715 | 0.00715 | 0.00715 |
| MAC | 0.28202 | 0.28202 | 0.28202 | 0.28202 | 0.28202 | |
| weight | 0.05336 | 0.10672 | 0.21343 | 0.42687 | 0.85374 | |
| KV cache | 2.05102 | 2.05102 | 2.05102 | 2.05102 | 2.05102 | |
| total | 2.39355 | 2.44691 | 2.55363 | 2.76706 | 3.19393 | |
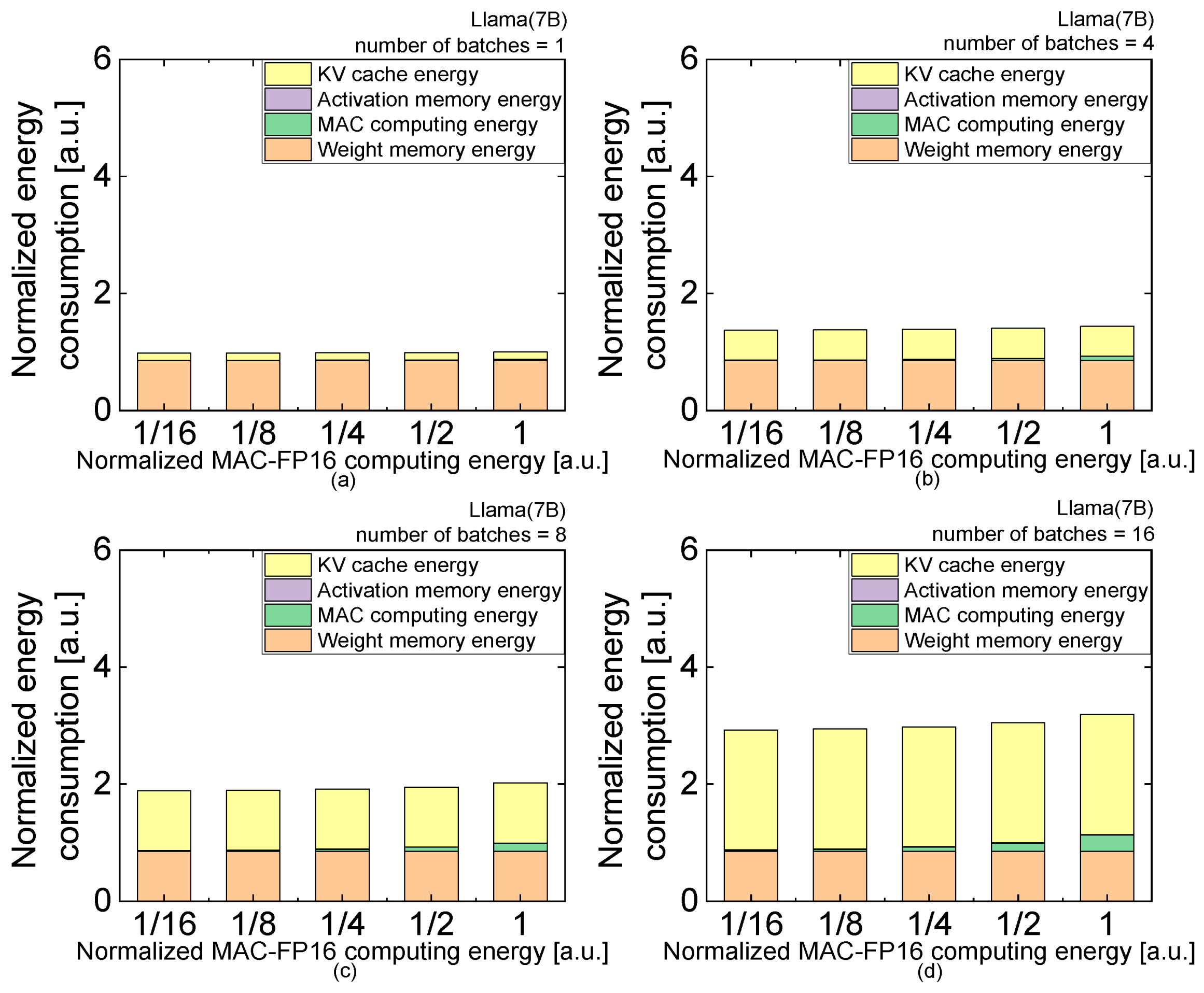
| (d) | Normalized MAC Energy per Bit | 1/16 | 1/8 | 1/4 | 1/2 | 1 |
| number of batches = 1 | activation | 4.47059 × 10−4 | 4.47059 × 10−4 | 4.47059 × 10−4 | 4.47059 × 10−4 | 4.47059 × 10−4 |
| MAC | 0.0011 | 0.0022 | 0.00441 | 0.00881 | 0.01763 | |
| weight | 0.85374 | 0.85374 | 0.85374 | 0.85374 | 0.85374 | |
| KV cache | 0.12819 | 0.12819 | 0.12819 | 0.12819 | 0.12819 | |
| total | 0.98348 | 0.98458 | 0.98678 | 0.99119 | 1 | |
| number of batches = 4 | activation | 0.00179 | 0.00179 | 0.00179 | 0.00179 | 0.00179 |
| MAC | 0.00441 | 0.00881 | 0.01763 | 0.03525 | 0.0705 | |
| weight | 0.85374 | 0.85374 | 0.85374 | 0.85374 | 0.85374 | |
| KV cache | 0.51276 | 0.51276 | 0.51276 | 0.51276 | 0.51276 | |
| total | 1.37269 | 1.37709 | 1.38591 | 1.40353 | 1.43879 | |
| number of batches = 8 | activation | 0.00358 | 0.00358 | 0.00358 | 0.00358 | 0.00358 |
| MAC | 0.00881 | 0.01763 | 0.03525 | 0.0705 | 0.14101 | |
| weight | 0.85374 | 0.85374 | 0.85374 | 0.85374 | 0.85374 | |
| KV cache | 1.02551 | 1.02551 | 1.02551 | 1.02551 | 1.02551 | |
| total | 1.89164 | 1.90045 | 1.91808 | 1.95333 | 2.02383 | |
| number of batches = 16 | activation | 0.00715 | 0.00715 | 0.00715 | 0.00715 | 0.00715 |
| MAC | 0.01763 | 0.03525 | 0.0705 | 0.14101 | 0.28202 | |
| weight | 0.85374 | 0.85374 | 0.85374 | 0.85374 | 0.85374 | |
| KV cache | 2.05102 | 2.05102 | 2.05102 | 2.05102 | 2.05102 | |
| total | 2.92954 | 2.94717 | 2.98242 | 3.05292 | 3.19393 | |
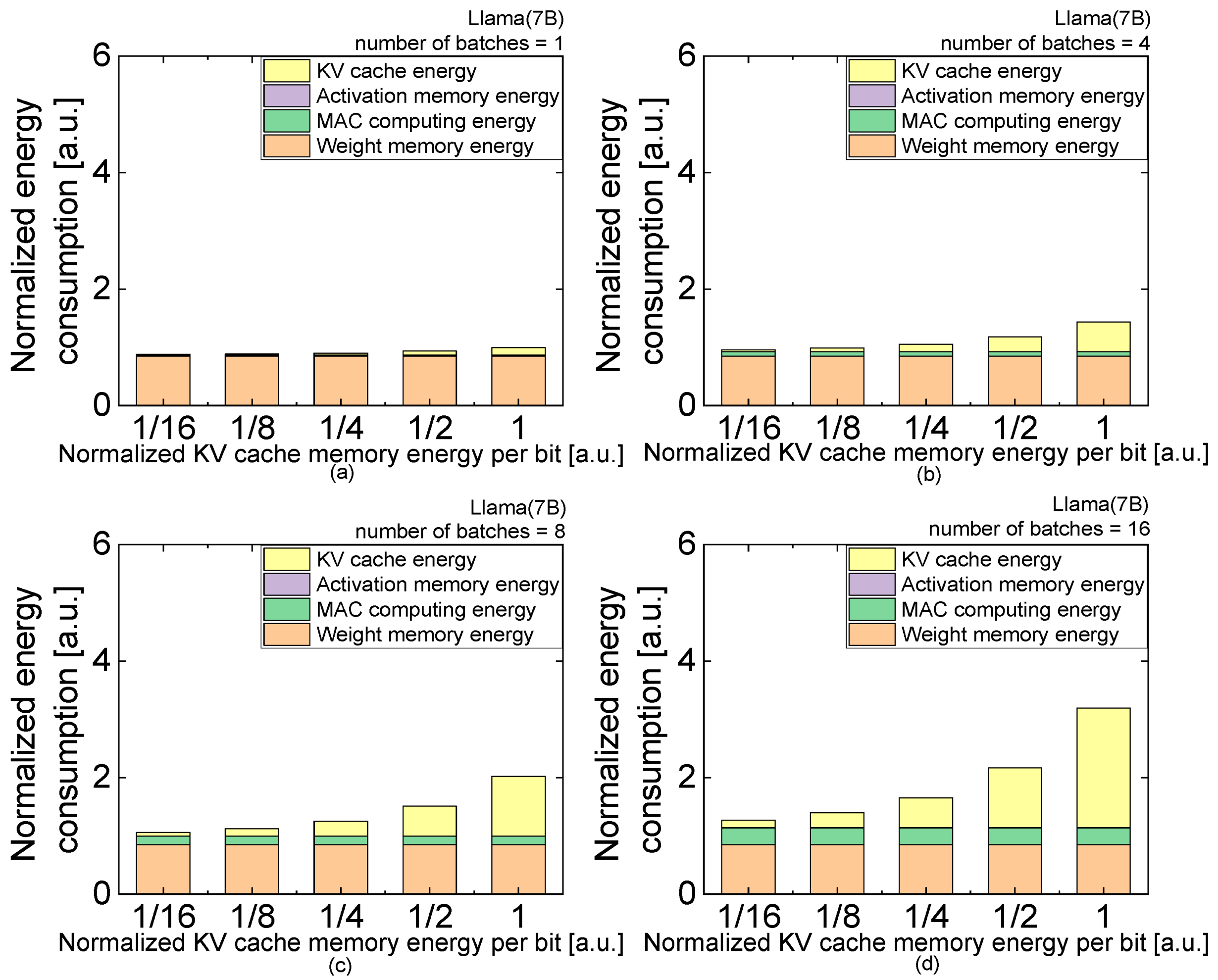
| (e) | Normalized KV Cache Energy per Bit | 1/16 | 1/8 | 1/4 | 1/2 | 1 |
| number of batches = 1 | activation | 4.47059 × 10−4 | 4.47059 × 10−4 | 4.47059 × 10−4 | 4.47059 × 10−4 | 4.47059 × 10−4 |
| MAC | 0.01763 | 0.01763 | 0.01763 | 0.01763 | 0.01763 | |
| weight | 0.85374 | 0.85374 | 0.85374 | 0.85374 | 0.85374 | |
| KV cache | 0.00801 | 0.01602 | 0.03205 | 0.06409 | 0.12819 | |
| total | 0.87982 | 0.88783 | 0.90386 | 0.93591 | 1 | |
| number of batches = 4 | activation | 0.00179 | 0.00179 | 0.00179 | 0.00179 | 0.00179 |
| MAC | 0.0705 | 0.0705 | 0.0705 | 0.0705 | 0.0705 | |
| weight | 0.85374 | 0.85374 | 0.85374 | 0.85374 | 0.85374 | |
| KV cache | 0.03205 | 0.06409 | 0.12819 | 0.25638 | 0.51276 | |
| total | 0.95808 | 0.99012 | 1.05422 | 1.18241 | 1.43879 | |
| number of batches = 8 | activation | 0.00358 | 0.00358 | 0.00358 | 0.00358 | 0.00358 |
| MAC | 0.14101 | 0.14101 | 0.14101 | 0.14101 | 0.14101 | |
| weight | 0.85374 | 0.85374 | 0.85374 | 0.85374 | 0.85374 | |
| KV cache | 0.06409 | 0.12819 | 0.25638 | 0.51276 | 1.02551 | |
| total | 1.06242 | 1.12651 | 1.2547 | 1.51108 | 2.02383 | |
| number of batches = 16 | activation | 0.00715 | 0.00715 | 0.00715 | 0.00715 | 0.00715 |
| MAC | 0.28202 | 0.28202 | 0.28202 | 0.28202 | 0.28202 | |
| weight | 0.85374 | 0.85374 | 0.85374 | 0.85374 | 0.85374 | |
| KV cache | 0.12819 | 0.25638 | 0.51276 | 1.02551 | 2.05102 | |
| total | 1.2711 | 1.39928 | 1.65566 | 2.16842 | 3.19393 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, I.; Mun, J.; Min, K.-S. Comparative Study on Energy Consumption of Neural Networks by Scaling of Weight-Memory Energy Versus Computing Energy for Implementing Low-Power Edge Intelligence. Electronics 2025, 14, 2718. https://doi.org/10.3390/electronics14132718
Yoon I, Mun J, Min K-S. Comparative Study on Energy Consumption of Neural Networks by Scaling of Weight-Memory Energy Versus Computing Energy for Implementing Low-Power Edge Intelligence. Electronics. 2025; 14(13):2718. https://doi.org/10.3390/electronics14132718
Chicago/Turabian StyleYoon, Ilpyung, Jihwan Mun, and Kyeong-Sik Min. 2025. "Comparative Study on Energy Consumption of Neural Networks by Scaling of Weight-Memory Energy Versus Computing Energy for Implementing Low-Power Edge Intelligence" Electronics 14, no. 13: 2718. https://doi.org/10.3390/electronics14132718
APA StyleYoon, I., Mun, J., & Min, K.-S. (2025). Comparative Study on Energy Consumption of Neural Networks by Scaling of Weight-Memory Energy Versus Computing Energy for Implementing Low-Power Edge Intelligence. Electronics, 14(13), 2718. https://doi.org/10.3390/electronics14132718