A CMOS Current Reference with Novel Temperature Compensation Based on Geometry-Dependent Threshold Voltage Effects
Abstract
1. Introduction
2. Proposed Architecture
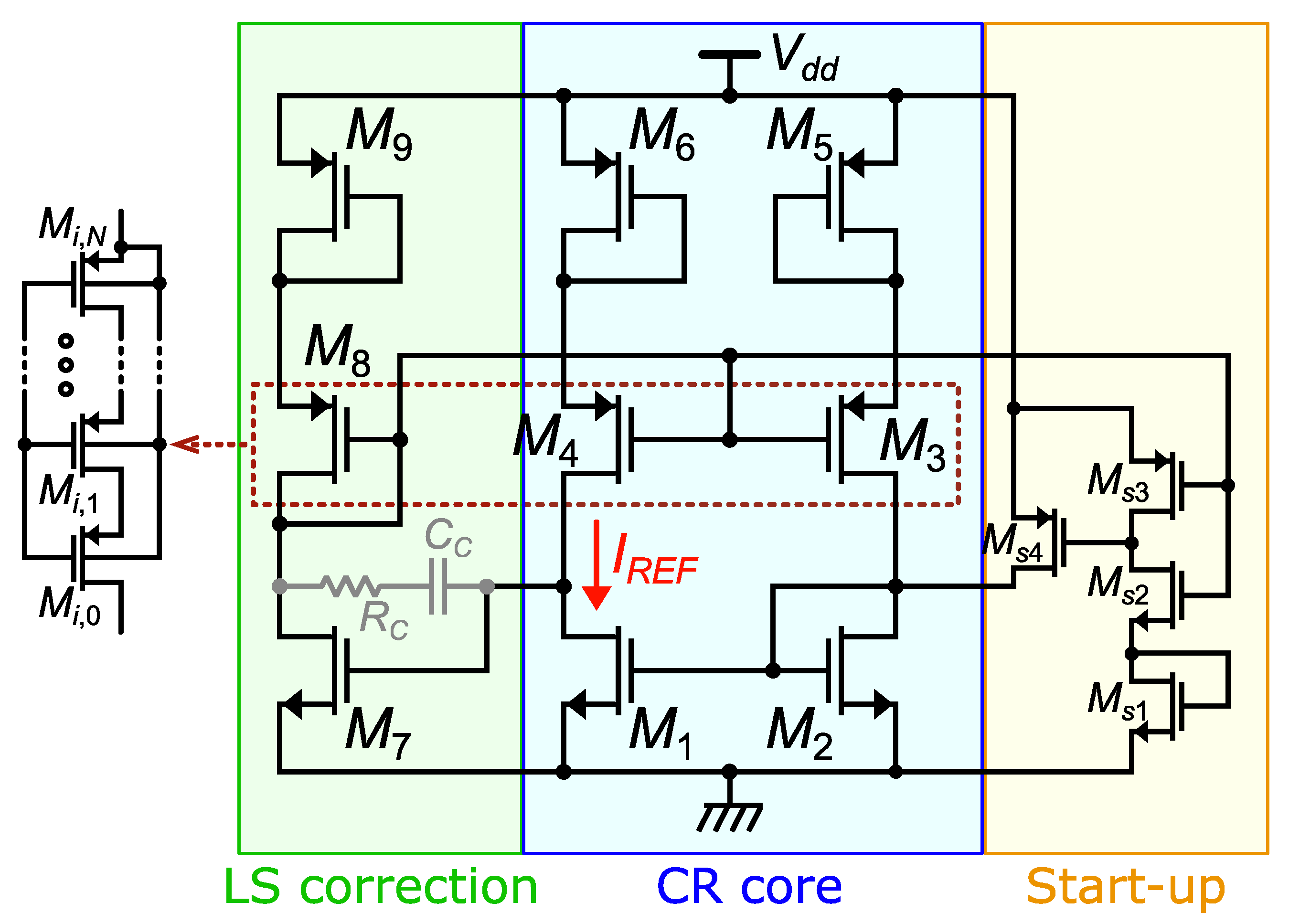
2.1. Current Reference Core
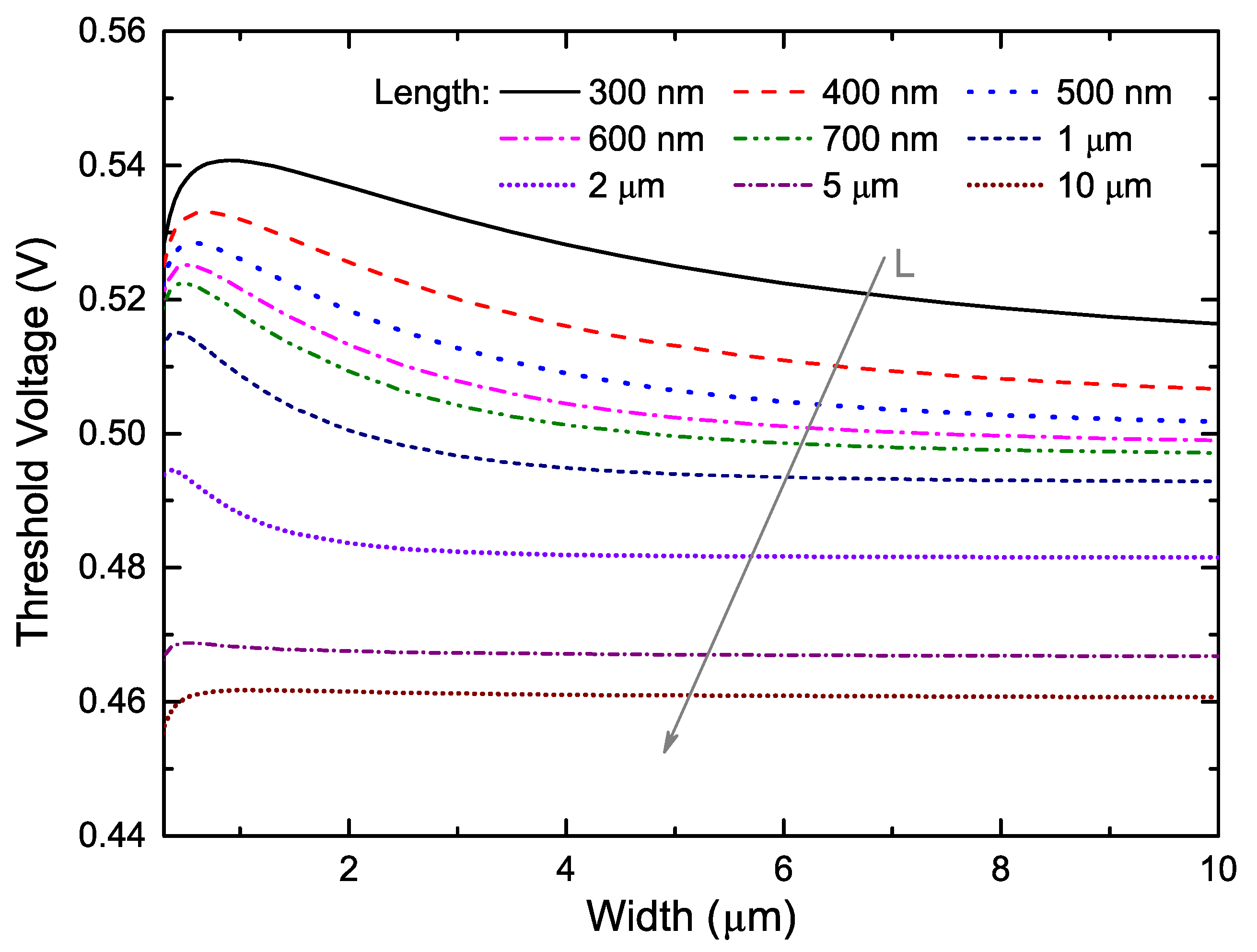
2.2. Proposed Temperature Compensation
2.3. Complete Current Reference Design
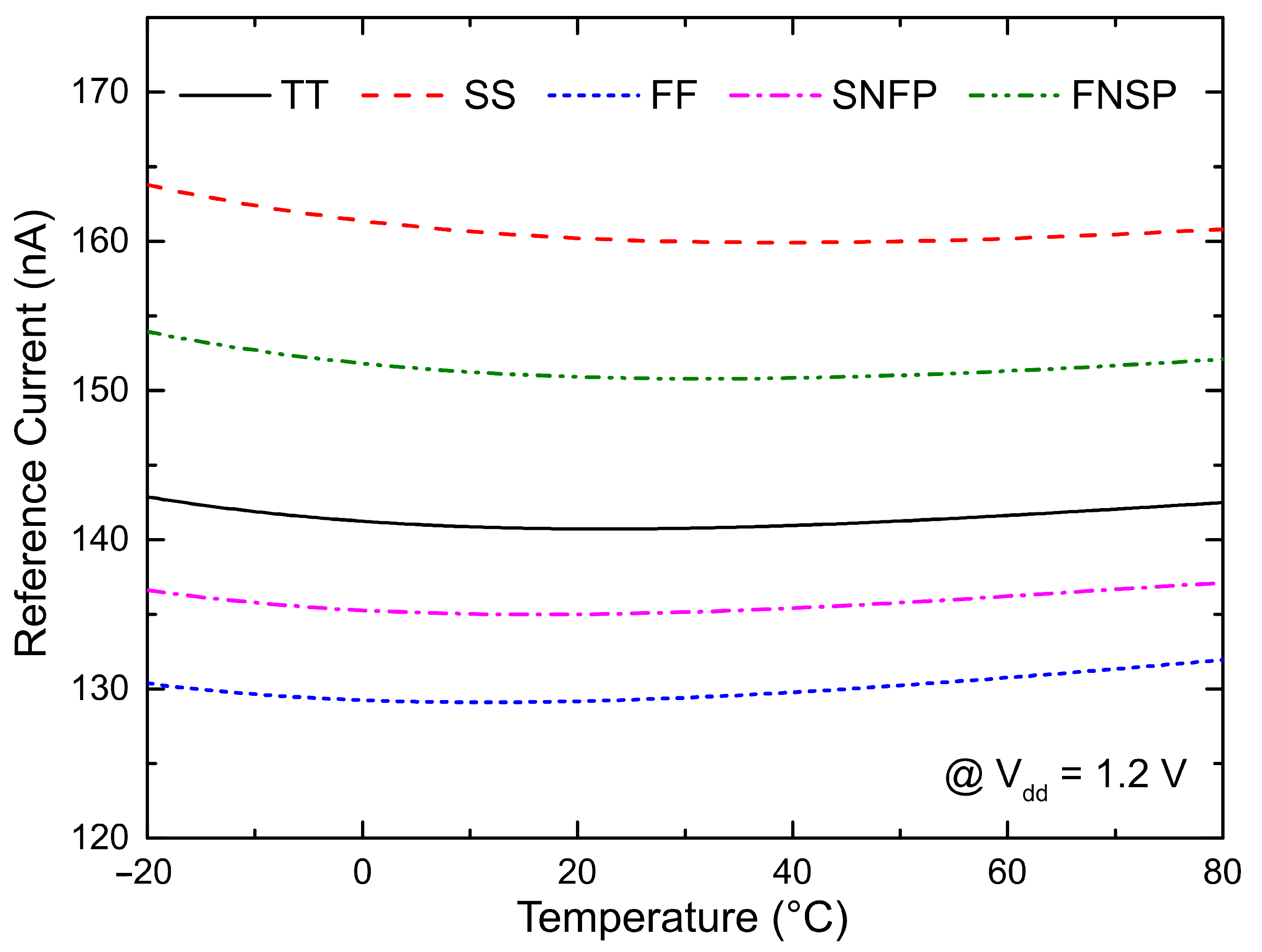
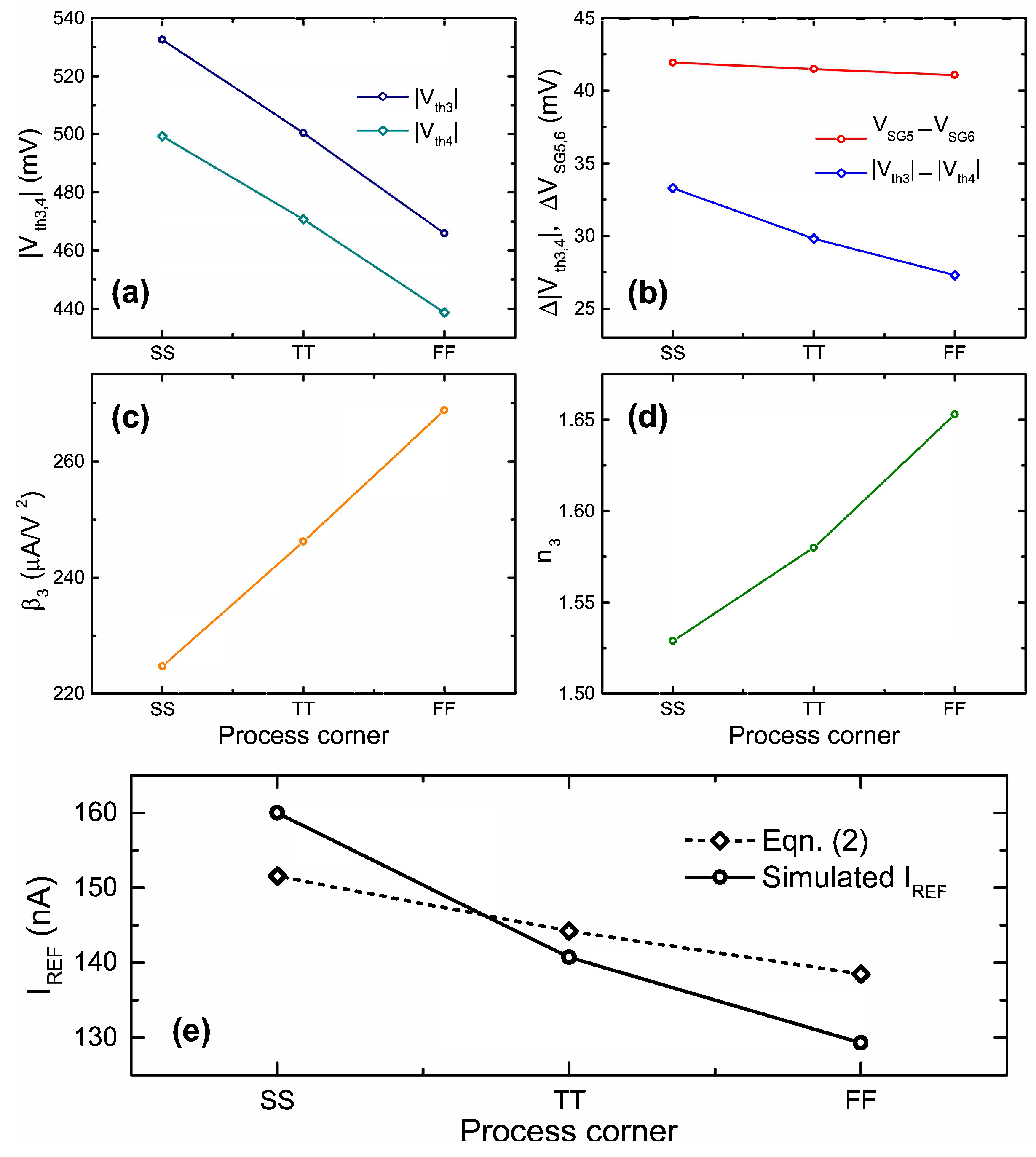
3. Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rezaeiyan, Y.; Kooliv, Y.; Zamani, M.; Shoaei, O.; Akbari, M.; Moradi, F.; Tang, K.T. A 4.5 µW Miniaturized 3-Channel Wireless Intra-Cardiac Acquisition System. IEEE Trans. Biomed. Circuits Syst. 2023, 17, 1097–1110. [Google Scholar] [CrossRef] [PubMed]
- Vohra, J.; Gupta, A.; Alioto, M. Imager with In-Sensor Event Detection and Morphological Transformations with 2.9pJ/pixel × frame Object Segmentation FOM for Always-On Surveillance in 40 nm. In Proceedings of the 2024 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 18–22 February 2024; pp. 104–106. [Google Scholar] [CrossRef]
- Zamani, M.; Rezaeiyan, Y.; Shoaei, O.; Serdijn, W.A. A 1.55 µW Bio-Impedance Measurement System for Implantable Cardiac Pacemakers in 0.18 µm CMOS. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 211–221. [Google Scholar] [CrossRef] [PubMed]
- Sheeraz, M.; Aslam, A.R.; Drakakis, E.M.; Heidari, H.; Altaf, M.A.B.; Saadeh, W. A Closed-Loop Ear-Worn Wearable EEG System with Real-Time Passive Electrode Skin Impedance Measurement for Early Autism Detection. Sensors 2024, 24, 7489. [Google Scholar] [CrossRef] [PubMed]
- Bijak, J.; Trawiński, T.; Szczygieł, M.; Kowalik, Z. Modelling and Investigation of Energy Harvesting System Utilizing Magnetically Levitated Permanent Magnet. Sensors 2022, 22, 6384. [Google Scholar] [CrossRef]
- Yalagala, B.P.; Zhang, J.; Das, R.; Heidari, H. Advancements in Energy Harvesting for Implantable Cardiovascular Devices. In Wireless Power Technologies for Biomedical Devices. Analog Circuits and Signal Processing; Springer: Cham, Switzerland, 2025. [Google Scholar] [CrossRef]
- Alioto, M. Enabling the Internet of Things: From Integrated Circuits to Integrated Systems; Springer: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Shaikh, F.K.; Zeadally, S. Energy harvesting in wireless sensor networks: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 55, 1041–1054. [Google Scholar] [CrossRef]
- Pullela, A.; Ali, A.; Jain, A.; Lee, I.; Abbas, Z. A 156pW Gate-Leakage Based Voltage/Current Reference for Low-Power IoT Systems. In Proceedings of the ISCAS 2022—IEEE International Symposium on Circuits and Systems, Austin, TX, USA, 27 May 2022–1 June 2022; pp. 1923–1927. [Google Scholar] [CrossRef]
- Catania, A.; Gagliardi, F.; Piotto, M.; Bruschi, P.; Dei, M. Ultralow-Power Inverter-Based Delta-Sigma Modulator for Wearable Applications. IEEE Access 2024, 12, 80009–80019. [Google Scholar] [CrossRef]
- Privitera, M.; Ballo, A.; Grasso, A.D.; Alioto, M. A 15-nA quiescent current capacitor-less LDO for sub-1V µW-powered fully-harvested systems. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 19–22 May 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Privitera, M.; Grasso, A.D.; Ballo, A.; Alioto, M. 0.6-V, µW-Power Four-Stage OTA With Minimal Components, and 100× Load Range. IEEE Solid-State Circuits Lett. 2024, 7, 311–314. [Google Scholar] [CrossRef]
- Sala, R.D.; Centurelli, F.; Scotti, G. A Novel Technique to Design Ultra-Low Voltage and Ultra-Low Power Inverter-Based OTAs. In Proceedings of the 2024 19th Conference on Ph.D Research in Microelectronics and Electronics (PRIME), Larnaca, Cyprus, 9–12 June 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Najafizadeh, L. Reference circuits for emerging applications-from extreme environment electronics to internet of things. In Proceedings of the MWSCAS 2017—IEEE 60th International Midwest Symposium on Circuits and Systems, Boston, MA, USA, 6–9 August 2017; pp. 1304–1307. [Google Scholar] [CrossRef]
- Moisello, E.; Bonizzoni, E.; Malcovati, P. A 0.756-ppm/°C Time-Domain-Based Curvature-Compensated Bandgap Reference. In Proceedings of the 2023 IEEE International Symposium on Circuits and Systems (ISCAS), Monterey, CA, USA, 21–25 May 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Moisello, E.; Bonizzoni, E.; Malcovati, P. MOSFET-Based Voltage Reference Circuits in the Last Decade: A Review. Micromachines 2024, 15, 1504. [Google Scholar] [CrossRef]
- Fassio, L.; Hanh, H.H.; Alioto, M. Event-Driven Voltage Reference with Bandgap-Class Temperature Coefficient Across-Corner with 100-pW Power at 0.8 V. In Proceedings of the 2024 IEEE European Solid-State Electronics Research Conference (ESSERC), Bruges, Belgium, 9–12 September 2024; pp. 273–276. [Google Scholar] [CrossRef]
- Gagliardi, F.; Ria, A.; Manfredini, G.; Piotto, M.; Bruschi, P. A Triode-Compensated CMOS Bandgap Core for Sub-250 mV Supply Voltages. In Proceedings of the 2022 17th Conference on Ph.D Research in Microelectronics and Electronics (PRIME), Villasimius, Italy, 12–15 June 2022; pp. 85–88. [Google Scholar] [CrossRef]
- Gagliardi, F.; Bruschi, P.; Piotto, M.; Sakouhi, S.; Dei, M. Single-Branch NMOS-Only Self-Cascoded Voltage Reference Operating down to 0.28-V Supply. In Proceedings of the 2025 23rd IEEE International NEWCAS Conference (NEWCAS), Paris, France, 22–25 June 2025. [Google Scholar]
- Gagliardi, F.; Bruschi, P.; Piotto, M.; Sakouhi, S.; Dei, M. A Multi-Self-Cascoded Voltage Reference with 2.73-ppm/V Line Sensitivity and 20.1-ppm/°C Temperature Coefficient at 0.45-V Supply. In Proceedings of the 2025 68th IEEE International Midwest Symposium on Circuits and Systems (MWSCAS), Lansing, MI, USA, 10–13 August 2025. [Google Scholar]
- Wikner, J.J.; Tan, N. Modeling of CMOS digital-to-analog converters for telecommunication. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1999, 46, 489–499. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, T.; Wang, C.; Gu, Z.; Li, Y.; Liu, Y. Design of a High Linearity Sinusoidal Current Generator Using Shifting Current Mirror Architecture. IEEE Trans. Instrum. Meas. 2022, 71, 4008905. [Google Scholar] [CrossRef]
- Lee, S.; Sánchez-Sinencio, E. Current Reference Circuits: A Tutorial. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 830–836. [Google Scholar] [CrossRef]
- Yang, W.-B.; Huang, Z.-Y.; Cheng, C.-T.; Lo, Y.-L. Temperature insensitive current reference for the 6.27 MHz oscillator. In Proceedings of the 2011 International Symposium on Integrated Circuits, Singapore, 12–14 December 2011; pp. 559–562. [Google Scholar] [CrossRef]
- Sebastiano, F.; Breems, L.J.; Makinwa, K.A.A.; Drago, S.; Leenaerts, D.M.W.; Nauta, B. A Low-Voltage Mobility-Based Frequency Reference for Crystal-Less ULP Radios. IEEE J. Solid-State Circuits 2009, 44, 2002–2009. [Google Scholar] [CrossRef]
- Gagliardi, F.; Catania, A.; Ria, A.; Bruschi, P.; Piotto, M. A Compact All-MOSFETs PVT-compensated Current Reference with Untrimmed 0.88%-(σ/μ). In Proceedings of the PRIME 2023—18th International Conference on Ph.D Research in Microelectronics and Electronics, Valencia, Spain, 18–21 June 2023; pp. 61–64. [Google Scholar] [CrossRef]
- Mohamed, A.R.; Chen, M.; Wang, G. Untrimmed CMOS Nano-Ampere Current Reference with Curvature-Compensation Scheme. In Proceedings of the ISCAS 2019—IEEE International Symposium on Circuits and Systems, Sapporo, Japan, 26–29 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Shima, T. Temperature insensitive current reference circuit using standard CMOS devices. In Proceedings of the 2007 50th Midwest Symposium on Circuits and Systems, Montreal, QC, Canada, 5–8 August 2007; pp. 181–184. [Google Scholar] [CrossRef]
- Rodovalho, L.H.; Toledo, P.; Bampi, S. A 0.6 V Current Reference Based on the MOSFET Forward-Body-Biased ZTC Condition. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 290–293. [Google Scholar] [CrossRef]
- Gagliardi, F.; Nannipieri, I.; Scognamiglio, M.; Contardi, S.; Ria, A. A PVT-Robust Beta-Multiplier Current Reference with Body-Effect-Based Temperature Dependency Modulation. In Proceedings of the PRIME 2024—19th International Conference on Ph.D Research in Microelectronics and Electronics, Larnaca, Cyprus, 9–12 June 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Lefebvre, M.; Bol, D. A nA-Range Area-Efficient Sub-100-ppm/°C Peaking Current Reference Using Forward Body Biasing in 0.11-µm Bulk and 22-nm FD-SOI. IEEE J. Solid-State Circuits 2025, 60, 579–592. [Google Scholar] [CrossRef]
- Amaravati, A.; Dave, M.; Baghini, M.S.; Sharma, D.K. 800-nA Process-and-Voltage-Invariant 106-dB PSRR PTAT Current Reference. IEEE Trans. Circuits Syst. II Express Briefs 2013, 60, 577–581. [Google Scholar] [CrossRef]
- Ji, Y.; Lee, J.; Kim, B.; Park, H.-J.; Sim, J.-Y. A 192-pW Voltage Reference Generating Bandgap-Vth With Process and Temperature Dependence Compensation. IEEE J. Solid-State Circuits 2019, 54, 3281–3291. [Google Scholar] [CrossRef]
- Wang, J.; He, J.; Law, M.-K.; Wang, X.; Liang, F.; Cheng, L. A 76.9 ppm/K Nano-Watt PVT-Insensitive CMOS Voltage Reference Operating From 4 to 300 K for Integrated Cryogenic Quantum Interface. IEEE J. Solid-State Circuits 2025. early access. [Google Scholar] [CrossRef]
- Van Staveren, J.; Almudever, C.G.; Scappucci, G.; Veldhorst, M.; Babaie, M.; Charbon, E.; Sebastiano, F. Voltage References for the Ultra-Wide Temperature Range from 4.2K to 300K in 40-nm CMOS. In Proceedings of the ESSCIRC 2019—IEEE 45th European Solid State Circuits Conference, Cracow, Poland, 23–26 September 2019; pp. 37–40. [Google Scholar] [CrossRef]
- Van Staveren, J.; Padalia, P.M.; Charbon, E.; Almudever, C.G.; Scappucci, G.; Babaie, M. Cryo-CMOS Voltage References for the Ultrawide Temperature Range From 300 K Down to 4.2 K. IEEE J. Solid-State Circuits 2024, 59, 2884–2894. [Google Scholar] [CrossRef]
- Hu, J.; Lu, C.; Xu, H.; Wang, J.; Liang, K.; Li, G. A novel precision CMOS current reference for IoT systems. AEÜ—Int. J. Electron. Commun. 2021, 130, 153577. [Google Scholar] [CrossRef]
- Azcona, C.; Calvo, B.; Celma, S.; Medrano, N.; Sanz, M.T. Precision CMOS current reference with process and temperature compensation. In Proceedings of the ISCAS 2014—IEEE International Symposium on Circuits and Systems, Melbourne, VIC, Australia, 1–5 June 2014; pp. 910–913. [Google Scholar] [CrossRef]
- Chouhan, S.S.; Halonen, K. A 0.67-µW 177-ppm/°C All-MOS Current Reference Circuit in a 0.18-µm CMOS Technology. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 723–727. [Google Scholar] [CrossRef]
- Lee, S.; Heinrich-Barna, S.; Noh, K.; Kunz, K.; Sánchez-Sinencio, E. A 1-nA 4.5-nW 289-ppm/°C Current Reference Using Automatic Calibration. IEEE J. Solid-State Circuits 2020, 55, 2498–2512. [Google Scholar] [CrossRef]
- Huang, W.; Liu, L.; Zhu, Z. A Sub-200nW All-in-One Bandgap Voltage and Current Reference Without Amplifiers. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 121–125. [Google Scholar] [CrossRef]
- Veit, D.; Oehm, J. A Current Reference With Multiple Nonlinear Current Mirrors to Reduce Noise, Mismatch, and Impact of Supply Voltage Variation. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 1729–1733. [Google Scholar] [CrossRef]
- Huang, Q.; Zhan, C.; Wang, L.; Li, Z.; Pan, Q. A −40 °C to 120 °C, 169 ppm/°C Nano-Ampere CMOS Current Reference. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1494–1498. [Google Scholar] [CrossRef]
- Ballo, A.; Grasso, A.D.; Privitera, M. A 28-nm, 0.5-V, 78.5-nA Switched Capacitor Current Reference with Active Trimming for sub-1V Implantable Medical Devices. In Proceedings of the 2023 IEEE International Symposium on Circuits and Systems (ISCAS), Monterey, CA, USA, 21–25 May 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Filanovsky, I.M.; Allam, A. Mutual Compensation of Mobility and Threshold Voltage Temperature Effects with Applications in CMOS Circuits. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 876–884. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Wang, R.; Sun, Z.; Huang, R. Body Bias Dependence of Bias Temperature Instability (BTI) in Bulk FinFET Technology. Energy Environ. Mater. 2021, 5, 1200–1203. [Google Scholar] [CrossRef]
- Enz, C.C.; Krummenacher, F.; Vittoz, E.A. An analytical MOS transistor model valid in all regions of operation and dedicated to low-voltage and low-current applications. Analog. Integr. Circuits Signal Process. 1995, 8, 83–114. [Google Scholar] [CrossRef]
- Dei, M. Heuristic Enz–Krummenacher–Vittoz (EKV) Model Fitting for Low-Power Integrated Circuit Design: An Open-Source Implementation. Electronics 2025, 6, 1162. [Google Scholar] [CrossRef]
- Kroell, K.E.; Ackermann, G.K. Threshold voltage of narrow channel field effect transistors. Solid-State Electron. 1976, 19, 77–81. [Google Scholar] [CrossRef]
- Kim, T.-H.; Eom, H.; Keane, J.; Kim, C. Utilizing reverse short channel effect for optimal subthreshold circuit design. In Proceedings of the ISLPED 2006—International Symposium on Low Power Electronics and Design, Tegernsee, Germany, 4–6 October 2006; pp. 127–130. [Google Scholar] [CrossRef]
- Khanna, V.K. Short-Channel Effects in MOSFETs. In NanoScience and Technology—Integrated Nanoelectronics; Springer: New Delhi, India, 2016. [Google Scholar] [CrossRef]
- Sze, S.M.; Li, Y.; Ng, K.K. Physics of Semiconductor Devices, 4th ed.; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Jooq, M.K.Q.; Bozorgmehr, A.; Mirzakuchaki, S. An ultra-miniature broadband operational transconductance amplifier utilizing 10 nm wrap-gate CNTFET technology. Analog. Integr. Circuits Signal Process. 2021, 107, 423–434. [Google Scholar] [CrossRef]
- Ballo, A.; Grasso, A.D.; Palumbo, G. Charge Pump Improvement for Energy Harvesting Applications by Node Pre-Charging. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3312–3316. [Google Scholar] [CrossRef]
- Gagliardi, F.; Ria, A.; Piotto, M.; Bruschi, P. A 114 ppm/°C-TC 0.78%-(σ/μ) Current Reference with Minimum-Current-Search Calibration. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 1561–1565. [Google Scholar] [CrossRef]
- Park, P.; Lee, J.; Cho, S. A PVT-Insensitive Sub-Ranging Current Reference Achieving 11.4-ppm/°C From −20 °C to 125 °C. IEEE J. Solid-State Circuits 2024, 59, 4057–4067. [Google Scholar] [CrossRef]
- Gagliardi, F.; Scognamiglio, M.; Ria, A.; Piotto, M.; Bruschi, P. All-MOSFETs Current Reference Featuring High-Order Segmented Curvature Compensation. In Proceedings of the ICECS 2024—31st IEEE International Conference on Electronics Circuits and Systems, Nancy, France, 18–20 November 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, J.; Goh, W.L. A 12.4-kHz on-chip RC oscillator with comparator offset cancellation for PVT variation tolerance. In Proceedings of the 2016 International Symposium on Integrated Circuits (ISIC), Singapore, 12–14 December 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Gagliardi, F.; Dei, M. Accuracy Enhancement of Resistor-String Digital-to-Analog Converters through Averaging Dynamic Element Matching. In Proceedings of the 2025 IEEE 28th International Symposium on Design and Diagnostics of Electronic Circuits and Systems (DDECS), Lyon, France, 5–7 May 2025; pp. 74–79. [Google Scholar] [CrossRef]
- Jiang, K.; Ji, Y.; Kosunen, M.; Kim, K. A 2.3nA-to-205nA Clock-Tunable Dynamic Current Reference with a Built-In 2nd-Order Current-Mode Low-Pass Filter and Coarse-Fine Regulation. In Proceedings of the 2025 23rd IEEE International NEWCAS Conference (NEWCAS), Paris, France, 22–25 June 2025. [Google Scholar]






| Device | Width (µm) | Length (µm) | Multiplicity | Stack |
|---|---|---|---|---|
| , , | 5 | 3 | 16, 16, 4 | 1 |
| 2 | 1 | 2 | 16 | |
| 7.52 | 3.76 | 1 | 16 | |
| , , | 5 | 0.5 | 16, 48, 4 | 1 |
| 1 | 1 | 1 | 16 | |
| , , | 1 | 0.3 | 1, 1, 8 | 1 |
| 0.25 | 5 | 1 | 2 |
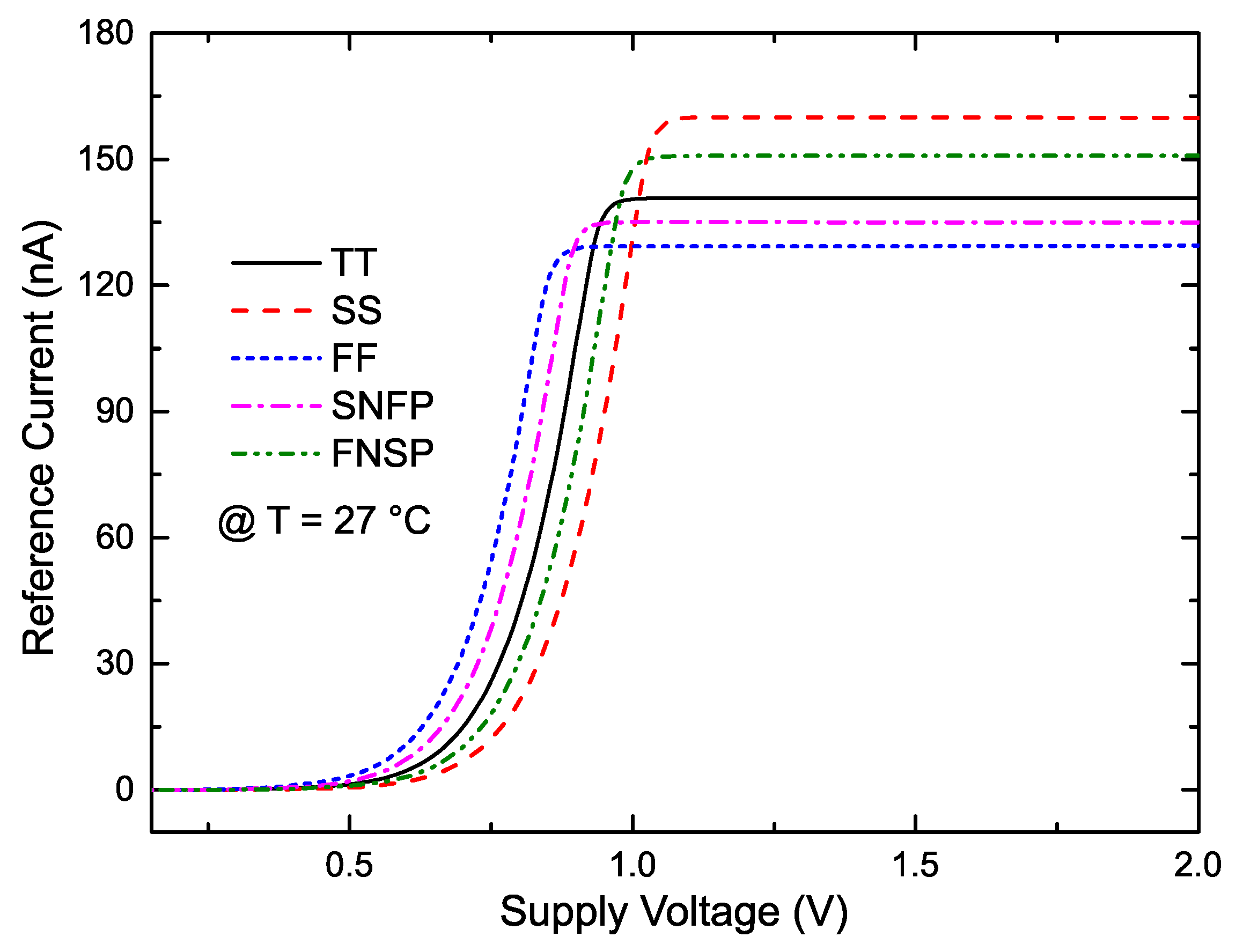
| TT | SS | FF | SNFP | FNSP | |
|---|---|---|---|---|---|
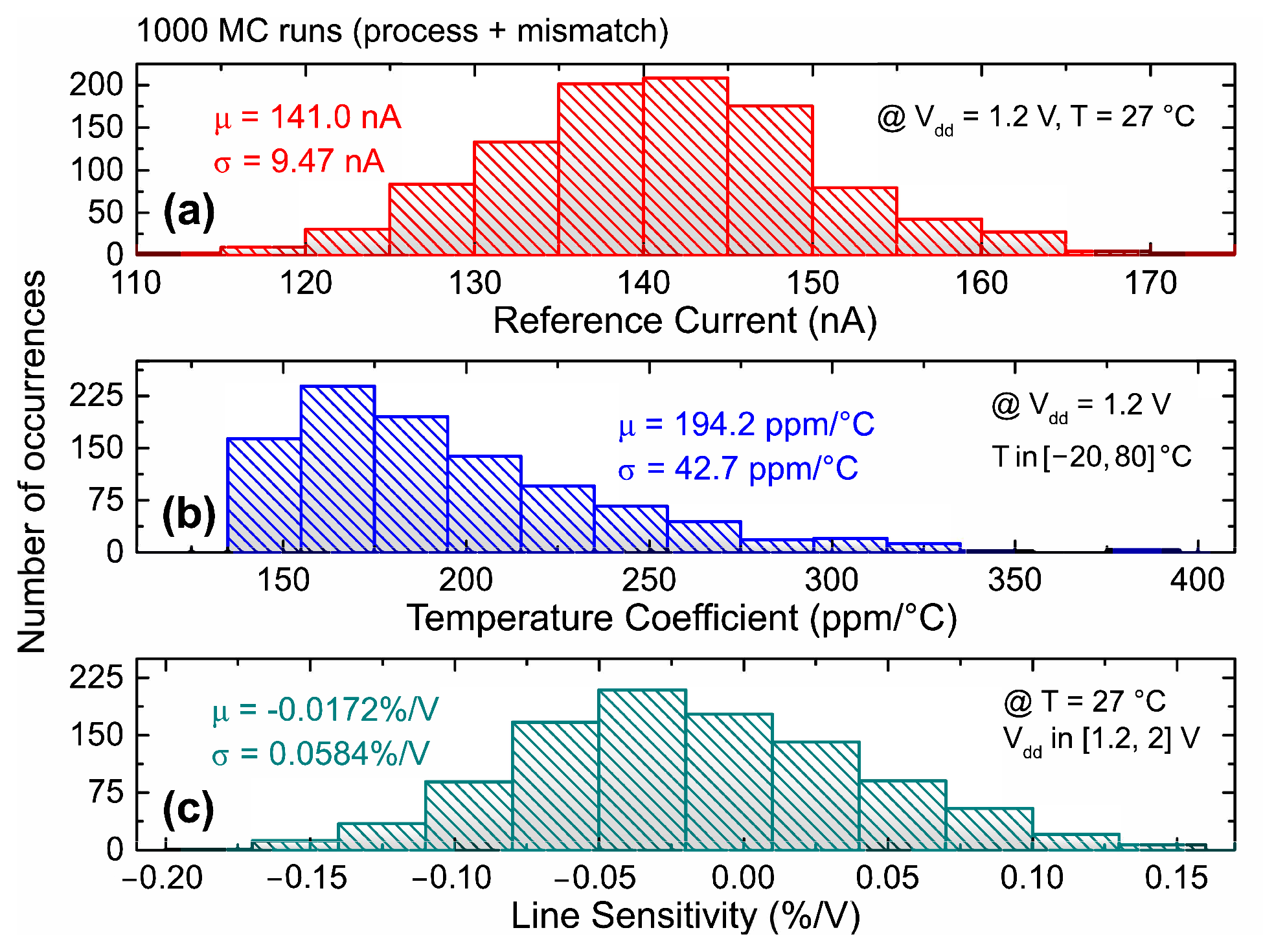
| (nA) | 140.7 | 160 | 129.3 | 135.1 | 150.8 |
| (nA) | 314.2 | 355.8 | 290.2 | 301.9 | 336.2 |
| TC (ppm/°C) | 152.8 | 242.2 | 219.6 | 157.8 | 208.7 |
| LS (%/V) | −0.0251 | −0.0999 | 0.171 | −0.0801 | 0.0375 |
| This Work | [55] TCAS-II 2024 | [37] AEÜ 2021 | [38] ISCAS 2014 | [27] ISCAS 2019 | [39] TCAS-II 2016 | [43] TCAS-II 2020 | [40] JSSC 2020 | [41] TCAS-II 2021 | [31] JSSC 2024 | [44] ISCAS 2023 | [42] TCAS-II 2023 | [56] JSSC 2024 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Techn. (nm) | 180 | 180 | 180 | 180 | 180 | 180 | 180 | 180 | 180 | 22 | 28 | 180 | 180 |
| Results type | Sim. | Sim. | Sim. | Sim. | Sim. | Meas. | Meas. | Meas. | Meas. | Meas. | Sim. | Meas. | Meas. |
| Approach | BM+ RSCE | BM+ SCC | BM | BM | BM+ ZTC | BM | BM | Auto calib. | BM+ BJT | BM | SC | BM | BJT+ DEM |
| CMOS only | Yes | Yes | No | No | Yes | Yes | Yes | Yes | No | No | Yes | Yes | No |
| Trimming | No | No | No | Yes | No | No | Yes | Yes | Yes | Yes | Yes | No | Yes |
| (V) | 1.2 | 1.4 | 0.6 | 1.2 | 1.2 | 1.25 | 0.8 | 1.5 | 2 | 0.75 | 0.5 | 2 | 1.3 |
| (nA) | 314.2 | 1916 | 345 | 1650 | 684 | 372 | 60.8 | N/A | 96 | 3.8 | 103 | 71.1·103 | 43.5·103 |
| (nA) | 141 * | 469 | 115 | 500 | 142 | 92.3 | 11.6 | 1 | 51 | 1.5 | 78.5 | 8.5·103 | 10.3·103 |
| (%) | 6.7 | 0.78 | 5.46 | 0.43 | 3.16 | 6.12 | 4.65 | 0.06 | 1.15 | 0.61 | 3.45 | 2.13 | 0.54 |
| range (°C) | −20, 80 | −20, 80 | −20, 120 | −40, 120 | −40, 85 | −40, 85 | −40, 120 | −20, 80 | −45, 125 | −40, 85 | −20, 60 | −35, 125 | −20, 125 |
| TC (ppm/°C) | 194 * | 114 * | 15.7 # | 119 † | 56.4 * | 177 * | 169 * | 289 * | 89 * | 89 * | 115 ‡ | 2740 | 11.4 |
| LS (%/V) | −0.017 * | 3.61 | 0.04 | 6.91 | 1.45 | 7.5 | 1.08 | 1.4 | 1.76 | 0.51 | 1.2 | 0.3 | 0.036 |
| RMS noise (pARMS) | 43.31 (0.1–10 Hz) | N/A | 14.7 (0.1–10 Hz) | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | 2750 (10–50 kHz) | 38.9 (0.01–10 Hz) |
| Area (mm2) | 0.00315 | 0.080 | 0.008 | N/A | N/A | 0.001 | 0.054 | 0.332 | 0.063 | 0.002 | 0.002 | 0.11 | 0.08 |
| FoM | 0.00231 | 13.5 | 0.001 | N/A | N/A | 0.428 | 3.23 | N/A | 1.09 | 0.0184 | 0.0453 | 47.3 | 0.00956 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gagliardi, F.; Ria, A.; Piotto, M.; Bruschi, P. A CMOS Current Reference with Novel Temperature Compensation Based on Geometry-Dependent Threshold Voltage Effects. Electronics 2025, 14, 2698. https://doi.org/10.3390/electronics14132698
Gagliardi F, Ria A, Piotto M, Bruschi P. A CMOS Current Reference with Novel Temperature Compensation Based on Geometry-Dependent Threshold Voltage Effects. Electronics. 2025; 14(13):2698. https://doi.org/10.3390/electronics14132698
Chicago/Turabian StyleGagliardi, Francesco, Andrea Ria, Massimo Piotto, and Paolo Bruschi. 2025. "A CMOS Current Reference with Novel Temperature Compensation Based on Geometry-Dependent Threshold Voltage Effects" Electronics 14, no. 13: 2698. https://doi.org/10.3390/electronics14132698
APA StyleGagliardi, F., Ria, A., Piotto, M., & Bruschi, P. (2025). A CMOS Current Reference with Novel Temperature Compensation Based on Geometry-Dependent Threshold Voltage Effects. Electronics, 14(13), 2698. https://doi.org/10.3390/electronics14132698









