1. Introduction
Special autonomous robotics systems (e.g., legged robots) have recently been successfully used in various reconnaissance missions. In 2009, DARPA started a legged squad support system (LS3) project to develop a legged robot that can function autonomously as a pack horse for a squad of soldiers or marines. Under the LS3 project, a series of quadruped robotic systems have been developed in the U.S., including “Spot,” “Mini-Spot” from Boston Dynamics, “Vision 60,” “Spirit 40” from Ghost Robotics, “Cheetah,” “Mini-Cheetah” from MIT, etc. Due to the substantial potential for future search and rescue missions, quadruped robotic development has also attracted international attention. It includes “ANYmal” from ANYbotics in Switzerland, “BEX” from Kawasaki Heavy Industries in Japan, “Go 1” from Unitree Robotics in China, and so on. However, those platforms with their out-of-the-box controllers have limited adaptability for challenging environments such as highly uneven, obstructed, and uncertain terrain [
1,
2]. Also, all existing quadruped robots suffer from limited agility, primarily due to high computational complexity that is often unaffordable for onboard systems [
3,
4] and slow mobility caused by inefficient real-time sensing capability [
5,
6]. Several control strategies have been developed to improve the locomotion of quadruped robots over uncertain terrains. Model predictive control (MPC) has emerged as a promising solution to incorporate constraints and optimization objectives directly in the control formulation [
7]. It has been widely applied in quadruped locomotion for its ability to handle multi-variable constraints and anticipate future states based on the given model. Early implementations, such as Di Carlo et al. [
8], demonstrated convex MPC formulations on MIT’s
Cheetah 3, enabling fast and efficient trajectory planning. These works, however, rely on simplified centroidal dynamics and assume relatively structured environments. Subsequent research [
9] proposed Whole body control (WBC) and whole body impulse control (WBIC) [
7,
10] to improve stability and dynamic consistency across different contact modes. In their implementation, traditional MPC is used to generate the center of mass (CoM) trajectory, whereas WBC focuses on following the generated CoM trajectory by manipulating the actuators and joint positions. This approach presents a viable way, as it provides a dynamically consistent formulation that makes it scalable to more complex systems as well as varied tasks; however, they are not effective in providing enough computations for frequent non-contact phases as required during high-speed running modes. To address this, ref. [
11] formulate WBC to follow both reaction forces and CoM trajectories by incorporating pre-computed reaction forces given by MPC as desired reaction forces and relaxing the floating base control. But this strategy is still inefficient when unstructured and uneven terrain operation is considered.
Alternative approaches—particularly learning-based methods—have demonstrated compelling results in challenging real-world conditions. For example, ref. [
12] proposed a reinforcement learning-based control pipeline for the ANYmal robot that enabled agile navigation through complex tasks such as stair climbing, gap crossing, and even parkour-style maneuvers. Nonetheless, their dependence on extensive training data, high computational demand, a clear view of foothold positions, and limited generalizability to out-of-distribution terrains remain key drawbacks in practical deployment. Despite recent advances, current quadruped control architectures lack an integrated framework that can simultaneously handle hybrid dynamic modeling, terrain uncertainty, and real-time control with minimal sensing dependencies. This gap becomes critical in field deployments where exteroceptive sensors are unreliable or unavailable. Thus, there is a need to identify and recognize the terrain at low computational costs before utilizing model predictive control for a quadruped robot working in an unstructured setting. Researchers in [
13] provided a simple and inexpensive way of classifying the terrain using only the time series data from the actuator. However, to further use this valuable information in a hierarchical way such that the optimization objective is solved at each time step has still not been addressed as evident in the literature survey of articles from [
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35].
This work aims to address these gaps by proposing a novel, proprioception-enhanced switching control framework. Our approach combines a bi-level hybrid dynamic model with a three-layer control architecture that integrates real-time IMU-based proprioceptive sensing, switching MPC for gait and trajectory adaptation, and distributed control for leg stability. This framework is designed to enhance adaptability, reduce computational complexity, and enable robust locomotion across a wide range of unstructured terrains at high speed. With this, the following challenges are addressed:
Lacking effective modeling techniques that consider the terrain and robotic limb reaction forces together.
Lacking robust control that provides quadruped robot stability in discontinuous events caused by uncertain terrains.
Lacking effective framework that considers both the modeling and control in a unified framework.
The development and validation of control strategies are elaborated here that can leverage both the simplified torso dynamics and the detailed leg dynamics by real-time feedback from a network of connected inertial measurement units (IMUs) placed at key locations of the quadruped robot skeleton. The new type of proprioceptive sensing-assisted control can improve the robot’s stability, adaptability, and overall performance even in challenging environments. Specifically, this paper introduces:
Situation-aware Hierarchical Bi-level Hybrid Dynamic Modeling: This strategy reduces the model complexity by integrating kinetic dynamics and multi-body dynamics hierarchically, thereby enhancing model agility by representing the multi-body dynamics in a distributed interconnected manner, and strengthens model scalability by incorporating a situation-driven multi-modal switched system modeling.
Hierarchical Hybrid Switching Control Framework: This strategy uses a three-layer hybrid control scheme that includes switching model predictive control to optimize the moving trajectory and gait schedule, robust distributed impulse torque control to enhance robotic leg robustness without increasing computational complexity, and fast-switched proportional derivative (PD) control to enhance the adaptability of quadruped robots.
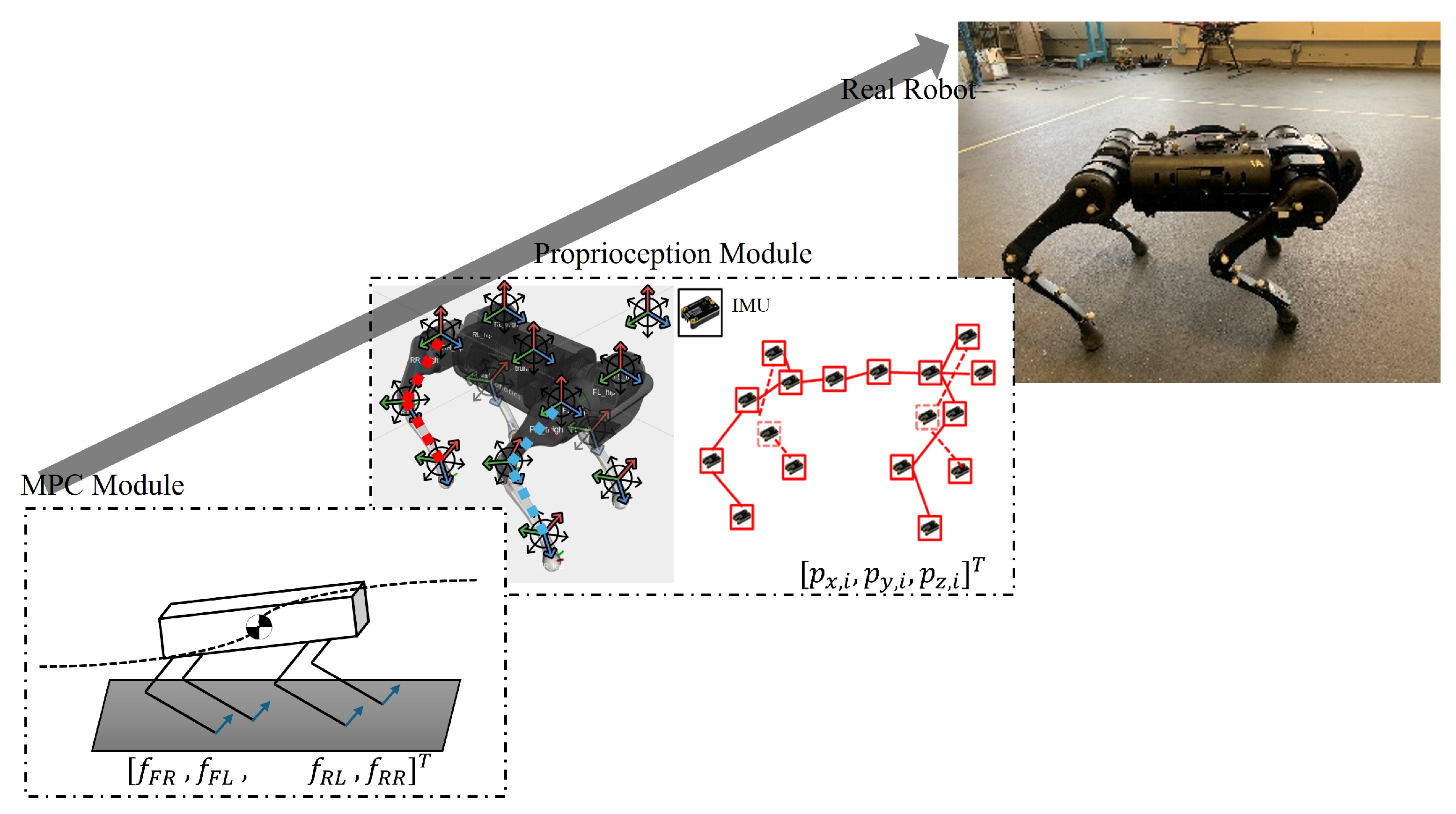
Figure 1 shows the control architecture, and
Figure 2 shows the overall framework. Both of these depict the data flow model that operates in a hierarchy. IMU-based proprioceptive state estimates, CoM trajectory, and the robot actuator states flow into the hybrid modeling and switched controller, and the solution of the co-joint algorithm feeds back into the quadruped robot, and the cycle continues until the goal is reached.
2. Methods
2.1. IMU-Based Proprioception Sensing
Proprioceptive sensing refers to the capability of biological creatures to sense the relative position of their bodies and limbs without relying on visual cues. This sense is critical for performing complex movements, maintaining balance, and reacting to unexpected changes in the environment. In robotic systems, proprioception is equally important, particularly for legged robots operating in harsh environments where external sensors like cameras or LiDAR may be obstructed, impaired by dust, rain, or darkness, or simply insufficient to provide the detailed information needed for precise control. Uneven terrains present unique challenges that make proprioceptive sensing not just beneficial but necessary for effective locomotion. Recent works, such as Chen et al. [
36], have shown that proprioceptive sensing can significantly improve energy efficiency and adaptability through optimized foothold planning and posture adjustment. These findings support the use of IMUs and internal sensors as a reliable alternative or complement to exteroceptive systems for terrain-adaptive locomotion. IMUs are efficient in providing instantaneous movement information but lack long-term tracking information due to inherent biases. This makes these sensors suitable for implementing them as a key proprioceptive tool. With the rise of computationally cheap off-the-shelf inertial measurement units researchers [
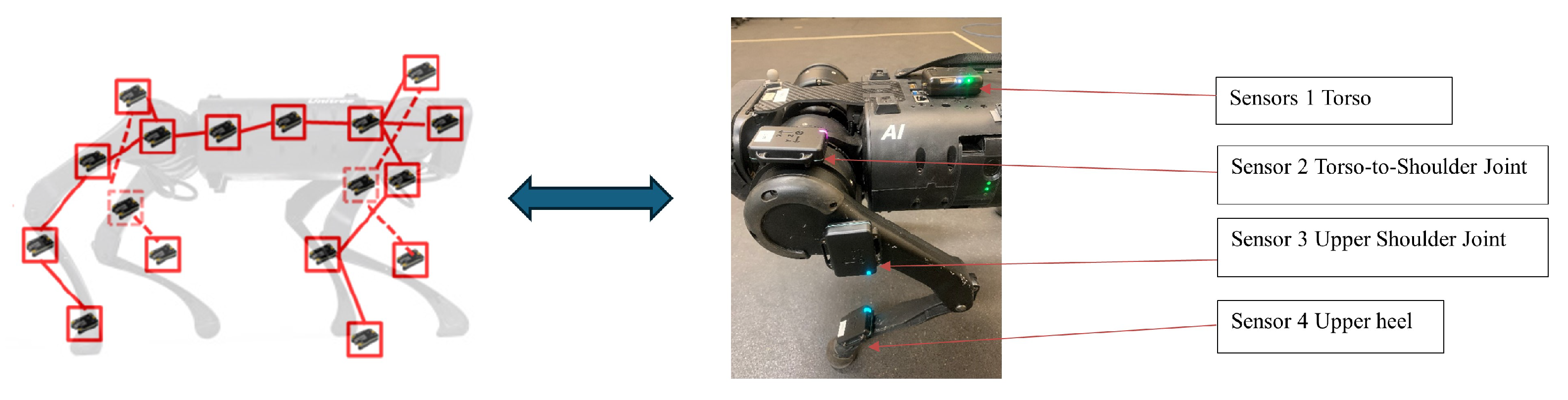
16] have been able to include multiple IMU units to estimate the traversed trajectory of the robots. However, they have not used an IMU to complement the proprioceptive sensing information. This paper introduces strategic placement of these IMUs on key joints of a four-legged robot that can enhance the robot’s proprioceptive capabilities as depicted in
Figure 3. Each IMU sensor provides localized data that, when integrated, offers a comprehensive understanding of the robot’s overall posture and movement dynamics, leading to a well-versed robotic dynamic model.
The challenges of modeling the quadruped robotic system lie in the trade-off between modeling accuracy and modeling complexity and the conflicts between limited onboard sensors and uncertain, challenging terrains. To overcome the challenges, this paper develops a model to reformulate the quadruped robot model hierarchically to enable parallel computing and use simple distributed proprioception sensors to enable enhanced state estimation. A specified form of the distributed multi-body dynamic model for the quadruped robot is shown in
Figure 3. Inertial measurement units (IMUs) were selected for proprioception due to their advantages at low energy cost, low latency, and easy integration with other sensors.
Each leg is modeled separately as shown below:
These equations are further simplified as
where
denotes the output of subsystem
, where
represents the coupling output and
is the corresponding output function for leg
.
Similarly, and represent the output of the front and back subsystems, respectively. represents subsystem state, represents subsystem input, and represents coupling input.
Unlike existing research for state estimation using IMUs, this subsection develops a novel unified two-layer deep mathematical model that thoroughly represents kinetic state space for the quadruped robot. This representation intelligently and seamlessly integrates the four key quadruped robot proprioceptive state estimation components, marking the first time this has been carried out. The structure of the developed quadruped robot kinetic state-space model is shown in
Figure 4.
Layer-1: Motion Pattern Model learning (High-level learning): The main goal of this layer is to process the raw data from multi-inertial sensors and generate the critical states that will be used for PVT estimation and quadruped robot proprioception in the next layer. Specifically, this layer includes four components, i.e.,
Motion Classification and Step Detection (MCSD) Model: To better classify motion and detect gaits, this block develops a novel Time-Series Continuous-State Markov Model (TS-CSMM). By using time-series inertial sensing data, the motion classification and step detection accuracy can be significantly improved.
Adaptive Kalman Filter (AKF): The developed AKF effectively reduces the effects of environmental noise and sensor errors adaptively.
Supervise Gait Length and Heading Estimation (SLH-E) Model: A time-series probability mathematical model is generated that can better supervise the gait length and heading estimation online.
IMU-based Position and Attitude Estimation Model: Using the inertial sensing data along with inertial navigation computation, a position and attitude estimation model is built. It integrates with the SLHE model to enable 3D quadruped robot proprioceptive sensing.
Next, using the learned motion pattern model as well as estimated navigation parameters, the uncertainties from the environment and unreliable data are compensated, allowing more accurate quadruped robot kinetic and whole-body model.
Layer-2: Motion Pattern Guided Quadruped Robot Modeling (Low-level learning): This layer aims to generate a time-series statistical mathematical model for 3D quadruped robot proprioceptive state estimation under harsh environments, e.g., GPS-denied areas, etc. Specifically, there are three key components developed in this layer, i.e.,
Continuous-Time Adaptive Particle Filter (CT-APT): To improve the accuracy of quadruped robot proprioceptive state-space modeling in real-time, the block CT-APT integrates a statistical approach with a particle filter.
Position, Velocity, Timing Estimation (PVT-E) Model: Integrating the SLH-E model with the IMU-based position and attitude estimation model from layer 1, a real-time PVT-E model is developed in Layer 2.
Quadruped Robot Proprioceptive State Model: Using the PVT-E model, the framework accurately computes the distance traveled as well as the elapsed time. A practical time-based objective moving model is generated in a 3D space, which is defined as the quadruped robot proprioceptive state model in this paper.
For proprioceptive modeling, vector
is constructed to represent values of 3D locations of joints relative to the body of the robot. And vector
is constructed to hold the ground reaction forces for each leg. This takes us to the goal of the presented development with a joint environment and quadruped robot state space as
2.2. Hybrid Dynamic Control Architecture
Quadruped robots operating in an unstructured and uneven terrain can be modeled as hybrid systems defined within a hybrid system framework to perform a quantitative analysis of gait scheduler or step planner. The framework proposed in this paper considers a quadruped robotic system as two coupled components, i.e., a floating base and four two-link legs. A step by step modeling is presented as follows: Numerous frameworks appear in literature for modeling such systems; these include [
14,
15]. According to the notations of the general framework, flow set (continuous-dynamics) is denoted by
, the jump set (discrete-dynamics) is denoted by
, the deferential equation is described by the flow map
, and the difference equation is defined by a jump map
. Then a hybrid dynamical system
can be expressed as
Collectively, the tuple
is called the data of
system.
Next, a controller that finds a series of optimal reaction forces for one gait cycle of locomotion by using MPC with a floating base model is expressed as [
7,
9,
11]
where
p,
, and
represent the robot’s vectored position, reaction force, and gravitational force in the world frame.
m is mass, and
is the number of contacts.
is the rotational inertial matrix.
Using the Hybrid Systems Framework Equation (
4) is rewritten as
Discrete-Dynamics:with
being the robot velocity and
being the robot angular velocity right before and after the discontinuous event (environmental impact).
The second controller is the body joint angle-torque controller, which takes in the reaction forces from the above equations and utilizes it to give joint torque, position, and velocity. The dynamic equation can be given in the similar form as [
7,
9,
11]
Discrete-Dynamics:where
are the generalized mass matrix, Coriolis force, gravitation force, joint torque, ground reaction force, and contact Jacobian, respectively.
is the acceleration of the floating base, and
is the vector of joint accelerations where
is the number of joints.
are the velocity of float base and joints before and after discontinuous events (environmental impact).
2.3. Proprioceptive Sensing Assisted Model Predictive Control
Model predictive control used in this framework produces a series of ground reaction forces that ensure the center of mass (CoM) follows the given trajectory. A predefined gait scheme with relaxed time bounding is fed, which makes this formulation a convex optimization problem. This makes it fast and easy to find the global minimum, unlike other nonlinear optimization formulations.
The floating base model, when approximated as a simple lumped mass, is prone to linearization errors due to the presence of the cross product term in Equation (
4). To fit this into convex MPC formulation, the following three assumptions [
8] are necessary: The first is that the roll and pitch angles are minor enough to be approximated from previous and next iteration steps. The second assumption is more related to the relaxed CoM trajectory tracking, which monitors the states the quadruped robot ends up in. If they are close enough to the commanded trajectory, they are qualified as executed. This assumption is further equated to the models saved inside the memory of robot. This is further presented in the event-triggered section. The last assumption is that the pitch and roll velocities and off-diagonal terms of inertia tensors are small enough to be ignored. With these assumptions, the following equations are listed:
where
is the Euler angle representation for the roll, pitch, and yaw for the robot.
is the rotational matrix.
are the inertial tensor forces in global and body frame, respectively.
With these assumptions, the discrete dynamics of the system is expressed as
where,
A general quadratic programming formulation is constructed using the above equations, which minimizes the state cost function as
subject to dynamics and initial constraints shown in Algorithm 1.
| Algorithm 1 Trajectory Optimization for Legged Robots |
- 1:
System Input (User Defined): Initial state of the system: Desired final state: Total time horizon: T Number of steps for each foot: - 2:
Initialize Decision Variables: CoM trajectory: Orientation: Foot positions: Contact forces: Phase duration for each foot: - 3:
Decide the Objective: Minimize the total energy or effort required for the motion: - 4:
Dynamics Constraints: Enforce dynamics constraints that relate CoM acceleration to contact forces given by equations in ( 9) and ( 10) above - 5:
Kinematic Constraints: Ensure that each foot stays within its workspace: - 6:
Contact and Force Constraints: Forces are only applied when feet are in contact: Non-slipping condition (Coulomb’s law):
where is the normal force, and is the friction coefficient. - 7:
Gait Discovery and Phase Duration: Use phase-based parameterization to optimize swing and stance duration : - 8:
Terrain Constraints: Ensure that foot height matches terrain height during stance phases: - 9:
Solve the QP using formulation in Equation (15): Optimize - 10:
Output: Optimized trajectories for: CoM position , Orientation , Foot positions , Contact forces
|
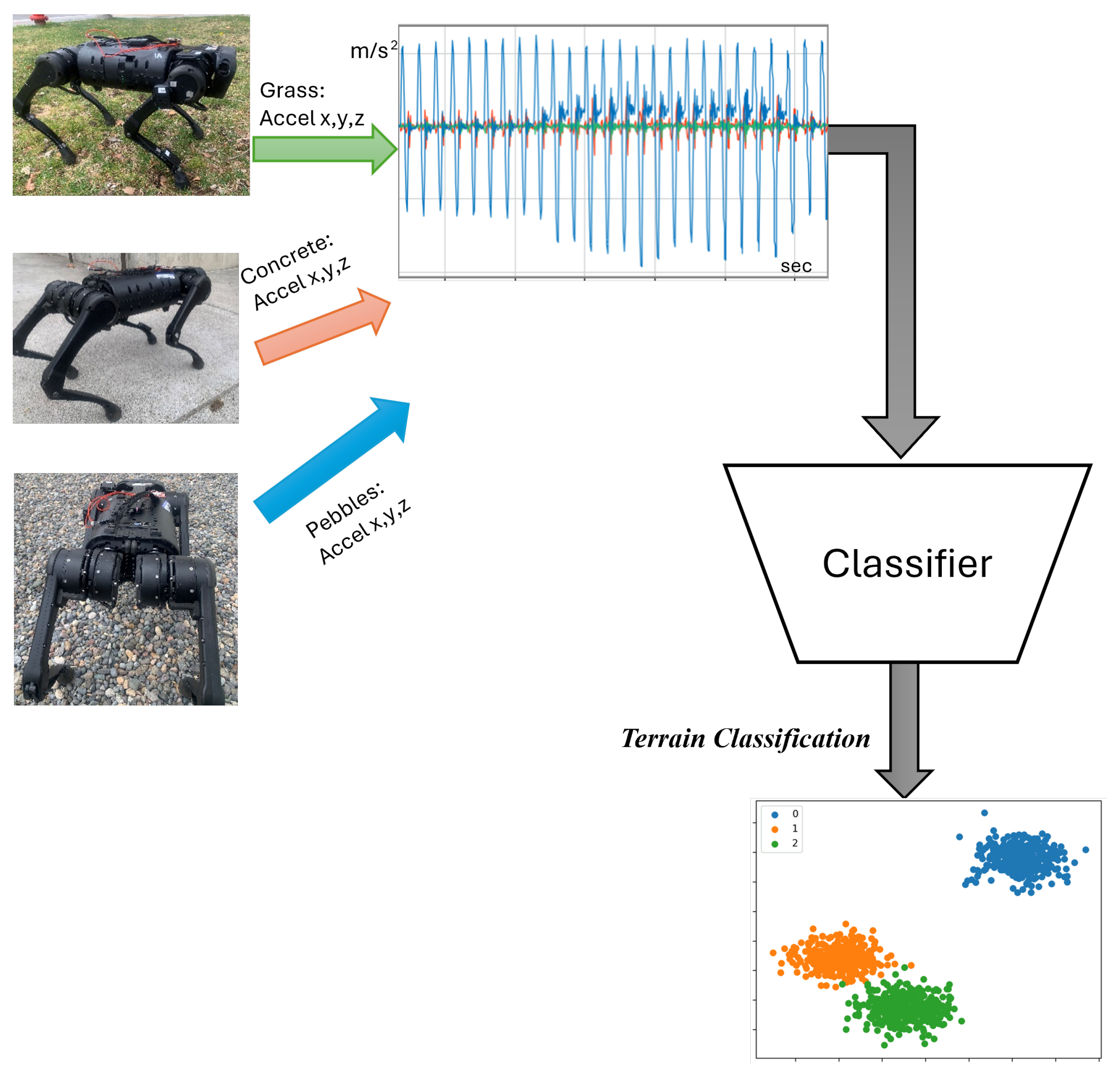
2.4. Motion Patterning and Terrain Adaptation
While proprioception is essential for state estimation and precise modeling of legged robots, exteroceptive sensors (IMU) provide crucial information about the robot’s surroundings, facilitating tasks such as navigation, obstacle avoidance, terrain analysis, and object manipulation. This subsection presents the significance of proprioception and exteroception in modeling and control design. Recognizing the high computational cost of processing high-dimensional data in real-time, a low-dimension embedding of the sensory data, as shown in
Figure 4, is learned, allowing for more efficient state estimation and environmental dynamics modeling. The low-dimensional data embedding is integrated into the proposed framework for state estimation and joint modeling.
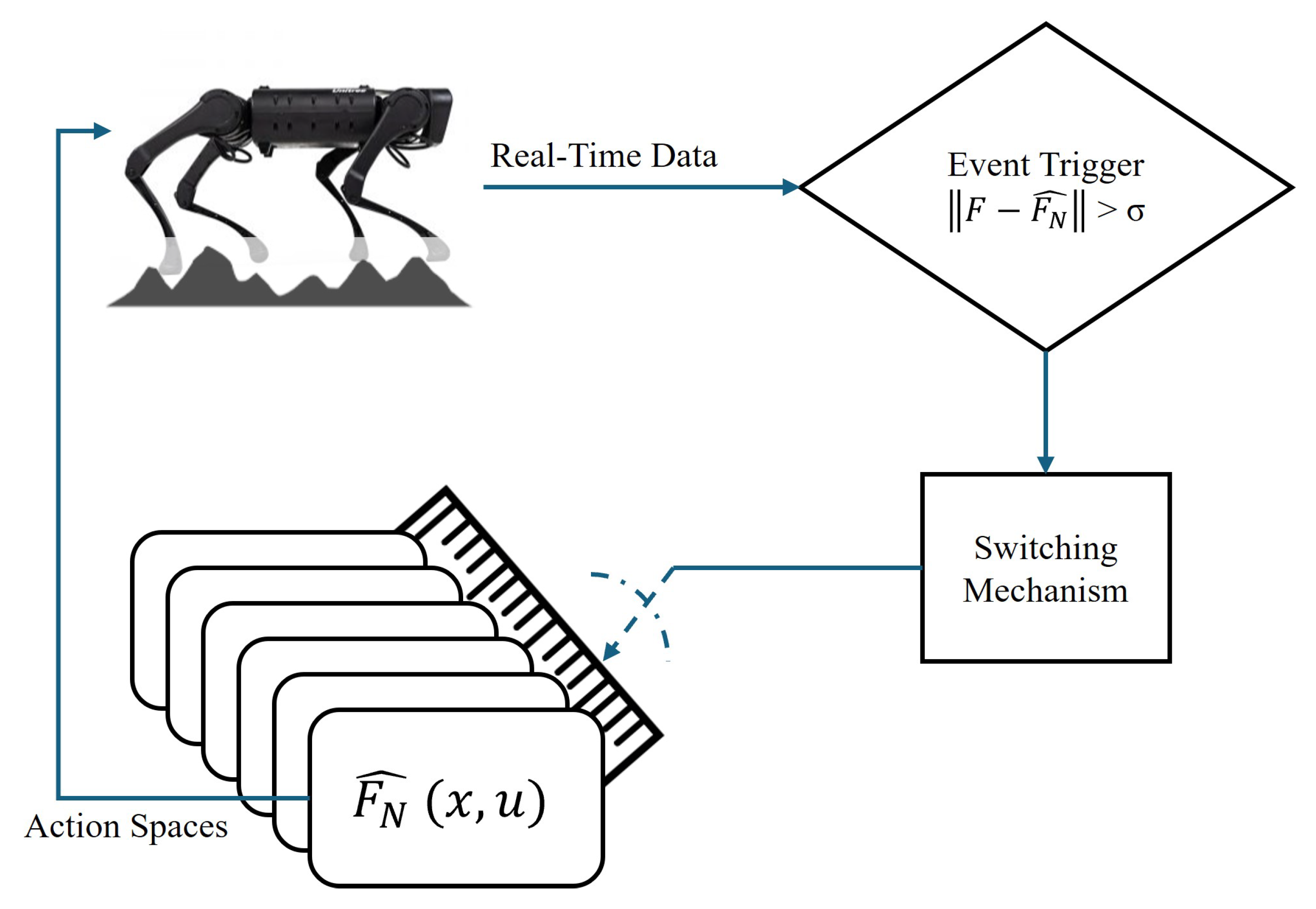
Figure 5 shows the process by which the multi-modal architecture is trained. The goal is to train
terrain models to comply with the equation
, which have different action spaces, and one model is triggered at one point in time. The triggering is completed by a switching mechanism that compares the real-time quadruped robot movement with estimated movement from an individual model that is trained as shown in
Figure 6.
2.4.1. Deep State Space for Continuous Motion Patterning
This part shows the development of the mechanism that estimates the practical time-based continuous motion pattern of the quadruped robot. The key idea here is to extend the traditional spatial motion pattern state space
into a novel spatio-temporal motion pattern state space
. According to [
34,
35] existing quadruped robot modeling research, the spatial motion pattern state space effectively transforms the collected IMU data, i.e., acceleration and angular rates
, to motion parameters, i.e.,
, under and identified motion pattern as:
Here,
and
represents the initial velocity and gravity, respectively;
represents the classified motion patterns under different terrains (e.g., walking on ice, running on grass, slow walking on rocky road, etc.), and
represents the i-th type of spatial motion pattern. It is important to note that quadruped robots might change their movement patterns continuously. Therefore, roughly switching among finite classified motion patterns might significantly degrade the parameter
estimation performance and seriously affect the accuracy of quadruped robot kinetic and whole-body modeling. To handle this intractable challenge, a novel spatial-temporal deep state space for representing continuously patterning trainees’ motion in real-time is given as follows:
Compared with the finite motion pattern set, that has been generated through spatial IMU data, our developed unique deep state-space-based continuous motion pattern is a time-based function that has been trained via spatio-temporal IMU data.
2.4.2. Online Motion Pattern Guided Quadruped Robot Model
The main tenet of the developed motion pattern guided model hinges on the following two key ideas:
Building a hierarchical deep learning architecture that processes the collected IMU data in different resolution levels to upgrade the accuracy level of quadruped robot modeling
Operating a two-layer deep learning algorithm in parallel that reduces the computational complexity and promotes its real-time efficiency.
Specifically, the proposed hierarchical deep learning is designed as
Layer 1: Motion Pattern Model learning (High-level learning)
A deep state-space continuous motion pattern model is trained through a novel 2-stage spatio-temporal NN:
Next, using the learned motion pattern model as well as estimated navigation parameters, the uncertainties from the environment and unreliable data are compensated, allowing a more accurate quadruped robot kinetic and whole-body model.
Layer 2: Motion Pattern Guided Quadruped Robot Modeling (Low-level learning)
To derive real-time navigation as well as deliver an accurate quadruped robot model, the starting location
and heading
, and the Cartesian projection can be represented as
with
being the nonlinear uncertainties from the environment. It is important to note that
can be obtained from the learned motion pattern model in Layer-1. However, even if one is able to generate a high-accuracy motion pattern model, the uncertainties
still cannot be fully compensated and will degrade the quadruped robot modeling and navigation performance. Therefore, a deep neural network-based uncertainty estimator is developed. It is used along with the learned motion pattern model to conduct high-accuracy and real-time quadruped robot modeling and navigation.
with the DNN-based uncertainty estimation being designed as
and DNN weights are updated as
Through hierarchical deep learning development, there is an improvement of the situation-aware quadruped robot kinetic and whole-body modeling and navigation accuracy and time efficiency through parallel computing shows the real deployment structure.
For the experimental results in a real-world setup, three different terrain classifications were used, and an unknown, highly uneven terrain was tested. With the help of this new mechanism, the accuracy of the model in real-world applications is increased. The final form of the equation with terrain uncertainties is written as
with
being the situation-aware dynamics model space basis set and
being the dimension of the constructed situation space.
is the real-time situation-aware robot dynamic model that is unknown due to the uncertainties for practical situations and terrains. Through effectively incorporating the uncertainties into the modeling, Equation (
24) can now solve the model predictive control with better accuracy.
4. Discussion
Robot Platform and Hardware Setup
The proposed control framework was implemented and tested on a pre-built quadruped robot Unitree-A1 platform with a modular architecture. Each leg is equipped with three actuated degrees of freedom (hip, thigh, and knee), driven by high-torque brushless DC motors with integrated encoders for joint feedback. The robot’s body is constructed from lightweight iron ore and carbon fiber composites, supporting a total payload of approximately 15 kg. For proprioceptive sensing, we integrated four low-cost MEMS-based inertial measurement units (IMUs) (x-IMU-3), strategically placed on the robot’s torso and one leg segment (
Figure 3). These IMUs provide real-time 6-DoF inertial data (acceleration and angular velocity) at 200 Hz. The sensors are connected to a central offboard computer (NVIDIA Jetson Xavier NX) wirelessly, which runs the hybrid dynamic modeling, sensor fusion, terrain classification, and switching MPC control loop in real time. All control algorithms were implemented in C++ and Python, with optimization routines solved using the OSQP QP solver. The full control pipeline runs at 120 Hz, while the terrain classifier operates asynchronously at 10 Hz. The system was tested indoors and outdoors over multiple terrain types, including flat concrete, grass, loose gravel, and sand, without relying on exteroceptive sensing.
Results
While there are a lot of highly dynamic robotic control implementations in the literature, most of them did not work well when the terrain was excessively uneven, as shown in the experiments (Link 1 and 2). In contrast to biological animals, which have a complex and versatile nervous system that gives instantaneous feedback from the ground reaction forces, which are almost independent of their brain’s reaction signals, these quadruped robotic systems lack this instantaneous feedback system. The goal was to replicate this nervous system parallel to its skeleton and independent of the model predictive control’s reaction force calculations. We set out with this research of replicating a “nervous system” of biological animals with the use of a network of IMUs, expecting to have an informed knowledge of the ground reaction forces. We were right in expecting the information would help in determining the right amount of torque required by each actuator; however, we were wrong in assuming the same torque calculations can be applied to all kinds of terrain. For example, we incorrectly assumed that we could use the same torque calculations for sandy surfaces and loose gravel with miniature rocks. The torque calculations for loose gravel would overshoot, while for sandy surfaces it was insufficient. Interestingly, for sandy surfaces and wet/muddy surfaces, the control calculations were relatively the same for a stable gait as opposed to the torque calculations for sandy surfaces and loose gravel. Hence, we decided to put an extra layer of terrain classification as an added knowledge base aiding torque calculations for a stable gait control across different terrain parameters. What surprised us was even though we had a small set of discrete terrain classifications, we were still able to navigate most of the previously unsuccessful experiments. From here, our next goal is to artificially generate intermediate imaginary terrain classifications between similar terrains and enlarge the model knowledge base for real-world applications without requiring prior training.
Figure 9 and
Figure 10 show the indoor experiment with position, velocity, acceleration, and ground reaction forces experienced by the quadruped robot with the commanded velocities as 0.5 m/s and trotting and pacing gaits as 1.0 m/s. This shows that state estimation and velocity command tracking are efficient and effective for indoor environments. Next, for the outdoor experiments, videos given in links 1 and 2 show the quadruped robot cannot maintain stability while using traditional reinforcement learning-enhanced controllers. The inability of the quadruped robot to determine the underlying uncertainty is apparent. However, when the quadruped robot is equipped with the developed situation-aware bi-level hybrid switched controller, its performance, including stability and resiliency, has been significantly improved even under uncertain outdoor environments. To benchmark the effectiveness of our proprioceptive switching MPC framework, we compared it against traditional MPC and reinforcement learning-based controllers across a variety of terrain conditions (e.g., rocky, sandy, and mixed debris). As shown in
Table 6, our method achieves a significantly lower position RMSE (0.5 m vs. 0.84 m for standard MPC), better velocity tracking, and a drastic reduction in instability events. Moreover, our framework maintains a fast average control cycle of 20 ms, enabling real-time deployment. These results confirm that integrating proprioceptive sensing with situation-aware switching leads to improved stability, responsiveness, and robustness, especially under uncertain terrain conditions.
Strengths, Limitations, and Generalizability
In summary, some of the key strengths of our methodology include terrain adaptability, sensor robustness, scalability, and modularity and real-time performance. In addition to these improvements, the authors also want to highlight some of the limitations still to be addressed in this field of research and hope to work on it in the future. These include: sensor drift, model dependency, and terrain class limitations. The low-cost IMUs, while fast and power-efficient, suffer from long-term drift. This “long-term” parameter varies with specific locomotion patterns, and periodic correction needs to be addressed in more depth. In terms of model dependency, our system, as with any other state-of-the-art implementation, does require prior knowledge of reasonably accurate dynamics models in the learning/data collection phase. Mismatches in these labels will degrade the performance. For terrain classification, while the authors had spent quite a lot of time gathering raw data for different terrains, intermediate or unseen terrain traversal was the main cause of reported instability in
Table 6. Our future work will address this limitation via online learning methods.
For researchers looking to adapt this methodology into their custom quadruped robot, the following generalization points need to be kept in mind:
Replacing the robot-specific dynamic model components with those tailored to the new platform (e.g., different limb morphology).
Adjusting the IMU sensor placements and retraining the terrain classification module using the new robot’s data.
Tuning MPC parameters and constraints to match the actuation capabilities and gait styles of the target robot.
This modular structure—combining proprioception, hybrid modeling, and switching control—makes the framework applicable to other legged platforms such as hexapods or humanoids, provided similar proprioceptive sensing and control primitives are available.
Contextualizing with Embodied Adaptive Control Approaches
Recent developments in biologically inspired control architectures have demonstrated the potential of embodied adaptive systems, which mimic neuromotor control seen in biological organisms. These systems often leverage spiking neural models, neuromechanical feedback, and dynamic learning to produce adaptive and robust locomotion. In particular, recent work on embodied motor neuron architectures has shown promise for integrating sensory feedback and control within the same computational units, offering low-latency, energy-efficient control mechanisms for dynamic and unstructured environments. Similarly, nullcline-based control strategies for piecewise-linear (PWL) oscillators provide a principled method to generate stable limit cycles and entrained gaits, with applications in rhythmic locomotion over uneven terrains. While our proposed framework does not explicitly adopt these bio-inspired mechanisms, it shares a number of design principles with embodied approaches:
It emphasizes distributed feedback through proprioceptive IMUs (analogous to biological sensory neurons).
It uses hierarchical and switching control, akin to how biological systems coordinate reflexive and voluntary motion layers.
It enables real-time adaptation to terrain perturbations, which is central to embodied locomotion control.
Future work can explore hybridizing the proposed model with embodied neuron-inspired architectures—for example, by replacing the switching logic with nullcline-based oscillators or integrating adaptive spiking neuron-based feedback for low-level torque modulation. This direction holds promise for further reducing computational cost while increasing biological plausibility and terrain generalization.