Secure Sharing of Electronic Medical Records Based on Blockchain and Searchable Encryption
Abstract
1. Introduction
2. Related Works
3. Proposed Framework
3.1. System Working Sequence
3.2. Basic Definition
- : Given the security parameter , the EMRSP randomly generates two keys, and . The variable serves as the static symmetric encryption key, and represents the CP-ABE key pair, where pk is the public key and msk is the main secret key.
- : Given the public key pk, the master secret key msk, and the user’s attribute, the EMRSP returns the corresponding attribute private key to the EMRDU. Given the security parameter , the EMRSP generates an encryption key .
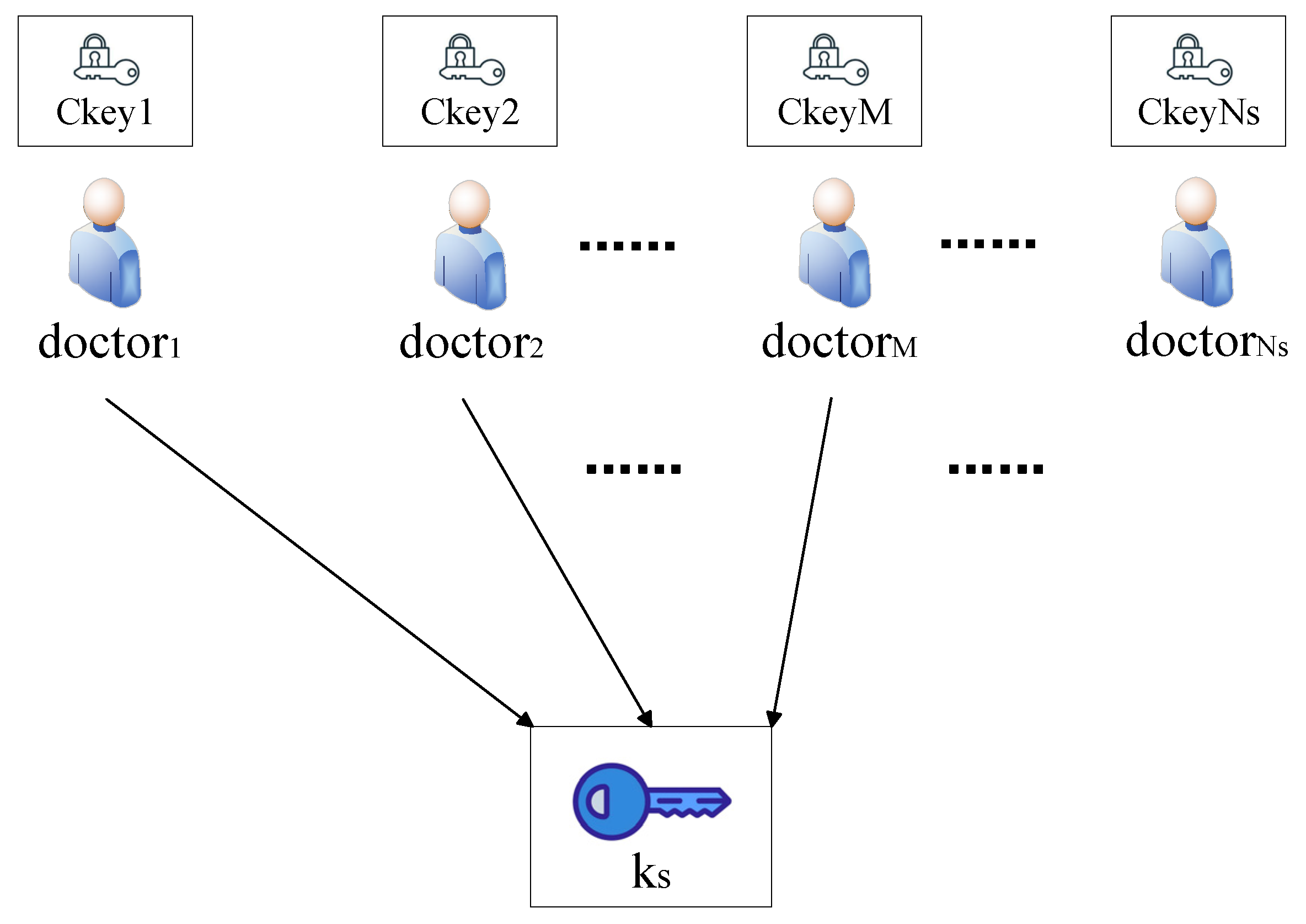
- : Given the public key , EMR set D, access policy, and symmetric key , the EMRSP outputs ciphertext C. The symmetric key is split into multiple shares using Shamir’s Secret Sharing, where represents the maximum number of all shares. The shares are encrypted to generate ciphertexts using CP-ABE. Then, the shares are sent to multiple trusted doctor nodes for storage. The encrypted data C will be stored in the IPFS.
- : This algorithm is designed for file index generation. Specifically, the EMRSP extracts a keyword set W from each original EMR file D and uses them to generate the file index I. I is encrypted using the key to generate the encrypted index . Then, the collection of all encrypted indexes is stored on the blockchain.
- : The query set is encrypted using to generate the trapdoor . The EMRDU sends the trapdoor to the search smart contract.
- : The search smart contract uses the encrypted index set and trapdoor to obtain the target file CID. Subsequently, the EMRDU can download the corresponding encrypted EMR from the IPFS via the CID.
- : The EMRDU use the attribute key ak to obtain from the specified doctor nodes. The symmetric key can be reconstructed only when a threshold number of shares is collected. The EMRDU downloads the corresponding EMR ciphertext via the CID. The symmetric key is used to obtain the ciphertext.
3.3. Specific Processes
3.3.1. Initialization
- Define two multiplicative cyclic groups and of prime order , and let be a generator of the group .
- Define a bilinear map e: .
- Select collision-resistant hash functions .
- Randomly choose and generate the master secret key .
- Generate a symmetric key .
- Output the system public parameters .
3.3.2. Key Generation
3.3.3. Encryption of EMR and Key
3.3.4. Index Generation
- Generate a -bit Bloom filter as the index I for each file in the EMR dataset.
- Select independent hash functions.
- Extract the keyword set from file D. The EMRSP inserts it into index I for each keyword by using hash functions.
- Given the security parameter , the encryption key is generated. are invertible matrices, and is a vector.
- The index I is encrypted under key sk, generating the ciphertext index . The encrypted index of files and their corresponding file CID form the access index for the EMR dataset , where is the maximum number of files. The encrypted index generation process is detailed in Algorithm 1:
| Algorithm 1: Index Generation |
| Input: , I |
| Output: |
| 1. Select random number , |
| 2. Initialize = [], = [] |
| 3: for j = 1 to Length(I) |
| 4: if then |
| 5: |
| 6: else × |
| 7: end else |
| 8: end if |
| 9: end for |
| 10: return |
3.3.5. Trapdoor Generation
- Generate a -bit Bloom filter Q for the query operation.
- Utilize l independent hash functions .
- For each query keyword , hash values are computed using the hash functions , and the results are inserted into the Bloom filter .
- The query string Q is encrypted with the key to generate the trapdoor. The EMRDU sends the trapdoor to the search smart contract and requests key shares from the trusted-doctor nodes. The trapdoor generation process is detailed in Algorithm 2:
| Algorithm 2: Trapdoor Generation |
| Input: , |
| Output: trapdoor |
| 1. Select random number , |
| 2. Initialize , |
| 3: for j = 1 to Length(I) |
| 4: if then |
| 5: |
| 6: else 7. |
| 8: end else |
| 9: end if |
| 10: end for 11: |
| 12: return |
3.3.6. Search Phase
| Algorithm 3: Search |
| Input: trapdoor , |
| Output: ID |
| 1: Extract from |
| 2: Calculate the inner product of index and trapdoor: |
| 3: |
| 4: if . Corresponding CID is added to ID |
| 5: else find the next file in the index collection |
| 6: return ID |
3.3.7. Decryption Phase
| Algorithm 4: Decryption |
| Input: , CID |
| Output: D |
| 1: if matcℎ(policy, ak) == false |
| 2: return |
| 3: end if |
| 4: else if matcℎ(policy, ak) == true |
| 5: return . |
| 6: end else 7. The symmetric key is reconstructed by applying Lagrange interpolation. 8. The destination file corresponding to CID is decrypted via , and the plaintext D is obtained. 9. return D |
4. Experimental Results and Analysis
4.1. Theoretical Evaluation
4.1.1. Security
4.1.2. Correctness
4.1.3. Single Point of Failure Resilience
4.2. Functionality Comparison
4.3. Experimental Results
- P: The running time of the bilinear pairing operation, which is 5.787 ms;
- M: The running time of the scalar multiplication operation, which is 2.355 ms;
- E: The running time of the exponentiation operation, which is 0.794 ms.
| Scheme | EncInd/ms | Trapdoor/ms | Search/ms |
|---|---|---|---|
| RKSE-SM9 | me(2M + E) | ls(M) | lsP |
| VMKS-ABE | (me + 1)E | ls(E) | lsP |
| Ours | 1.062 | 77.894 | 0.01 |
4.3.1. Index Generation Time
4.3.2. Trapdoor Generation Time
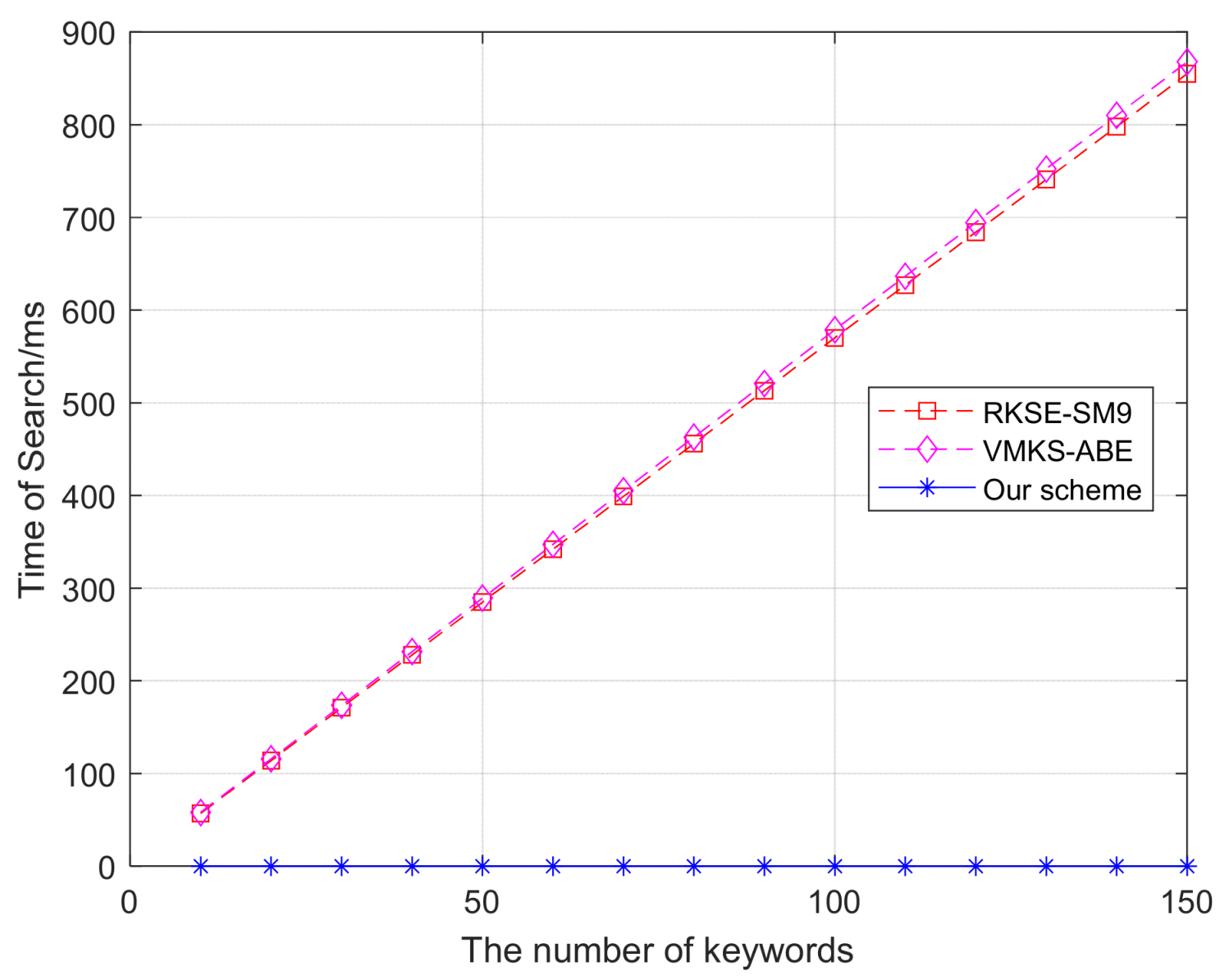
4.3.3. Search Time
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tariq, U.U.; Sabrina, F.; Rashid, M.M.; Gordon, S.; Lin, Y.F.; Wang, Z.L.; Azad, S. Blockchain-Based Secured Data Sharing in Healthcare: A Systematic Literature Review. IEEE Access 2025, 13, 45415–45435. [Google Scholar] [CrossRef]
- Dobrzykowski, D.D.; Tarafdar, M. Linking Electronic Medical Records Use to Physicians’ Performance: A Contextual Analysis. Decis. Sci. 2017, 48, 7–38. [Google Scholar] [CrossRef]
- Lin, C.; Huang, X.Y.; He, D.B. Efficient Blockchain-Based Electronic Medical Record Sharing with Anti-Malicious Propagation. IEEE Trans. Serv. Comput. 2023, 16, 3294–3304. [Google Scholar] [CrossRef]
- Zhu, P.; Hu, J.; Li, X.T.; Zhu, Q.Y. Using blockchain technology to enhance the traceability of original achievements. IEEE Trans. Eng. Manag. 2023, 70, 1693–1707. [Google Scholar] [CrossRef]
- Wu, D.Y.; Xu, Z.W.; Chen, B.; Zhang, Y.J.; Han, Z. Enforcing access control in information-centric edge networking. IEEE Trans. Commun. 2021, 69, 353–364. [Google Scholar] [CrossRef]
- Zhu, P.; Hu, J.; Zhang, Y.; Li, X.T. Enhancing traceability of infectious diseases: A blockchain-based approach. Inf. Process. Manag. 2021, 58, 102570. [Google Scholar] [CrossRef]
- Nizamuddin, N.; Salah, K.; Azad, M.A.; Arshad, J.; Rehman, M.H. Decentralized document version control using ethereum blockchain and IPFS. Comput. Electr. Eng. 2019, 76, 183–197. [Google Scholar] [CrossRef]
- Islam, M.S.; Ameedeen, M.A.B.; Ajra, H.; Ismail, Z.B. Blockchain-enabled Secure Privacy-preserving System for Public Health-center Data. Int. J. Adv. Comput. Sci. Appl. IJACSA 2023, 14, 1147–1154. [Google Scholar] [CrossRef]
- Waghe, P.U.; Kumar, A.S.; Prasad, A.B.; Rao, V.S.; Thenmozhi, E.; Godla, S.R.; El-Ebiary, Y.A.B. Blockchain-Enabled Cybersecurity Framework for Safeguarding Patient Data in Medical Informatics. Int. J. Adv. Comput. Sci. Appl. IJACSA 2024, 15, 797–808. [Google Scholar] [CrossRef]
- Elghoul, M.K.; Bahgat, S.F.; Hussein, A.S.; Hamad, S.H. Securing Patient Medical Records with Blockchain Technology in Cloud-based Healthcare Systems. Int. J. Adv. Comput. Sci. Appl. IJACSA 2023, 14, 330–337. [Google Scholar] [CrossRef]
- Venkatesh, R.; Hanumantha, B.S. Electronic medical records protection framework based on quantum blockchain for multiple hospitals. Multimed. Tools Appl. 2023, 83, 42721–42734. [Google Scholar] [CrossRef]
- Sun, J.; Ren, L.L.; Wang, S.P.; Yao, X.M. A blockchain-based framework for electronic medical records sharing with fine-grained access control. PLoS ONE 2020, 15, e0239946. [Google Scholar] [CrossRef] [PubMed]
- Khatoon, A. A Blockchain-Based Smart Contract System for Healthcare Management. Electronics 2020, 9, 94. [Google Scholar] [CrossRef]
- Prathap, R.; Mohanasundaram, R. Enhancing security by two-way decryption of message passing of EMR in public cloud. Int. J. Intell. Enterp. 2021, 8, 239–250. [Google Scholar] [CrossRef]
- Lee, J.S.; Chew, C.J.; Liu, J.Y.; Chen, Y.C.; Tsai, K.Y. Medical blockchain: Data sharing and privacy preserving of EHR based on smart contract. J. Inf. Secur. Appl. 2022, 65, 103117. [Google Scholar] [CrossRef]
- Mhamdi, H.; Ayadi, M.; Ksibi, A.; Al-Rasheed, A.; Soufiene, B.; Hedi, S. SEMRAchain: A Secure Electronic Medical Record Based on Blockchain Technology. Electronics 2022, 11, 3617. [Google Scholar] [CrossRef]
- Bera, S.; Prasad, S.; Rao, Y.S. Verifiable and Boolean keyword searchable attribute-based signcryption for electronic medical record storage and retrieval in cloud computing environment. J. Supercomput. 2023, 79, 20324–20382. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Gao, W.J.; Yang, M.; Hao, R. Enabling Secure Data sharing with data deduplication and sensitive information hiding in cloud-assisted Electronic Medical Systems. Clust. Comput. 2022, 26, 3839–3854. [Google Scholar] [CrossRef]
- Luo, H.T.; Mei, N.S.; Du, C. EMR sharing system with lightweight searchable encryption and rights management. Clust. Comput. 2024, 27, 6341–6353. [Google Scholar] [CrossRef]
- Park, H. Security and privacy model of an electronic medical record system. Int. J. Healthc. Technol. Manag. 2022, 19, 303–323. [Google Scholar] [CrossRef]
- Zhu, D.X.; Sun, Y.; Li, N.F.; Song, L.J.; Zheng, J. Secure electronic medical records sharing scheme based on blockchain and quantum key. Clust. Comput. 2023, 27, 3037–3054. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Qin, B.D.; Zheng, D. Registered Keyword Searchable Encryption Based on SM9. Appl. Sci. 2023, 13, 3226. [Google Scholar] [CrossRef]
- Wu, Z.G.; Wang, H.J.; Wan, J.; Zhang, L.; Huang, J. An Inner Product Predicate-Based Medical Data-Sharing and Privacy Protection System. IEEE Access 2024, 12, 68680–68696. [Google Scholar] [CrossRef]






| Scheme | RKSE-SM9 | VMKS-ABE | Ours |
|---|---|---|---|
| IPFS | × | × | √ |
| Decentralization search | × | √ | √ |
| Low cost | × | × | √ |
| Software Environment | Detailed Information |
|---|---|
| Operating system | Ubuntu 20.04.6 |
| Docker | v24.0.5 |
| Docker Compose | v1.29.2 |
| Golang | v1.17.1 |
| Hyperledger fabric | v2.5.4 |
| Node | v22.12.0 |
| Npm | v10.9.0 |
| Python | v3.8.10 |
| Hardware Environment | Detailed Information |
|---|---|
| CPU | i9-12900H |
| Memory | 16 GB |
| Hard disk | 100 GB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, A.; Tian, H. Secure Sharing of Electronic Medical Records Based on Blockchain and Searchable Encryption. Electronics 2025, 14, 2679. https://doi.org/10.3390/electronics14132679
Zhao A, Tian H. Secure Sharing of Electronic Medical Records Based on Blockchain and Searchable Encryption. Electronics. 2025; 14(13):2679. https://doi.org/10.3390/electronics14132679
Chicago/Turabian StyleZhao, Aomen, and Hongliang Tian. 2025. "Secure Sharing of Electronic Medical Records Based on Blockchain and Searchable Encryption" Electronics 14, no. 13: 2679. https://doi.org/10.3390/electronics14132679
APA StyleZhao, A., & Tian, H. (2025). Secure Sharing of Electronic Medical Records Based on Blockchain and Searchable Encryption. Electronics, 14(13), 2679. https://doi.org/10.3390/electronics14132679





