Probabilistic Shaping Based on Single-Layer LUT Combined with RBFNN Nonlinear Equalization in a Photonic Terahertz OFDM System
Abstract
1. Introduction
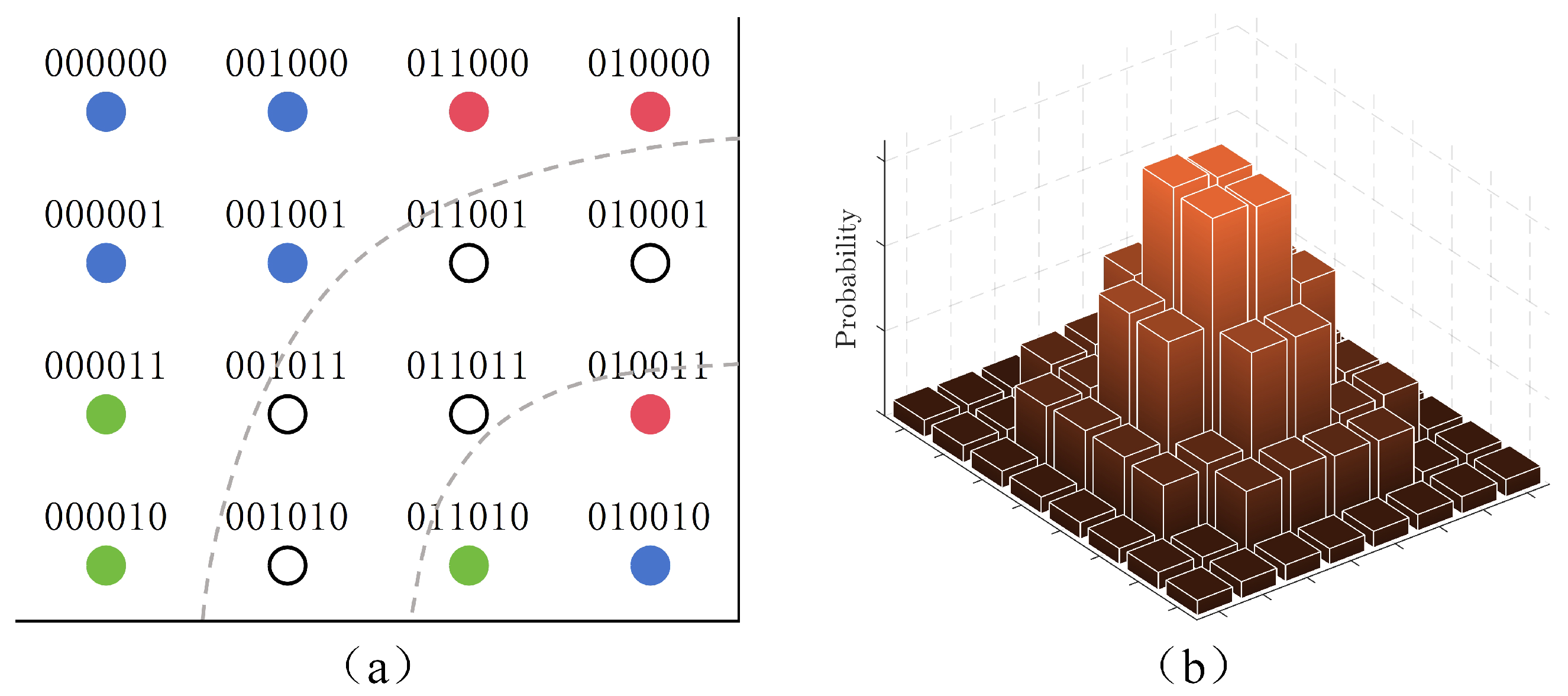
- We present a PS scheme based on a single-layer lookup table (LUT-PS) that adjusts the symbol distribution by using a specific LUT architecture and a flexible shaping proportion to realize probabilistic shaping.
- We propose a joint scheme combining LUT-PS and RBFNN equalization to further mitigate nonlinear distortion.
- We demonstrate the transmission of 16-QAM OFDM signals over a photonic terahertz-over-fiber system at 400 GHz.
2. Principle
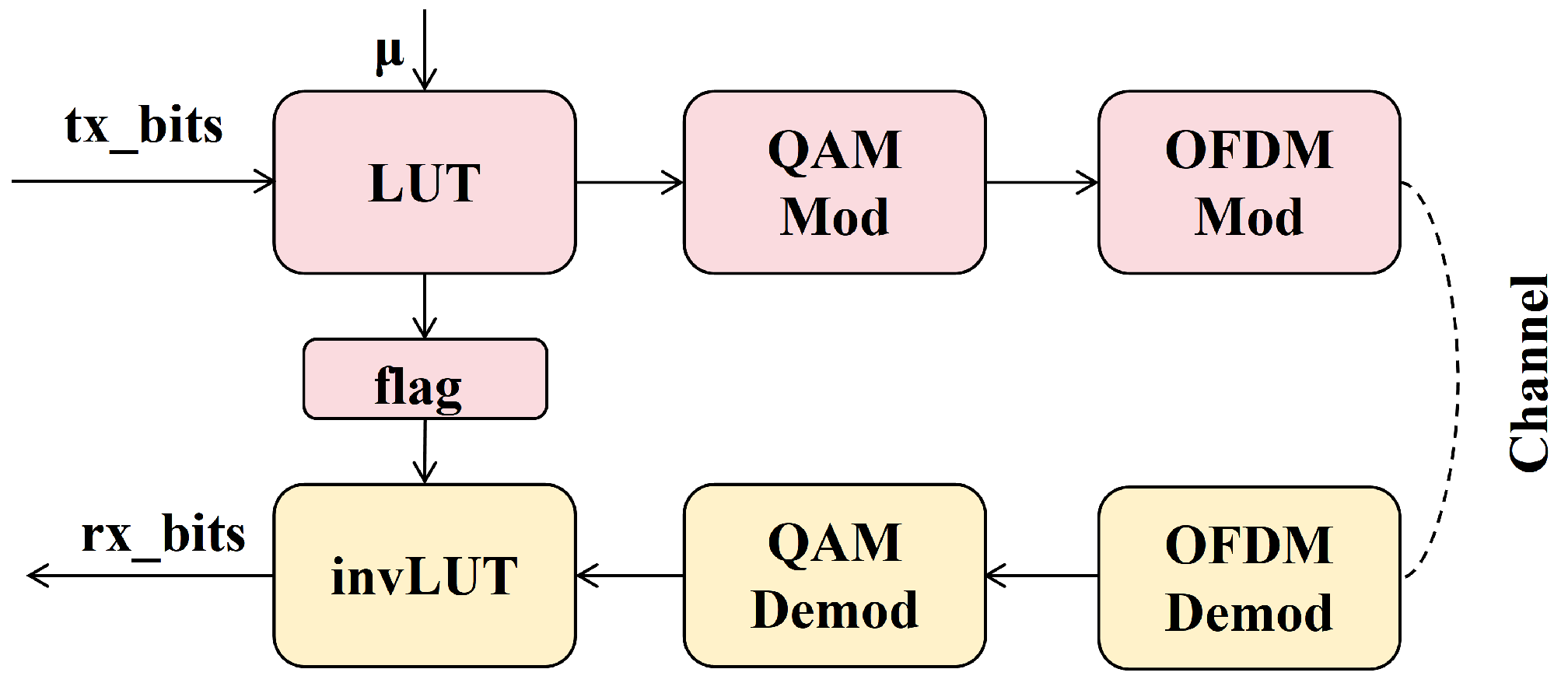
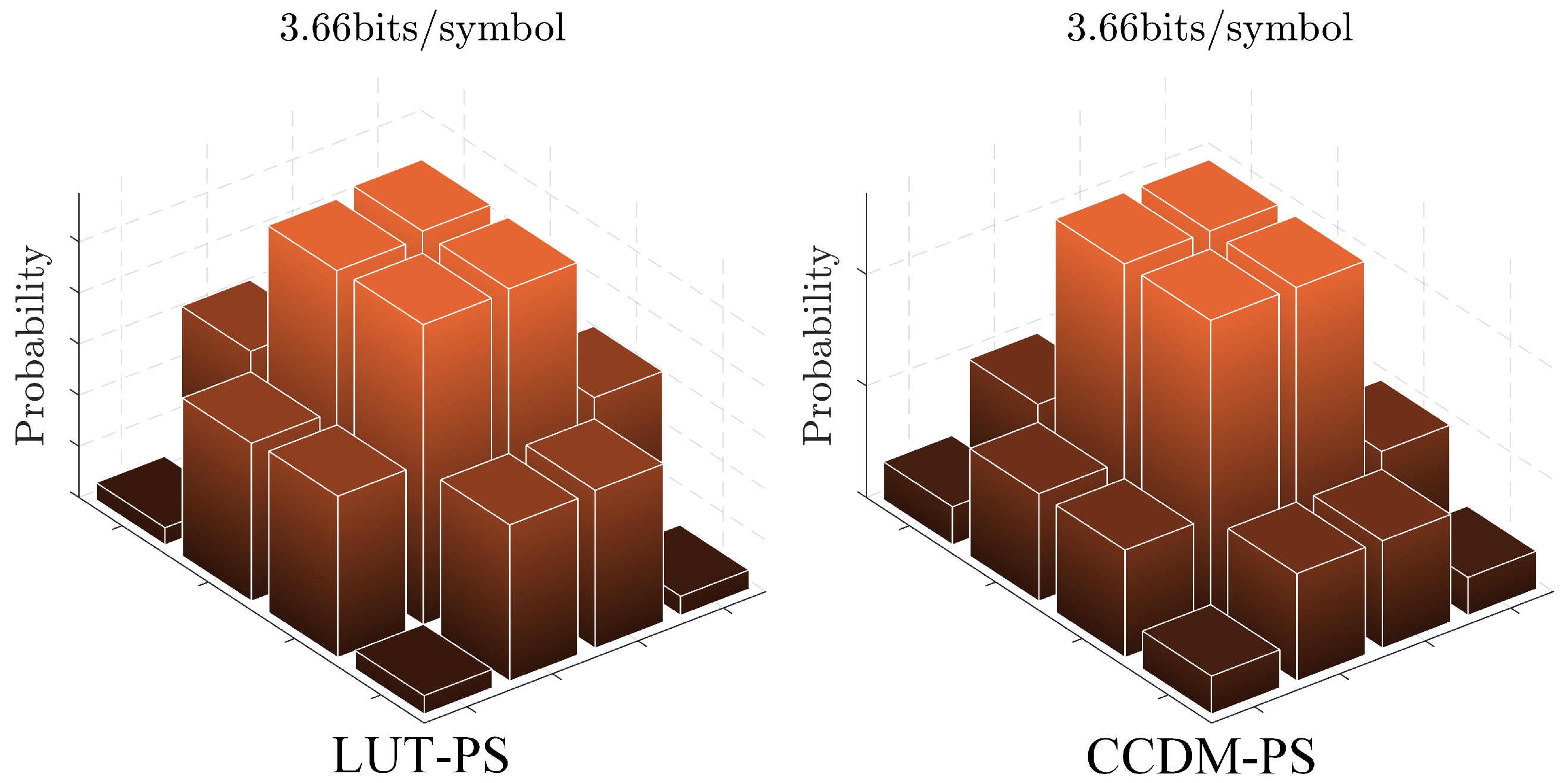
2.1. PS Based on Single-Layer LUT
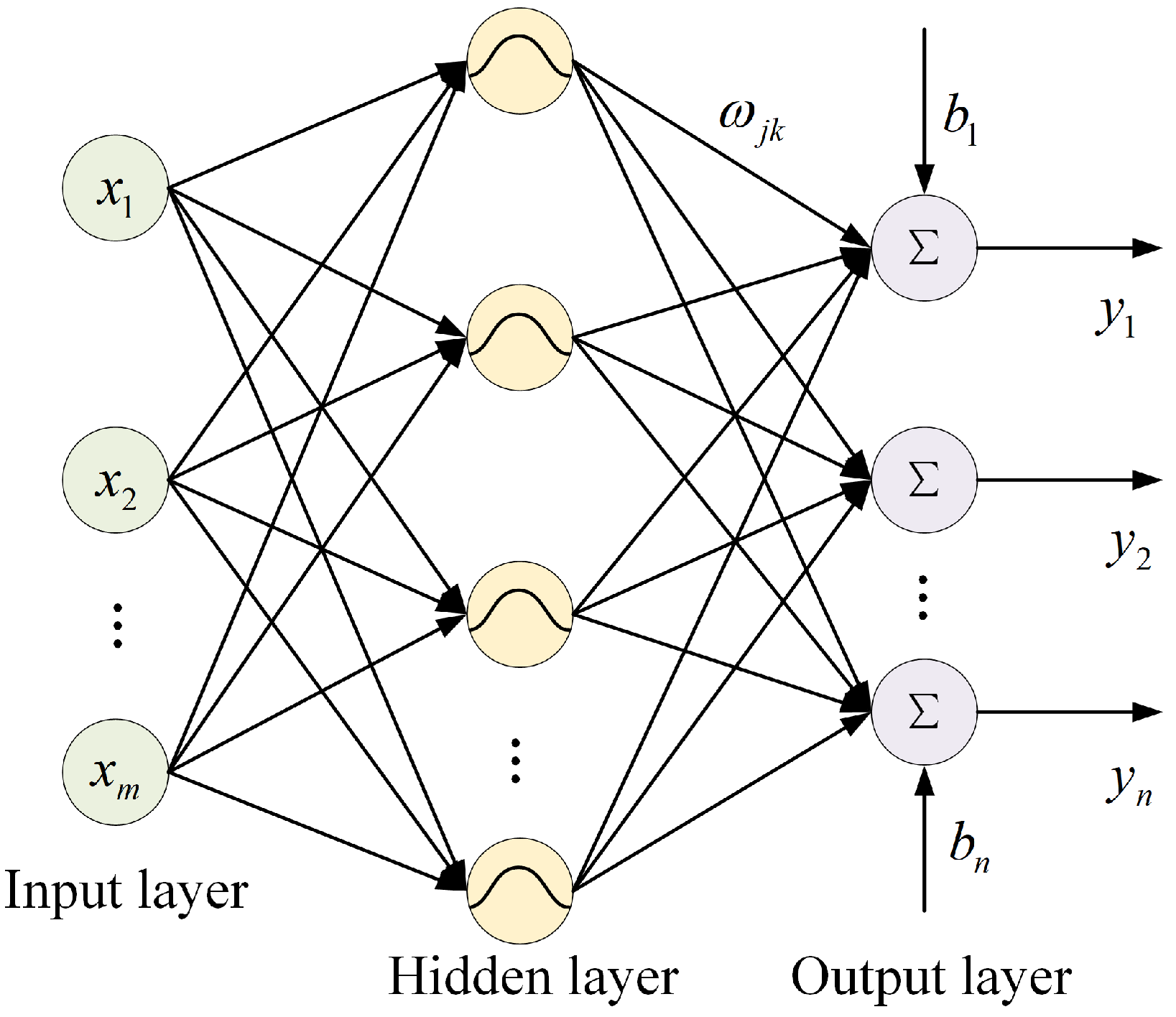
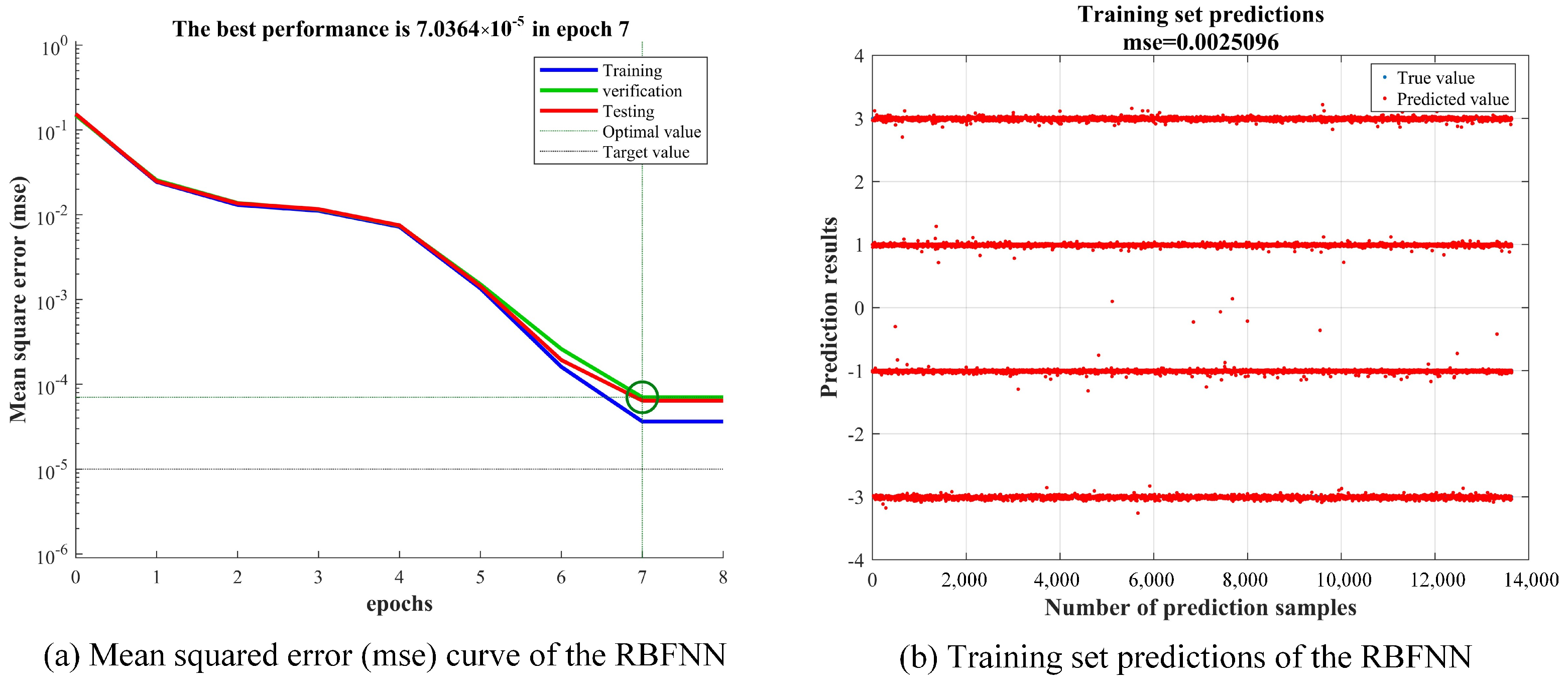
2.2. RBFNN Nonlinear Equalization
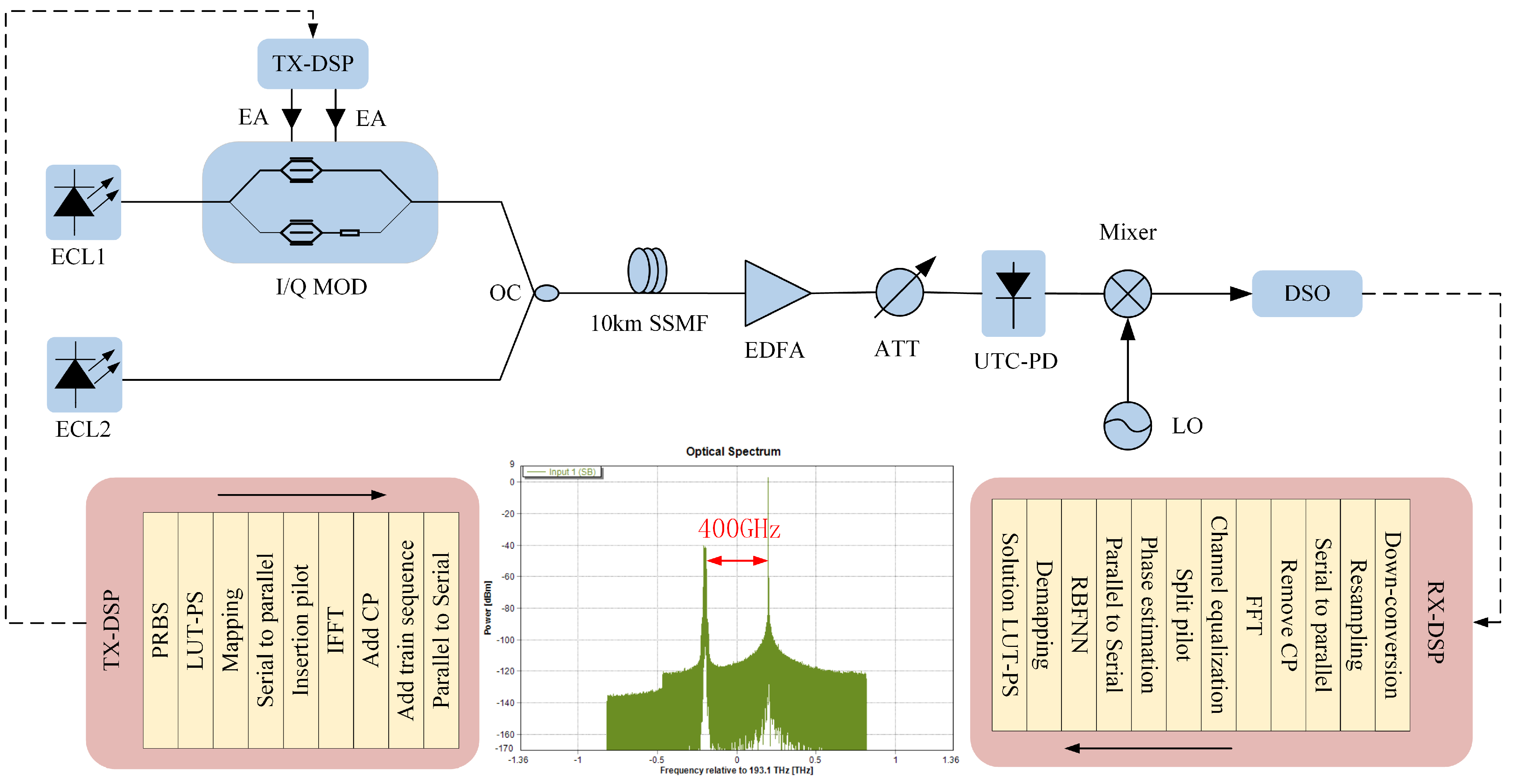
3. Simulation Setup
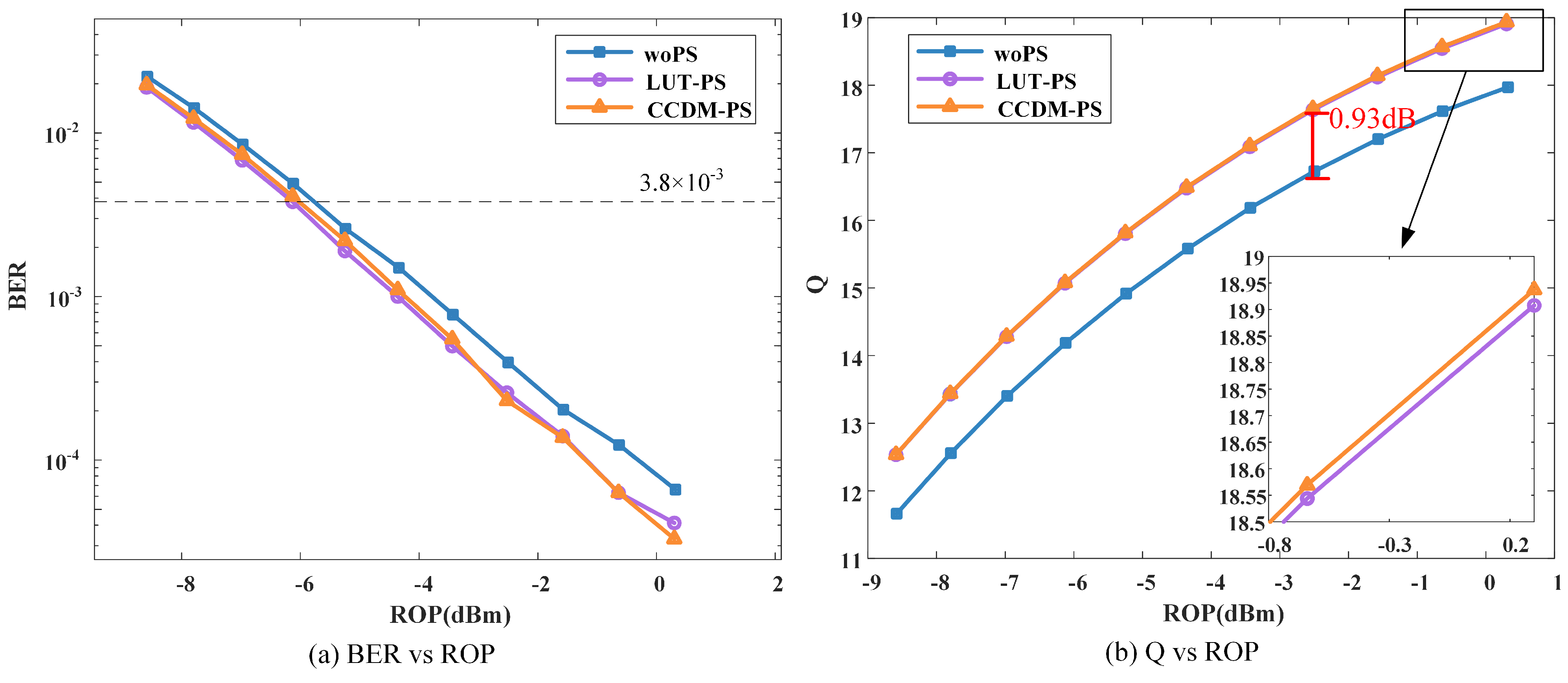
4. Analysis of Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kawanishi, T. THz and photonic seamless communications. J. Lightwave Technol. 2019, 37, 1671–1679. [Google Scholar] [CrossRef]
- Song, H.-J.; Lee, N. Terahertz communications: Challenges in the next decade. IEEE Trans. Terahertz Sci. Technol. 2022, 12, 105–117. [Google Scholar] [CrossRef]
- Nagatsuma, T. THz communication systems. In Proceedings of the Optical Fiber Communication Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017. [Google Scholar]
- Wang, Y. Key Technologies and Spectrum-Efficient Utilization for 6G Terahertz Communications. In Proceedings of the 2025 6th International Conference on Electrical, Electronic Information and Communication Engineering (EEICE), Shenzhen, China, 18–20 April 2025; pp. 655–658. [Google Scholar]
- Jiang, W.; Zhou, Q.; He, J.; Habibi, M.A.; Melnyk, S.; El-Absi, M.; Han, B.; Renzo, M.D.; Schotten, H.D.; Luo, F.-L.; et al. Terahertz Communications and Sensing for 6G and Beyond: A Comprehensive Review. IEEE Commun. Surv. Tutor. 2024, 26, 2326–2381. [Google Scholar] [CrossRef]
- Li, W.; Zeng, H.; Huang, L.; Gong, S.; Cao, H.; Wang, W.; Wang, Z.; Zhou, H.; Liang, S.; Yang, Z.; et al. A Review of Terahertz Solid-State Electronic/Optoelectronic Devices and Communication Systems. Chin. J. Electron. 2025, 34, 26–48. [Google Scholar] [CrossRef]
- Yu, J.; Wang, Y.; Ding, J.; Zhang, J.; Li, W.; Wang, F.; Wang, C.; Wang, K.; Tan, Y.; Zhu, M.; et al. Broadband photon-assisted terahertz communication and sensing. J. Lightwave Technol. 2023, 41, 3332–3349. [Google Scholar] [CrossRef]
- Li, K.; Chen, Y.; Huang, Y.; Li, Y.; Han, Y.; Fu, J.; Yu, J. 16-QAM vector terahertz-wave signal generation by simple MZM-based optical frequency comb. IEEE Photon. J. 2021, 13, 7900308. [Google Scholar] [CrossRef]
- Yu, J.; Li, K.; Chen, Y.; Zhao, L.; Huang, Y.; Li, Y.; Ma, J.; Shan, F. Terahertz-wave generation based on optical frequency comb and single Mach-Zehnder modulator. IEEE Photon. J. 2020, 12, 7900808. [Google Scholar] [CrossRef]
- Li, K.; Yu, J. Photonics-aided terahertz-wave wireless communication. J. Lightwave Technol. 2022, 40, 4186–4195. [Google Scholar] [CrossRef]
- Ding, J.; Yu, J.; Li, W.; Wang, K.; Zhou, W.; Zhang, J.; Zhu, M.; Xie, T.; Yu, J.; Zhao, F. High-speed and long-distance photonics-aided terahertz wireless communication. J. Lightwave Technol. 2023, 41, 143–171. [Google Scholar] [CrossRef]
- Yin, L.; He, J. Modulated-symbol domain matched filtering scheme for photonic-assisted integrated sensing and communication system based on a single OFDM waveform. Opt. Lett. 2024, 49, 2153–2156. [Google Scholar] [CrossRef]
- Mallick, K.; Mandal, P.; Dutta, B.; Kuiri, B.; Santra, S.; Mukherjee, R.; Patra, A.S. Bidirectional OFDM based MMW/THzW over fiber system for next generation communication. IEEE Photon. J. 2021, 13, 7301207. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, Y.; Yin, P.; Ma, J.; Li, K.; Li, Y.; Li, X.; Yu, J. Coherent optical orthogonal frequency division multiplexing with index modulation. In Proceedings of the 18th International Conference on Optical Communications and Networks (ICOCN), Huangshan, China, 5–8 August 2019; pp. 1–3. [Google Scholar]
- Peng, L.; Luo, D.; Xiao, Y.; Li, F. A photonics-aided MMW OFDM joint radar and communication system with velocity accuracy improvement. In Proceedings of the IEEE Applied Sensing Conference (APSCON), Bengaluru, India, 23–25 January 2023; pp. 1–3. [Google Scholar]
- Guo, X.; Xu, R. Probabilistically Shaped 3D-32QAM Constellation Design for Visible Light Communication. IEEE Photon. Technol. Lett. 2025, 37, 583–586. [Google Scholar] [CrossRef]
- Wang, Z.; Xiao, Y.; Wang, S.; Yan, Y.; Wang, B.; Chen, Y.; Zhou, Z.; He, J.; Yang, L. Probabilistic shaping based constellation encryption for physical layer security in OFDM RoF system. Opt. Express 2021, 29, 17890–17902. [Google Scholar] [CrossRef]
- Wang, S.; Lu, Z.; Li, W.; Jia, S.; Zhang, L.; Qiao, M.; Pang, X.; Idrees, N.; Saqlain, M.; Gao, X.; et al. 26.8-m THz wireless transmission of probabilistic shaping 16-QAM-OFDM signals. APL Photon. 2020, 5, 056105. [Google Scholar] [CrossRef]
- Cui, H.; Sun, Z.; Huang, X.; Tang, D.; Xie, F.; Qiao, Y. Trellis-coded modulation-enabled probabilistic shaping with simplified Viterbi decoder for bandwidth-limited IMDD systems. IEEE Photon. J. 2023, 15, 7202110. [Google Scholar] [CrossRef]
- Yoshida, T.; Karlsson, M.; Agrell, E. Hierarchical distribution matching for probabilistically shaped coded modulation. J. Lightwave Technol. 2019, 37, 1579–1589. [Google Scholar] [CrossRef]
- Civelli, S.; Secondini, M. Hierarchical distribution matching for probabilistic amplitude shaping. Entropy 2020, 22, 958. [Google Scholar] [CrossRef]
- Lin, J.; Xu, S.; Wang, Q.; Zhang, J.; Ge, J.; Wang, S.; Ou, Z.; Ma, Y.; Zhou, W.; Yu, J. D-Band 4.6 km 2 × 2 MIMO Photonic-Assisted Terahertz Wireless Communication Utilizing Iterative Pruning Deep Neural Network-Based Nonlinear Equalization. Photonics 2024, 11, 1009. [Google Scholar] [CrossRef]
- Liao, T.; Xue, L.; Huang, L.; Hu, W.; Yi, L. Training data generation and validation for a neural network-based equalizer. Opt. Lett. 2020, 45, 5113–5116. [Google Scholar] [CrossRef]
- Aldaya, I.; Giacoumidis, E.; Tsokanos, A.; Jarajreh, M.; Wen, Y.; Wei, J.; Campuzano, G.; Abbade, M.L.F.; Barry, L.P. Compensation of nonlinear distortion in coherent optical OFDM systems using a MIMO deep neural network-based equalizer. Opt. Lett. 2020, 45, 5820–5823. [Google Scholar] [CrossRef]
- Duan, W.; Liu, Y.; Huang, Y.; Wang, Y.; Liu, X.; Yu, J. Nonlinear equalization based on CV-CNN for 16-QAM coherent optical OFDM signal at 350 GHz. In Proceedings of the 4th International Conference on Neural Networks and Information Communication (NNICE), Guangzhou, China, 19–21 January 2024; pp. 1260–1263. [Google Scholar]
- Shi, J.; Sang, B.; Zhou, W.; Zhao, L.; Ding, J.; Yu, J. Sparse I/Q-joint DNN nonlinear equalization based on progressive pruning for a photonics-aided 256-QAM MMW communication system. Opt. Lett. 2023, 48, 602–605. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Li, K.; Zhang, F.; Zhang, Y.; Zhang, H.; Yu, J. PS-16QAM-OFDM with Nonlinear Equalization Based on RBF Neural Network by 350GHz Photonic Terahertz System. In Proceedings of the 2024 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 2–5 November 2024; pp. 1–4. [Google Scholar]

| Input | Output | ||
|---|---|---|---|
| 0101 | 2 | 0000 | 18 |
| 0111 | 2 | 0010 | 18 |
| 1101 | 2 | 1000 | 18 |
| 1111 | 2 | 1010 | 18 |
| 0001 | 10 | 0001 | 10 |
| 0011 | 10 | 0011 | 10 |
| 0100 | 10 | 0100 | 10 |
| 0110 | 10 | 0110 | 10 |
| 1001 | 10 | 1001 | 10 |
| 1011 | 10 | 1011 | 10 |
| 1100 | 10 | 1100 | 10 |
| 1110 | 10 | 1110 | 10 |
| 0000 | 18 | 0101 | 2 |
| 0010 | 18 | 0111 | 2 |
| 1000 | 18 | 1101 | 2 |
| 1010 | 18 | 1111 | 2 |
| μ | 1/11 | 1/9 | 1/7 | 1/5 | 1/3 | 1 |
| BER | 3.3003 | 3.3003 | 4.1254 | 3.3003 | 4.4004 | 6.6007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Li, K.; Zhang, F.; Yu, J. Probabilistic Shaping Based on Single-Layer LUT Combined with RBFNN Nonlinear Equalization in a Photonic Terahertz OFDM System. Electronics 2025, 14, 2677. https://doi.org/10.3390/electronics14132677
Huang Y, Li K, Zhang F, Yu J. Probabilistic Shaping Based on Single-Layer LUT Combined with RBFNN Nonlinear Equalization in a Photonic Terahertz OFDM System. Electronics. 2025; 14(13):2677. https://doi.org/10.3390/electronics14132677
Chicago/Turabian StyleHuang, Yuting, Kaile Li, Feixiang Zhang, and Jianguo Yu. 2025. "Probabilistic Shaping Based on Single-Layer LUT Combined with RBFNN Nonlinear Equalization in a Photonic Terahertz OFDM System" Electronics 14, no. 13: 2677. https://doi.org/10.3390/electronics14132677
APA StyleHuang, Y., Li, K., Zhang, F., & Yu, J. (2025). Probabilistic Shaping Based on Single-Layer LUT Combined with RBFNN Nonlinear Equalization in a Photonic Terahertz OFDM System. Electronics, 14(13), 2677. https://doi.org/10.3390/electronics14132677






