Exploring Tabu Tenure Policies with Machine Learning
Abstract
1. Introduction
2. Background
2.1. Optimum Satisfiability Problem
2.2. Tabu Search
2.3. Machine Learning
3. Literature Review
3.1. Tabu Tenure
3.2. Machine Learning for Parameter Setting
4. Methodology
4.1. Input Characteristics for Tabu Policies
4.2. Baseline Analysis of Tabu Tenure Policies
- 1.
- First, we analyze how different tabu tenure ranges affect solution quality to establish baseline performance and determine promising ranges for further investigation. This analysis identifies the sensitivity of the OptSAT problem to tabu tenure parameters. The baseline follows the dynamic tabu tenure policy proposed by Bentsen et al. [15], which draws the tabu tenure randomly from an interval defined by two fixed parameters with and . However, this range is tuned to solve a wide variety of binary integer problems, of which the OptSAT is only one example. Therefore, the parameters and are varied to check the influence of different interval ranges on performance. Without understanding this baseline performance, we would lack the context needed to evaluate whether our ML approaches offer meaningful improvements. We have also presented the best solution obtained by a commercial MIP solver to understand the potential room for improvements.
- 2.
- Second, we investigate how specific search characteristics can be leveraged to formulate better tabu tenure policies. We focus particularly on incorporating the type of move (improving vs. non-improving) into policy formulation, motivated by findings from the analysis made by Glover and Laguna [5]. Based on the importance of move types, we have formulated a novel move-type-based policy. It also implements a dynamic tabu tenure, which is drawn randomly from an interval defined through two fixed parameters but with differentiating ranges based on move type. To find the policy, we assign different tenure ranges based on whether a move is improving or non-improving and determine which configuration gives better performance. The policy can serve as a baseline that can be compared against ML-derived policies and potentially included among promising policies for the SL method.
4.3. Self-Adaptive Policy with Reinforcement Learning
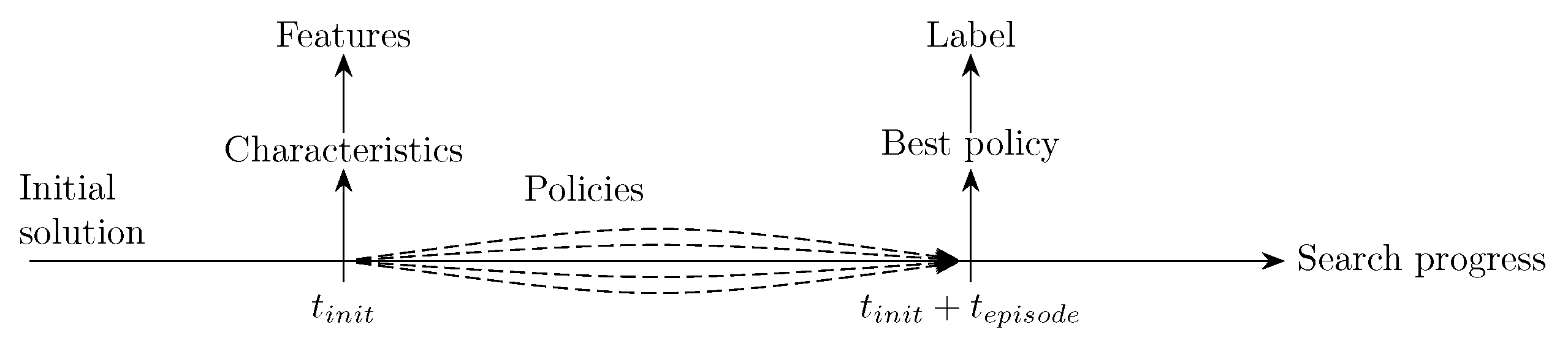
- Decision point: For this method, we propose predicting tabu tenure value at each search iteration, where each iteration corresponds to a timestep , where is the total number of iterations.
- State: A state at iteration t consists of input characteristics defined in Table 2:where t defines for current iteration, and represents the previously used tabu tenure.
- Action: The action is to select a tabu tenure value for the current move as a discrete value from interval.
- Reward: The reward is given only at the end of the episode and reflects the quality of solution found during the search.where is the best solution value found during the episode, and is the best known upper bound for the current problem instance.
- Transition function: The state transition preserves the static instance parameters while updating the search parameters . The previous action transitions to , and the time step increases by one. Thus, the next state is as follows:
4.4. Policy Selection with Supervised Learning
- Random policy: The tabu tenure value for each iteration is drawn at random from a uniform distribution .
- Objective coefficient-based policy: The tabu tenure value is dynamically determined using the objective coefficient value of the variable which becomes tabu. The policy scales the coefficient value between its minimum and maximum values of all objective coefficients in the instance and later maps it onto the range between and . If the calculated value is less than the average of and , it picks a random integer value between and . Otherwise, it picks a random integer between .
- Frequency-based policy: The tabu tenure value is determined by considering how frequently each variable has been designated as tabu in the past. If a normalized variable’s tabu frequency (normalized by the maximum frequency observed across all variables) exceeds , the policy assigns a larger tabu tenure by randomly selecting an integer value between and . Otherwise, it assigns a smaller tenure by randomly selecting an integer value between and and .
- Move-type-based policy: The tabu tenure value is based on the type of the move in the current iteration (see Section 4.2). The specific rules of this policy are established empirically through a series of experiments presented in Section 5.2.
4.5. Machine Learning Algorithms
4.6. Design of Computational Study
- Examination of how tabu tenure parameter adjustments affect TS performance (Section 5.1);
- Assessment of the performance of move-type-based policy (Section 5.2);
- Development of self-adaptive policy with RL (Section 5.3);
- Evaluation of policy selection approach with ML (Section 5.4).
5. Results and Discussion
5.1. Influence of Tabu Tenure on Algorithm Performance
5.2. Move-Type-Based Policy
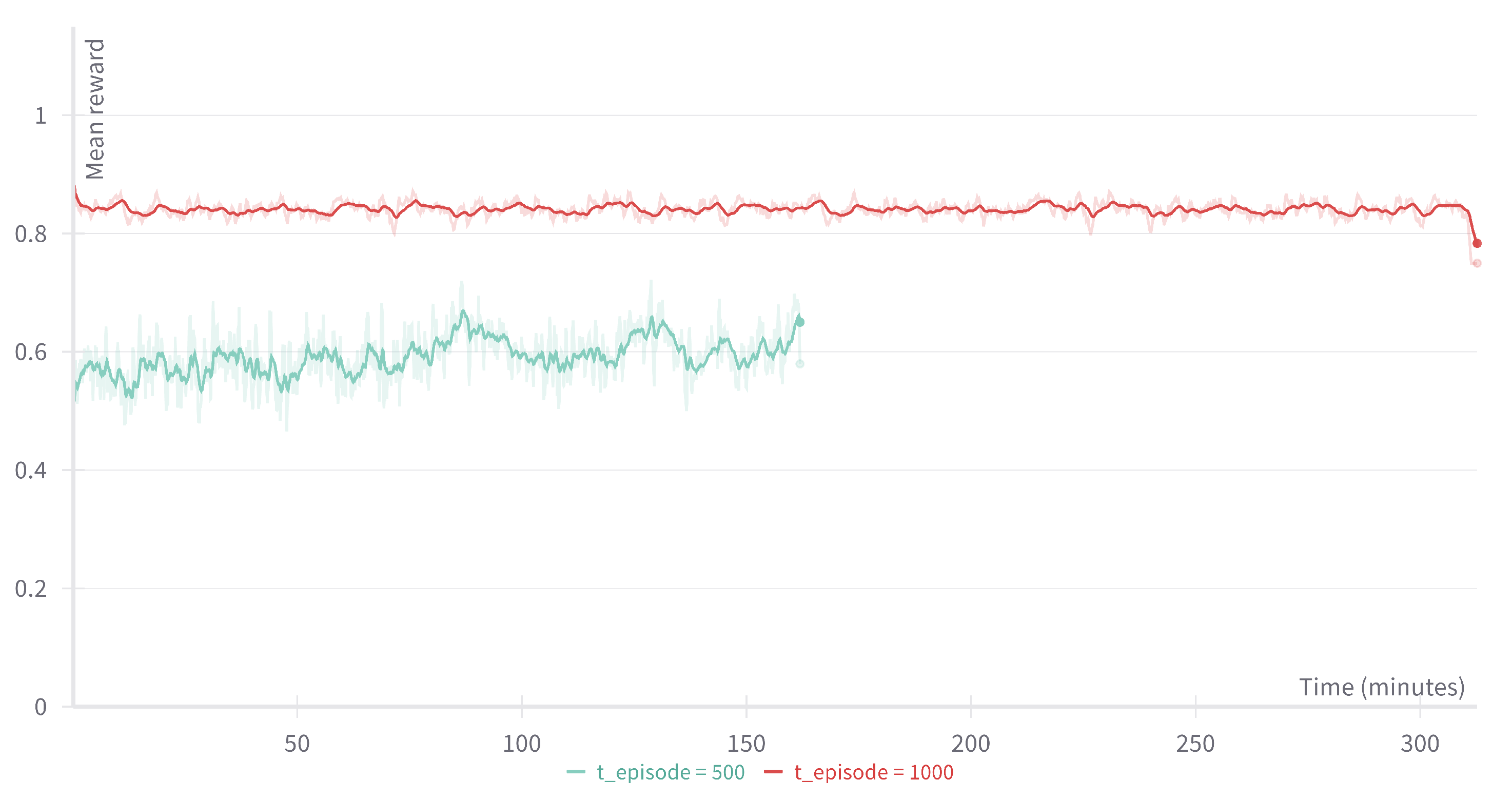
5.3. Policy with Reinforcement Learning
- 1.
- Problem complexity: As shown in Section 5.1, the impact of using different tabu tenure policies can be relatively small. The nature of local search means that promising policies may be lost during training due to the many factors that affect search trajectories.
- 2.
- 3.
- Action similarity: Adjacent tabu tenure values often produce similar search behaviors, making it difficult for the algorithm to distinguish performance differences between similar actions.
- 4.
- State representation limitations: Our state representation uses general search metrics rather than detailed move histories. This abstraction may lack information to fully characterize the search state.
5.4. Policy with Supervised Learning
- 1.
- Insufficient training data: The relationship between search state and optimal tabu tenure policy is complex, requiring more data to capture meaningful patterns. The current dataset is not enough to build this relationship.
- 2.
- Similar performance across policies: The dataset class distribution shows that different tabu tenure policies perform similarly across problem instances. This small performance gap creates a difficult classification problem where a correct prediction offers minimal benefit. Like in the RL approach, the tabu tenure selection impact involves complex dependencies that can be difficult to capture.
- 3.
- Feature representation limitations: The current feature set may lack expressiveness to distinguish between states where different policies would be optimal. More search-specific features might be necessary to capture information representing search states.
- 4.
- Instance similarity: As instance characteristics had a minimal impact on prediction, we can also attribute this to the similar structural properties of the selected OptSAT benchmark instances.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TS | Tabu Search |
| ML | Machine Learning |
| OptSAT | Optimum Satisfiability Problem |
| SAT | Boolean Satisfiability Problem |
| ILP | Integer Linear Programming Problem |
| SL | Supervised Learning |
| RL | Reinforcement Learning |
| MDPs | Markov Decision Processes |
| PPO | Proximal Policy Optimization |
| RF | Random Forest |
References
- Laguna, M.; Barnes, J.W.; Glover, F.W. Tabu search methods for a single machine scheduling problem. J. Intell. Manuf. 1991, 2, 63–73. [Google Scholar] [CrossRef]
- Taillard, É.; Badeau, P.; Gendreau, M.; Guertin, F.; Potvin, J.Y. A tabu search heuristic for the vehicle routing problem with soft time windows. Transp. Sci. 1997, 31, 170–186. [Google Scholar] [CrossRef]
- Sun, M. Solving the uncapacitated facility location problem using tabu search. Comput. Oper. Res. 2006, 33, 2563–2589. [Google Scholar] [CrossRef]
- Belfares, L.; Klibi, W.; Lo, N.; Guitouni, A. Multi-objectives tabu search based algorithm for progressive resource allocation. Eur. J. Oper. Res. 2007, 177, 1779–1799. [Google Scholar] [CrossRef]
- Glover, F.; Laguna, M. Tabu search. In Handbook of Combinatorial Optimization; Du, D.Z., Pardalos, P.M., Eds.; Springer: Boston, MA, USA, 1998; Volumes 1–3, pp. 2093–2229. [Google Scholar] [CrossRef]
- Devarenne, I.; Mabed, H.; Caminada, A. Adaptive tabu tenure computation in local search. In Evolutionary Computation in Combinatorial Optimization: 8th European Conference, EvoCOP 2008, Naples, Italy, 26–28 March 2008; Springer: Berlin/Heidelberg, Germany, 2008; Volume 4972, pp. 1–12. [Google Scholar] [CrossRef]
- Løkketangen, A.; Olsson, R. Generating meta-heuristic optimization code using ADATE. J. Heuristics 2010, 16, 911–930. [Google Scholar] [CrossRef]
- Sugimura, M.; Parizy, M. A3TUM: Automated Tabu Tenure Tuning by Unique Move for Quadratic Unconstrained Binary Optimization. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, GECCO ’24 Companion, Melbourne, Australia, 14–18 July 2024; pp. 1963–1971. [Google Scholar] [CrossRef]
- Davoine, T.; Hammer, P.L.; Vizvári, B. A heuristic for Boolean optimization problems. J. Heuristics 2003, 9, 229–247. [Google Scholar] [CrossRef]
- Schaefer, T.J. The complexity of satisfiability problems. In Proceedings of the 10th Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 1–3 May 1978; pp. 216–226. [Google Scholar]
- da Silva, R.; Hvattum, L.M.; Glover, F. Combining solutions of the optimum satisfiability problem using evolutionary tunneling. MENDEL 2020, 26, 23–29. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—Part I. ORSA J. Comput. 1989, 1, 190–205. [Google Scholar] [CrossRef]
- Arntzen, H.; Hvattum, L.M.; Løkketangen, A. Adaptive memory search for multidemand multidimensional knapsack problems. Comput. Oper. Res. 2006, 33, 2508–2525. [Google Scholar] [CrossRef]
- Hvattum, L.M.; Løkketangen, A.; Glover, F. Adaptive memory search for Boolean optimization problems. Discrete Appl. Math. 2004, 142, 99–109. [Google Scholar] [CrossRef]
- Bentsen, H.; Hoff, A.; Hvattum, L.M. Exponential extrapolation memory for tabu search. EURO J. Comput. Optim. 2022, 10, 100028. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine Learning: Algorithms, real-world applications and research directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; Volume 4. [Google Scholar]
- Danielsen, K.; Hvattum, L.M. Solution-based versus attribute-based tabu search for binary integer programming. Int. Trans. Oper. Res. 2025, 32, 3780–3800. [Google Scholar] [CrossRef]
- Bachelet, V.; Talbi, E.G. COSEARCH: A co-evolutionary metaheuristic. In Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; Volume 2, pp. 1550–1557. [Google Scholar]
- Montemanni, R.; Moon, J.N.J.; Smith, D.H. An improved tabu search algorithm for the fixed-spectrum frequency-assignment problem. IEEE Trans. Veh. Technol. 2003, 52, 891–901. [Google Scholar] [CrossRef]
- Blöchliger, I. Suboptimal Colorings and Solution of Large Chromatic Scheduling Problems. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2005. [Google Scholar] [CrossRef]
- Galinier, P.; Hao, J.K. Hybrid evolutionary algorithms for graph coloring. J. Comb. Optim. 1999, 3, 379–397. [Google Scholar] [CrossRef]
- Vasquez, M.; Hao, J.K. A “logic-constrained” knapsack formulation and a tabu algorithm for the daily photograph scheduling of an earth observation satellite. Comput. Optim. Appl. 1999, 20, 137–157. [Google Scholar] [CrossRef]
- Lü, Z.; Hao, J.K. Adaptive tabu search for course timetabling. Eur. J. Oper. Res. 2010, 200, 235–244. [Google Scholar] [CrossRef]
- Battiti, R.; Tecchiolli, G. The reactive tabu search. ORSA J. Comput. 1994, 6, 126–140. [Google Scholar] [CrossRef]
- Glover, F.; Hao, J.K. The case for strategic oscillation. Ann. Oper. Res. 2011, 183, 163–173. [Google Scholar] [CrossRef]
- Karimi-Mamaghan, M.; Mohammadi, M.; Meyer, P.; Karimi-Mamaghan, A.M.; Talbi, E.G. Machine learning at the service of meta-heuristics for solving combinatorial optimization problems: A state-of-the-art. Eur. J. Oper. Res. 2022, 296, 393–422. [Google Scholar] [CrossRef]
- Kärcher, J.; Meyr, H. A machine learning approach for predicting the best heuristic for a large scaled capacitated lotsizing problem. OR Spectrum 2025, 1–43. [Google Scholar] [CrossRef]
- Quevedo, J.; Abdelatti, M.; Imani, F.; Sodhi, M. Using reinforcement learning for tuning genetic algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Lille, France, 10–14 July 2021; pp. 1503–1507. [Google Scholar]
- Benlic, U.; Epitropakis, M.G.; Burke, E.K. A hybrid breakout local search and reinforcement learning approach to the vertex separator problem. Eur. J. Oper. Res. 2017, 261, 803–818. [Google Scholar] [CrossRef]
- Aleti, A.; Moser, I.; Meedeniya, I.; Grunske, L. Choosing the appropriate forecasting model for predictive parameter control. Evol. Comput. 2014, 22, 319–349. [Google Scholar] [CrossRef] [PubMed]
- Niroumandrad, N.; Lahrichi, N.; Lodi, A. Learning tabu search algorithms: A scheduling application. Comput. Oper. Res. 2024, 170, 106751. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Zheng, A.; Casari, A. Feature Engineering for Machine Learning: Principles and Techniques for Data Scientists; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hossin, M.; Sulaiman, M.N. A review on evaluation metrics for data classification evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1. [Google Scholar]
- Raffin, A.; Hill, A.; Gleave, A.; Kanervisto, A.; Ernestus, M.; Dormann, N. Stable-Baselines3: Reliable reinforcement learning implementations. J. Mach. Learn. Res. 2021, 22, 1–8. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- CPLEX Optimizer. 2019. Available online: https://www.ibm.com/support/pages/downloading-ibm-ilog-cplex-enterprise-server-v1290 (accessed on 28 June 2025).
- Nikanjam, A.; Morovati, M.M.; Khomh, F.; Braiek, B.B. Faults in deep reinforcement learning programs: A taxonomy and a detection approach. Autom. Softw. Eng. 2022, 29, 8. [Google Scholar] [CrossRef]
- Thrun, S.; Schwartz, A. Issues in using function approximation for reinforcement learning. In Proceedings of the 1993 Connectionist Models Summer School; Psychology Press: Hove, UK, 2014; pp. 255–263. [Google Scholar]
- Sutton, R.S. Temporal Credit Assignment in Reinforcement Learning. Ph.D. Thesis, University of Massachusetts Amherst, Amherst, MA, USA, 1984. [Google Scholar]
- Devidze, R.; Kamalaruban, P.; Singla, A. Exploration-guided reward shaping for reinforcement learning under sparse rewards. Adv. Neural Inf. Process. Syst. 2022, 35, 5829–5842. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Birattari, M.; Kacprzyk, J. Tuning Metaheuristics: A Machine Learning Perspective; Springer: Berlin/Heidelberg, Germany, 2009; Volume 197. [Google Scholar]
- Malik, M.M. A hierarchy of limitations in machine learning. arXiv 2020, arXiv:1709.06560. [Google Scholar]
- Lones, M.A. Avoiding common machine learning pitfalls. Patterns 2024, 5, 101046. [Google Scholar] [CrossRef]
- Yates, W.B.; Keedwell, E.C.; Kheiri, A. Explainable optimisation through online and offline hyper-heuristics. ACM Trans. Evol. Learn. 2025, 5, 1–29. [Google Scholar] [CrossRef]
| Study | Static | Dynamic | Reactive | Fixed | Random | Solution | Move | Time |
|---|---|---|---|---|---|---|---|---|
| Glover [12] | ✓ | ✓ | ||||||
| Bentsen et al. [15] | ✓ | ✓ | ||||||
| Glover and Laguna [5] | ✓ | ✓ | ||||||
| Bachelet and Talbi [19] | ✓ | ✓ | ||||||
| Montemanni et al. [20] | ✓ | ✓ | ||||||
| Galinier and Hao [22] | ✓ | ✓ | ||||||
| Devarenne et al. [6] | ✓ | ✓ | ||||||
| Vasquez and Hao [23] | ✓ | ✓ | ||||||
| Lü and Hao [24] | ✓ | ✓ | ✓ | |||||
| Løkketangen and Olsson [7] | ✓ | ✓ | ✓ | |||||
| Battiti and Tecchiolli [25] | ✓ | ✓ | ||||||
| Blöchliger [21] | ✓ | ✓ | ||||||
| Devarenne et al. [6] | ✓ | ✓ | ||||||
| Glover and Hao [26] | ✓ | ✓ |
| Category | Characteristic | Variable |
|---|---|---|
| Instance | Number of variables | n |
| Number of clauses | m | |
| Number of non-zeros | z | |
| Left-hand-side density | ||
| Average number of literals in the clause | ||
| Search | The best value of the dynamic move evaluation function at iteration t | |
| Number of local optima in the last iterations | ||
| Number of times applying the aspiration criteria in the last iterations | ||
| Number of variables currently being tabu | ||
| Time | Identification of the search progress | t |
| Policy | Policy (tabu tenure) that has been recently used |
| Class 25 | Class 27 | Class 28 | Class 36 | Class 37 | Avg. | ||
|---|---|---|---|---|---|---|---|
| 7 | 22 | 21,904 | 20,456 | 22,534 | 20,120 | 22,619 | 21,527 |
| (101) | (71) | (413) | (66) | (434) | |||
| 1 | 15 | 21,940 | 20,505 | 22,546 | 20,157 | 22,624 | 21,554 |
| (124) | (58) | (446) | (60) | (450) | |||
| 1 | 3 | 21,881 | 20,481 | 22,463 | 20,148 | 22,567 | 21,508 |
| (270) | (94) | (490) | (81) | (480) | |||
| CPLEX | 22,072 | 20,598 | 22,833 | 20,255 | 22,917 | 21,735 | |
| Best gap % | |||||||
| Impr. | Non-Impr. | Class 25 | Class 27 | Class 28 | Class 36 | Class 37 | Avg. | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 9 | 15 | 21,931 | 20,490 | 225,36 | 20,148 | 22,613 | 21,544 |
| (118) | (63) | (444) | (63) | (453) | |||||
| 9 | 15 | 1 | 8 | 21,958 | 20,521 | 22,551 | 20175 | 22,628 | 21,567 |
| (103) | (53) | (448) | (58) | (453) | |||||
| 1 | 8 | 1 | 8 | 21,960 | 20,518 | 22,533 | 20,173 | 22,610 | 21,559 |
| (158) | (62) | (461) | (57) | (464) | |||||
| 9 | 15 | 9 | 15 | 21,926 | 20,480 | 22,541 | 20,137 | 22,626 | 21,542 |
| (90) | (63) | (429) | (63) | (450) | |||||
| Policy | Class 25 | Class 27 | Class 28 | Class 36 | Class 37 | Avg. |
|---|---|---|---|---|---|---|
| SL model | 21,959 | 20,521 | 22,554 | 20,176 | 22,628 | 21,568 |
| (103) | (54) | (446) | (51) | (454) | ||
| Random | 21,940 | 20,505 | 22,546 | 20,157 | 22,624 | 21,554 |
| (124) | (58) | (446) | (60) | (450) | ||
| Objective coefficient-based | 21,944 | 20,513 | 22,527 | 20,167 | 22,605 | 21,551 |
| (146) | (59) | (460) | (69) | (464) | ||
| Frequency-based | 21,946 | 20,509 | 22,540 | 20,166 | 22,615 | 21,555 |
| (120) | (58) | (446) | (60) | (456) | ||
| Move-type-based | 21,958 | 20,521 | 22,551 | 20,175 | 22,628 | 21,567 |
| (103) | (53) | (448) | (58) | (453) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konovalenko, A.; Hvattum, L.M. Exploring Tabu Tenure Policies with Machine Learning. Electronics 2025, 14, 2642. https://doi.org/10.3390/electronics14132642
Konovalenko A, Hvattum LM. Exploring Tabu Tenure Policies with Machine Learning. Electronics. 2025; 14(13):2642. https://doi.org/10.3390/electronics14132642
Chicago/Turabian StyleKonovalenko, Anna, and Lars Magnus Hvattum. 2025. "Exploring Tabu Tenure Policies with Machine Learning" Electronics 14, no. 13: 2642. https://doi.org/10.3390/electronics14132642
APA StyleKonovalenko, A., & Hvattum, L. M. (2025). Exploring Tabu Tenure Policies with Machine Learning. Electronics, 14(13), 2642. https://doi.org/10.3390/electronics14132642








